Motion Decoupling and Dynamic Response of Permanent Magnet Maglev Bogie
-
摘要:
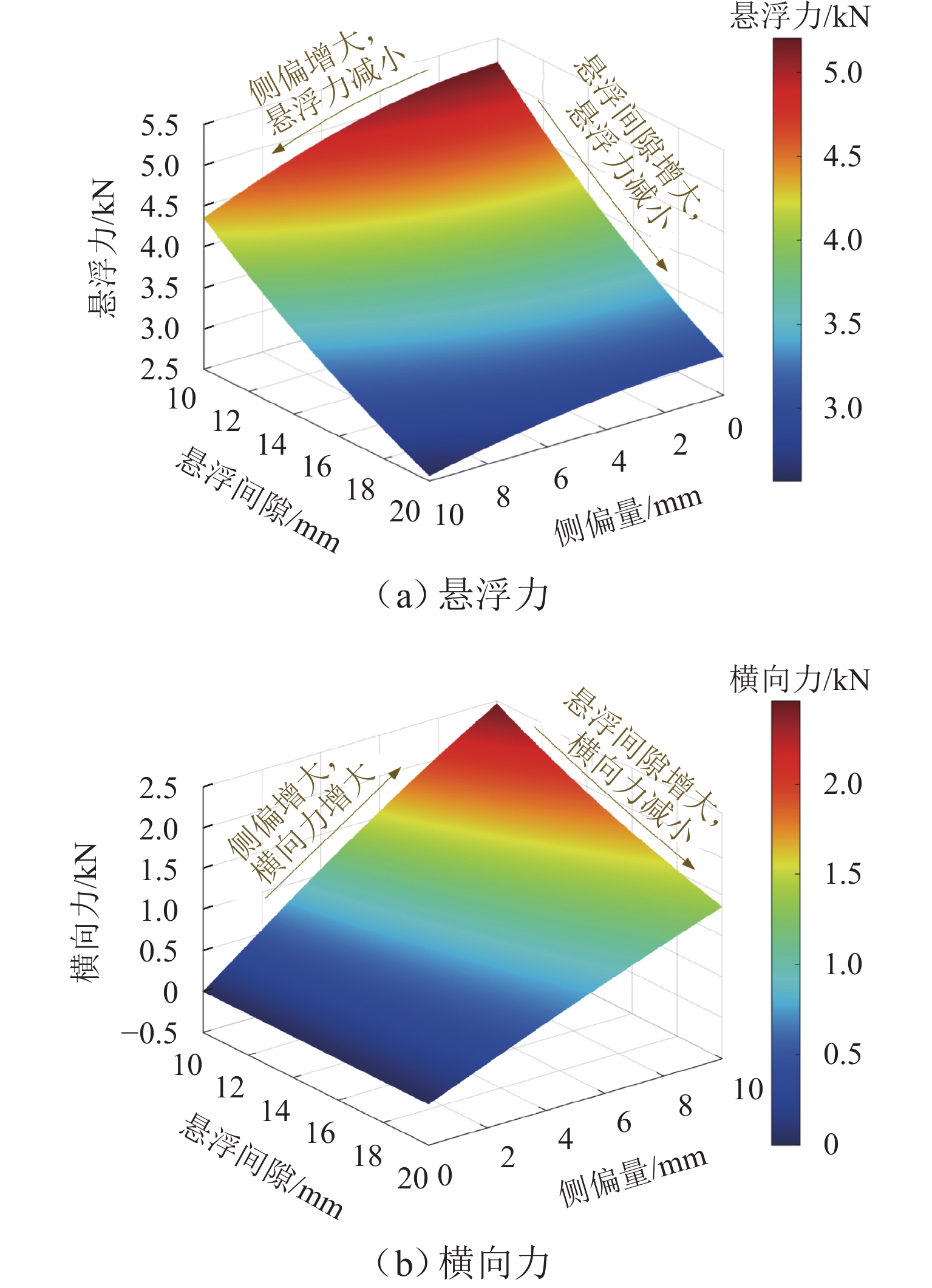
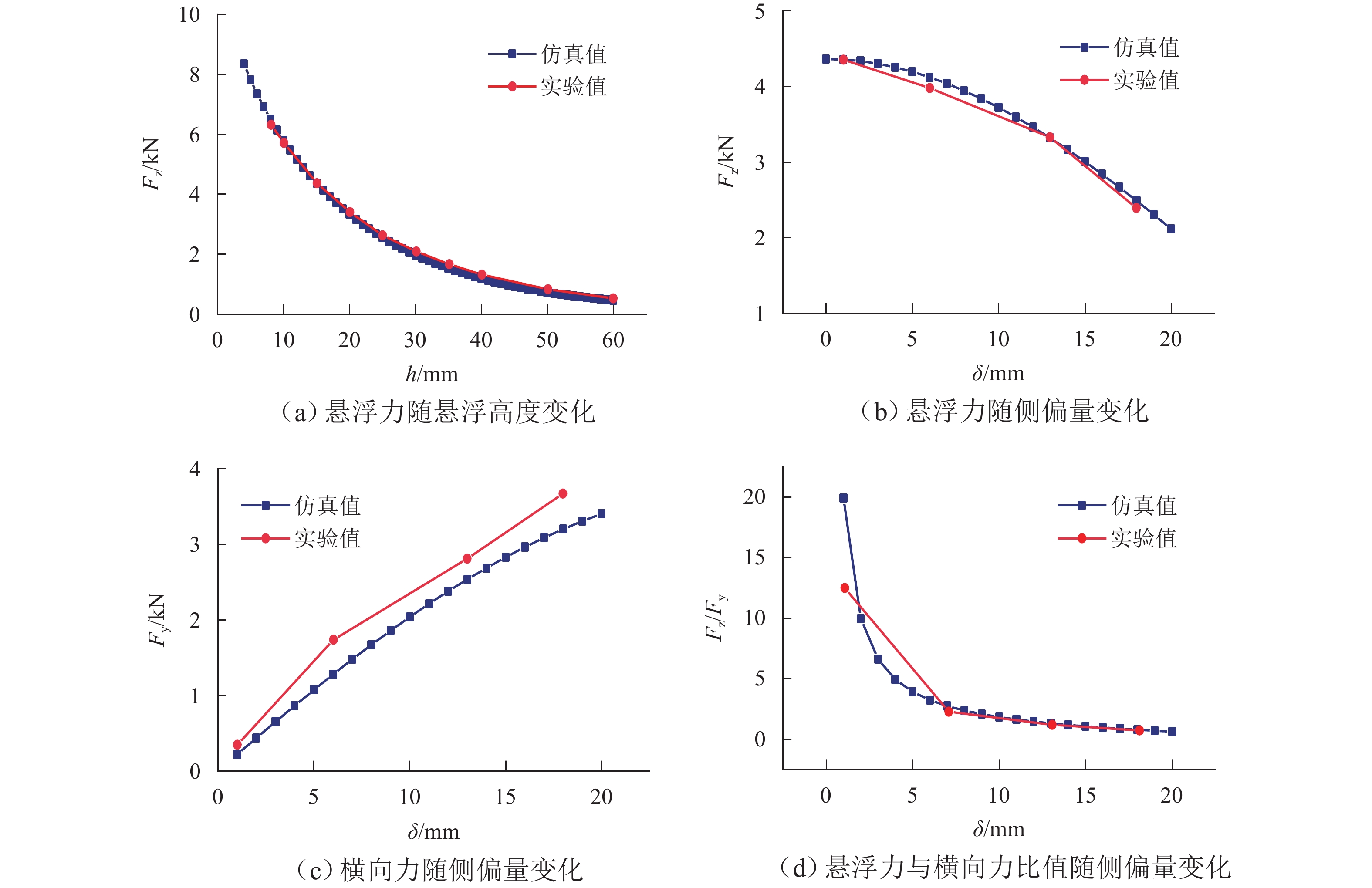
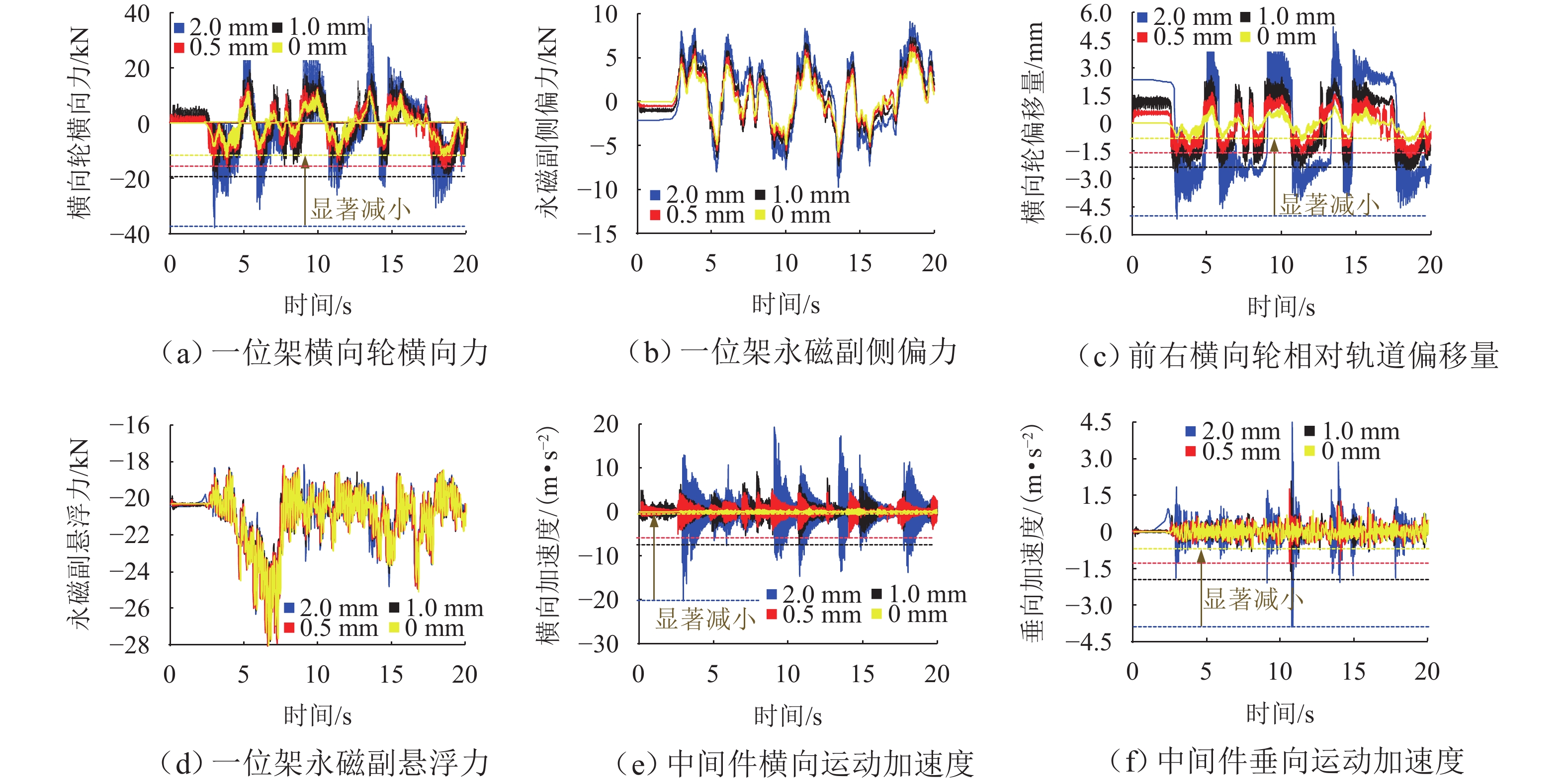
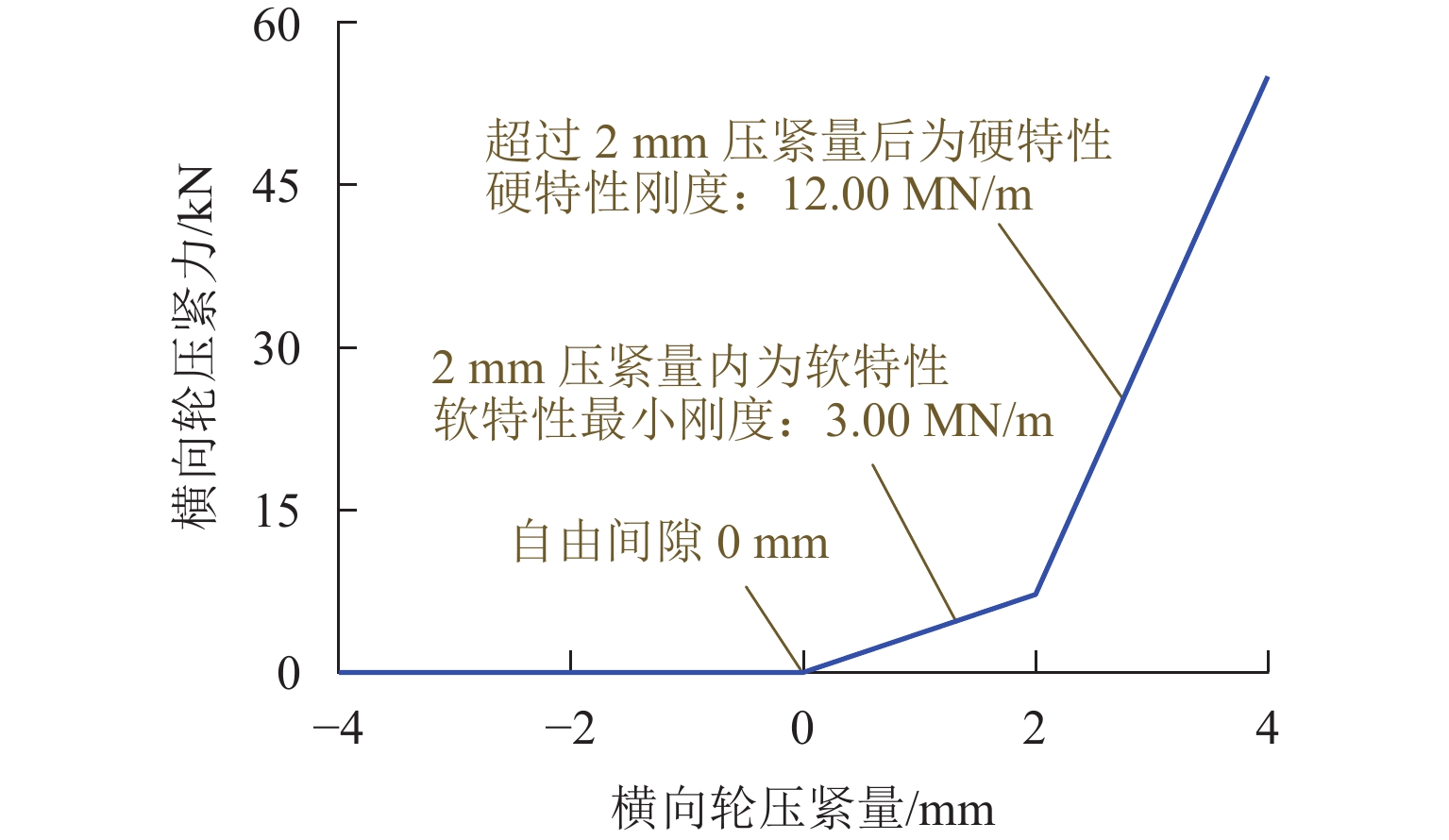
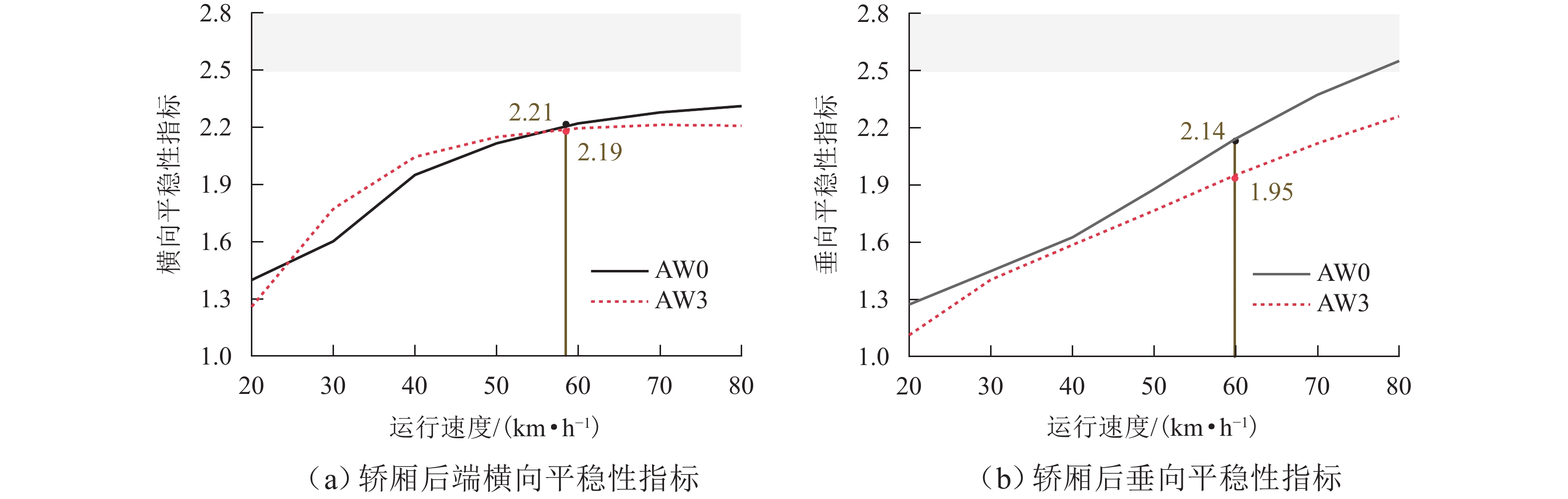
针对永磁磁浮“红轨”列车转向架在悬浮与导向性能上的不足，提出一种新型转向架方案并开展动力学研究. 首先，采用有限元法分析Halbach阵列磁场与磁力特性，明确永磁侧偏对导向性能及运动解耦对稳定悬浮的影响机制；其次，详细阐述新型转向架结构设计，构建车辆系统动力学模型，重点研究车辆直线运行及通过R50小半径曲线时转向架关键部件的动力学响应；最后，探究横向轮自由间隙与刚度对转向架冲击振动的影响. 研究结果表明：当横向轮自由间隙设为0，刚度值设为6 × 106 N/m时，转向架冲击振动得到有效抑制；车辆过曲线时，转向架在永磁侧偏力作用下，以横向轮紧贴曲线内侧来平衡离心力，与传统轨道车辆动力学特性明显不同；在运行速度≤60 km/h工况下，空载（AW0）状态时车辆的横向与垂向平稳性指标均优于超载（AW3）状态，且两者平稳性指标均控制在2.5以内.
Abstract:To address levitation and guidance performance deficiencies in permanent magnet maglev “Red Rail” train bogies, an innovative bogie scheme was proposed, and dynamic analyses were performed. First, the finite element method was used to analyze the Halbach array’s magnetic field and force characteristics and clarify the influence of lateral offset of the permanent magnet on guidance performance and that of motion decoupling on stable levitation. Next, the innovative bogie’s structural design was detailed, and a vehicle system dynamics model was built to investigate the dynamic responses of key bogie components during straight-line operation and passing through a 50-m radius curve (R50). Finally, the impact of free gaps and stiffness of lateral wheels on bogie impact vibration was explored. The results show that when the free gap of lateral wheels is 0, and the stiffness is 6 × 106 N/m, bogie impact vibration is effectively suppressed. When the train passes through a curve, the bogie balances centrifugal force by keeping lateral wheels in close contact with the inner curve side under the lateral offset force of a permanent magnet, which is distinct from traditional rail vehicle dynamics. When the speed is no more than 60 km/h, the lateral and vertical ride quality indices of no-load (AW0) vehicles outperform those in overload (AW3), with both indices controlled below 2.5.
-
Key words:
- permanent magnet /
- bogie /
- magnetic levitation /
- lateral offset of permanent magnet /
- dynamic response
-
永磁磁浮技术具有无机械摩擦、能耗低的特点，在轨道交通、工业轴承、医疗设备、加速器等领域应用广泛[1-4]. 作为新兴轨道交通技术，永磁磁浮技术具有绿色环保、维护成本低的优势，江西理工大学研发的“红轨”列车是国际首例实现该技术工程化的代表性成果[5]. 相较于其他磁浮技术[6-8]，永磁磁浮节能明显，但存在悬浮力不足、缺乏自稳定性等短板. 当前，将强磁材料（如钕铁硼[9]）以Halbach阵列形式运用到永磁磁浮技术中，能大幅提升悬浮能力，为其工程化应用开辟了可行道路.
在此背景下，学者们围绕磁场与磁力计算方法、磁力特性与优化、振动控制与稳定性等进行了深入研究. 其中，等效面电流法[10]、等效磁荷法[11]以及有限元法[12]是研究磁场分布的常用工具；Maxwell应力张量法[13]和虚功法[14]为精确计算磁力提供了有效手段. Mallinson[15]于1973年首次在平面磁结构中发现单边磁通现象；Halbach[16]于1979年在粒子加速多极磁体优化研究中提出Halbach阵列，通过周期性旋转磁体磁化方向，实现了单侧磁场显著增强、另一侧磁场抵消的定向场效应；Bachovchin等[17]对比了Halbach阵列与简单环形磁铁在磁悬浮轴承中的性能差异，证实了前者可显著提升磁轴承的承载力与刚度；赵春发等[18]构建了Halbach阵列车载永磁体与永磁轨道的有限元模型，探究了磁力随悬浮间隙、横向偏移、摇头角等位姿参数的变化规律及其相关程度；Jiang等[19]研究了永磁磁浮列车Halbach阵列磁体宽度和厚度对悬浮力影响，得到了限定条件下利用率最佳的磁体尺寸；李博涵等[20]分析了Halbach阵列结构参数对横向力的影响，探明了磁体厚度、相邻磁体磁化角度对最大横向力和横向刚度的影响；Rovers等[21]研究发现Halbach阵列中永磁体间相互作用力显著，经解析模型计算和有限元仿真验证，该力会导致安装结构发生明显变形，其研究为执行器及有关永磁悬浮结构设计提供了参考；Sun等[22]利用Maxwell张量法，对永磁与超导混合悬浮系统中永磁Halbach阵列结构参数进行了优化，为提升该磁悬浮系统的承载能力和横向稳定性提供了思路；Hekmati等[23]通过优化永磁导轨Halbach阵列的磁化角度，显著提升了对高温超导体的悬浮力，为永磁导轨设计提供了依据；Zhou等[24]基于Halbach阵列构建了垂向悬浮力解析模型，通过多参数优化磁轨结构尺寸，提出了7模块Halbach阵列结构，有效提升了悬浮系统性能.
在振动控制与稳定性研究方面：高涛等[25]通过单自由度永磁磁浮模型研究发现，单靠弹簧阻尼悬挂很难从根本上改善永磁磁浮固有的零阻尼特性，结合电磁悬浮结构可提升系统的抗扰动能力；唐文冰等[26]归纳了现有磁悬浮轨道交通的悬浮导向原理与结构特点，提出基于永磁斥力与电磁吸力、永磁斥力与超导钉扎的混合磁悬浮导向结构，但尚未从理论角度验证其悬浮导向性能；陈花顺等[27]针对永磁阵列悬浮结构（MAS）的横向侧偏问题，研究了斥力型与吸力型电磁导向方案，为解决永磁悬浮导向问题提供了思路，但该构型导向控制范围仅有几个毫米，使得有效控制成为了新的关键问题；Musolino等[28]提出了一种被动永磁磁悬浮系统，通过导轨导体动生电流与电枢永磁体的相互作用产生稳定力，解决了传统永磁悬浮不稳定问题，其探讨的导电板和零磁通线圈2种配置方式，为高速电磁发射场景下磁悬浮系统的发展提供了新思路；Sun等[29]采用变刚度控制方法开发了可变磁通路径永磁磁浮平台，通过磁体旋转调节磁力，实现稳定悬浮与运动控制；Long等[30]提出了以主动控制电磁力弥补阻尼、抑制振荡，提升永磁电动磁浮系统的动态稳定性，具有良好适用性；Wu等[31]针对永磁电动悬浮系统提出了永磁被动阻尼方案，通过在两侧布置Halbach阵列阻尼磁体，将纵向的阻尼特性转化为抑制系统振荡的阻尼力，以抑制悬浮系统振荡和降低导向系统振荡幅度，但该系统对低频干扰敏感，研究尚未深入探讨其影响.
总体而言，现有永磁悬浮被动方案研究较少，更多聚焦于结合电磁控制的方案. “红轨”列车采用永磁与电磁混合的模式，通过电磁力实现系统稳态调控[32]. 然而，实践表明，该列车存在导向缺陷. 前期理论研究和现场试验确定其根源在于永磁磁浮导向复杂以及存在轨道刚度不连续、几何不平顺及磁场不平顺等多重因素叠加. 为此，本文针对永磁磁浮的导向特性展开研究，剖析并整理出影响稳定悬浮的运动解耦问题以及影响导向的永磁侧偏与姿态不稳定问题；随后，提出了一种新型永磁磁浮转向架设计方案，并通过动力学仿真，详细分析了车辆直线、曲线运行时关键部件的动力学响应，探讨了横向轮的最优间隙与刚度设置.
1. 技术概述
1.1 悬挂式空轨转向架技术
当前，悬挂式空轨多采用轮胎式转向架，该技术已在德国、日本、中国等国家[33]商业落地. 永磁磁浮悬挂式空轨尚未投入商用，处于技术验证与研究阶段. 轮胎式转向架技术相对成熟，各类转向架遵循相同的技术原理. 以国内某悬挂式空轨为例，其轮胎式转向架见图1（a）；“红轨”列车的永磁磁浮转向架见图1（b）；本文提出的永磁磁浮转向架见图1（c）. 三者的技术共性与差异见表1.
表 1 轮胎式与2种永磁磁浮转向架技术对比Table 1. Technical comparison among tire-type and two types of permanent magnet maglev bogies类型 承载 导向/抗侧滚 牵引 制动 轮胎式 充气轮胎 横向轮与稳定轮 旋转电机 电制动与机械制动 兴国线 永磁副 导向/稳定轮 直线电机 电制动与机械制动 本文研究 永磁副 横向轮与姿态轮 直线电机 机械制动 3种转向架技术承载原理不同，但除以下3个方面外，其他技术基本一致：1） 永磁磁浮以永磁副取代轮胎；2） 采用直线感应电机取代旋转电机；3） 用轨道制动板取代转向架上旋转制动盘.
兴国试验线运行以来，暴露出了一些问题. 经分析，现阶段主要问题如下：
1） 轨道梁承载部位在底部，呈开口结构，承载后底部张开量增大，车辆运行时开口持续变化，影响了平稳性.
2） 因制造、安装等误差，转向架4个磁浮点难共面，磁力不均导致磁浮不稳、产生冲击，而且作为整体式结构，一侧受冲击易影响另一侧，相互激扰，降低了平稳性.
3） 制动器置于转向架顶部，制动时点头现象明显，对行车带来不利影响.
4） 永磁磁浮特性独特，引发的导向问题比轮胎式更显著.
1.2 既有永磁磁浮存在的问题
1.2.1 永磁磁浮导向问题
永磁磁浮系统通过上部与下部Halbach阵列间的磁斥力实现悬浮. 将上部与下部Halbach阵列相对面的垂直距离定义为悬浮间隙（h），上部Halbach阵列断面中心线相对下部Halbach阵列中心线的横向偏移量定义为永磁侧偏量（简称侧偏量，δ）. 当车载磁体出现侧偏时，永磁体间会产生横向力，导致车辆无法横向自复位. 因此，深入研究永磁体的侧偏特性对认识这一现象至关重要. 为此，利用Ansoft Maxwell软件构建Halbach阵列有限元模型（图2（a）），图2（b）为其断面结构，其中箭头指向表示磁化方向. 模型中，轨道磁体宽度为30 mm，厚度为22 mm，由5块永磁体沿横向排列组成Halbach阵列；车载磁体宽度为30 mm，厚度为60 mm，也由5块永磁体组成Halbach阵列.
图 2 Halbach永磁阵列结构及有限元模型Figure 2. Structure of Halbach permanent magnet array and its finite element model车辆和轨道两侧分别用钕铁硼N45和N52M永磁材料构建Halbach阵列，磁材性能参数见表2.
表 2 钕铁硼N45 和 N52M永磁材料参数Table 2. Parameters of NdFeB N45 and N52M permanent magnet materials牌号 矫顽力/（kA•m−1） 相对磁导率 剩余磁感应强度/T N45 955.20 1.14 1.37 N52M 1114.40 1.04 1.46 以悬浮间隙（10.00～20.00 mm）和侧偏量（0～10.00 mm）为变量，按1.00 mm步长设置231个工况，系统分析二者对悬浮力和横向力的协同影响. 首先，为揭示二者对磁场分布的影响规律，无侧偏工况选取了10.00、20.00 mm 2种悬浮间隙，磁场结果见图3（a）、（b），d为观测磁场位置与磁体表面的距离，B为磁感应强度；有侧偏工况则基于该2种悬浮间隙，选取了10 mm 侧偏量，磁场结果见图3（c）、（d）. 图3（e）、（f）分别为车载永磁体Halbach阵列和永磁轨道Halbach阵列磁体的静磁场分布，Halbach阵列静磁场主要聚集于单侧，且随悬浮高度增加呈非线性衰减.
由图3可知：Halbach阵列斥力型磁浮结构产生的磁力源于车载与轨道永磁体共同形成的叠加磁场；无侧偏工况下，磁场对称性分布，受悬浮间隙影响；有侧偏工况下，磁场因侧偏失去对称性.
图4为悬浮力、横向力随悬浮间隙与侧偏量变化情况. 由图4可知：磁体对中时，横向力为0；存在侧偏时，悬浮力和横向力均随悬浮间隙增大而减小，且悬浮力随侧偏量增大而减小，横向力随侧偏量增大而增大. 由于横向力方向与侧偏方向相同，因此，横向力呈现出负刚度特性，导致系统动态稳定性下降. 当转向架运行姿态不稳时，易诱发列车振动或失稳，故车辆侧偏是影响运行的关键因素之一，须加以控制.
图 4 悬浮力、横向力随悬浮间隙与侧偏量变化Figure 4. Variation of levitation force and lateral force with levitation gap and lateral offset1.2.2 永磁磁浮运动解耦问题
当转向架有4个及以上支撑点位，且各个支撑点位的垂向刚度很大（如钢轮与钢轨）时，为适应轨道变形、超高因素导致的扭曲，每个支撑位置与转向架的垂向连接需具备足够柔度. 为了减小轨道扭曲影响，转向架的轴距应尽可能小. 轴距越小，轨道扭曲激励引起的动力学响应越小，但会削弱转向架抗点头能力，必要时须设置相应止挡.
永磁磁浮在垂向具有一定弹性，类似轮胎支撑，可通过单点永磁单自由度模型的响应主频计算悬浮刚度. 不同悬浮间隙（相当于不同载荷）下的悬浮刚度k=(2πf)2m，f 为响应主频，m为相应悬浮间隙下的承载质量.
计算40%AW3、50%AW3、60%AW3、70%AW3、AW0（空载）和AW3（超载）状态下永磁磁浮系统的垂向刚度. 设定AW0状态下的质量为
24800 kg，AW3状态下的质量为33400 kg，悬浮点数量为24个（按4个悬浮架，每个悬浮架设6个单点永磁磁浮进行配置）. 不同悬浮间隙下永磁悬浮系统的磁浮刚度见表3.表 3 不同悬浮间隙下永磁磁浮系统的垂向刚度Table 3. Vertical stiffness of permanent magnet maglev system with different levitation gaps悬浮间
隙/mm单点载
荷/kN响应主
频/Hz悬浮刚度/
（MN·m−1）20.10 5.5 3.6 0.28 16.40 6.8 3.9 0.42 13.90 8.2 4.4 0.62 12.00 9.6 4.6 0.83 11.40 10.1 5.0 1.02 8.70 13.7 5.5 1.66 由表3可知，单点磁浮载荷较小，但悬浮刚度较大，响应主频与不考虑二系悬挂时的一系悬挂沉浮频率相当. 轮胎式转向架轴重约5 t，一对轮胎垂向刚度约0.50 MN/m，不考虑二系悬挂的沉浮频率约1.6 Hz. 显然，永磁磁浮系统的一系频率过高，因此转向架支撑点间应实现运动解耦.
1.3 单点等比例磁体磁力测试及模型验证
图5为单点等比例磁体磁力测试平台. 为验证仿真模型的准确性，将平台测试结果与仿真结果对比分析，如图6. 由图6可得：悬浮力（Fz）和横向力（Fy）均受悬浮间隙和侧偏量的影响，呈明显非线性关系；侧偏量增大，悬浮力下降，横向力上升；悬浮力与横向力比值随侧偏量增大而减小，0～5 mm内骤降，15 mm时比值约为1.
图 5 单点等比例Halbach阵列磁力测试平台Figure 5. Magnetic force testing platform of single-point equal-proportion Halbach array因此，车辆应用时需控制偏移量，以确保悬浮性能和横向力可控. 仿真与实验值的吻合度高，验证了永磁仿真模型可靠，可为后续研究提供支撑.
图 6 单点等比例磁体磁力测试结果Figure 6. Magnetic force testing results of single-point equal-proportion magnet2. 创新转向架整体设计及结构特点
2.1 总体技术要求
创新转向架设计的总体技术参照了兴国试验线的相关要求. 其中，列车采用2编组（Mc + Mc）形式，转向架结构适配既有轨道梁结构尺寸（其内部高
1200 mm、宽1200 mm）.2.2 转向架总体及关键部件
2.2.1 转向架布置形式
一节轿厢由2台转向架支撑，二者通过悬挂摆臂实现横向摆动，且在转向架、摆臂及轿厢间设置有减振器、牵引装置、空气弹簧等元件.
2.2.2 转向架结构
由图1（c）可知，转向架为三大件结构，包括左、右磁浮架和中间体. 左右磁浮架结构对称，通过绕中间体销轴转动实现运动解耦. 磁浮系统布置于轨道梁中部，牵引系统设于底部，以有效减小轨道梁开口变形对悬浮与导向力的影响. 姿态轮与轨道梁垂向常接触，以稳定转向架姿态. 磁浮架主要由构架、横向轮等功能件构成.
1） 构架组成及功能件安装
磁浮架呈“口”字形，由下纵梁、上纵梁及2根立柱组成. 磁体固定于上纵梁下表面，横向轮布置于上纵梁两端，所处水平面略高于磁体悬浮位置；直线电机初级固定于下纵梁下表面；垂向防撞轮设于立柱与上纵梁连接处；下纵梁靠近立柱位置的上表面设机械制动夹钳安装座，底部固定直线电机；下纵梁中部上表面设制动拉杆安装座，中部开销孔与中间体销轴配合.
2） 横向轮设计
横向轮起横向限位和减振作用，采用铝合金内圈，外层包裹橡胶层的形式，刚度通过橡胶层厚度和软硬程度调节. 横向轮沿转轴有横动量并设复位簧，以减小构架垂向运动时横向轮与接触面的摩擦.
3） 直线电机配置
每台转向架安装2台直线感应电机，分别置于左、右磁浮架底部. 每节车有2个转向架，共配备4台直线感应电机.
4） 机械制动装置说明
采用液压制动夹钳，以主动制动模式工作，可实现常用、紧急、停放等多种制动工况. 每节车配备4套该装置，对称安装在左右磁浮架上.
5） 中间体结构功能
中间体用于吊挂车体和稳定转向架姿态，上部布置受流器；中部设有销轴，其销轴两端安装姿态轮，与轨道梁中部水平梁常接触控制姿态. 为防止销轴失效，中间体设有防脱键；横轴断裂时，防脱键压在磁浮架上，防止车厢掉落.
3. 动力学论证
基于创新转向架结构特点构建动力学模型，且模型中的高度值设定遵循如下规则：以车辆处于空车AW0状态时，垂向防撞轮恰好接触轨面（此时设定悬浮间隙为5.00 mm）为名义零高度状态，并以永磁轨上平面为参考面. 在建模型中，轨道参考面较兴国线参考面向上抬升了700 mm （图7）.
3.1 总体技术要求
3.1.1 悬浮力和侧偏力计算模型
当永磁体尺寸确定后，悬浮力和侧偏力的大小由悬浮间隙和侧偏量这2个关键参数决定.
1） 悬浮力计算
无侧偏时，依据图6（a），对于长度为100 mm、厚度为60 mm、宽度为5 × 30 mm的Halbach永磁阵列，其承载力可近似为图8（a）中的指数表达式. 而在动力学模型中，每个磁体的长度为500 mm，无侧偏状态下的悬浮力为
46.1585 e−0.049h kN. 当存在侧偏时，悬浮力会被削弱. 依据图6（b），在悬浮间隙为15.00 mm时，悬浮力与侧偏量的关系式可用图8（b）中的二次多项式表示. 为便于研究，将其除以无侧偏时的悬浮力（4.39 kN）进行规范化处理，从而得到修正系数（−0.0011 δ2−0.0037| δ| +1.0075 ）. 假设不同悬浮间隙下，悬浮力的修正系数保持不变，则悬浮力为
图 8 无侧偏/有侧偏时悬浮力拟合曲线Figure 8. Fitting curves of levitation force without/with lateral offsetFz(h,δ)=46.1585e−0.049h×(−0.0011δ2−0.0037|δ|+1.0075). (1) 2） 侧偏力计算
由图4（b）可知，当悬浮间隙不变时，侧偏力与侧偏量基本呈线性关系. 为简化侧偏力的计算过程，根据悬浮间隙确定相应的侧偏刚度. 在模型中，侧偏力等于侧偏量与侧偏刚度的乘积.
对于长度为100 mm的磁体，依据图4（a），当悬浮间隙为10.00 mm时，侧偏刚度为0.25 kN/mm；悬浮间隙为20.00 mm时，侧偏刚度为0.14 kN/mm. 由此按该两点确定的线性关系可得侧偏刚度ky= （0.36−0.011h） kN/mm， h取值为0～20 mm. 在动力学模型中，车载磁体长度为500 mm，因此，侧偏力的计算式为
Fy(h,δ)=kyδ=(1800−55h)δ. (2) 3.1.2 单点永磁磁浮子结构
单点永磁磁浮子结构由代表轨道和车辆的2个刚体构成. 在子结构中，车辆体相对轨道体仅有垂向运动1个自由度，但可设置侧偏量. 当子结构被调入主模型后，轨道体与主模型轨道相应点固结，车辆体与主模型中相应转向架固结. 在车辆体和轨道体之间建立悬浮力和侧偏力模型，同时，在子结构模型中设置垂向止挡. 当悬浮间隙≤5.00 mm时，悬浮力输出值固定为100 kN；当悬浮间隙>5.00 mm时，悬浮力按式（1）计算，侧偏力则始终按式（2）计算.
3.1.3 永磁磁浮基本状态
表 5 AW0状态不同侧偏量下悬浮间隙、侧偏力及修正系数Table 5. Levitation gap, lateral offset force, and correction coefficient under different lateral offsets in AW0 condition侧偏量/mm 悬浮间隙/mm 侧偏力/N 修正系数/% 0 22.81 0 100.00 −5 21.86 2988.4 96.15 −10 19.60 7222.4 86.05 −15 15.51 14201.4 70.45 −20 8.09 27106.5 49.40 表 6 AW3状态不同侧偏量下悬浮间隙、侧偏力及修正系数Table 6. Levitation gap, lateral offset force, and correction coefficient under different lateral offsets in AW3 condition侧偏量/mm 悬浮间隙/mm 侧偏力/N 修正系数/% 0 16.74 0 100.00 −5 15.78 4659.2 96.15 −10 13.52 10564.1 86.05 −15 9.44 19213.9 70.45 −17 7.05 24008.7 62.67 −18 5.63 26829.5 58.45 −19 4.16 29848.3 54.01 −20 2.03 33764.7 49.40 AW0状态下，该单自由度系统的振荡频率约为3.5 Hz，与1.2.2节中表3给出悬浮间隙为20.10 mm时的接近，从而验证了1.2.2节关于运动解耦分析的合理性.
由表6可知：当侧偏量超过18 mm后，悬浮间隙小于5.00 mm，此时垂向止挡提供100 kN的恒外力，故在准静态状况下，为确保系统的稳定性和安全性，最大侧偏不宜超过18 mm；在动态变化时，应进一步限制侧偏量，否则车辆通过小半径曲线时，极可能发生止挡碰撞现象. 此外，在AW3状态下，该单自由度系统的振荡频率约为3.5 Hz，与AW0状态下的相同，这一结果与1.2.2节表3中关于悬浮间隙减小频率增大的分析存在差异. 经分析推测，该差异可能与1.2.2节所阐述的永磁磁浮强迫响应特性以及本节所研究的自由响应特性有关.
3.2 车辆系统动力学建模
对于多刚体系统，通常可采用格朗日方程[34]描述系统的运动状态，如式（3）.
ddt(∂L∂˙qi)−∂L∂qi=Qi,i=1,2,⋯,N, (3) 式中：L=T−V，为拉格朗日函数，T为动能，V 为势能；qi 为广义坐标，i为系统具有的自由度；Qi为广义力.
利用SIMPACK软件搭建车辆系统动力学模型. 图9为转向架多体动力学模型，其中磁浮架相对中间体能够实现转动，横向轮与姿态轮赋予旋转自由度. 前车2台转向架的横向轮和姿态轮均设置复位弹簧，可沿转轴横向移动，每台转向架有20个自由度；后车2台转向架对应位置未设置复位弹簧（可视为弹簧卡滞，用于对比复位簧作用），每台转向架有14个自由度. 该车辆动力学模型参考了“红轨” 列车的相关成果，具备一定合理性.
3.3 关键部件动力学响应及参数优化
3.3.1 AW3状态直线运行
设定运行速度为60 km/h，初始状态下横向轮自由间隙为2.0 mm，径向刚度为1.2 × 107 N/m. 对AW3状态直线运行开展动力学仿真计算，具体结果见图10. 由图10可知：
图 10 转向架直线运行的动力学响应结果Figure 10. Dynamic response results of bogie during straight-line operation1） 对于一位转向架横向轮的横向力：初始时左侧轮受到向右的微小横向力，右侧轮与轨道梁脱开，如此两侧轮交替变换受力状态；同侧轮受力基本相同，2个横向轮的横向合力峰值约60 kN，无对角同时受力情况，表明每个永磁副的侧偏力基本相同，而侧偏力合力峰值约32 kN. 由于一侧横向轮的受力基本相同，前右轮的侧偏量具有足够代表性. 负值表示横向轮右移受力，正值表示左移脱开，故两侧横向轮总是一侧受力另一侧脱开.
2） 对于一位架永磁副悬浮力，初始有明显增载过程，由线路局部抬升引起；姿态轮与轨道梁间隙约1 mm，当间隙耗尽时，两侧姿态轮的受力差值会产生力矩，以平衡转向架的侧滚力矩；中间件的横向运动冲击较大，横向运动加速度有数个冲击峰值；垂向冲击峰值水平较低，表明永磁侧偏才是引发冲击的主因.
3） 一位架横向轮设复位簧有冲击性摩擦力，峰值约500 N；而横向轮沿轴垂向运动受阻，摩擦力会显著增大，峰值约4 kN.
3.3.2 AW3状态直线运行参数优化
为改善基本状态下的冲击振动问题，本节聚焦于横向轮自由间隙与径向刚度这2项关键参数. 初始状态设定为：横向轮自由间隙为0的临界接触状态，此时侧偏量约为0.005 mm，侧偏力约为4.0 N，悬浮间隙约为16.70 mm；姿态轮间隙约为0.7 mm.
在相同计算条件下，分析2.0、1.0、0.5、0 mm自由间隙下的动力学响应，具体结果见图11. 由图11可知：随自由间隙减小，横向轮横向力和侧偏量显著减小；永磁副侧偏力略减，悬浮力则基本相同；中间件运动加速度减小最为显著.
图 11 不同横向轮自由间隙下直线运行动力学响应结果Figure 11. Dynamic response results of bogie during straight-line operation under different free gaps of lateral wheel综上，消除自由间隙对于解决永磁侧偏引发的振动问题至关重要. 计算横向轮采用了“硬”特性，其径向刚度设定为12.00 MN/m. 若径向刚度过大，则转向架适应横向轮接触面的变形能力将会受到较大影响，在确保满足零自由间隙条件基础上，应尽可能降低横向轮刚度. 若采用“软”轮，则“软”轮的刚度应显著大于永磁侧偏刚度，否则系统会出现横向失稳. 依据3.1.1节中基于台架试验所得的永磁副侧偏刚度公式，在AW3状态下，永磁副的侧偏刚度为920.00 N/mm. 每台转向架有4个永磁副，所以合成的侧偏刚度为3.68 MN/m. 4个横向轮中只有2个能同时发挥作用，所以每个横向轮的刚度不能低于1.84 MN/m. 为了留有足够的裕量，可将每个横向轮的刚度取值为3.00 MN/m. 然而，永磁副侧偏刚度呈现出复杂的非线性特性. 为了避免失稳后计算中断，在模型中加入了具有止挡特性的横向轮特性. 假定横向轮“软”特性在2 mm弹性间隙耗尽后，呈现“硬”止挡特性，详见图12.
图 12 零自由间隙下具有二级刚度的横向轮模型Figure 12. Lateral wheel model with secondary stiffness under zero free gap在0自由间隙条件下，其他计算条件不变，分析3.00、4.00、5.00、6.00 MN/m横向轮刚度下的动力学响应，具体结果见图13. 结果显示：随横向刚度增大，横向轮横向力和侧偏量略有减小；永磁副侧偏力和悬浮力基本保持相同；中间件的横向运动加速度随横向轮刚度的增大而减小，垂向运动加速度则基本保持在较低的相同水平.
图 13 不同横向轮自由间隙下直线运行动力学响应结果Figure 13. Dynamic response results of bogie during straight-line operation under different free gaps of lateral wheel由上述结果可得：1） 仅当横向轮刚度不低于4.00 MN/m时，转向架横向冲击振动才不显著. 由于一台转向架上的永磁侧偏合成横向刚度为3.68 MN/m，因此，任何一个横向轮的径向刚度都不应低于转向架的总侧偏刚度；2） 为防止横向失稳，模型中加入了止挡刚度，并设置了2 mm的止挡间隙. 若采用的“软”横向轮的刚度未超过4.00 MN/m，则在结构上须考虑止挡功能. 不过，4.00 MN/m的横向轮刚度意味着横向轮产生1 mm半径变形需要4 kN的压力，所述的“软”横向轮在一定程度上仍具有较高的抗变形能力.
3.3.3 AW3状态通过R50曲线
以横向轮间隙0、横向轮刚度6.00 MN/m为参数，计算模型在AW3状态通过R50最小半径水平曲线时的动力学响应，以检验参数对曲线通过的适应性，如图14. 运行速度设定为20 km/h，此时轿厢的未被平衡离心加速度为0.063g.
图 14 通过R50曲线时车载磁体力矩平衡及横向力平衡示意Figure 14. Balance of on-board magnetic force torque and lateral force when passing through R50 curve曲线设置为：直线段—10 m进缓和曲线段—50 m圆曲线段—10 m出缓和曲线段—直线段，线路无超高. 设定车辆顺时针通过曲线，右侧为曲线内侧.
不考虑弯道线路不平顺以反映基本特征，动力学响应结果见图15. 永磁磁浮车辆在通过小半径曲线时展现出与其他轨道交通车辆不同的动力学特征. 具体表现为：转向架并未贴靠曲线外侧，而是在侧偏力作用下，通过横向轮紧贴曲线内侧来平衡离心力. 通过小半径曲线时，横向轮具有限位作用，转向架前后限位点位于磁体外侧，致使车载磁体中心线（左右磁体合成的中心线）的名义位置在轨道中心线内侧，车载磁体在侧偏力作用下进一步向曲线内侧贴靠，直至内侧横向轮限制其侧偏量（图14（a））.
图 15 转向架通过R50曲线时的动力学响应结果Figure 15. Dynamic response results of bogie when passing through R50 curve由图15可知：1） 横向轮的合成横向力为32.4 kN； 4个永磁副的合成横向力为37.2 kN；用车辆1/4总质量（
8350 kg）乘以离心加速度可得未被平衡离心力为4.8 kN，三者达成平衡（图14（b））. 2） 通过曲线时转向架相对车体回转，后横向轮的力显著大于前横向轮，由此形成14.90 kN•m 的顺时针力矩. 需要平衡的反力矩主要来自二系悬挂的纵向力，其阻力矩为14.42 kN•m，极小一部分阻力矩来自永磁副. 3） 一位转向架上后磁体的力略超过前磁体0.2 kN，形成的阻力矩约为0.48 kN•m，三者达成平衡. 在侧滚方向，转向架受到来自车体顺时针的侧滚力矩3.40 kN•m，主要由左右侧悬浮力差形成的侧滚力矩平衡. 4） 由于姿态轮未提供侧滚力矩，右侧姿态轮增载较大，左侧姿态轮减载较大；图15（e）中两侧永磁副的侧偏量相同，约8.90 mm，依据3.1.3节可知，悬浮力损失约13.5%，已超过外侧永磁副减载量；悬浮间隙由直线稳定状态下的16.70 mm 下降至15.45 mm，而内侧永磁副在增载和侧偏共同作用下悬浮间隙由直线稳定状态下的16.70 mm下降至12.20 mm；在通过小半径曲线时，转向架中间件的振动加速度存在尖峰，但幅值很小.3.3.4 平稳性指标[35]
设定横向轮间隙为0、横向轮刚度为6.00 MN/m，以10 km/h为速度增量，将20～80 km/h运行速度区间划分为7个工况，计算平稳性指标. 选取轿厢后端为观测点，图16为AW0与AW3状态下，列车直线运行时轿厢后端的平稳性指标.
图 16 轿厢后端横向与垂向平稳性指标Figure 16. Transverse and vertical ride comfort index at rear of train carriage由图16可知：运行速度60 km/h及以下时，AW0状态下的横向平稳性与垂向平稳性普遍优于AW3状态，且两项指标均未超过2.5；同时，在该速度范围内，无论AW0还是AW3状态，垂向平稳性均优于横向平稳性；当速度达到80 km/h时，AW0状态下的垂向平稳性指标超过了2.5.
4. 结 论
1） 本文针对永磁悬浮系统剖析了影响稳定悬浮的运动解耦问题及导向存在的永磁侧偏与姿态不稳定问题. 为此，提出一种新型永磁磁浮转向架结构设计方案，并详述了其总体构造及功能部件.
2） 采用有限元模型与磁浮性能测试相结合方式，定性分析了悬浮力、横向力与悬浮间隙和侧偏量的非线性关系；结合指数拟合与修正系数得出了悬浮力和侧偏力的近似计算式.
3） 分析了AW3状态下车辆直线运行和通过R50曲线时转向架关键部件的动力学响应. 针对横向轮自由间隙和刚度值开展优化研究，得到名义自由间隙应设置为0，优化后的刚度值为6 MN/m.
4） 在通过小半径曲线时，永磁磁浮车辆展现出独特的动力学特征，即转向架不会贴靠曲线外侧，而是在侧偏力作用下，通过横向轮紧贴曲线内侧来平衡离心力.
致谢：中国博士后科学基金面上项目（2024M762698）；轨道交通运载系统全国重点实验室自主课题（2025RVL-T12）.
-
图 2 Halbach永磁阵列结构及有限元模型
Figure 2. Structure of Halbach permanent magnet array and its finite element model
图 4 悬浮力、横向力随悬浮间隙与侧偏量变化
Figure 4. Variation of levitation force and lateral force with levitation gap and lateral offset
图 5 单点等比例Halbach阵列磁力测试平台
Figure 5. Magnetic force testing platform of single-point equal-proportion Halbach array
图 6 单点等比例磁体磁力测试结果
Figure 6. Magnetic force testing results of single-point equal-proportion magnet
图 8 无侧偏/有侧偏时悬浮力拟合曲线
Figure 8. Fitting curves of levitation force without/with lateral offset
图 10 转向架直线运行的动力学响应结果
Figure 10. Dynamic response results of bogie during straight-line operation
图 11 不同横向轮自由间隙下直线运行动力学响应结果
Figure 11. Dynamic response results of bogie during straight-line operation under different free gaps of lateral wheel
图 12 零自由间隙下具有二级刚度的横向轮模型
Figure 12. Lateral wheel model with secondary stiffness under zero free gap
图 13 不同横向轮自由间隙下直线运行动力学响应结果
Figure 13. Dynamic response results of bogie during straight-line operation under different free gaps of lateral wheel
图 14 通过R50曲线时车载磁体力矩平衡及横向力平衡示意
Figure 14. Balance of on-board magnetic force torque and lateral force when passing through R50 curve
图 15 转向架通过R50曲线时的动力学响应结果
Figure 15. Dynamic response results of bogie when passing through R50 curve
图 16 轿厢后端横向与垂向平稳性指标
Figure 16. Transverse and vertical ride comfort index at rear of train carriage
表 1 轮胎式与2种永磁磁浮转向架技术对比
Table 1. Technical comparison among tire-type and two types of permanent magnet maglev bogies
类型 承载 导向/抗侧滚 牵引 制动 轮胎式 充气轮胎 横向轮与稳定轮 旋转电机 电制动与机械制动 兴国线 永磁副 导向/稳定轮 直线电机 电制动与机械制动 本文研究 永磁副 横向轮与姿态轮 直线电机 机械制动 
下载: 导出CSV
表 2 钕铁硼N45 和 N52M永磁材料参数
Table 2. Parameters of NdFeB N45 and N52M permanent magnet materials
牌号 矫顽力/（kA•m−1） 相对磁导率 剩余磁感应强度/T N45 955.20 1.14 1.37 N52M 1114.40 1.04 1.46
下载: 导出CSV
表 3 不同悬浮间隙下永磁磁浮系统的垂向刚度
Table 3. Vertical stiffness of permanent magnet maglev system with different levitation gaps
悬浮间
隙/mm单点载
荷/kN响应主
频/Hz悬浮刚度/
（MN·m−1）20.10 5.5 3.6 0.28 16.40 6.8 3.9 0.42 13.90 8.2 4.4 0.62 12.00 9.6 4.6 0.83 11.40 10.1 5.0 1.02 8.70 13.7 5.5 1.66
下载: 导出CSV
表 5 AW0状态不同侧偏量下悬浮间隙、侧偏力及修正系数
Table 5. Levitation gap, lateral offset force, and correction coefficient under different lateral offsets in AW0 condition
侧偏量/mm 悬浮间隙/mm 侧偏力/N 修正系数/% 0 22.81 0 100.00 −5 21.86 2988.4 96.15 −10 19.60 7222.4 86.05 −15 15.51 14201.4 70.45 −20 8.09 27106.5 49.40
下载: 导出CSV
表 6 AW3状态不同侧偏量下悬浮间隙、侧偏力及修正系数
Table 6. Levitation gap, lateral offset force, and correction coefficient under different lateral offsets in AW3 condition
侧偏量/mm 悬浮间隙/mm 侧偏力/N 修正系数/% 0 16.74 0 100.00 −5 15.78 4659.2 96.15 −10 13.52 10564.1 86.05 −15 9.44 19213.9 70.45 −17 7.05 24008.7 62.67 −18 5.63 26829.5 58.45 −19 4.16 29848.3 54.01 −20 2.03 33764.7 49.40
下载: 导出CSV
-
[1] 赵川,孙凤,裴文哲,等. 永磁悬浮技术的实现机理与发展现状[J]. 机械工程学报,2023,59(17): 189-207. doi: 10.3901/JME.2023.17.189ZHAO Chuan, SUN Feng, PEI Wenzhe, et al. Realization mechanism and development of permanent magnetic levitation: a review[J]. Journal of Mechanical Engineering, 2023, 59(17): 189-207. doi: 10.3901/JME.2023.17.189 [2] WU T, ZHANG W Y. Review on key development of magnetic bearings[J]. Machines, 2025, 13(2): 113. doi: 10.3390/machines13020113 [3] DABBAGH S R, ALSEED M M, SAADAT M, et al. Biomedical applications of magnetic levitation[J]. Advanced NanoBiomed Research, 2022, 2(3): 2100103. doi: 10.1002/anbr.202100103 [4] CHAVANNE J, LE BEC G. Prospects for the use of permanent magnets in future accelerator facilities[C]// 5th International Particle Accelerator Conference. Dresden:[s.n.], 2014: 968-973. [5] ZHOU F Z, YANG J, HU H L, et al. Study of repulsive permanent magnetic levitation mechanism and its dynamic characteristics[J]. Scientific Reports, 2024, 14: 29859. doi: 10.1038/s41598-024-81439-2 [6] 邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001 [7] 马卫华,罗世辉,张敏,等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报,2021,21(1): 199-216.MA Weihua, LUO Shihui, ZHANG Min, et al. Research review on medium and low speed maglev vehicle[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 199-216. [8] BARBOSA F C. High speed intercity and urban passenger transport maglev train technology review: a technical and operational assessment[C]//2019 Joint Rail Conference. Snowbird: American Society of Mechanical Engineers, 2019: V001T08A002. [9] GUTFLEISCH O, WILLARD M A, BRÜCK E, et al. Magnetic materials and devices for the 21st century: stronger, lighter, and more energy efficient[J]. Advanced Materials, 2011, 23(7): 821-842. doi: 10.1002/adma.201002180 [10] 陈春涛,吴新振,郑晓钦,等. 基于改进等效面电流法的永磁电机气隙磁场解析计算[J]. 中国电机工程学报,2021,41(增1): 315-323.CHEN Chuntao, WU Xinzhen, ZHENG Xiaoqin, et al. Analytical calculation of air-gap magnetic field of permanent-magnet motor based on improved equivalent surface current method[J]. Proceedings of the CSEE, 2021, 41(S1): 315-323. [11] 柴凯,朱石坚,杨庆超,等. 三磁体型隔振器的性能分析和实验研究[J]. 振动与冲击,2018,37(6): 36-41.CHAI Kai, ZHU Shijian, YANG Qingchao, et al. Analysis and test for the performances of a tri-magnet vibration isolator[J]. Journal of Vibration and Shock, 2018, 37(6): 36-41. [12] 叶建和,占鹏飞,曾金成,等. Halbach型磁浮列车永磁轨道的空间磁场计算模型[J]. 磁性材料及器件,2024,55(5): 6-11.YE Jianhe, ZHAN Pengfei, ZENG Jincheng, et al. Calculation model of space magnetic field of Halbach-type permanent magnetic guideway in maglev trains[J]. Journal of Magnetic Materials and Devices, 2024, 55(5): 6-11. [13] GHOSH M K, GAO Y, DOZONO H, et al. Proposal of Maxwell stress tensor for local force calculation in magnetic body[C]//2018 IEEE International Magnetics Conference (INTERMAG). Singapore: IEEE, 2018: 1-4. [14] TANG W B, XIAO L Y, XIA D, et al. 2-D and 3-D analytical calculation of the magnetic field and levitation force between two halbach permanent magnet arrays[J]. IEEE Transactions on Magnetics, 2021, 57(4):8300208. [15] MALLINSON J. One-sided fluxes: a magnetic curiosity?[J]. IEEE Transactions on Magnetics, 1973, 9(4):678-682. [16] HALBACH K. Design of permanent multipole magnets with oriented rare earth cobalt material[J]. Nuclear Instruments and Methods, 1980, 169(1): 1-10. doi: 10.1016/0029-554X(80)90094-4 [17] BACHOVCHIN K D, HOBURG J F, POST R F. Magnetic fields and forces in permanent magnet levitated bearings[J]. IEEE Transactions on Magnetics, 2012, 48(7): 2112-2120. doi: 10.1109/TMAG.2012.2188140 [18] 赵春发,刘浩东,冯洋,等. 五位姿参数下车载永磁体与永磁轨道之间的磁力特性研究[J]. 西南交通大学学报,2024,59(4): 804-811. doi: 10.3969/j.issn.0258-2724.20240049ZHAO Chunfa, LIU Haodong, FENG Yang, et al. Magnetic force characteristics between on-board permanent magnet and permanent magnetic rail considering five pose parameters[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 804-811. doi: 10.3969/j.issn.0258-2724.20240049 [19] JIANG Y, DENG Y F, ZHU P H, et al. Optimization on size of halbach array permanent magnets for magnetic levitation system for permanent magnet maglev train[J]. IEEE Access, 2021, 9: 44989-45000. doi: 10.1109/ACCESS.2021.3058124 [20] 李博涵,吴兴文,池茂儒,等. 基于Halbach阵列的永磁悬浮车辆悬浮系统磁力特性研究[J]. 机械,2024,51(10): 21-28,58. doi: 10.3969/j.issn.1006-0316.2024.10.003LI Bohan, WU Xingwen, CHI Maoru, et al. Magnetic force characteristics of permanent maglev vehicle levitation system based on Halbach array[J]. Machinery, 2024, 51(10): 21-28,58. doi: 10.3969/j.issn.1006-0316.2024.10.003 [21] ROVERS J M M, JANSEN J W, LOMONOVA E A, et al. Calculation of the static forces among the permanent magnets in a halbach array[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4372-4375. doi: 10.1109/TMAG.2009.2021860 [22] SUN R X, ZHENG J, LI H T, et al. Halbach structure parameter optimization by Maxwell tensor method for PML in manned hybrid maglev[J]. Journal of Magnetism and Magnetic Materials, 2024, 610: 172566. doi: 10.1016/j.jmmm.2024.172566 [23] HEKMATI A, MAFI H. Impact of magnetization angles in permanent magnet guideways on high-temperature superconductors’ levitation[J]. IEEE Transactions on Magnetics, 2016, 52(9): 9000209. [24] ZHOU F Z, YANG J, JIA L M. Structure size optimization and magnetic circuit design of permanent magnet levitation system based on halbach array[J]. IEEE Access, 2023, 11: 113244-113254. doi: 10.1109/ACCESS.2023.3323596 [25] 高涛,杨杰,贾利民,等. 考虑机械阻尼结构的永磁悬浮系统动态特性研究[J]. 铁道学报,2021,43(11): 61-68. doi: 10.3969/j.issn.1001-8360.2021.11.008GAO Tao, YANG Jie, JIA Limin, et al. Study on dynamic characteristics of permanent magnet suspension system based on mechanical damping structure[J]. Journal of the China Railway Society, 2021, 43(11): 61-68. doi: 10.3969/j.issn.1001-8360.2021.11.008 [26] 唐文冰,肖立业,王粟,等. 磁悬浮轨道交通中的磁悬浮导向方式研究综述[J]. 电工电能新技术,2022,41(5): 45-60. doi: 10.12067/ATEEE2108022TANG Wenbing, XIAO Liye, WANG Su, et al. Summary of research on levitation-guidance modes in maglev rail transportation technology[J]. Advanced Technology of Electrical Engineering and Energy, 2022, 41(5): 45-60. doi: 10.12067/ATEEE2108022 [27] 陈花顺,彭月,杨杰. 稀土永磁悬浮阵列的电磁导向结构设计[J]. 稀土,2023,44(4): 214-224.CHEN Huashun, PENG Yue, YANG Jie. Design and feasibility analysis of electromagnetic guidance structure based on MAS array[J]. Chinese Rare Earths, 2023, 44(4): 214-224. [28] MUSOLINO A, RAUGI M, RIZZO R, et al. Stabilization of a permanent-magnet MAGLEV system via null-flux coils[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1242-1247. doi: 10.1109/TPS.2015.2404781 [29] SUN F, PEI W Z, ZHAO C, et al. Permanent maglev platform using a variable flux path mechanism: stable levitation and motion control[J]. IEEE Transactions on Magnetics, 2022, 58(7): 8300410. [30] LONG Z Q, HE G, XUE S. Study of EDS & EMS hybrid suspension system with permanent-magnet halbach array[J]. IEEE Transactions on Magnetics, 2011, 47(12): 4717-4724. doi: 10.1109/TMAG.2011.2159237 [31] WU C, LI G C, WANG D, et al. Dynamic characterization of permanent magnet electrodynamic suspension system with a novel passive damping magnet scheme[J]. Journal of Sound and Vibration, 2025, 599: 118849. doi: 10.1016/j.jsv.2024.118849 [32] 杨杰,高涛,邓永芳,等. 永磁磁浮空轨系统的研究与设计[J]. 铁道学报,2020,42(10): 30-37. doi: 10.3969/j.issn.1001-8360.2020.10.005YANG Jie, GAO Tao, DENG Yongfang, et al. Study and design on suspended permanent maglev rail transit system[J]. Journal of the China Railway Society, 2020, 42(10): 30-37. doi: 10.3969/j.issn.1001-8360.2020.10.005 [33] LI Y, XU Y G, YAN H Y, et al. Suspended monorail system: a new development of an urban rail transit system with low passenger capacity[C]//ICTE 2015. Dailan:American Society of Civil Engineers. 2015: 3180-3186. [34] 哈尔滨工业大学理论力学教研室. 理论力学Ⅰ[M]. 8版. 北京:高等教育出版社,2016. [35] 中华人民共和国国家市场监督管理总局,中国国家标准化管理委员会. 机车车辆动力学性能评定及试验鉴定规范:GB/T 5599—2019[S]. 北京:中国标准出版社,2019. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 30
- HTML全文浏览量: 24
- PDF下载量: 10
- 被引次数: 0