Super-Twisting Sliding Mode Control of Linear Magnetic Drive System Based on Fuzzy Variable Gain
-
摘要:
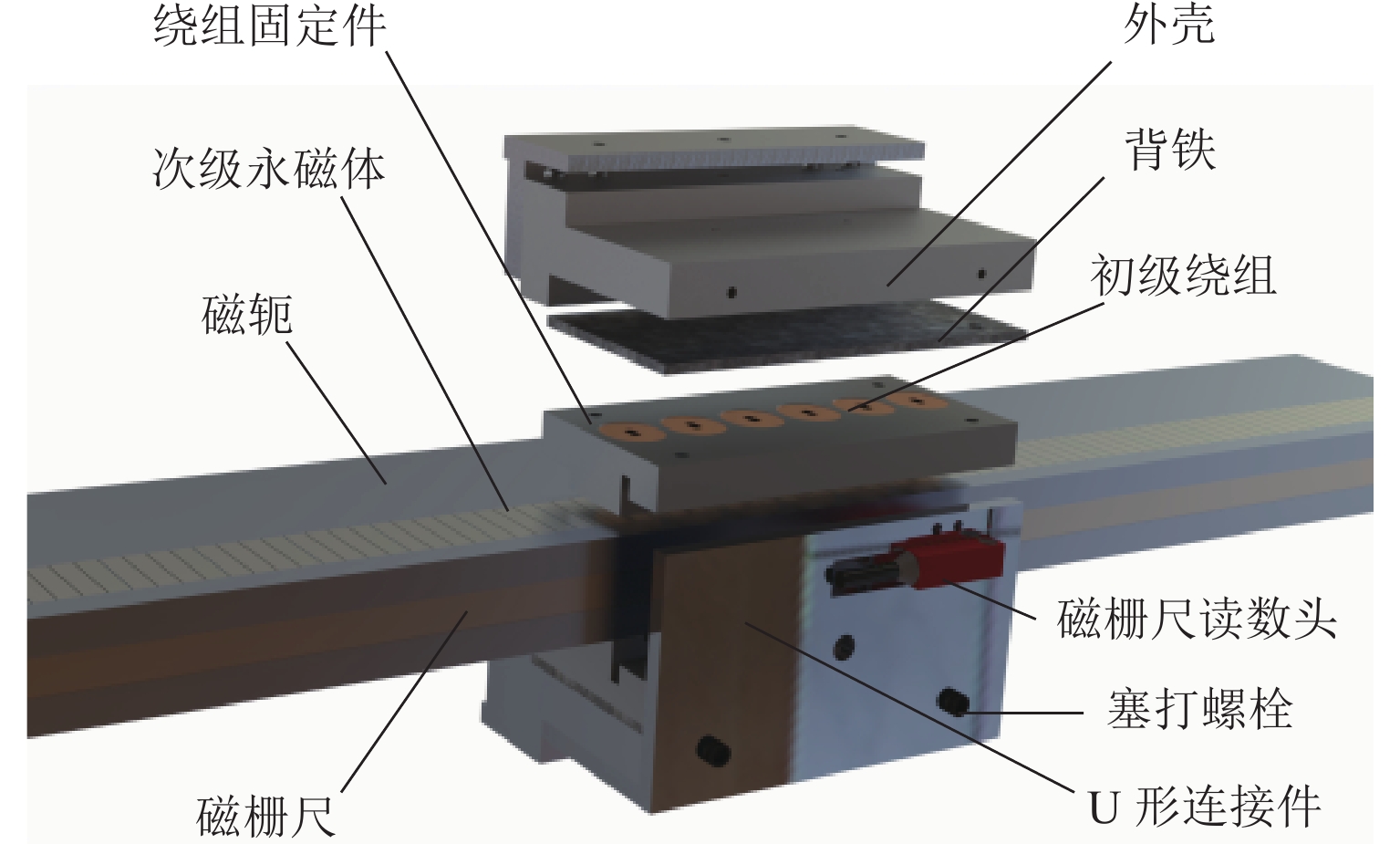
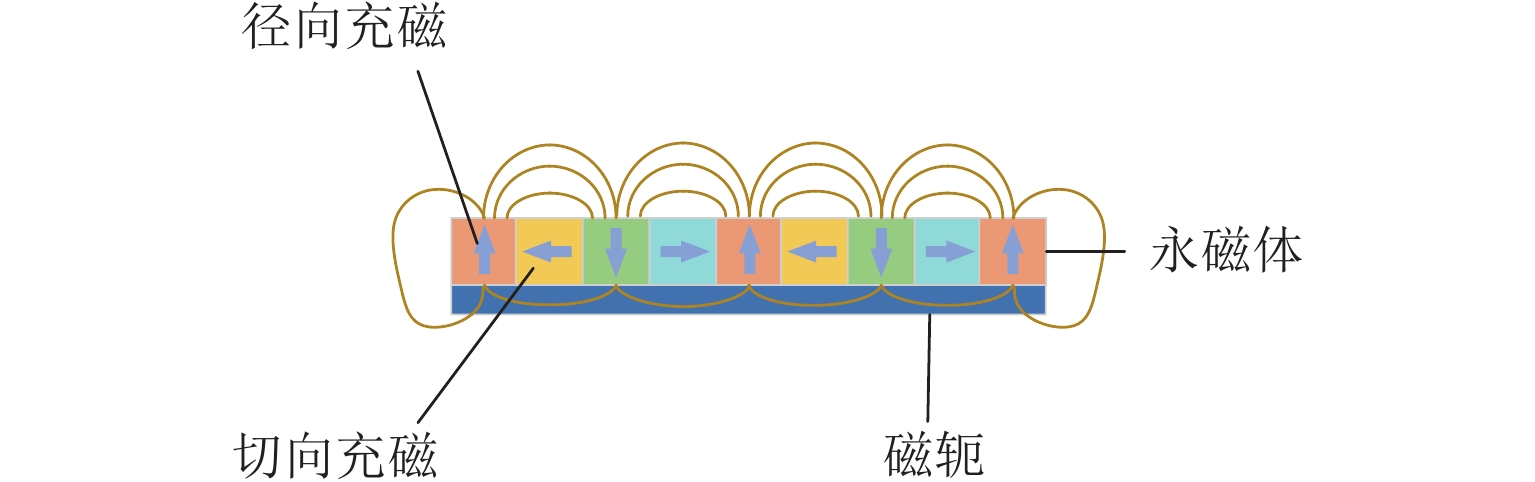
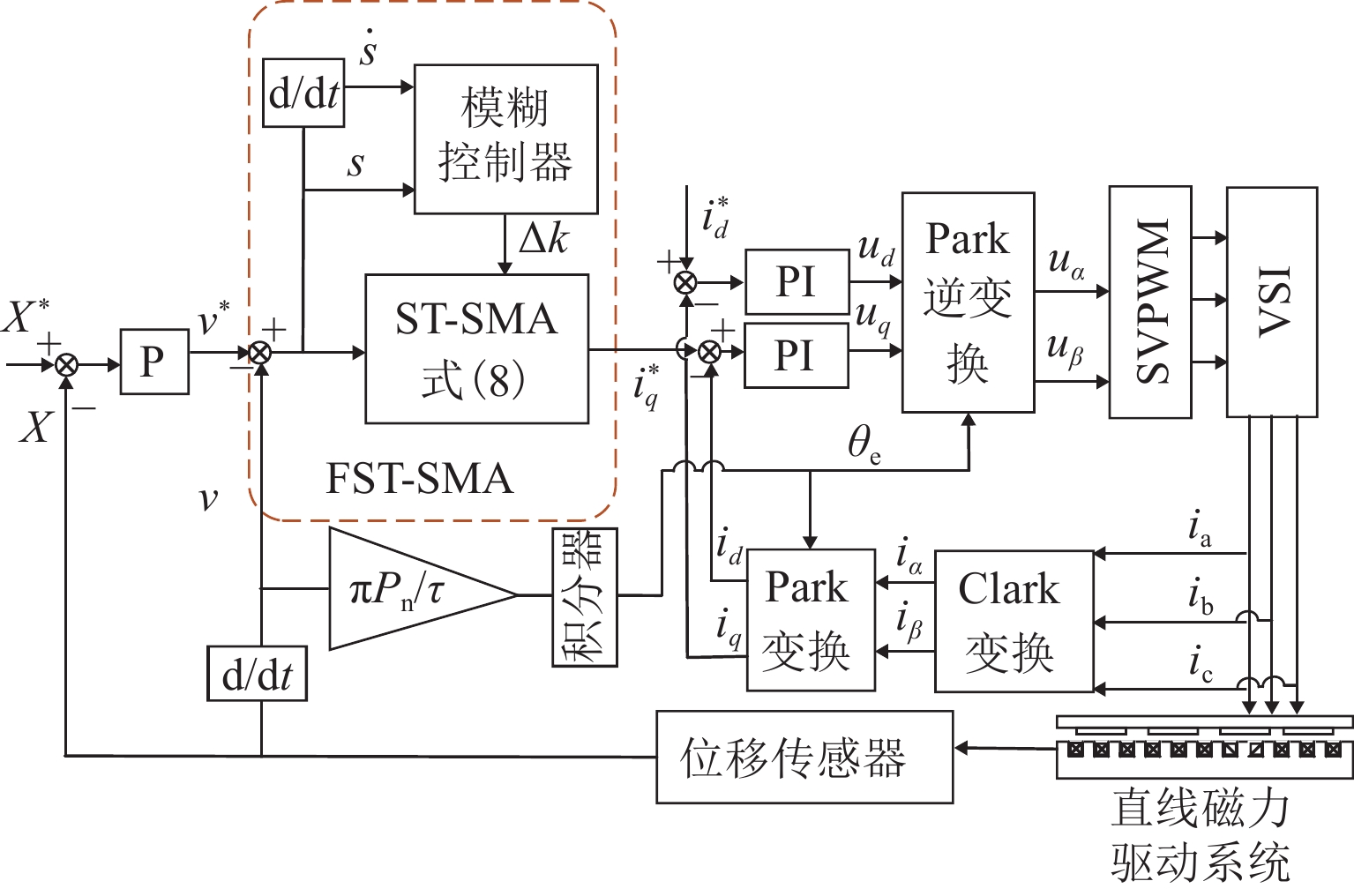
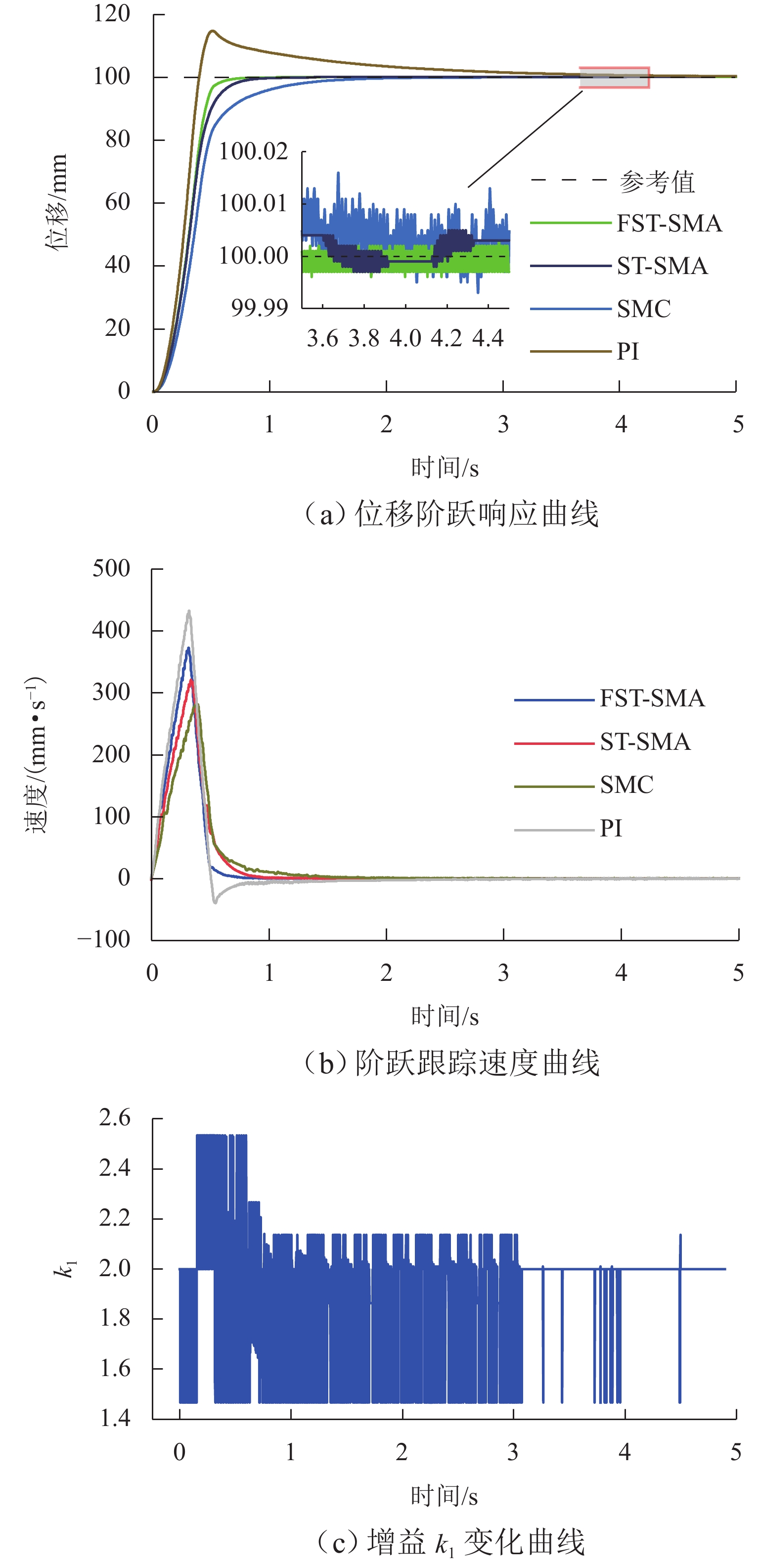
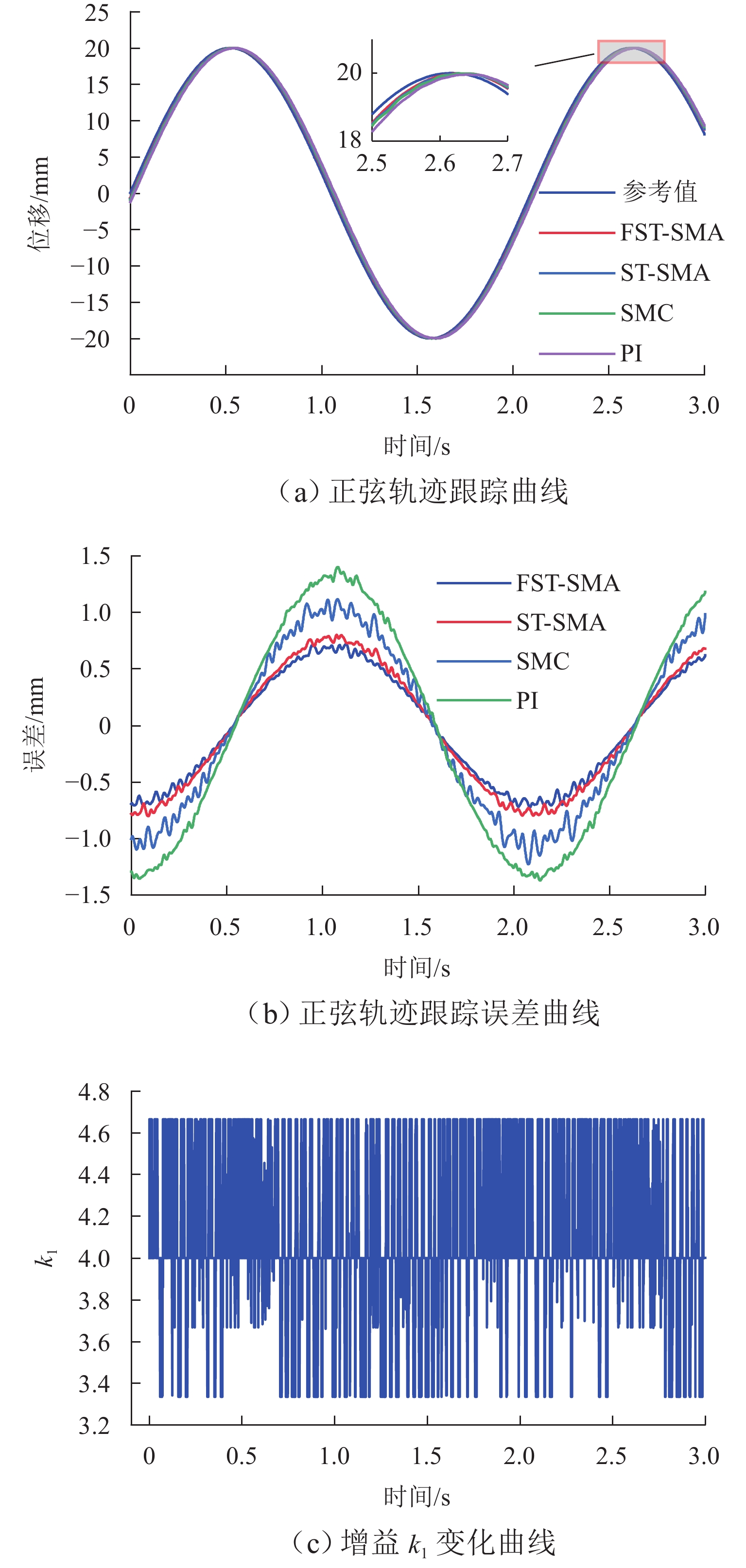
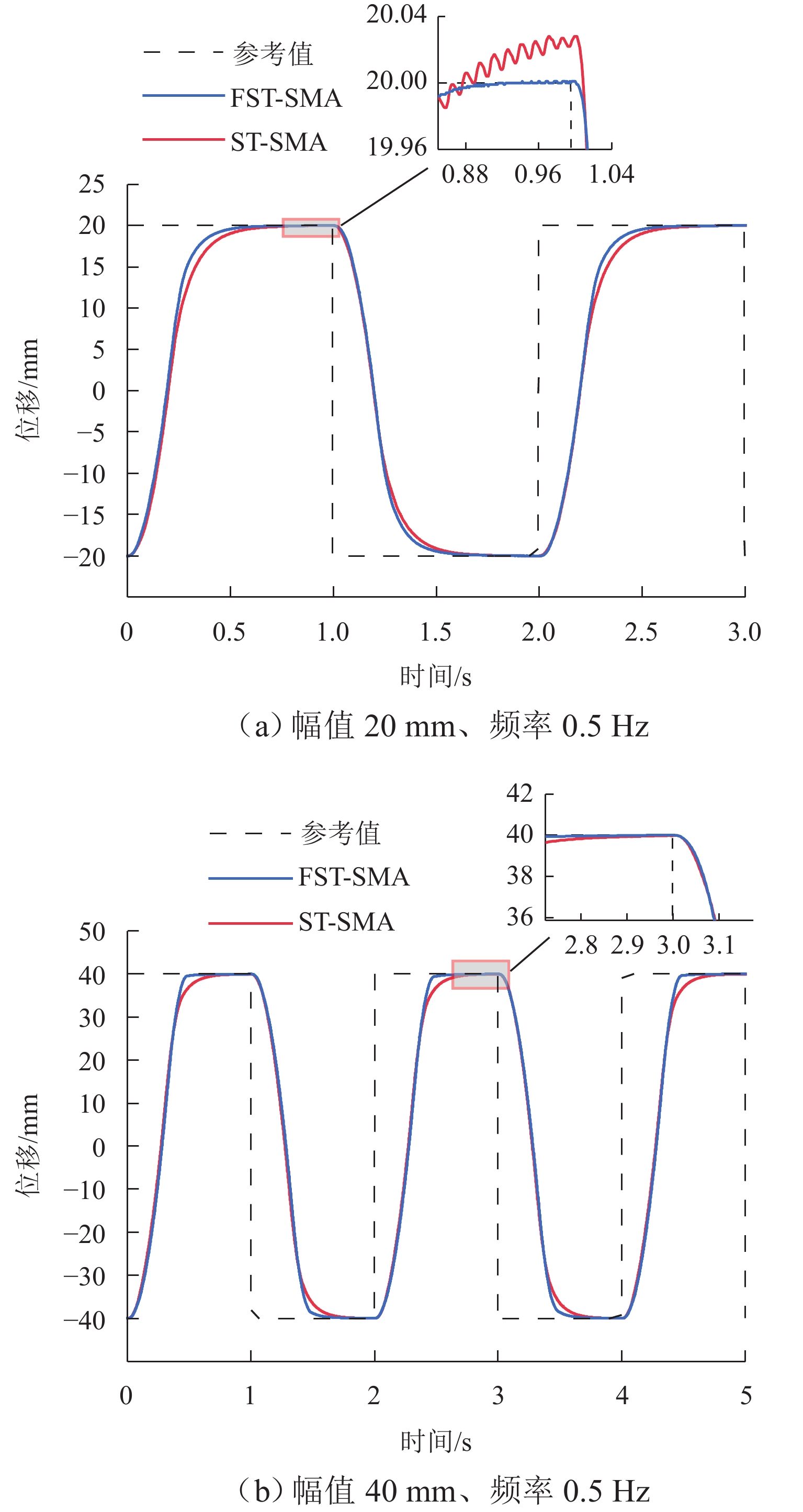
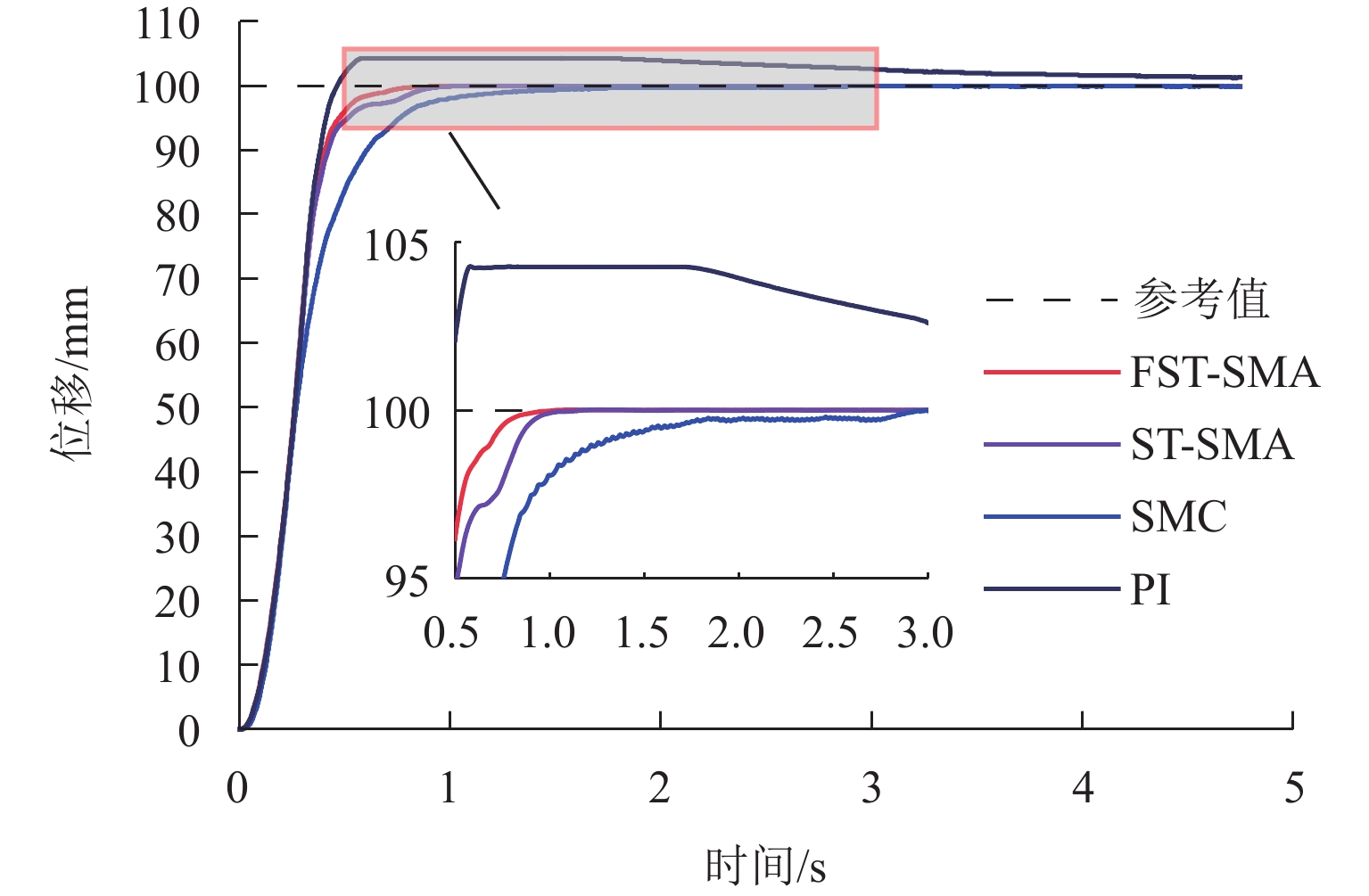
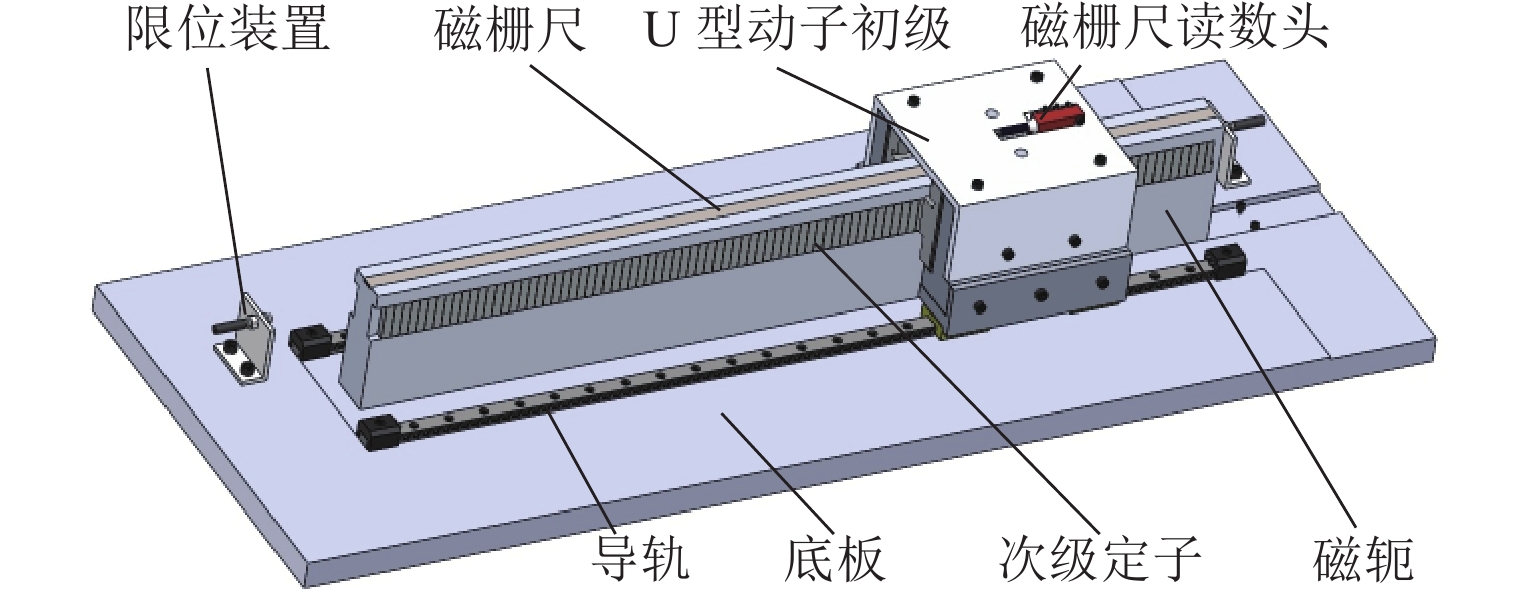
针对直线磁力驱动系统的位置跟踪精度易受外部扰动等不确定因素影响以及滑模控制中的抖振问题，提出一种基于模糊变增益的超螺旋滑模控制策略. 首先，介绍直线磁力驱动系统的工作原理，建立含扰动的直线磁力驱动系统数学模型；其次，使用超螺旋滑模算法设计速度控制器，实现系统精确、快速的收敛，并通过Lyapunov函数证明系统稳定性，进一步地，使用模糊算法对超螺旋滑模增益进行自适应调节；最后，对所提复合控制方法进行实验验证. 结果表明：基于模糊变增益的超螺旋滑模控制位置跟踪精度高，响应速度快；相对于超螺旋滑模控制，阶跃位置跟踪响应时间缩短28%，稳态误差从3 μm减小到1 μm，并且没有抖振现象；正弦位置跟踪相位差减小13%，位置跟踪精度提升14%；方波位置跟踪有更好的动态性能；施加扰动后，系统到达稳态时间减小13%，受到负载之后的延迟时间减小80%，抗扰性能大幅提升.
Abstract:To enhance the position tracking accuracy of the linear magnetic drive system susceptible to uncertainties such as external perturbations and address the jitter in sliding mode control, a super-twisting sliding mode control strategy was proposed based on the fuzzy variable gain. First, the working principle of the linear magnetic drive system was introduced, and its mathematical model was established with perturbations considered. Next, a speed controller based on the super-twisting sliding mode algorithm was designed to ensure fast and accurate system convergence. The stability of the system was verified by using the Lyapunov function, and the gain of the algorithm was adaptively adjusted via a fuzzy algorithm. Finally, the proposed composite control method was validated through experiments. Results demonstrate that super-twisting sliding mode control based on the fuzzy variable gain achieves high position tracking accuracy and fast response. Compared to that of the original super-twisting sliding mode control, the step position tracking response time is reduced by 28%, and the steady state error decreases from 3 µm to 1 µm. There is no jitter. The phase difference in sinusoidal position tracking is reduced by 13%, and the tracking accuracy increases by 14%. Additionally, square wave position tracking exhibits enhanced dynamic performance. The time of the system to reach a steady state declines by 13% after perturbations are applied, and the delay time is reduced by 80% after the load is applied, significantly enhancing perturbation resistance.
-
图 4 不同k1值下位移、速度变化曲线
Figure 4. Displacement and velocity variation curves for different values of k1
图 7 直线磁力驱动系统控制系统结构
Figure 7. Structure of control system of linear magnetic drive system
图 12 负载扰动下阶跃轨迹跟踪控制系统位移曲线
Figure 12. Displacement curves of step trajectory tracking control system under load perturbation
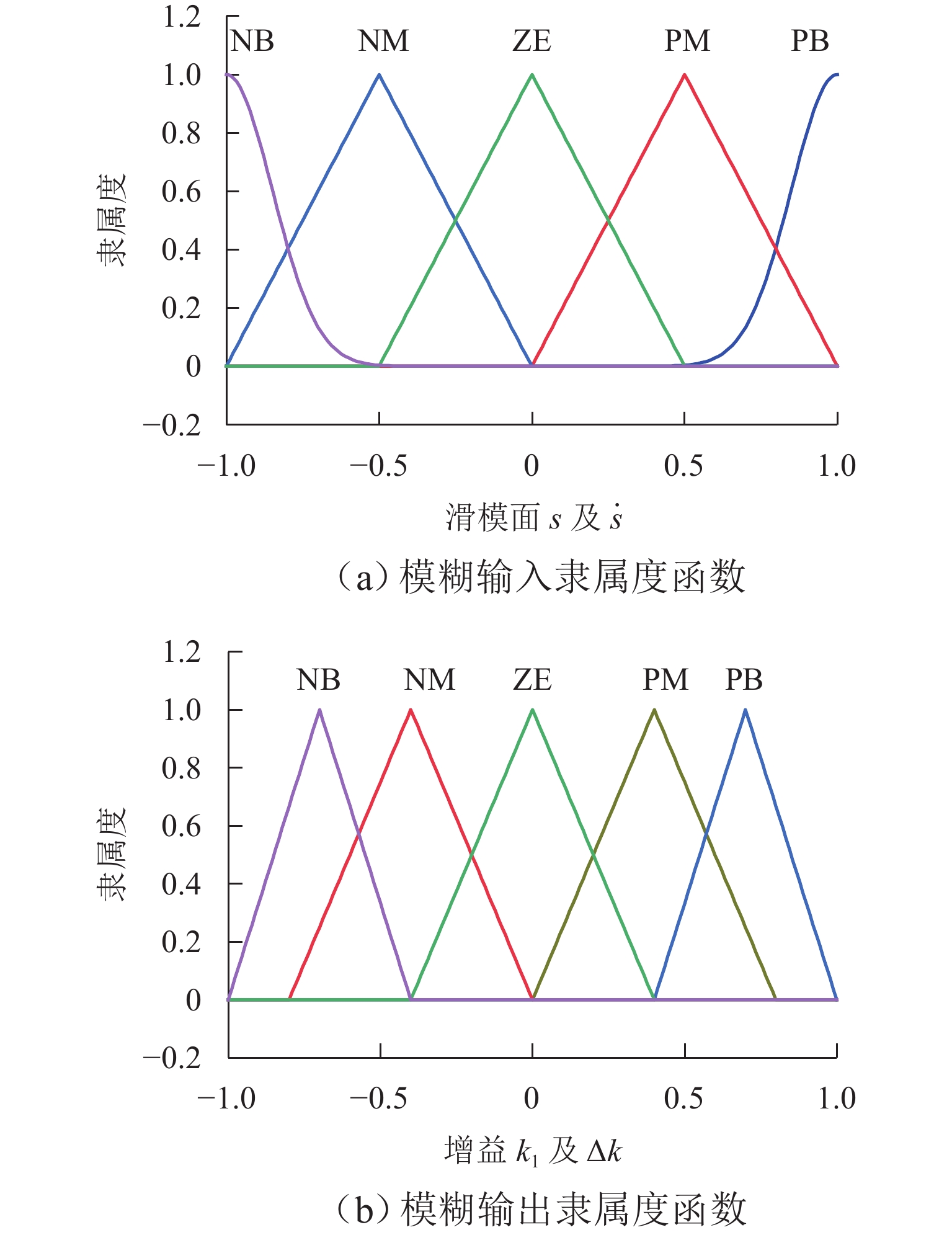
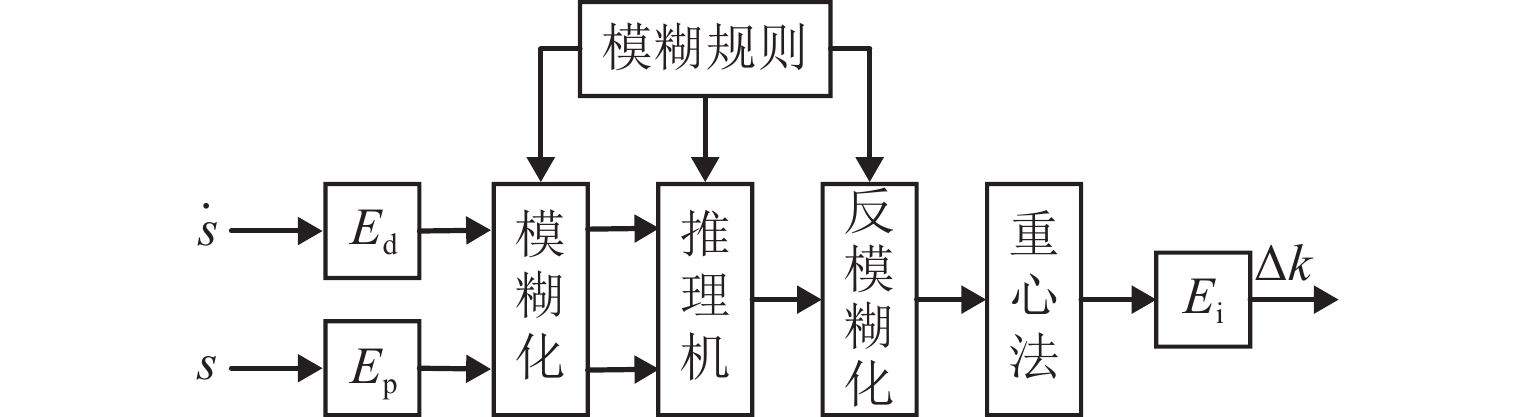
表 1 模糊规则
Table 1. Fuzzy rules
s $\dot s$ NB NM ZE PM PB NB PB PM ZE NM NB NM PM PM ZE NM NM ZE ZE ZE ZE ZE ZE PM NM NM ZE PM PM PB NB NM ZE PM PB 
下载: 导出CSV
表 2 直线磁力驱动系统参数表
Table 2. Parameters of linear magnetic drive system
参数 M/kg Pn τ/mm ψf/Wb R/Ω Lq/mH Ld/mH 取值 2.99 5 12 5.5 3.8 0.85 0.85
下载: 导出CSV
表 3 控制器参数表
Table 3. Controller parameters
控制方法 参数 FST-SMA 位置环 Kp=11；速度环 k1=2, k2=10,
Ep=1.2，Ed=0.8，Ei=0.5ST-SMA 位置环 Kp=11；速度环 k1=2, k2=10 PI 位置环 Kp=11；速度环 kp=5, ki=2
下载: 导出CSV
表 4 正弦轨迹跟踪控制器参数表
Table 4. Parameters of sinusoidal trajectory tracking controller
控制方法 参数 FST-SMA 位置环 Kp=80；速度环 k1=4, k2=20,
Ep=1.2，Ed=0.8，Ei=0.5ST-SMA 位置环 Kp=80；速度环 k1=4, k2=20 PI 位置环 Kp=80；速度环 kp=10, ki=6
下载: 导出CSV
-
[1] 卢琴芬,沈燚明,叶云岳. 永磁直线电动机结构及研究发展综述[J]. 中国电机工程学报,2019,39(9): 2575-2588.LU Qinfen, SHEN Yiming, YE Yunyue. Development of permanent magnet linear synchronous motors structure and research[J]. Proceedings of the CSEE, 2019, 39(9): 2575-2588. [2] CUI F R, SUN Z L, XU W, et al. Comparative analysis of bilateral permanent magnet linear synchronous motors with different structures[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 142-150. doi: 10.30941/CESTEMS.2020.00019 [3] CHEN S Y, CHIANG H H, LIU T S, et al. Precision motion control of permanent magnet linear synchronous motors using adaptive fuzzy fractional-order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741-752. doi: 10.1109/TMECH.2019.2892401 [4] WANG M Y, KANG K, ZHANG C M, et al. Precise position control in air-bearing PMLSM system using an improved anticipatory fractional-order iterative learning control[J]. IEEE Transactions on Industrial Electronics, 2024, 71(6): 6073-6083. doi: 10.1109/TIE.2023.3290251 [5] 赵川,孙凤,裴文哲,等. 永磁悬浮平台的分散串级控制方法[J]. 西南交通大学学报,2022,57(3): 618-626. doi: 10.3969/j.issn.0258-2724.20210960ZHAO Chuan, SUN Feng, PEI Wenzhe, et al. Independent cascade control method for permanent magnetic levitation platform[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 618-626. doi: 10.3969/j.issn.0258-2724.20210960 [6] JIN J J, WANG X, ZHAO C, et al. Characteristics analysis of an electromagnetic actuator for magnetic levitation transportation[J]. Actuators, 2022, 11(12): 377.1-377.16. [7] 康劲松,丁浩,倪菲,等. 计及悬浮系统影响的高速磁浮直线同步电机建模方法[J]. 西南交通大学学报,2024,59(4): 729-736. doi: 10.3969/j.issn.0258-2724.20230431KANG Jingsong, DING Hao, NI Fei, et al. Modeling of high-speed maglev linear synchronous motors considering influence of suspension system[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 729-736. doi: 10.3969/j.issn.0258-2724.20230431 [8] 丰富,胡海林,钟德鸣,等. 基于改进互联型全阶观测器的直线感应电机在线参数辨识[J]. 西南交通大学学报,2024,59(4): 776-785. doi: 10.3969/j.issn.0258-2724.20230507FENG Fu, HU Hailin, ZHONG Deming, et al. Online parameter identification of linear induction motors based on improved interconnected full-order observer[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 776-785. doi: 10.3969/j.issn.0258-2724.20230507 [9] ZHAO X M, FU D X. Adaptive neural network nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. IEEE Access, 2019, 7: 180361-180372. doi: 10.1109/ACCESS.2019.2958569 [10] MAN F, WANG R K, CHEN Q Y, et al. Research on speed sensorless control of permanent magnet linear synchronous motor based on PID neural network[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS). Harbin: IEEE, 2019: 1-4. [11] 刘志坚,蓝益鹏,徐泽来. 磁悬浮平台直线同步电动机悬浮系统的分数阶反步控制[J]. 电机与控制应用,2023,50(11): 52-58. doi: 10.12177/emca.2023.127LIU Zhijian, LAN Yipeng, XU Zelai. Fractional order backstepping control of linear synchronous motor suspension system of magnetic levitation platform[J]. Electric Machines & Control Application, 2023, 50(11): 52-58. doi: 10.12177/emca.2023.127 [12] 钟永彬,高健,冯富原,等. 基于闭环辨识模型的永磁同步直线电机分数阶反馈控制方法[J]. 中国机械工程,2023,34(23): 2773-2780,2793. doi: 10.3969/j.issn.1004-132X.2023.23.001ZHONG Yongbin, GAO Jian, FENG Fuyuan, et al. Fractional-order feedback control method for PMLSMs based on closed-loop identification model[J]. China Mechanical Engineering, 2023, 34(23): 2773-2780,2793. doi: 10.3969/j.issn.1004-132X.2023.23.001 [13] MANI P, RAJAN R, SHANMUGAM L, et al. Adaptive fractional fuzzy integral sliding mode control for PMSM model[J]. IEEE Transactions on Fuzzy Systems, 2019, 27(8): 1674-1686. doi: 10.1109/TFUZZ.2018.2886169 [14] LI B X, ZHAO X. Neural network-based adaptive sliding mode control for T-S fuzzy fractional order systems[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2023, 70(12): 4549-4553. [15] CHEN S Y, LEE C Y. Compensatory fuzzy neural network control with dynamic parameters estimation for linear voice coil actuator[J]. Precision Engineering, 2017, 48: 191-202. doi: 10.1016/j.precisioneng.2016.12.002 [16] 黄家才,张玎橙,施昕昕. 基于复合积分滑模的永磁同步电机硬件在环位置控制[J]. 电机与控制学报,2014,18(12): 108-114.HUANG Jiacai, ZHANG Dingcheng, SHI Xinxin. PMSM position control with hardware-in-loop based on composite integral sliding mode[J]. Electric Machines and Control, 2014, 18(12): 108-114. [17] 付东学,赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报,2020,35(4): 717-723.FU Dongxue, ZHAO Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723. [18] 武志涛,李帅,程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报,2022,37(10): 2503-2512.WU Zhitao, LI Shuai, CHENG Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512. [19] BAIK I C, KIM K H, YOUN M J. Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J]. IEEE Transactions on Control Systems Technology, 2000, 8(1): 47-54. doi: 10.1109/87.817691 [20] LEVANT A. Homogeneity approach to high-order sliding mode design[J]. Automatica, 2005, 41(5): 823-830. doi: 10.1016/j.automatica.2004.11.029 [21] BARTOLINI G, FERRARA A, USAI E. Chattering avoidance by second-order sliding mode control[J]. IEEE Transactions on Automatic Control, 1998, 43(2): 241-246. doi: 10.1109/9.661074 [22] 张庆超,马瑞卿,皇甫宜耿,等. 电机转速环节SuperTwisting算法二阶滑模控制律设计与研究[J]. 西北工业大学学报,2016,34(4): 669-676ZHANG Qingchao, MA Ruiqing, HUANGFU Yigeng, et al. Second-order sliding mode control based on super-twisting algorithm for the speed outer loop of motors[J]. Journal of Northwestern Polytechnical University, 2016, 34(4): 669-676. [23] 谢浩然,胡纯福,卢萌,等. 基于级联线性-非线性自抗扰控制器的永磁直线同步电机速度控制策略研究[J]. 中国电机工程学报,2024,44(15): 6158-6169.XIE Haoran, HU Chunfu, LU Meng, et al. Research on speed control strategy for permanent magnet linear synchronous motor based on cascaded linear-nonlinear active disturbance rejection controller[J]. Proceedings of the CSEE, 2024, 44(15): 6158-6169. [24] PATEL V, DI GENNARO S, BUCCELLA C, et al. Super twisting sliding mode controller for PMSM fed with multilevel inverter for E-transportation[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia). Nanjing: IEEE, 2020: 238-244. [25] LASCU C, BOLDEA I, BLAABJERG F. Super-twisting sliding mode control of torque and flux in permanent magnet synchronous machine drives[C]//IECON 2013 - 39th Annual Conference of the IEEE Industrial Electronics Society. Vienna: IEEE, 2013: 3171-3176. [26] 李鹏,郑志强. 基于类二次型Lyapunov函数的Super-twisting算法收敛性分析[J]. 控制与决策,2011,26(6): 949-952.LI Peng, ZHENG Zhiqiang. Convergence of super-twisting algorithm based on quadratic-like Lyapunov function[J]. Control and Decisign, 2011, 26(6): 949-952. [27] MORENO J A, OSORIO M. Strict Lyapunov functions for the super-twisting algorithm[J]. IEEE Transactions on Automatic Control, 2012, 57(4): 1035-1040. doi: 10.1109/TAC.2012.2186179 -
下载:
点击查看大图
计量
- 文章访问数: 53
- HTML全文浏览量: 25
- PDF下载量: 8
- 被引次数: 0