基于Sobol’ 法的高速磁浮列车单点悬浮系统全局灵敏度分析

倪菲; 范琳; 徐俊起; 林国斌; 贾万涛

doi:10.3969/j.issn.0258-2724.20240545

基于Sobol’ 法的高速磁浮列车单点悬浮系统全局灵敏度分析

doi: 10.3969/j.issn.0258-2724.20240545

倪菲^{1, 2,},
范琳^{2, 3},
徐俊起^{1, 2},
林国斌^{1, 2},
贾万涛^4, ,

1.
同济大学磁浮交通工程技术研究中心，上海 201804
2.
同济大学高速磁浮运载技术全国重点实验室，上海 201804
3.
同济大学交通学院，上海 201804
4.
西北工业大学数学与统计学院，陕西西安 710129

基金项目: 国家自然科学基金项目（52232013）

详细信息

作者简介:
倪菲（1985—），女，副研究员，研究方向为磁浮列车不确定性量化与鲁棒控制，E-mail：fei.ni@tongji.edu.cn

通讯作者:
贾万涛（1987—），男，副教授，研究方向为非线性随机动力学，E-mail：jiawantao@nwpu.edu.cn

中图分类号: U24；U271
计量
- 文章访问数: 142
- HTML全文浏览量: 62
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2024-10-19
- 修回日期: 2025-01-27
- 网络出版日期: 2025-04-17
- 刊出日期: 2025-02-27

Global Sensitivity Analysis of Single-Point Levitation System for High-Speed Maglev Train Based on Sobol’ Method

NI Fei^{1, 2
,},
FAN Lin^{2, 3},
XU Junqi^{1, 2},
LIN Guobin^{1, 2},
JIA Wantao^{4
, ,}

1.
National Maglev Transportation Engineering R & D Center, Tongji University, Shanghai 201804, China
2.
State Key Laboratory of High-Speed Maglev Transportation Technology, Shanghai 201804, China
3.
College of Transportation, Tongji University, Shanghai 201804, China
4.
School of Mathematics and Statistics, Northwestern Polytechnical University, Xi’an 710129, China

摘要

摘要:
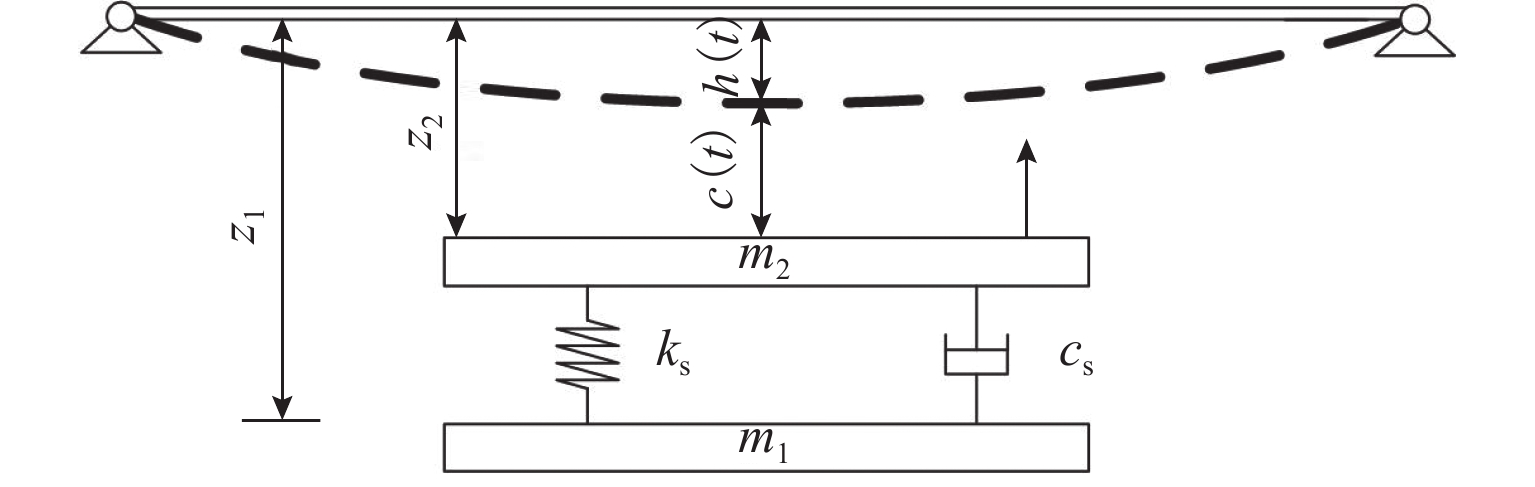
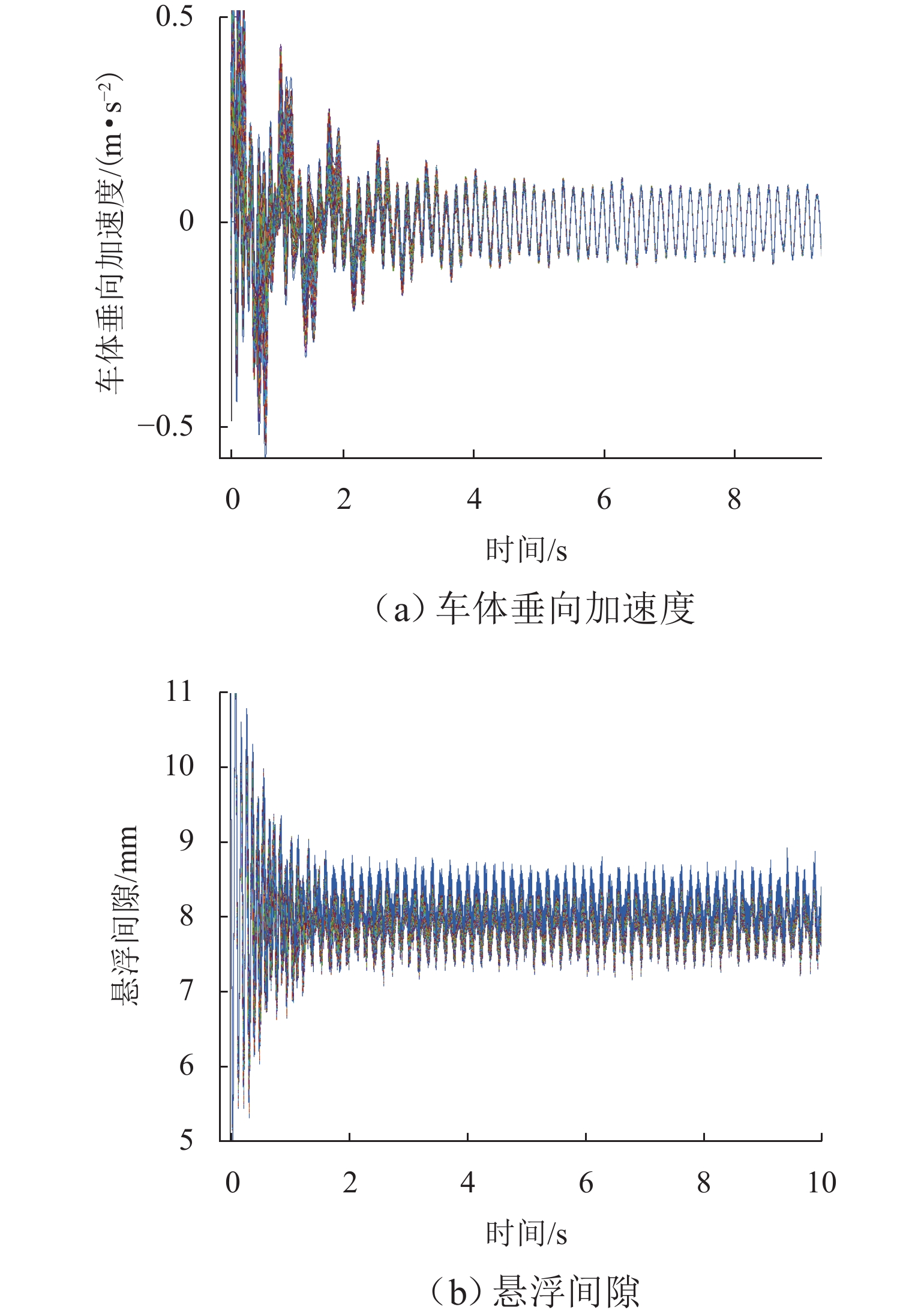
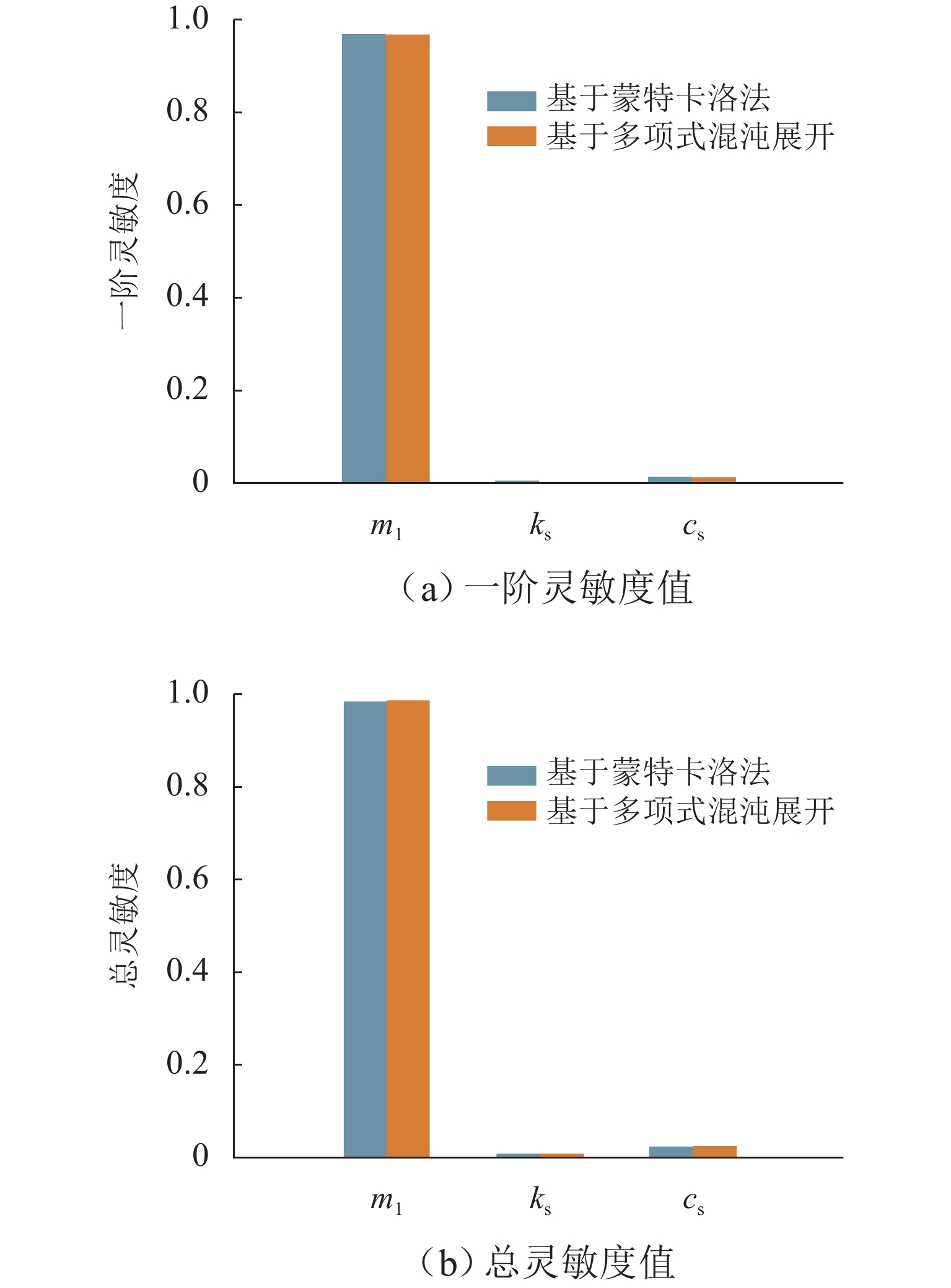
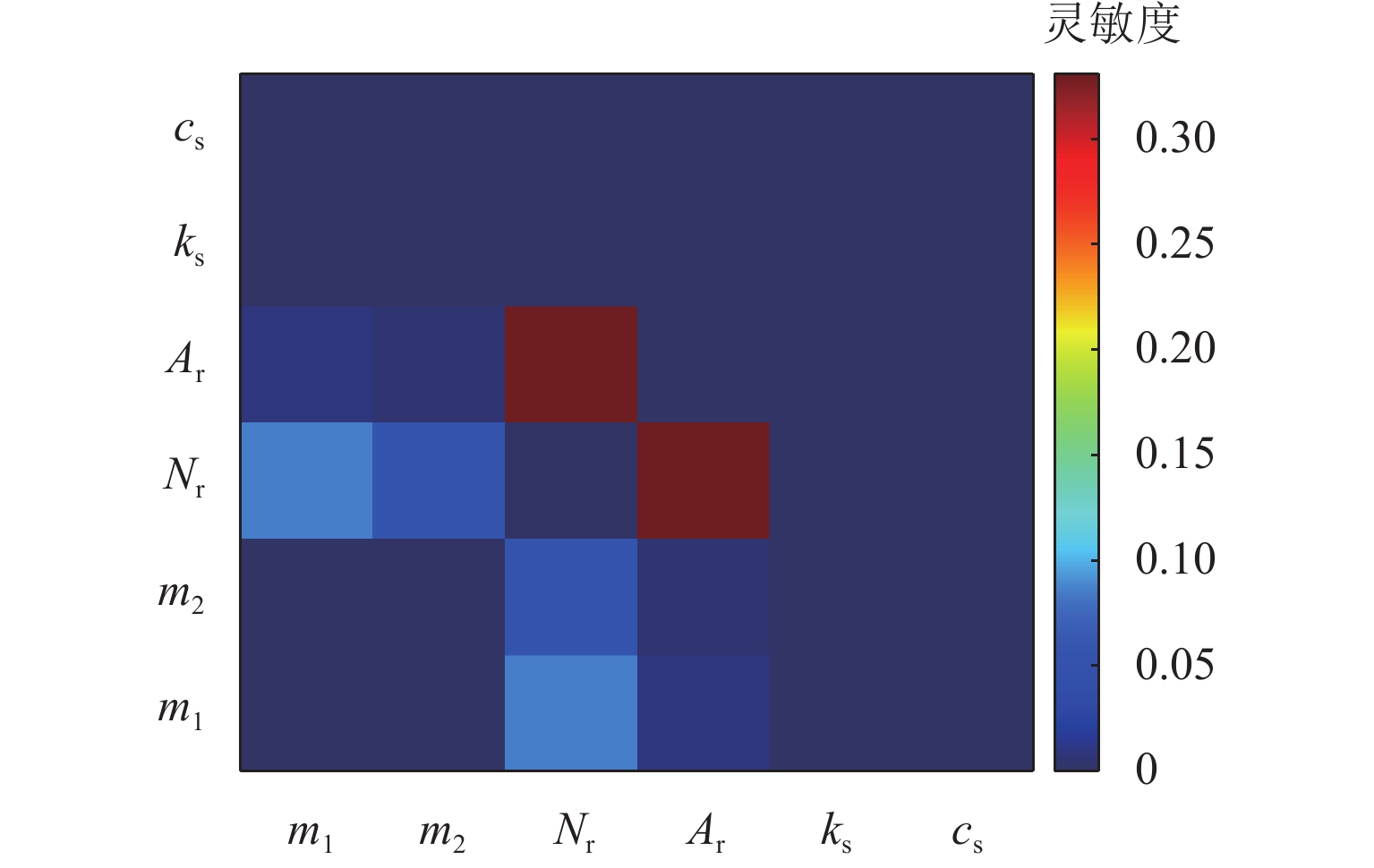
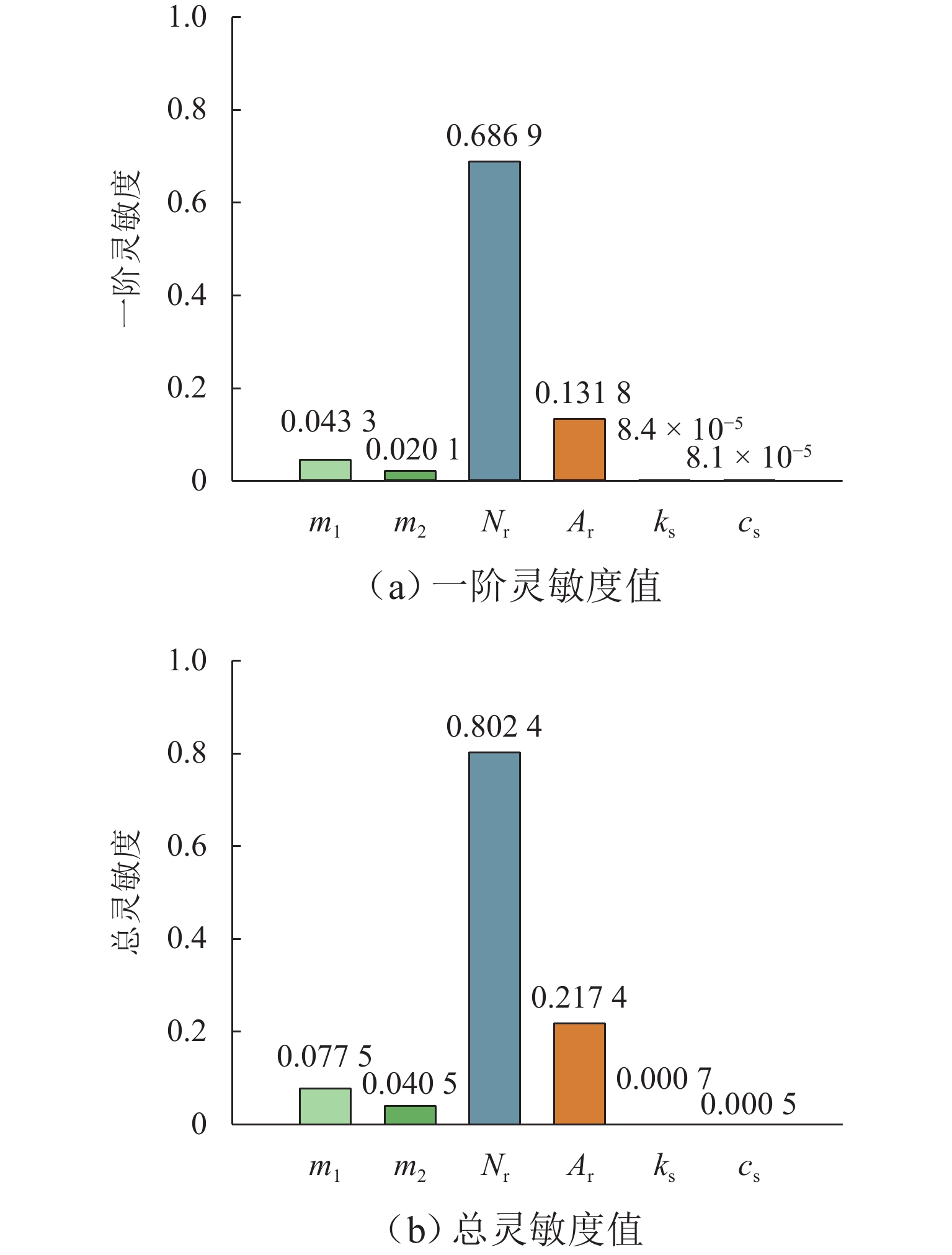
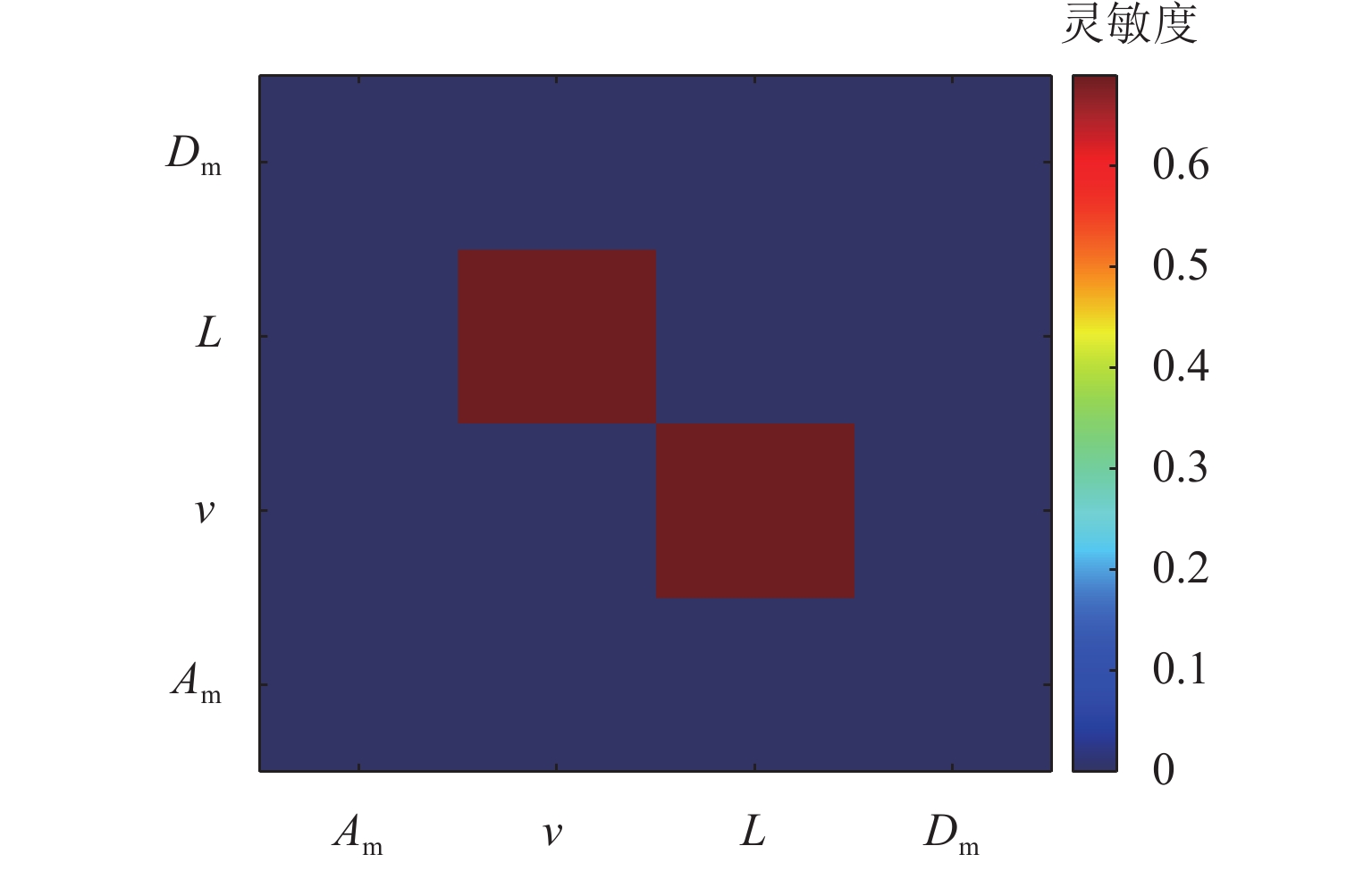
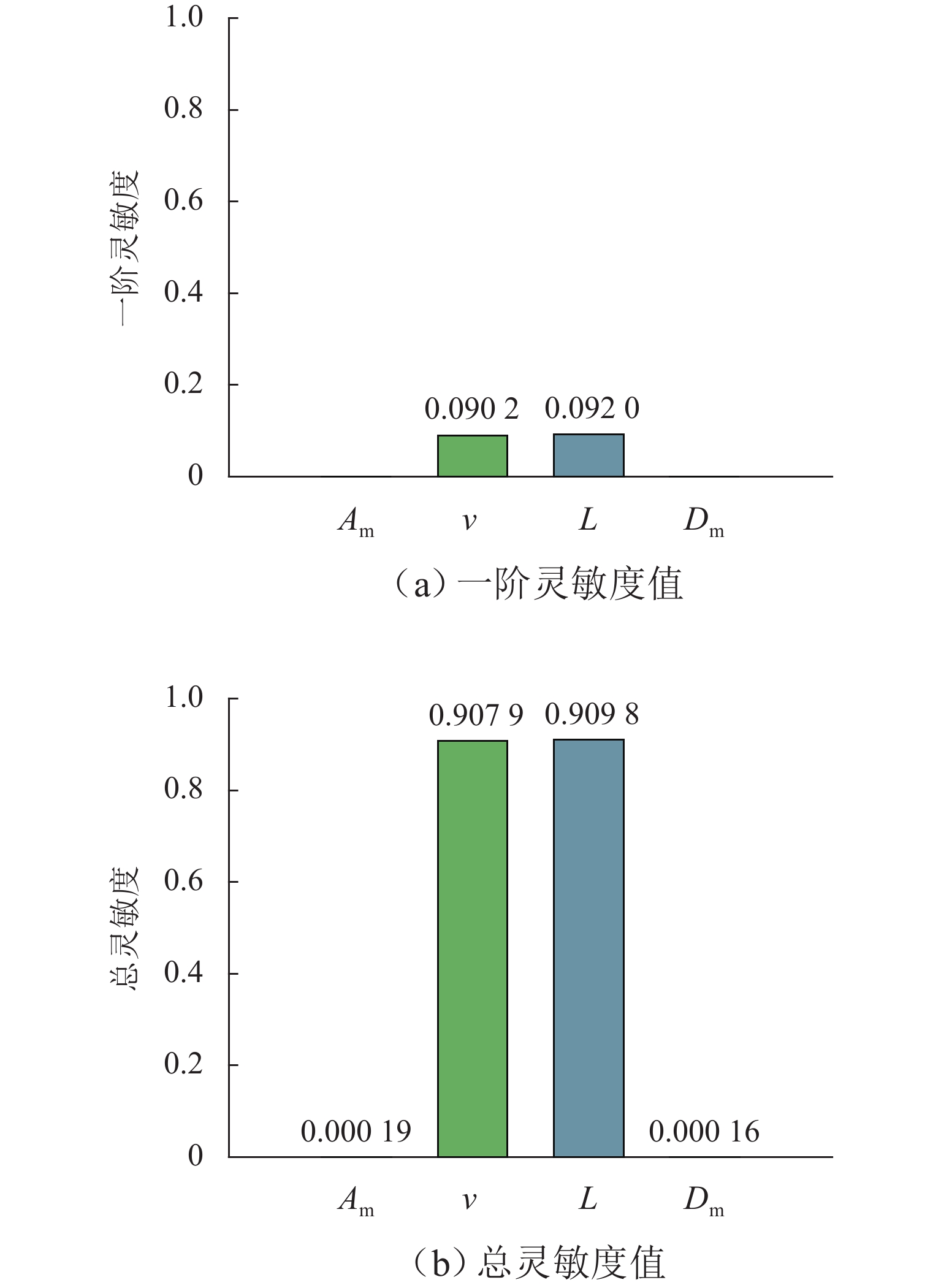
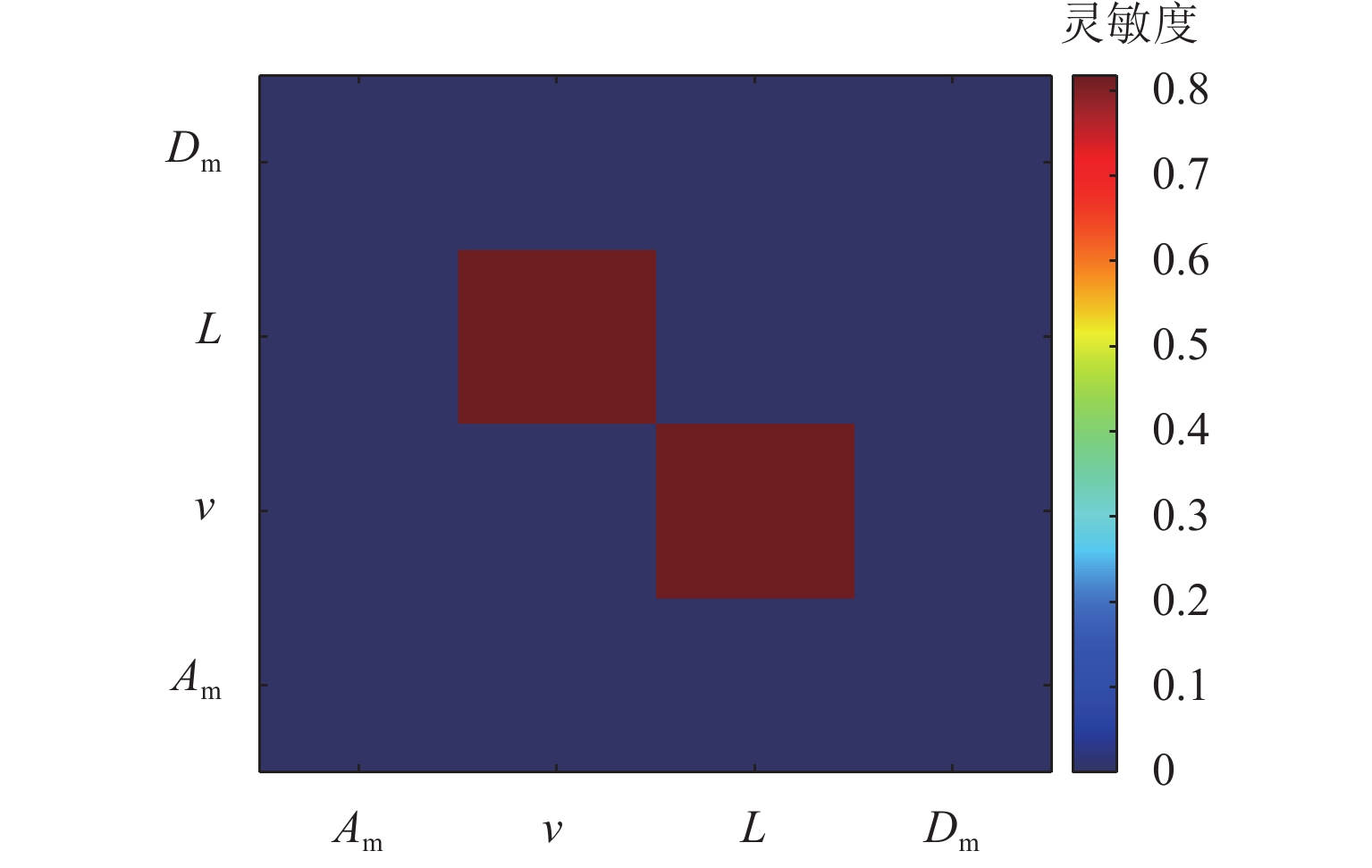
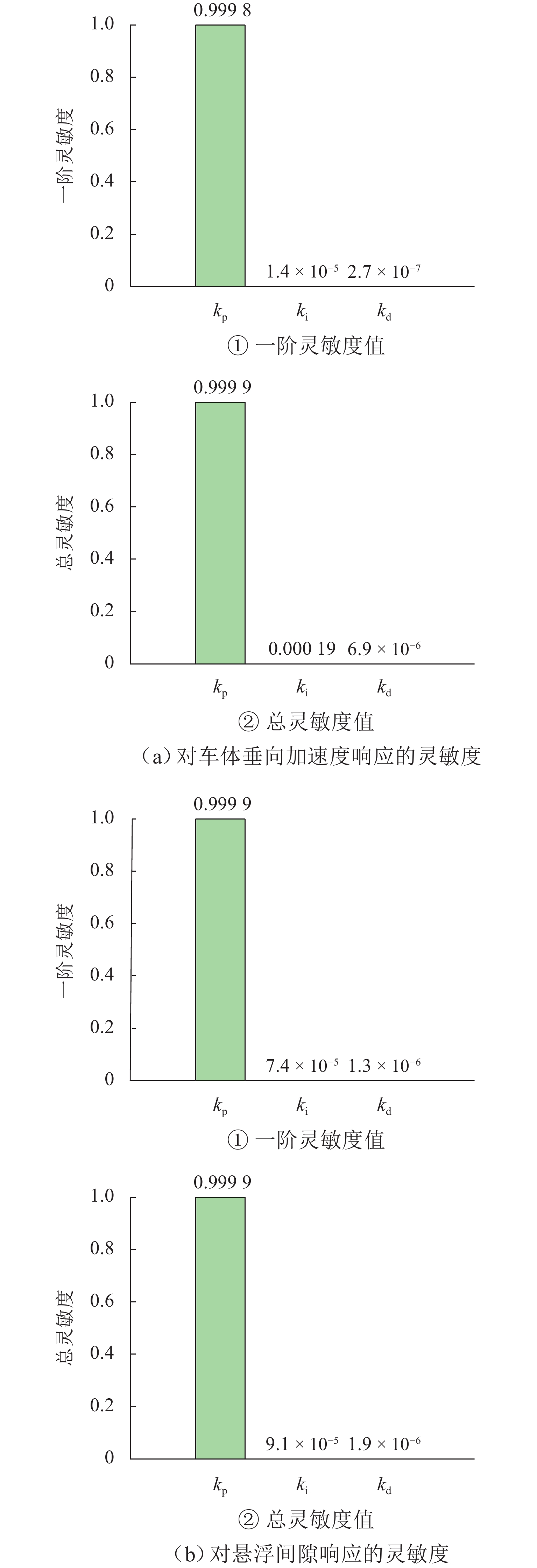
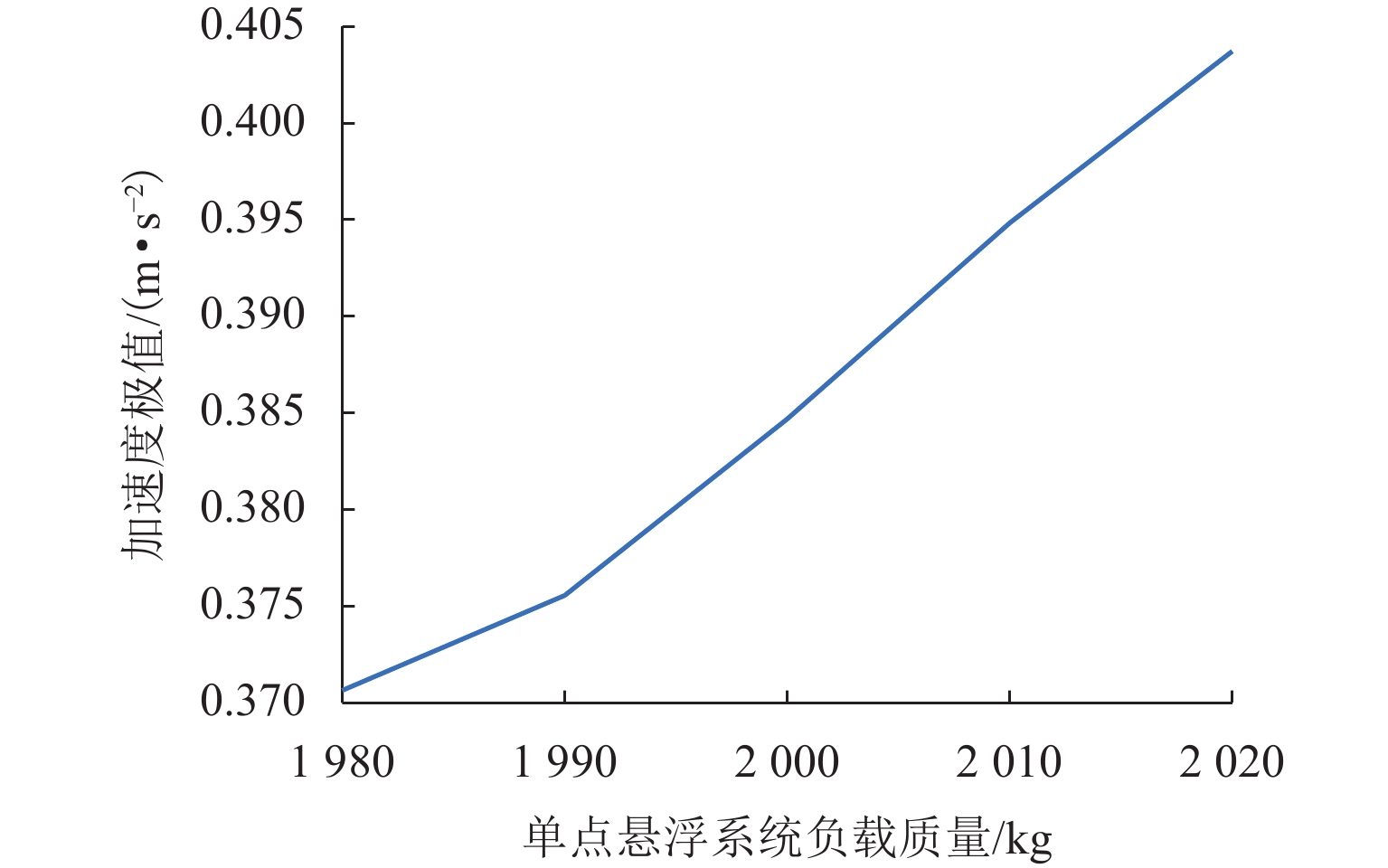
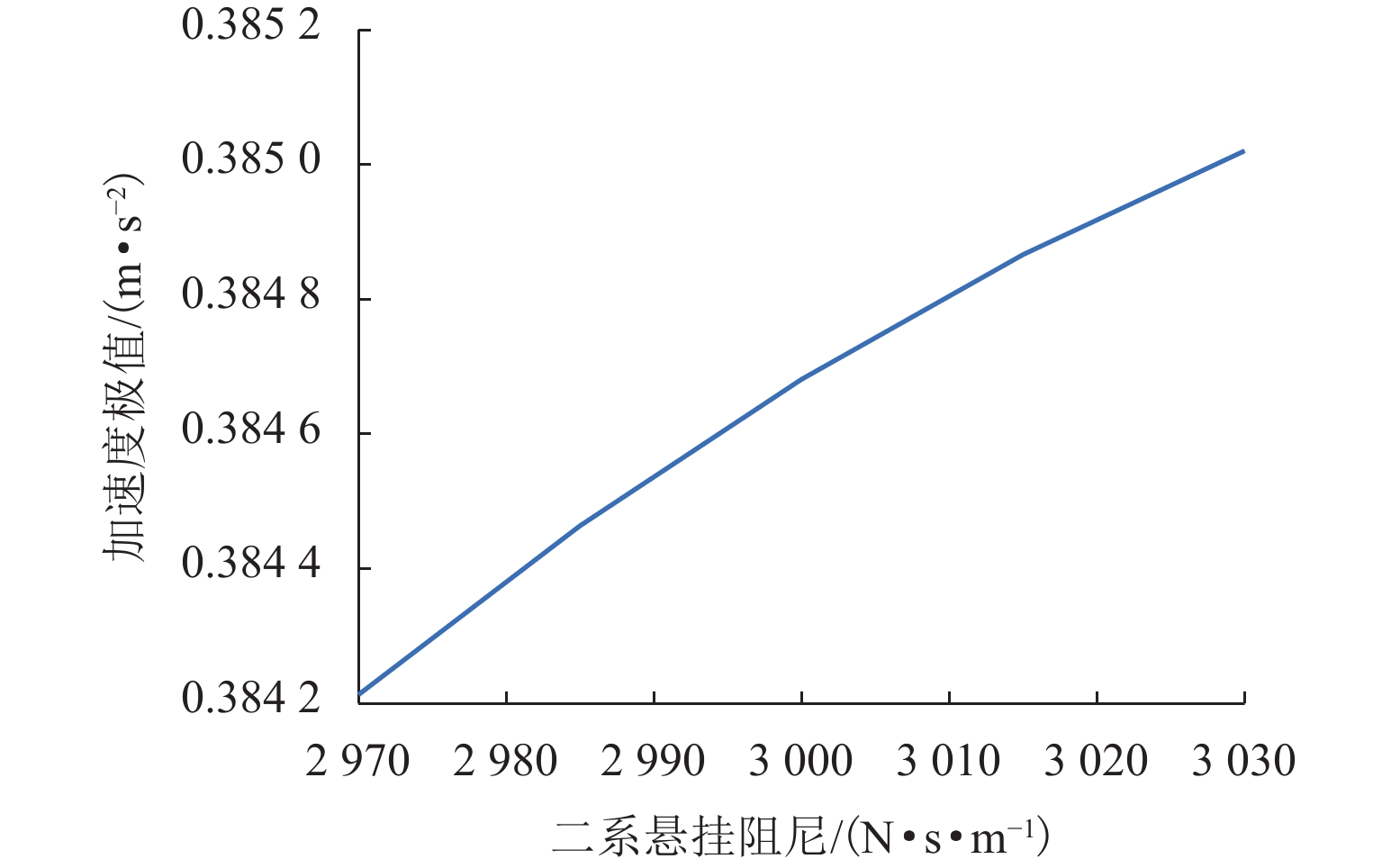
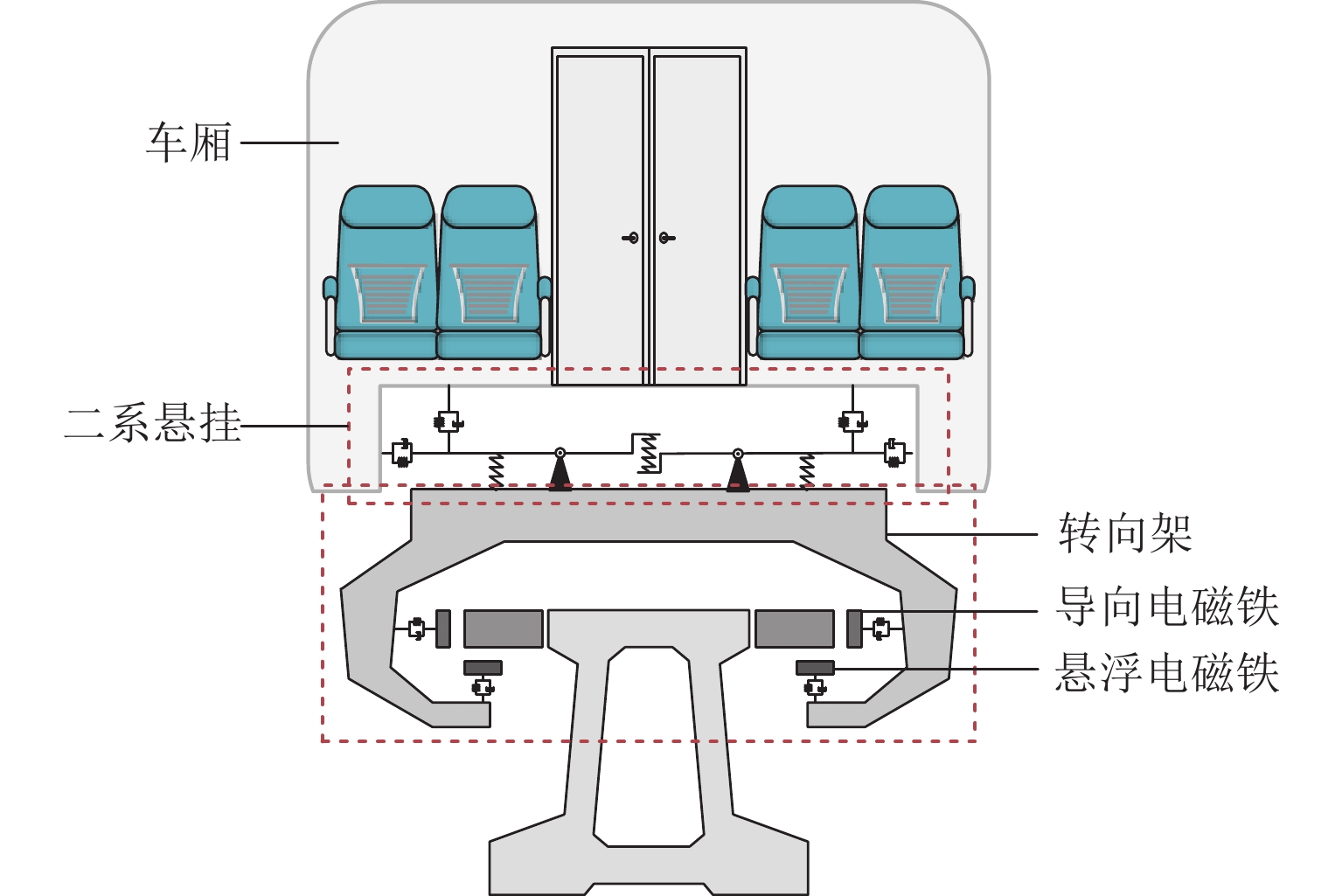
本文针对高速磁浮列车悬浮系统中不确定性参数对系统动态响应的影响展开研究，旨在为磁浮列车的优化设计提供理论依据. 首先，将高速磁浮列车悬浮系统简化为包含二系悬挂的单点悬浮系统，并构建相应的多项式混沌展开（PCE）模型；在此基础上，采用Sobol’ 法进行全局灵敏度分析，相较于在原始模型上进行蒙特卡洛仿真求解Sobol’ 灵敏度的方法，基于PCE模型的求解方法将计算效率提升了73倍，且计算误差控制在0.004以内；进一步地，深入分析车辆结构参数、轨道不平顺参数以及悬浮控制参数对悬浮系统间隙响应和车体垂向加速度的影响规律，识别了关键影响参数及其交互效应. 研究结果表明：电磁铁线圈匝数和电磁铁铁芯有效面积对车体垂向加速度及悬浮系统间隙响应影响较大，总灵敏度指数均大于0.20，而电磁铁质量和二系悬挂参数对其影响相对较小，总灵敏度指数均小于0.10；列车运行速度与轨道不平顺波长对悬浮间隙和车体垂向加速度的影响显著，总灵敏度指数均大于0.80，且二者之间存在明显的交互作用；在悬浮控制参数中，间隙响应对比例系数的变化最为敏感，总灵敏度指数接近1.00.
- 高速磁浮列车 /
- 电磁悬浮系统 /
- 灵敏度分析 /
- Sobol’ 法 /
- 多项式混沌展开
Abstract:
The impact of uncertain parameters on the dynamic response of the high-speed maglev train levitation system was investigated, aiming to provide a theoretical foundation for the optimal design of maglev trains. Firstly, the high-speed maglev train levitation system was simplified to a single-point levitation system incorporating secondary suspension, and a corresponding polynomial chaos expansion (PCE) model was established. On this basis, the Sobol’ method was employed for global sensitivity analysis. Compared to the method of solving Sobol’ sensitivity through Monte Carlo simulation on the original model, the PCE-based approach enhances computational efficiency by 73 times while maintaining the calculation error within 0.004. Furthermore, the influence patterns of vehicle structural parameters, track irregularity parameters, and levitation control parameters on the levitation gap response and the vertical acceleration of the train body were analyzed, identifying key influencing parameters and their interaction effects. The results indicate that the coil turns of the electromagnet and the effective area of the electromagnet core significantly affect the vertical acceleration of the train body and the levitation gap response, with total sensitivity indexes exceeding 0.20, whereas the electromagnet mass and the secondary suspension parameters have a relatively minor impact, with total sensitivity indexes less than 0.10. The train operating speed and track irregularity wavelength significantly influence the levitation gap and the vertical acceleration of the train body, with total sensitivity indexes exceeding 0.80 and a notable interaction effect between the two. Among the levitation control parameters, the gap response is most sensitive to changes in the proportional coefficient, with the total sensitivity index approaching 1.00.
- high-speed maglev train /
- electromagnetic levitation system /
- sensitivity analysis /
- Sobol’ method /
- polynomial chaos expansion

HTML全文

图 1 高速磁浮列车结构

Figure 1. Structure of high-speed maglev train

下载: 全尺寸图片幻灯片

图 2 单点悬浮系统结构

Figure 2. Single-point levitation system

下载: 全尺寸图片幻灯片

图 3 车辆结构参数变化下的悬浮系统动态响应

Figure 3. Dynamic responses of levitation system under variations in vehicle structural parameters

下载: 全尺寸图片幻灯片

图 4 两种灵敏度求解方法对比

Figure 4. Comparison between two sensitivity analysis methods

下载: 全尺寸图片幻灯片

图 5 车辆结构参数对车体垂向加速度响应的灵敏度

Figure 5. Sensitivity of vehicle structural parameters to vertical acceleration response of train body

下载: 全尺寸图片幻灯片

图 6 车辆结构参数对车体垂向加速度响应的二阶灵敏度

Figure 6. Second-order sensitivity of vehicle structural parameters to vertical acceleration response of train body

下载: 全尺寸图片幻灯片

图 7 车辆结构参数对悬浮间隙响应的灵敏度

Figure 7. Sensitivity of vehicle structural parameters to levitation gap response

下载: 全尺寸图片幻灯片

图 8 车辆结构参数对悬浮间隙响应的二阶灵敏度

Figure 8. Second-order sensitivity of vehicle structural parameters to levitation gap response

下载: 全尺寸图片幻灯片

图 9 轨道不平顺参数对车体垂向加速度响应的灵敏度

Figure 9. Sensitivity of track irregularity parameters to vertical acceleration response of train body

下载: 全尺寸图片幻灯片

图 10 轨道不平顺参数对车体垂向加速度响应二阶灵敏度

Figure 10. Second-order sensitivity of track irregularity parameters to vertical acceleration response of train body

下载: 全尺寸图片幻灯片

图 11 轨道不平顺参数对悬浮间隙响应的灵敏度

Figure 11. Sensitivity of track irregularity parameters to levitation gap response

下载: 全尺寸图片幻灯片

图 12 轨道不平顺参数对悬浮间隙响应的二阶灵敏度

Figure 12. Second-order sensitivity of track irregularity parameters to levitation gap response

下载: 全尺寸图片幻灯片

图 13 悬浮控制参数对车体垂向加速度、悬浮间隙响应的灵敏度

Figure 13. Sensitivity of levitation control parameters to vertical acceleration of train body and levitation gap response

下载: 全尺寸图片幻灯片

图 14 车体垂向加速度极值与单点悬浮系统负载质量关系

Figure 14. Relationship between extreme values of vertical acceleration of train body and load mass of single-point levitation system

下载: 全尺寸图片幻灯片

图 15 车体垂向加速度极值与二系悬挂阻尼关系

Figure 15. Relationship between extreme values of vertical acceleration of train body and secondary suspension damping

下载: 全尺寸图片幻灯片

表 1 单点悬浮系统模型参数

Table 1. Parameters of single-point levitation system model

参数数值

A_r/m² 0.115

m₁/kg 2000

m₂/kg 750

k_s/（N·m⁻¹） 150000

c_s/（N·s·m⁻¹） 3000

N_r/匝 270

下载: 导出CSV

表 2 轨道不平顺参数

Table 2. Parameters of track irregularities

参数数值

A_m/m 0.001

v/（km·h⁻¹） 600

L/m 25

D_m/W ${10}^{-11}$

下载: 导出CSV

参考文献(27)

[1]	翟明达,李晓龙,龙志强,等. 基于Youla参数化的高速磁浮列车悬浮系统控制与优化设计[J]. 同济大学学报(自然科学版),2023,51(3): 341-350. ZHAI Mingda, LI Xiaolong, LONG Zhiqiang, et al. Control and optimization design of magnetic levitation system of highspeed maglev train based on Youla parameterization[J]. Journal of Tongji University (Natural Science), 2023, 51(3): 341-350.
[2]	邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001 DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001
[3]	余志武,张鹏,丁叁叁. 轨道梁参数随机的磁悬浮列车-轨道梁系统概率密度演化分析[J]. 铁道学报,2023,45(12): 138-147. doi: 10.3969/j.issn.1001-8360.2023.12.015 YU Zhiwu, ZHANG Peng, DING Sansan. Probability density evolution analysis of maglev train-guideway system with random guideway parameters[J]. Journal of the China Railway Society, 2023, 45(12): 138-147. doi: 10.3969/j.issn.1001-8360.2023.12.015
[4]	卜秀孟,王力东,黎清蓉,等. 高速磁浮车-桥耦合振动控制参数影响分析[J]. 西南交通大学学报,2024,59(4): 848-857,866. doi: 10.3969/j.issn.0258-2724.20230534 BU Xiumeng, WANG Lidong, LI Qingrong, et al. Influence analysis of vibration control parameters for high-speed maglev train-bridge coupling[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 848-857,866. doi: 10.3969/j.issn.0258-2724.20230534
[5]	CHEN J B, YANG J S, JENSEN H. Structural optimization considering dynamic reliability constraints via probability density evolution method and change of probability measure[J]. Structural and Multidisciplinary Optimization, 2020, 62(5): 2499-2516. doi: 10.1007/s00158-020-02621-4
[6]	刘伟,赵春发,娄会彬,等. 基于虚拟激励法的磁浮车桥耦合系统随机振动分析[J]. 西南交通大学学报,2024,59(4): 823-831. doi: 10.3969/j.issn.0258-2724.20240035 LIU Wei, ZHAO Chunfa, LOU Huibin, et al. Stochastic vibration analysis of maglev train-bridge coupling system based on pseudo excitation method[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 823-831. doi: 10.3969/j.issn.0258-2724.20240035
[7]	TARANTOLA S, FERRETTI F, LO PIANO S, et al. An annotated timeline of sensitivity analysis[J]. Environmental Modelling & Software, 2024, 174: 105977.1-105977.8.
[8]	BAZYLEVA V, GARIBAY V M, ROY D. Trajectory-based global sensitivity analysis in multiscale models[J]. Scientific Reports, 2024, 14(1): 13902.1-13902.8.
[9]	XU Z X, WANG X Z, GUO L, et al. Stability evaluation of slope based on global sensitivity analysis[J]. Complexity, 2024, 2024(1): 2333859.1-2333859.17.
[10]	孟春成,亐道远,段晓晨. 城市轨道交通土建工程造价非线性预测与反演[J]. 西南交通大学学报,2025,60(1): 137-146. MENG Chuncheng, QU Daoyuan, DUAN Xiaochen. Nonlinear prediction and inversion of civil engineering cost of urban rail transit[J]. Journal of Southwest Jiaotong University, 2025, 60(1): 137-146.
[11]	陈秉智,汪驹畅. 基于Sobol’ 法的轨道车辆前端吸能结构灵敏度分析[J]. 铁道学报,2020,42(3): 63-68. doi: 10.3969/j.issn.1001-8360.2020.03.008 CHEN Bingzhi, WANG Juchang. Global sensitivity analysis of energy-absorbing structure for rail vehicle based on sobol’ method[J]. Journal of the China Railway Society, 2020, 42(3): 63-68. doi: 10.3969/j.issn.1001-8360.2020.03.008
[12]	邵永生,李成,成明. 基于Sobol’ 法的轨道车辆平稳性的全局灵敏度分析[J]. 铁道科学与工程学报,2018,15(3): 748-754. doi: 10.3969/j.issn.1672-7029.2018.03.027 SHAO Yongsheng, LI Cheng, CHENG Ming. Global sensitivity analysis on ride quality of railway vehicle based on the Sobol’ method[J]. Journal of Railway Science and Engineering, 2018, 15(3): 748-754. doi: 10.3969/j.issn.1672-7029.2018.03.027
[13]	刘涛,徐鼎皓,陈秉智. Sobol’ 法轨道车辆吸能薄壁管灵敏度分析[J]. 大连交通大学学报,2019,40(4): 39-44. LIU Tao, XU Dinghao, CHEN Bingzhi. Sensitivity analysis of thin-walled tube for rail vehicle based on Sobol’ method[J]. Journal of Dalian Jiaotong University, 2019, 40(4): 39-44.
[14]	侯宇飞. 车辆蛇行稳定的全局灵敏度研究[D]. 北京:北京交通大学,2023.
[15]	高广军,卓天宇,关维元. 高速列车曲线通过性能分析及脱轨影响因素研究[J]. 铁道科学与工程学报,2024,21(3): 901-912. GAO Guangjun, ZHUO Tianyu, GUAN Weiyuan. Analysis of high-speed train curve negotiation performance and research on factors affecting derailment[J]. Journal of Railway Science and Engineering, 2024, 21(3): 901-912.
[16]	刘博,尚晓兵,晁涛,等. 基于PCE的飞行器不确定性量化方法[J]. 系统仿真学报,2018,30(12): 4555-4562. LIU Bo, SHANG Xiaobing, CHAO Tao, et al. Uncertainty quantification method for aircraft using PCE model[J]. Journal of System Simulation, 2018, 30(12): 4555-4562.
[17]	周生通,张沛,肖乾,等. 单盘悬臂转子启动过程峰值响应全局灵敏度分析[J]. 振动与冲击,2021,40(11): 17-25. ZHOU Shengtong, ZHANG Pei, XIAO Qian, et al. Global sensitivity analysis for peak response of a cantilevered rotor with single disc during start-up[J]. Journal of Vibration and Shock, 2021, 40(11): 17-25.
[18]	EHRE M, PAPAIOANNOU I, STRAUB D. Global sensitivity analysis in high dimensions with PLS-PCE[J]. Reliability Engineering & System Safety, 2020, 198: 106861.1-106861.14.
[19]	DUAN X J, YAN L, ZENG S J. Planning and analysis on UAV trajectory based on PCE method[J]. Journal of System Simulation, 2022, 34(1): 145.
[20]	肖乾,程玉琦,罗佳文,等. 车辆/轨道耦合作用下高速列车车轮振动影响灵敏度分析[J]. 交通运输工程学报,2021,21(6): 160-169. XIAO Qian, CHENG Yuqi, LUO Jiawen, et al. Sensitivity analysis of high-speed train wheel vibration influenced by vehicle-track coupling[J]. Journal of Traffic and Transportation Engineering, 2021, 21(6): 160-169.
[21]	韩旭,向活跃,李永乐. 考虑参数不确定性的列车-桥梁垂向耦合振动的PC-ARMAX代理模型研究[J]. 工程力学,2021,38(11): 180-188. doi: 10.6052/j.issn.1000-4750.2020.11.0812 HAN Xu, XIANG Huoyue, LI Yongle. Coupled vibration of vertical random vehicle-bridge system considering parameter uncertainty based on PC-ARMAX model[J]. Engineering Mechanics, 2021, 38(11): 180-188. doi: 10.6052/j.issn.1000-4750.2020.11.0812
[22]	ZHOU K, YOU T W, GONG D, et al. Effects of uncertain suspension parameters on dynamic responses of the railway vehicle system[J]. Probabilistic Engineering Mechanics, 2023, 71: 103405.1-103405.14.
[23]	吴杨俊,徐翠强,陈杰,等. 内燃动力包隔振参数灵敏度分析及优化设计[J]. 中南大学学报(自然科学版),2021,52(11): 3872-3884. doi: 10.11817/j.issn.1672-7207.2021.11.010 WU Yangjun, XU Cuiqiang, CHEN Jie, et al. Sensitivity analysis and optimization design of parameters of vibration isolation for power pack[J]. Journal of Central South University (Science and Technology), 2021, 52(11): 3872-3884. doi: 10.11817/j.issn.1672-7207.2021.11.010
[24]	SUDRET B. Global sensitivity analysis using polynomial chaos expansions[J]. Reliability Engineering & System Safety, 2008, 93(7): 964-979.
[25]	王志强,龙志强,李晓龙. 高速磁浮列车搭接结构悬浮系统仿真分析[J]. 西南交通大学学报,2024,59(3): 590-599. doi: 10.3969/j.issn.0258-2724.20210932 WANG Zhiqiang, LONG Zhiqiang, LI Xiaolong. Simulation analysis of levitation system of high-speed maglev trains with joint structure[J]. Journal of Southwest Jiaotong University, 2024, 59(3): 590-599. doi: 10.3969/j.issn.0258-2724.20210932
[26]	黎松奇. EMS磁浮列车悬浮系统振动机理及抑制方法研究[D]. 成都:西南交通大学,2016.
[27]	邹逸鹏,刘放,庞振华,等. 轨道不平顺激励下高速磁浮列车垂向动力学仿真[J]. 机械科学与技术,2021,40(2): 281-286. ZOU Yipeng, LIU Fang, PANG Zhenhua, et al. Vertical dynamics simulation of high speed maglev vehicle under track irregularity excitation[J]. Mechanical Science and Technology for Aerospace Engineering, 2021, 40(2): 281-286.