超导电动悬浮非对称系统多目标优化设计

王津; 葛琼璇; 赵鲁

doi:10.3969/j.issn.0258-2724.20240477

超导电动悬浮非对称系统多目标优化设计

doi: 10.3969/j.issn.0258-2724.20240477

王津^{1, 2,},
葛琼璇^{1, 2, ,},
赵鲁¹

1.
中国科学院电工研究所高密度电磁动力与系统全国重点实验室，北京 100190
2.
中国科学院大学，北京 100049

基金项目: 国家重点研发计划（2023YFB4302501-02）

详细信息

作者简介:
王津（1994—），女，博士研究生，研究方向大功率电力电子与直线驱动，E-mail：wj2021syg@mail.iee.ac.cn

通讯作者:
葛琼璇（1967—），女，研究员，博士生导师，研究方向为高压大功率变流器控制技术、高性能电机牵引控制技术，E-mail： gqx@mail.iee.ac.cn

中图分类号: xxx
计量
- 文章访问数: 42
- HTML全文浏览量: 22
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2024-09-24
- 修回日期: 2025-03-07
- 网络出版日期: 2025-05-14

Multi-objective Optimization of Asymmetric Null-Flux Coils for Superconducting Electrodynamic Suspension System

WANG Jin^{1, 2
,},
GE Qiongxuan^{1, 2
, ,},
ZHAO Lu¹

1.
State Key Laboratory of High Density Electromagnetic Power and Systems, Institute of Electrical Engineering, Chinese Academy of Sciences, Haidian District, Beijing 100190, China
2.
University of Chinese Academy of Sciences, Shijingshan District, Beijing 100049, China

摘要

摘要:
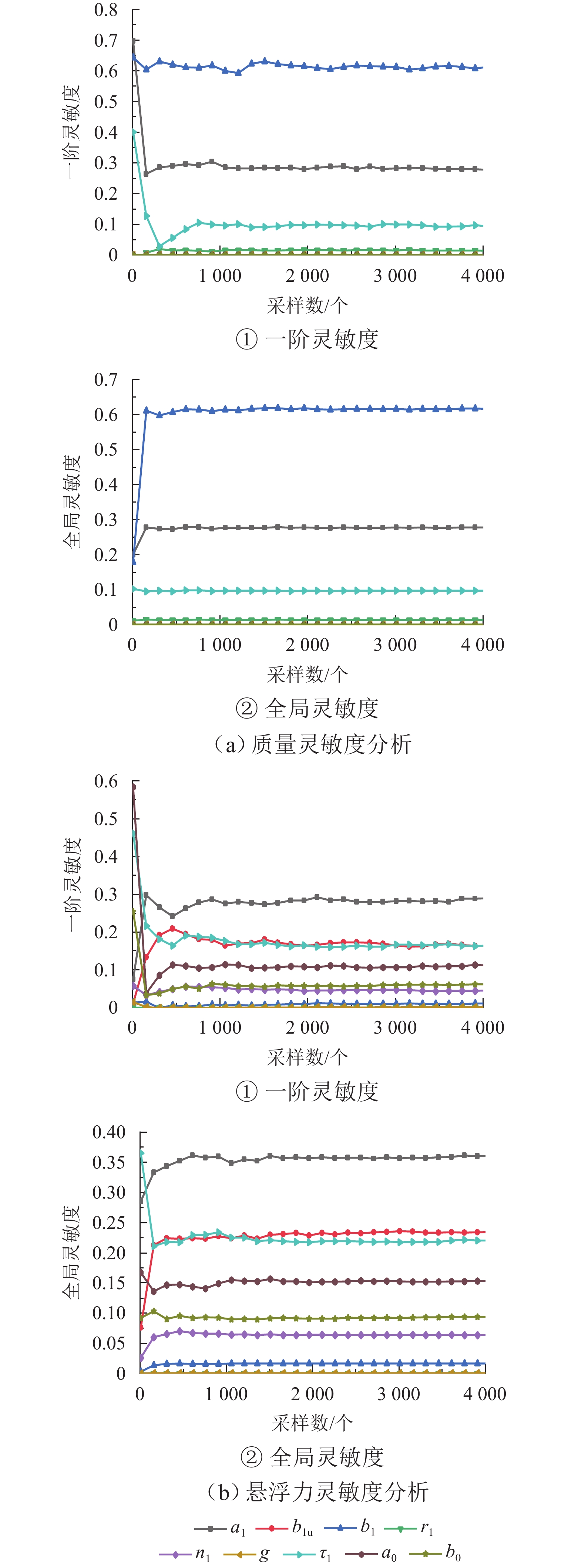
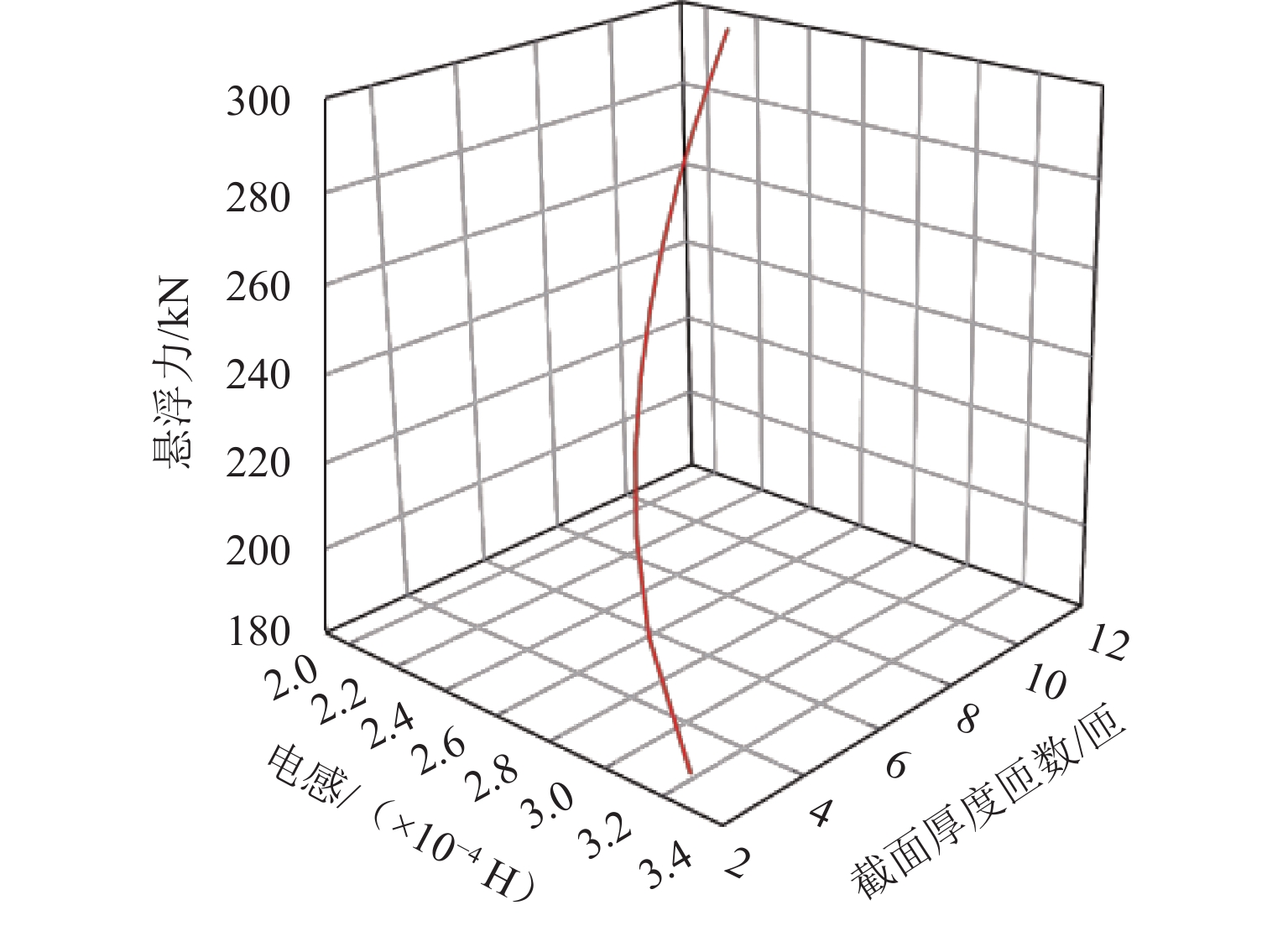
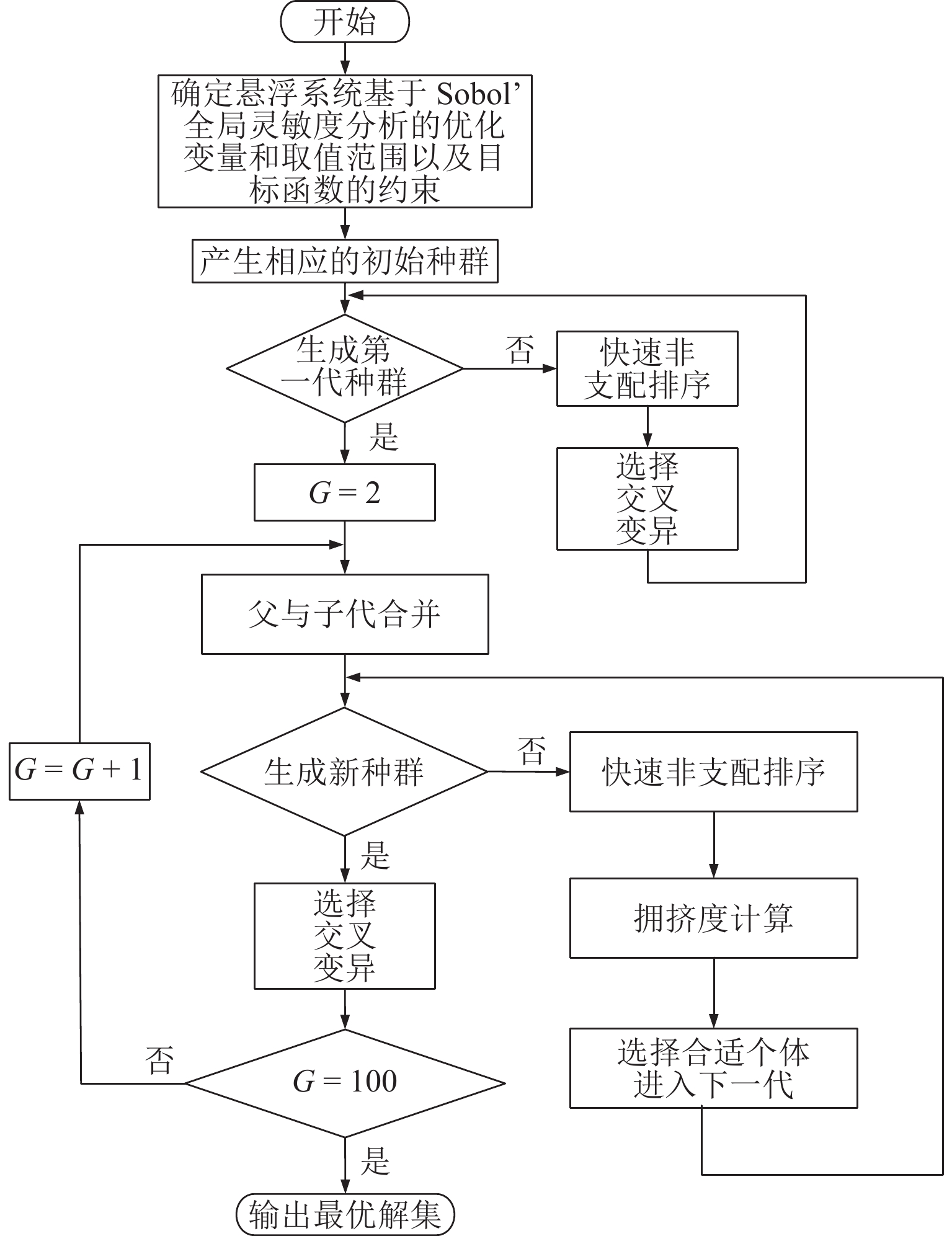
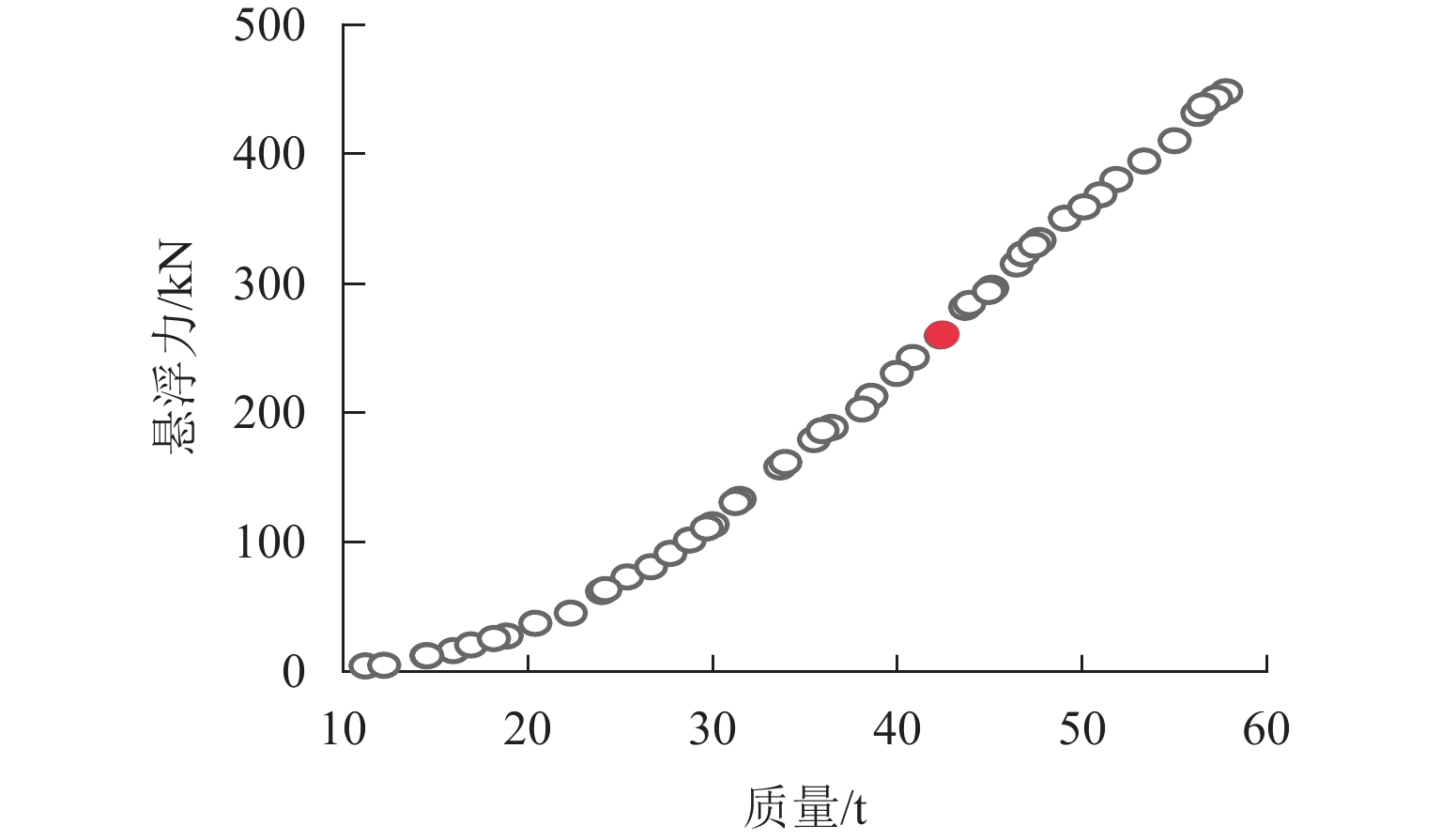
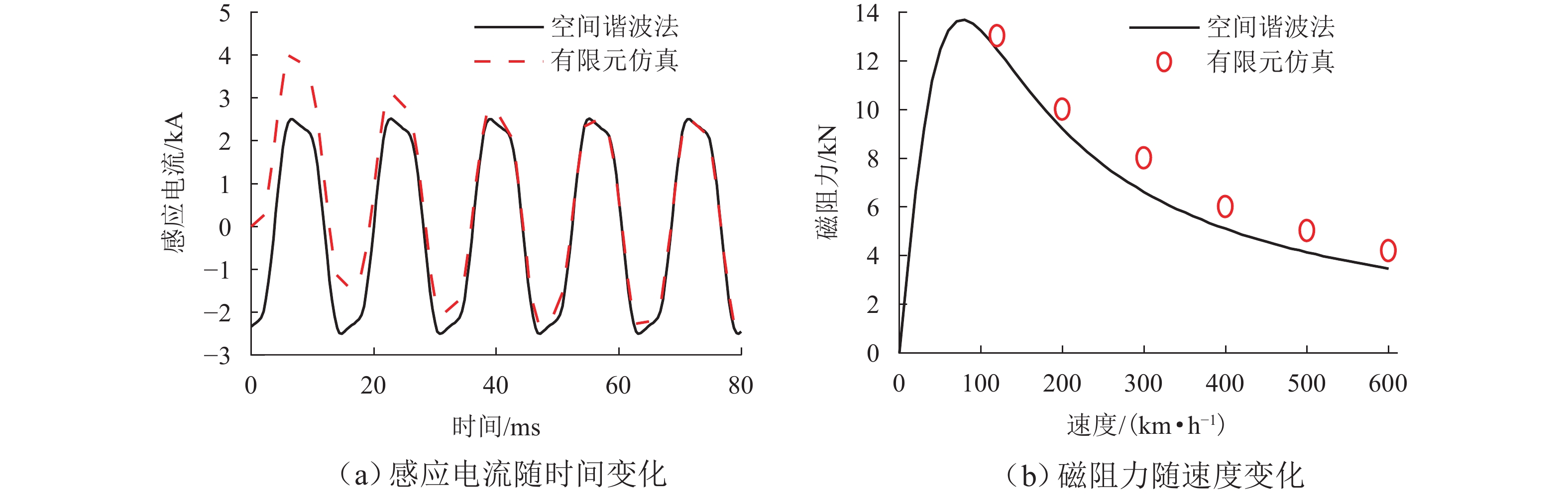
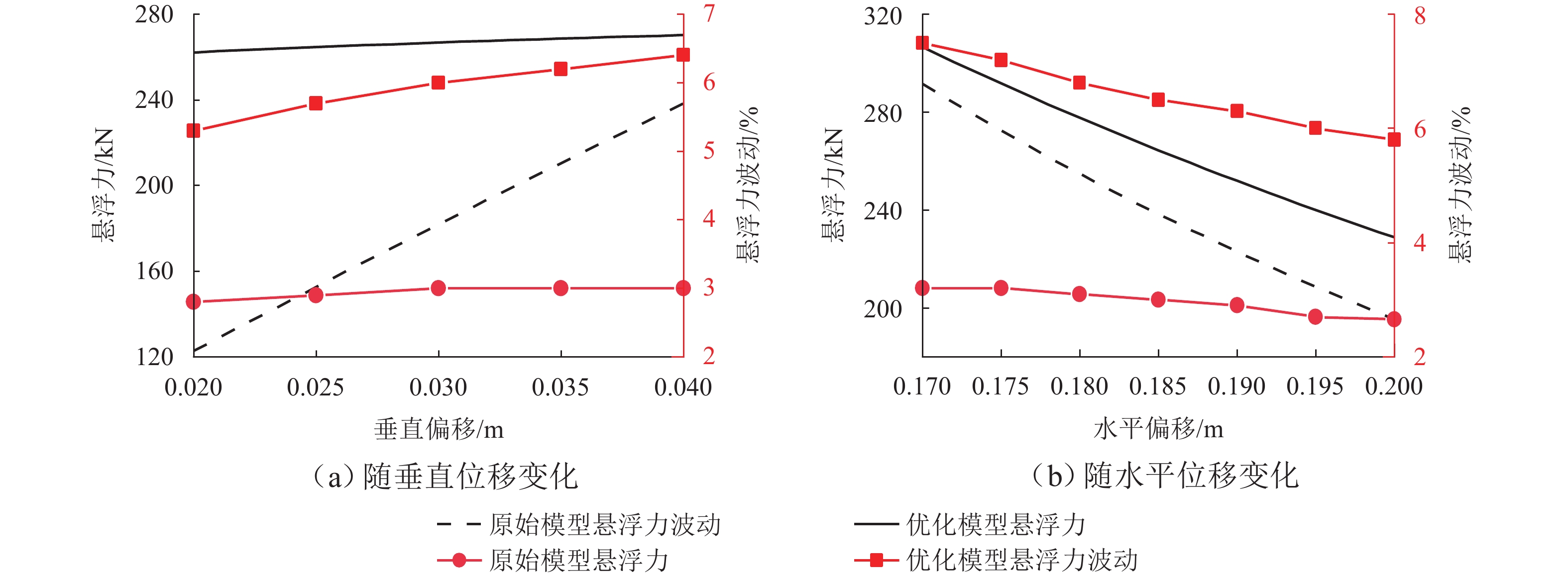
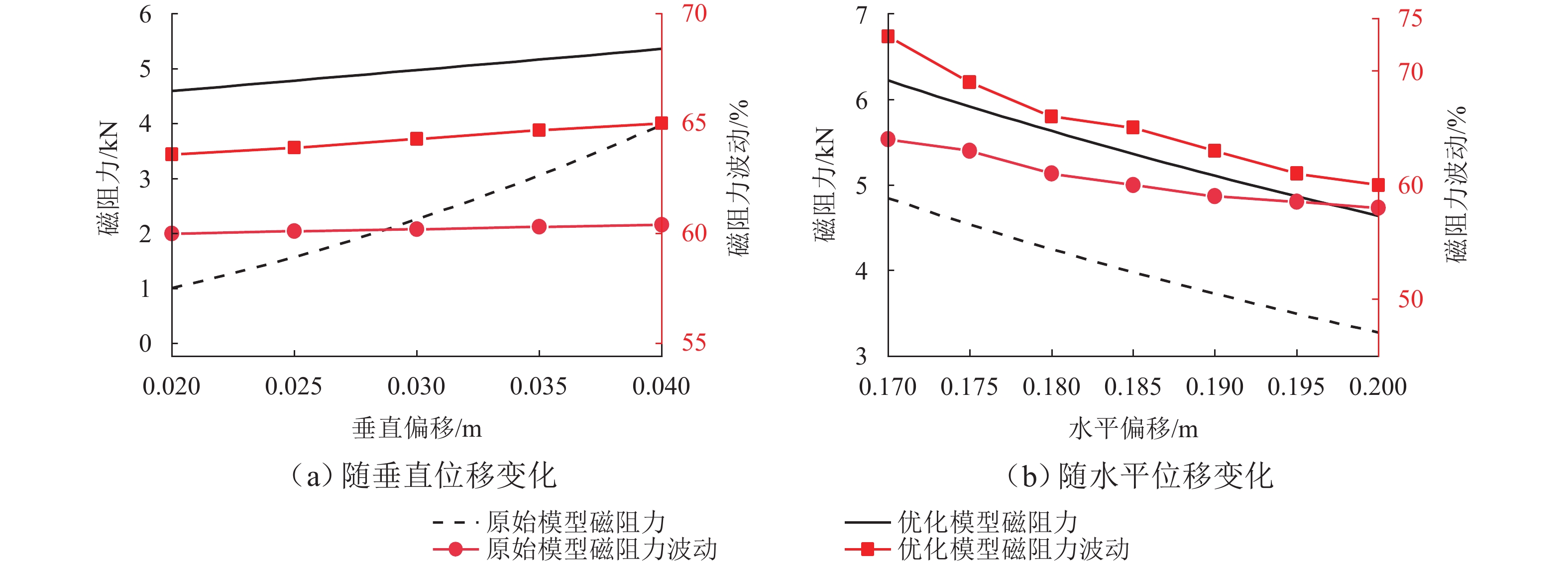
为提高超导电动悬浮系统性能，基于全局灵敏度分析和多目标优化算法，提出一种非对称悬浮线圈优化设计方法. 首先，基于空间谐波法建立超导电动悬浮系统的数学模型，计算超导磁体的磁感应强度以及悬浮线圈的电磁力；其次，对此模型进行非对称优化设计，采用Sobol’敏感性分析方法，以悬浮力和每公里悬浮线圈质量为目标，计算各设计参数的灵敏度，并基于灵敏度分析结果进行非支配排序遗传算法Ⅱ（NSGA-Ⅱ）优化设计；最后，通过有限元进行仿真分析，验证空间谐波法解析模型，并对优化前后的模型进行比较. 研究结果表明：空间谐波法建立的悬浮系统模型与有限元模型具有一致性；相比优化前，优化后的非对称悬浮系统悬浮力提高8.3%，每公里铺设线圈质量降低12.9%；垂直位移0.02～0.04 m时，悬浮力由262.2 kN增加到270.2 kN，磁阻力由4.5 kN增加到5.4 kN；水平位移0.17～0.20 m时，悬浮力由306.5 kN减小到228.8 kN，磁阻力由6.2 kN减小为4.6k N；悬浮力、磁阻力的波动分别约为6%、65%. 研究揭示了悬浮力和磁阻力随着位移方向的变化规律，验证了非对称设计在提升悬浮力和轻量化方面的优势，为超导电动悬浮系统的优化设计提供理论参考.
- 电动悬浮 /
- 灵敏度分析 /
- 非支配排序遗传算法II /
- 有限元仿真 /
- 超导磁体
Abstract:
In order to improve the performance of superconducting electrodynamic suspension system, an optimal design method of asymmetric null-flux coils was proposed based on global sensitivity analysis and multi-objective optimization algorithm. Firstly, the mathematical model of superconducting electrodynamic suspension system was established based on space harmonic method. Then the magnetic flux intensity of the superconducting magnets and electromagnetic forces of the null-flux coils were calculated. Secondly, the model was designed asymmetrically. Sobol' sensitivity analysis method was used to calculate the sensitivity of each design parameter with the levitation force and the mass of the null-flux coils per kilometer as the objectives. Based on the optimization parameters obtained from the sensitivity analysis, NSGA-II optimization design was carried out and the optimization results were obtained. Finally, finite element method was carried out to verify the analytic model of space harmonic method. The model before and after optimization was compared. The results indicated that the suspension system model established by space harmonic method was consistent with the finite element model. Compared with the initial system, the levitation force of the optimized asymmetric suspension system was increased by 8.3%, the mass of null-flux coils per kilometer was reduced by 12.9%, the levitation force increased from 262.2 kN to 270.2 kN and the drag force increased from 4.5 kN to 5.4 kN when the vertical deviation was 0.02～0.04 m. The levitation force decreased from 306.5 kN to 228.8 kN and the drag force decreased from 6.2 kN to 4.6 kN when the horizontal deviation was 0.17～0.2 m. The levitation force fluctuation was about 6% and the drag force fluctuation was about 65%. It revealed the variation patterns of levitation and drag forces with respect to offset directions, demonstrating the advantages of asymmetric design in enhancing levitation force and achieving lightweight performance. This provided a theoretical reference for the optimal design of superconducting electrodynamic suspension systems.
- electrodynamic suspension /
- sensitivity analysis /
- nondominated sorting genetic algorithm II /
- finite element method /
- superconducting magnets.

HTML全文

图 1 EDS系统截面

Figure 1. Cross-section of EDS.

下载: 全尺寸图片幻灯片

图 2 EDS单侧结构

Figure 2. Single-side EDS system structure diagram.

下载: 全尺寸图片幻灯片

图 3 超导线圈与8字线圈的几何关系和对应参数

Figure 3. Structure diagram and geometry parameters of the SCMs and NFCs

下载: 全尺寸图片幻灯片

图 4 不同采样规模下质量和悬浮力的灵敏度分析

Figure 4. Sensitivity of the levitation of different sampling size

下载: 全尺寸图片幻灯片

图 5 悬浮力、线圈电感与线圈截面宽度的关系

Figure 5. Relationships between the levitation force, inductance and cross-section width

下载: 全尺寸图片幻灯片

图 6 基于Sobol’的NSGA-Ⅱ流程

Figure 6. The Sobol’-based NSGA-II algorithm flow chart

下载: 全尺寸图片幻灯片

图 7 悬浮力与质量的Pareto前沿

Figure 7. Pareto front of levitation force to mass.

下载: 全尺寸图片幻灯片

图 8 空间谐波法与有限元模型对比

Figure 8. Comparison of space harmonic technique and finite element model.

下载: 全尺寸图片幻灯片

图 9 悬浮力优化前后对比

Figure 9. Comparison of the levitation force of the initial system and the optimal system.

下载: 全尺寸图片幻灯片

图 10 磁阻力优化前后对比

Figure 10. Comparison of the drag force of the initial system and the optimal system

下载: 全尺寸图片幻灯片

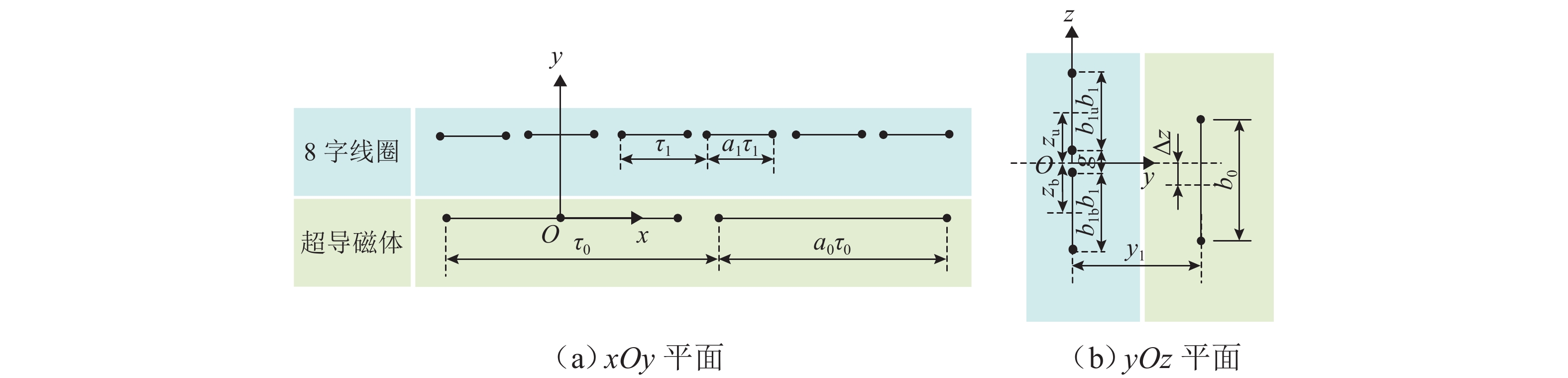
表 1 EDS系统关键参数

Table 1. Main parameters of EDS

线圈	符号	描述	幅值
8字线圈	a₁	长度与极距比例	0.778
	b_1u	上线圈高度占比	0.500
	b_1b	下线圈高度占比	0.500
	b₁	上下线圈总高度/m	0.680
	z_u	上线圈中心高度/m	0.380
	z_b	下线圈中心高度/m	0.380
	c₁	线圈截面长度/m	0.060
	c₂	线圈截面宽度/m	0.040
	N_g	线圈匝数	24
	S_g	截面线圈每匝面积/mm²	100
	τ₁	极距/m	0.450
	g	上下线圈间隙/m	0.080
	r₁	线圈圆角半径/m	0.115
超导线圈	a₀	长度与极距比例	0.793
	b₀	高度/m	0.500
	d₁	线圈截面长度/m	0.040
超导线圈	d₂	线圈截面宽度/m	0.070
	N_s	线圈匝数	1400
	I_s	额定电流/A	500
	τ₀	极距/m	1.350
	y₁	8字线圈与超导线圈水平距离/m	0.185
	Δz	8字线圈与超导线圈中心垂直位移/m	0

下载: 导出CSV

表 2 设计参数及其变量范围

Table 2. Value range of design parameters

参数	变量范围	参数	变量范围
a₁	[0.700,0.900]	g/m	[0.060,0.100]
b_1u	[0.200,0.300]	τ₁/m	[0.400,0.600]
b₁/m	[0.200,0.800]	a₀	[0.700,0.800]
r₁/m	[0.100,0.200]	b₀/m	[0.200,0.600]
n₁/匝数	[2,12]

下载: 导出CSV

表 3 优化方案参数

Table 3. Indicator comparison of initial and optimization scheme

参数	目标值	参数	目标值
a₁	0.580	τ₁/m	0.600
b_1u	0.350	a₀	0.800
n₁/匝	12	b₀/m	0.500

下载: 导出CSV

参考文献(26)

[1]	NASIRI-ZARANDI R, HEKMATI A. A review of suspension and traction technologies in maglev trains[C]//2019 International Power System Conference (PSC). Tehran: IEEE, 2019: 129-135.
[2]	PHAENKONGNGAM T, CHINNAWONG K, PATUMASUIT N, et al. Reviewing propulsion & levitation system for magnetic levitation train[C]//2021 9th International Electrical Engineering Congress (iEECON). Pattaya: IEEE, 2021: 185-188.
[3]	熊嘉阳,邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报,2021,21(1): 177-198. XIONG Jiayang, DENG Zigang. Research progress of high-speed maglev rail transit[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 177-198.
[4]	刘士苋,王磊,王路忠,等. 电动悬浮列车及车载超导磁体研究综述[J]. 西南交通大学学报,2023,58(4): 734-753. doi: 10.3969/j.issn.0258-2724.20220621 LIU Shixian, WANG Lei, WANG Luzhong, et al. Review on electrodynamic suspension trains and on-board superconducting magnets[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 734-753. doi: 10.3969/j.issn.0258-2724.20220621
[5]	张榕欣,蔡小培,汤雪扬,王一. 超导电动磁浮道岔线形设计与侧向过岔速度优化研究[J/OL]. 西南交通大学学报,1-10[2024-11-29]. https://link.cnki.net/urlid/51.1277.u.20241129.1331.020. ZHANG Rongxin, CAI Xiaopeng, TANG Xueyang, et al. Linear design of superconducting electric magnetic levitation turnouts andoptimization of lateral speed over turnouts [J/OL]. Journal of southwest jiaotong university, 1-10[2024-11-29]. https://link.cnki.net/urlid/51.1277.u.20241129.1331.020.
[6]	赵春发,李煜寒,彭也也,杨晶,宁晓芳,冯洋. 超导电动悬浮列车明线气动特性及其对悬浮状态的影响[J/OL]. 西南交通大学学报,1-10[2024-12-05]. https://link.cnki.net/urlid/51.1277.u.20241204.1756.013. ZHAO Chunfa, LI Yuhan, PENG Yeye, et al. Aerodynamic characteristics of the open air of superconducting maglev train and its influence on the levitation state[J/OL]. Journal of southwest jiaotong university, 1-10[2024-12-05]. https://link.cnki.net/urlid/51.1277.u.20241204.1756.013.
[7]	MURAI T, IWAMATSU M, YOSHIOKA H. Optimized design of 8-figure null-flux coils in EDS maglev[J]. IEEJ Transactions on Industry Applications, 2003, 123(1): 9-14. doi: 10.1541/ieejias.123.9
[8]	MURAI T, FUJIWARA S. Design of coil specifications in EDS maglev using optimization program[J]. IEEJ Transactions on Industry Applications, 1997, 117(7): 905-911. doi: 10.1541/ieejias.117.905
[9]	CHEN Y J, FENG J. Optimization of guideway coil dimensions for a magnetic levitation system[J]. IEEE Transactions on Magnetics, 1997, 33(5): 4335-4344. doi: 10.1109/20.620443
[10]	CUI L B, LUO J, SU Z H, et al. Fast optimization of null-flux coils for superconducting electrodynamic suspension train with RSM and AMGA[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(5): 3602308.1-3602308.8.
[11]	王志涛,蔡尧,龚天勇,等. 基于场–路–运动耦合模型的超导电动悬浮列车特性研究[J]. 中国电机工程学报,2019,39(4): 1162-1171. WANG Zhitao, CAI Yao, GONG Tianyong, et al. Characteristic studies of the superconducting electrodynamic suspension train with a field-circuit-motion coupled model[J]. Proceedings of the CSEE, 2019, 39(4): 1162-1171.
[12]	GONG X X, LU Q F, LI Y X. Multi-objective optimization for the levitation system of the electrodynamic suspension train with HTS magnets[C]//2021 13th International Symposium on Linear Drives for Industry Applications (LDIA). Wuhan: IEEE, 2021: 1-6.
[13]	HUANG H, DENG Z G, LI H T, et al. Numerical simulation of dynamic electromagnetic characteristics of superconducting electrodynamic suspension (EDS) train[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(5): 3601105.1-.3601105.5.
[14]	NING X F, ZHAO C F, YU Q S, et al. Suspension and guidance performance of a new superconducting EDS system using the 8-shaped ground coils with nonequal turns[J]. IEEE Transactions on Applied Superconductivity, 2024, 34(4): 3601511.1-3601511.11.
[15]	王小农,黄靖宇. 超导电动磁浮列车悬浮和导向特性[J]. 同济大学学报(自然科学版),2022,50(10): 1482-1489. WANG Xiaonong, HUANG Jingyu. Levitation and guidance characteristics of superconducting electrodynamic maglev train[J]. Journal of Tongji University (Natural Science), 2022, 50(10): 1482-1489.
[16]	YONEZU T, WATANABE K, SUZUKI E, et al. Study on electromagnetic force characteristics acting on levitation/guidance coils of a superconducting maglev vehicle system[J]. IEEE Transactions on Magnetics, 2017, 53(11): 8300605.1-8300605.5.
[17]	NONAKA S, HIROSAKI T, KAWAKAMI E. Analysis of characteristics of repulsive magnetic levitated train using a space harmonic technique[J]. Electrical Engineering in Japan, 1980, 100(5): 80-88. doi: 10.1002/eej.4391000512
[18]	RIBANI P L, URBANO N. Study on figure-eight-shaped coil electrodynamic suspension magnetic levitation systems without cross-connection[J]. IEEE Transactions on Magnetics, 2000, 36(1): 358-365. doi: 10.1109/20.822547
[19]	Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1/2/3): 271-280.
[20]	宋健,佘湖清,李超,等. 基于Sobol’灵敏度分析的火箭弹自力弹射多目标约束优化[J]. 推进技术,2022,43(12): 40-48. SONG Jian, SHE Huqing, LI Chao, et al. Multi-object constraint optimization of rocket self-ejection based on sobol’Sensitivity analysis[J]. Journal of Propulsion Technology, 2022, 43(12): 40-48.
[21]	倪菲,范琳,徐俊起,林国斌,等. 基于Sobol′法的高速磁浮列车单点悬浮系统全局灵敏度分析[J/OL]. 西南交通大学学报,1-12[2025-02-07]. https://link.cnki.net/urlid/51.1277.U.20250227.1256.002. NI Fei, FAN Lin, XU Junqi, et al. Global sensitivity analysis of single electromagnet levitation system for high-speed maglev train based on the Sobol' method [J/OL]. Journal of southwest jiaotong university, 1-12[2025-02-07]. https://link.cnki.net/urlid/51.1277.U.20250227.1256.002.
[22]	谭富星,李凯,于淼,等. 超导电动悬浮试验线悬浮系统设计及验证[J]. 机车电传动,2024(3): 13-18. TAN Fuxing, LI Kai, YU Miao, et al. Design and verification of levitation system for superconducting electrodynamic suspension test line[J]. Electric Drive for Locomotives, 2024(3): 13-18.
[23]	OHASHI S, UEDA N. Dependence of the quenched SC coil position on the transient motion of the superconducting magnetically levitated bogie[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 3600604.1-3600604.4.
[24]	LEE H W, KIM K C, LEE J. Review of maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1917-1925. doi: 10.1109/TMAG.2006.875842
[25]	邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001 DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001
[26]	徐杰. 超导磁悬浮列车用直线发电机的设计与特性解析分析[D]. 北京:北京交通大学,2020.