Influence of Bridge Parameters on Vehicle-Bridge Coupling Stability of Maglev System
-
摘要:
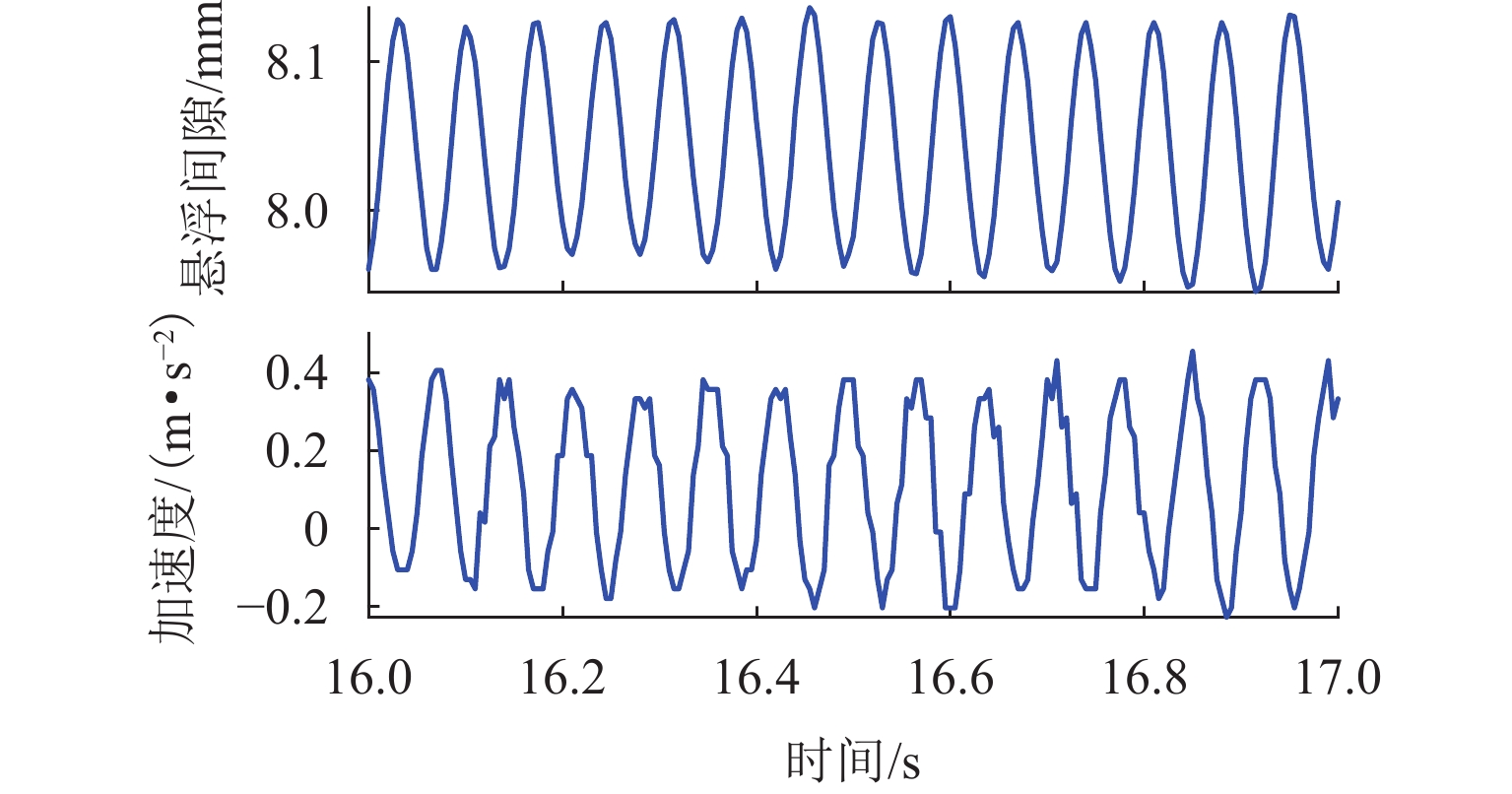
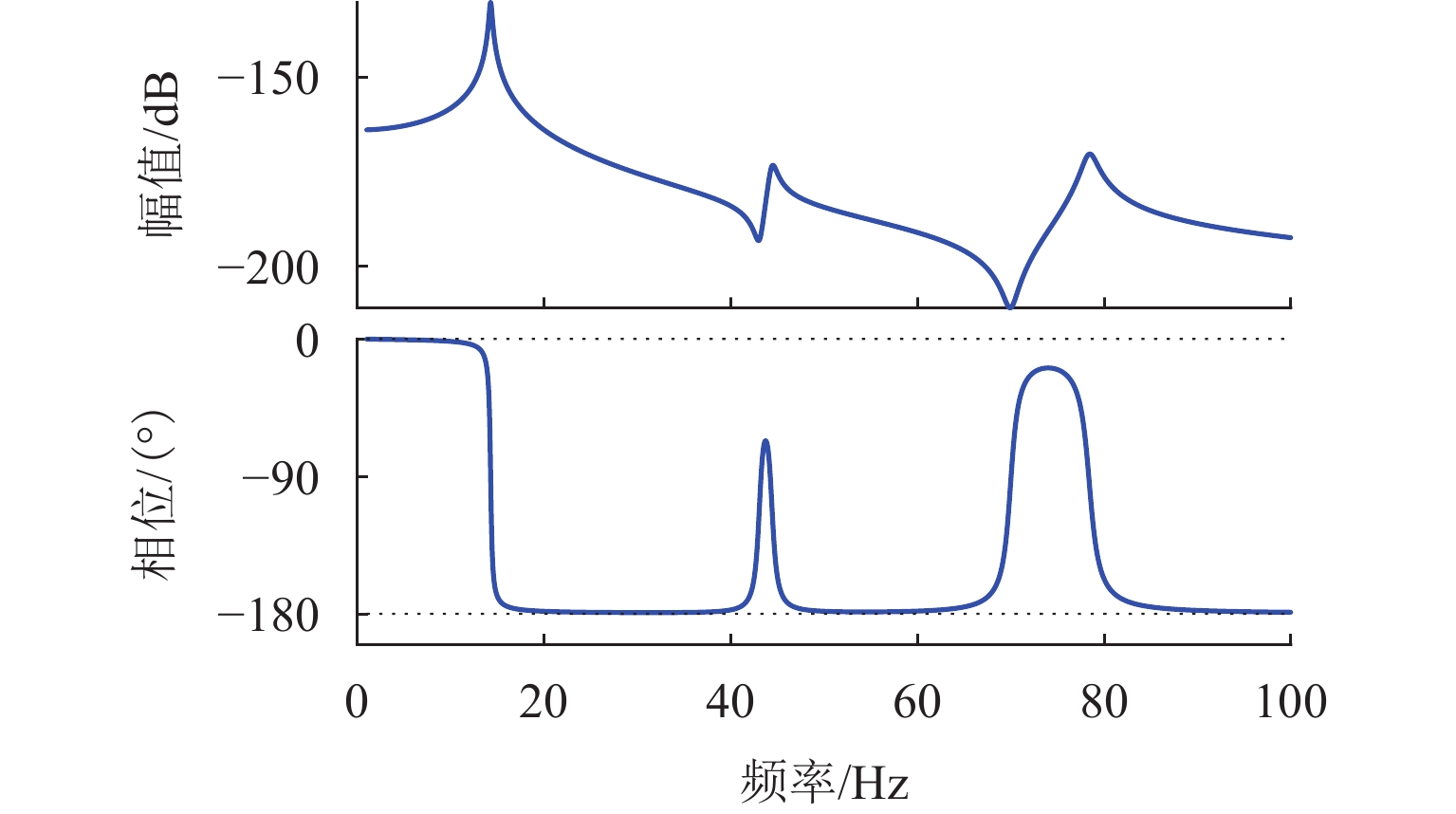
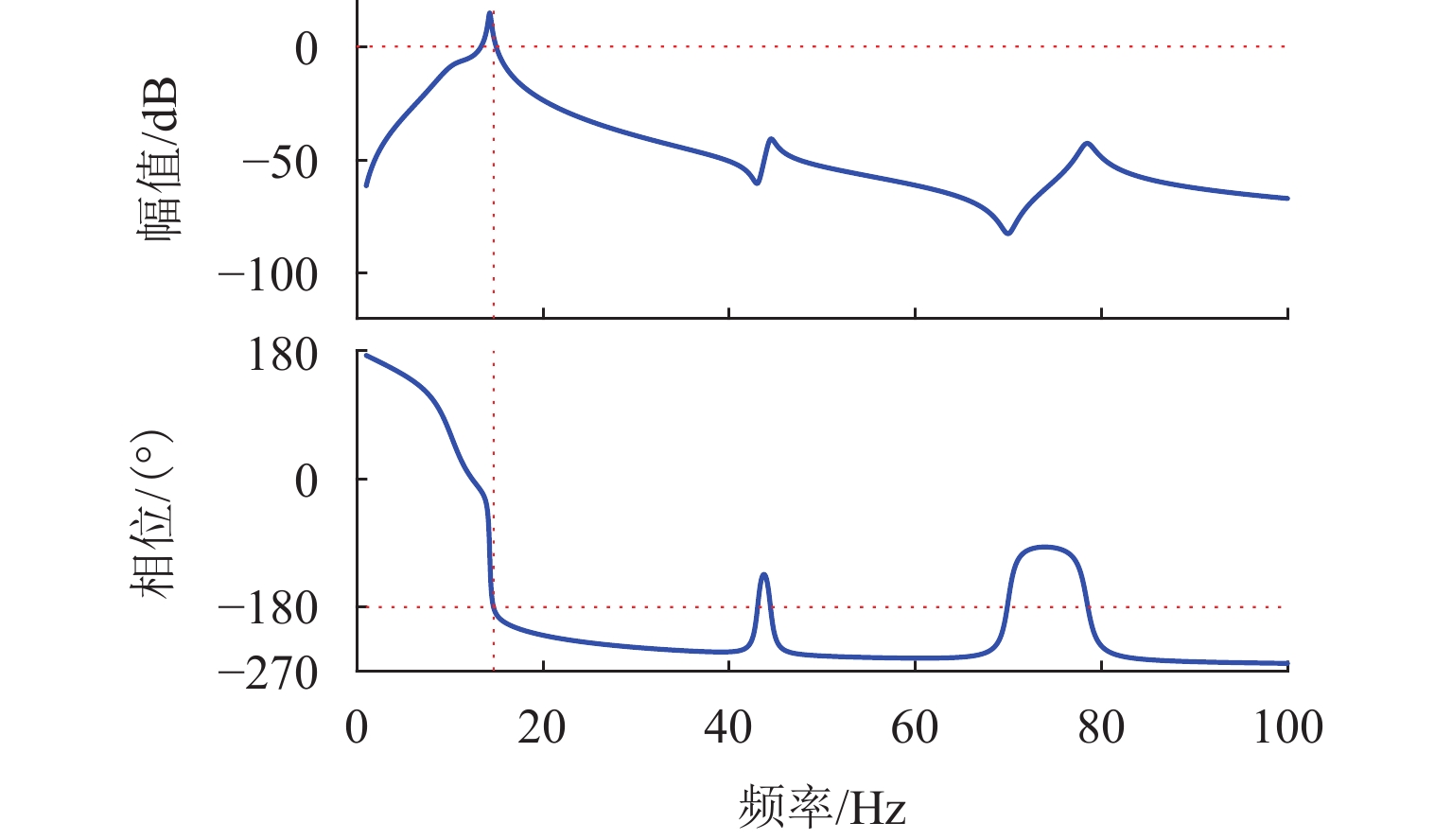
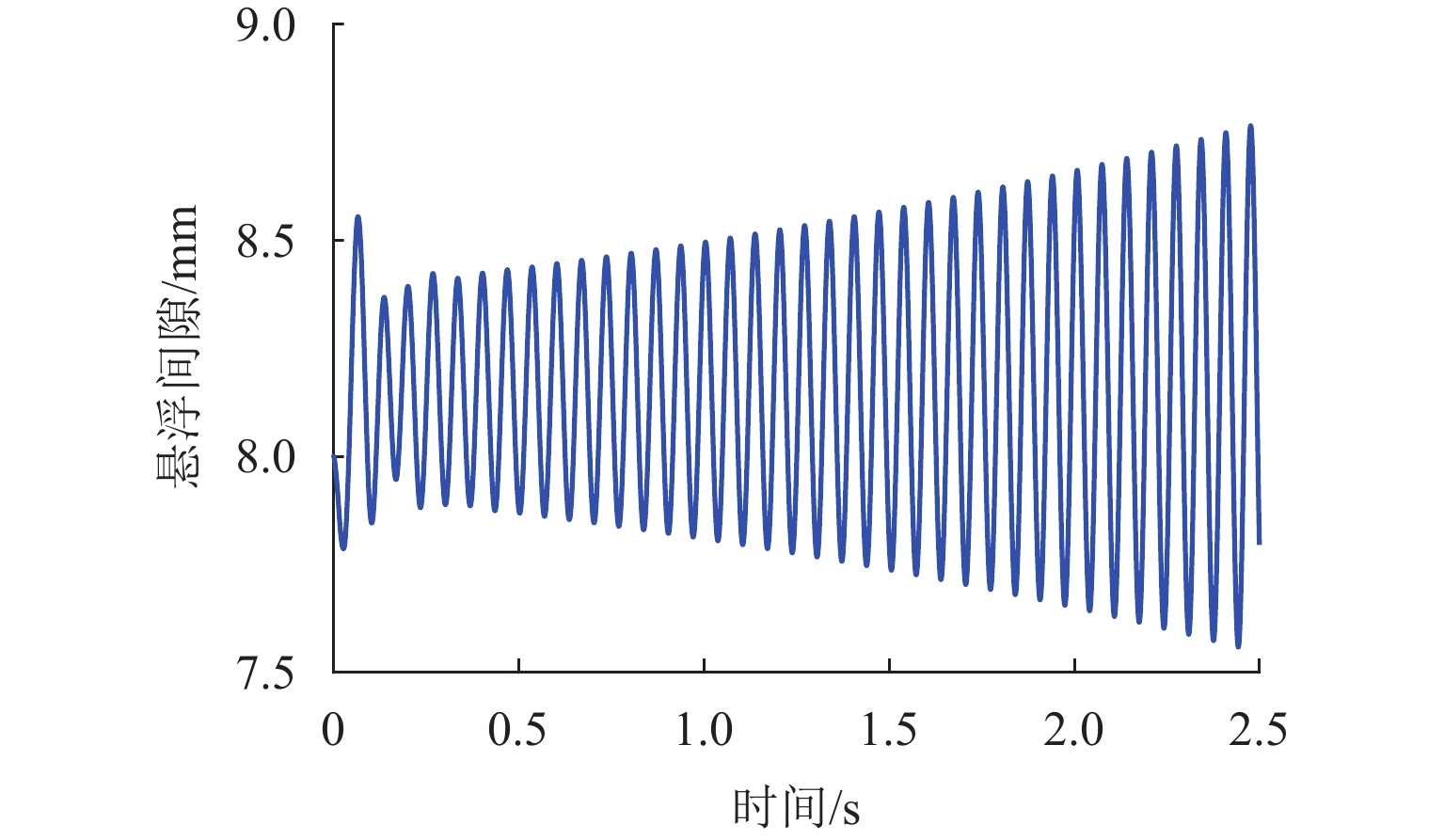
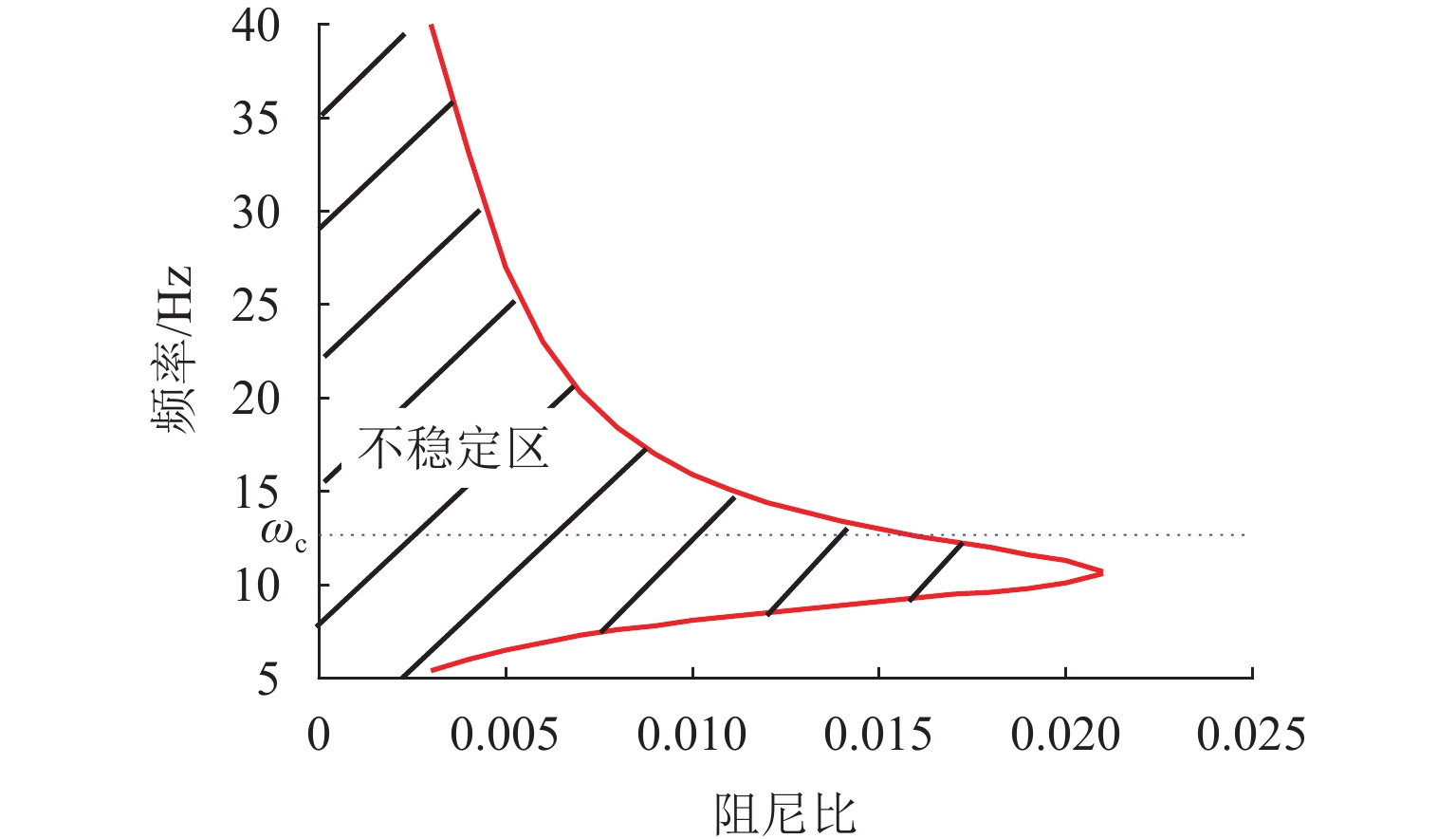
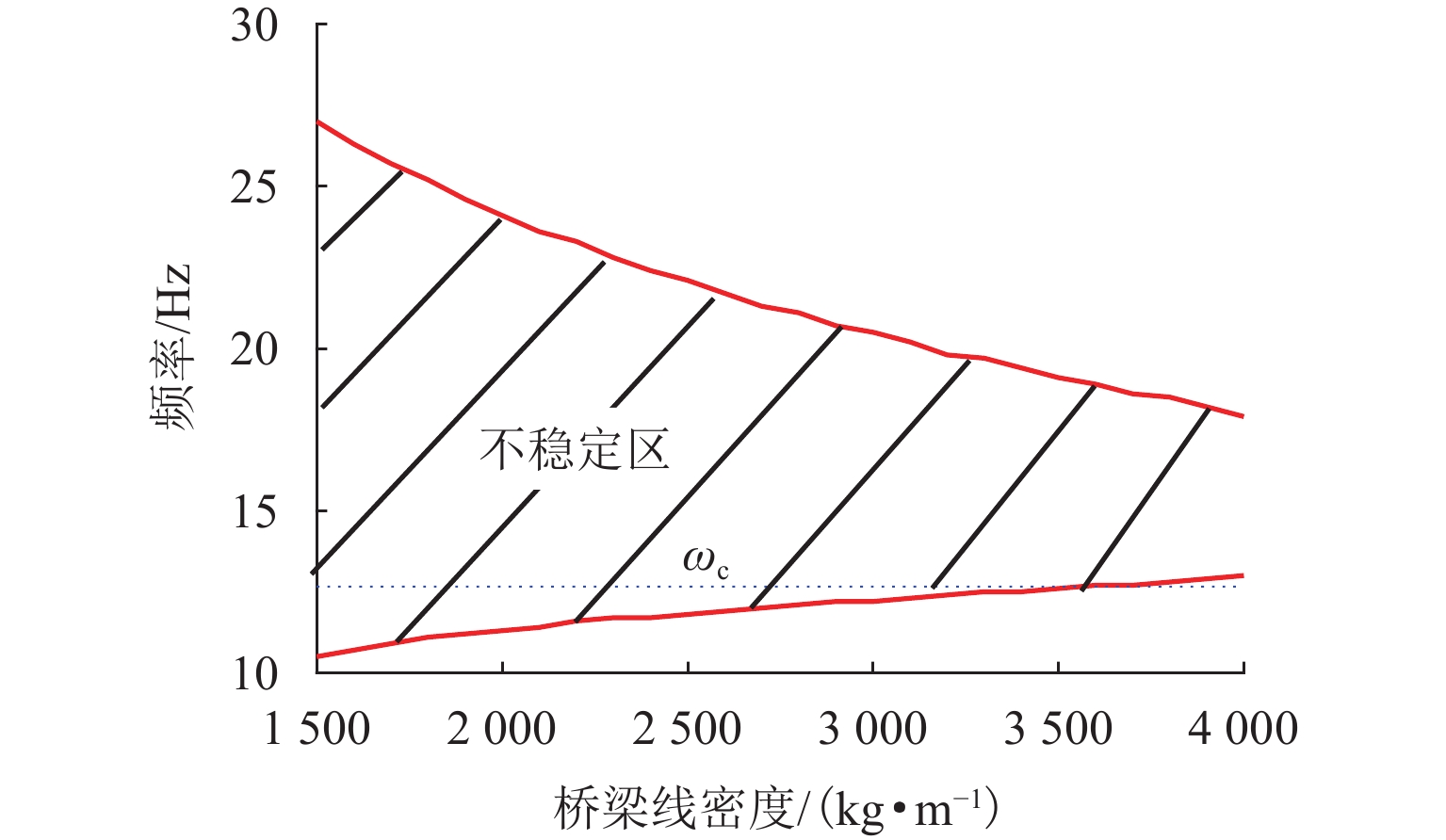
为解决磁浮交通车-桥耦合自激振动问题并指导磁浮桥梁的设计,基于模态分析法建立桥梁的数学模型,研究桥梁的参数对磁浮列车车-桥耦合稳定性的影响. 首先,以磁浮工程某外伸型高架桥梁为例,用模态分析法建立弹性支撑结构的桥梁数学模型,探讨支墩位置对桥梁模态频率的影响;其次,结合磁浮列车悬浮控制系统的模型构建车-桥耦合系统模型,通过分析其开环频率特性研究自激振动发生的原因;最后,探讨桥梁的一阶模态频率、跨径、阻尼比、线密度等参数对车-桥耦合稳定性的影响. 研究表明:桥梁一阶模态频率接近或高于悬浮临界频率易导致闭环不稳定,故一阶模态频率高于10 Hz的轻质梁易引发车-桥耦合自激振动;大跨径梁的模态频率和模态增益更低,稳定性优于小跨径梁;桥梁的阻尼比、线密度越小,不稳定的频率范围越宽;相比两端支撑梁,在桥梁长度和截面固定情况下外伸梁的一阶模态频率随跨径减小呈先增后减的趋势,其最高频率可高出53.9%,更容易进入不稳定频率范围,因此,在磁浮工程中应尽量避免使用这类短跨外伸梁.
Abstract:To solve the self-excited vibration problem during vehicle-bridge coupling in the maglev transportation and guide maglev bridge design, a mathematical model of the bridge was established based on the modal analysis method, so as to study the influence of the bridge parameters on the stability of the vehicle-bridge coupling in the maglev system. Firstly, by taking a stretched overpass in a maglev project as an example, the mathematical model of the overpass with elastic support structures was established using the modal analysis method, and the influence of the pier position on the modal frequencies of the overpass was studied. Secondly, according to the levitation control system model of the maglev train, the vehicle-bridge coupling system model was established. Then, the causes of self-excited vibration were studied by analyzing its open-loop frequency characteristics. Finally, the effects of parameters, including the first-order modal frequency of the overpass, the span, the damping ratio, and the line density on the stability of vehicle-bridge coupling were discussed. The results show that when the first-order modal frequency of the overpass is close to or higher than the critical levitation frequency, the closed loop may be unstable. Therefore, a light bridge with the first-order modal frequency of above 10 Hz is more likely to induce self-excited vibration during vehicle-bridge coupling; long-span bridges have lower modal frequencies and gains and are more stable than short-span bridges; a smaller damping ratio and line density of the overpass mean wider unstable frequency range; compared to girders with supports at both ends, under the fixed bridge length and cross-section, the first-order modal frequency of the stretched bridge shows a trend of first increasing and then decreasing as the span decreases, with the maximum frequency exceeding 53.9%, which makes it more likely to fall into the unstable frequency range. Therefore, the short-span stretched bridges should be excluded from maglev projects as much as possible.
-
Key words:
- maglev train /
- vehicle-girder coupled /
- vibration /
- girder /
- parameters
-
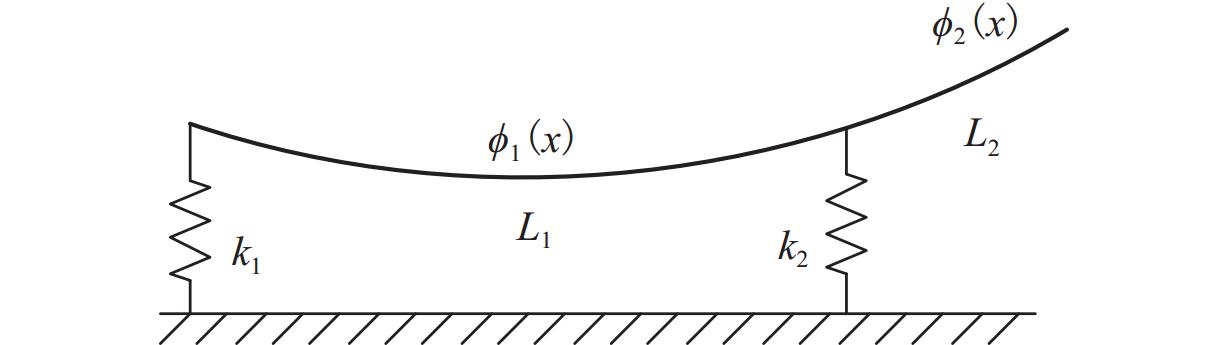
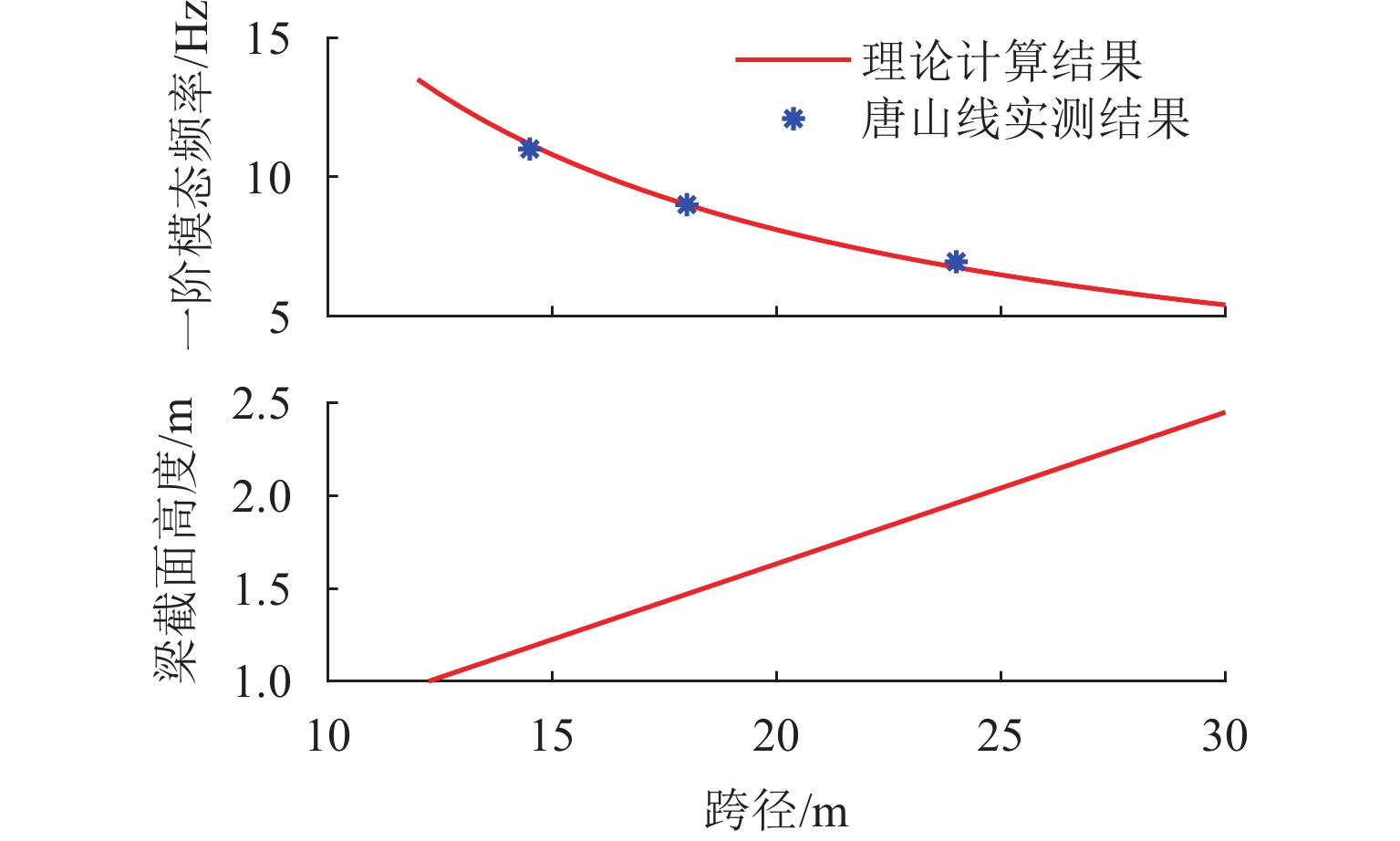
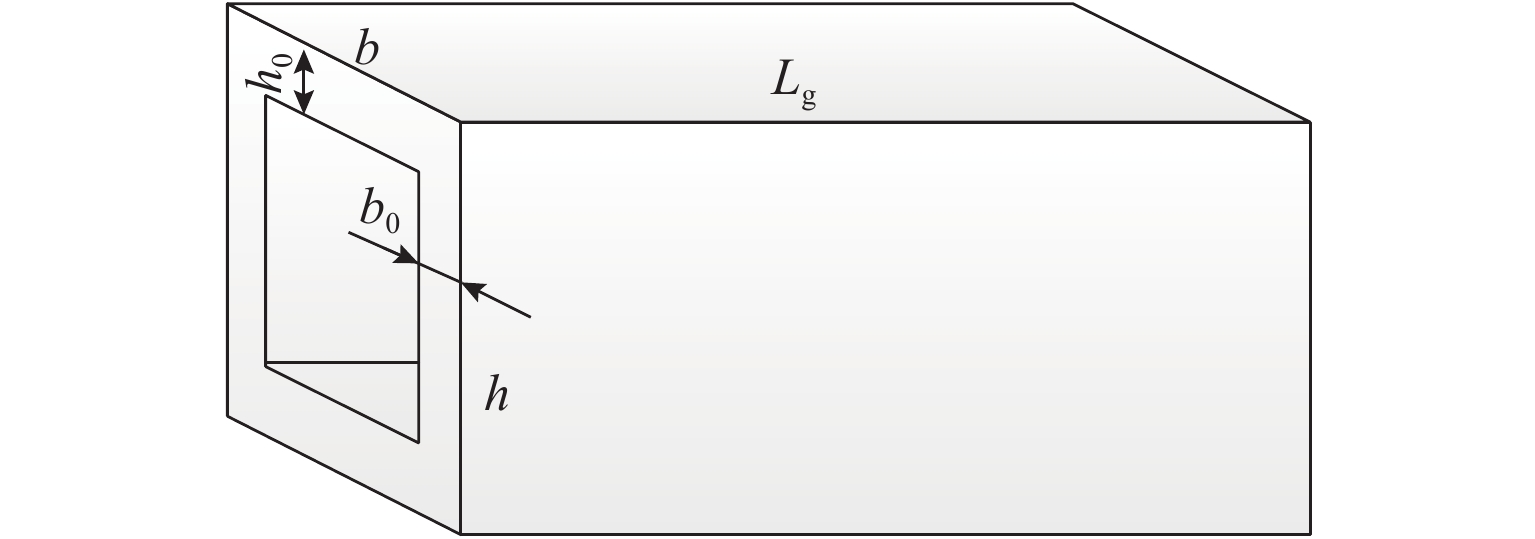
表 1 不同跨径下外伸梁的前三阶模态频率
Table 1. Simplified structure of asymmetrical stretched bridge
Hz 跨径/m 弹性支撑 简支支撑 一阶 二阶 三阶 一阶 二阶 三阶 10.0 16.05 23.23 54.10 16.98 38.54 106.22 11.0 16.55 26.00 51.22 17.45 44.56 93.50 12.0 14.86 33.96 48.67 15.95 55.81 96.44 12.5 13.92 38.10 49.09 14.99 56.89 114.08 13.0 13.02 39.68 52.96 13.94 54.86 118.95 14.0 11.40 37.84 62.92 12.07 48.29 108.58 14.5 10.75 36.56 64.57 11.42 45.67 102.91 表 2 悬浮系统的主要参数
Table 2. Main parameters of levitation system
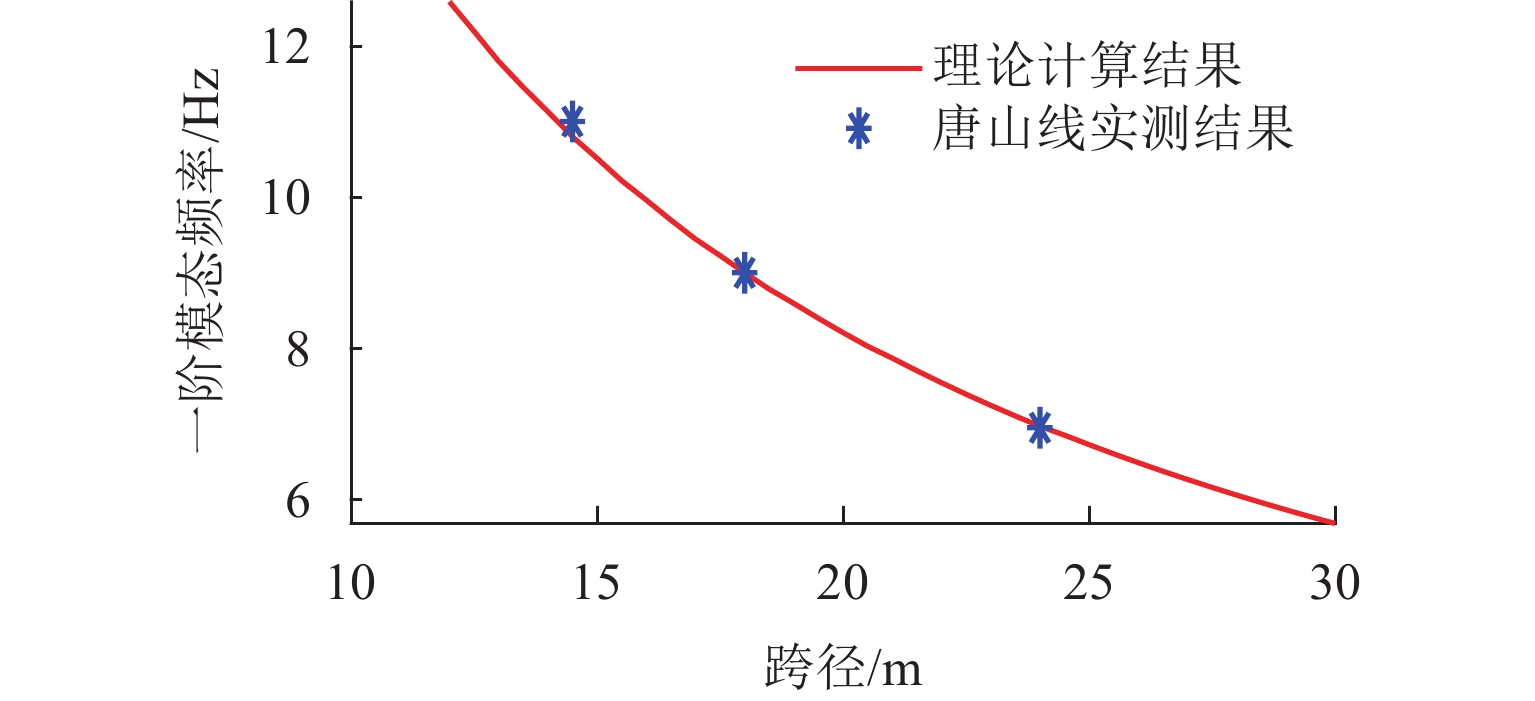
参数 数值 参数 数值 A/m2 0.018 48 kp 5 000 N/匝 360 kd 50 R/Ω 0.55 kc 40 z0/mm 8 μ0/(H·m−1) 4π × 10−7 m1/kg 650 表 3 唐山试验线几种典型的桥梁一阶模态频率
Table 3. First-order modal frequencies of typical bridges in Tangshan test line
编号 跨径/m 一阶模态频率/Hz 梁类型 L1_1 12.5* 13.80 外伸混凝土箱梁 L1_3 14.5 11.00 简支混凝土箱梁 L1_6 18.0 9.00 简支混凝土箱梁 L1_8 18.0 9.10 简支混凝土箱梁 L2_29 24.0 6.80 简支混凝土箱梁 L2_30 24.0 7.00 简支混凝土箱梁 注:* 表示L1_1梁全长为14.5 m,支墩间距为12.5 m. -
[1] 吴会超,罗建利,周文,等. 中低速磁浮车岔耦合振动研究[J]. 西南交通大学学报,2022,57(3): 483-489. doi: 10.3969/j.issn.0258-2724.20210829WU Huichao, LUO Jianli, ZHOU Wen, et al. Coupled vibration between low-medium speed maglev vehicle and turnout[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 483-489. doi: 10.3969/j.issn.0258-2724.20210829 [2] 王淼,宋振森,滕念管. 高速磁浮列车−柔性轨道梁横向耦合振动[J]. 铁道科学与工程学报,2022,19(2):301-309.WANG Miao, SONG Zhensen, TENG Nianguan. Lateral coupling vibration of high-speed maglev train and flexible guideway-beam[J]. Journal of Railway Science and Engineering, 2022, 19(2):301-309. [3] ALBERTS T E, OLESZCZUK G, HANASOGE A M. Stable levitation control of magnetically suspended vehicles with structural flexibility[C]//2008 American Control Conference. Seattle: IEEE, 2008: 4035-4040. [4] 任晓博,赵春发,冯洋,等. 中低速磁浮车辆-轨道-桥梁垂向耦合振动仿真分析[J]. 铁道标准设计,2019,63(2): 70-76.REN Xiaobo, ZHAO Chunfa, FENG Yang, et al. Numerical analysis on vertical coupled vibration of medium-low speed maglev vehicle-track-viaduct system[J]. Railway Standard Design, 2019, 63(2): 70-76. [5] 唐昊天,黄凤华,王淼,等. 中速磁浮列车-桥道-桥梁系统耦合振动分析[J]. 铁道科学与工程学报,2023,20(7): 2395-2406.TANG Haotian, HUANG Fenghua, WANG Miao, et al. Coupling vibration analysis of medium speed maglev vehicle-track-bridge system[J]. Journal of Railway Science and Engineering, 2023, 20(7): 2395-2406. [6] WANG D X, WANG C G, LI S Y, et al. Numerical investigation on dynamic interactions of non-contact maglev vehicle and two-span steel continuous bridge induced by high-frequency vibration modes[J/OL]. Journal of Vibration and Control, [2024-07-20], https://journals.sagepub.com/doi/pdf/10.1177/10775463241262546. [7] WANG D X, LI X Z. Research on vibration mechanism of the low-to-medium-speed maglev train-track-at-ground-structure system[J]. Advances in Structural Engineering, 2023, 26(10): 1803-1817. doi: 10.1177/13694332231175393 [8] 曾国锋,韩紫平,刘鸣博,等. 电磁悬浮型高速磁浮车-岔垂向动力响应[J]. 同济大学学报(自然科学版),2023,51(3): 303-313.ZENG Guofeng, HAN Ziping, LIU Mingbo, et al. Vertical dynamic response of electromagnetic suspension highspeed maglev vehicle-turnout[J]. Journal of Tongji University (Natural Science), 2023, 51(3): 303-313. [9] 杨光. 中低速磁浮简支轨道梁竖向挠跨比限值探讨[J]. 铁道建筑技术,2019(9): 38-43. doi: 10.3969/j.issn.1009-4539.2019.09.009YANG Guang. Discussion on vertical limited ratio value of deflection to span of simply-supported girder in low-to-medium speed maglev line[J]. Railway Construction Technology, 2019(9): 38-43. doi: 10.3969/j.issn.1009-4539.2019.09.009 [10] 王理达. 中低速磁浮桥梁关键技术研究[D]. 成都:西南交通大学,2014. [11] 李小珍,王渝文,胡启凯,等. 不同桥跨对中低速磁浮列车-简支梁系统竖向耦合振动影响机理研究[J]. 振动与冲击,2022,41(19): 8-15.LI Xiaozhen, WANG Yuwen, HU Qikai, et al. Influence mechanisms of different bridge spans on vertical coupled vibration of low and medium speed maglev train-simply supported beam system[J]. Journal of Vibration and Shock, 2022, 41(19): 8-15. [12] 唐语,刘放,邹逸鹏,等. 中低速磁浮车辆-道岔主动梁刚柔耦合振动分析[J]. 机械科学与技术,2022,41(4): 500-504.TANG Yu, LIU Fang, ZOU Yipeng, et al. Analysis on coupling vibration of mid-low speed maglev vehicle on active turnout girder[J]. Mechanical Science and Technology for Aerospace Engineering, 2022, 41(4): 500-504. [13] 邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001 [14] 唐语,刘放,吴涛,等. 中低速磁浮道岔主动梁动力学分析[J]. 起重运输机械,2021(10): 28-32. doi: 10.3969/j.issn.1001-0785.2021.10.016TANG Yu, LIU Fang, WU Tao, et al. Dynamic analysis of active beam of medium and low speed maglev turnout[J]. Hoisting and Conveying Machinery, 2021(10): 28-32. doi: 10.3969/j.issn.1001-0785.2021.10.016 [15] 刘伟,赵春发,娄会彬,等. 基于虚拟激励法的磁浮车-桥耦合系统随机振动分析[J]. 西南交通大学学报,2024,59(4): 823-831. doi: 10.3969/j.issn.0258-2724.20240035LIU Wei, ZHAO Chunfa, LOU Huibin, et al. Stochastic vibration analysis of maglev train-bridge coupling system based on pseudo excitation method[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 823-831. doi: 10.3969/j.issn.0258-2724.20240035 [16] 向活跃,刘科宏,李永乐. 列车荷载作用下的磁浮轨道梁响应极值条件[J]. 西南交通大学学报,2025,60(1): 27-34,136. doi: 10.3969/j.issn.0258-2724.20220835XIANG Huoyue, LIU Kehong, LI Yongle. Extremum conditions of response of maglev guideway under train loads[J]. Journal of Southwest Jiaotong University, 2025, 60(1): 27-34,136. doi: 10.3969/j.issn.0258-2724.20220835 [17] 娄会彬,魏凌云,彭也也,等. 中低速磁浮列车-桥道-T构梁耦合振动[J]. 铁道建筑,2025,65(2): 83-88. doi: 10.3969/j.issn.1003-1995.2025.02.14LOU Huibin, WEI Lingyun, PENG Yeye, et al. Coupled vibration of rapid maglev train-track-T-shaped girder[J]. Railway Engineering, 2025, 65(2): 83-88. doi: 10.3969/j.issn.1003-1995.2025.02.14 [18] 娄会彬,彭也也,赵春发,等. T构梁温度和收缩徐变效应对磁浮车-桥-桥耦合振动的影响[J]. 铁道建筑,2025,65(1): 93-98. doi: 10.3969/j.issn.1003-1995.2025.01.16LOU Huibin, PENG Yeye, ZHAO Chunfa, et al. Influence of temperature and shrinkage creep effects of T-shaped rigid frame girder on coupled vibration of urban maglev vehicle-track-bridge system[J]. Railway Engineering, 2025, 65(1): 93-98. doi: 10.3969/j.issn.1003-1995.2025.01.16 [19] 杨志南,冯洋,刘东生,等. 悬浮控制参数对磁浮车辆与道岔梁耦合振动的影响分析[J]. 机械,2022,49(2): 38-46. doi: 10.3969/j.issn.1006-0316.2022.02.006YANG Zhinan, FENG Yang, LIU Dongsheng, et al. Influence of levitation control parameters on coupled vibration between maglev vehicles and switch girder[J]. Machinery, 2022, 49(2): 38-46. doi: 10.3969/j.issn.1006-0316.2022.02.006 [20] 卜秀孟,王力东,黎清蓉,等. 高速磁浮车-桥耦合振动控制参数影响分析[J]. 西南交通大学学报,2024,59(4): 848-857,866. doi: 10.3969/j.issn.0258-2724.20230534BU Xiumeng, WANG Lidong, LI Qingrong, et al. Influence analysis of vibration control parameters for high-speed maglev train-bridge coupling[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 848-857,866. doi: 10.3969/j.issn.0258-2724.20230534 [21] 侯龙刚,梁树林,池茂儒. 中低速磁浮道岔处车轨耦合振动抑制方法研究[J]. 机车电传动,2022(5): 49-55.HOU Longgang, LIANG Shulin, CHI Maoru. Research on vehicle-rail coupling vibration at turnout and suppression method of medium and low speed maglev vehicle[J]. Electric Drive for Locomotives, 2022(5): 49-55. [22] ZHOU D F, LI J, HANSEN C H. Suppression of the stationary maglev vehicle–bridge coupled resonance using a tuned mass damper[J]. Journal of Vibration and Control, 2013, 19(2): 191-203. doi: 10.1177/1077546311430716 [23] 周丹峰. EMS型磁浮列车车轨耦合自激振动问题研究[D]. 长沙:国防科学技术大学,2011. [24] ZHOU D F, YANG Q, WANG L C, et al. Stability and control of maglev vehicle–girder coupled system considering torsional vibration of the girder[J]. ISA Transactions, 2021, 111: 309-322. doi: 10.1016/j.isatra.2020.11.006 [25] 中华人民共和国住房和城乡建设部. 中低速磁浮交通设计规范:CJJ/T 262—2017[S]. 北京:中国建筑工业出版社,2017. [26] 李苗,马卫华,龚俊虎,等. 中低速磁浮车辆-桥梁耦合系统动力性能试验[J]. 交通运输工程学报,2022,22(1): 141-154.LI Miao, MA Weihua, GONG Junhu, et al. Dynamic performance test of medium and low speed maglev vehicle-bridge coupled system[J]. Journal of Traffic and Transportation Engineering, 2022, 22(1): 141-154. -





 下载:
下载: