Prestress Optimization of Suspended Domes with Plant Growth Simulation Algorithm Based on Multi-Mechanism Fusion
-
摘要:
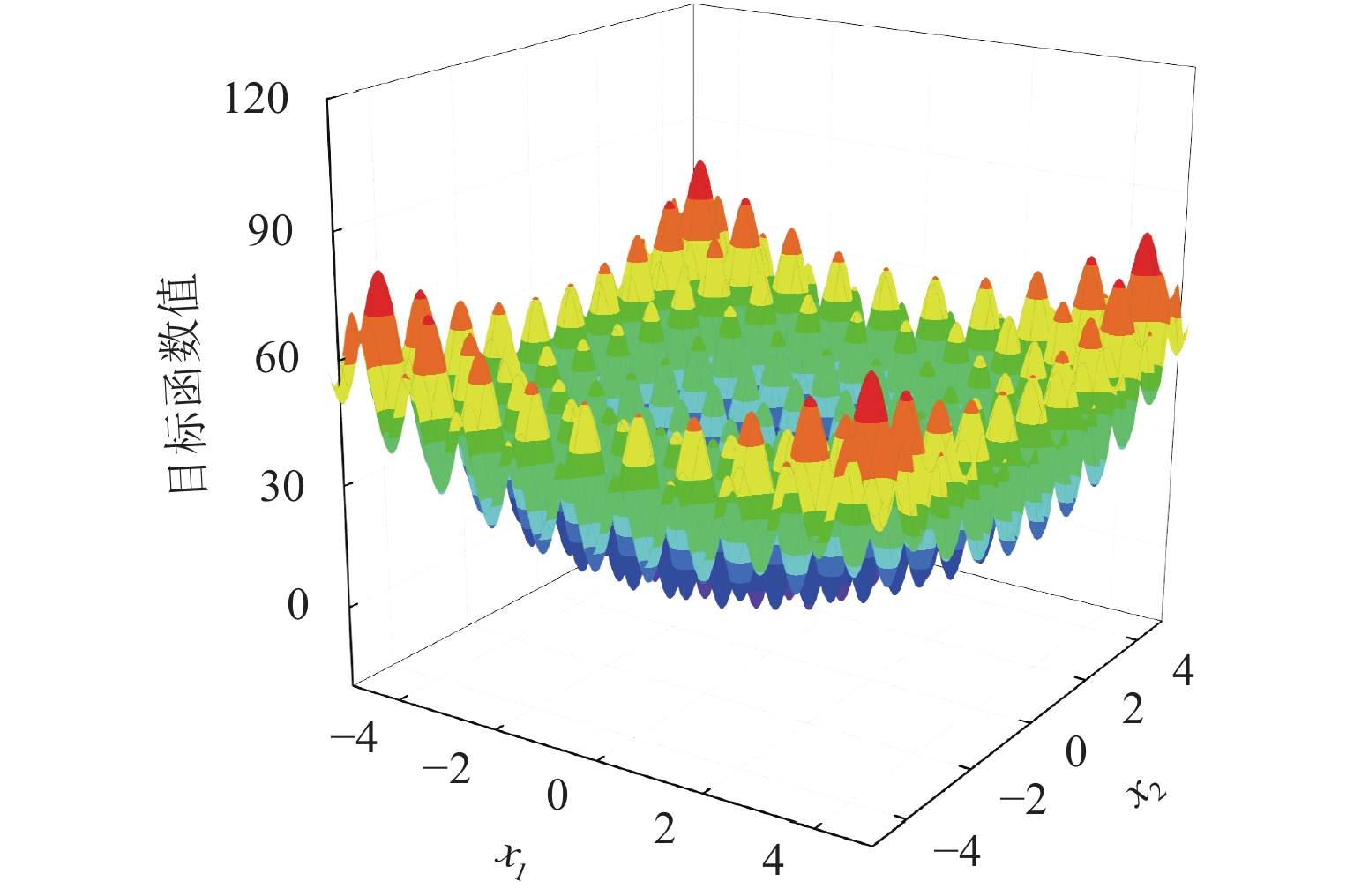
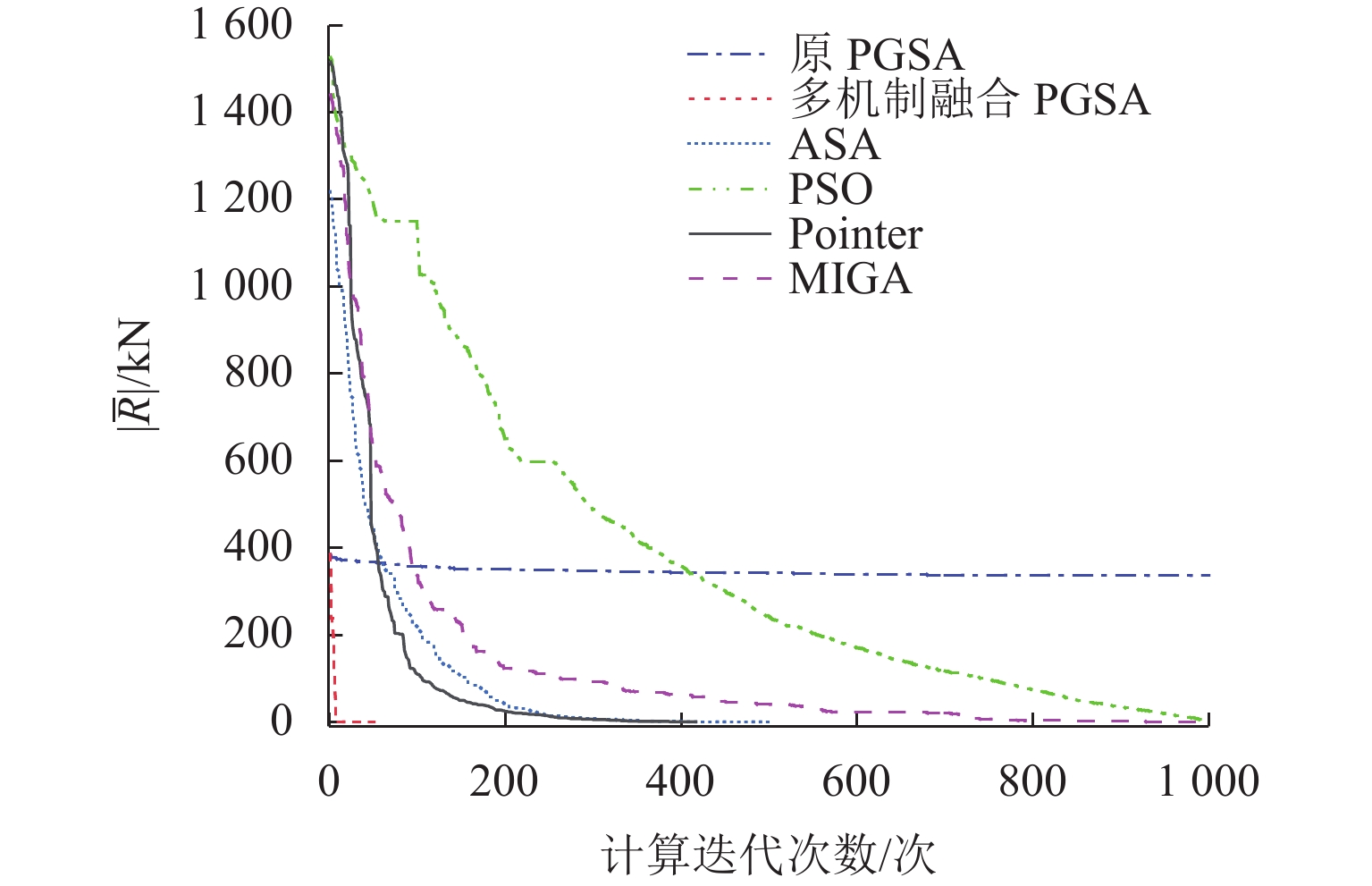
针对模拟植物生长算法(PGSA)以固定步长搜索难以收敛于全局最优解、对初始生长点选取依赖性强和生长空间巨大的局限性，提出自适应变步长搜索、高斯扰动变异和生长空间筛选3种机制的新策略，建立基于多机制融合的模拟植物生长算法(多机制融合PGSA)，进一步采用多机制融合PGSA对弦支穹顶结构进行预应力优化，并与其他优化算法进行对比. 结果表明：与原PGSA相比，引入自适应变步长搜索机制，可避免算法陷入局部最优解，引入高斯扰动变异机制，可解决由于初始生长点的选取不当而造成优化结果不佳的问题，引入生长空间筛选机制，可在算法收敛后有效终止生长，显著缩小生长空间(降幅最大达97.64%)；与其他优化算法相比，多机制融合PGSA的迭代次数最少(仅为45次)，且优化得到的支座平均水平径向反力绝对值最小(仅为0.004 kN)，验证了该算法的适用性.
Abstract:To address the limitations of difficult convergence to the global optimal solution with fixed step search, strong dependence on the selection of initial growth point, and huge growth space for the plant growth simulation algorithm (PGSA), a new strategy for search mechanism of adaptive variable step, Gauss perturbation mutation mechanism, and screening mechanism of growth space was proposed. On this basis, the PGSA based on multi-mechanism fusion (multi-mechanism fusion PGSA) was established. The prestress optimization of suspended domes was further carried out by using the multi-mechanism fusion PGSA and compared with other algorithms. The results show that compared with the original PGSA, the introduction of search mechanism of adaptive variable step can avoid the algorithm falling into local optimal solutions; the introduction of Gauss perturbation mutation mechanism can solve the problem of poor optimization results caused by the improper selection of initial growth points, and the introduction of screening mechanism of growth space can effectively terminate the growth after the algorithm converges, thus significantly reducing the growth space by 97.64%. The number of iterations of multi-mechanism fusion PGSA is the smallest (only 45), and the absolute value of the average horizontal radial reaction of supports after optimization is minimal (only 0.004 kN) in comparison with other algorithms. Therefore, the applicability of this algorithm is verified.
-
图 3 仅引入自适应变步长搜索机制的PGSA优化过程
Figure 3. PGSA optimization process introducing searching mechanism of adaptive variable step only
图 4 仅引入高斯扰动变异机制的PGSA优化过程
Figure 4. PGSA optimization process introducing Gauss perturbation mutation mechanism only
图 5 引入生长空间筛选机制的PGSA优化过程
Figure 5. PGSA optimization process introducing screening mechanism of growth space
表 1 仅引入自适应变步长搜索机制的PGSA优化结果
Table 1. PGSA optimization results introducing searching mechanism of adaptive variable step only
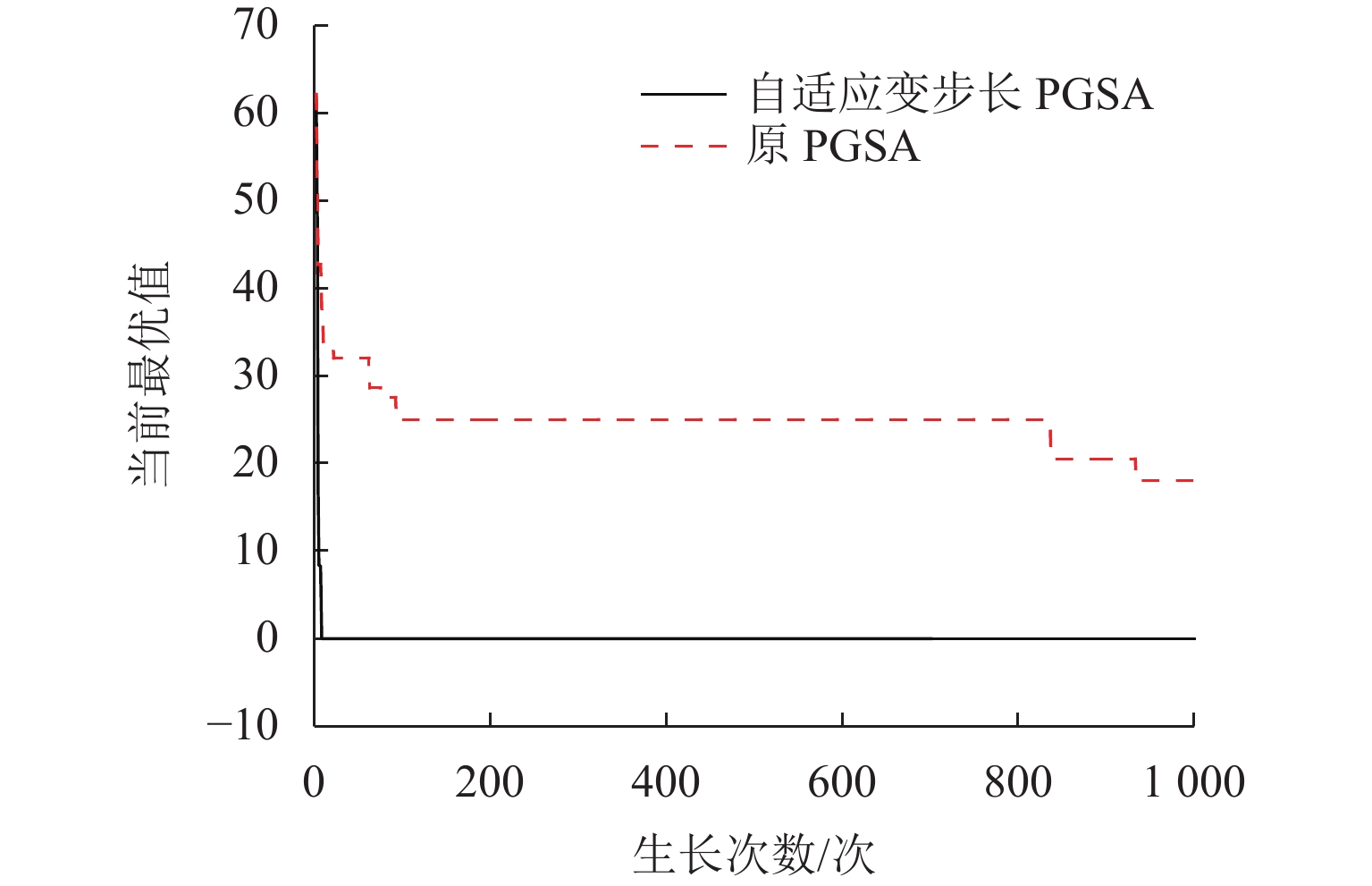
算法 收敛生长次数/次 优化结果 寻优耗时/s 生长空间 O 不收敛 18.00 60.742 6012 × 3A 7 0 301.199 24562 × 3注：算法O、A分别对应于图3中的原PGSA、自适应变步长PGSA 
下载: 导出CSV
表 2 仅引入高斯扰动变异机制的PGSA优化结果
Table 2. PGSA optimization results introducing Gauss perturbation mutation mechanism only
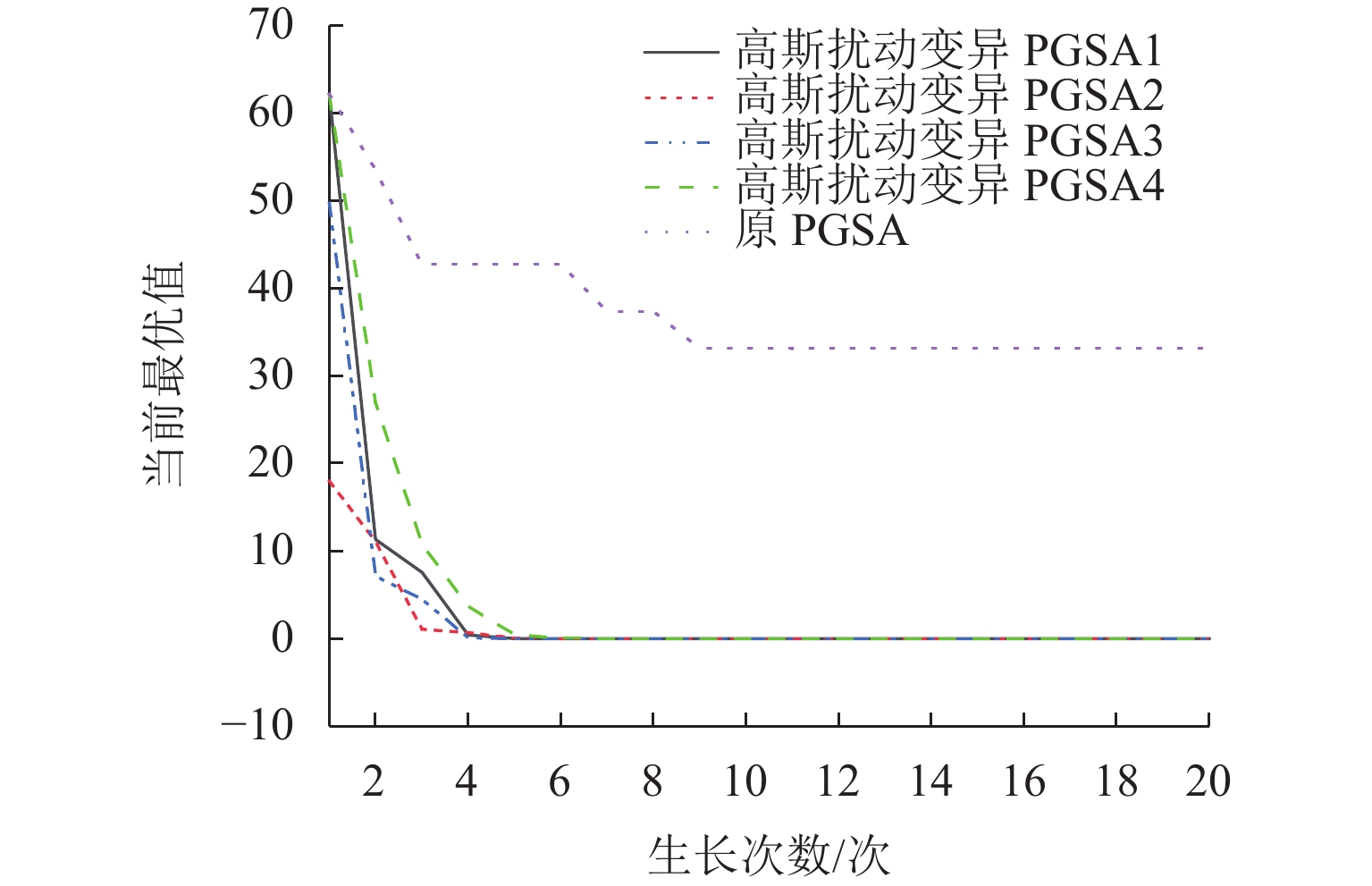
算法 初始生长点 收敛生长次数/次 优化结果 寻优耗时/s 生长空间 O $ {x_j} = 3.6 $ 不收敛 18.00 60.742 6012 × 3B1 $ {x_j} = 3.6 $ 15 0 658.209 28472 × 3B2 $ {x_j} = 3.0 $ 14 0 681.205 29081 × 3B3 $ {x_j} = 2.6 $ 14 0 849.400 28687 × 3B4 $ {x_j} = - 3.6 $ 16 0 601.005 28286 × 3注：算法B1～B4分别对应于图4中的高斯扰动变异PGSA1～PGSA4
下载: 导出CSV
表 3 引入生长空间筛选机制的PGSA优化结果
Table 3. PGSA optimization results introducing screening mechanism of growth space
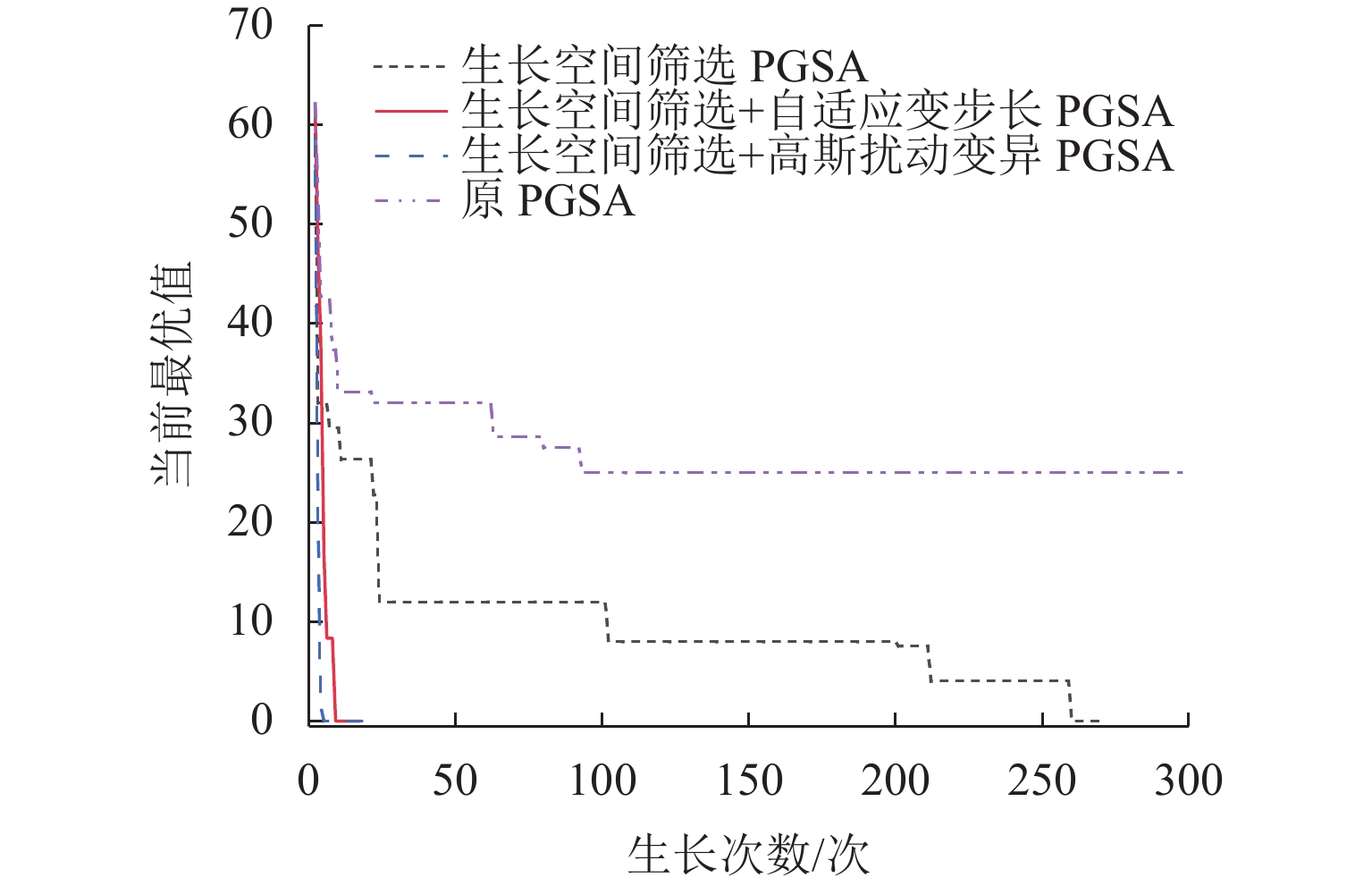
算法 收敛生长次数 优化结果 寻优耗时/s 生长空间 O 不收敛 18.00 60.742 6012 × 3C 265 0 2.767 746 × 3 C + A 8 0 0.051 142 × 3 C + B 11 0 0.244 533 × 3 注：算法C、C + A和C + B分别对应于图5中的生长空间筛选PGSA、生长空间筛选 + 自适应变步长PGSA和生长空间筛选 + 高斯扰动变异PGSA
下载: 导出CSV
表 4 多机制融合PGSA优化结果
Table 4. Optimization results of multi-mechanism fusion PGSA
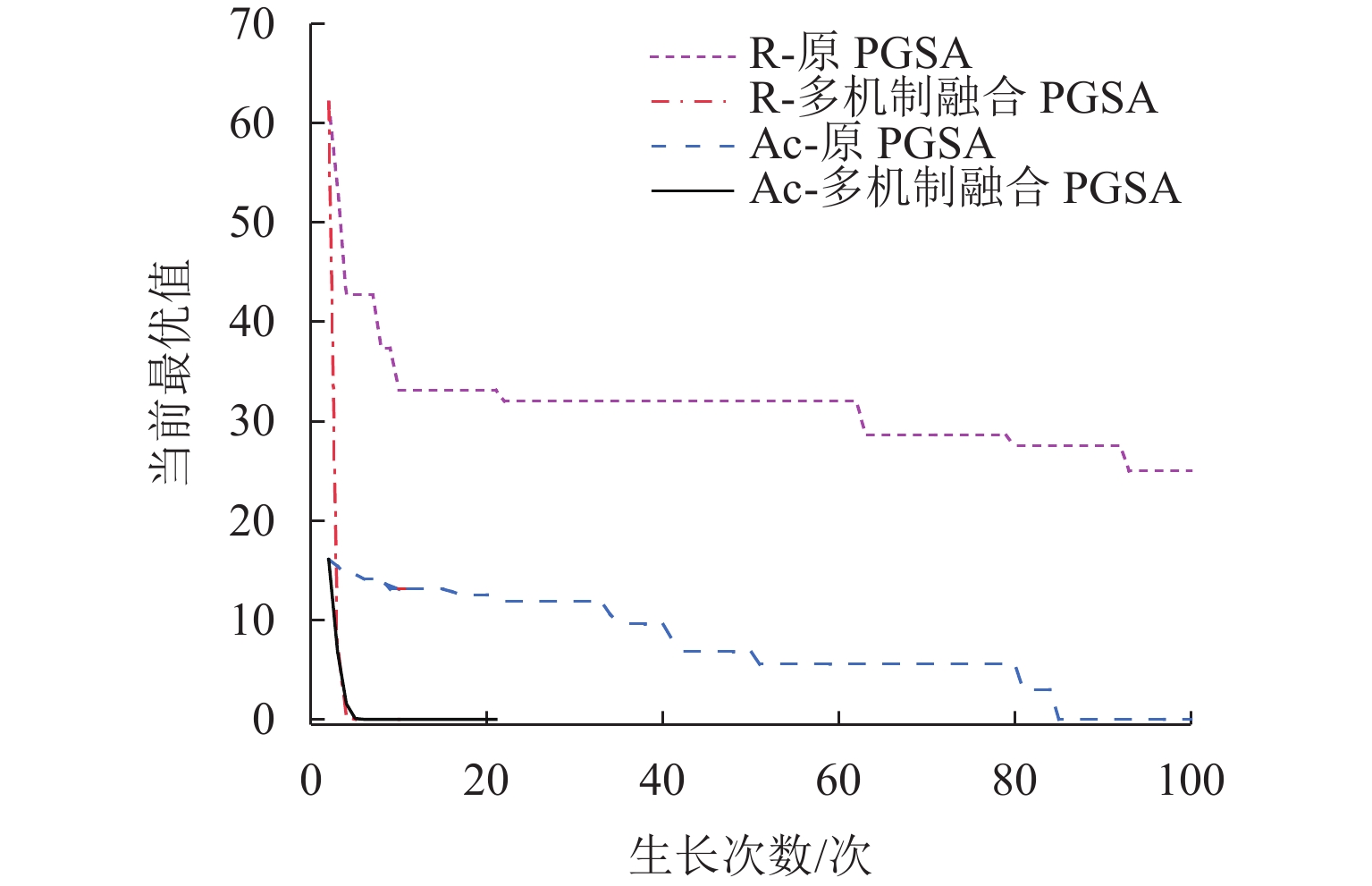
算法 收敛生长次数/次 寻优效果 寻优耗时/s 生长空间 R-O 不收敛 18.00 60.742 6012 × 3R-A+B+C 10 0.00 0.185 489 × 3 Ac-O 85 0.00 45.011 4746 × 3Ac-A+B+C 11 0.00 0.279 644 × 3 注：算法R-A+B+C、Ac-A+B+C分别对应于图7中的R-多机制融合PGSA、Ac-多机制融合PGSA
下载: 导出CSV
表 5 构件和材料规格
Table 5. Specifications of members and materials
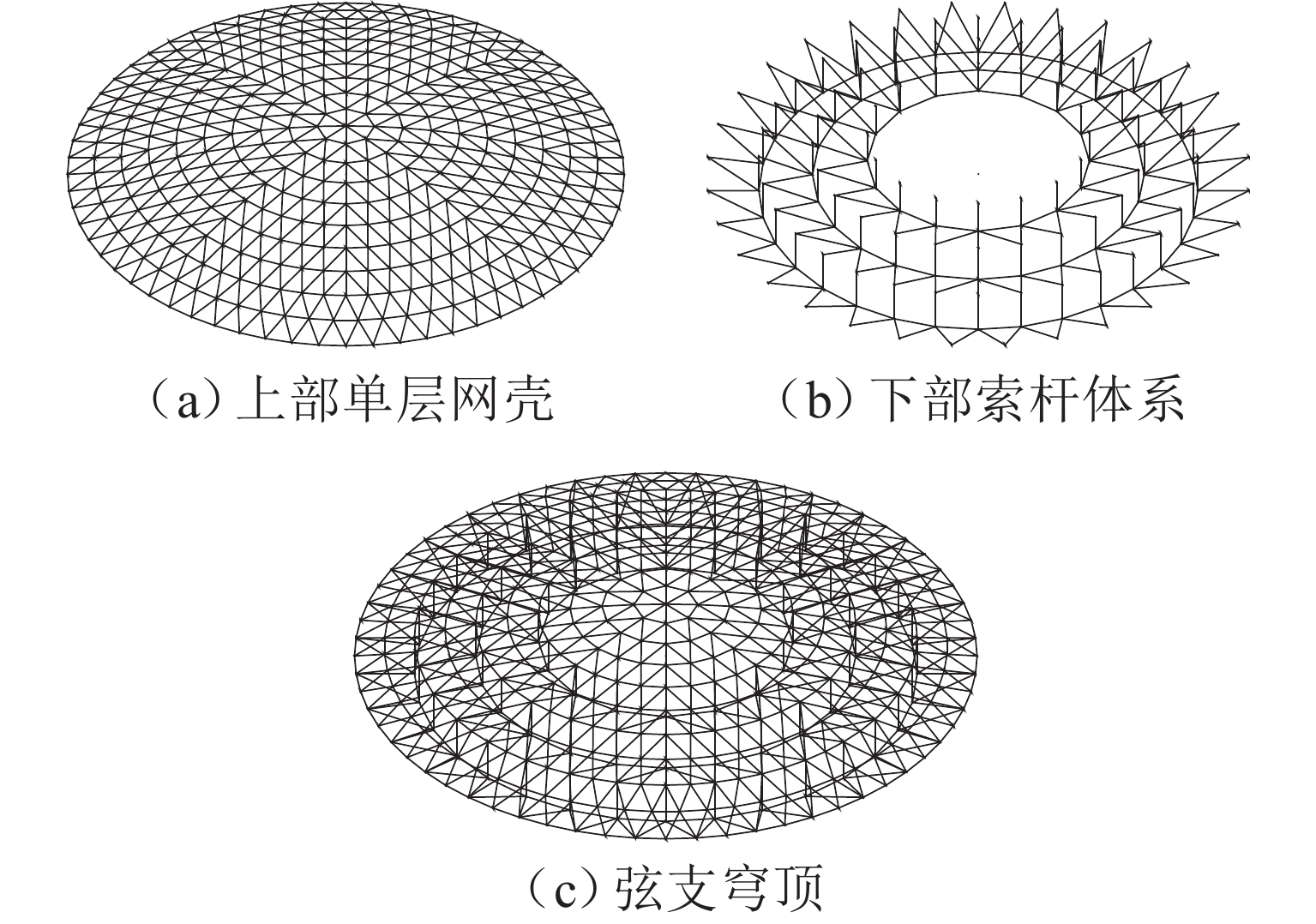
结构部位 构件 材质 规格 上部单层
网壳凯威特
部分径向杆 Q355B ϕ245 × 14 环向杆 Q355B ϕ245 × 14 斜杆 Q355B ϕ219 × 12 联方
部分环向杆 Q355B ϕ219 × 12 斜杆 Q355B ϕ203 × 12 下部索杆
体系撑杆 Q355B ϕ180 × 8 环向索 内圈 平行钢丝束， 1670 级ϕ5 × 61 中圈 平行钢丝束， 1670 级ϕ5 × 91 外圈 平行钢丝束， 1670 级ϕ5 × 139 径向索 平行钢丝束， 1670 级ϕ5 × 55
下载: 导出CSV
表 6 不同优化算法的关键参数设定
Table 6. Key parameter setting for different optimization algorithms
算法 关键参数 原 PGSA 步长为 5，Kmax = 1000 多机制融合PGSA dmin=0.1，d0=50，Kmax = 1000 ，s=0.3，Cs=100PSO 粒子个数为 10，惯性权重和全局增量均为 0.9 ASA 初始温度为 1.0，退火相对速率为 1.0，最大收敛步数为 5 MIGA 子群规模为 10，交叉概率为 1.0，变异概率为 0.01 Pointer 任务时间为 1，失败点的罚值和目标值均为1.0×1030
下载: 导出CSV
-
[1] KAWAGUCHI M, ABE M, TATEMICHI I. Design, tests and realization of “suspen-dome” system[J]. Journal of the International Association for Shell and Spatial Structures, 1999, 40(3): 179-192. [2] 姜正荣, 邱俊明, 石开荣, 等. 考虑杆件初弯曲的弦支穹顶结构非线性屈曲分析[J]. 西南交通大学学报, 2025, 60(3): 561-568.JIANG Zhengrong, QIU Junming, SHI Kairong, et al. Nonlinear buckling analysis of suspended domes considering initial curvature of members[J]. Journal of Southwest Jiaotong University, 2025, 60(3): 561-568. [3] 闫翔宇, 巩昊, 陈志华, 等. H型钢弦支穹顶结构弹塑性稳定性分析[J]. 空间结构, 2022, 28(3): 39-48.YAN Xiangyu, GONG Hao, CHEN Zhihua, et al. Elastic-plastic stability analysis of H-beam suspendome[J]. Spatial Structures, 2022, 28(3): 39-48. [4] 于敬海, 韩平, 李路川, 等. 天津中医药大学体育馆不连续支承弦支穹顶结构抗火分析[J]. 建筑结构, 2024, 54(9): 81-87, 94.YU Jinghai, HAN Ping, LI Luchuan, et al. Fire resistance analysis of suspen-dome structure with discontinuous support in gymnasium of Tianjin University of Traditional Chinese Medicine[J]. Building Structure, 2024, 54(9): 81-87, 94. [5] 陈丰, 潘睿, 王四清. 张家界大成俄罗斯马戏城主馆屋盖结构的稳定性、抗连续倒塌及施工模拟分析[J]. 建筑结构, 2020, 50(20): 54-58.CHEN Feng, PAN Rui, WANG Siqing. Analysis on the stability, progressive collapse resistance and construction simulation of the roof structure of Dacheng Russian Circus City main pavilion in Zhangjiajie[J]. Building Structure, 2020, 50(20): 54-58. [6] 李璐. 张弦结构在景德镇游泳馆中的应用[J]. 建筑结构, 2021, 51(增2): 335-339.LI Lu. Application of string structure in Jingdezhen swimming center[J]. Building Structure, 2021, 51(S2): 335-339. [7] 姜正荣, 王仕统, 石开荣, 等. 厚街体育馆大跨度椭圆抛物面弦支穹顶结构的非线性屈曲分析[J]. 土木工程学报, 2013, 46(9): 21-28.JIANG Zhengrong, WANG Shitong, SHI Kairong, et al. Nonlinear buckling analysis of long-span elliptic paraboloid suspended dome structure for Houjie Gymnasium[J]. China Civil Engineering Journal, 2013, 46(9): 21-28. [8] CHEN Y, YAN J Y, SAREH P, et al. Feasible prestress modes for cable-strut structures with multiple self-stress states using particle swarm optimization[J]. Journal of Computing in Civil Engineering, 2020, 34(3): 04020003. doi: 10.1061/(ASCE)CP.1943-5487.0000882 [9] POLLINI N. Gradient-based prestress and size optimization for the design of cable domes[J]. International Journal of Solids and Structures, 2021, 222: 111028. [10] KAVEH A, REZAEI M. Optimal design of double-layer domes considering different mechanical systems via ECBO[J]. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 2018, 42(4): 333-344. [11] 邱俊明. 弦支穹顶结构的预应力多目标优化及静力稳定性分析[D]. 广州: 华南理工大学, 2022. [12] 姜正荣, 苏延, 石开荣, 等. 交替提升与张拉的索穹顶结构施工优化方法[J]. 西南交通大学学报, 2024, 59(3): 663-669.JIANG Zhengrong, SU Yan, SHI Kairong, et al. Construction optimization method for cable domes with alternately lifting and tensioning[J]. Journal of Southwest Jiaotong University, 2024, 59(3): 663-669. [13] 李彤, 王春峰, 王文波, 等. 求解整数规划的一种仿生类全局优化算法——模拟植物生长算法[J]. 系统工程理论与实践, 2005, 25(1): 76-85.LI Tong, WANG Chunfeng, WANG Wenbo, et al. A global optimization bionics algorithm for solving integer programming—plant growth simulation algorithm[J]. Systems Engineering-theory & Practice, 2005, 25(1): 76-85. [14] 石开荣, 姜正荣, 潘文智. 基于模拟植物生长算法的空间结构优化方法[M]. 北京: 科学出版社, 2022. [15] SUN H X, ZHANG H, LEI Z M. Research on wind power optimization scheduling based on improved plant growth simulation algorithm[C]//Proceedings of 2019 Chinese Intelligent Automation Conference. Singapore: Springer, 2020: 473-481. [16] LI Y Q, WANG L, LIU F, et al. Optimization for minimum manufacturing costs of tower cranes based on the plant growth simulation algorithm[J]. Engineering Optimization, 2023, 55(2): 236-256. [17] 吕俊锋. 基于改进PGSA的高层悬挂结构优化设计方法及施工模拟分析[D]. 广州: 华南理工大学, 2018. [18] 石开荣, 林金龙, 姜正荣. 基于双生长点并行生长机制的模拟植物生长算法及其结构优化[J]. 建筑结构学报, 2022, 43(8): 240-247.SHI Kairong, LIN Jinlong, JIANG Zhengrong. Plant growth simulation algorithm based on double growth point parallel growth mechanism and its structural optimization[J]. Journal of Building Structures, 2022, 43(8): 240-247. [19] JIANG Z R, LIN Q P, SHI K R, et al. A novel PGSA–PSO hybrid algorithm for structural optimization[J]. Engineering Computations, 2019, 37(1): 144-160. doi: 10.1108/EC-01-2019-0025 [20] 姜正荣, 林全攀, 石开荣, 等. 基于混合智能优化算法的弦支穹顶结构预应力优化[J]. 华南理工大学学报(自然科学版), 2018, 46(9): 36-42.JIANG Zhengrong, LIN Quanpan, SHI Kairong, et al. Prestress optimization of suspended dome structures based on mixed intelligent optimization algorithm[J]. Journal of South China University of Technology (Natural Science Edition), 2018, 46(9): 36-42. [21] 姜正荣, 苏延, 石开荣, 等. 基于阶段生长PGSA的索穹顶结构预应力优化[J]. 华南理工大学学报(自然科学版), 2022, 50(11): 133-140, 154.JIANG Zhengrong, SU Yan, SHI Kairong, et al. Prestress optimization of cable domes with plant growth simulation algorithm based on stage growth[J]. Journal of South China University of Technology (Natural Science Edition), 2022, 50(11): 133-140, 154. [22] 张一帆. 基于改进模拟植物生长算法的桁架结构优化设计[D]. 邯郸: 河北工程大学, 2022. [23] 李顺, 郭星. 一种改进的自适应步长的萤火虫算法[J]. 微电子学与计算机, 2018, 35(8): 93-96, 100.LI Shun, GUO Xing. An improved glowworm swarm optimization alogorithm with adaptive step[J]. Microelectronics & Computer, 2018, 35(8): 93-96, 100. [24] 苏昌旺. 弦支穹顶结构的预应力优化方法与静力稳定性研究[D]. 广州: 华南理工大学, 2024. [25] 中华人民共和国住房和城乡建设部, 国家质量监督检验检疫总局. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017. [26] 赖宇阳, 方立桥, 李明, 等. Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012. -
下载:
点击查看大图
计量
- 文章访问数: 20
- HTML全文浏览量: 10
- PDF下载量: 0
- 被引次数: 0