落石冲击荷载计算方法研究

王玉锁; 田四明; 杨竣翔; 王明年; 王伟; 李传宝; 赵状; 肖鹏

doi:10.3969/j.issn.0258-2724.20240019

落石冲击荷载计算方法研究

doi: 10.3969/j.issn.0258-2724.20240019

王玉锁^1,,
田四明²,
杨竣翔¹,
王明年^1, ,,
王伟²,
李传宝²,
赵状¹,
肖鹏^{1, 3}

1.
西南交通大学土木工程学院，四川成都 611756
2.
中国铁路经济规划研究院有限公司，北京 100080
3.
西藏大学工学院，西藏拉萨 850000

基金项目: 四川省自然科学基金项目（2022NSFSC1127）；中央高校基本科研业务费专项资金（2682023CX075）

详细信息

作者简介:
王玉锁（1974—），男，副教授，博士，研究方向为隧道及地下工程，E-mai：lwangysuo@swjtu.edu.cn

通讯作者:
王明年（1965—），男，教授，博士，研究方向为隧道及地下工程，E-mail：19910622@163.com

中图分类号: P642.21
计量
- 文章访问数: 35
- HTML全文浏览量: 10
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2024-01-09
- 录用日期: 2025-05-12
- 修回日期: 2024-04-18
- 网络出版日期: 2025-05-19

Research on the Calculation Method of Falling Rock Impact Load

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 611756, China
2.
China Railway Economic and Planning Research Institute, Beijing 100080, China
3.
College of Engineering, Tibet University, Tibet 850000, China

摘要

摘要:
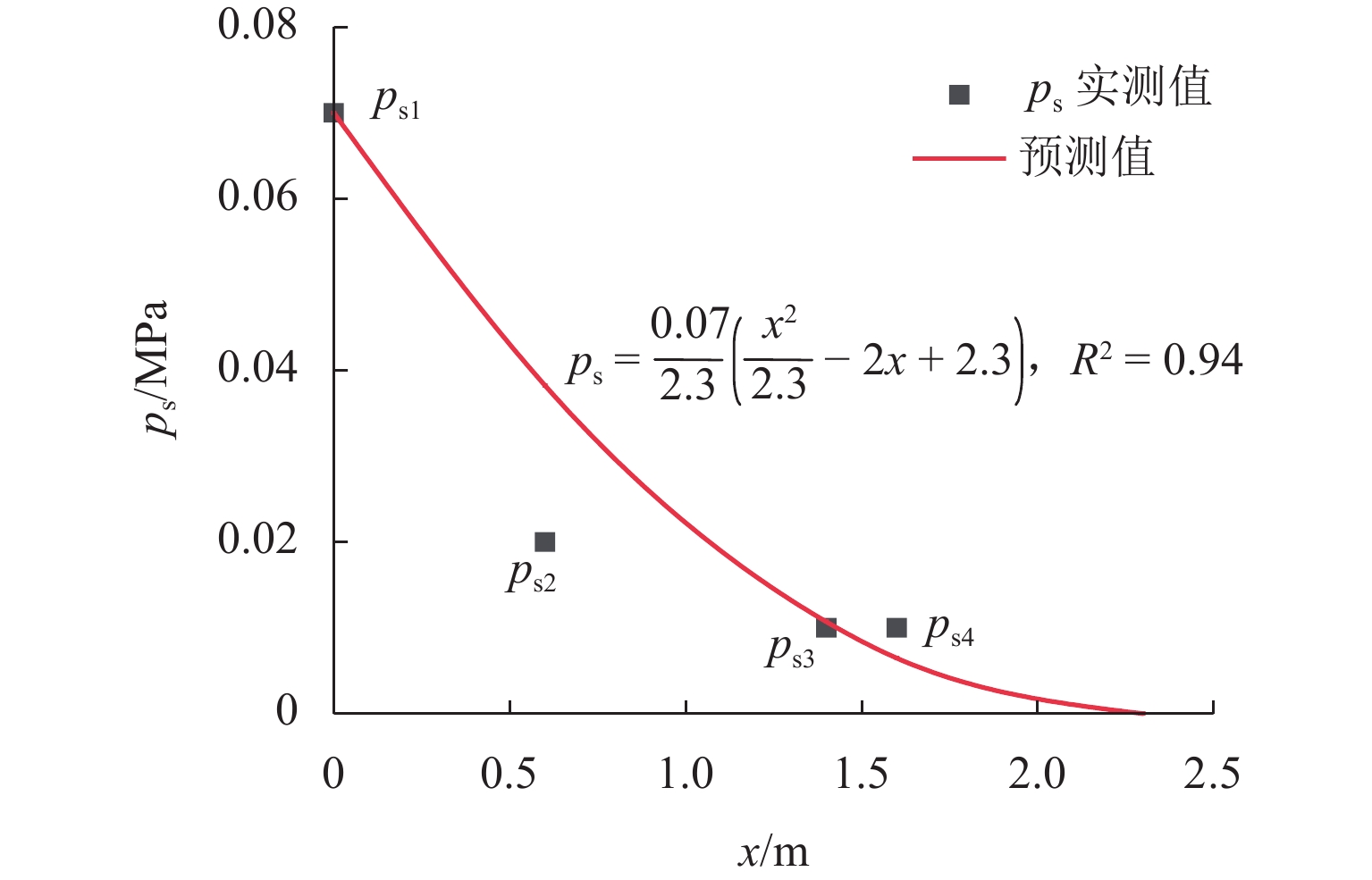
为明晰落石冲击力与冲击荷载的关系，定义能反映落石、缓冲土层及结构间相互作用的综合反射系数（其值越大说明对结构的冲击效应越显著），提出基于波动理论的落石冲击荷载计算方法. 通过落石冲击上覆缓冲土层拱形结构试验研究落石冲击荷载的大小和分布特征，得到综合反射系数的取值和影响规律，并利用所提出的计算方法分析落石冲击荷载和落石冲击力的关系；进一步明确结构的落石冲击荷载在横剖面上呈对称抛物线分布，可由拱顶处最大冲击压力峰值和结构跨度控制的二次抛物线曲线方程表征. 结果表明：在落石自由下落高度10 m及缓冲土层厚2.0 m范围内，综合反射系数与缓冲土层厚度呈显著负相关性；缓冲土层厚度2.0 m时其受落石形状及下落高度影响较小，可取0.55；当厚度为1.0 m和0.5 m时，立方体落石的综合反射系数要大于球面体或锥体落石，且与落石下落高度呈正相关性；结构所受落石冲击荷载的合力与落石对缓冲土层的冲击力与缓冲土层厚度和落石形状有关，当缓冲土层厚为2.0 m时二者接近，前者稍小于后者，将落石冲击荷载合力等于落石冲击力对结构设计是偏于安全的，当缓冲土层厚小于2.0 m时则反之，且厚度越小相差的倍数越大；缓冲土层厚1.0 m时，立方体落石冲击荷载合力较落石冲击力平均增大约20倍，而球顶锥体的增大约3倍，缓冲土层厚0.5 m时，两种形状的落石冲击荷载合力较落石冲击力平均增大分别约30倍和10倍；相同条件下，立方体落石的冲击荷载合力大于球顶锥体的，且随落石下落高度增大或缓冲土层厚度减小，立方体与球顶锥体相差倍数越大.
- 落石冲击荷载 /
- 缓冲土层 /
- 综合反射系数 /
- 落石冲击力
Abstract:
To clarify the relationship between rockfall impact force and impact load in civil engineering, a comprehensive reflection coefficient is introduced to reflect the interaction between falling rocks, cushioning soil layers, and structures (a higher value indicates a more significant impact effect on the structure). A rockfall impact load calculation method based on wave theory is proposed. The size and distribution characteristics of rockfall impact loads were studied through experiments on arched structures with overlying cushioning soil layers subjected to rockfall impacts. The values and influencing patterns of the comprehensive reflection coefficient were obtained. The proposed calculation method was used to analyze the relationship between rockfall impact loads and rockfall impact forces. Through the research, it was clarified that the rockfall impact load on the structure presents a symmetrical parabolic distribution on the cross-section and can be characterized by a quadratic parabolic curve equation controlled by the maximum impact pressure peak at the arch crown and the structural span. The results indicate that within a range of 10 meters of free fall height for falling rocks and a cushioning soil layer thickness of 2.0 meters, there is a significant negative correlation between the comprehensive reflection coefficient and the thickness of the cushioning soil layer. When the thickness of the cushioning soil layer is 2.0 meters, its influence on the shape and free fall height of the falling rock is relatively small, and a value of 0.55 can be used. When the thickness is 1.0 meter and 0.5 meters, the comprehensive reflection coefficient of cuboid falling rocks is greater than that of spherical or conical falling rocks, and it is positively correlated with the falling height of the rocks. The relationship between the resultant force of rockfall impact loads on the structure and the impact force of rocks on the cushioning soil layer depends on the thickness of the cushioning soil layer and the shape of the falling rocks. When the thickness of the cushioning soil layer is 2.0 meters, the two are close, with the former slightly smaller than the latter, making the resultant force of rockfall impact loads equal to the rockfall impact force on the structure, which leans towards safety in structural design. However, when the thickness of the cushioning soil layer is less than 2.0 meters, the reverse is true, and the smaller the thickness, the greater the difference. When the thickness of the cushioning soil layer is 1.0 meter, the average increase of cuboid falling rocks is about 20 times larger than that of spherical or conical ones, and when the thickness is 0.5 meters, the average increase is about 30 and 10 times respectively for the two shapes. Under the same conditions, the resultant impact load of cuboid falling rocks is greater than that of spherical or conical ones, and the difference between them increases as the falling height of the rocks increases or the thickness of the cushioning soil layer decreases.
- impact load of falling rock /
- buffer soil layer /
- composite reflection coefficient /
- impact force of falling rock

HTML全文

图 1 落石冲击荷载计算模型

Figure 1. Calculation model of falling rock impact load

下载: 全尺寸图片幻灯片

图 2 测点布置及编号

Figure 2. Layout and numbering of measurement points

下载: 全尺寸图片幻灯片

图 3 落石冲击荷载测点值

Figure 3. Measurement point value of falling rock impact load

下载: 全尺寸图片幻灯片

图 4 p_s及其分布形式（单位：MPa）

Figure 4. p_s and its distribution form （unit: MPa）

下载: 全尺寸图片幻灯片

图 5 落石冲击荷载分布形式

Figure 5. Distribution forms of falling rock impact load

下载: 全尺寸图片幻灯片

图 6 落石冲击荷载试验实测值与预测值对比

Figure 6. Comparison of measured and predicted values of falling rock impact load test

下载: 全尺寸图片幻灯片

图 7 p_s1理论与试验结果对比

Figure 7. Comparison of theoretical calculation results and test results of maximum impact pressure peak p_s1

下载: 全尺寸图片幻灯片

图 8 落石冲击力和落石冲击荷载（合力）对比

Figure 8. Comparison of falling rock impact force and impact load （resultant force）

下载: 全尺寸图片幻灯片

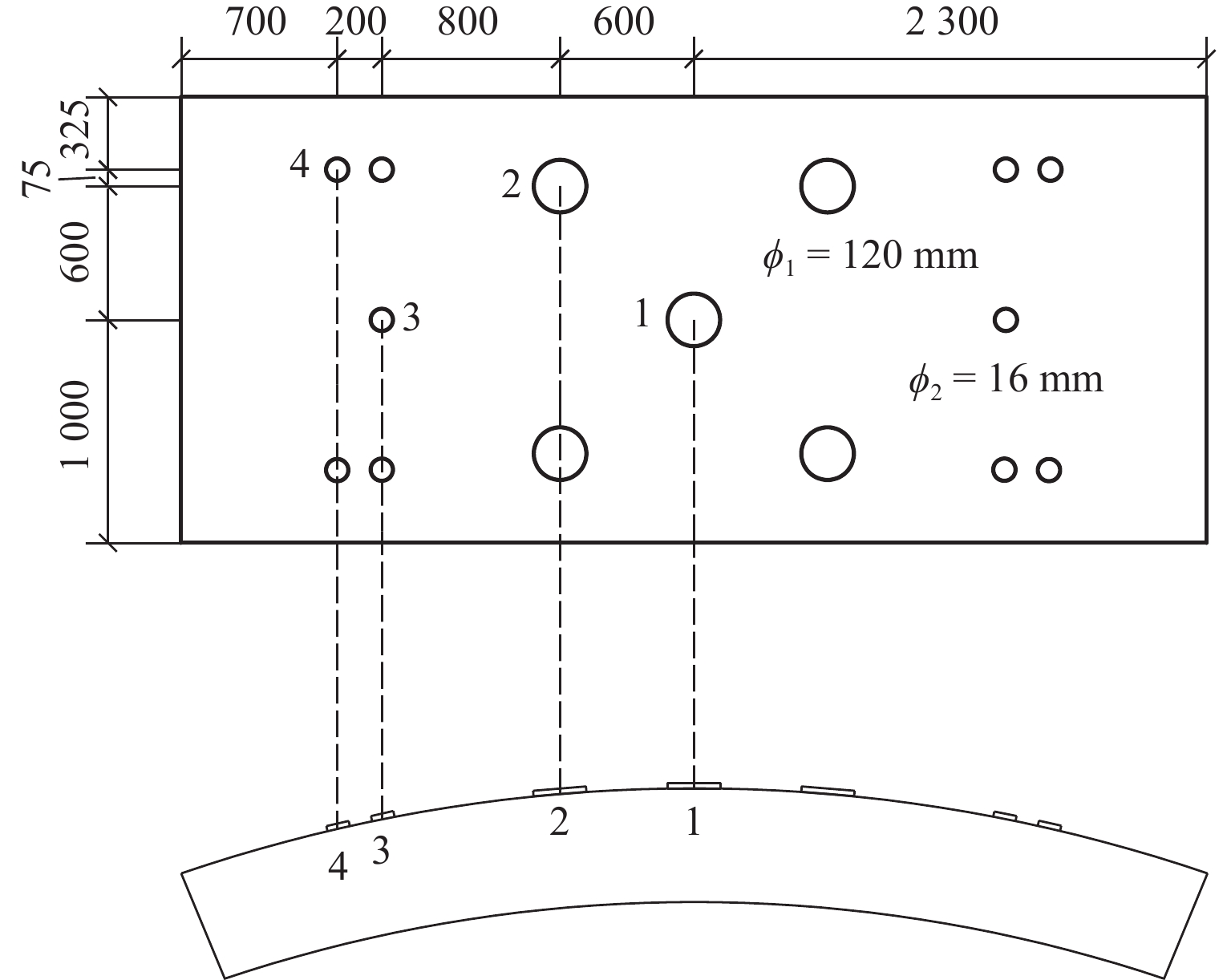
表 1 落石冲击荷载试验结果

Table 1. Test results of falling rock impact load

工况	落石形状	落石质量 M/kg	h/m	H/m	冲击深度 δ_max/m	F_max/kN	S/m²	p_max/MPa	p_s1/MPa	p_s2/MPa	p_s3/MPa	p_s4/MPa
1	立方体	2200	2.0	1	0.17	266	1.00	0.27	0.07	0.02	0.01	0.01
2		2200	2.0	5	0.40	226	1.00	0.23	0.18	0.06	0.02	0.01
3		2200	2.0	10	0.51	836	1.00	0.84	0.32	0.11	0.02	0.01
4		2200	1.0	1	0.08	87	1.00	0.09	0.33	0.11	0.02	0.02
5		2200	1.0	5	0.15	135	1.00	0.13	1.50	0.12	0.02	0.02
6		2200	1.0	10	0.22	266	1.00	0.27	2.28	0.11	0.02	0.02
7		2200	0.5	1	0.08	49	1.00	0.05	1.03	0.15	0.02	0.02
8		2200	0.5	5	0.11	314	1.00	0.31	2.24	0.32	0.02	0.02
9		2200	0.5	10	0.19	645	1.00	0.64	4.8	0.41	0.03	0.03
10	球顶锥体	2280	2.0	1	0.35	181	1.45	0.12	0.07	0.01	0.01	0.01
11		2280	2.0	5	0.48	541	1.57	0.34	0.16	0.06	0.02	0.01
12		2280	2.0	10	0.66	870	1.57	0.55	0.29	0.11	0.02	0.01
13		2280	1.0	1	0.22	231	0.79	0.46	0.37	0.03	0.01	0.01
14		2280	1.0	5	0.35	234	1.45	0.16	0.44	0.08	0.01	0.02
15		2280	1.0	10	0.45	828	1.57	0.53	0.59	0.14	0.02	0.05
16		2280	0.5	1	0.24	281	0.61	0.46	0.65	0.03	0.01	0.01
17		2280	0.5	5	0.30	367	0.96	0.38	1.24	0.07	0.01	0.05
18		2280	0.5	10	0.37	469	1.20	0.39	3.56	0.95	0.03	0.03

下载: 导出CSV

表 2 落石冲击最大压力峰值相关性分析

Table 2. Correlation analysis of maximum pressure peak of falling rock impact

因变量	落石形状	缓冲土层厚度	落石高度
皮尔逊相关性	−0.232	−0.625^**	0.498^*
显著性（双尾）	0.353	0.006	0.036
个案数	18	18	18
注：*. 在 0.01 级别（双尾），相关性显著；. 在 0.05 级别（双尾），相关性显著.

下载: 导出CSV

表 3 综合反射系数

Table 3. Comprehensive reflection coefficient

工况	落石形状	h/m	H/m	k_f
工况	落石形状	h/m	H/m	取值	平均值
1	立方体	2.0	1	0.29	0.53
2			5	0.88
3			10	0.42
4		1.0	1	3.99	6.50
5			5	11.72^*
6			10	9.00
7		0.5	1	21.43^*	7.50
8			5	7.32
9			10	7.63
10	球顶锥体	2.0	1	0.62	0.57
11			5	0.51
12			10	0.58
13		1.0	1	0.84	1.63
14			5	2.86
15			10	1.18
16		0.5	1	1.45	4.71
17			5	3.33
18			10	9.34
注：带*数值按异常值未参与平均值计算.

下载: 导出CSV

表 4 p_s1理论计算结果与试验结果对比

Table 4. Comparison of theoretical calculation results and test results of maximum impact pressure peak p_s1

工况	理论 F_max/KN	理论 δ_max/m	S/m²	p_s1/MPa
工况	理论 F_max/KN	理论 δ_max/m	S/m²	理论	试验	误差
1	202.3	0.17	1.00	0.10	0.07	0.43
2	593.8	0.36	1.00	0.28	0.18	0.56
3	935.5	0.49	1.00	0.45	0.32	0.41
4	202.3	0.17	1.00	1.25	0.33	2.79
5	593.8	0.36	1.00	3.67	1.5	1.45
6	935.5	0.49	1.00	5.78	2.28	1.54
7	202.3	0.17	1.00	1.48	1.03	0.44
8	593.8	0.36	1.00	4.34	2.24	0.94
9	935.5	0.49	1.00	6.84	4.80	0.43
10	189.6	0.19	0.68	0.14	0.07	1.00
11	556.6	0.40	1.57	0.18	0.16	0.13
12	877.0	0.55	1.57	0.29	0.29	0
13	189.6	0.19	0.68	0.43	0.37	0.16
14	556.6	0.40	1.57	0.55	0.44	0.25
15	877.0	0.55	1.57	0.87	0.59	0.47
16	189.6	0.19	0.68	1.28	0.65	0.97
17	556.6	0.40	1.57	1.63	1.24	0.31
18	877.0	0.55	1.57	2.57	3.56	−0.28
注：误差=（理论−试验） /试验.

下载: 导出CSV

表 5 落石冲击力与落石冲击荷载（合力）比较

Table 5. Comparison of falling rock impact force and impact load （resultant force）

h/m	形状	工况	F_max/kN	P/kN	（P−F_max）/F_max
h/m	形状	工况	F_max/kN	P/kN	值	平均值
2.0	立方体	1	266	194	−0.27	−0.11
		2	226^*	498	1.20^*
		3	836	886	0.06
	球顶椎体	10	181	194	0.07	−0.06
		11	541	443	−0.18
		12	870	803	−0.08
1.0	立方体	4	87	914	9.51	20.69
		5	135	4153	29.85
		6	266	6312	22.69
	球顶椎体	13	231	1024	3.44	2.87
		14	234	1218	4.20
		15	828	1633	0.97
0.5	立方体	7	49	2851	56.86	31.75
		8	314	6201	18.77
		9	645	13288	19.61
	球顶椎体	16	281	1799	5.41	11.26
		17	367	3433	8.37
		18	469	9856	20.01
注：带 * 值按异常值未参与平均值计算.

下载: 导出CSV

参考文献(26)

[1]	铁道第二勘测设计院. 铁路工程设计技术手册. 隧道[M]. 北京:中国铁道出版社,1999.
[2]	交通部第二公路勘察设计研究院. 公路路基设计规范:JTJ013—95 [S]. 北京:人民交通出版社,1995.
[3]	LABIOUSE V, DESCOEUDRES F, MONTANI S. Experimental study of rock sheds impacted by rock blocks[J]. Structural Engineering International, 1996, 6(3): 171-176.
[4]	YOSHIDA H, MASUYA H, IHARA T, et al. Experimental study of impulsive design load for rock sheds[J]. IABSE Proceedings, 1988, 127:61-74.
[5]	DI PRISCO C, VECCHIOTTI M. Design charts for evaluating impact forces on dissipative granular soil cushions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(11): 1529-1541. doi: 10.1061/(ASCE)GT.1943-5606.0000363
[6]	CHEN T J, ZHANG G C, XIANG X. Research on rockfall impact process based on viscoelastic contact theory[J]. International Journal of Impact Engineering, 2023, 173: 104431.1-104431.8.
[7]	KAWAHARA S, MURO T. Effects of dry density and thickness of sandy soil on impact response due to rockfall[J]. Journal of Terramechanics, 2006, 43(3): 329-340. doi: 10.1016/j.jterra.2005.05.009
[8]	杨其新,关宝树. 落石冲击力计算方法的试验研究[J]. 铁道学报,1996,18(1): 101-106. doi: 10.3321/j.issn:1001-8360.1996.01.017 YANG Qixin, GUAN Baoshu. Test and research on calculating method of falling stone impulsive force[J]. Journal of the China Railway Society, 1996, 18(1): 101-106. doi: 10.3321/j.issn:1001-8360.1996.01.017
[9]	ZHAO P, XIE L Z, LI L P, et al. Large-scale rockfall impact experiments on a RC rock-shed with a newly proposed cushion layer composed of sand and EPE[J]. Engineering Structures, 2018, 175: 386-398. doi: 10.1016/j.engstruct.2018.08.046
[10]	吴建利,胡卸文,梅雪峰,等. 落石冲击混凝土板与缓冲层组合结构的动力响应[J]. 水文地质工程地质,2021,48(1): 78-87. WU Jianli, HU Xiewen, MEI Xuefeng, et al. Dynamic response of RC slab with cushion layer composed of sandy soil to rockfall impact[J]. Hydrogeology & Engineering Geology, 2021, 48(1): 78-87.
[11]	YU B X, ZHOU X J, TANG J H, et al. Impact resistance performance and optimization of the sand-EPE composite cushion in rock sheds[J]. Journal of Mountain Science, 2024, 21(2): 676-689. doi: 10.1007/s11629-023-8403-0
[12]	BHATTI A Q, KISHI N. Impact response of RC rock-shed girder with sand cushion under falling load[J]. Nuclear Engineering and Design, 2010, 240(10): 2626-2632. doi: 10.1016/j.nucengdes.2010.07.029
[13]	何思明,沈均,吴永. 滚石冲击荷载下棚洞结构动力响应[J]. 岩土力学,2011,32(3): 781-788. doi: 10.3969/j.issn.1000-7598.2011.03.024 HE Siming, SHEN Jun, WU Yong. Rock shed dynamic response to impact of rock-fall[J]. Rock and Soil Mechanics, 2011, 32(3): 781-788. doi: 10.3969/j.issn.1000-7598.2011.03.024
[14]	王玉锁,李俊杰,李正辉,等. 落石冲击力评定的离散元颗粒流数值模拟[J]. 西南交通大学学报,2016,51(1): 22-29. doi: 10.3969/j.issn.0258-2724.2016.01.004 WANG Yusuo, LI Junjie, LI Zhenghui, et al. Assessment of rockfall impact force by particle flow code numerical simulation based on discrete element model[J]. Journal of Southwest Jiaotong University, 2016, 51(1): 22-29. doi: 10.3969/j.issn.0258-2724.2016.01.004
[15]	裴向军,刘洋,王东坡. 滚石冲击棚洞砂土垫层耗能缓冲机理研究[J]. 四川大学学报(工程科学版),2016,48(1):15-22. PEI Xiangjun,LIU Yang,WANG Dongpo. Study on the energy dissipation of sandy soil cushions on the rock-shed under rockfall impact load[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(1):15-22.
[16]	王玉锁,周良,李正辉,等. 落石冲击下单压式拱形明洞的力学响应[J]. 西南交通大学学报,2017,52(3):505-515. WANG Yusuo, ZHOU Liang, LI Zhenghui, et al. Mechanical responses of single-pressure arch-shaped open tunnel structure under rockfall impaction[J]. Journal of Southwest Jiaotong University, 2017, 52(3):505-515.
[17]	王玉锁,王涛,周良,等. 跨中受落石冲击的拱形护桥明洞力学响应[J]. 隧道建设(中英文),2018,38(1): 22-32. WANG Yusuo, WANG Tao, ZHOU Liang, et al. Mechanical responses of arched protection shed of bridge under rock-fall impaction on midspan of rooftop[J]. Tunnel Construction, 2018, 38(1): 22-32.
[18]	王玉锁,周良,王涛,等. 落石冲击下单压式拱形明洞的回填方式[J]. 中国铁道科学,2018,39(2): 71-79. doi: 10.3969/j.issn.1001-4632.2018.02.09 WANG Yusuo, ZHOU Liang, WANG Tao, et al. Backfill modes of single-pressure arch-shaped open tunnel under rockfall impact[J]. China Railway Science, 2018, 39(2): 71-79. doi: 10.3969/j.issn.1001-4632.2018.02.09
[19]	中华人民共和国住房和城乡建设部. 铁路工程结构可靠性设计统一标准:GB 50216—2019[S]. 北京:中国计划出版社,2019.
[20]	中华人民共和国住房和城乡建设部. 建筑结构可靠性设计统一标准GB 50068—2018[S]. 北京:中国建筑工业出版社,2018.
[21]	KRAUTHAMMER T, PUGLISI R D. Simplified analysis of buried reinforced concrete Arches under simulated nuclear loads[J]. Computers & Structures, 1992, 43(6): 1029-1039.
[22]	周健南,金丰年,范华林,等. 震后地下拱结构的抗冲击波动载能力评估[J]. 工程力学,2012,29(2): 159-164,171. ZHOU Jiannan, JIN Fengnian, FAN Hualin, et al. Residual dynamic resistance of seismic damaged underground arch[J]. Engineering Mechanics, 2012, 29(2): 159-164,171.
[23]	钱七虎. 钱七虎院士论文选集[M]. 北京:科学出版社,2007.
[24]	中华人民共和国住房和城乡建设部. 建筑抗震设计规范:GB50011—2010(2016年版)[S]. 北京:中国建筑工业出版社,2016.
[25]	王玉锁,杨竣翔,肖宗扬,等. 落石对缓冲土层的冲击力及冲击深度理论与试验研究[J]. 西南交通大学学报,西南交通大学学报,2024,9(5): 1078-1085. WANG Yusuo, YANG Junxiang, XIAO Zongyang, et al. Theoretical and test study of impact force and impact depth of falling rocks on buffering soil layers[J]. Journal of Southwest Jiaotong University, 2024, 9(5): 1078-1085.
[26]	黄晓玉,王兰会. SPSS 24.0 统计分析[M]. 北京:中国人民大学出版社,2021.