Optimized Control Method for Guidance System of High-Speed Maglev Train
-
摘要:
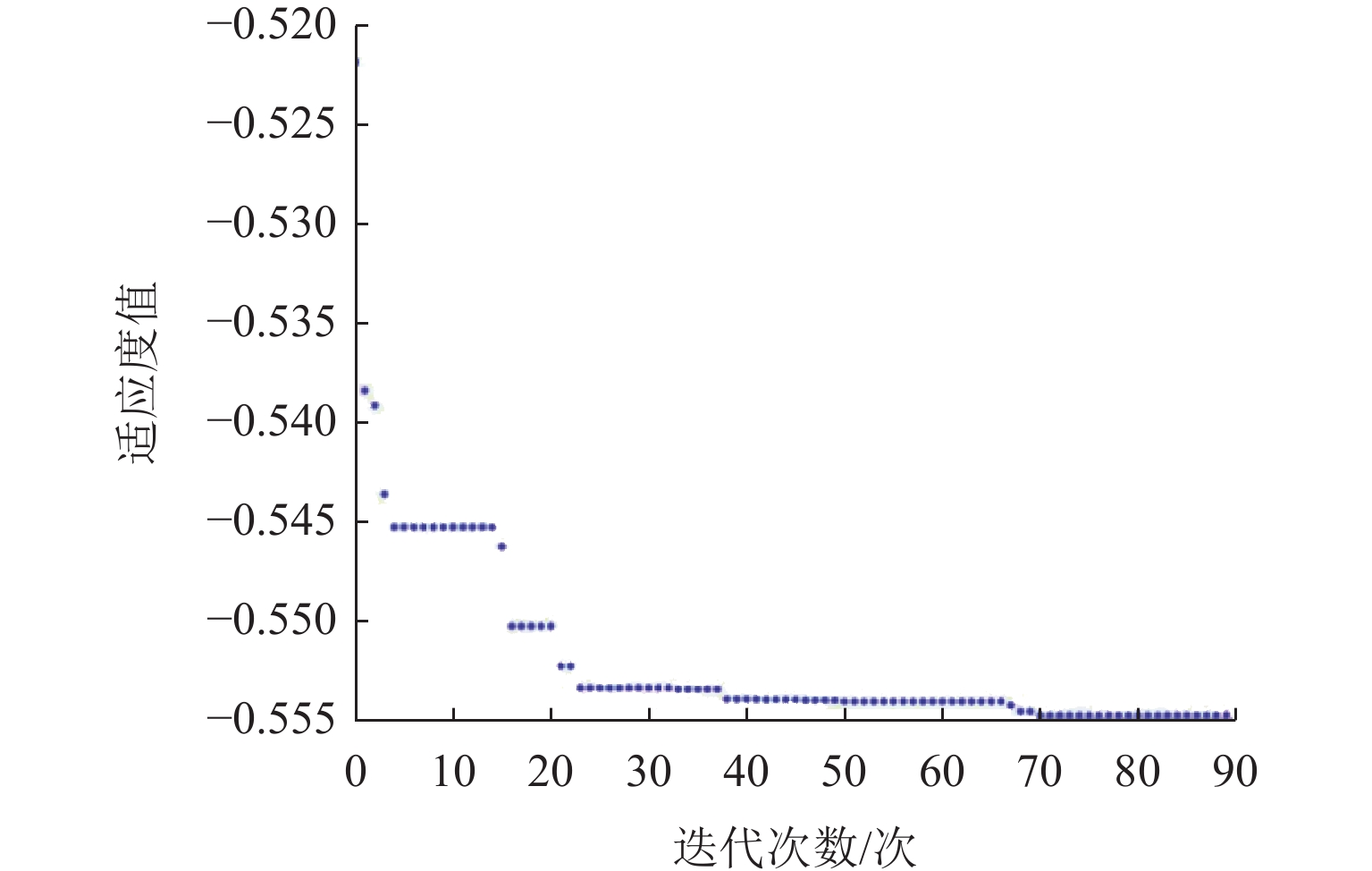
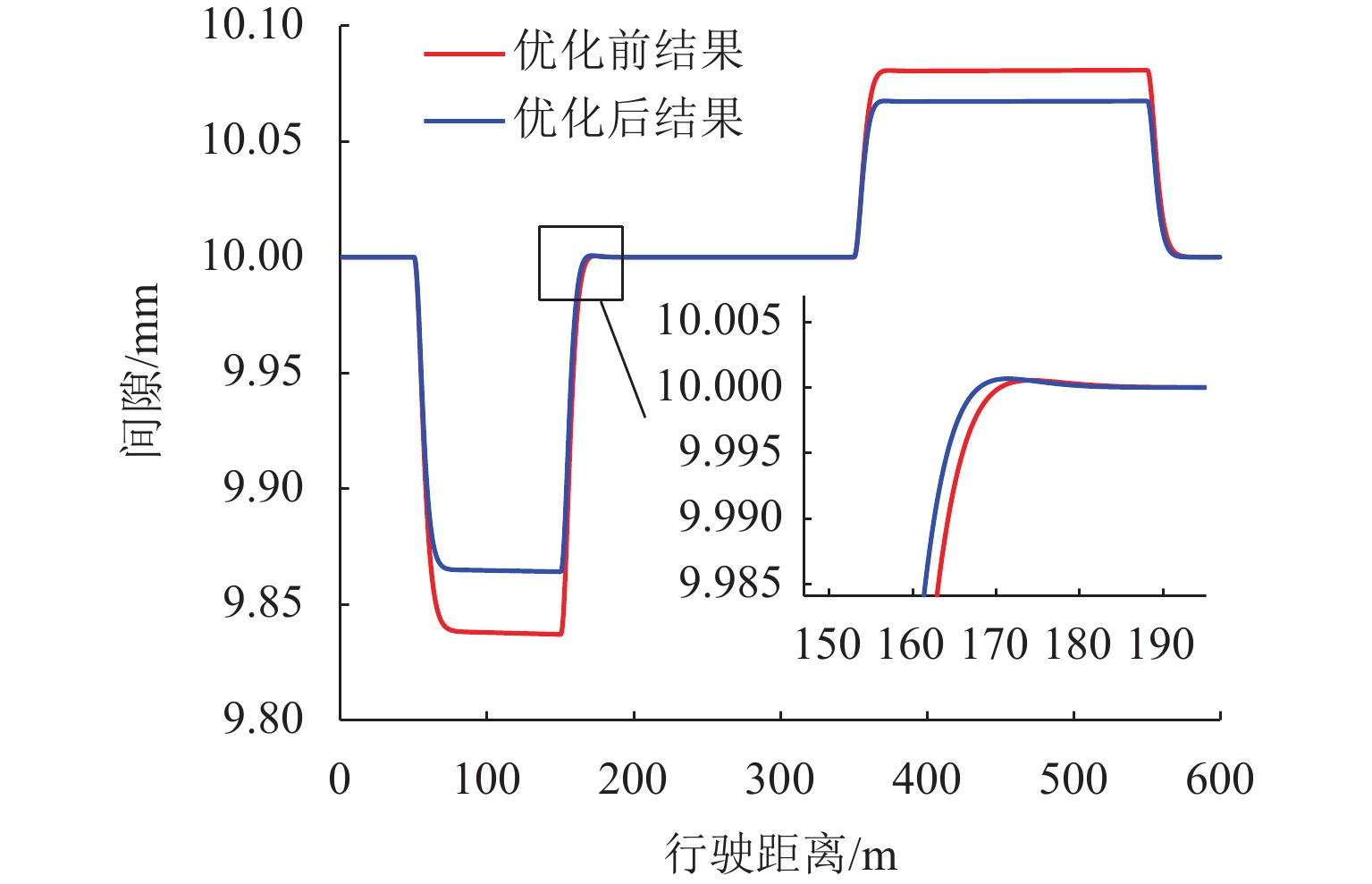
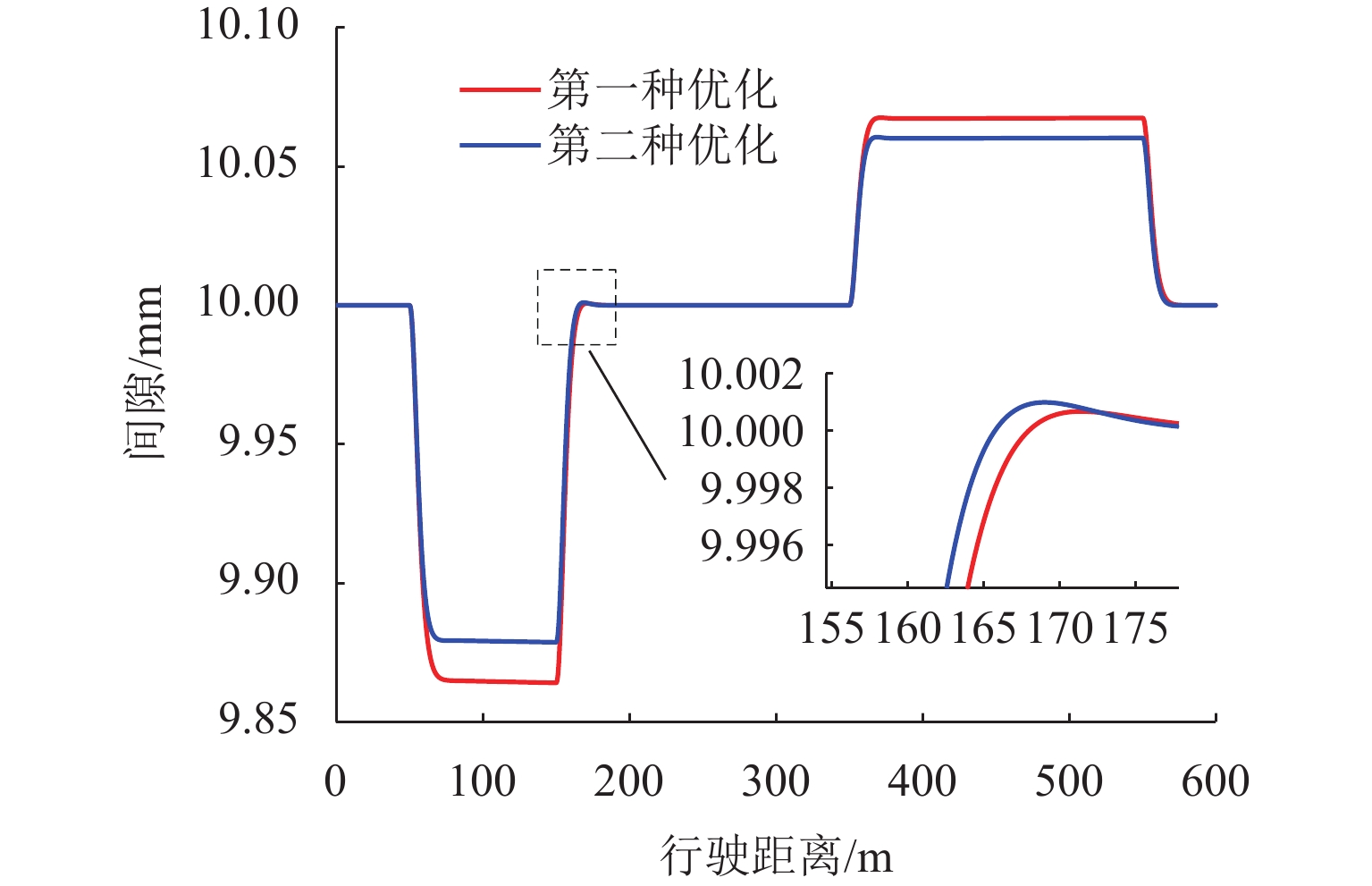
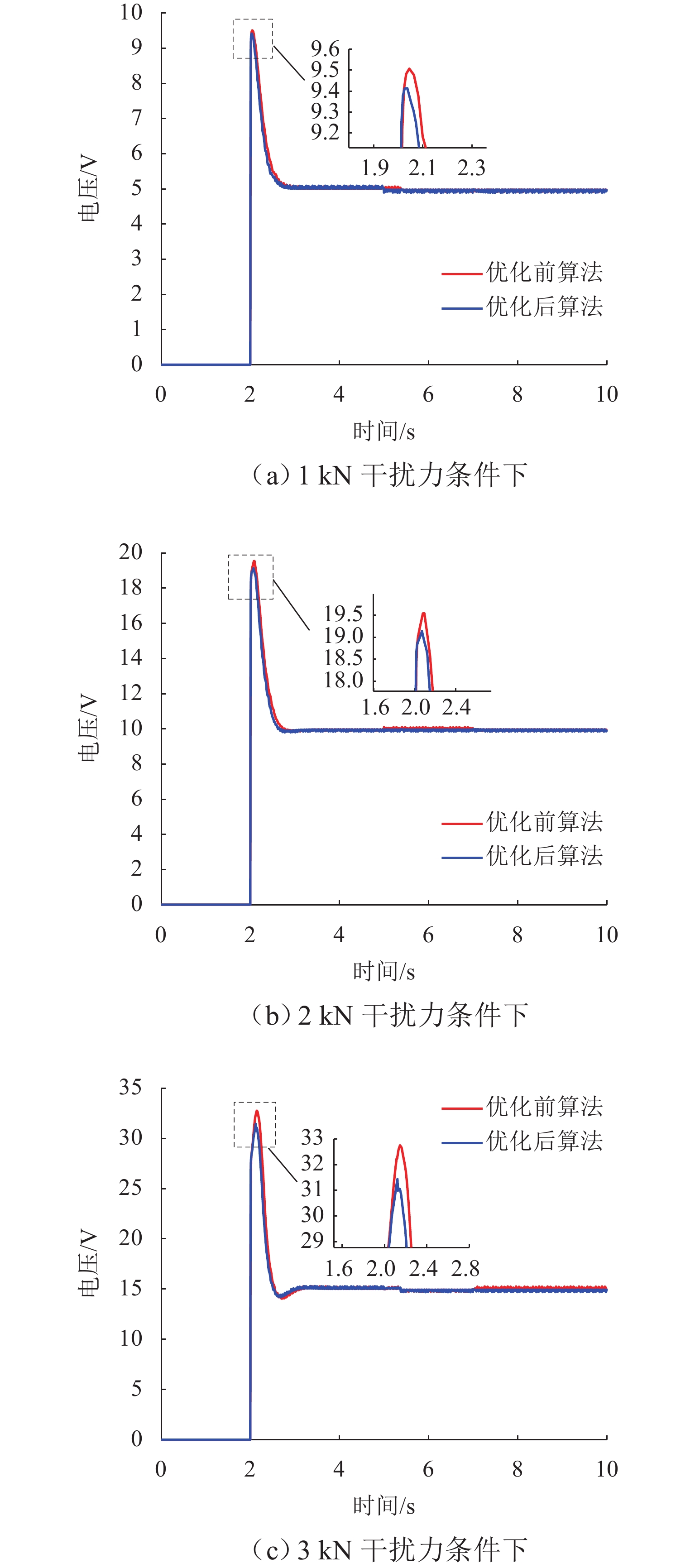
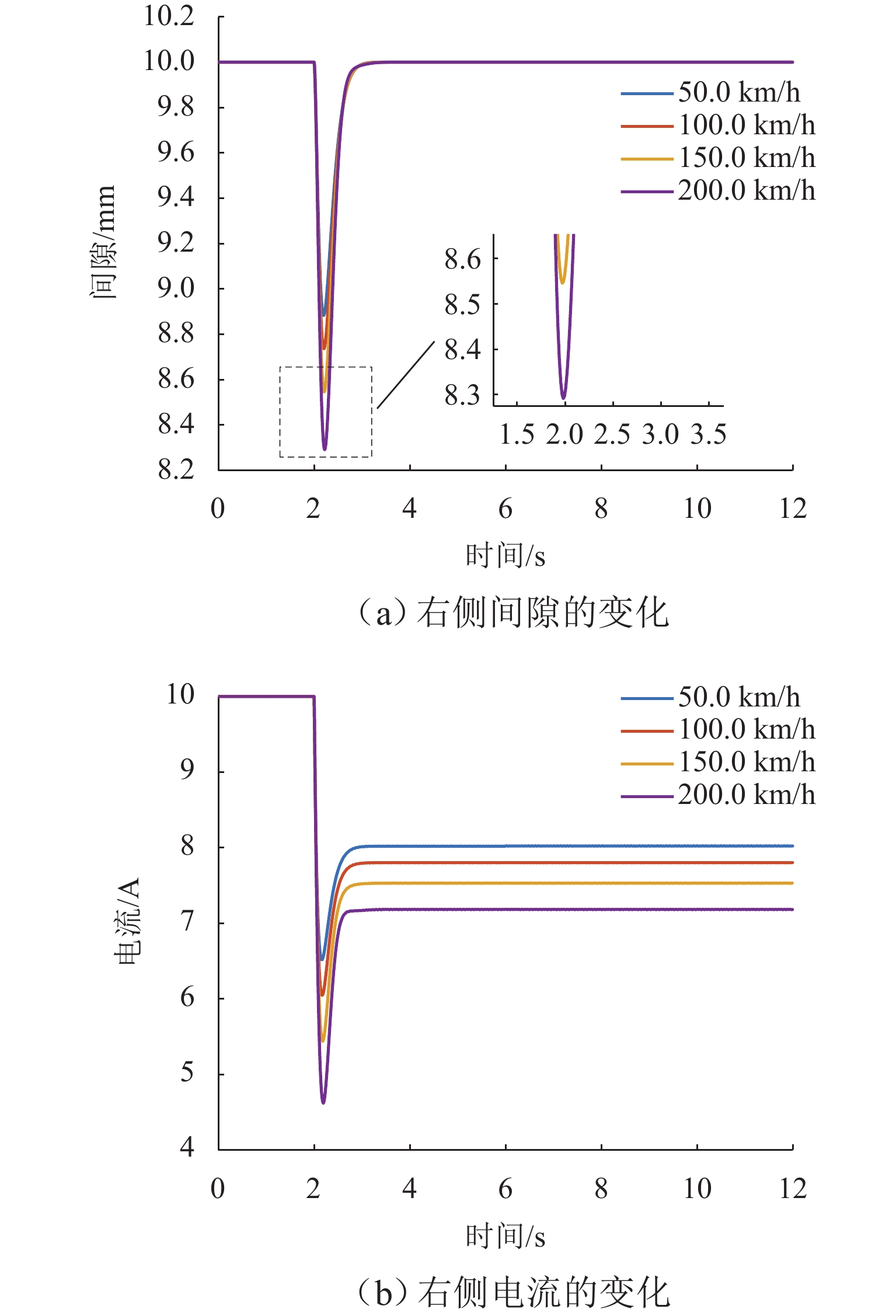
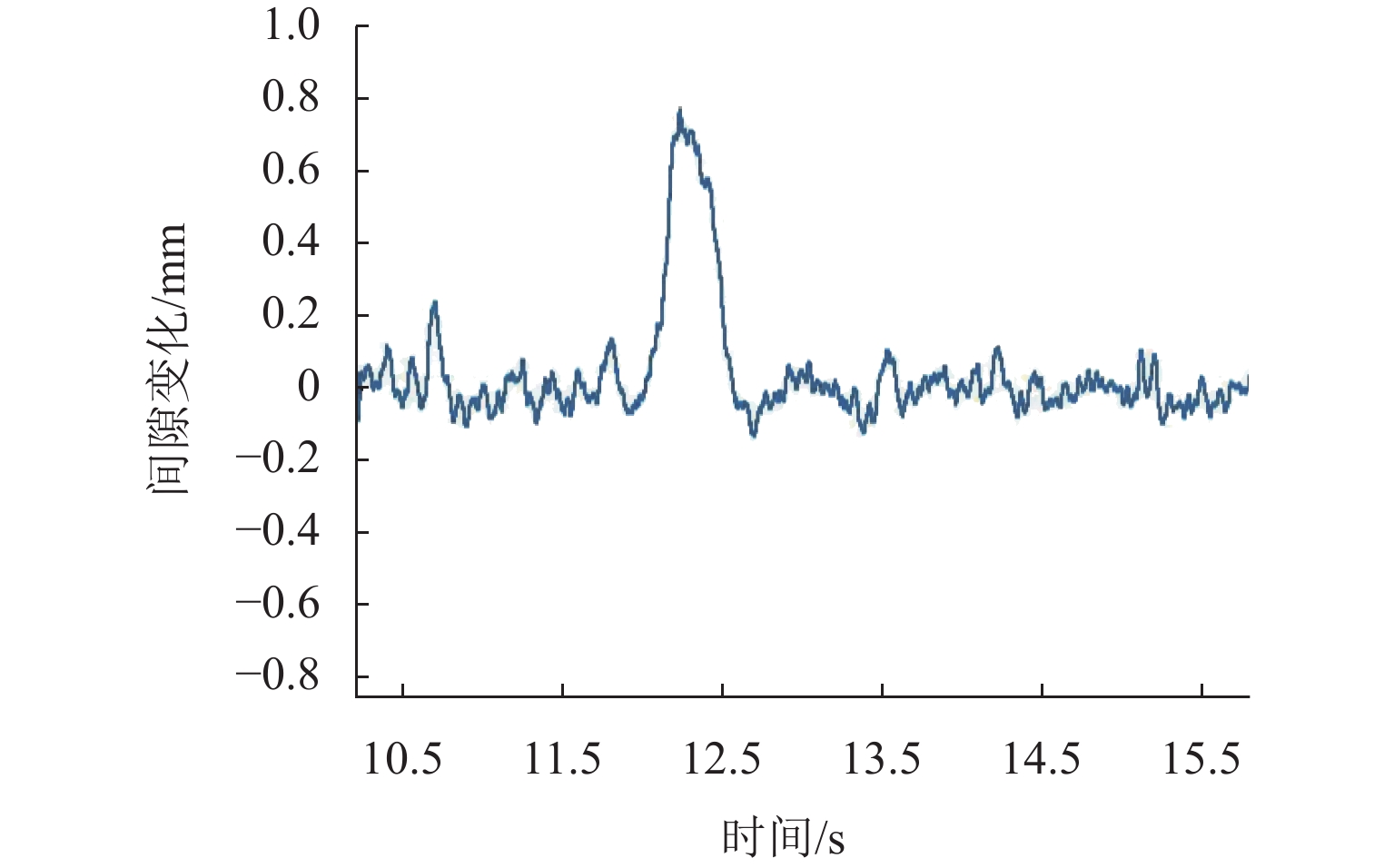
为进一步优化和改善高速磁浮列车导向系统的控制性能，以高速磁浮列车导向系统为研究对象，在基于搭接结构导向系统的数学模型基础上进行导向控制器的设计和仿真实验；分析高速磁浮列车在通过弯道时的情况，考虑了2种工作条件（磁浮列车以不同速度通过弯道、磁浮列车受到不同大小的侧向干扰力）建立考虑扰动的导向系统数学模型，采用线性二次型最优控制方法设计导向系统标称控制器，并利用粒子群优化算法对控制器参数进行优化；建立了导向系统的仿真模型，通过仿真平台分析导向系统在2种特定工作条件下的系统响应，并将优化前后算法进行对比. 研究结果表明：1、2、3 kN模拟干扰力情况下，导向间隙波动幅值分别减小9.46%、9.70%、11.82%，相比于优化前的算法，优化后导向系统间隙恢复速度有所提升；优化后的算法在改善列车通过弯道及受到横风干扰时的性能方面均具有一定的提升作用，证明了优化算法的有效性及可靠性.
Abstract:To further enhance the control performance of the guidance system for high-speed maglev trains, the guidance system was taken as the research subject, and the design and simulation of a guidance controller were carried out based on the mathematical model of a jointed guidance system. The behavior of the maglev train navigating through curves was analyzed under two operating conditions: different velocities while navigating curves and varying magnitudes of lateral disturbance forces. A mathematical model incorporating these disturbances was developed, and a nominal guidance controller was designed using the linear quadratic regulator (LQR) method. The controller parameters were then optimized using a particle swarm optimization (PSO) algorithm. A simulation model of the guidance system was established, and the system’s responses under the two specific operating conditions were analyzed using a simulation platform. A comparison between the algorithms before and after optimization was conducted. The results indicate that, under simulated disturbance forces of 1 kN, 2 kN, and 3 kN, the fluctuation amplitudes of the guidance gap are reduced by 9.46%, 9.70%, and 11.82%, respectively. Furthermore, the recovery velocity of the guidance gap is improved with the optimized algorithm compared to the pre-optimization version. The optimized algorithm also improves the train’s performance when navigating curves and when subjected to crosswind disturbances.
-
Key words:
- maglev train /
- guidance system /
- particle swarm optimization /
- optimized control
-
图 3 不同速度条件下的导向间隙和导向电流
Figure 3. Guidance gap and guidance current under different velocity conditions
图 7 优化前、后90 km/h右侧间隙对比
Figure 7. Comparison of right-side gap before and after optimization at 90 km/h
图 8 2种优化思路导向系统右侧间隙对比
Figure 8. Comparison of right-side gap in guidance system using two optimization approaches
图 9 优化前后右侧导向间隙变化对比
Figure 9. Comparison of changes in right-side guidance gap before and after optimization
图 10 优化前后系统输入u的变化对比
Figure 10. Comparison of changes in system input u before and after optimization
图 11 考虑涡流影响时不同速度下导向系统右侧间隙、电流的变化
Figure 11. Variation in right-side gap and current of guidance system at different velocities considering influence of eddy currents
表 1 高速磁浮列车物理参数表
Table 1. Physical parameters of high-speed maglev train
符号 物理意义 数值 $ {\mu }_{0} $/（N·A−2） 真空磁导率 4π×10−7 $ N $ 线圈绕组匝数 200 $ A $/m2 电磁铁磁极面积 0.552 $ R $/Ω 线圈绕组电阻 2.77 $ {L}_{0} $/H 电磁铁线圈的等效电感 0.1387 $ {{\textit{z}}}_{0} $/m 平衡点间隙 0.01 $ {i}_{0} $/A 平衡点的工作电流 10 $ {m}_{{\mathrm{l}}} $/kg 左侧一组导向电磁铁质量 390 $ {m}_{{\mathrm{r}}} $/kg 右侧一组导向电磁铁质量 390 $ {m}_{{\mathrm{d}}} $/kg 一个导向单元的等效质量 550 
下载: 导出CSV
表 2 不同速度下导向力损失情况表
Table 2. Loss of guiding force at different velocities
速度/（km·h−1） 导向力/N 降比/% 0 604.0 100 429.5 28.89 200 383.0 36.59 300 382.0 36.75 400 381.5 36.84 500 381.2 36.89 600 381.2 36.89
下载: 导出CSV
-
[1] 吴云飞. EMS型高速磁浮列车导向控制系统及其仿真[J]. 黑龙江科技学院学报,2006,16(4): 244-247.WU Yunfei. Guidance control system and simulation research of EMS type high-speed maglev vehicle[J]. Journal of Heilongjiang Institute of Science and Technology, 2006, 16(4): 244-247. [2] 郝阿明,龙志强,常文森. 考虑轨道不平顺的高速磁浮列车导向系统控制器设计[J]. 系统仿真学报,2008,20(22): 6234-6237.HAO Aming, LONG Zhiqiang, CHANG Wensen. Guidance controller design of high speed maglev train considering random irregularity of guideway[J]. Journal of System Simulation, 2008, 20(22): 6234-6237. [3] 郝阿明,龙志强,常文森. 高速磁浮列车导向系统的鲁棒控制器设计[J]. 铁道学报,2008,30(6): 40-45.HAO Aming, LONG Zhiqiang, CHANG Wensen. Design of the robust controller of the guidance system in high-speed maglev train[J]. Journal of the China Railway Society, 2008, 30(6): 40-45. [4] ZHAI M D, HAO A M, LI X L, et al. Research on the active guidance control system in high speed maglev train[J]. IEEE Access, 2019, 7: 741-752. doi: 10.1109/ACCESS.2018.2885784 [5] LI B W, LI X L, WANG Z Q, et al. Design of ADRC for guidance system of high speed maglev train[C]//2020 Chinese Automation Congress (CAC). Shanghai: IEEE, 2020: 1471-1476. [6] 郝阿明,佘龙华,常文森. EMS型高速磁浮列车自适应导向控制器设计[J]. 控制工程,2008,15(2): 116-119,170. doi: 10.3969/j.issn.1671-7848.2008.02.002HAO Aming, SHE Longhua, CHANG Wensen. Adaptive controller design of guidance system of EMS high speed maglev train[J]. Control Engineering of China, 2008, 15(2): 116-119,170. doi: 10.3969/j.issn.1671-7848.2008.02.002 [7] 朴明伟,曹玉峰,梁树林,等. 高速磁浮列车组装模型及导向原理[J]. 中国铁道科学,2008,29(4): 103-108.PIAO Mingwei, CAO Yufeng, LIANG Shulin, et al. Assembled model and guidance principle of high-speed maglev train[J]. China Railway Science, 2008, 29(4): 103-108. [8] 马铁刚. 高速磁浮车主动悬浮导向控制稳定性研究[D]. 大连:大连交通大学,2005. [9] 朴明伟,梁世宽,薛世海,等. 高速磁浮列车主动悬浮与导向的2-DOF控制[J]. 中国铁道科学,2006,27(4): 80-85.PIAO Mingwei, LIANG Shikuan, XUE Shihai, et al. 2-DOF control of active levitation and guidance in high-speed maglev train[J]. China Railway Science, 2006, 27(4): 80-85. [10] 吴海鹏. 高速磁浮车小半径曲线运行性能的研究[D]. 大连:大连交通大学,2007. [11] 吴云飞. 高速磁浮列车导向控制系统仿真研究[D]. 成都:西南交通大学,2006. [12] 王汝宁. 高速磁浮列车的转向运动相关问题研究[D]. 长沙:国防科学技术大学,2010. [13] 赵春霞. EMS型高速磁浮列车导向动力学研究[D]. 长沙:国防科学技术大学,2014. [14] 李博文. 高速磁浮列车主动导向系统优化控制算法研究[D]. 长沙:国防科技大学,2021. [15] 龙长林. 基于数值方法的磁浮列车新型导向电磁铁电磁特性分析[D]. 长沙:国防科学技术大学,2008. [16] 刘少克,龙长林,陈贵荣,等. 高速磁悬浮列车新型导向电磁铁分析[J]. 机车电传动,2010(1): 49-51.LIU Shaoke, LONG Changlin, CHEN Guirong, et al. Analysis of new guide electromagnet for high-speed maglev train[J]. Electric Drive for Locomotives, 2010(1): 49-51. [17] DING S S, SUN J J, HAN W T, et al. Modeling and analysis of a novel guidance magnet for high-speed maglev train[J]. IEEE Access, 2019(7):133324-133334. [18] 张德. 高速列车横风挡风装置空气动力学性能的数值分析[D]. 北京:北京交通大学,2013. [19] 杨永刚,陈大伟,梅元贵. 600 km/h高速磁浮列车明线交会横向气动性能[J]. 振动与冲击,2022,41(1): 137-146.YANG Yonggang, CHEN Dawei, MEI Yuangui. Lateral aerodynamic performance of 600 km/h high-speed maglev train during open line intersection[J]. Journal of Vibration and Shock, 2022, 41(1): 137-146. [20] 左志超. 高速磁浮列车导向系统的容错控制问题研究[D]. 长沙:国防科技大学,2019. [21] 郑涛. 风速对高速列车气动力的影响研究[J]. 时代农机,2019,46(8): 59,62. -
下载:
点击查看大图
计量
- 文章访问数: 24
- HTML全文浏览量: 11
- PDF下载量: 7
- 被引次数: 0