Nonlinear Aerodynamic Force Identification and Nonlinear Flutter Analysis Based on Autoencoder
-
摘要:
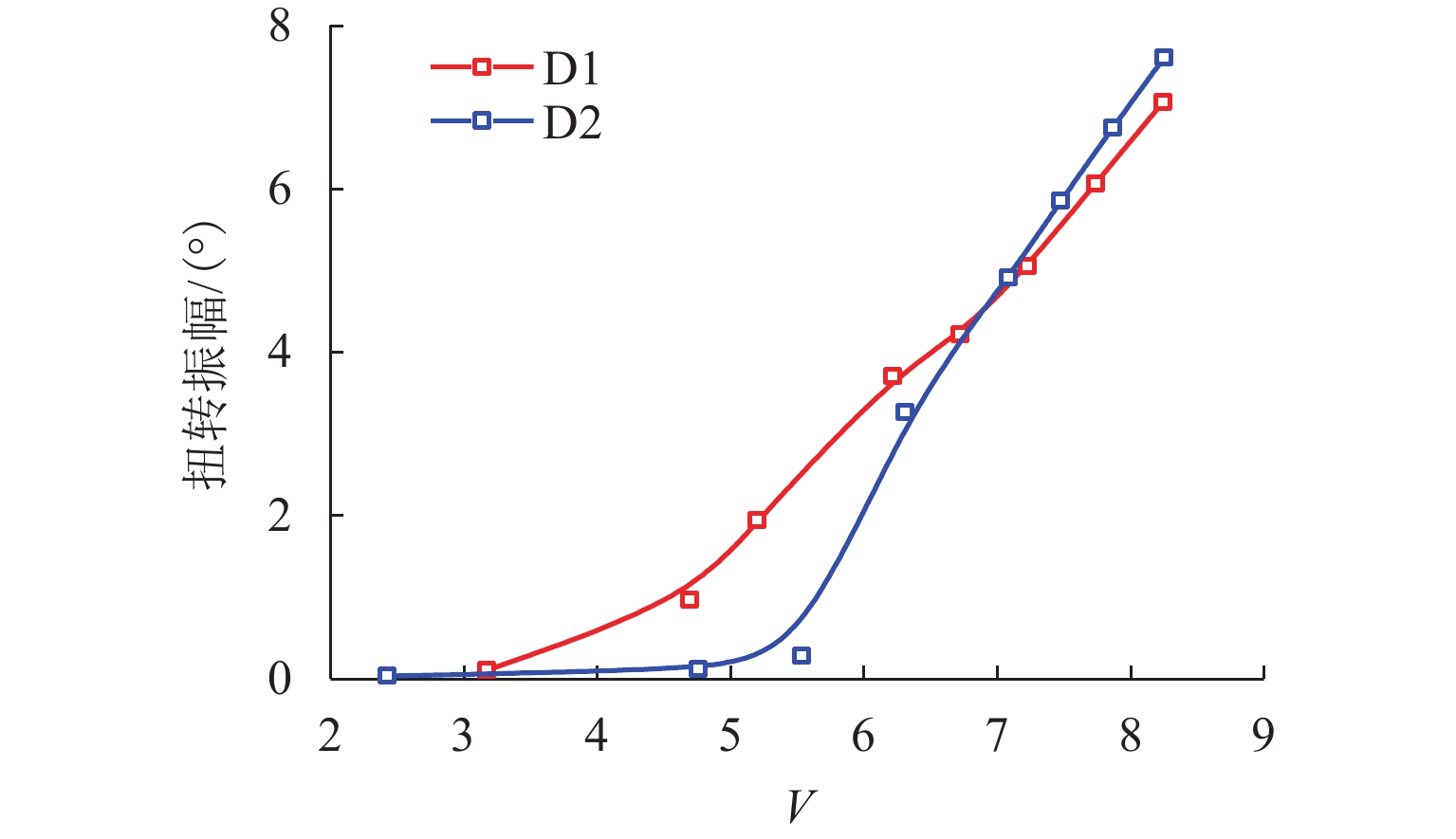
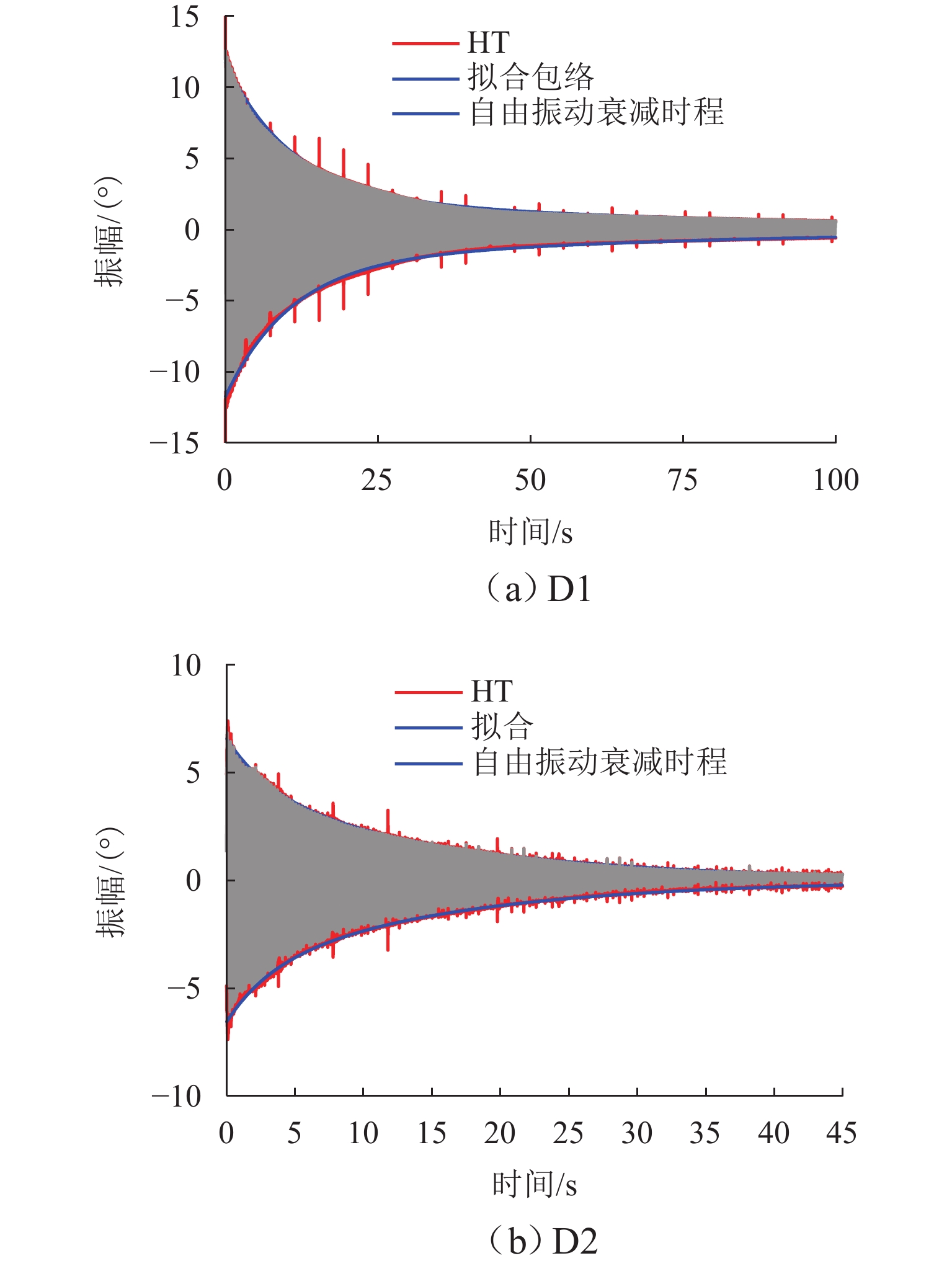
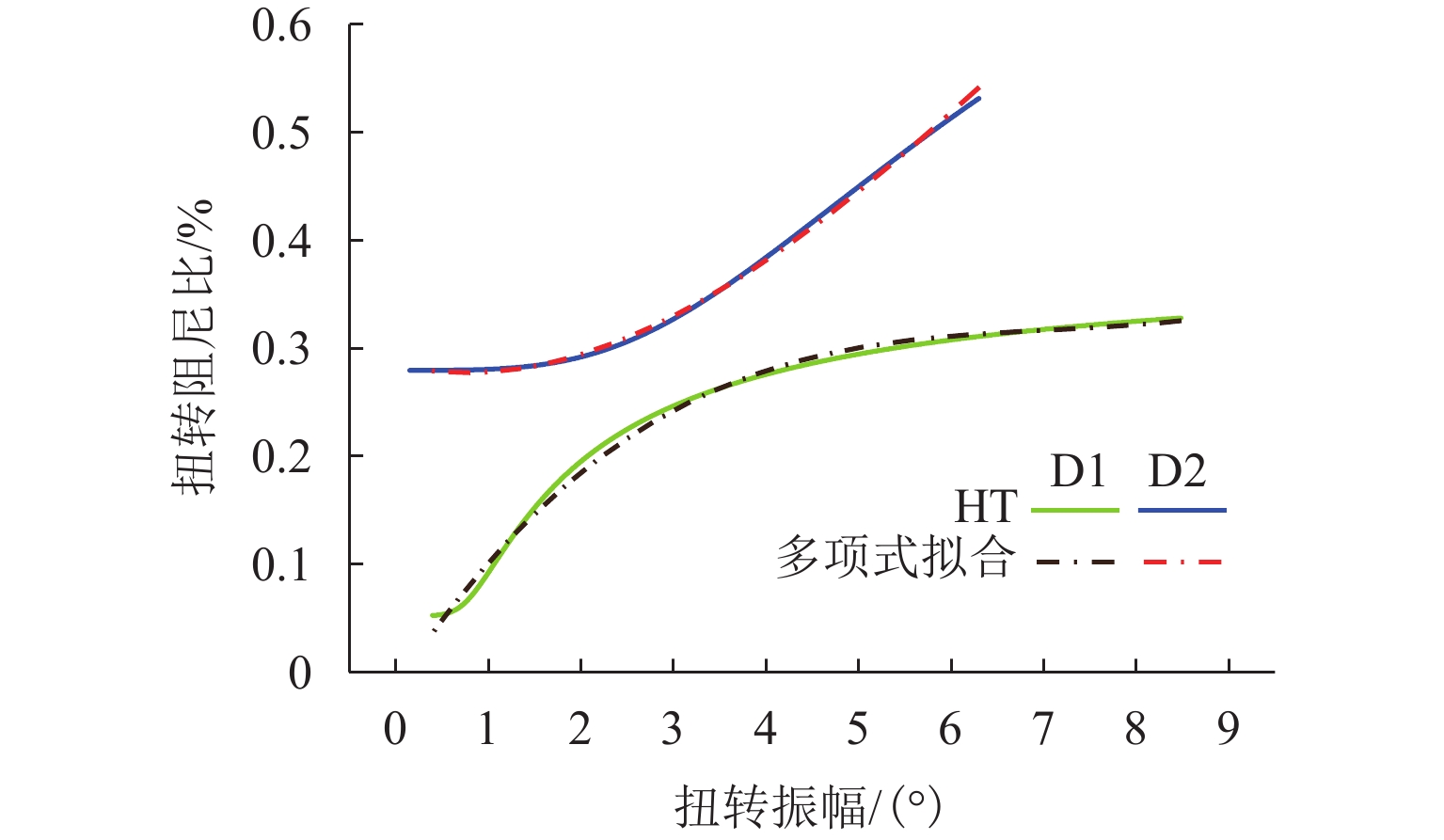
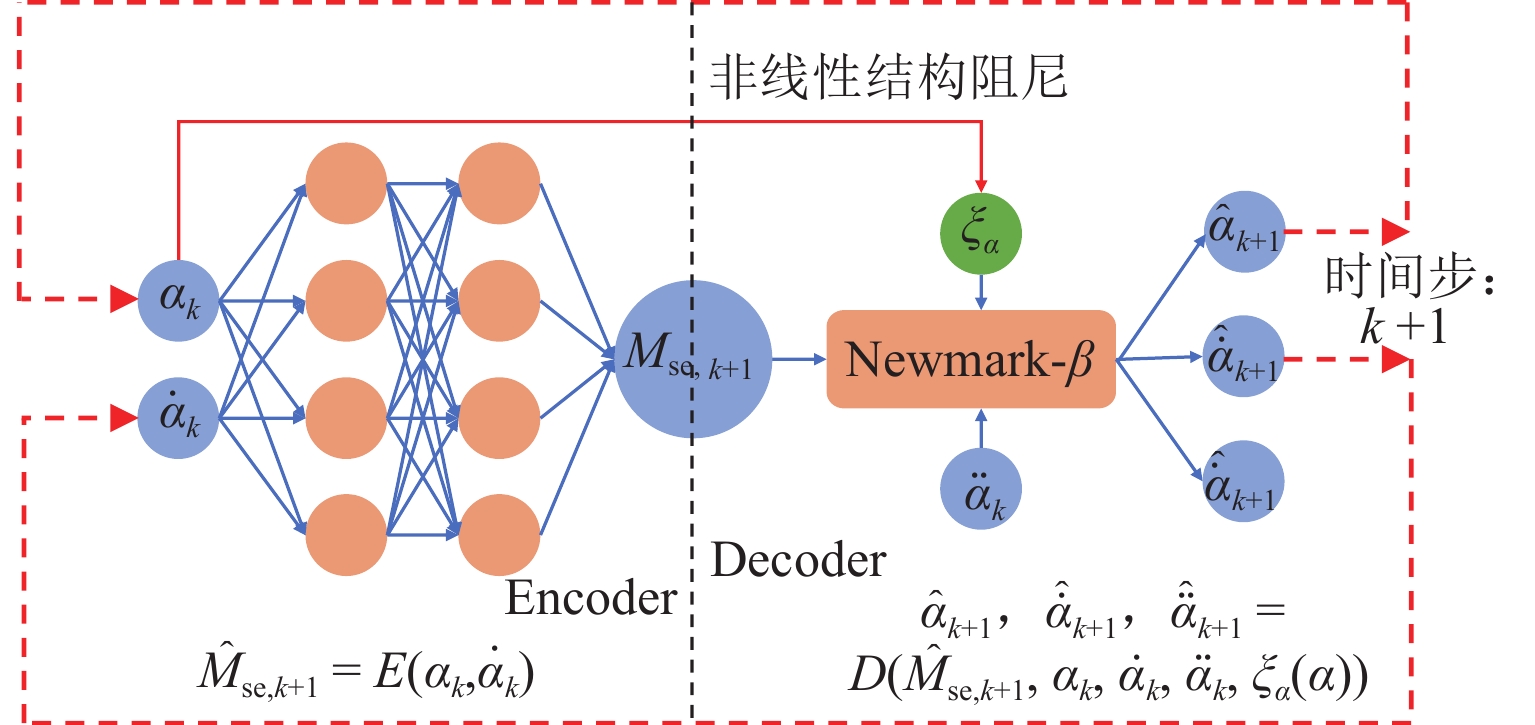
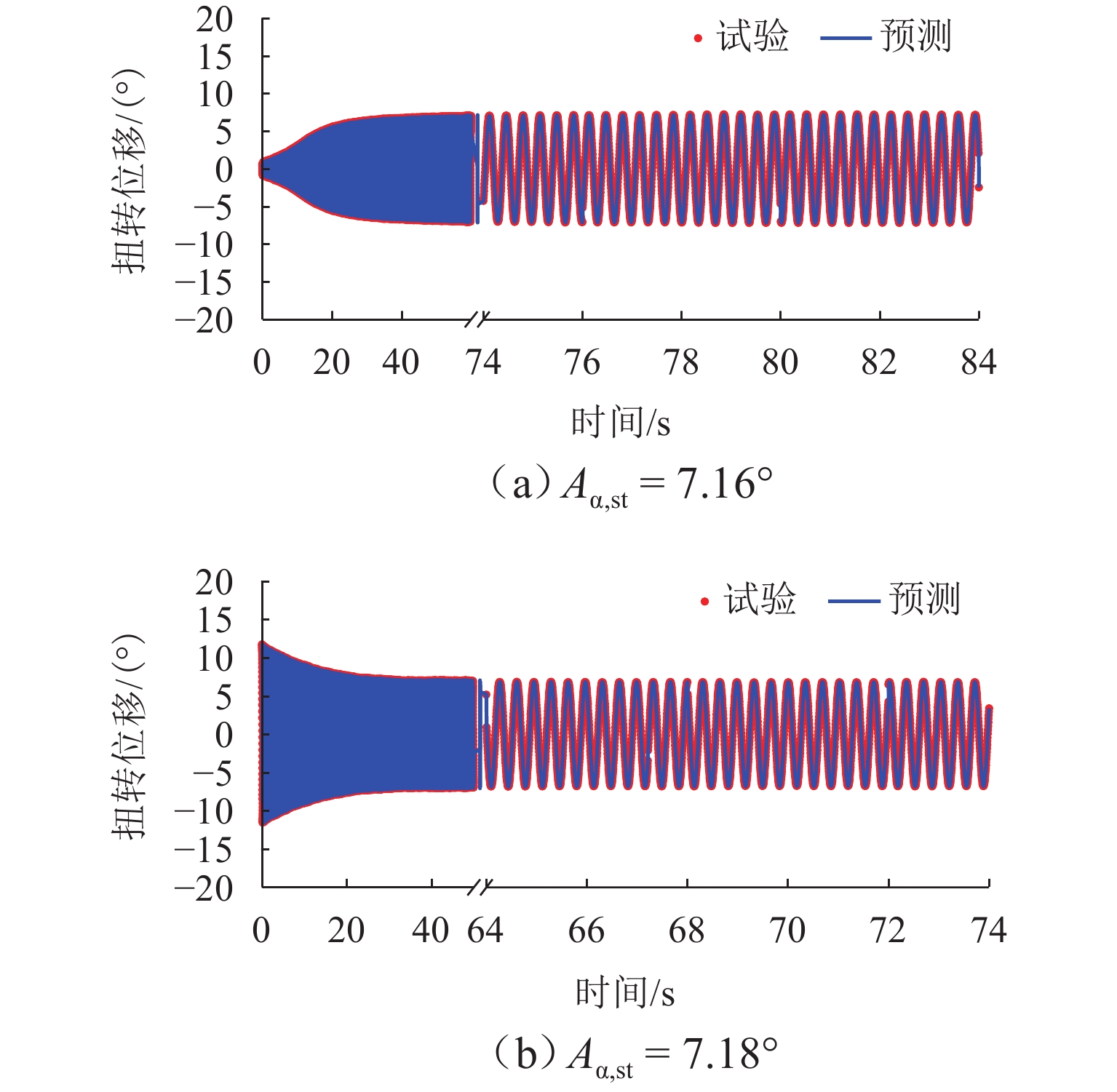
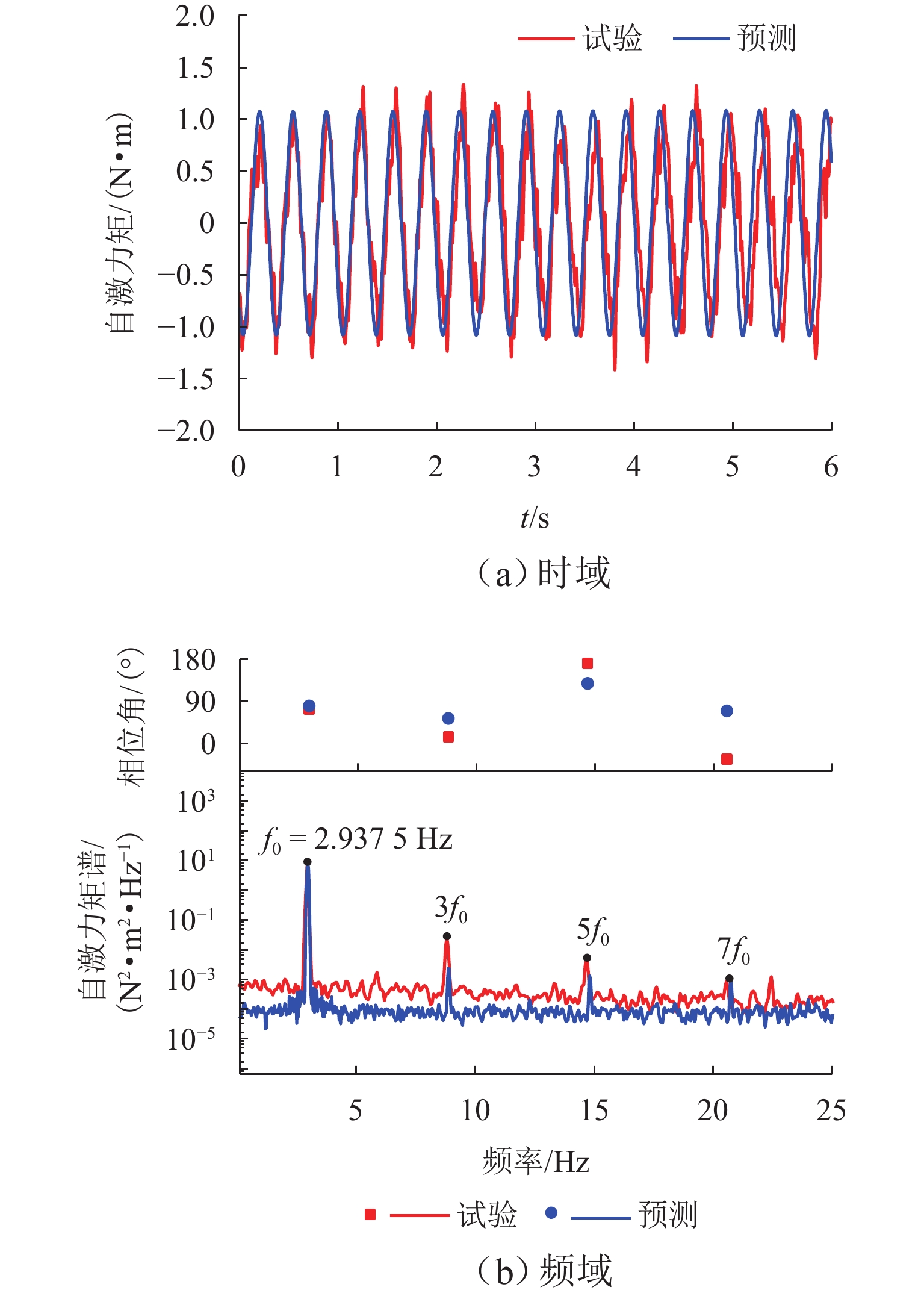
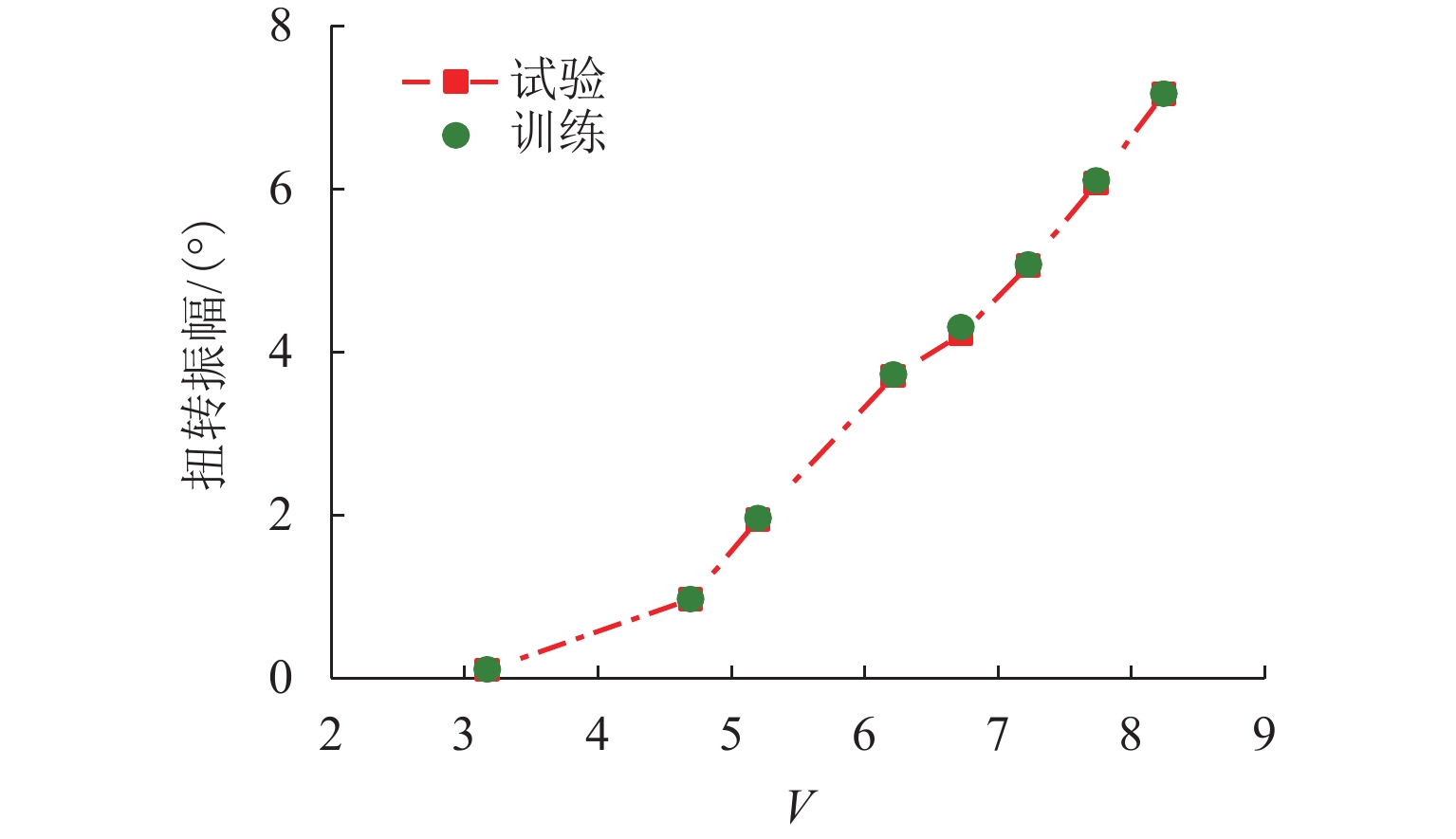
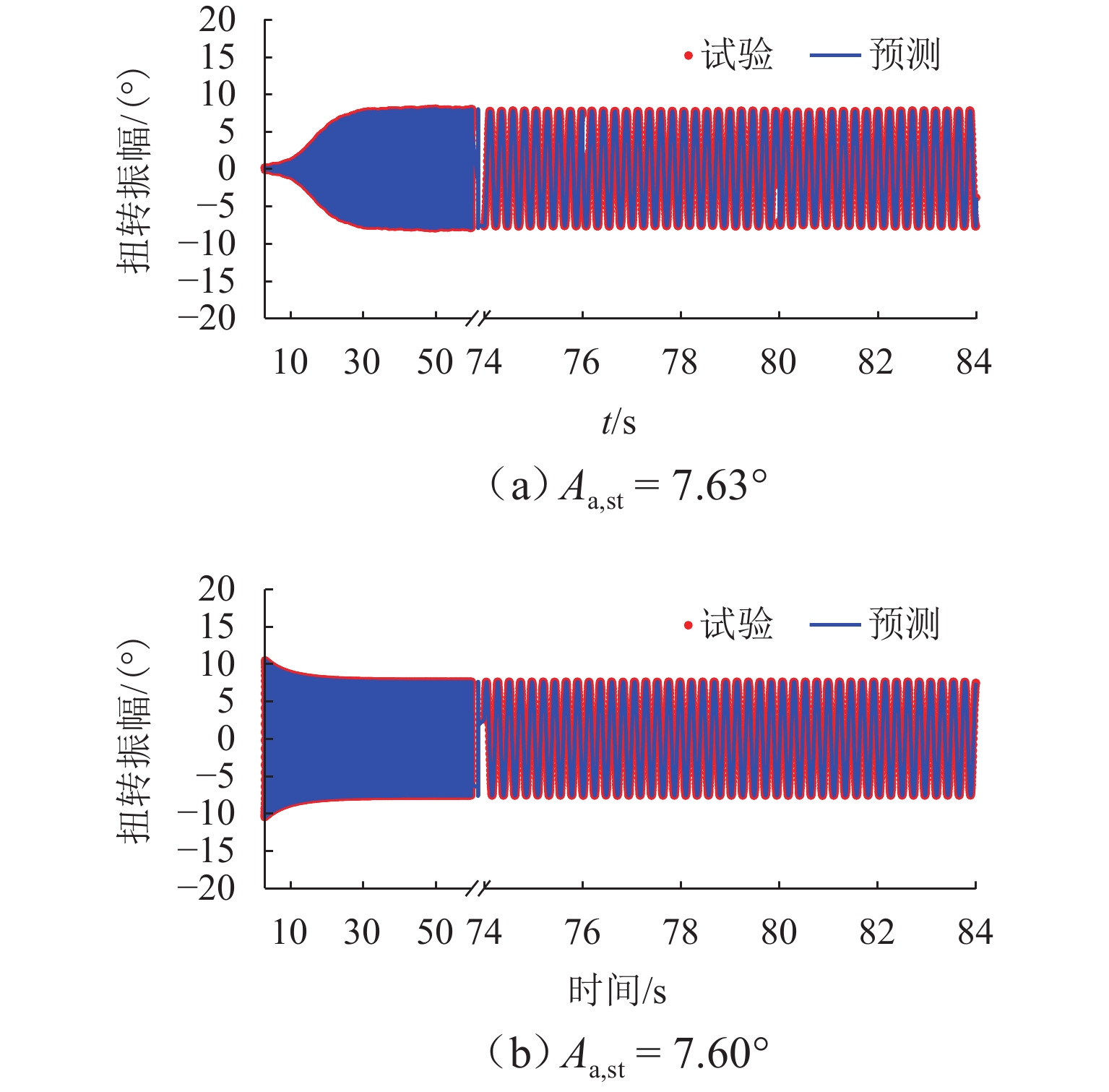
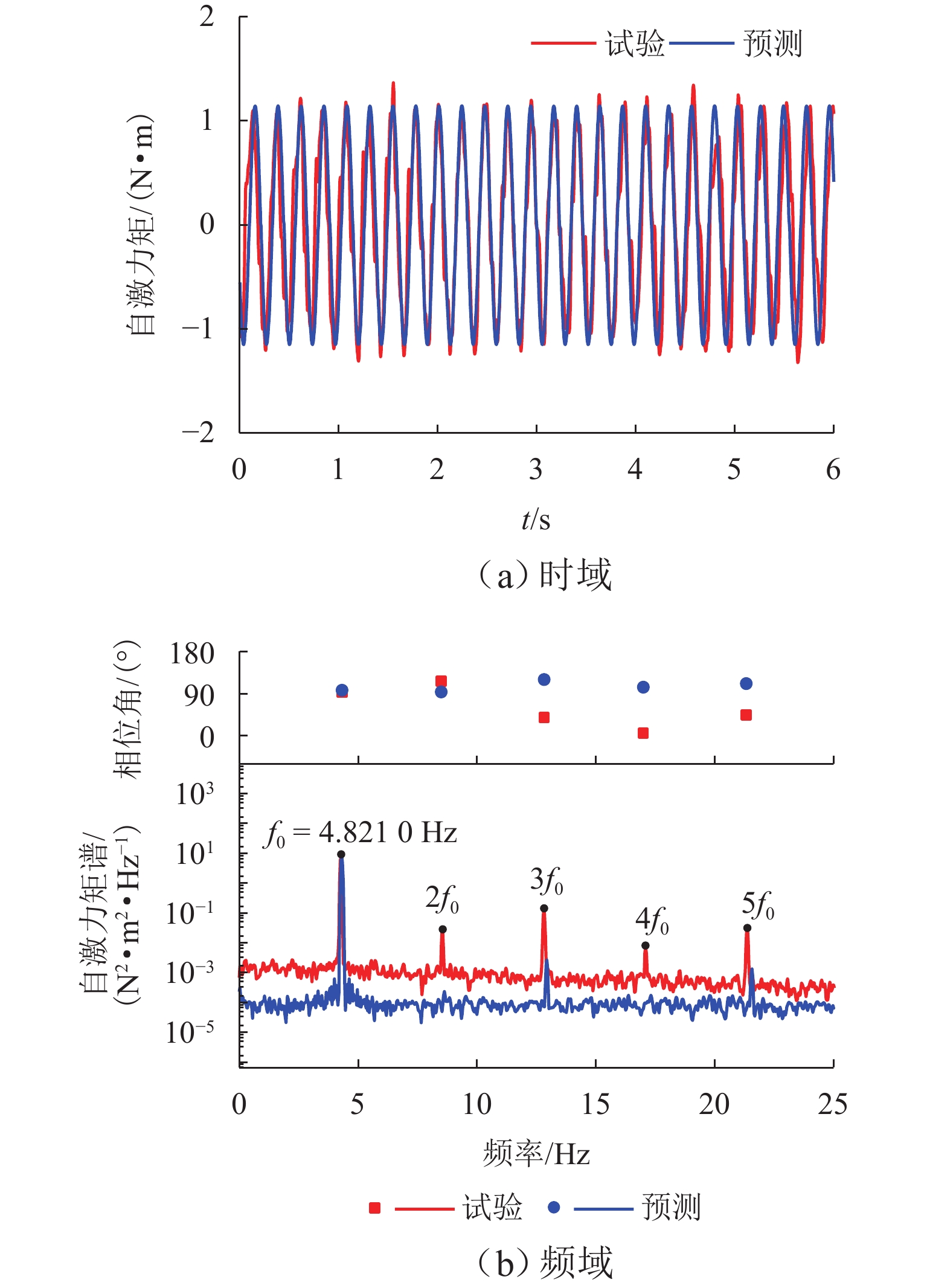
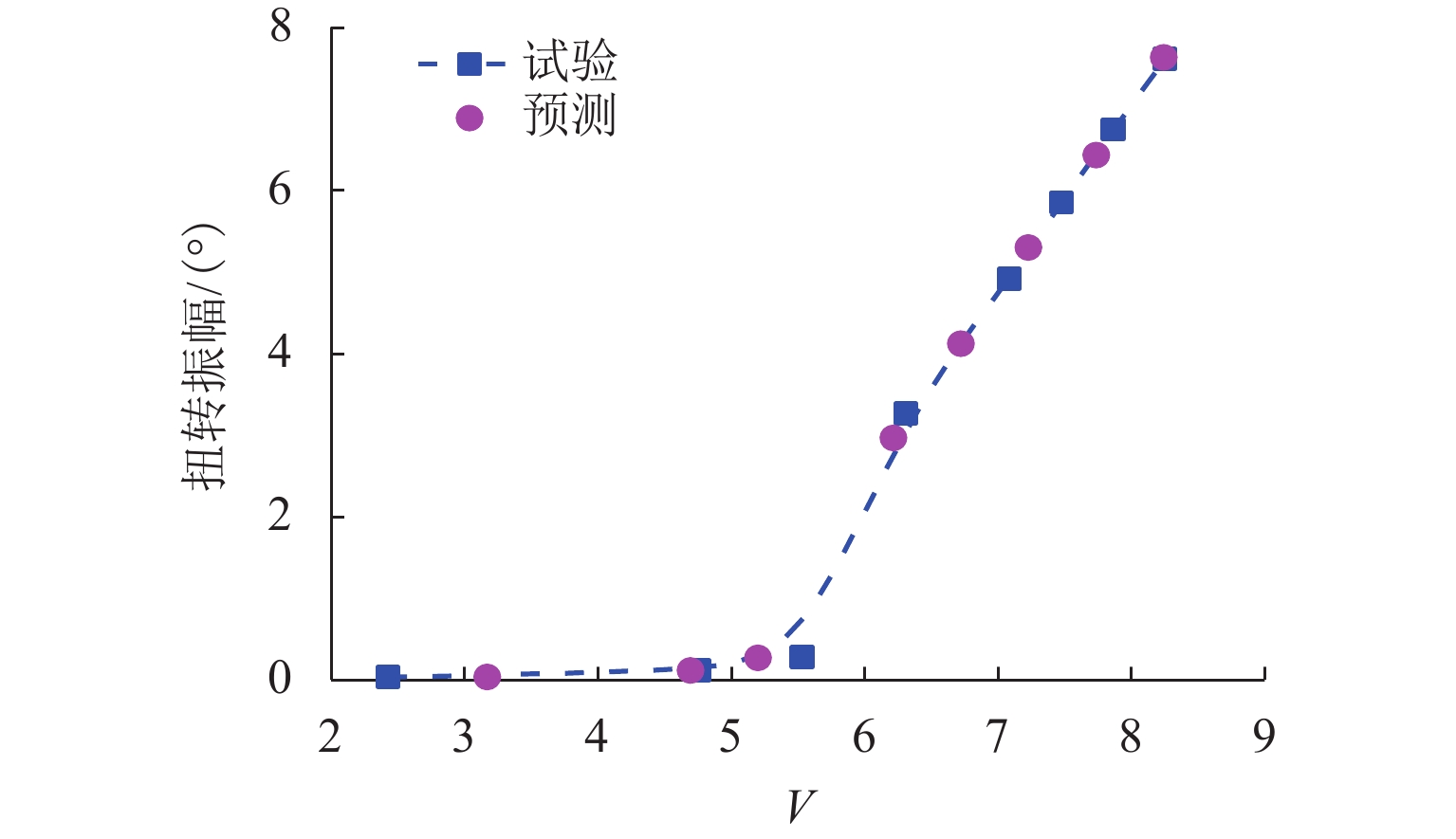
为实现非线性动力系统的非线性气动力辨识和非线性颤振计算，提出一种基于神经网络方法和运动方程数值求解方法的自编码器模型. 以5∶1矩形断面为研究对象，通过节段模型自由振动风洞试验，详细测试系统非线性阻尼的振幅依存性和非线性颤振稳态振幅响应，明确该断面在不同折算风速下稳态振幅的唯一性；基于试验数据对所提出的自编码器模型进行训练，获取精准描述与位移和速度相关的非线性气动力编码器模型，实现不同动力参数下5∶1矩形断面非线性颤振运动时程分析. 研究结果表明：所提出的自编码器模型能够仅依赖自由振动风洞试验而无需测力或测压试验，即可精确辨识包含奇数次高次谐波分量的非线性气动力时程；能够精确复现不同初始条件下断面非线性颤振运动时程和不同折算风速下的稳态振幅响应，扭转稳态振幅最大误差不超过5%，平均误差为1.15%；具有较高的拓展性，可为后续相关研究提供参考.
Abstract:In order to identify the nonlinear aerodynamic forces and calculate nonlinear flutters of a nonlinear dynamic system, an autoencoder model based on the neural network method and numerical solution of motion equation was proposed. The 5∶1 rectangular cross-section was taken as the research object. Through free vibration wind tunnel tests of the sectional model, the amplitude dependence of the nonlinear damping and the steady-state amplitude responses of the nonlinear flutter of the system were tested, and it was clarified that the tested cross-section had the only steady-state flutter response at different reduced wind speeds. Based on the experimental data, the proposed autoencoder model was trained. The nonlinear aerodynamic force encoder model that accurately described displacement and speed was obtained to realize motion time-history analysis of the nonlinear flutter of the 5∶1 rectangular cross-section under different dynamic parameters. Research results show that the proposed autoencoder model can accurately identify the nonlinear aerodynamic force time-history containing high-order harmonic components only by relying on a free vibration wind tunnel test without the need to carry out force or pressure tests; the proposed model can accurately reproduce the motion time-history of nonlinear flutter under different initial conditions and the steady-state amplitude responses at different reduced wind speeds. The maximum error of torsional steady-state amplitude is less than 5%, and the average error is 1.15%. It has high extensibility and can provide a reference for subsequent related research.
-
Key words:
- nonlinear flutter /
- wind tunnel test /
- neural network /
- encoder /
- decoder
-
图 4 不同初始激励下的运动响应时程
Figure 4. Motion response time-history under different initial excitations
图 5 稳态扭转响应振幅随折算风速的变化
Figure 5. Variation of steady-state torsional response amplitude with reduced wind speed
图 7 非线性结构阻尼随扭转振幅的变化
Figure 7. Variation of nonlinear structural damping with torsional amplitude
图 9 训练预测值和试验值对比 （$ V=8.24 $）
Figure 9. Comparison of prediction results in training and testing results ($ V=8.24 $)
图 10 气动力训练预测值和试验值对比（$ V=8.24 $）
Figure 10. Comparison of prediction results in aerodynamic force training and testing results ($ V=8.24 $)
图 11 不同折算风速下非线性颤振响应 （D1）
Figure 11. Nonlinear flutter responses at different reduced wind speeds (D1)
图 12 非线性颤振运动时程验证预测值和试验值对比（$ V=8.24 $）
Figure 12. Comparison of prediction results and testing results for motion time-history of nonlinear flutter ($ V=8.24 $)
图 13 气动力验证预测值和试验值对比（$ V=8.24 $）
Figure 13. Comparison of prediction results and testing results of aerodynamic force ($ V=8.24 $)
图 14 不同折算风速下非线性颤振响应 （D2）
Figure 14. Nonlinear flutter responses at different reduced wind speeds (D2)
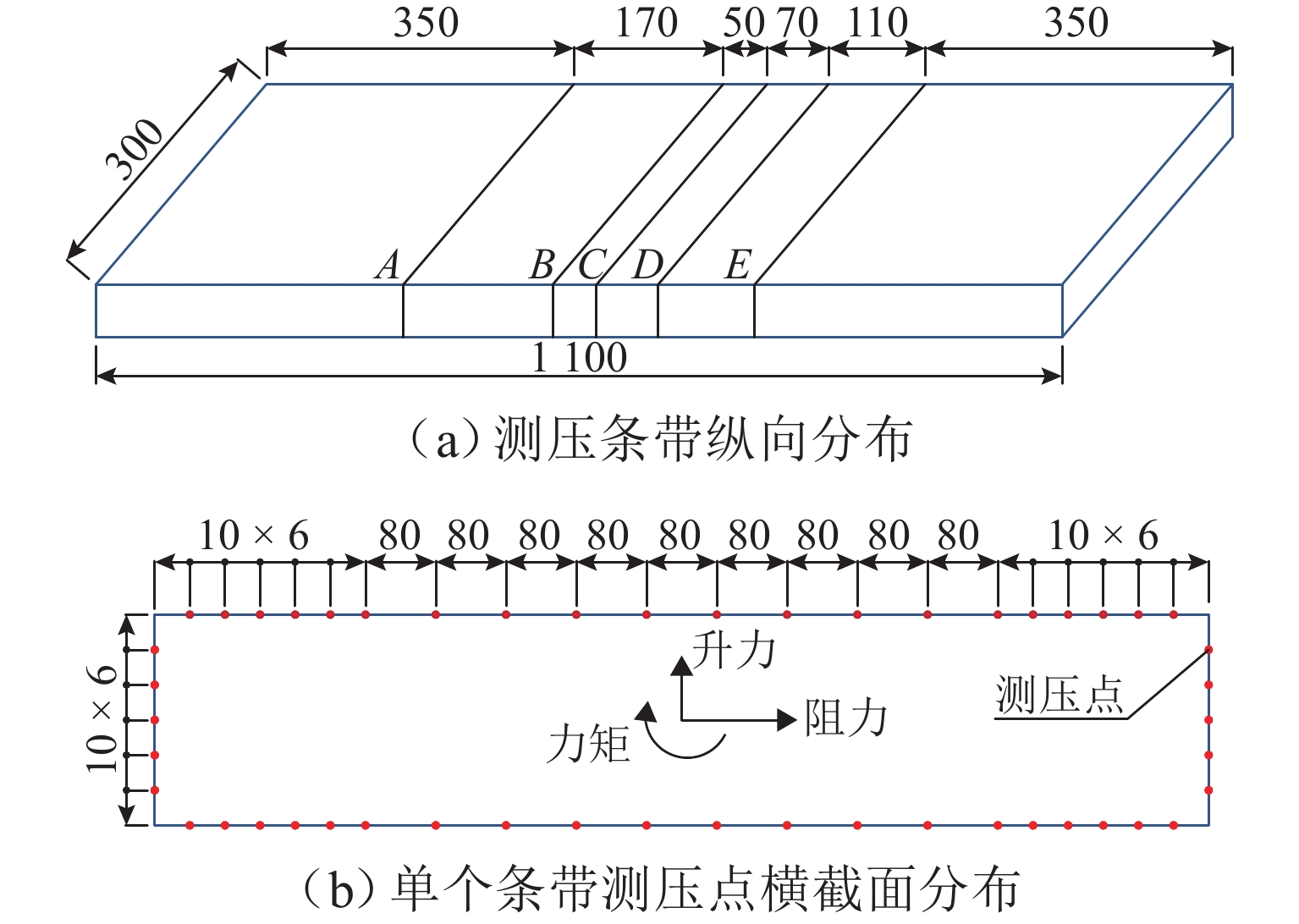
表 1 节段模型试验动力参数
Table 1. Dynamic parameters of sectional model test
动力参数
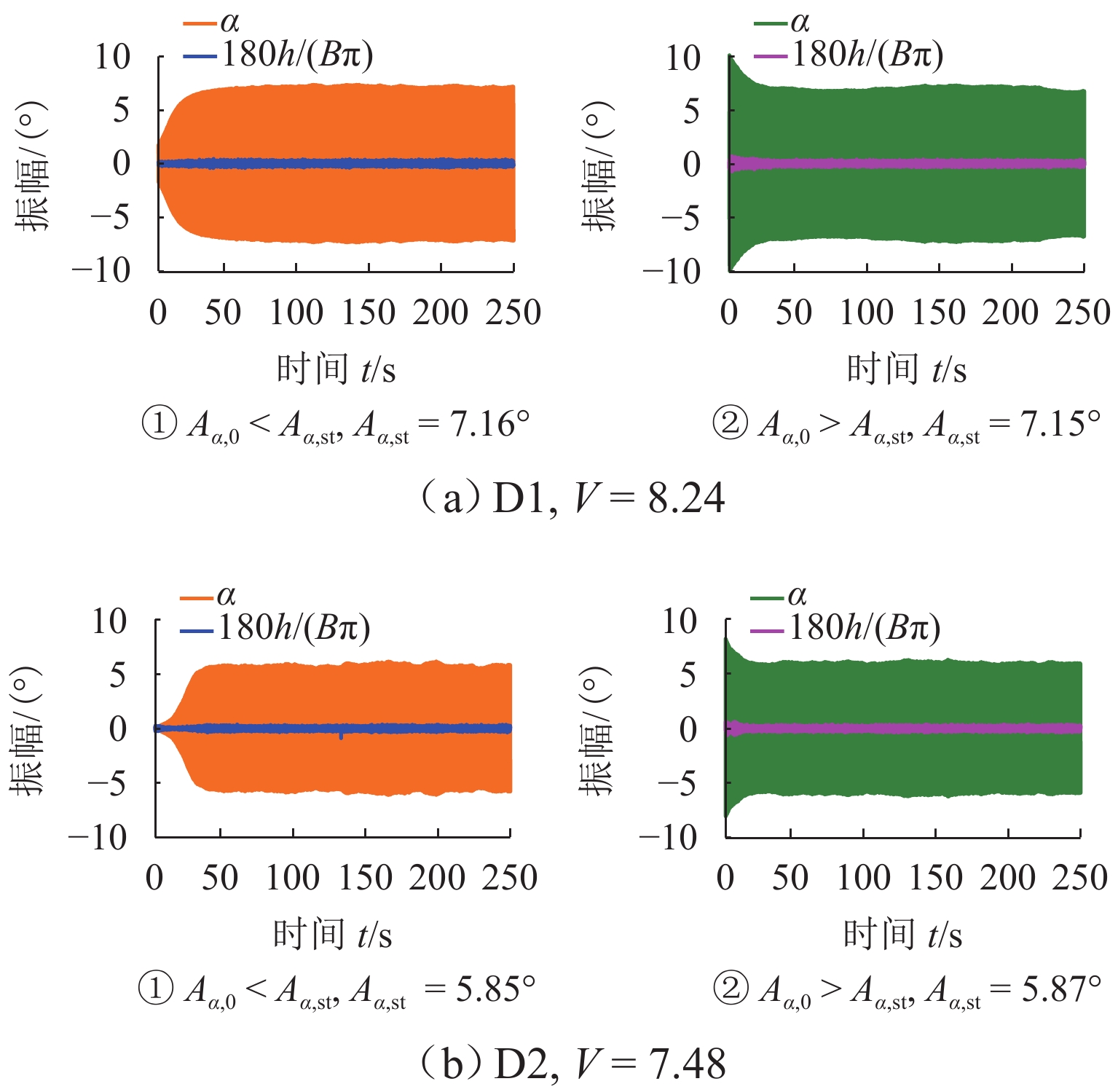
类型m/kg I/（kg•m2•m−1） fh/Hz ft/Hz D1 18.56 0.4928 1.768 3.038 D2 15.36 0.2152 1.875 4.435 
下载: 导出CSV
-
[1] SCANLAN R H, TOMKO J J. Airfoil and bridge deck flutter derivatives[J]. Journal of the Engineering Mechanics Division, 1971, 97(6): 1717-1737. doi: 10.1061/JMCEA3.0001526 [2] 林思源. 矩形和流线型箱梁断面非线性自激气动力特性研究[D]. 成都:西南交通大学,2019. [3] WU B, WANG Q, LIAO H L, et al. Effects of vertical motion on nonlinear flutter of a bridge girder[J]. Journal of Bridge Engineering, 2020, 25(11): 04020093.1-04020093.14. [4] 许福友,陈艾荣. 印尼Suramadu大桥颤振试验与颤振分析[J]. 土木工程学报,2009,42(1): 35-40. doi: 10.3321/j.issn:1000-131X.2009.01.006XU Fuyou, CHEN Airong. Flutter test and analysis for the Suramadu Bridge in Indonesia[J]. China Civil Engineering Journal, 2009, 42(1): 35-40. doi: 10.3321/j.issn:1000-131X.2009.01.006 [5] 杨猛,王云飞,赵家斌,等. 考虑气动力跨向振幅依存性和相关性的桥梁涡振响应分析[J]. 西南交通大学学报,2025,60(1):45-52.YANG Meng, WANG Yunfei, ZHAO Jiabin, et al. Vortex-induced vibration response of bridges considering both spanwise variation of vibration amplitude and correlation of aerodynamic forces[J]. Journal of Southwest Jiaotong University, 2025, 60(1):45-52. [6] YING X Y, XU F Y, ZHANG M J, et al. Numerical explorations of the limit cycle flutter characteristics of a bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 169: 30-38. doi: 10.1016/j.jweia.2017.06.020 [7] 朱乐东,高广中. 典型桥梁断面软颤振现象及影响因素[J]. 同济大学学报(自然科学版),2015,43(9): 1289-1294,1382.ZHU Ledong, GAO Guangzhong. Influential factors of soft flutter phenomenon for typical bridge deck sections[J]. Journal of Tongji University (Natural Science), 2015, 43(9): 1289-1294,1382. [8] 朱乐东,高广中. 双边肋桥梁断面软颤振非线性自激力模型[J]. 振动与冲击,2016,35(21): 29-35.ZHU Ledong, GAO Guangzhong. A nonlinear self-excited force model for soft flutter phenomenon of a twin-side-girder bridge section[J]. Journal of Vibration and Shock, 2016, 35(21): 29-35. [9] 王骑. 大跨度桥梁断面非线性自激气动力与非线性气动稳定性研究[D]. 成都:西南交通大学,2011. [10] 伍波,王骑,廖海黎. 扁平箱梁颤振后状态的振幅依存性研究[J]. 中国公路学报,2019,32(10): 96-106.WU Bo, WANG Qi, LIAO Haili. Characteristics of amplitude dependence of a flat box girder in a post-flutter state[J]. China Journal of Highway and Transport, 2019, 32(10): 96-106. [11] WU B, WANG Q, LIAO H L, et al. Hysteresis response of nonlinear flutter of a truss girder: experimental investigations and theoretical predictions[J]. Computers & Structures, 2020, 238: 106267.1-106267.17. [12] GAO G Z, ZHU L D, HAN W S, et al. Nonlinear post-flutter behavior and self-excited force model of a twin-side-girder bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 177: 227-241. doi: 10.1016/j.jweia.2017.12.007 [13] WU B, CHEN X Z, WANG Q, et al. Characterization of vibration amplitude of nonlinear bridge flutter from section model test to full bridge estimation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 197: 104048.1-104048.14. [14] CHU S R, SHOURESHI R, TENORIO M. Neural networks for system identification[J]. IEEE Control Systems Magazine, 1990, 10(3): 31-35. doi: 10.1109/37.55121 [15] NARENDRA K S, PARTHASARATHY K. Identification and control of dynamical systems using neural networks[J]. IEEE Transactions on Neural Networks, 1990, 1(1): 4-27. doi: 10.1109/72.80202 [16] MASRI S F, CHASSIAKOS A G, CAUGHEY T K. Identification of nonlinear dynamic systems using neural networks[J]. Journal of Applied Mechanics, 1993, 60(1): 123-133. doi: 10.1115/1.2900734 [17] CHEN X Z. Estimation of stochastic crosswind response of wind-excited tall buildings with nonlinear aerodynamic damping[J]. Engineering Structures, 2013, 56: 766-778. doi: 10.1016/j.engstruct.2013.05.044 [18] 王骑,廖海黎,李明水,等. 桥梁断面非线性自激气动力经验模型[J]. 西南交通大学学报,2013,48(2): 271-277. doi: 10.3969/j.issn.0258-2724.2013.02.013WANG Qi, LIAO Haili, LI Mingshui, et al. Empirical mathematical model for nonlinear motion-induced aerodynamic force of bridge girder[J]. Journal of Southwest Jiaotong University, 2013, 48(2): 271-277. doi: 10.3969/j.issn.0258-2724.2013.02.013 [19] RIZZO F, CARACOGLIA L. Artificial Neural Network model to predict the flutter velocity of suspension bridges[J]. Computers & Structures, 2020, 233: 106236.1-106236.20. [20] ABBAS T, KAVRAKOV I, MORGENTHAL G, et al. Prediction of aeroelastic response of bridge decks using artificial neural networks[J]. Computers & Structures, 2020, 231: 106198.1-106198.20. [21] GOODFELLOW I, BENGIO Y, COURVILLE A. Deep Learning[M]. Cambridge:MIT Press, 2016. [22] 谢明志,樊丁萌,蒋志鹏,等.基于计算机视觉的混凝土结构裂缝检测研究现状与展望[J/OL]. 西南交通大学学报,1-20[2024-10-03]. http://kns.cnki.net/kcms/detail/51.1277.u.20240913.1853.002.html. [23] KINGMA D, BA J. Adam: A method for stochastic optimization[J]. Computer Science, 2017(v9): 1-13. [24] 邱锡鹏. 神经网络与深度学习[M]. 北京:机械工业出版社,2020. [25] ZHANG M J, XU F Y, YING X Y. Experimental investigations on the nonlinear torsional flutter of a bridge deck[J]. Journal of Bridge Engineering, 2017, 22(8): 04017048.1-04017048.13. -
下载:
点击查看大图
计量
- 文章访问数: 189
- HTML全文浏览量: 70
- PDF下载量: 34
- 被引次数: 0