基于误差交叉耦合的多电磁铁悬浮系统滑模协同控制

孙友刚; 徐俊起; 贺祯宇; 李丰荥; 陈琛; 林国斌

doi:10.3969/j.issn.0258-2724.20210924

基于误差交叉耦合的多电磁铁悬浮系统滑模协同控制

doi: 10.3969/j.issn.0258-2724.20210924

孙友刚^{1, 2, 3,},
徐俊起^{2, 3, ,},
贺祯宇¹,
李丰荥¹,
陈琛²,
林国斌^{2, 3}

1.
同济大学铁道与城市轨道交通研究院，上海 201804
2.
同济大学国家磁浮交通工程技术研究中心，上海 201804
3.
同济大学磁浮技术铁路行业重点实验室，上海 201804

基金项目: 国家重点研发计划（2016YFB1200602）；国家自然科学基金（51905380，52072269）；上海市多网多模式轨道交通协同创新中心基金（28002360012）；上海市级科技重大专项（2021SHZDZX0100）；湖南创新型省份建设专项（2020GK2084）

详细信息

作者简介:
孙友刚（1989—），男，副教授，博士，研究方向为磁浮列车动力学及控制，E-mail：1989yoga@tongji.edu.cn

通讯作者:
徐俊起（1977—），男，高级工程师，博士，研究方向为电磁悬浮控制理论与应用，E-mail：xujunqi@tongji.edu.cn

中图分类号: U237
计量
- 文章访问数: 499
- HTML全文浏览量: 108
- PDF下载量: 28
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-15
- 修回日期: 2022-03-10
- 刊出日期: 2022-04-13

Sliding Mode Cooperative Control of Multi-Electromagnet Suspension System Based on Error Cross Coupling

SUN Yougang^{1, 2, 3
,},
XU Junqi^{2, 3
, ,},
HE Zhenyu¹,
LI Fengxing¹,
CHEN Chen²,
LIN Guobin^{2, 3}

1.
Institute of Rail Transit, Tongji University, Shanghai 201804, China
2.
National Maglev Transportation Engineering R & D Center, Tongji University, Shanghai 201804, China
3.
Key Laboratory of Maglev Technology in Railway Industry，Tongji University, Shanghai 201804, China

摘要

摘要:
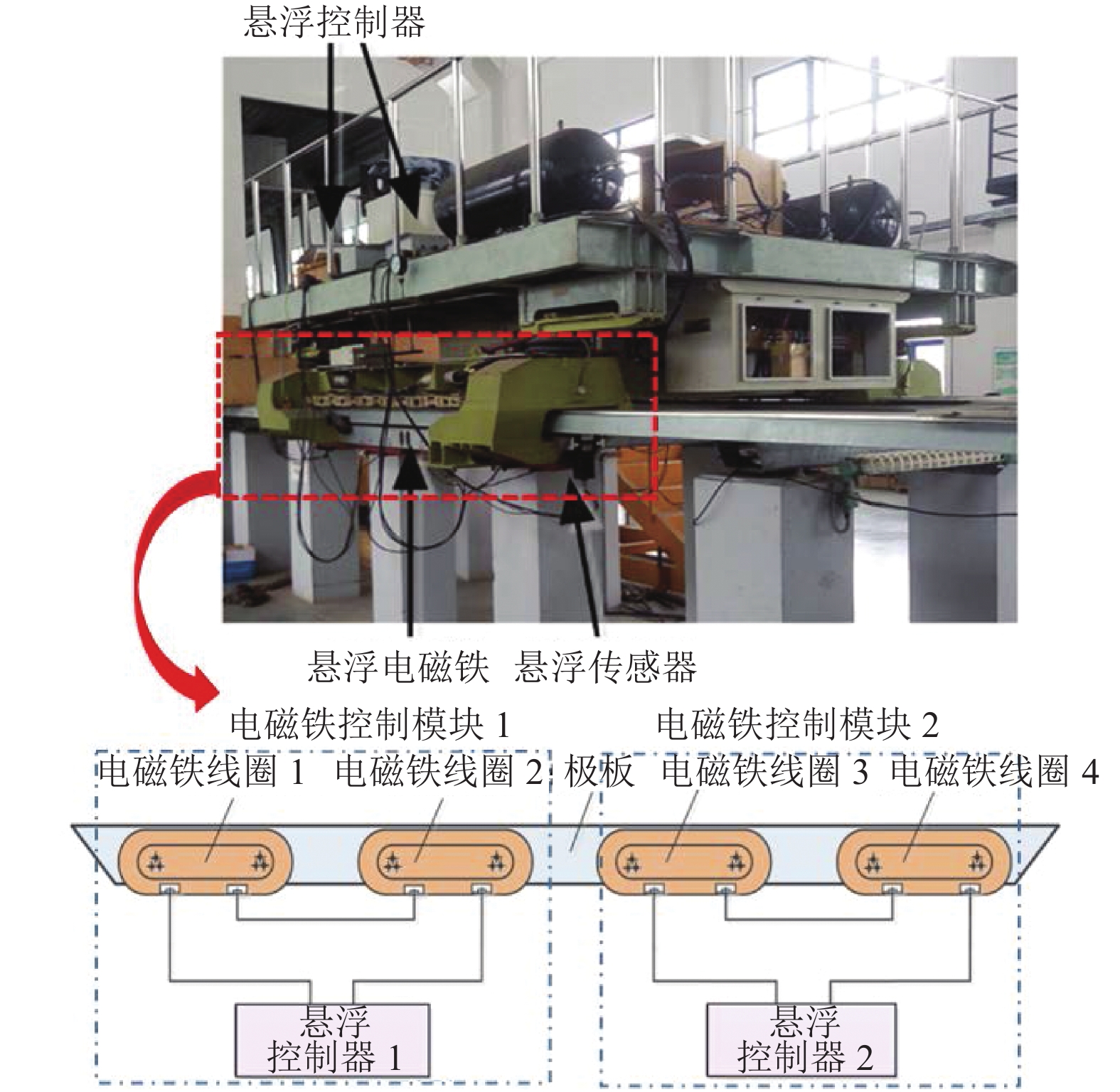
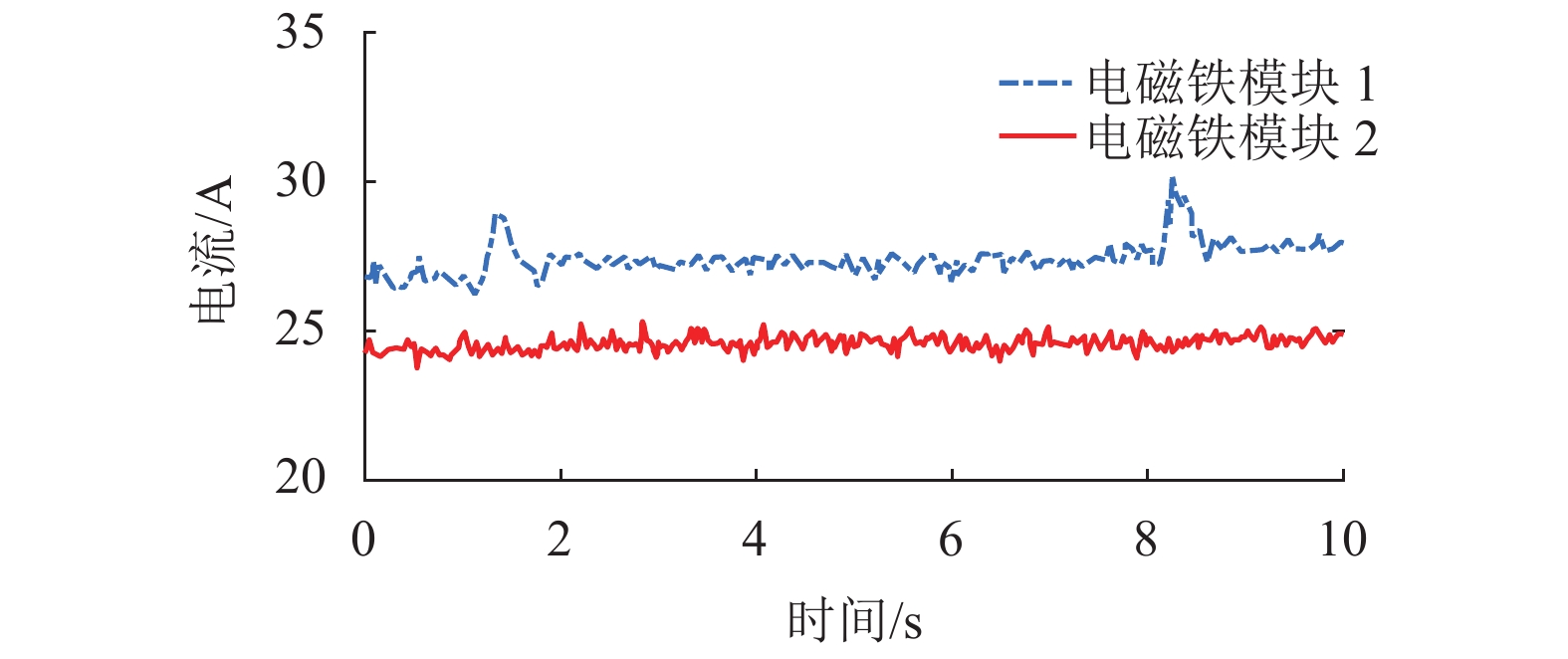
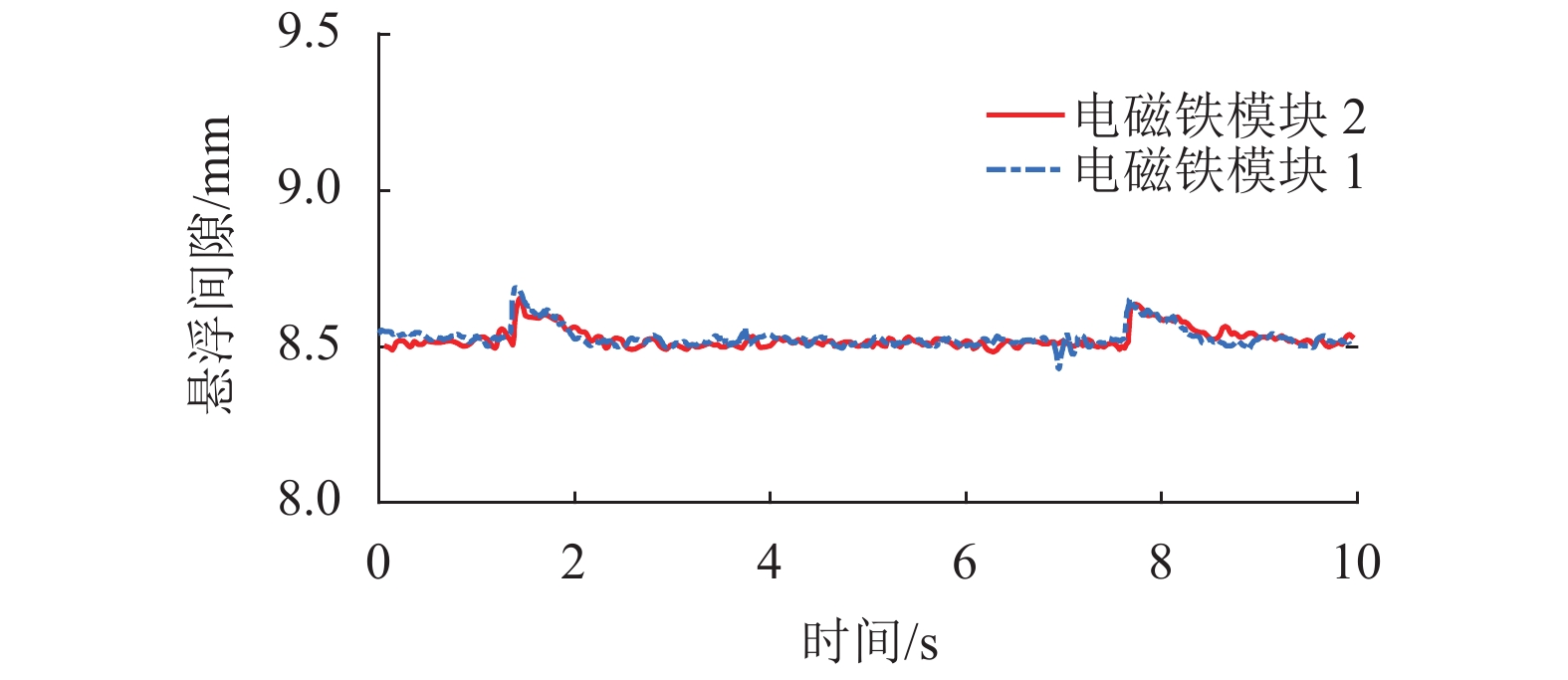
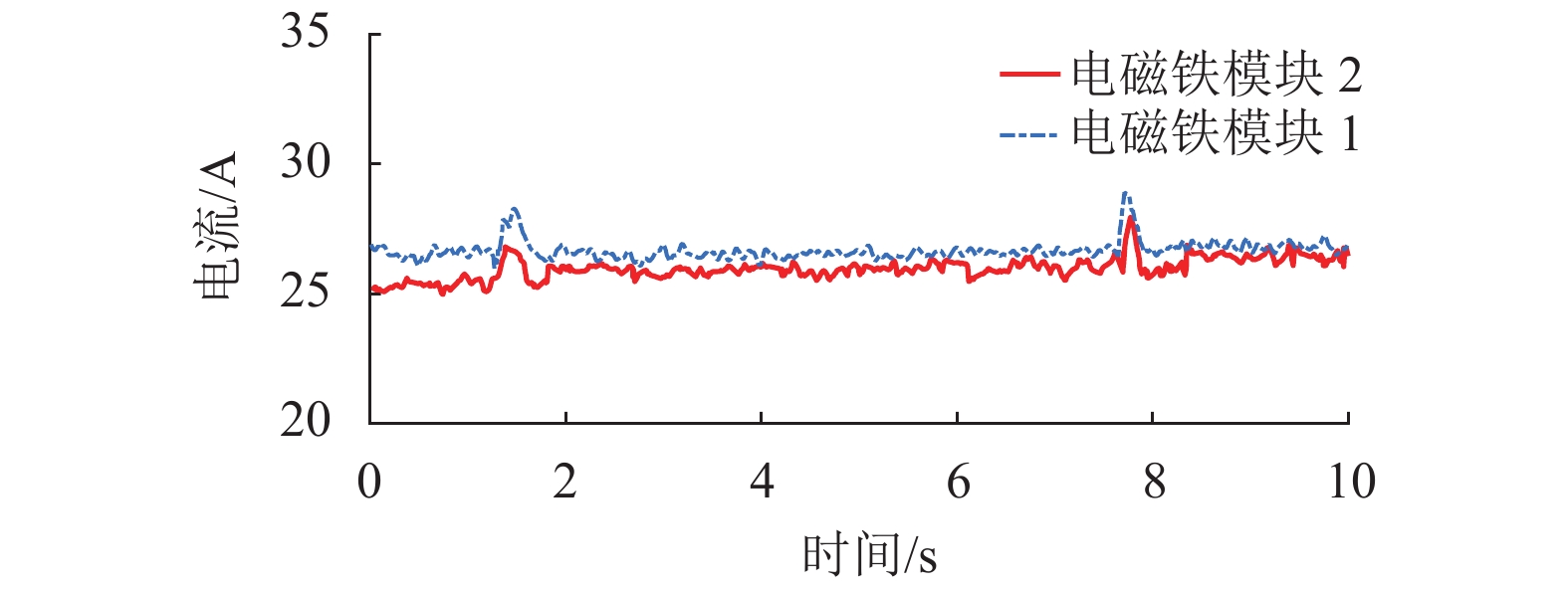
针对磁浮列车传统的单点悬浮控制方法没有考虑多电磁铁间的协调同步问题，将多电磁铁的跟踪误差交叉耦合来设计高精度的协同控制方法，在减少了多点悬浮系统的跟踪误差和同步误差的同时，提高了系统抗干扰能力. 首先，通过动力学分析了考虑未知扰动的4个电磁铁（2个控制模块）悬浮系统的动力学特征；其次，针对系统中的未知扰动，引入干扰观测器来估计扰动并进行扰动补偿；然后，考虑到相邻电磁铁控制模块之间存在耦合动力学特性，设计一种误差交叉耦合的滑模协同控制器；最后，在不作任何线性化处理的前提下，证明了闭环系统的渐近稳定性. 研究结果表明：通过多电磁铁的悬浮架实验证明所提方法可以考虑补偿电磁铁模块之间的协调关系，抑制扰动的影响，减小间隙跟踪误差达40%，显著减少了电磁铁之间的耦合扰动作用.
- 磁浮列车 /
- 多点悬浮系统 /
- 滑模协同控制 /
- 干扰观测器 /
- 误差交叉耦合
Abstract:
As to the problem that traditional signal point suspension control method of maglev train lacks consideration of coordination and synchronization of multiple electromagnets, a novel coordination control method is developed through tracking error cross-coupling. The novel method can reduce tracking error and synchronization error of multiple points suspension system and enhance anti-disturbance ability at the same time. Firstly, through dynamic analysis, the dynamic equations of four electro magnets (two control modules) suspension system considering unknown disturbance are established. Secondly, in order to estimate and compensate the unknown disturbance of the system, a disturbance observer is introduced. Next, considering the coupling dynamic characteristics of adjacent electromagnet control modules, a sliding mode coordinated controller of error cross coupling is designed. Finally, the asymptotic stability of the closed-loop system is proved without linearization. The experiments show that the presented control method can compensate the coordination relationship of electromagnet modules, suppress the effect of disturbance, reduce the synchronization error by 40%, and inhibit the coupling disturbance between electro magnets significantly.
- maglev train /
- multipoint suspension system /
- sliding mode cooperative control /
- disturbance observer /
- error cross coupling

HTML全文

图 1 悬浮架同侧多电磁铁悬浮系统

Figure 1. Multi-electromagnet suspension system on the same side of suspension frame

下载: 全尺寸图片幻灯片

图 2 多电磁铁悬浮系统动力学模型

Figure 2. Dynamic model of multi-electromagnet suspension system

下载: 全尺寸图片幻灯片

图 3 带观测器的滑模协同控制系统框图

Figure 3. Block diagram of sliding mode cooperative control system with observer

下载: 全尺寸图片幻灯片

图 4 带多电磁铁模块的悬浮架试验平台

Figure 4. Suspension frame test platform with multi-electromagnet modules

下载: 全尺寸图片幻灯片

图 5 悬浮间隙波动实验结果（PID控制器）

Figure 5. Experimental results of suspension airgap fluctuation （PID controller）

下载: 全尺寸图片幻灯片

图 6 悬浮电流波动实验结果（PID控制器）

Figure 6. Experimental results of suspension current fluctuation （PID controller）

下载: 全尺寸图片幻灯片

图 7 悬浮间隙波动实验结果（滑模协同控制）

Figure 7. Experimental results of suspension airgap fluctuation （sliding mode cooperative control）

下载: 全尺寸图片幻灯片

图 8 悬浮电流波动实验结果（滑模协同控制）

Figure 8. Experimental results of suspension current fluctuation （sliding mode cooperative control）

下载: 全尺寸图片幻灯片

表 1 磁悬浮系统参数

Table 1. Magnetic levitation system parameters

物理参数	取值	物理参数	取值
m_s/kg	750	μ₀/（H·m⁻¹）	4π × 10⁻⁷
N_m	340	A/m²	0.0196
δ_d/m	0.008	g/（m·s⁻²）	9.8

下载: 导出CSV

参考文献(17)

[1]	BOLDEA I, TUTELEA L N, XU W, et al. Linear electric machines, drives, and MAGLEVs: an overview[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7504-7515. doi: 10.1109/TIE.2017.2733492
[2]	马卫华,罗世辉,张敏,等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报,2021,21(1): 199-216. MA Weihua, LUO Shihui, ZHANG Min, et al. Research review on medium and low speed maglev vehicle[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 199-216.
[3]	翟婉明,赵春发. 磁浮车辆/轨道系统动力学(I): 磁/轨相互作用及稳定性[J]. 机械工程学报,2005,41(7): 1-10. doi: 10.3321/j.issn:0577-6686.2005.07.001 ZHAI Wanming, ZHAO Chunfa. Dynamics of maglev vehicle/guideway systems(I): magnet/rail interaction and system stability[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 1-10. doi: 10.3321/j.issn:0577-6686.2005.07.001
[4]	赵春发,翟婉明. 磁浮车辆/轨道系统动力学(Ⅱ): 建模与仿真[J]. 机械工程学报,2005,41(8): 163-175. doi: 10.3321/j.issn:0577-6686.2005.08.029 ZHAO Chunfa, ZHAI Wanming. Dynamics of maglev vehicle/guideway systems(Ⅱ): modeling and simulation[J]. Chinese Journal of Mechanical Engineering, 2005, 41(8): 163-175. doi: 10.3321/j.issn:0577-6686.2005.08.029
[5]	蒋启龙,张昆仑,李熹. 单磁铁悬浮系统的数字控制[J]. 铁道学报,1999,21(5): 45-48. JIANG Qilong, ZHANG Kunlun, LI Xi. Digital control for single-magnet suspension system[J]. Journal of the China Railway Society, 1999, 21(5): 45-48.
[6]	龙志强,洪华杰,周晓兵. 磁浮列车的非线性控制问题研究[J]. 控制理论与应用,2003,20(3): 399-402. doi: 10.3969/j.issn.1000-8152.2003.03.016 LONG Zhiqiang, HONG Huajie, ZHOU Xiaobing. Research of nonlinear control for maglev train[J]. Control Theory & Applications, 2003, 20(3): 399-402. doi: 10.3969/j.issn.1000-8152.2003.03.016
[7]	汪科任,罗世辉,张继业. 磁悬浮控制器设计及静悬浮稳定性分析[J]. 西南交通大学学报,2017,52(1): 118-126. doi: 10.3969/j.issn.0258-2724.2017.01.017 WANG Keren, LUO Shihui, ZHANG Jiye. Design of magnetic levitation controller and static stability analysis[J]. Journal of Southwest Jiaotong University, 2017, 52(1): 118-126. doi: 10.3969/j.issn.0258-2724.2017.01.017
[8]	王亮,王立德,王永翔. 多点悬浮系统的解耦及控制系统设计[J]. 自动化技术与应用,2004,23(1): 12-15. doi: 10.3969/j.issn.1003-7241.2004.01.004 WANG Liang, WANG Lide, WANG Yongxiang. Decoupling of multispot suspension system and its control design[J]. Techniques of Automation and Applications, 2004, 23(1): 12-15. doi: 10.3969/j.issn.1003-7241.2004.01.004
[9]	李奇南,徐德鸿. 四电磁铁支撑钢板磁悬浮系统气隙交叉耦合控制[J]. 中国电机工程学报,2010,30(33): 129-134. LI Qinan, XU Dehong. Gap cross-coupling control for 4-electromagnet supported steel plate magnetic suspension system[J]. Proceedings of the CSEE, 2010, 30(33): 129-134.
[10]	徐俊起,林国斌,陈琛,等. 负载扰动下磁浮车辆多点悬浮建模与控制[J]. 同济大学学报(自然科学版),2020,48(9): 1353-1363. doi: 10.11908/j.issn.0253-374x.20103 XU Junqi, LIN Guobin, CHEN Chen, et al. Modeling and control of multi-point levitation of maglev vehicle under loading disturbance[J]. Journal of Tongji University (Natural Science), 2020, 48(9): 1353-1363. doi: 10.11908/j.issn.0253-374x.20103
[11]	赵伟. 磁浮列车多点悬浮系统的无模型自适应控制器模块化设计方法研究[D]. 北京: 北京交通大学, 2020.
[12]	徐秀栋,黄攀峰,孟中杰. 空间绳系机器人逼近目标协调控制方法[J]. 航空学报,2013,34(5): 1222-1231. XU Xiudong, HUANG Panfeng, MENG Zhongjie. Coordinated control method of space tethered robot for approaching targets[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1222-1231.
[13]	褚文博,罗禹贡,韩云武,等. 基于规则的分布式电驱动车辆驱动系统失效控制[J]. 机械工程学报,2012,48(10): 90-95,102. doi: 10.3901/JME.2012.10.090 CHU Wenbo, LUO Yugong, HAN Yunwu, et al. Rule-based traction system failure control of distributed electric drive vehicle[J]. Journal of Mechanical Engineering, 2012, 48(10): 90-95,102. doi: 10.3901/JME.2012.10.090
[14]	张昭遂,孙元章,李国杰,等. 超速与变桨协调的双馈风电机组频率控制[J]. 电力系统自动化,2011,35(17): 20-25,43. ZHANG Zhaosui, SUN Yuanzhang, LI Guojie, et al. Frequency regulation by doubly fed induction generator wind turbines based on coordinated overspeed control and pitch control[J]. Automation of Electric Power Systems, 2011, 35(17): 20-25,43.
[15]	王树宏,孙友刚,董达善. 基于观测器和输出受限的磁浮列车悬浮控制[J]. 控制工程,2020,27(8): 1440-1444. WANG Shuhong, SUN Yougang, DONG Dashan. Suspension control for maglev train systems based on state observer and output constraints[J]. Control Engineering of China, 2020, 27(8): 1440-1444.
[16]	张敏,马卫华,李铁,等. 线圈串接方式对悬浮控制性能的影响仿真[J]. 机械工程学报,2019,55(12): 149-156. doi: 10.3901/JME.2019.12.149 ZHANG Min, MA Weihua, LI Tie, et al. Simulation of the influence of coil connectionmode on levitation control performance[J]. Journal of Mechanical Engineering, 2019, 55(12): 149-156. doi: 10.3901/JME.2019.12.149
[17]	孙友刚,李万莉,林国斌,等. 低速磁浮列车悬浮系统动力学建模及非线性控制[J]. 同济大学学报(自然科学版),2017,45(5): 741-749. SUN Yougang, LI Wanli, LIN Guobin, et al. Dynamic modeling and nonlinear control research on magnetic suspension systems of low-speed maglev train[J]. Journal of Tongji University (Natural Science), 2017, 45(5): 741-749.