基于不等磁路面积设计方法的磁轴承刚度

胡余生; 李立毅; 郭伟林; 李欣

doi:10.3969/j.issn.0258-2724.20210888

基于不等磁路面积设计方法的磁轴承刚度

doi: 10.3969/j.issn.0258-2724.20210888

胡余生^{1, 2,},
李立毅^1, ,,
郭伟林²,
李欣^2,

1.
哈尔滨工业大学电气工程学院，黑龙江哈尔滨 150000
2.
珠海格力电器股份有限公司，广东珠海 519000

详细信息

作者简介:
胡余生（1978—），男，高级工程师（教授级），博士研究生，研究方向为磁悬浮制冷离心压缩机，E-mail：dewtutg@163.com

通讯作者:
李立毅（1969—），男，教授，博士生导师，研究方向为特种电机，E-mail：gldqhys@163.com

中图分类号: TH133.3
计量
- 文章访问数: 292
- HTML全文浏览量: 86
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-15
- 修回日期: 2022-04-11
- 刊出日期: 2022-05-17

Support Stiffness of Magnetic Bearing Based on Unequal Magnetic Circuit Area Design Method

HU Yusheng^{1, 2
,},
LI Liyi^{1
, ,},
GUO Weilin²,
LI Xin^2
,

1.
Deptment of Electrical Engineering, Harbin Institute of Technology, Harbin 150000, China
2.
Gree Electric Appliance Inc. of Zhuhai, Zhuhai 519000, China

摘要

摘要:
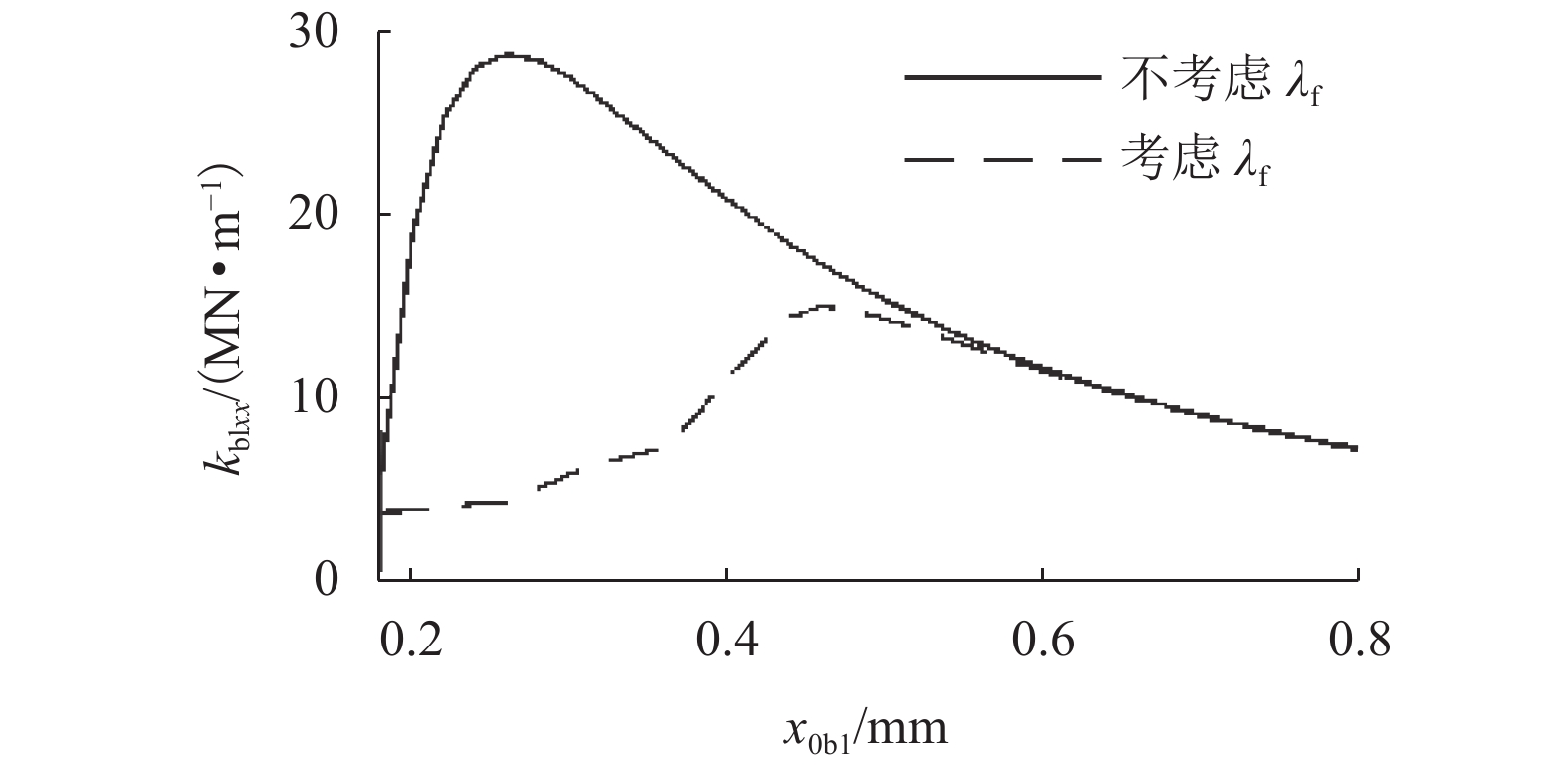
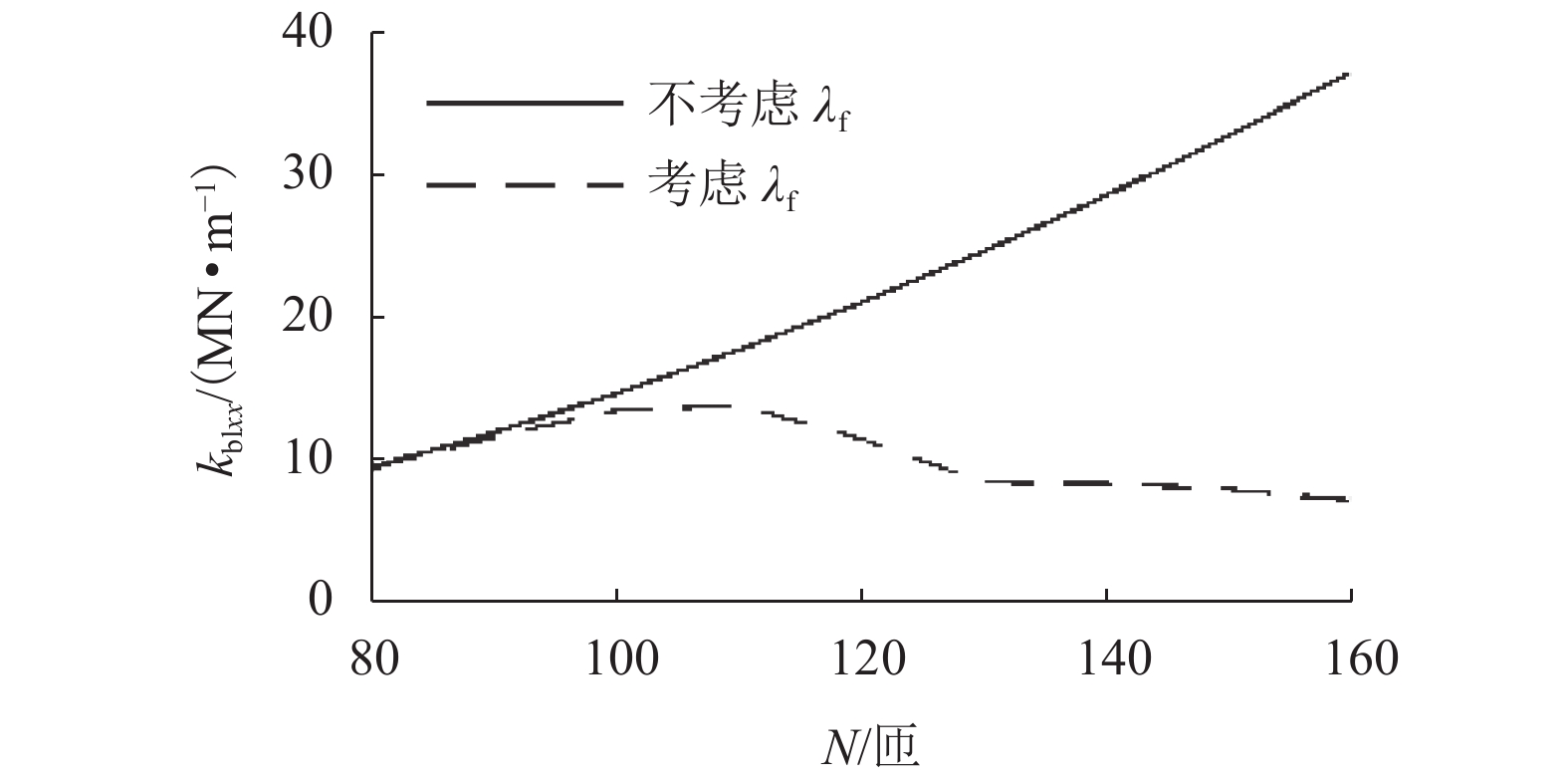
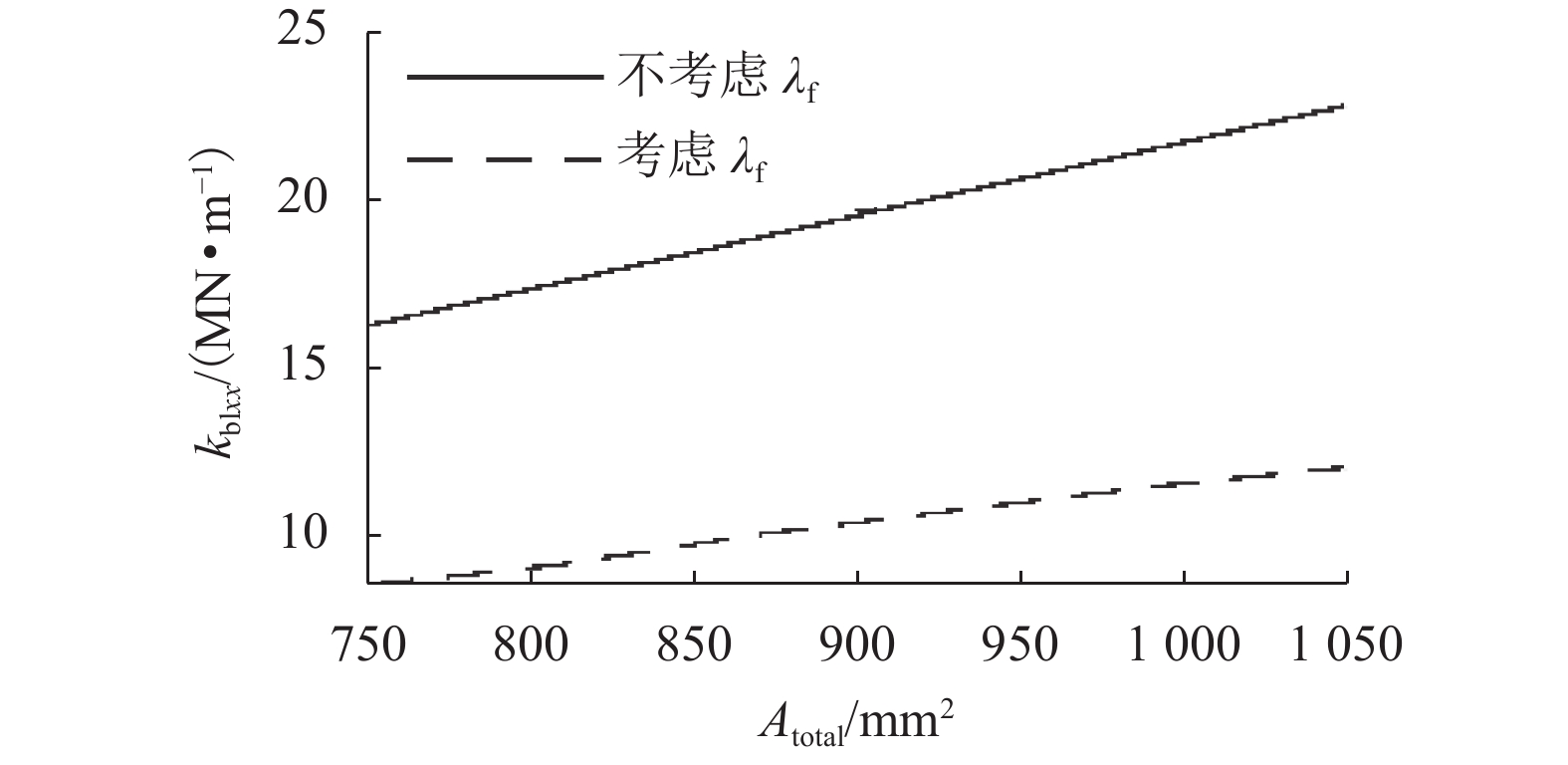
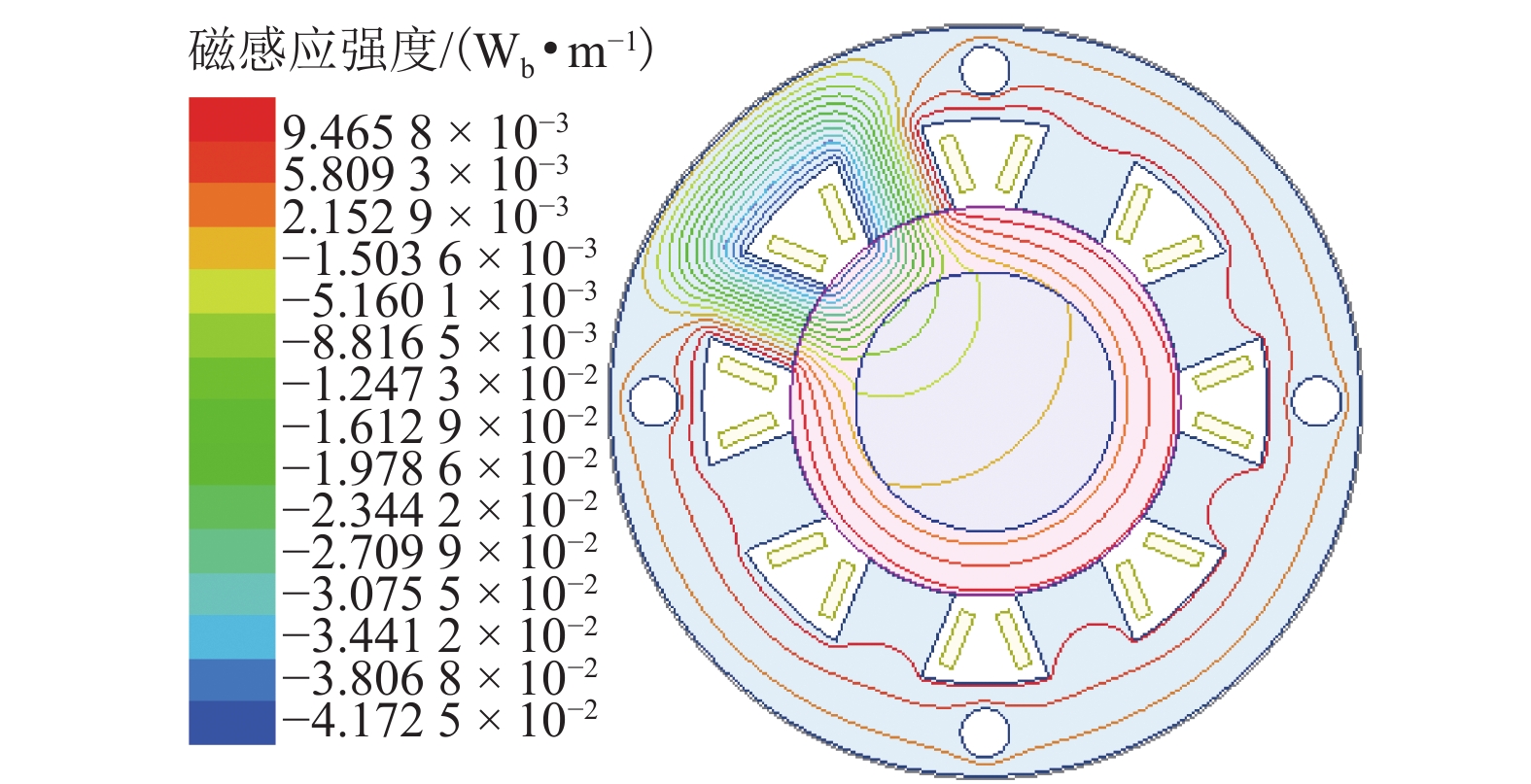
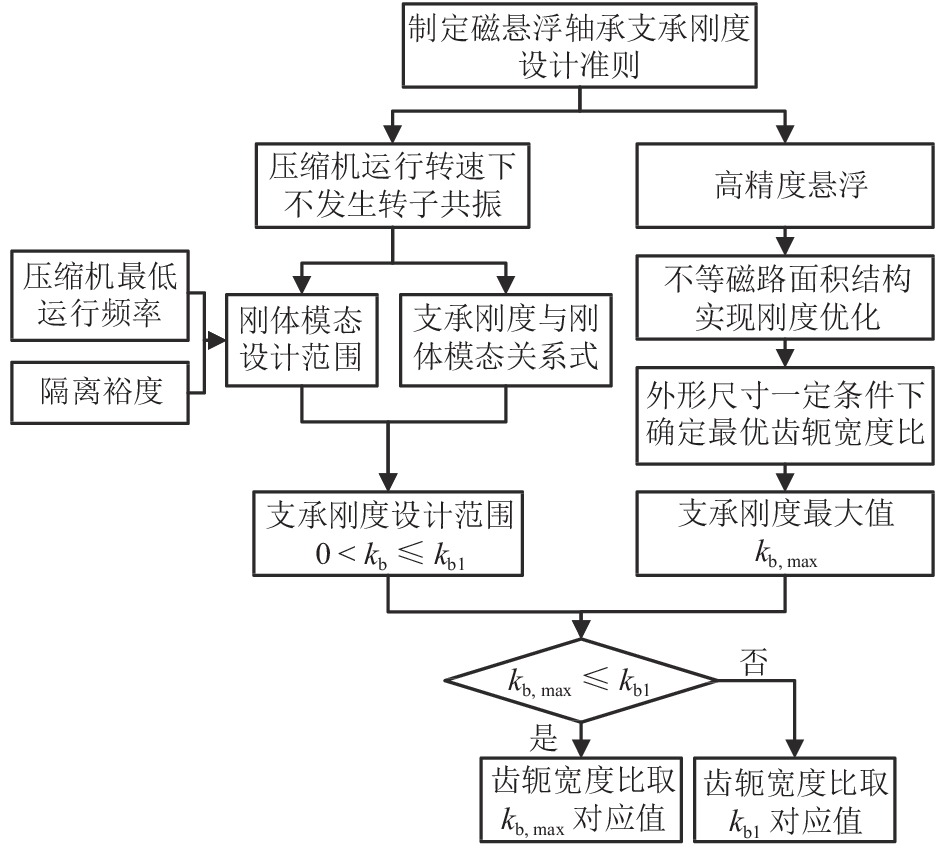
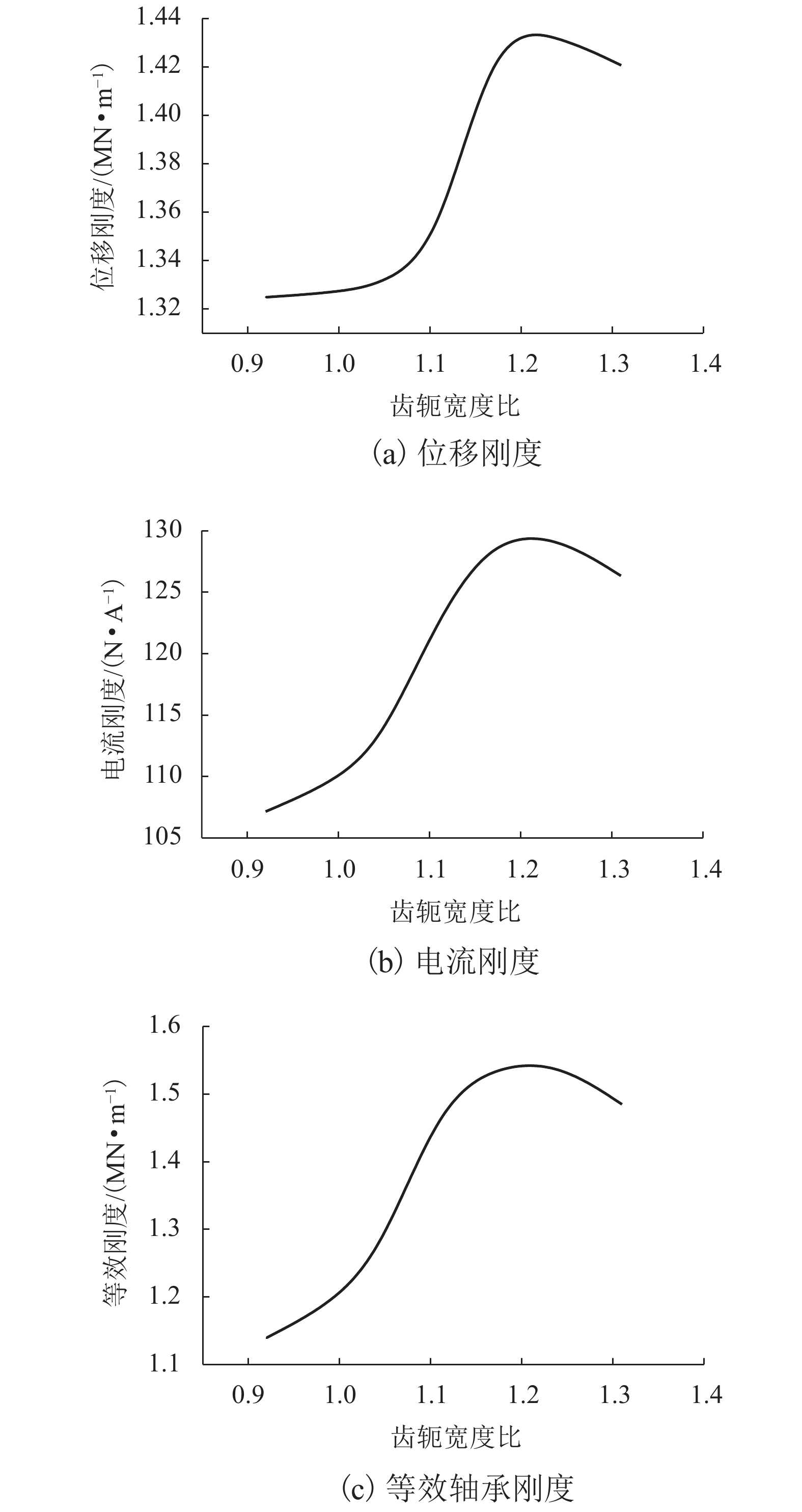
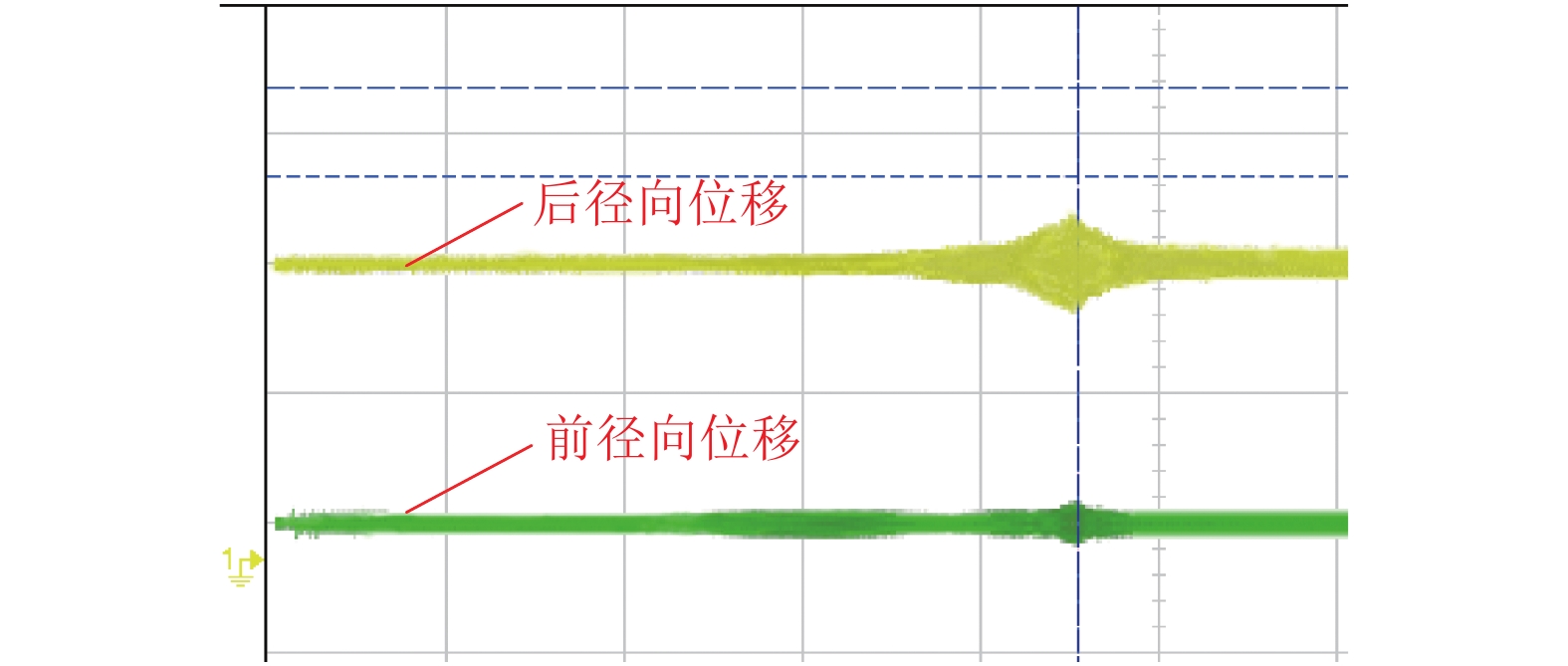
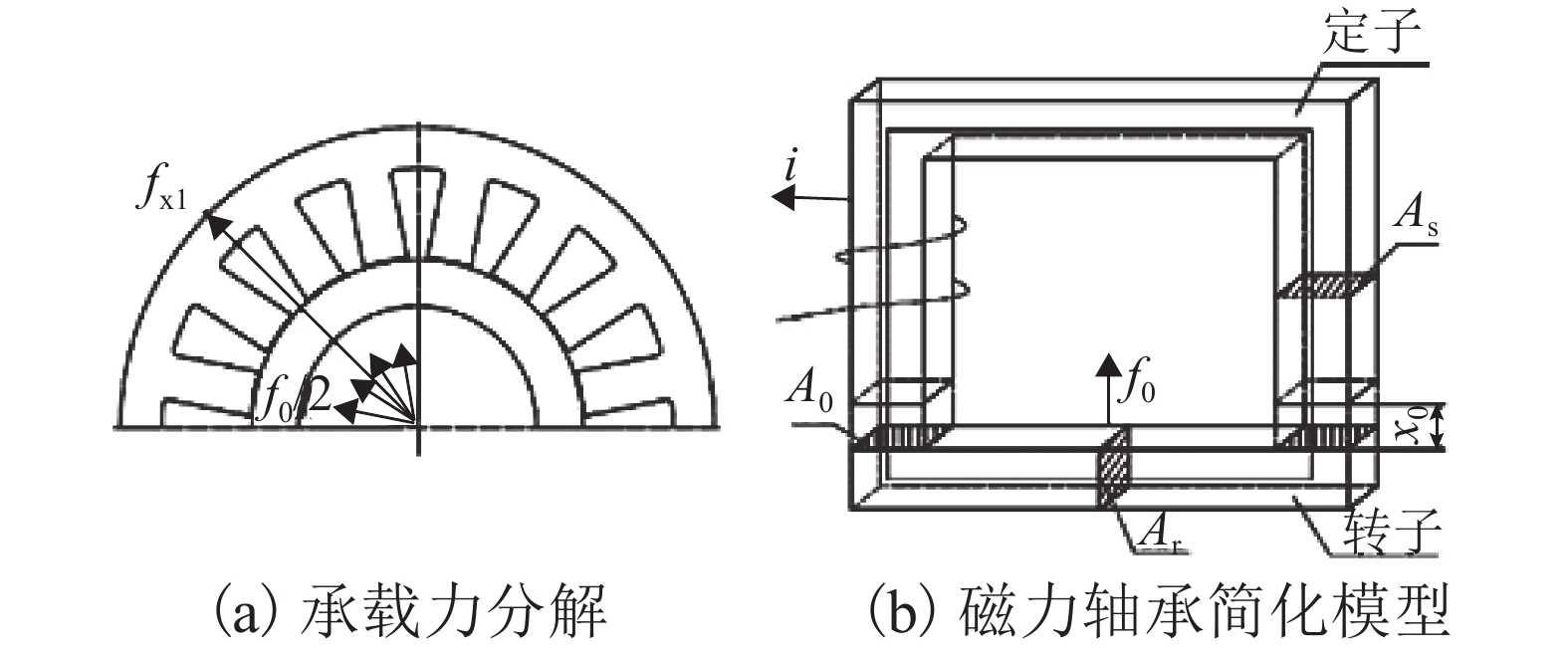
磁悬浮转子需同时满足抗干扰与共振隔离需求，为了从磁悬浮轴承结构角度奠定设计基础，基于磁悬浮轴承结构参数对支承刚度的影响，对高刚度磁悬浮轴承设计方法展开研究. 首先，通过磁悬浮轴承刚度解析式推导，分析磁悬浮轴承结构参数对支承刚度的影响因素，确定支承刚度优化方向；其次，提出高刚度磁悬浮轴承设计方法，分析支承刚度的优化效果；最后，通过转子固有频率测试及压缩机升频实验，验证所提出方法的可行性. 结果表明：在压缩机样机中，磁悬浮轴承采用不等磁路面积结构，在齿轭宽度比为1.2时，可使轴承在最恶劣工况，即对应最大控制电流时，支承刚度较常规等磁路面积结构提高了25%，压缩机在工况运行区间有效避免共振，为工程应用中磁悬浮轴承刚度优化设计提供参考.
- 磁悬浮轴承 /
- 支承刚度 /
- 结构优化 /
- 不等磁路面积
Abstract:
The magnetic suspension rotor needs to meet the requirements of anti-interference and resonance isolation at the same time, in order to lay the design foundation from the perspective of magnetic bearing structure, the design method of high stiffness magnetic bearing is studied based on the influence of magnetic bearing structural parameters on support stiffness. Firstly, through the derivation of the analytical formula of the stiffness of the magnetic bearing, the influencing factors of the structural parameters on the support stiffness are analyzed, and the optimization direction of the support stiffness is determined; Secondly, the design method of high stiffness magnetic bearing is proposed, and the optimization effect of support stiffness is analyzed; Finally, the feasibility of the proposed method is verified by rotor natural frequency test and compressor frequency rise experiment. The results show that in the compressor prototype, when the magnetic bearing adopts the structure of unequal magnetic circuit area with the tooth yoke width ratio 1.2, the support stiffness of the magnetic bearing under the worst working condition, that is, the maximum control current, can improve by 25% compared with the equal magnetic circuit area, and the compressor can effectively avoid resonance in the operating range, which provides a reference for the optimization design of the support stiffness of magnetic bearing in engineering application.
- magnetic bearing /
- support stiffness /
- structure optimization /
- unequal magnetic circuit area

HTML全文

图 1 磁力轴承出力模型

Figure 1. Capacity model of magnetic bearing

下载: 全尺寸图片幻灯片

图 2 四自由度磁悬浮转子系统

Figure 2. Magnetic suspension rotor system with 4 degree-of-freedom

下载: 全尺寸图片幻灯片

图 3 支承刚度随磁极的变化

Figure 3. Relationship between support stiffness and number of poles

下载: 全尺寸图片幻灯片

图 4 支承刚度随气隙的变化

Figure 4. Relationship between support stiffness and air gap

下载: 全尺寸图片幻灯片

图 5 支承刚度随匝数的变化

Figure 5. Relationship between support stiffness and number of turns

下载: 全尺寸图片幻灯片

图 6 支承刚度随磁极面积的变化

Figure 6. Relationship between support stiffness and magnetic pole area

下载: 全尺寸图片幻灯片

图 7 等磁路面积结构下磁力线分布

Figure 7. Distribution of magnetic force line with equal magnetic circuit area structure

下载: 全尺寸图片幻灯片

图 8 支承刚度设计方法

Figure 8. Design method for magnetic bearing stiffness

下载: 全尺寸图片幻灯片

图 9 不同控制电流下的磁密分布

Figure 9. Distribution of magnetic flux density with different control currents

下载: 全尺寸图片幻灯片

图 10 x = 0，i_b = 0时轴承刚度与齿轭宽度比关系

Figure 10. Relationship between stiffness and the width ratio of tooth to yoke with x = 0，i_b = 0

下载: 全尺寸图片幻灯片

图 11 x = 0，i_b = 4 A时轴承刚度与齿轭宽度比关系

Figure 11. Relationship between stiffness and the width ratio of tooth to yoke with x = 0，i_b = 4 A

下载: 全尺寸图片幻灯片

图 12 转子结构及加速度传感器布置示意

Figure 12. Magnetic suspension centrifuge rotor and position of acceleration sensor

下载: 全尺寸图片幻灯片

图 13 转子升频过程轴承位移曲线

Figure 13. Displacement curves of bearing in the process of frequency rise

下载: 全尺寸图片幻灯片

参考文献(13)

[1]	XU Y P, SHEN Q, ZHANG Y, et al. Dynamic modeling of the active magnetic bearing system operating in base motion condition[J]. IEEE Access, 2020, 8: 166003-166013. doi: 10.1109/ACCESS.2020.3022996
[2]	KIM C S, JUNG H H, PARK B K. A study on the optimal design for a magnetic bearing-rotor with maximum stiffness using a genetic algorithm[J]. Journal of the Korean Society of Manufacturing Process Engineers, 2013, 12(6): 167-174. doi: 10.14775/ksmpe.2013.12.6.167
[3]	YANG G J, XU Y, SHI Z G, et al. Characteristic analysis of rotor dynamics and experiments of active magnetic bearing for HTR-10GT[J]. Nuclear Engineering and Design, 2007, 237(12/13): 1363-1371.
[4]	JUNG H H, KANG S H, CHO B H, et al. A design technique for a magnetic bearing-rotor in a turbo blower considering critical speeds[J]. Advanced Materials Research, 2012, 569: 564-567. doi: 10.4028/www.scientific.net/AMR.569.564
[5]	FUJIWARA H, YANAGIHARA K, MATSUSHITA O, et al. Design of active magnetic bearing rotors and their control method for passing through fourth bending critical speed[J]. Mechanical Engineering Journal, 2019, 6(3): 00481.1-00481.11.
[6]	任正义,朱健国,杨立平. 基于ANSYS Workbench的飞轮转子临界转速计算分析[J]. 机械工程师,2019(9): 23-24,27. REN Zhengyi, ZHU Jianguo, YANG Liping. Calculation and analysis on critical speed of flywheel rotor based on ANSYS workbench[J]. Mechanical Engineer, 2019(9): 23-24,27.
[7]	蒋启龙,胡振球. 轴向主动磁轴承的改进不完全微分PID控制[J]. 西南交通大学学报,2015,50(2): 241-246. doi: 10.3969/j.issn.0258-2724.2015.02.006 JIANG Qilong, HU Zhenqiu. Improved incomplete derivative PID control of axial active magnetic bearing[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 241-246. doi: 10.3969/j.issn.0258-2724.2015.02.006
[8]	黎松奇,张昆仑. 单磁铁悬浮系统自激振动的稳定性分析及抑制[J]. 西南交通大学学报,2015,50(3): 410-416. doi: 10.3969/j.issn.0258-2724.2015.03.004 LI Songqi, ZHANG Kunlun. Self-excited vibration of single-magnet suspension system: stability analysis and inhibition[J]. Journal of Southwest Jiaotong University, 2015, 50(3): 410-416. doi: 10.3969/j.issn.0258-2724.2015.03.004
[9]	CHITTLANGIA V, LIJESH K P, AKASH K, et al. Optimum design of an active magnetic bearing considering the geometric constraints[J]. Technology Letters, 2014, 1(3): 23-30.
[10]	LIJESH K P, HIRANI H. Optimization of eight pole radial active magnetic bearing[J]. Journal of Tribology, 2015, 137(2): 024502.1-024502.7.
[11]	周瑾,高天宇,董继勇,等. 基于Isight的径向磁悬浮轴承结构优化设计[J]. 轴承,2018(7): 6-11. ZHOU Jin, GAO Tianyu, DONG Jiyong, et al. Optimal design for structure of radial magnetic bearings based on isight[J]. Bearing, 2018(7): 6-11.
[12]	KANG K, PALAZZOLO A. Homopolar magnetic bearing saturation effects on rotating machinery vibration[J]. IEEE Transactions on Magnetics, 2012, 48(6): 1984-1994. doi: 10.1109/TMAG.2012.2182776
[13]	GERAMI A, ALLAIRE P, FITTRO R. Control of magnetic bearing with material saturation nonlinearity[J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 137(6): 061002.1-061002.10.