永磁电磁混合Halbach阵列电动悬浮的稳定性控制

罗成; 张昆仑; 王滢

doi:10.3969/j.issn.0258-2724.20210868

永磁电磁混合Halbach阵列电动悬浮的稳定性控制

doi: 10.3969/j.issn.0258-2724.20210868

罗成^{1, 2,},
张昆仑^{1, 2},
王滢^{1, 2}

1.
西南交通大学电气工程学院，四川成都 611756
2.
西南交通大学磁浮技术与磁浮列车教育部重点实验室，四川成都 611756

基金项目: 中央高校基本科研业务费科技创新项目（2682022CX001）；国家重点研发计划（2018YFC0809505）

详细信息

作者简介:
罗成（1987—），男，实验师，博士，研究方向为电动悬浮，E-mail：luocheng1987.happy@163.com

中图分类号: TM154.1；U266.4
计量
- 文章访问数: 449
- HTML全文浏览量: 293
- PDF下载量: 39
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-09
- 修回日期: 2022-03-11
- 刊出日期: 2022-03-17

Stability Control of Electrodynamic Suspension with Permanent Magnet and Electromagnet Hybrid Halbach Array

LUO Cheng^{1, 2
,},
ZHANG Kunlun^{1, 2},
WANG Ying^{1, 2}

1.
School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China
2.
Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle of Ministry of Education, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
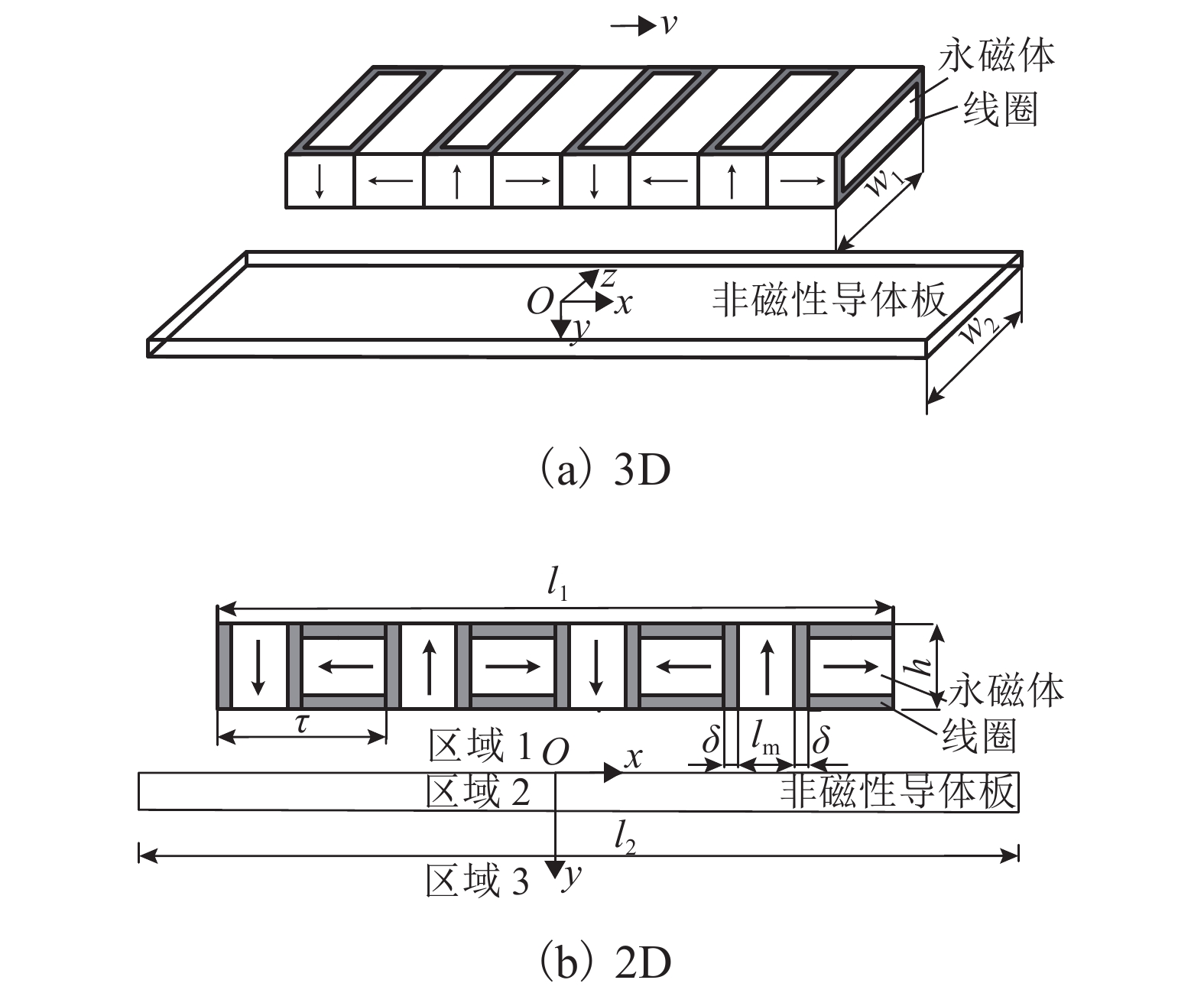
为了研究不同控制方法下永磁电磁混合Halbach阵列的电动悬浮稳定性，首先，利用电磁场理论对系统悬浮力2D解析式进行了推导，并搭建有限元模型对其进行了验证；其次，建立了系统垂向动力学模型，设计了基于气隙反馈的定气隙PID控制器和变气隙PID控制器；最后，仿真分析了系统受到外界扰动时的悬浮气隙及线圈电流波形. 研究结果表明：当系统受到1 mm轨道沉降扰动时，两种控制器均能使系统稳定运行于额定状态，且动态过程一致；当系统受到 ±1000 N扰动力作用时，定气隙PID控制器可使系统稳定悬浮于额定气隙30 mm位置，且稳态线圈电流分别为2.12 A/mm²和 −2.17 A/mm²，变气隙PID控制器则使系统分别稳定悬浮于28.5 mm及31.6 mm位置，且稳态线圈电流均为0.
- Halbach阵列 /
- 电动悬浮 /
- 解析计算 /
- 有限元模型 /
- 系统稳定性
Abstract:
In order to study the suspension stability of the electrodynamic suspension (EDS) with permanent magnet (PM) and electromagnet hybrid halbach array under different control methods, Firstly, the 2D levitation force analytical expression was derived by using the electromagnetic field theory and the corresponding finite element model (FEM) was built to verify the suspension force analytical expression. Secondly, the vertical dynamic model of the system was established, and the fixed air gap PID controller and variable air gap PID controller based on the air gap feedback were designed respectively. Finally, the system suspension air gap and current density waveforms under external disturbances were simulated and analyzed. The simulation results indicate that both controllers can make the system suspend stably at the rated state and have the same dynamic process under the 1 mm track settlement disturbance. When the system is disturbed by the ± 1000 N disturbing force, the fixed air gap PID controller can make the system suspend stably at the 30 mm rated air gap, and apply the steady state coil current of 2.12 A/mm² and −2.17 A/mm² respectively. The variable air gap PID controller makes the system suspend stably at 28.5 mm and 31.6 mm respectively, and applies the steady-state coil current of 0.
- Halbach array /
- electrodynamic suspension /
- analytical calculation /
- finite element model /
- system stability

HTML全文

在交通强国战略加快推进、交通运输领域基础设施建设逐步完善的背景下，隧道施工技术日趋成熟，长大隧道（长度超过1.00 km）不断涌现. 目前，我国已建成了世界最长的双洞高速公路隧道—秦岭终南山隧道（18.02 km）^[1]，海拔3000 m以上的世界最长隧道—新关角隧道（32.70 km）^[2]，以及亚洲最长的单孔双线高速铁路隧道—秦岭天华山隧道（16.00 km）^[3]. 面对隧道建设技术的持续革新和隧道需求的井喷式增长，我国隧道建设的规模和难度已位居世界第一，超长、超深隧道建设迎来新的发展机遇.

在隧道建设过程中，地质条件复杂，视觉环境不良，施工作业难度大，具有一定的风险^[4]. 因此，隧道施工期间的组织管理成为规避事故风险、保证施工效率的重要途径. Sousa等^[5]研究了隧道施工过程中的事故案例，强调隧道组织管理在降低施工风险，减少施工事故方面的重要性. Zhu等^[6]调查统计了我国2010年～2020年发生的重大隧道施工事故发现，低下的组织管理水平会导致施工过程中事故频发. 值得注意的是，施工车辆的运输组织管理已成为严重制约施工安全和施工效率的重点环节，隧道内的渣土运输、人员输送、交通物流配送等成为限制施工效率的瓶颈问题. 施工车辆在路况恶劣、能见度低的长大隧道内交通组织紊乱，不仅严重影响施工进度，还会增加运输安全隐患.

考虑到隧道内错综复杂的交通线路，科学的运输组织管理势在必行. 特别是长大隧道施工过程中对于施工交通流的合理组织和有效管控有利于提高施工效率，保障施工安全. 目前，国内外已有一些学者对隧道的运输组织管理进行了相关研究. Jiang等^[7]通过VISSIM对隧道出入口车辆的运行情况进行仿真模拟，提出隧道施工期间隧道出入口及其周边的交通流组织优化方案. Liu等^[8]在权衡施工车辆运输效率和安全性的基础上，建立了包含限高、限重、限速等约束条件的双目标车辆运输路径优化模型. 林杉等^[9]提出了一种高速公路隧道交通瓶颈元胞自动机模型，为制定隧道内的交通流组织方案提供依据. 高壮^[10]基于重载铁路的线路条件研究设计出 2 种隧道内无砟轨道施工物流组织方案，极大地提高了施工组织效率. 然而，现有的大多数研究都是从宏观的角度提出广泛的、借鉴性较强的交通物流组织方案，尚未有着眼于隧道内部交通冲突疏解的多工种施工车辆时刻表和运行路径的优化研究.

车辆时刻表和路径规划的协同优化问题在铁路开行方案和列车时刻表制定，公交循环计划，集装箱码头智能转运车路径、时刻规划以及智能机器人路径规划（避撞）等领域具有广泛的应用^[11-14]. Zhang等^[11]从宏观层面提出了一种基于扩展时空网络的列车运行周期表模型来得到最佳列车循环方案. 王志建等^[12]根据公交车IC刷卡数据构建了多模式公交路网模型来设计满足乘客多种需求的路径规划方案. Cherif等^[13]基于Peri网对自动化智能转运车在码头的时间调度和路径规划问题进行了研究. 徐翔斌等^[14]将多自动引导车（AGV）的路径转化为离散时空网络下的路径，建立基于离散时空网络的路径优化模型. 由此可见，虽然车辆时刻表和路径的协同优化问题近年来受到了广泛关注，但是少有研究关注到隧道内部施工车辆的时刻表与运行路径的协同优化问题. 与一般隧道相比，长大隧道内道路线形差，施工车辆需求大，面临比上述领域更为棘手的难题. 如果不规定施工车辆的发车频率和路径时刻表，那么混乱、不均匀、不规律的发车会使车辆间产生过多的交通冲突，迫使车辆停止运行，进行掉头、避让、后退等操作，将严重影响施工效率.

在疏解冲突方面，Zhang等^[15]针对自动导引车的离线路径规划问题，提出了一种无冲突路径规划方法. 李珣等^[16]建立了基于元胞自动机的精细化车道模型，研究新的交通流模型在减少车辆堵塞方面的作用. 李英帅等^[17]建立交通冲突预测模型，对直线式单泊位公交停靠站设置进行优化. 本文考虑到长大隧道内部的恶劣路况和复杂交通流促使多工种施工车辆间形成交通冲突的实际情况，对施工车辆的发车时刻表和运行路径的进行协同优化，实现交通冲突的有效消除，保证施工安全.

为解决上述难题，本文立足于施工车辆作业过程，构建路网层面的车辆时刻表和运行路径协同优化模型，并将模型重构为整数线性规划模型，利用GUROBI进行求解，制定施工车辆总运行时间最短的运输组织方案. 该优化方案能够有效疏解车辆间的交通冲突，协助调度员实施决策调度，使施工车辆在保证安全的前提下高效完成运输任务.

1. 问题描述

一般隧道的路况简单，施工过程中需求单一，多数研究侧重于其微观层面的组织管理. 而长大隧道内部道路狭长，路况复杂，需要从宏观层面对施工车辆的运输组织进行规划与管理. 在长大隧道施工作业的过程中，不同工种的施工车辆要求在指定需求点完成运渣、运材料、运人等任务.

1.1 隧道交通网络拓扑建模

长大隧道内的施工道路交通网络由正线、平导线、横洞等交错构成的复杂方格状道路网络，包含节点和路段2种基本要素. 其中，节点为路段间的交叉点，代表路段的交叉口. 交叉口按照交叉方式可分为“十字型交叉”和“T字型交叉”. 路段是连接节点的线段，代表供车辆行驶的道路，按照可供车辆行驶的方向数量分为单向路段和双向路段. 其拓扑结构如图1 所示.

图 1 隧道内部基本交通单元拓扑

Figure 1. Topological diagram of basic traffic units inside the tunnel

下载: 全尺寸图片幻灯片

本文考虑了长大隧道内部的多样运输需求，包括运渣需求、运材料需求和运人需求. 因此，施工车辆由运渣车辆、运材料车辆和运人车辆组成，对应于不同类型的需求点. 施工车辆的作业流程包括：驶入隧道、到达需求点并完成指定运输任务、驶出隧道. 根据隧道内节点及路段间的物理连接关系，图2展示出了隧道内部的交通网络及其拓扑图.

图 2 隧道内部交通网络拓扑

Figure 2. Topological diagram of traffic network inside the tunnel

下载: 全尺寸图片幻灯片

由于隧道内部单、双向路段混合共存，行驶环境恶劣，且施工车辆本身体积大、运载质量大，其在运输过程中容易在交叉口和单向路段发生交通冲突，形成通行瓶颈，妨碍其他车辆正常通行. 根据产生原因可将交通冲突分为交叉冲突、相向冲突和赶超冲突，如图3所示. 交叉冲突是指车辆在很短的时间范围内到达同一交叉点而产生的冲突；相向冲突是指对向行驶的车辆在单向路段上相遇而产生的冲突；赶超冲突是指不同的速度的车辆在单向路段上同向行驶而产生的冲突.

图 3 交通冲突类型

Figure 3. Types of traffic conflicts

下载: 全尺寸图片幻灯片

2. 模型构建

在模型中，车辆时刻表的决策变量属于整数变量，车辆的运行路径由表示车辆是否经过某路段的一系列0-1变量决定.

2.1 模型假设

为了简化问题，方便后续模型的建立和求解，本文做出以下假设：

假设1. 施工车辆的运行路径分为去程和返程方向. 另外，为简化求解过程，指定车辆在去程和返程期间任意路段上的唯一可行方向，即简化车辆去程和返程方向上的有向弧集合.

假设2. 施工车辆的限速条件预先给定，其在路段上的运行时间范围由最高和最低限速确定.

假设3. 隧道内，同向行驶的车辆遵循先到先服务（FIFO）原则，即同向行驶的车辆中，先到达某路段的车辆先从该路段离开.

2.2 数学描述

隧道内的拓扑网络由有向网络 ${\mathcal{G}}=({\mathcal{N}}, {\mathcal{A}})$ 表示， $\mathcal{N}$ 为节点集合， $\mathcal{A}$ 为路段集合，节点 $i, j \in \mathcal{N}$ ，有向弧 $(i, j) \in \mathcal{A}$ ， $i \neq j$ . $\mathcal{U}=\{1,2\}$ 表示车辆的行驶方向集合，用 $t, u_{\mathrm{a}} \in \mathcal{U}$ 进行索引. 当 $u=1$ 或 $u_{\mathrm{a}}=1$ 时，车辆从隧道入口向需求点行驶，当 $t=2$ 或 $u_{\mathrm{a}}={2}$ 时，车辆从需求点向隧道出口行驶. $\mathcal{A}_{u}$ 表示 $u$ 方向上的路段集合， $\mathcal{A}_{{\mathrm{s}}}$ 表示单向路段集合， $\mathcal{K}$ 表示车辆集合，用 $k, k_{\mathrm{a}} \in \mathcal{K}$ 进行索引.

1）车辆行驶路径的0-1决策变量：

${x}_{i,j}^{k,u}=\left\{\begin{array}{l} 1,\quad 若车辆k在u方向上经过路段\left(i,j\right) \\ 0,\quad 其他 \end{array}.\right.$

2）车辆时刻表的决策变量：

$h^{k}$ 为车辆 $k$ 的发车间隔.

3）车辆到达和离开路段事件的相关变量：

$a_{i,j}^{k,u}$ 为车辆 $k$ 在 ${u}$ 方向上到达路段 $(i, j)$ 的时刻，

$d_{i,j}^{k,u}$ 为车辆 $k$ 在 ${u}$ 方向上离开路段 $(i, j)$ 的时刻.

2.3 目标函数和约束条件

隧道内多工种施工车辆的运输组织方案在保证系统安全的基础上，设计施工车辆的发车时刻表，合理安排运行路径，尽可能高效率地完成各项运输任务. 因此，模型以最小化所有车辆的运行（行驶）总时间为目标建立目标函数. 每辆车的行驶时长为 $\displaystyle\sum\limits_{\left( i,{{d}_{{\mathrm{s}}}} \right)\in \mathcal{A}}{d_{i,{{d}_{{\mathrm{s}}}}}^{k,2}}-\displaystyle\sum\limits_{\left( {{o}_{{\mathrm{s}}}},j \right)\in \mathcal{A}}{a_{{{o}_{{\mathrm{s}}}},j}^{k,1}}$ ，目标函数表示如式（1）所示.

$\min \quad {\textit{Z}} = \sum\limits_{k \in \mathcal{K}} {\left( {\sum\limits_{\left( {i,{d_{\mathrm{s}}}} \right) \in \mathcal{A}} {d_{i,{d_{\mathrm{s}}}}^{k,2}} - \sum\limits_{\left( {{o_{\mathrm{s}}},j} \right) \in \mathcal{A}} {a_{{o_{\mathrm{s}}},j}^{k,1}} } \right)},$

(1)

式中： $o_{{\mathrm{s}}}$ 为隧道入口，即车辆去程方向上的起点 $o_{k, 1}$ ； $d_{{\mathrm{s}}}$ 为隧道出口，即车辆返程方向上的终点 $d_{k, 2}$ .

1）车辆路径约束

车辆 $k$ 在 ${u}$ 方向上从起点 $o_{k, {u}}$ 出发，沿着路段驶过中间节点后到达终点 $d_{k,u}$ ，需满足所有车辆的路径均被规划（式（2）～（3））. 对于去程，车辆的起点为隧道入口，终点为相应需求点. 对于返程，车辆的起点为需求点，终点为隧道出口.

$\sum\limits_{\left( {{o_{k,u}},j} \right) \in {\mathcal{A}_u}} {x_{{o_{k,u}},j}^{k,u}} = 1,\quad {\mkern 1mu} {\mkern 1mu} \forall k \in \mathcal{K},\quad u \in \mathcal{U},$

(2)

$\sum\limits_{\left( {i,{d_{k,u}}} \right) \in {\mathcal{A}^u}} {x_{i,{d_{k,u}}}^{k,u}} = 1.$

(3)

2）流量守恒约束

中间节点必须满足流量守恒约束，即节点流入等于节点流出，如式（4）所示.

$\begin{split} &\sum\limits_{\left( {i_{\mathrm{a}},i} \right) \in {\mathcal{A}_u}} {x_{i_{\mathrm{a}},i}^{k,u}} = \sum\limits_{\left( {i,j} \right) \in {\mathcal{A}_u}} {x_{i,j}^{k,u}} {\mkern 1mu} ,\quad \forall i \in \mathcal{N}\backslash \left\{ {{o_{k,u}},{d_{k,u}}} \right\}, \\ &\quad k \in \mathcal{K},u \in \mathcal{U}. \end{split}$

(4)

3）路径和时刻联系约束

只有车辆经过某一路段，才能得到其在该路段上的到达时刻和离开时刻，满足式（5）～（6）. 其中， $M$ 是一个非常大的正数. 式（5）中，当车辆 $k$ 在方向 ${u}$ 上经过路段 $(i, j)$ ，即 $x_{i,j}^{k,u}=1$ 时， $0 \leqslant a_{i, j}^{k, u} \leqslant M$ ，规定了 $a_{i, j}^{k, u}$ 的取值范围，强调了其非负特性，使 $a_{i, j}^{k,u}$ 具有实际意义. 而当车辆 $k$ 在 ${u}$ 方向上不经过路段 $(i, j)$ ，即 $x_{i, j}^{k, u}=0$ 时， $-M \leqslant a_{i, j}^{k,u} \leqslant 0$ ， $a_{i, j}^{k,u}$ 不具有实际意义. 式（6）中的 $d_{i,j}^{k,u}$ 同理.

$\begin{split} &\left( {x_{i,j}^{k,u} - 1} \right) M \leqslant a_{i,j}^{k,u} \leqslant x_{i,j}^{k,u} M,\quad {\mkern 1mu} {\mkern 1mu} \forall \left( {i,j} \right) \in \mathcal{A}, \\ &\quad k \in \mathcal{K},u \in \mathcal{U}, \end{split}$

(5)

$\begin{split} &\left( {x_{i,j}^{k,u} - 1} \right) M \leqslant d_{i,j}^{k,u} \leqslant x_{i,j}^{k,u} M,\quad {\mkern 1mu} {\mkern 1mu} \forall \left( {i,j} \right) \in \mathcal{A}, \\ &\quad k \in \mathcal{K},u \in \mathcal{U}. \end{split}$

(6)

4）发车间隔约束

在隧道中，受到技术条件和安全性能的限制，施工车辆需要满足一定的发车间隔要求，即满足式（7）.

$h_{\min } \leqslant h_{k} \leqslant h_{\max }, \forall k \in \mathcal{K},$

(7)

式中： $h_{\text {min }}$ 、 $h_{\max }$ 分别为给定的最小和最大发车间隔.

5）路网进入时间约束

为保证车辆有序运行，车辆 $k$ 进入路网的时间由已出发车辆的发车间隔决定，满足式（8）.

$\sum\limits_{\left( {{o_{\mathrm{s}}},j} \right) \in {\mathcal{A}_1}} {a_{{o_{\mathrm{s}}},j}^{k,1}} = \sum\limits_{k_{\mathrm{a}} = 1}^k {{h_{k_{\mathrm{a}}}}} ,{\mkern 1mu} {\mkern 1mu} \forall k \in \mathcal{K},$

(8)

式中： ${\mathcal{A}_1}$ 为去程方向上的路段集合.

6）路网运行时间约束

路网运行时间是指从第一辆车驶入路网开始直到最后一辆车驶出路网的总时间，即施工车队对于路网的使用周期. 路网存在一个最大的运行时间，在现实情况中可能是隧道内路段的最大工作时长或施工队的最长工时. 最后执行运输任务的车辆 $K$ 必须在到达路网的最大运行时间 $t_{\text{max}}$ 之前离开路网，即满足式（9）.

$\sum\limits_{\left( i,{{d}_{{\mathrm{s}}}} \right)\in {{\mathcal{A}}^{2}}}{d_{i,{{d}_{{\mathrm{s}}}}}^{K,2}}\leqslant {{t}_{\text{max}}}$

(9)

7）路段运行时间约束

车辆在路段上的行驶时间范围取决于路段的长度和限速条件，满足式（10）.

$\tau _{i,j,k}^{\text{(r)}} \geqslant \frac{{{l_{i,j}}}}{{v_{\max {\mathrm{k}} }}},\quad \forall \left( {i,j} \right) \in \mathcal{A},\; k \in \mathcal{K},$

(10)

式中： $l_{i j}$ 为路段 $(i, j)$ 的长度， $v_{\max {\mathrm{k}}}$ 为车辆 $k$ 的最大行驶速度， $\tau_{i j, k}^{({\mathrm{r}})}$ 表示车辆 $k$ 在路段 $(i, j)$ 上的运行时间.

8）路段到达和离开时刻约束

车辆离开某一路段的时刻等于到达该路段的时刻与路段上的行驶时间之和，即满足式（11）. 除了起始路段外，车辆到达某一路段的时刻等于离开上一路段的时刻，即满足约束条件（12）.

$d_{i, j}^{k, u}=a_{i, j}^{k, u} + \tau_{i, j, k}^{({\mathrm{r}})}, \quad \forall(i, j) \in \mathcal{A}, \;k \in \mathcal{K},\; u \in U$

(11)

$\begin{split} & a_{i,j}^{k,u} = \sum\limits_{\left( {i_{\mathrm{a}},i} \right) \in {\mathcal{A}^u}} {d_{i_{\mathrm{a}},i}^{k,u}} ,\quad \forall \left( {i,j} \right) \in {\mathcal{A}_u}, \\ &\quad i \ne {o_{k,u}},i \ne j,\; k \in \mathcal{K},\; u \in \mathcal{U}. \end{split}$

(12)

9）去程和返程联系约束

对于车辆 $k$ ，其去程的终点和返程的起点相同，都为执行任务的需求点. 另外，车辆从返程起点出发的时刻等于离开去程终点的时刻与需求点服务时间之和，满足式（13）.

$\sum\limits_{\left( {{o_{k,2}},j} \right) \in {\mathcal{A}_2}} {a_{{o_{k,2}},j}^{k,2}} = \sum\limits_{\left( {i_{\mathrm{a}},{d_{k,1}}} \right) \in {\mathcal{A}_1}} {d_{i_{\mathrm{a}},{d_{k,1}}}^{k,1}} + \tau _{{d_{k,1}}}^{(\text{w})},\quad \forall k \in \mathcal{K},$

(13)

式中： $\boldsymbol{\tau}_{d_{k, 1}}^{({\mathrm{w}})}$ 表示需求点的服务时间.

10）冲突疏解约束

为避免施工车辆间的碰撞、追尾事故，保障隧道内的运输安全，需要对车辆间的交叉冲突、相向冲突和赶超冲突进行疏解.

11）交叉冲突疏解

若2辆车在短时间内到达同一交叉点，则会形成交叉冲突. 所以要求到达同一交叉口车流的时间间隔必须满足可保障安全的最低时间限制，满足式（14）.

$\begin{split} & \left| {a_{j,i}^{k,u} - d_{i_{\mathrm{a}},j}^{k_{\mathrm{a}},u_{\mathrm{a}}}} \right| + \left( {1 - x_{j,i}^{k,u}} \right) M + \left( {1 - x_{i_{\mathrm{a}},j}^{k_{\mathrm{a}},u_{\mathrm{a}}}} \right) M \geqslant \\ &\quad \tau _{\min }^{(\text{m})},\quad \forall j \in \mathcal{N},\;\left( {j,i} \right) \in \mathcal{A},\;\left( {i_{\mathrm{a}},j} \right) \in \mathcal{A},\;k,k_{\mathrm{a}} \in \mathcal{K}, \\ &\quad k \ne k_{\mathrm{a}},\;u,u_{\mathrm{a}} \in \mathcal{U}, \end{split}$

(14)

式中： $\tau_{\mathrm{mim}}^{(\mathrm{m})}$ 表示最小会车时间间隔.

12）相向冲突疏解约束

若2辆车在单向路段上相向而行，则会发生相向冲突. 为了避免这类情况的发生，需要保证先到达的车辆对于路段的优先使用权，满足式（15）.

$\begin{split} &\left( {a_{i,j}^{k,u} - a_{j,i}^{k_{\mathrm{a}},u_{\mathrm{a}}}} \right) \left( {a_{i,j}^{k,u} - d_{j,i}^{k_{\mathrm{a}},u_{\mathrm{a}}}} \right) + \left( {1 - x_{i,j}^{k,u}} \right) M +\\ &\quad \left( {1 - x_{j,i}^{k_{\mathrm{a}},u_{\mathrm{a}}}} \right) M \geqslant 1,\quad \forall \left( {i,j} \right) \in \mathcal{A}^{{\mathrm{s}}}, \\ &\quad k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}},\;u,u_{\mathrm{a}} \in \mathcal{U} . \end{split}$

(15)

13）赶超冲突疏解约束

若2辆车在单向路段上同向而行，由于速度不同，可能会发生赶超冲突. 在现实情况中，车辆一般遵守先到先服务的原则，满足式（16）.

$\begin{split} &\left( {a_{i,j}^{k,u} - a_{i,j}^{k_{\mathrm{a}},u_{\mathrm{a}}}} \right) \left( {d_{i,j}^{k,u} - d_{i,j}^{k_{\mathrm{a}},u_{\mathrm{a}}}} \right) \geqslant 0,\quad \forall \left( {i,j} \right) \in \mathcal{A}_{{\mathrm{s}}}, \\ &\quad k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}},\;u,u_{\mathrm{a}} \in \mathcal{U}. \end{split}$

(16)

14）路段瓶颈约束

隧道内的每一路段都有通行能力限制. 当行驶车辆大于路段通行能力时，该路段成为瓶颈路段，路网安全性大幅度降低，所以需要满足式（17）.

$\sum\limits_{k \in \mathcal{K}} {\sum\limits_{u \in \mathcal{U}} {x_{i,j}^{k,u}} } \leqslant {C_{i,j}},\quad \forall \left( {i,j} \right) \in \mathcal{A} ,$

(17)

式中： $C_{i, j}$ 表示路段 $(i, j)$ 的最大通行能力.

15）变量约束

车辆运行路径和时刻表的决策变量以及车辆到达和离开路段事件的相关变量满足式（18）.

$\left\{ \begin{array}{l} {x}_{i,j}^{k,u}\in \left\{0,1\right\},\quad \forall(i,j)\in \mathcal{A},\;k\in \mathcal{K},\;u\in \mathcal{U},\\ {a}_{i,j}^{k,u},{d}_{i,j}^{k,u},{h}_{k}\geqslant 0{\text{且为整数}}, \quad \forall(i,j)\in \mathcal{A},\;k\in \mathcal{K},\;u\in \mathcal{U},\end{array}\right.$

(18)

3. 模型重构

本文建立的模型为整数非线性规划模型，为方便求解，结合假设1的简化条件对模型进行线性化处理，为接下来使用GUROBI求解模型做准备.

首先，通过引入 $M$ ，对式（11）和式（12）进行了线性化处理，得到式（19）和式（20）.

$\begin{split} &d_{i,j}^{k,u} \geqslant a_{i,j}^{k,u} + \tau _{i,j,k}^{(\text{r})} - M \left( {1 - x_{i,j}^{k,u}} \right), \\ &\quad \forall \left( {i,j} \right) \in \mathcal{A},\;k \in \mathcal{K},\;u \in \mathcal{U} \end{split}$

(19)

$\begin{split} &a_{i,j}^{k,u} \geqslant \sum\limits_{\left( {i_{\mathrm{a}},i} \right) \in {\mathcal{A}_u}} {d_{i_{\mathrm{a}},i}^{k,u}} - M \left( {1 - x_{i,j}^{k,u}} \right), \\ &\quad \forall \left( {i,j} \right) \in {\mathcal{A}_u},\;i \ne {o_{k,u}},\;i \ne j,\;k \in \mathcal{K},\;u \in \mathcal{U} \end{split}$

(20)

根据假设1，简化后模型中去程和返程上的有向弧均为单向弧，则式（14）可简化为式（21）. 另外，由于GUROBI可对绝对值进行运算，不对式（14）进行线性化处理.

$\begin{split} &\left| {\sum\limits_{u \in \mathcal{U}} {a_{j,i}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {d_{i_{\mathrm{a}},j}^{k_{\mathrm{a}},u}} } \right| + \left( {1 - \sum\limits_{u \in \mathcal{U}} {x_{j,i}^{k,u}} } \right) M + \\ &\quad \left( {1 - \sum\limits_{u \in \mathcal{U}} {x_{i_{\mathrm{a}},j}^{k_{\mathrm{a}},u}} } \right) M \geqslant \tau _{\min }^{(\text{m})},\quad \forall j \in \mathcal{N},\;\left( {i,j} \right) \in \mathcal{A}, \\ &\quad \left( {i_{\mathrm{a}},j} \right) \in \mathcal{A},\;k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}} \end{split}$

(21)

类似地，式（15）可简化为式（22）. 式（22）的线性化处理的结果如式（23）～（26）所示. 需要注意： $\delta_{i, j, k, k_{\mathrm{a}}}$ 为0-1变量，用于辅助式（22）的线性化处理. 当 $\delta_{i, j, k, k_{\mathrm{a}}}=1$ 时，式（23）和（25）的约束条件成立，式（24）和（26）的约束条件被放松，表明此时车 $k_{\mathrm{a}}$ 先进入路段，且在车 $k$ 进入路段之前就离开路段，保证不发生相向冲突. 同理，当 $\delta_{i, j, k, k_{\mathrm{a}}}=0$ 时，式（24）和（26）的约束条件成立，式（23）和（25）的约束条件被放松，表明此时车 $k$ 先进入路段，且在车 $k_{\mathrm{a}}$ 进入路段之前就离开路段，保证不发生相向冲突.

$\begin{split} &\left( {\sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {a_{j,i}^{k_{\mathrm{a}},u}} } \right) \left( {\sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {d_{j,i}^{k_{\mathrm{a}},u}} } \right) +\\ &\quad \left( {1 - \sum\limits_{u \in \mathcal{U}} {x_{i,j}^{k,u}} } \right) M + \left( {1 - \sum\limits_{u \in \mathcal{U}} {x_{i_{\mathrm{a}},j}^{k_{\mathrm{a}},u}} } \right) M \geqslant 1,\\ &\quad \forall \left( {i,j} \right) \in \mathcal{A}^{{\mathrm{s}}},\;k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}} , \end{split}$

(22)

$\begin{split} &\sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {a_{j,i}^{k_{\mathrm{a}},u}} \geqslant 1 - \left( {1 - {\delta _{i,j,k,k_{\mathrm{a}}}}} \right) M - \\ &\quad\left( {2 - \sum\limits_{u \in \mathcal{U}} {x_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {x_{j,i}^{k_{\mathrm{a}},u}} } \right) M,\quad \forall \left( {i,j} \right) \in \mathcal{A}_{{\mathrm{s}}},\;\\ &\quad k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}} \end{split}$

(23)

$\begin{split} &\sum\limits_{u \in \mathcal{U}} {a_{j,i}^{k_{\mathrm{a}},u}} - \sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k,u}} \geqslant 1 - {\delta _{i,j,k,k_{\mathrm{a}}}} M - \\ &\quad \left( {2 - \sum\limits_{u \in \mathcal{U}} {x_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {x_{j,i}^{k_{\mathrm{a}},u}} } \right) M,\quad \forall \left( {i,j} \right) \in \mathcal{A}_{{\mathrm{s}}},\\&\quad k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}}, \end{split}$

(24)

$\begin{split} &\sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {d_{j,i}^{k_{\mathrm{a}},u}} \geqslant 1 - \left( {1 - {\delta _{i,j,k,k_{\mathrm{a}}}}} \right) M - \\ &\quad\left( {2 - \sum\limits_{u \in \mathcal{U}} {x_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {x_{j,i}^{k_{\mathrm{a}},u}} } \right) M,\quad \forall \left( {i,j} \right) \in \mathcal{A}_{{\mathrm{s}}},\\&\quad k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}}, \end{split}$

(25)

$\begin{split} &\sum\limits_{u \in \mathcal{U}} {a_{j,i}^{k_{\mathrm{a}},u}} - \sum\limits_{u \in \mathcal{U}} {d_{i,j}^{k,u}} \geqslant 1 - {\delta _{i,j,k,k_{\mathrm{a}}}} M - \\ &\quad\left( {2 - \sum\limits_{u \in \mathcal{U}} {x_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {x_{j,i}^{k_{\mathrm{a}},u}} } \right) M,\quad \forall \left( {i,j} \right) \in \mathcal{A}_{{\mathrm{s}}},\\&\quad k,k_{\mathrm{a}} \in \mathcal{K},\;k \ne k_{\mathrm{a}}. \end{split}$

(26)

与式（15）的处理方式相同，式（16）可简化为式（27），线性化处理结果如式（28）、（29）所示. $\xi_{i, j, k, k_{\mathrm{a}}}$ 为0-1变量. 当 $\xi_{i, j, k, k_{\mathrm{a}}}=1$ 时， $k$ 车先进入路段，先离开路段，保证不发生赶超冲突；当 $\xi_{i, j, k, k_{\mathrm{a}}}=0$ 时，车 $k_{\mathrm{a}}$ 先进入路段，先离开路段，保证不发生赶超冲突.

$\begin{split} &\left( {\sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k_{\mathrm{a}},u}} } \right) \left( {\sum\limits_{u \in \mathcal{U}} {d_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {d_{i,j}^{k_{\mathrm{a}},u}} } \right) \\ &\quad\geqslant 0,\quad \forall \left( {i,j} \right) \in \mathcal{A}_{{\mathrm{s}}},\;k,k_{\mathrm{a}} \in \mathcal{K}, \end{split}$

(27)

$\begin{split} & - M {\xi _{i,j,k,k_{\mathrm{a}}}} \leqslant \sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {a_{i,j}^{k_{\mathrm{a}},u}} \leqslant \left( {1 - {\xi _{i,j,k,k_{\mathrm{a}}}}} \right) M, \\ &\quad \forall \left( {i,j} \right) \in \mathcal{A}^{{\mathrm{s}}},\;k,k_{\mathrm{a}} \in \mathcal{K}, \end{split}$

(28)

$\begin{split} & - M {\xi _{i,j,k,k_{\mathrm{a}}}} \leqslant \sum\limits_{u \in \mathcal{U}} {d_{i,j}^{k,u}} - \sum\limits_{u \in \mathcal{U}} {d_{i,j}^{k_{\mathrm{a}},u}} \leqslant \left( {1 - {\xi _{i,j,k,k_{\mathrm{a}}}}} \right) M, \\ &\quad \forall \left( {i,j} \right) \in \mathcal{A}^{{\mathrm{s}}},\;k,k_{\mathrm{a}} \in \mathcal{K}, \end{split}$

(29)

$\delta_{i, j, k, k_{\mathrm{a}}}, \xi_{i, j, k, k_{\mathrm{a}}} \in\{0,1\}, \quad\forall(i, j) \in \mathcal{A}^{{\mathrm{s}}},\; k^{2}, k_{\mathrm{a}} \in \mathcal{K}$

(30)

4. 案例分析

某长大隧道项目共有20辆施工车辆执行运渣、运材料、运人任务，包括12辆运渣车、4辆运材料车和4辆运人车. 隧道只有一个出入口，所有施工车辆均从该口驶入驶出隧道.

4.1 隧道网络拓扑

与一般隧道不同，长大隧道内部道路狭长，单双向路段混合，路网呈现纵横交错的结构. 本文将隧道抽象为近似3 × 5的网格结构，并对各节点进行编号，如所示. 其中，黄色节点为隧道出入口，绿色节点为运渣需求点，紫色节点为运材料需求点，红色节点为运人需求点，蓝色节点为中间节点. 可以看出，紫色节点，即运材料需求点也是隧道施工过程中的断点. 节点之间通过路段连接，有向双线箭头代表双向路段，有向单线箭头代表单向路段，路段上的数值代表节点间的距离. 根据假设1，对去程和返程方向上的有向弧进行简化，在去程方向上规定右行和下行有向弧，在返程方向上规定左行和上行的有向弧，如所示. 令V_q为图5中对应的节点. $q \in \{0,1,\cdots,16\}$ .

图 4 隧道网络拓扑图

Figure 4. Tunnel network topology diagram

下载: 全尺寸图片幻灯片

图 5 去返程方向的隧道网络拓扑图

Figure 5. Tunnel network topology diagram in inbound and outbound directions

下载: 全尺寸图片幻灯片

4.2 编制隧道交通组织方案

模型求解时，运行计算机硬件环境为Intel （R） Core （TM） i5-6200U CPU，主频2.40 GHz，内存8 GB；软件环境为Windows10系统，使用Python调用GUROBI求解器. 在该案例中，基于铁路隧道工程施工技术指南^[18]，通过调查成兰铁路跃龙门隧道施工组织实际案例^[19]，对各参数进行了规定和限制. 参考成兰铁路龙门隧道案例中车队的施工周期要求，规定路网的最大运行时间为100 min. 考虑到铁路隧道工程施工技术指南中提出的安全规范，结合成兰铁路跃龙门隧道案例涉及的车速限制，我们令运渣车（KM）和运材料车（KC）的最高限速为30 km/h，运人车（KP）的最高限速为40 km/h，车辆的最小和最大发车间隔分别为1 min和4 min，最小会车时间间隔和安全时间间隔均为1 min，单向路段和双向路段的最大通行能力分别为10辆和20辆车. 案例中20辆施工车辆根据最短行驶路径和最高行驶速度得到的施工运输组织初始方案，见表1. 然后本文使用GUROBI求解器，经过1661 s后求解得到基于重构的整数线性规划模型的施工运输组织优化方案，见表2.

表 1 施工运输组织初始方案

Table 1. Initial construction organization scheme

编号	车辆进入隧道运行方案		车辆离开隧道运行方案
编号	始发时刻	运行路径	始发时刻	运行路径
KP1	0	0-1-2-5-8-11-14	13	14-11-8-5-4-1-0
KP2	1	0-1-4-5-8-11-14	14	14-11-8-5-2-1-0
KP3	2	0-1-4-5-8-11-14	15	14-11-8-5-2-1-0
KP4	3	0-1-4-5-8-11-14	16	14-11-8-5-2-1-0
KC1	4	0-1-2-3-6-9	15	9-6-3-2-1-0
KC2	5	0-1-2-3-6-9	16	9-6-3-2-1-0
KC3	6	0-1-2-3-6-9	17	9-6-3-2-1-0
KC4	7	0-1-2-3-6-9	18	9-6-3-2-1-0
KM1	8	0-1-4-7-10-13	23	13-10-7-4-1-0
KM2	9	0-1-4-7-10-13-14-16	27	16-14-13-10-7-4-1-0
KM3	10	0-1-4-5-8-11-14-15	27	15-14-11-8-5-2 1-0
KM4	11	0-1-4-7-10-13	26	13-10-7-4-1-0
KM5	12	0-1-4-7-10-13-14-16	30	16-14-13-10-7-4-1-0
KM6	13	0-1-4-5-8-11-14-15	30	15-14-11-8-5-2-1-0
KM7	14	0-1-4-7-10-13	29	10-7-4-1-0
KM8	15	0-1-4-7-10-13-14-16	33	16-14-13-10-7-4-1-0
KM9	16	0-1-4-5-8-11-14-15	33	15-14-11-8-5-2-1-0
KM10	17	0-1-4-7-10-13	32	13-10-7-4-1-0
KM11	18	0-1-4-7-10-13-14-16	36	16-14-13-10-7-4-1-0
KM12	19	0-1-4-5-8-11-14-15	36	15-14-11-8-5-2-1-0

下载: 导出CSV

| 显示表格

表 2 施工运输组织优化方案

Table 2. Optimization construction organization scheme

编号	车辆进入隧道运行方案		车辆离开隧道运行方案
编号	始发时刻	运行路径	始发时刻	运行路径
KP1	0	0-1-2-5-8-11-14	13	14-11-8-5-4-1-0
KP2	1	0-1-4-7-8-11-14	14	14-13-10-7-4-1-0
KP3	5	0-1-4-7-8-11-14	18	14-13-10-7-4-1-0
KP4	9	0-1-4-7-8-11-14	22	14-11-8-5-4-1-0
KC1	13	0-1-4-5-6-9	24	9-6-5-4-1-0
KC2	17	0-1-2-5-6-9	28	9-6-5-2-1-0
KC3	18	0-1-4-5-6-9	29	9-6-3-2-1-0
KC4	22	0-1-2-3-6-9	33	9-6-5-4-1-0
KM1	23	0-1-4-7-10-13	38	13-10-7-4-1-0
KM2	27	0-1-4-7-10-13-14-16	45	16-14-11-8-5-2-1-0
KM3	31	0-1-4-7-8-11-14-15	48	15-14-13-10-7-4-1-0
KM4	34	0-1-4-7-10-13	49	13-10-7-4-1-0
KM5	35	0-1-4-7-8-11-14-16	53	16-14-11-8-5-2-1-0
KM6	39	0-1-2-5-8-11-14-15	56	15-12-11-8-5-2-1-0
KM7	42	0-1-4-7-10-13	57	13-10-7-4-1-0
KM8	46	0-1-4-7-8-11-14-16	64	16-14-11-8-5-2-1-0
KM9	47	0-1-2-5-8-11-14-15	64	15-14-11-8-5-4-1-0
KM10	49	0-1-4-7-10-13	64	13-10-7-4-1-0
KM11	53	0-1-4-7-10-13-14-16	71	16-14-11-8-7-4-1-0
KM12	57	0-1-2-5-8-11-12-15	74	15-14-11-8-5-4-1-0

下载: 导出CSV

| 显示表格

表1中加粗划线的节点表示车辆在该节点与其他车辆发生了交叉冲突. 易看出，优化前车辆KP1与KM3、KM9、KC2，KP2与KC3，KP3与KM9、KC4，KP4与KM6，KC1与KM12，KM1与KM10，KM2与KM11，KM3与KM7，KM6与KM10间发生了交叉冲突，甚至车辆KP2与KC3间存在3个交叉冲突点. 车辆KM3与KM9，车辆KM6与KM12在V₁₄与V₁₅间的路段发生了相向冲突. 对比表1和表2可以发现，优化前后施工车辆的时刻表发生了很大的变化. 车辆KP2、KC3、KM1、KM5、KM9与前车的发车间隔保持1 min没有变化，车辆KM10与前车的发车间隔从1 min增至2 min，车辆KM4、KM7与前车的发车间隔从1 min增加至3 min，剩下车辆与前车的发车间隔从1 min增加至4 min. 另外，优化前，对于需求点相同的车辆，其运行路径大多相同. 例如：需求点为V₁₄的车辆KP2、KP3、KP4的运行路径

多数为V₀→V₁→V₄→V₅→V₈→V₁₁→V₁₄→V₁₁→V₈→V₅→V₄→V₁→V₀；需求点为V₉的车辆KC1、KC2、KC3、KC4的运行路径都为V₀→V₁→V₂→V₃→V₆→V₉→V₆→V₃→V₂→V₁→V₀→V₁. 这容易导致车辆对某路段的使用频率过高，从而产生冲突，例如：V₁与V₂间路段的高使用率导致V₁与V₂的交叉冲突点过多. 而优化后，对于需求点相同的车辆，其运行路径大多不同. 这是因为各个车辆需要尽量避免沿着相同路径行驶，减少某个路段的使用压力，规避交通冲突，保证安全行驶. 事实上，优化方案还可以在限速范围内改变车辆的行驶速度来调整车辆在路段上的运行时间，间接改变车辆的路径时刻表，达到延缓或提前到达某一节点的时刻来规避交通冲突，保证运行安全. 综上分析，本文所提出的优化方案主要从调整发车时刻表、改变车辆运行路径、调节路段行驶时间3个途径来减少交通冲突.

初始方案、优化方案的目标函数值和交通冲突数量如表3所示. 优化前后，目标函数值，即车辆的总运行（行驶）时间均为512 min，没有发生变化，交通冲突数量从21个减到0个. 因此，可以得出，对多工种施工车辆的时刻表和路径进行规划，可以在不增加车辆总运行（行驶）时间，即目标函数值（512 min）的基础上有效规避交通冲突，保证隧道内部施工期间车辆的行驶安全. 实际上，不同于理论计算结果，当隧道内部车辆间发生交通冲突时，车辆总运行时间不仅会大幅度增加，还可能引发严重的交通事故. 本案例的优化方案在不牺牲车辆理想运行（行驶）时间的条件下完全避免了交通冲突，保证了隧道内部施工车辆的畅通运行. 为进一步清晰直观地对比初始方案与优化方案的优劣，刻画2种方案优化前后的效果，我们绘制隧道运输组织初始方案和优化方案的时空轨迹图，如图6和图7所示. 图中的黑色五角星代表交叉冲突点，红色直线的交点代表相向冲突点. 优化后，图中的交通冲突点得以消除，各个车辆的路径时刻表从紧张危险、交错纵横的状态转变为疏散安全、平衡有序的状态. 另外，观察交通冲突的涉及对象和发生时刻可发现，车辆容易在去程方向上与其他返程方向上的车辆发生冲突. 这是因为去程方向和返程方向的目标方向不一致，车辆运行路径容易产生交叉相错. 初始方案的路径时刻表只能先保证去程方向上车辆的有序规律发车，难以进一步确保返程方向上车辆对于冲突的规避，而优化方案可以通过进一步调整路径时刻表来继续保证返程方向上车辆的有序安全运行. 由此可知，考虑交通冲突的长大隧道内部多工种施工车辆时刻表和运行路径的协同优化，使得隧道内部交通网络的安全性得到提高，车辆间的交通冲突得以疏解，施工任务能够高效安全完成，减少了意外事故发生的可能性.

表 3 初始和优化方案的目标函数值和交通冲突数量

Table 3. Objective function values and number of traffic conflicts for initial and optimization schemes

方案	目标函数值/min	交通冲突数量/个
方案	目标函数值/min	交叉	相向	赶超
初始方案	512	19	2	0
优化方案	512	0	0	0

下载: 导出CSV

| 显示表格

图 6 隧道运输组织初始方案时空轨迹图

Figure 6. Space-time trajectory map of initial scheme of tunnel transportation organization

下载: 全尺寸图片幻灯片

图 7 隧道运输组织优化方案时空轨迹图

Figure 7. Space-time trajectory map of optimization scheme of tunnel transportation organization

下载: 全尺寸图片幻灯片

综上分析，本文提出的考虑交通冲突的长大隧道内部多工种施工车辆的时刻表和运行路径系统优化模型及GUROBI求解方法具备可行性，能够在短时间内得到效果较好的优化方案，应用于隧道内部运输组织方案编制，可操作性强.

5. 结论与展望

1）在隧道施工任务执行过程中，需求点相同的施工车辆容易发生交通冲突，不同目标方向（去程和返程）的车辆容易发生交通冲突. 本文所提出的优化方案主要从调整发车时刻表、改变车辆运行路径、调节路段行驶时间3个途径来减少交通冲突. 在案例中优化得到的多工种施工车辆运输组织方案不增加车辆的总运行（行驶）时间，即目标函数值（512 min），使车辆间的交通冲突数量从21个减为0个，提高了施工效率，保证了运输安全.

2）本文提出的隧道内部多工种施工车辆的时刻表和运行路径协同优化模型可应用于各种隧道施工项目，也可以通过设置时间窗，考虑车辆装配过程，考虑车辆的循环运输计划等来进一步完善模型，扩大其应用场景，同时也是后续的重要研究方向.

图 1 永磁电磁混合Halbach阵列电动悬浮示意

Figure 1. Diagram of PM and electromagnet hybrid Halbach array EDS system

下载: 全尺寸图片幻灯片

图 2 2D有限元模型

Figure 2. 2D FEM

下载: 全尺寸图片幻灯片

图 3 悬浮力随运行速度的变化曲线

Figure 3. Variation curve of suspension force with running speed

下载: 全尺寸图片幻灯片

图 4 定气隙PID控制仿真框图

Figure 4. Simulation block diagram of fixed air gap PID control

下载: 全尺寸图片幻灯片

图 5 变气隙PID控制仿真框图

Figure 5. Simulation block diagram of variable air gap PID control

下载: 全尺寸图片幻灯片

图 6 悬浮气隙及线圈电流密度

Figure 6. Suspension air gap and coil current density

下载: 全尺寸图片幻灯片

图 7 悬浮气隙及线圈电流密度(变气隙)

Figure 7. Suspension air gap and coil current density (variable air gap )

下载: 全尺寸图片幻灯片

表 1 模型参数

Table 1. Model parameters

参数	数值	参数	数值
永磁体剩磁 B_r/T	1.25	线圈宽度/mm	10
永磁体横向宽度/mm	200	线圈电流体密度 J/ （ A•mm⁻²)）	6
永磁体长度/mm	80	导体板横向宽度/mm	200
永磁体高度/mm	100	导体板长度/mm	1600
一对极模块数 m	4	导体板厚度 d/mm	20
阵列总长度/mm	800	导体板电导率/ （S•m⁻¹）	3.8 × 10⁷
阵列模块数 N	8	气隙 g/mm	30

下载: 导出CSV

参考文献(22)

[1]	POST R F, RYUTOV D. The Inductrack concept: A new approach to magnetic levitation[R]. Springfield: Office of Scientific and Technical Information (OSTI), 1996.
[2]	罗成,张昆仑,靖永志. 新型Halbach阵列永磁电动悬浮系统垂向稳定性[J]. 交通运输工程学报,2019,19(2): 101-109. doi: 10.3969/j.issn.1671-1637.2019.02.010 LUO Cheng, ZHANG Kunlun, JING Yongzhi. Vertical stability of permanent magnet EDS system with novel Halbach array[J]. Journal of Traffic and Transportation Engineering, 2019, 19(2): 101-109. doi: 10.3969/j.issn.1671-1637.2019.02.010
[3]	CHENG Y W, HE G, LONG Z Q. Vertical dynamic stability analysis of EDS levitation systems based on Halbach magnet arrays[C]//2009 Chinese Control and Decision Conference. Guilin: IEEE, 2009: 3726-3730.
[4]	郑杰. 感应线圈对磁浮系统性能影响研究[D]. 长沙: 国防科学技术大学, 2006.
[5]	CHEN S S, ZHU S, CAI Y. On the unsteady-motion theory of magnetic forces for maglev[R]. Argonne : Office of Scientific and Technical Information (OSTI), 1996.
[6]	ZHU S, CAI Y, ROTE D M, et al. Magnetic damping for maglev[J]. Shock and Vibration, 1998, 5: 119-128. doi: 10.1155/1998/480273
[7]	HAN Q H. Analysis and modeling of the EDS maglev system based on the Halbach permanent magnet array[D]. Orlando: University of Central Florida, 2004.
[8]	KO W. Modeling and analysis of the EDS maglev system with the Halbach magnet array[D]. Orlando: University of Central Florida, 2007.
[9]	HAN C, KO W, LIN K C, et al. Study of a hybrid magnet array for an electrodynamic maglev control[J]. Journal of Magnetics, 2013, 18(3): 370-374. doi: 10.4283/JMAG.2013.18.3.370
[10]	贺光. 基于Halbach结构的永磁电动与电磁混合悬浮技术研究[D]. 长沙: 国防科学技术大学, 2010.
[11]	LONG Z Q, HE G, XUE S. Study of EDS & EMS hybrid suspension system with permanent-magnet halbach array[J]. IEEE Transactions on Magnetics, 2011, 47(12): 4717-4724. doi: 10.1109/TMAG.2011.2159237
[12]	闫宇壮,李云钢,程虎. 电动电磁混合磁浮悬浮稳定性及技术特性分析[J]. 中国电机工程学报,2007,27(6): 53-56. doi: 10.3321/j.issn:0258-8013.2007.06.012 YAN Yuzhuang, LI Yungang, CHENG Hu. Analysis of levitation stability and technology characters of EDS and EMS hybrid maglev[J]. Proceedings of the CSEE, 2007, 27(6): 53-56. doi: 10.3321/j.issn:0258-8013.2007.06.012
[13]	陈殷,张昆仑. Halbach永磁阵列空间磁场的解析计算[J]. 磁性材料及器件,2014,45(1): 1-4,9. doi: 10.3969/j.issn.1001-3830.2014.01.001 CHEN Yin, ZHANG Kunlun. Analytic calculation of the magnetic field created by Halbach permanent magnets array[J]. Journal of Magnetic Materials and Devices, 2014, 45(1): 1-4,9. doi: 10.3969/j.issn.1001-3830.2014.01.001
[14]	LUO C, ZHANG K L, DUAN J H, et al. Study of permanent magnet electrodynamic suspension system with a novel halbach array[J]. Journal of Electrical Engineering & Technology, 2020, 15(2): 969-977.
[15]	陈殷,张昆仑. 板式双边永磁电动悬浮电磁力计算[J]. 电工技术学报,2016,31(24): 150-156. CHEN Yin, ZHANG Kunlun. Calculation of electromagnetic force of plate type null double side permanent magnet electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 150-156.
[16]	雷银照. 时谐电磁场解析方法[M]. 北京: 科学出版社, 2000.
[17]	MELCHER J R. Continuum electromechanics[M]. Cambridge: The MIT Press, 1981.
[18]	KIM W J. High-precision planar magnetic levitation[D]. Cambridge: Massachusetts Institute Technology, 1997.
[19]	宋玉晶,张鸣,朱煜. Halbach永磁阵列磁场解析求解及推力建模[J]. 电工技术学报,2014,29(11): 61-67. doi: 10.3969/j.issn.1000-6753.2014.11.008 SONG Yujing, ZHANG Ming, ZHU Yu. Modeling of halbach array magnetic field and motor thrust[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 61-67. doi: 10.3969/j.issn.1000-6753.2014.11.008
[20]	赵博, 张洪亮. Ansoft12在工程电磁场中的应用[M]. 北京: 水利水电出版社, 2010.
[21]	王莉,张昆仑. 基于零功率控制策略的混合磁悬浮系统[J]. 西南交通大学学报,2005,40(5): 667-672. doi: 10.3969/j.issn.0258-2724.2005.05.022 WANG Li, ZHANG Kunlun. Hybrid magnetic suspension system based on zero power control strategy[J]. Journal of Southwest Jiaotong University, 2005, 40(5): 667-672. doi: 10.3969/j.issn.0258-2724.2005.05.022
[22]	王莉. 混合EMS磁悬浮系统研究[D]. 成都: 西南交通大学, 2006.

施引文献

附加材料(0)

访问统计

点击查看大图

图(7) / 表(1)

计量

文章访问数: 449
HTML全文浏览量: 293
PDF下载量: 39
被引次数: 0

1. 问题描述
1.1 隧道交通网络拓扑建模
2. 模型构建
2.1 模型假设
2.2 数学描述
2.3 目标函数和约束条件
3. 模型重构
4. 案例分析
4.1 隧道网络拓扑
4.2 编制隧道交通组织方案
5. 结论与展望

永磁电磁混合Halbach阵列电动悬浮的稳定性控制

doi: 10.3969/j.issn.0258-2724.20210868

作者简介: 罗成（1987—），男，实验师，博士，研究方向为电动悬浮，E-mail：luocheng1987.happy@163.com

计量

出版历程

Stability Control of Electrodynamic Suspension with Permanent Magnet and Electromagnet Hybrid Halbach Array

1. 问题描述

1.1 隧道交通网络拓扑建模

2. 模型构建

2.1 模型假设

2.2 数学描述

2.3 目标函数和约束条件

3. 模型重构

4. 案例分析

4.1 隧道网络拓扑

4.2 编制隧道交通组织方案

5. 结论与展望

计量

出版历程

目录

1. 问题描述

1.1 隧道交通网络拓扑建模

2. 模型构建

2.1 模型假设

2.2 数学描述

2.3 目标函数和约束条件

3. 模型重构

4. 案例分析

4.1 隧道网络拓扑

4.2 编制隧道交通组织方案

5. 结论与展望

作者简介:
罗成（1987—），男，实验师，博士，研究方向为电动悬浮，E-mail：luocheng1987.happy@163.com