Application of Active Magnetic Bearing in Waste Heat Generator
-
摘要:
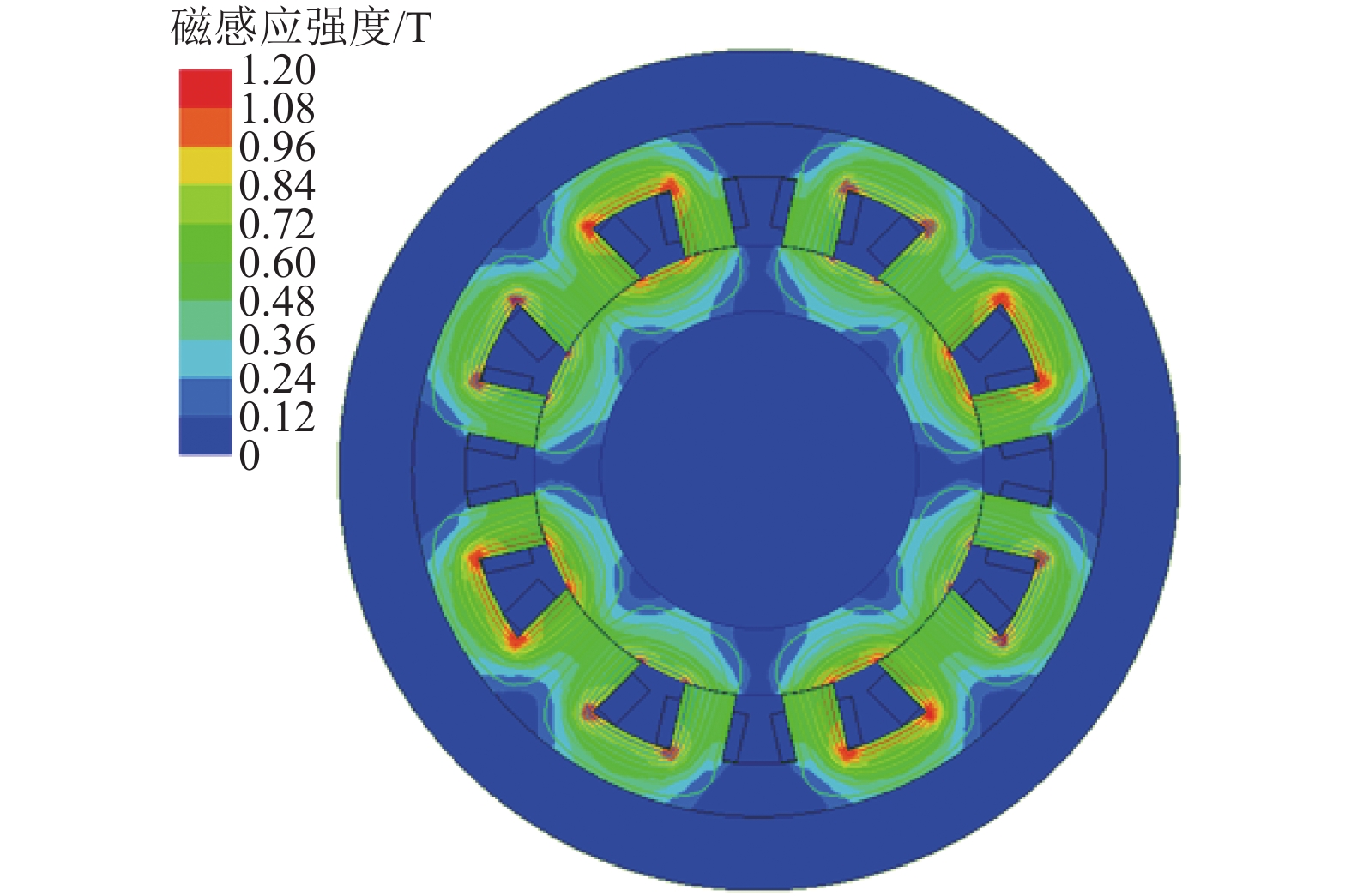
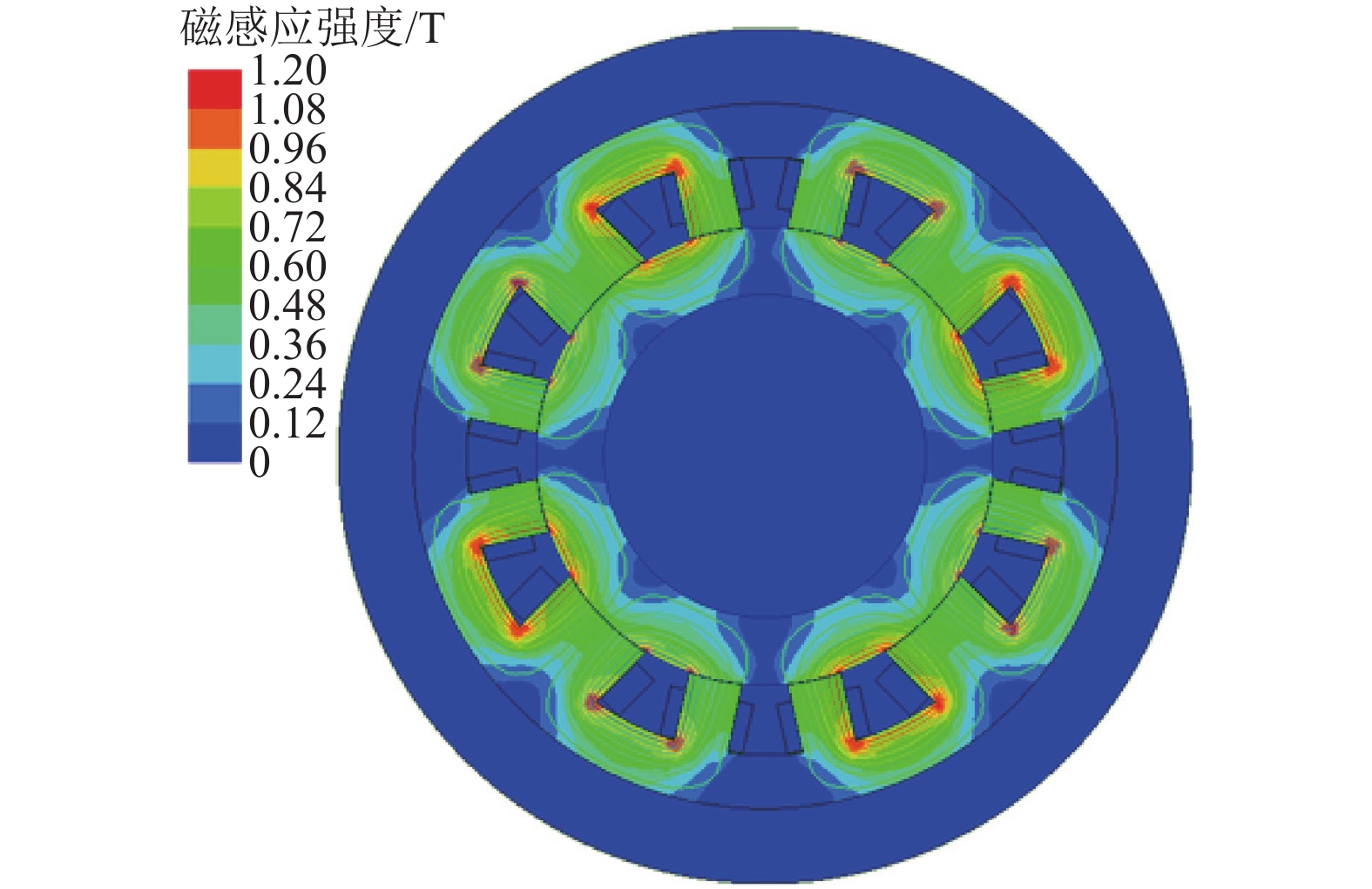
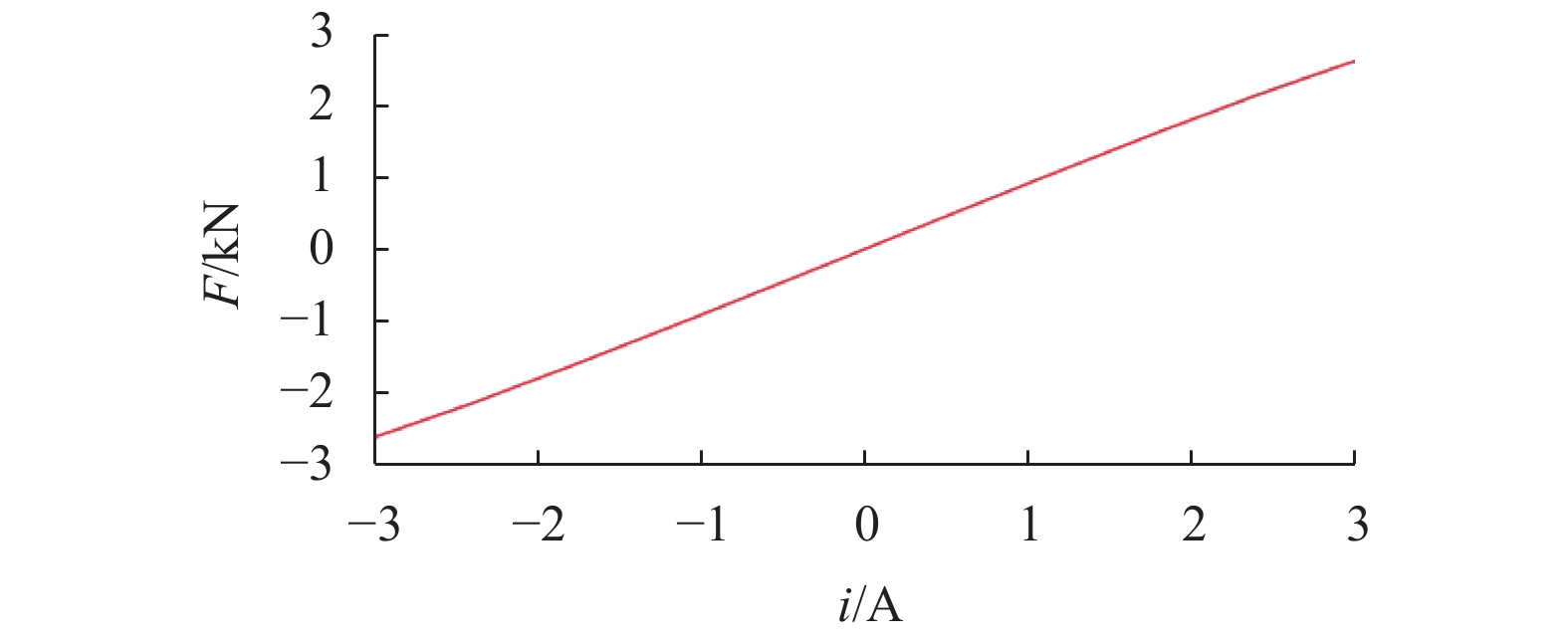
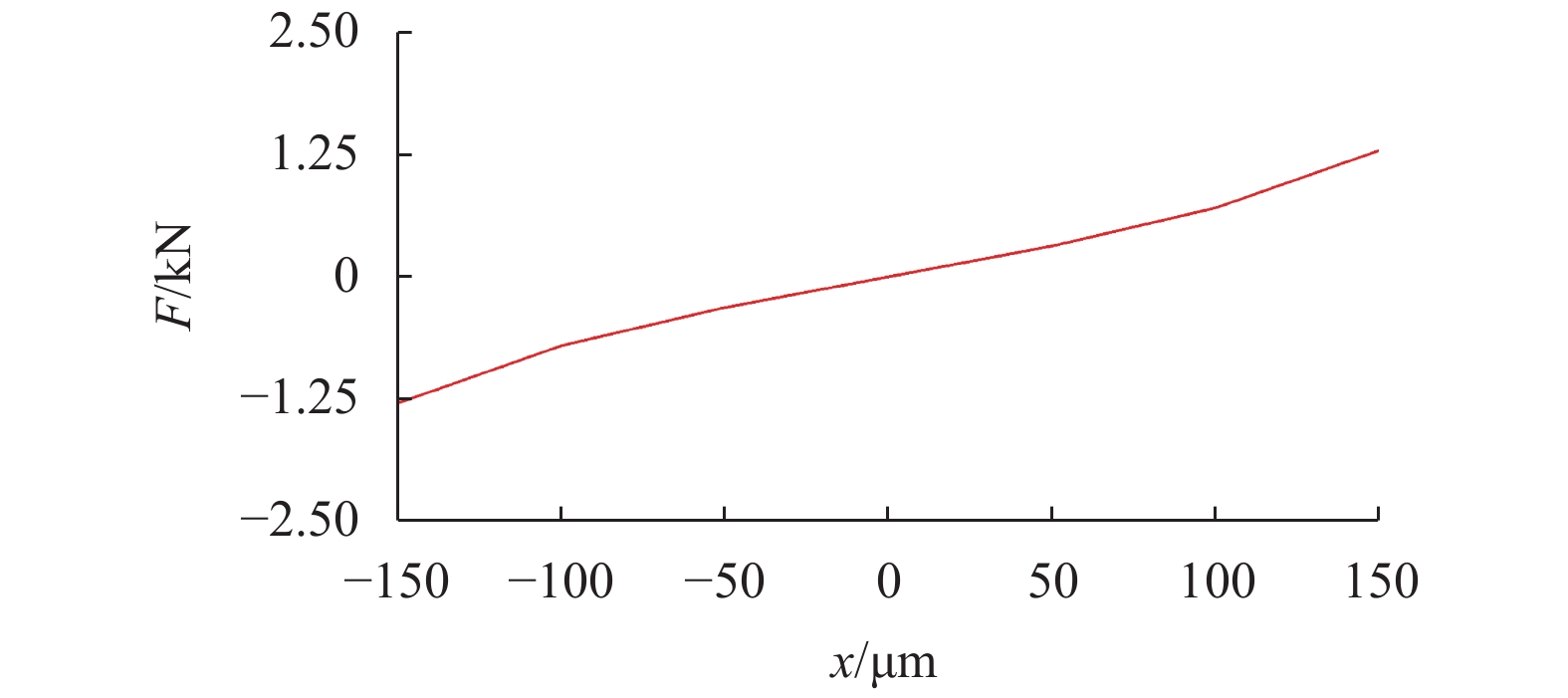
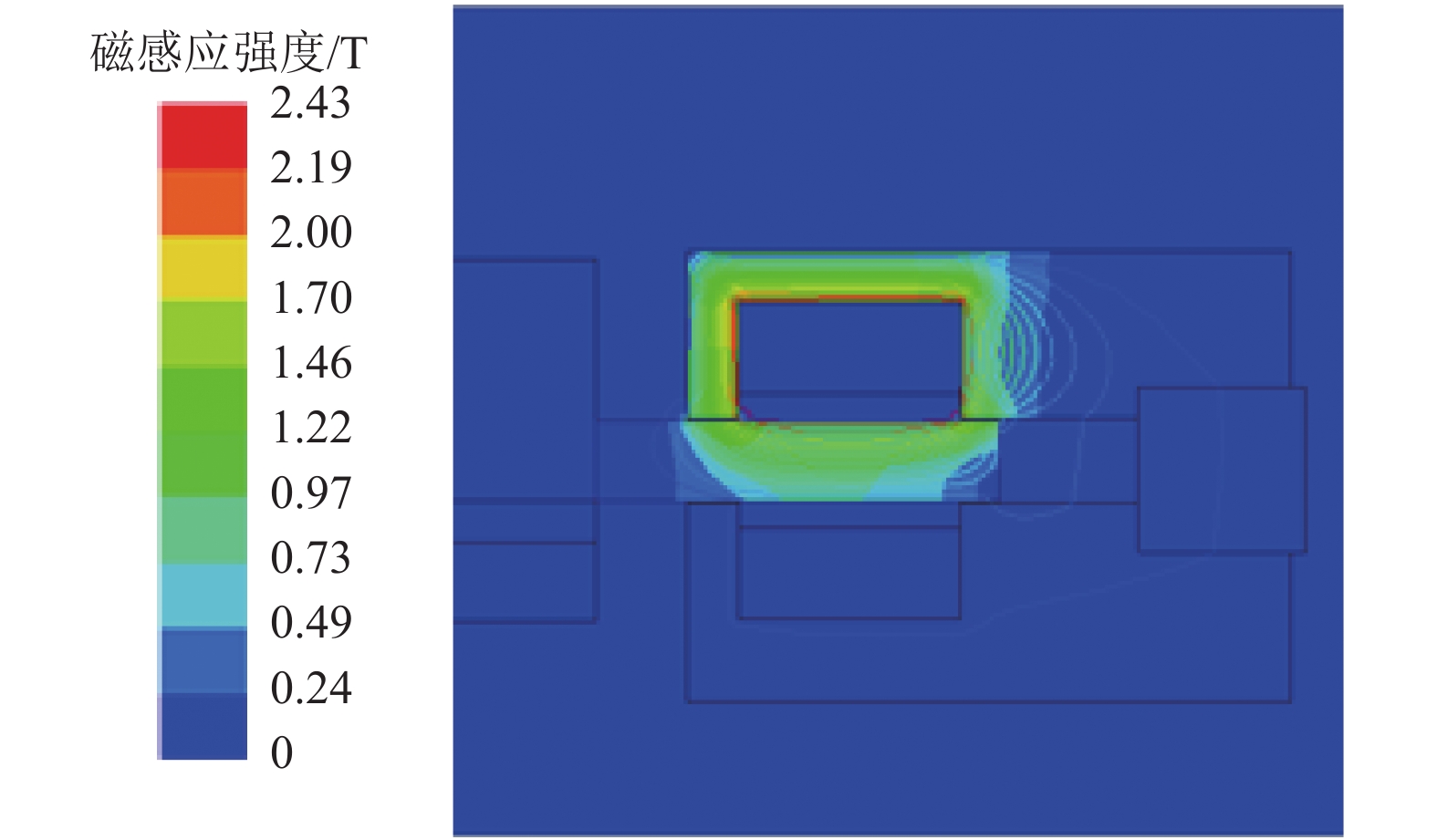
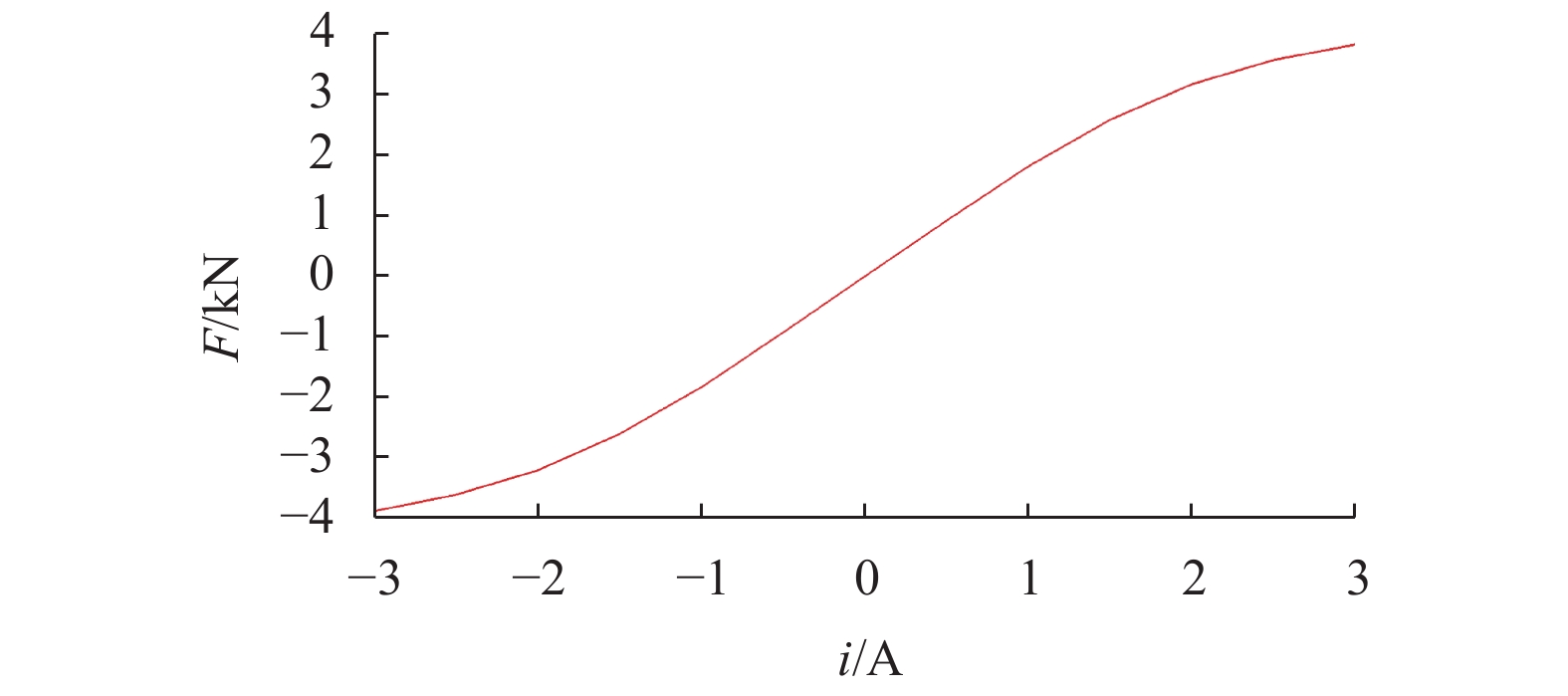
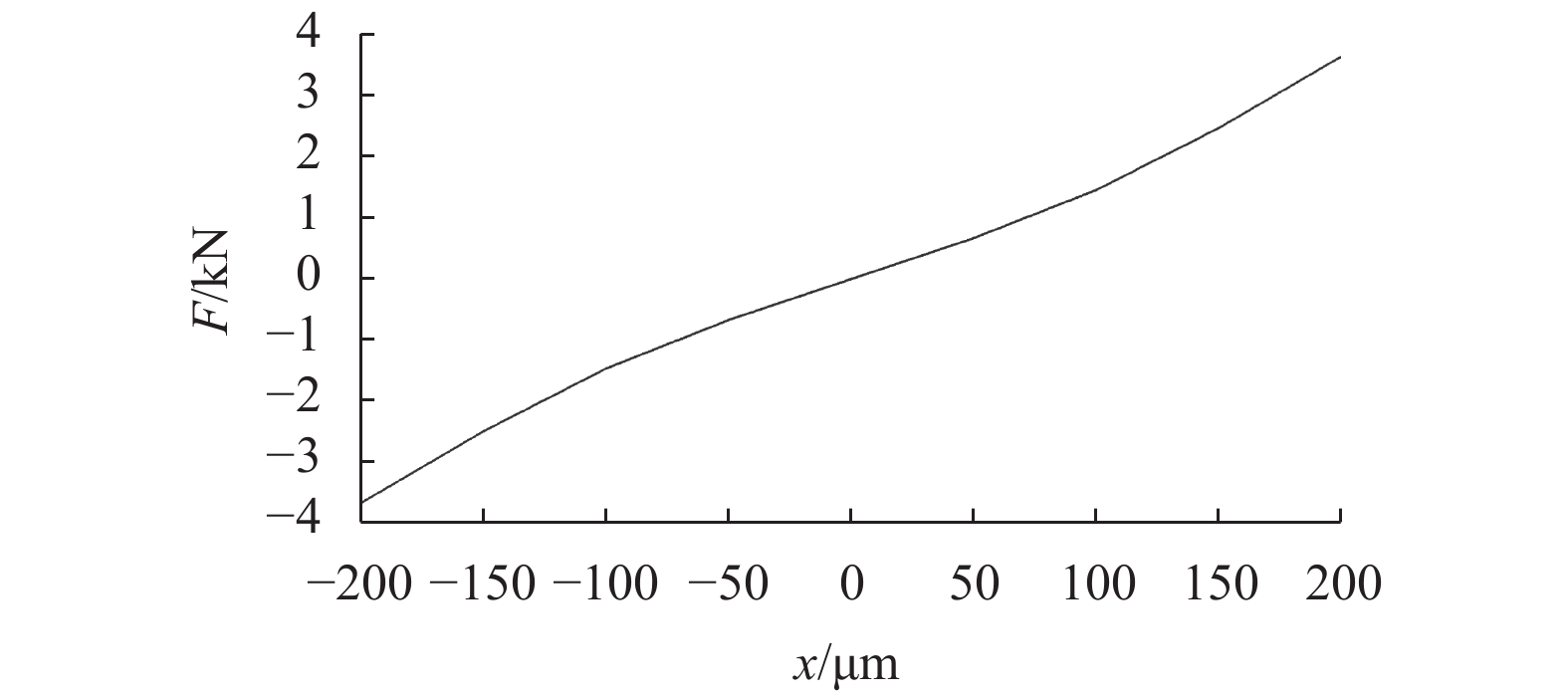
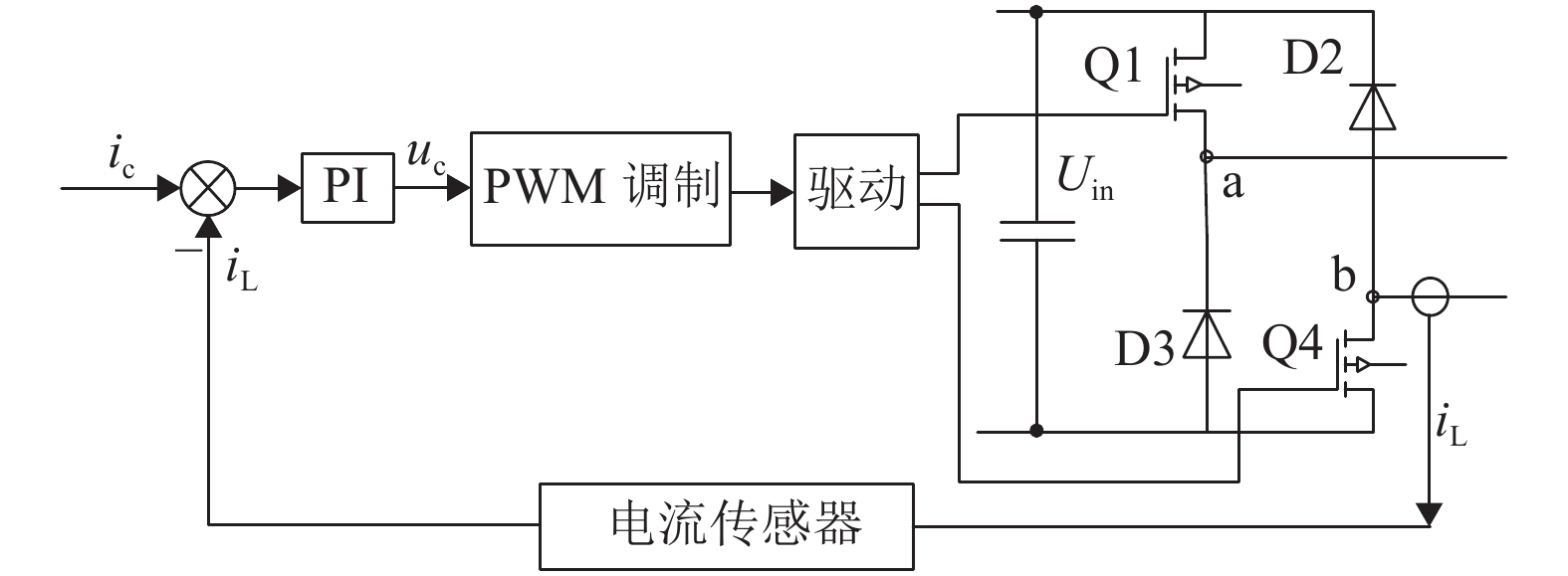
针对传统余热发电设备存在发电效率低、成本高、体积大等问题，设计了一款装备5自由度（5-DOF）主动磁悬浮轴承的余热发电机，用于余热发电有机朗肯循环系统. 首先，基于电机转子轴径限制和最大承载力要求，确定径向磁悬浮轴承和轴向磁悬浮轴承的结构形式，采用一维磁路模型和二维有限元分析，计算并校核磁悬浮轴承的尺寸和性能参数；其次，为保证磁悬浮轴承的稳定裕度，采用三电平PWM功率放大器降低输出电流纹波，利用不完全微分PID控制器和不平衡补偿算法实现5自由度稳定悬浮；最后，将该磁悬浮余热发电机应用到实际客户现场，从稳定裕度、承载力和轴振峰峰值3个维度验证磁悬浮余热发电机的可靠性. 现场试验结果表明：磁悬浮余热发电机系统运行稳定可靠，实现了满功率发电和长期运行考核；在全工况运行范围，磁悬浮轴承系统的灵敏度函数小于12 dB，余热发电机转子振动峰峰值小于53 μm，满足ISO14839-3规定的长期稳定运行要求；轴向承载力最大达到3 600 N，满足实际工况需求.
-
关键词:
- 有机朗肯余热发电机 /
- 主动磁悬浮轴承 /
- 三电平PWM功率放大器 /
- 转子不平衡补偿
Abstract:Aiming at the problems of low efficiency, high cost and large volume of the traditional waste heat power generation equipment, a waste heat generator equipped with the 5-DOF (5-degree of freedom) active magnetic bearing for Organic Rankine waste heat generation system was designed. Firstly, based on the rotor diameter limit and maximum bearing capacity requirements, the structural forms of radial and axial magnetic bearings were determined. Furthermore, the dimensions and performance parameters of magnetic bearings were calculated and checked by one-dimensional magnetic circuit model and two-dimensional finite element analysis. Secondly, in order to ensure the stability margin of the magnetic bearing, a three-level PWM (pulse-width modulation) power amplifier was used to reduce the output current ripple, and an incomplete differential PID controller incorporated with unbalance compensation were used to realize the 5-DOF stable suspension. Finally, the waste heat generator equipped with magnetic bearing was applied to the actual customer site. The reliability of the waste heat generator was verified from three dimensions of stability margin, bearing capacity and shaft peak-to-peak value. The field test results show that the waste heat generator system has operated stably and reliably in all operation conditions, and can achieve full-power generation and long-term operation. The sensitivity function of the magnetic bearing system is less than 12 dB, and the peak-to-peak vibration value of the rotor of the waste heat generator is less than 53 μm, which meet the long-term stable operation requirements of ISO14839. The maximum axial bearing capacity reaches 3 600 N, which meets the requirements of actual working conditions.
-
图 1 磁悬浮轴承余热发电机的结构示意
Figure 1. Schematic diagram of magnetic bearing waste heat generator
图 2 径向磁轴承E型电磁铁结构及尺寸定义
Figure 2. Structure and dimension definition of E-type electromagnet for radial magnetic bearing
图 4 上线圈电流最大、下线圈电流为0的磁场分布
Figure 4. Magnetic field distribution when the top coil current is maximum and the bottom coil is zero
图 5 电磁力与控制电流的关系曲线
Figure 5. Relationship between the electromagnetic force and the control current
图 6 电磁力与转子位移的关系曲线
Figure 6. Relationship between the electromagnetic force and the rotor displacement
图 7 轴向磁轴承电磁铁结构及尺寸定义
Figure 7. Structure and dimension definition of the electromagnet for the axial magnetic bearing
图 9 上端线圈电流为0、下线圈电流最大的磁场分布
Figure 9. Magnetic field distribution when the top coil current is zero and the bottom coil current is maximum
图 10 电磁力随控制电流变化曲线
Figure 10. Relationship between the electromagnetic force and the control current
图 11 电磁力与转子位移的关系曲线
Figure 11. Relationship between the electromagnetic force and the rotor displacement
图 12 磁悬浮轴承余热发电机现场安装
Figure 12. Site installation drawing of waste heat generator with magnetic bearing
图 16 额定转速时空载与负载条件下灵敏度函数对比
Figure 16. Sensitivity function comparison between no-load and full load at rated speed
图 17 实际测量的轴向磁轴承电流增益曲线
Figure 17. Measured curves of the current-force coefficient of axial magnetic bearing
图 18 整个转速范围内的转子轴振峰峰值曲线
Figure 18. Peak-to-peak curves of rotor shaft vibration in the whole speed range
表 1 径向磁轴承设计输入条件
Table 1. Input conditions of radial magnetic bearing
变量 符号 数值 备注 额定气隙/mm x0 0.3 最大磁感应强度/T Bmax 1.20 最大承载力/N Fmax 2 250 径向转子外径/mm Dr2 170.0 接口尺寸 定子内径/mm Ds1 170.6 
下载: 导出CSV
表 2 轴向磁轴承设计输入条件
Table 2. Input conditions of axial magnetic bearing
变量 符号 数值 额定气隙/mm x0 0.4 最大磁感应强度/T Bmax 1.25 最大承载力/N Fmax 2 600 电机内部安装外径/mm dlim 394
下载: 导出CSV
表 3 额定转速条件下，空载与负载运行的敏感性函数峰值
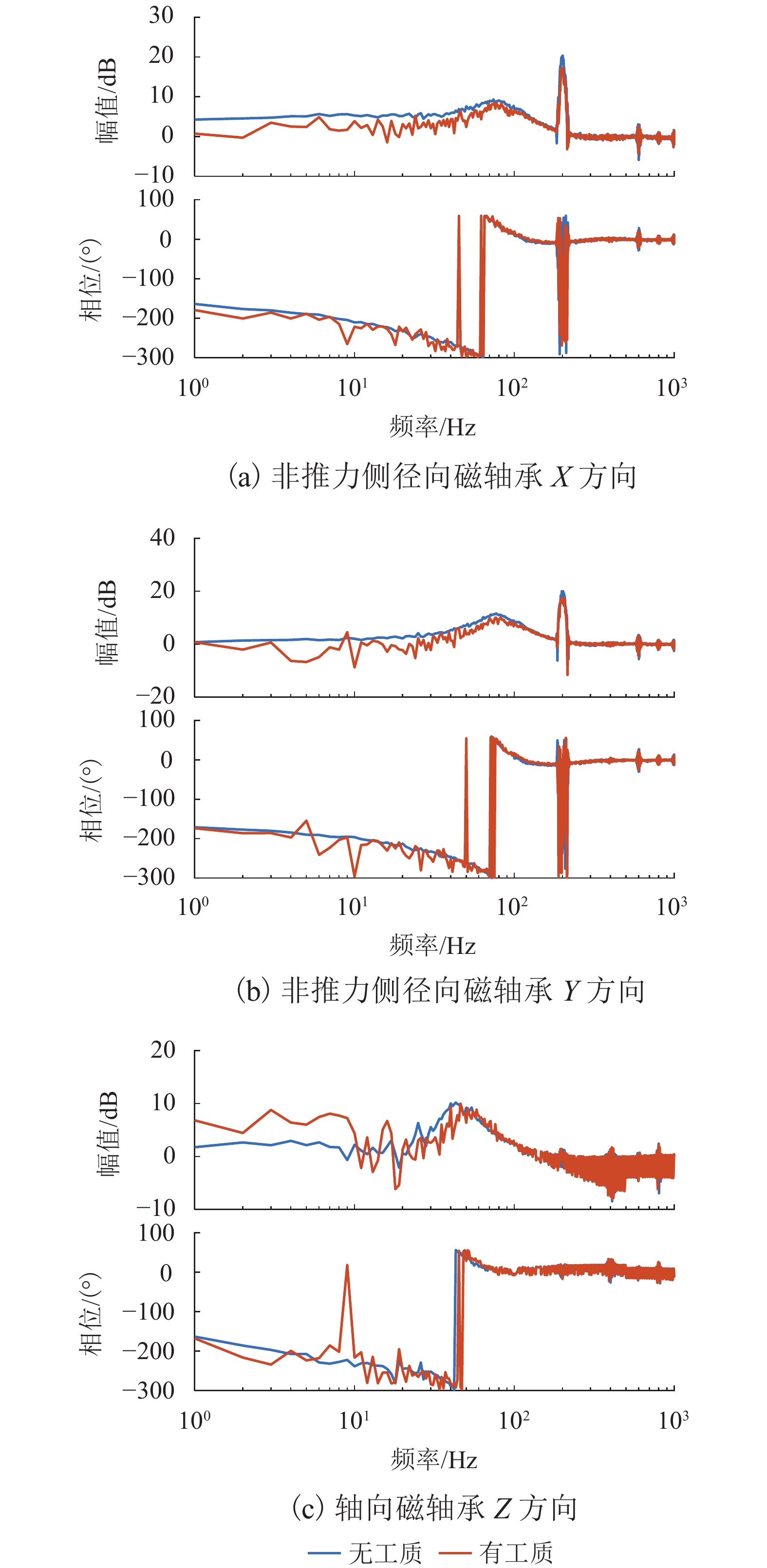
Table 3. Sensitivity function peaks of no-load and load operations at rated speed
类别 工况 峰值/dB 转速/krpm 非推力侧径向磁轴承 X 方向 无工质 9.34 4.44 有工质 8.47 4.50 非推力侧径向磁轴承 Y 方向 无工质 11.65 4.62 有工质 10.07 4.92 推力侧径向磁轴承 X 方向 无工质 8.97 3.90 有工质 7.30 4.86 推力侧径向磁轴承 Y 方向 无工质 9.54 3.66 有工质 7.58 3.24 轴向磁轴承 Z 方向 无工质 10.19 2.58 有工质 10.00 2.76
下载: 导出CSV
-
[1] 孟祥睿, 马新灵. 有机朗肯循环低品位热能发电技术[M]. 郑州: 河南科技出版社, 2015. [2] 纪历. 低温余热磁悬浮发电机转子轴系振动机理研究[J]. 电机与控制学报,2019,23(11): 67-75.JI Li. Vibration mechanism analysis of magnetic levitation rotor system for low temperature waste heat power generation[J]. Electric Machines and Control, 2019, 23(11): 67-75. [3] 孙立佳,任小坤,高元景,等. 高速透平发电机的特点及相关技术研究[J]. 低温与超导,2015,43(8): 23-26.SUN Lijia, REN Xiaokun, GAO Yuanjing, ea al. Study on feature and related technology of high speed turbine generator[J]. Cryogenics & Superconductivity, 2015, 43(8): 23-26. [4] 梁欣. 余热发电高速永磁电机设计与分析[D]. 武汉: 华中科技大学, 2019. [5] 戴其城. 涡轮直驱余热发电机组中锥形永磁同步电机的研究[D]. 长沙: 湖南大学, 2018. [6] 胡业发, 周祖德, 江征风. 磁力轴承的基础理论与应用[M]. 北京: 机械工业出版社, 2006. [7] 王大彪,段 捷,胡哺松,等. 有机朗肯循环发电技术发展现状[J]. 节能技术,2015,33(191): 235-242.WANG Dabiao, DUAN Jie, HU Bu song, et al. Status of organic Rankine cycle power generation technology[J]. Energy Conservation Technology, 2015, 33(191): 235-242. [8] 占智军,祝长生. E型径向电磁轴承的参数设计及特性分析[J]. 机电工程,2013,30(3): 267-272.ZHAN Zhijun, ZHU Changsheng. Parameters design and characteristics analysis of E-core radial magnetic bearings[J]. Journal of Mechanical & Electrical Engineering, 2013, 30(3): 267-272. [9] 杨贝,张宁,张海波,等. 径向磁悬浮轴承的结构设计和数值模拟[J]. 低温与超导,2015,43(4): 31-35,42.YANG Bei, ZHANG Ning, ZHANG Haibo, et al. Design and simulation of radial active magnetic bearings[J]. Cryogenics & Superconductivity, 2015, 43(4): 31-35,42. [10] 代燕杰. 磁悬浮推力轴承的电磁性能分析及结构设计[D]. 济南: 山东大学, 2008. [11] 吴宝贵. 轴向磁悬浮轴承的研究[D]. 南京: 南京航空航天大学, 2008. [12] 邹望蠡. 轴向磁轴承的拓扑结构及参数优化设计[D]. 南京: 南京航空航天大学, 2014. [13] 刘程子. 适用于高速电机的混合型磁悬浮轴承设计及控制策略的研究[D]. 南京: 南京航空航天大学, 2014. [14] 魏坚. 磁悬浮飞轮电池支承控制系统的硬件设计与算法研究[D]. 武汉: 武汉理工大学, 2010. [15] 刘建明. 电磁轴承结构设计与转子动力学分析[D]. 合肥: 合肥工业大学, 2007. [16] 李冰. 电磁轴承系统集成化技术的研究[D]. 南京: 南京航空航天大学, 2003. [17] 郑坚强. 电磁轴承有限元分析结构设计及控制[D]. 杭州: 浙江大学, 2004. [18] 周传月,JOACHIM S. 基于Madyn_2000的磁悬浮轴承控制器的设计[J]. 风机技术,2017,59(4): 51-59,78.ZHOU Chuanyue, JOACHIM S. Design of magnetic bearing controller using Madyn 2000[J]. Chinese Journal of Turbomachinery, 2017, 59(4): 51-59,78. [19] 杨先,李洪斌. 有机朗肯循环发电技术的原理及应用[J]. 大众科技,2020,22(9): 61-63. doi: 10.3969/j.issn.1008-1151.2020.09.019YANG Xian, LI Hongbin. Principle and application organic Rankine cycle power generation technology[J]. Popular Science & Technology, 2020, 22(9): 61-63. doi: 10.3969/j.issn.1008-1151.2020.09.019 [20] HERZOG R, BUHLER P, GAHLER C, et al. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 580-586. doi: 10.1109/87.531924 [21] 宋腾,韩邦成,郑世强,等. 基于最小位移的磁悬浮转子变极性 LMS 反馈不平衡补偿[J]. 振动与冲击,2015,34(7): 24-32.SONG Teng, HAN Bangcheng, ZHENG Shiqiang, et al. Variable polarity LMS feedback based on displacement nulling to compensate unbalance of magnetic bearing[J]. Journal of Vibration and Shock, 2015, 34(7): 24-32. -
下载:
点击查看大图
计量
- 文章访问数: 306
- HTML全文浏览量: 178
- PDF下载量: 19
- 被引次数: 0