基于自抗扰技术的机械-电磁悬浮复合隔振控制

黄翠翠; 李晓龙; 杨洋; 龙志强

doi:10.3969/j.issn.0258-2724.20210850

基于自抗扰技术的机械-电磁悬浮复合隔振控制

doi: 10.3969/j.issn.0258-2724.20210850

国防科技大学智能科学学院，湖南长沙 410073

基金项目: 国家重点研发计划（2016YFB1200600）

详细信息

作者简介:
黄翠翠（1992—），女，博士研究生，研究方向为电磁悬浮与推进技术，E-mail：708849069@qq.com

通讯作者:
龙志强（1967—），男，教授，博士，研究方向为电磁悬浮与推进控制、智能诊断与容错控制、智能系统安全控制，E-mail： zhqlong@nudt.edu.cn

中图分类号: TP273
计量
- 文章访问数: 220
- HTML全文浏览量: 69
- PDF下载量: 14
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-01
- 录用日期: 2022-03-22
- 修回日期: 2022-03-14
- 刊出日期: 2022-03-24

Mechanical-Electromagnetic Suspension Compound Vibration Isolation Control Based on Active Disturbance Rejection Technology

College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China

摘要

摘要:
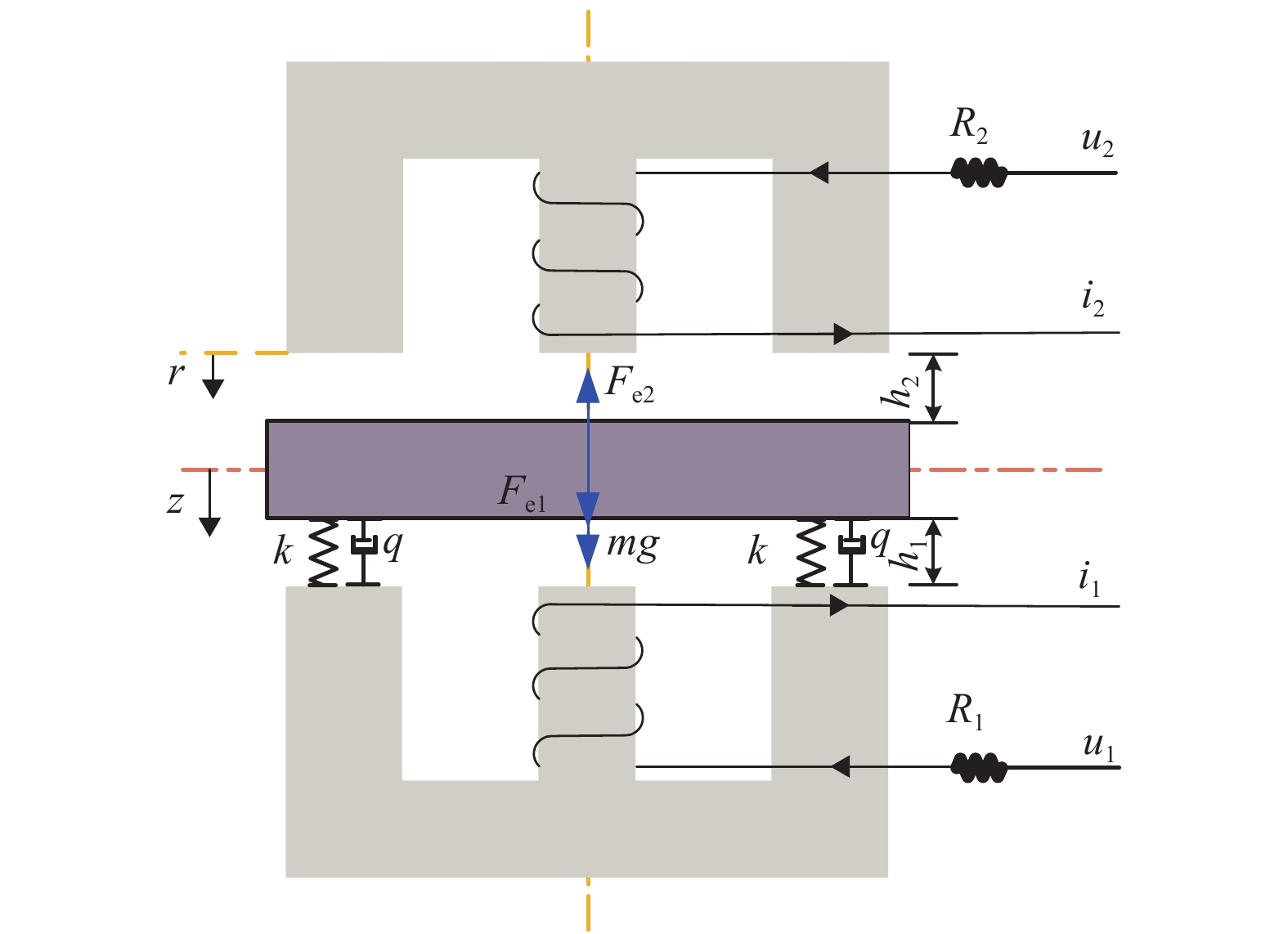
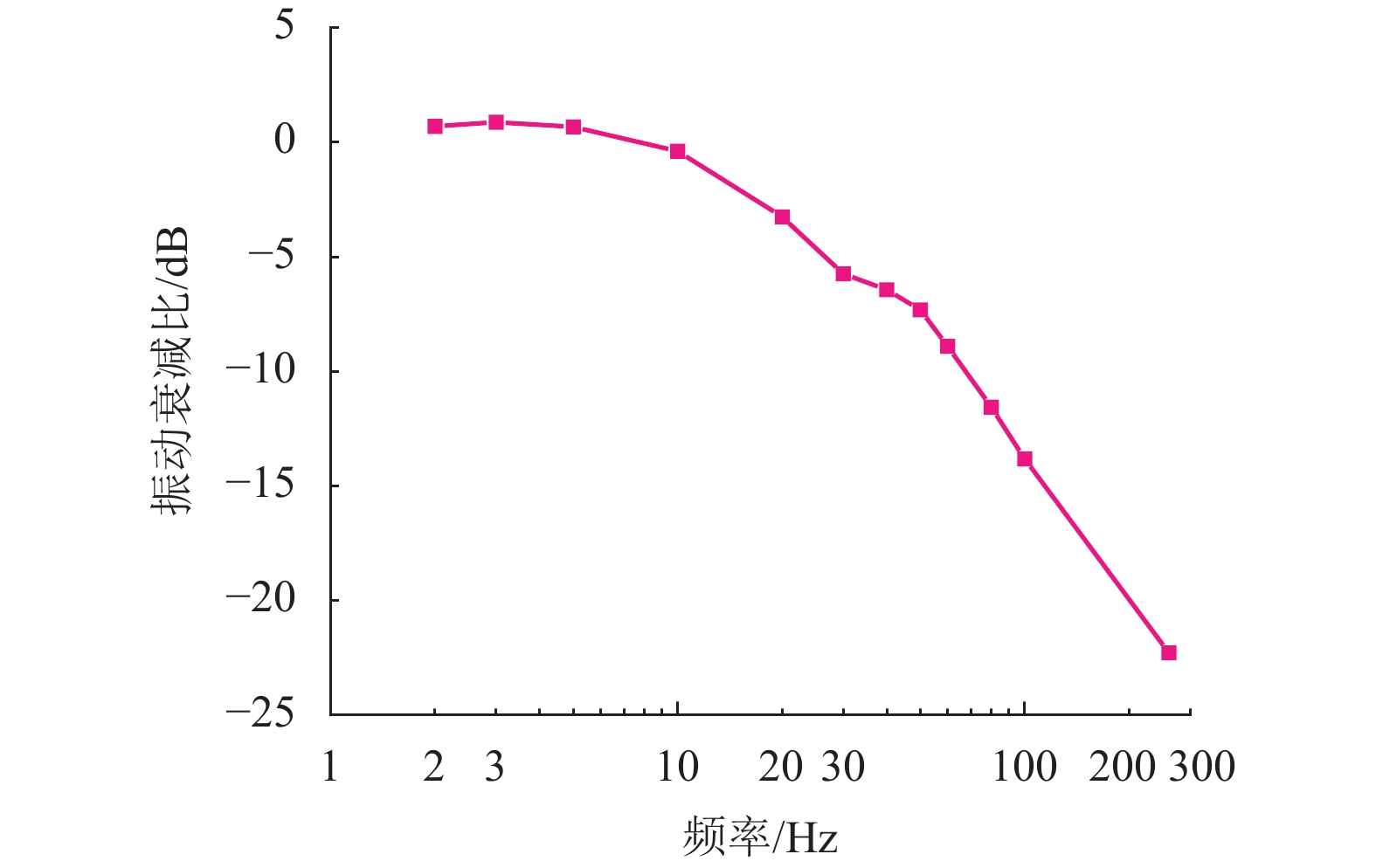
为了研究宽频带的隔振问题，以使系统具有较好的隔振效果，提出将电磁悬浮隔振与机械隔振相结合的复合隔振系统. 首先，对所设计的隔振系统进行动力学建模，分析线性化后的模型控制特性；其次，针对系统振动控制问题，提出基于自抗扰技术的控制器设计方案，并通过仿真实现了复合隔振系统的自抗扰控制；最后，在复合隔振平台上验证了该控制方案的可行性. 研究结果表明：在0~10 Hz频段控制系统能实现较好的低频跟随效果，在10~100 Hz频段幅值衰减逐渐增大，在100~300 Hz频段的隔振效果超过−14.9 dB. 本文所提出的控制方案为复合隔振系统控制提供了一种新思路.
- 复合隔振 /
- 隔振控制 /
- 电磁悬浮 /
- 自抗扰控制
Abstract:
In order to study broadband vibration isolation and make a system have better vibration isolation performance, a compound vibration isolation system combining electromagnetic suspension isolation and mechanical spring isolation is proposed. First, a dynamic model of the designed vibration isolation system is established, and the control characteristics of the linearized model are analyzed. Aiming at the problem of system vibration control, a controller design scheme based on active disturbance rejection technology is then presented, and the active disturbance rejection control of system is realized by simulation. Finally, the feasibility of the control scheme is verified on a compound vibration isolation platform. The experimental results show that the control system in 0−10 Hz frequency band can achieve good performance of low-frequency tracking, the amplitude attenuation increases gradually in 10−100 Hz, and the vibration isolation effect in 100−300 Hz frequency band exceeds −14.9 dB. The control scheme proposed in this paper provides a new idea for the control of the compound vibration isolation system.
- compound vibration isolation /
- active vibration control /
- electromagnetic suspension /
- active disturbance rejection control

HTML全文

图 1 复合隔振平台示意

Figure 1. Schematic diagram of a compound vibration isolation platform

下载: 全尺寸图片幻灯片

图 2 复合隔振系统受力分析

Figure 2. Force analysis of compound vibration isolation system

下载: 全尺寸图片幻灯片

图 3 带电流反馈的开环系统模型

Figure 3. Open loop system model with current feedback

下载: 全尺寸图片幻灯片

图 4 控制系统架构

Figure 4. Framework of control system

下载: 全尺寸图片幻灯片

图 5 控制系统仿真图

Figure 5. Simulation results of control system

下载: 全尺寸图片幻灯片

图 6 复合隔振平台实物

Figure 6. Photograph of compound vibration isolation platform

下载: 全尺寸图片幻灯片

图 7 自抗扰控制仿真与实验结果对比

Figure 7. Comparison between simulation and test results of the active disturbance rejection control

下载: 全尺寸图片幻灯片

参考文献(13)

[1]	龙志强,郝阿明,陈革,等. 磁悬浮控制的主动式隔振平台研究[J]. 宇航学报,2003,24(5): 510-514. LONG Zhiqiang, HAO Aming, CHEN Ge, et al. The research of active isolation platform with magnetically levitated control[J]. Journal of Astronautics, 2003, 24(5): 510-514.
[2]	SHAHADAT M M Z, MIZUNO T, ISHINO Y, et al. Active vibration isolation using negative stiffness and displacement cancellation controls: Comparison based on vibration isolation performance[J]. Control Engineering Practice, 2005, 37: 55-66.
[3]	RASID S M R, MIZUNO T, ISHINO Y, et al. Design and control of active vibration isolation system with an active dynamic vibration absorber operating as accelerometer[J]. Journal of Sound and Vibration, 2019, 438: 175-190. doi: 10.1016/j.jsv.2018.09.037
[4]	KIM M H, KIM H Y, KIM H C, et al. Design and control of a 6-DOF active vibration isolation system using a Halbach magnet array[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(4): 2185-96. doi: 10.1109/TMECH.2016.2539349
[5]	GONG Z, DING L, YUE H, et al. System integration and control design of a maglev platform for space vibration isolation[J]. Journal of Vibration and Control, 2019, 25(11): 1720-1736.
[6]	SUN Y, MENG K, YUAN S, et al. Modeling electromagnetic force and axial-stiffness for an electromagnetic negative-stiffness spring toward vibration isolation[J]. IEEE Transactions on Magnetics, 2019, 55(3): 1-10. doi: 10.1109/TMAG.2019.2897913
[7]	何琳,李彦,杨军. 磁悬浮-气囊主被动混合隔振装置理论和实验[J]. 声学学报,2013,38(2): 241-249. HE Lin, LI Yan, YANG Jun. Theory and experiment of passive-active hybrid vibration isolation mounts using electromagnetic actuator and air spring[J]. Acta Acustica, 2013, 38(2): 241-249.
[8]	马建国, 帅长庚, 李彦. 磁悬浮-气囊主被动混合隔振器力学特性及主动隔振实验研究[J]. 振动与冲击 2018, 37(19) : 198-204. MA Jianguo, SHUAI Changgeng, LI Yan. Dynamic characteristics of maglev-air bag active-passive hybrid vibration isolators and active vibration isolation tests. Journal of Vibration and Shock 2018, 37(19): 206-212.
[9]	文湘隆. 基于气磁主被动混合隔振的浮筏若干问题研究[D]. 武汉: 武汉理工大学, 2018.
[10]	陈绍青. 电磁式主被动复合隔振器关键技术研究[D]. 合肥: 中国科学技术大学, 2013.
[11]	韩京清,袁露林. 跟踪—微分器的离散形式[J]. 系统科学与数学,1999,19(3): 268-273. doi: 10.3969/j.issn.1000-0577.1999.03.003 HAN Jingqing, YUAN Lulin. The discrete form of tracking-differentiator[J]. Journal of Systems Science and Mathematical Sciences, 1999, 19(3): 268-273. doi: 10.3969/j.issn.1000-0577.1999.03.003
[12]	韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策,1995,10(1): 85-88. HAN Jingqing. The “extended state observer” of a class of uncertain systems[J]. Control and Decision, 1995, 10(1): 85-88.
[13]	韩京清. 非线性状态误差反馈控制律—NLSEF[J]. 控制与决策,1995,10(3): 221-225. doi: 10.3321/j.issn:1001-0920.1995.03.007 HAN Jingqing. Nonlinear state error feedback control law-NLSEF[J]. Control and Decision, 1995, 10(3): 221-225. doi: 10.3321/j.issn:1001-0920.1995.03.007