Design and Implementation of Magnetic Suspension Vibration Isolation Platform with Quasi-Zero Stiffness Based on Fuzzy PID Control
-
摘要:
为有效降低系统固有频率,获得外部振动在多频段的强衰减,以永磁电磁混合作动器为负刚度结构提出并设计了一种准零刚度的磁悬浮隔振平台,实现了基于模糊PID (proportional integral differential)算法的振动主动控制系统. 首先,通过特性分析与参数计算,基于准零刚度理论完成了准零刚度磁悬浮隔振平台的方案设计;其次,建立磁悬浮隔振系统模型,提出基于模糊PID算法的振动主动控制策略,可主动调节系统的等效刚度和阻尼;最后,基于Speedgoat实时目标机开发振动主动控制系统,搭建隔振测试平台,并开展了隔振性能测试. 研究结果表明:本文设计的准零刚度磁悬浮隔振平台通过采用模糊PID的控制策略能够主动调节PID参数,动态调整系统的等效刚度和阻尼;外部振动频率在20~100 Hz频率段内,振动衰减率大于80%;外部振动频率在100~500 Hz频率段内,振动衰减率大于90%.
Abstract:In order to effectively reduce the natural frequency of systems and realize the strong attenuation of external vibrations in multiple frequency bands, a magnetic suspension vibration isolation platform with quasi-zero stiffness was designed, in which the permanent-magnet and electromagnetic hybrid actuator was the negative stiffness structure, and an active vibration control system based on fuzzy PID (proportional integral differential) algorithm was implemented. Firstly, based on the theory of quasi-zero stiffness, the scheme of the magnetic suspension vibration isolation platform with quasi-zero stiffness was designed through characteristic analysis and parameter calculation; secondly, the model of the magnetic suspension vibration isolation system was established, and the active vibration control strategy based on fuzzy PID algorithm was designed to actively adjust the equivalent stiffness and damping of the system; finally, an active vibration control system was developed based on the Speedgoat real-time target machine. A vibration isolation test platform was built, and a series of vibration isolation performance tests were carried out. The results show that the magnetic suspension vibration isolation platform with quasi-zero stiffness can actively adjust PID parameters by adopting a fuzzy PID control strategy and dynamically adjust the equivalent stiffness and damping of the system. When the external vibration frequency is 20–100 Hz, the vibration attenuation rate is greater than 80%; when the external vibration frequency is 100–500 Hz, the vibration attenuation rate is greater than 90%.
-
为了减小外部振动的传递,实现被隔振对象振动量级衰减,各种隔振装置和振动控制技术应运而生. 被动隔振装置一般由弹簧与阻尼元件构成,结构简单,刚度较大,不需要外部能量输入,但是受系统固有频率与承载能力的矛盾限制,被动隔振装置的低频隔振效果较差,导致隔振带宽较窄[1-2]. 主动隔振通过主动控制策略使隔振装置产生与外部振动相反的运动,刚度和阻尼可在线调节,广泛应用于航空航天、道路桥梁等领域中[3-4]. 主被动复合隔振是在被动隔振的基础上,通过增加主动隔振装置的一种新型隔振技术,目前是隔振领域研究的热点[5-7].
但是,传统隔振装置的刚度均是正刚度,并且存在系统刚度与隔振效果和承载能力不可兼得的矛盾问题. 因此,文献[8]首次提出了准零刚度理论,通过在正刚度机构中并联负刚度结构,在保证承载力不受影响的前提下使系统达到准零刚度状态,实现了飞机和支架的低频隔振. 文献[9]将永磁铁引入到负刚度机构模型的设计,设计了一种基于电磁式的准零刚度隔振系统. 文献[10]通过加装隔磁层来减小磁场耦合效应的不利影响,通过改变电流的大小实现了负刚度的动态调节. 文献[11]将空气弹簧作为正刚度机构,将电磁弹簧作为负刚度机构,研究了基于磁气混合的准零刚度隔振系统,设计了模糊控制器,获得了良好的准零刚度特性.
然而,电磁隔振平台需要设计专门的主动控制系统. 针对隔振系统的主动振动控制策略,很多学者基于传统的PID (proportional integral differential)算法开展了大量工作,取得了很好的效果[12-14]. 但是,磁悬浮隔振结构复杂,传统的PID算法不能有效适应外部振动变化,不能通过主动调节PID参数实现系统等效刚度和阻尼的动态调节,难以满足系统全过程、多频段的减振需求.
因此,本文基于准零刚度理论,提出并设计了一种准零刚度磁悬浮隔振平台. 该平台具有低固有频率、高承载能力,宽隔振频带等优点. 但是,隔振效果受电流和永磁体的影响较大,也存在不稳定等问题. 为了能够动态调节准零刚度磁悬浮隔振平台的刚度和阻尼,设计基于模糊PID算法的振动主动控制系统,以实现外部振动在多频段的强衰减.
1. 准零刚度磁悬浮隔振平台
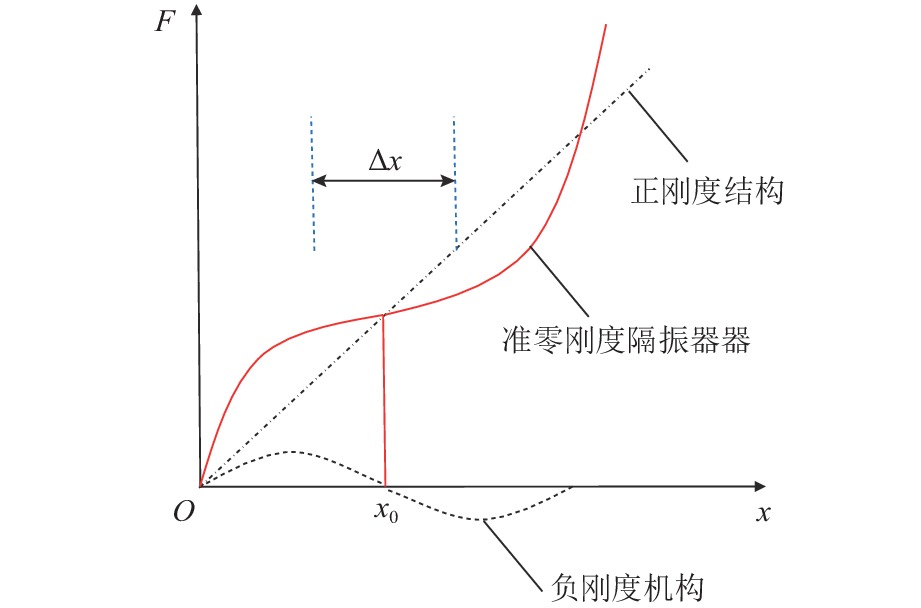
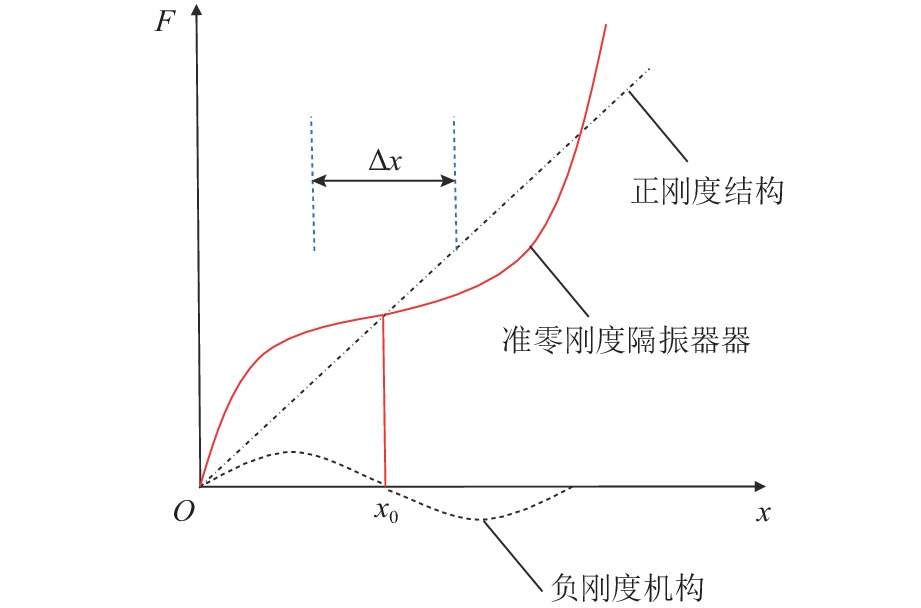
传统隔振装置刚度通常为正刚度,隔振效果与承载能力不可兼得,通过在正刚度机构中并联负刚度结构,在保证承载力不受影响的前提下能够使系统达到准零刚度状态. 如图1所示. 图中:x为变形量;F为承载力. 准零刚度隔振器的工作原理是利用正负刚度机构并联,通过结构设计和参数计算,使得系统总刚度在平衡点x0的某一邻域Δx内正负刚度大致相抵,在平衡点附近系统的总刚度趋于0.
准零刚度隔振器的承载能力由正刚度机构决定,与只使用正刚度机构的隔振器承载能力几乎相同,因此,可以有效保证承载力不受影响. 负刚度机构可以有效降低系统的总刚度,进而降低系统固有频率,实现较为不错的低频隔振效果,从而达到拓宽隔振频带的目的.
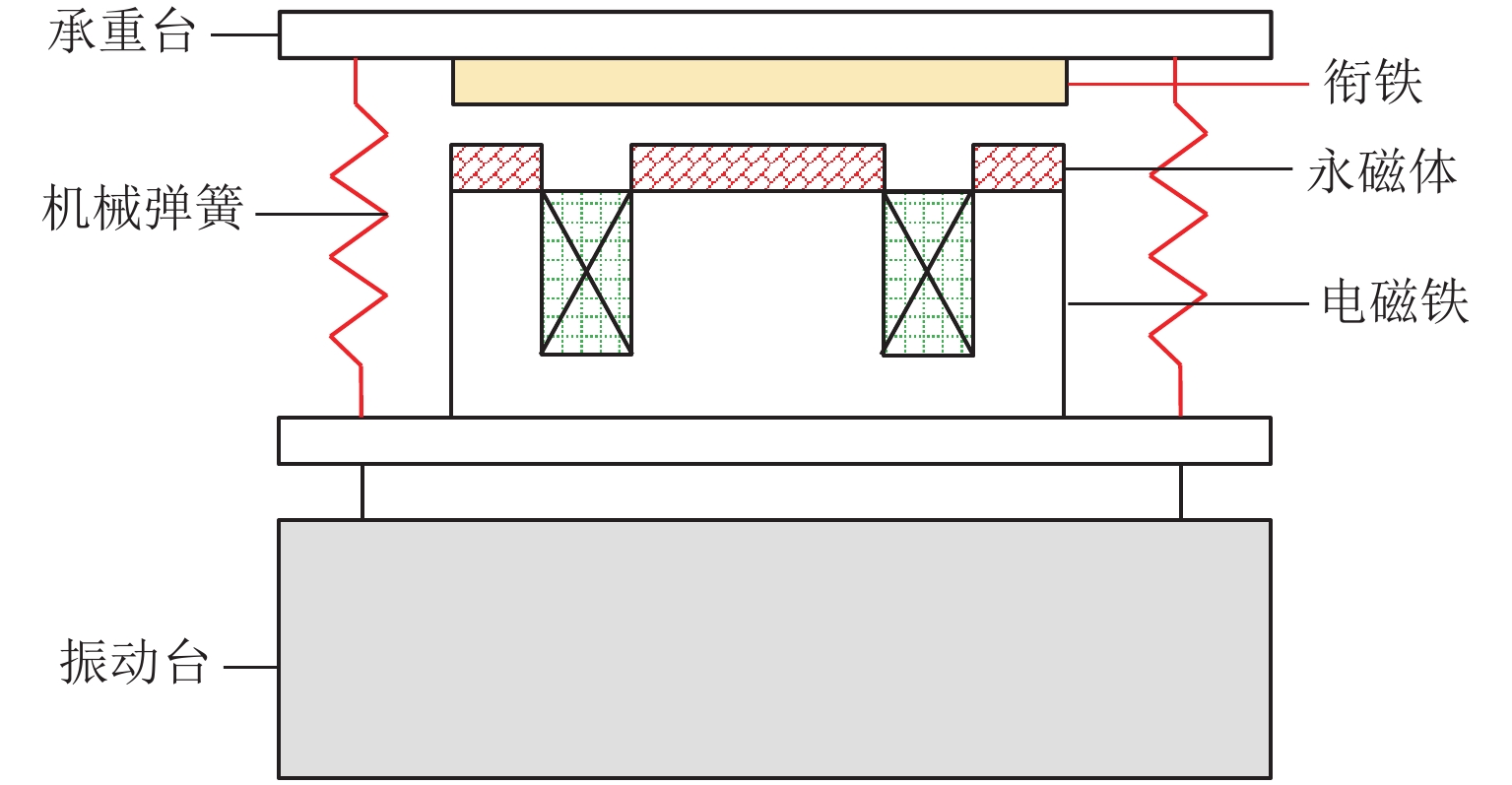
因此,基于准零刚度理论,以永磁电磁混合作动器为负刚度结构,以机械弹簧为正刚度机构,将正刚度机构与负刚度机构并联,提出并设计了一种准零刚度磁悬浮隔振平台. 其中,作为正刚度机构的机械弹簧通过预压缩为被隔振对象提供支撑力,无电流条件下,通过平衡永磁电磁混合作动器与衔铁之间的电磁吸力,使被隔振对象始终处在初始平衡位置附近. 永磁电磁混合作动器中永磁体主要用来提供负刚度,减小或者平衡机械弹簧带给系统的正刚度,进而使系统的总刚度在平衡点附近达到准零刚度状态. 永磁电磁混合作动器中电磁铁能够通过改变电压和电流的大小和方向,进而改变永磁电磁混合作动器的磁场强度,最终实现动态调整电磁吸力的目标.
本文设计的准零刚度磁悬浮隔振平台不仅能够通过永磁体减小系统的总刚度,同时还能够动态调整系统的等效刚度和等效阻尼,从而实现较为不错的低频隔振效果,从而满足多频段的减振需求. 准零刚度磁悬浮隔振平台的整体结构如图2所示.
为了满足准零刚度磁悬浮隔振平台的设计需求,作为正刚度机构的机械弹簧采用的是强度高、性能好的节距圆柱螺旋弹簧,弹簧材料为牌号65 Mn的碳素弹簧钢丝,整个磁悬浮隔振平台共安装4个对称的机械弹簧. 机械弹簧提供的正刚度为86.461 N/mm.
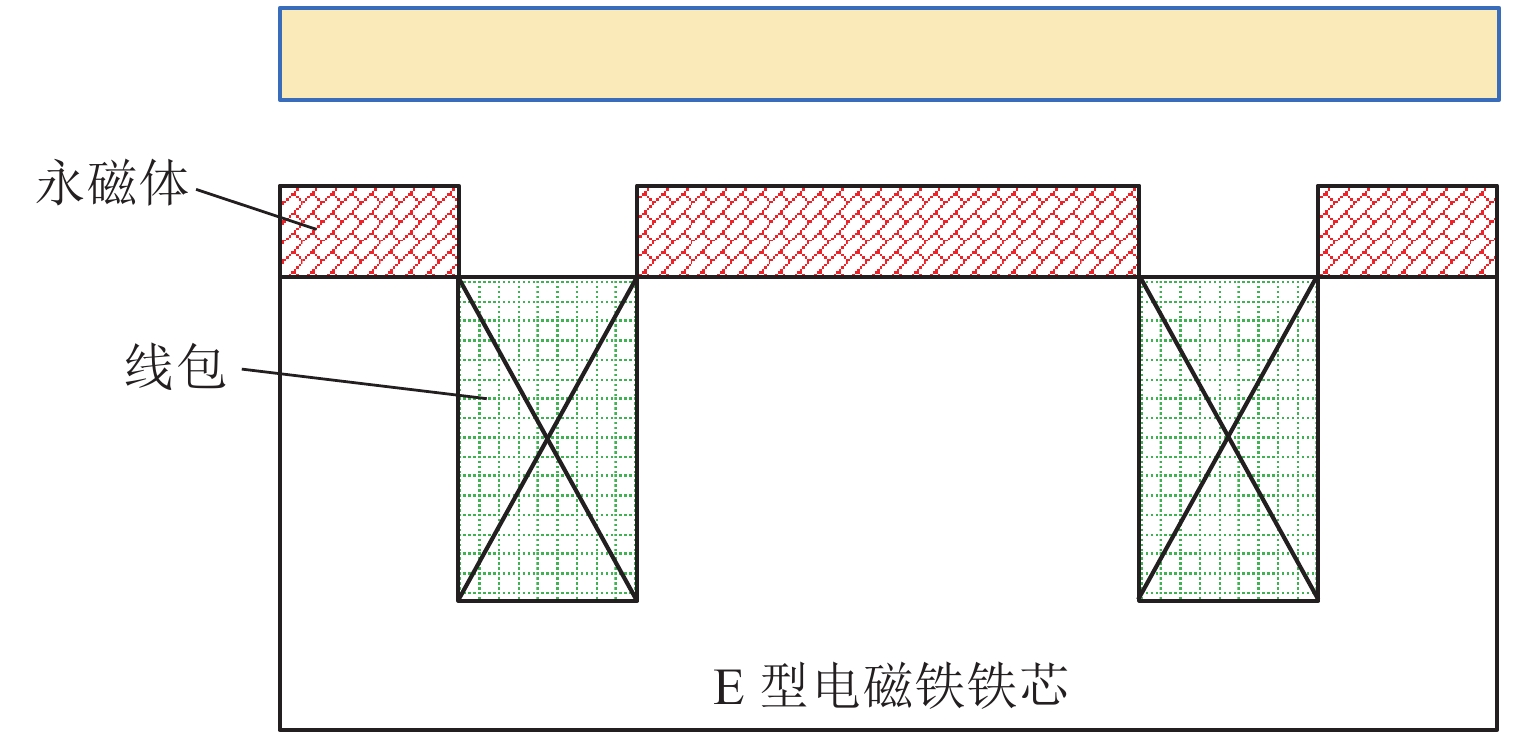
永磁电磁混合作动器是准零刚度磁悬浮隔振平台的负刚度结构,其结构如图3所示. 其中,永磁体主要用来提供负刚度,电磁铁主要通过改变电压和电流的大小和方向,进而改变永磁电磁混合作动器的磁场强度,最终实现动态调整电磁吸力的目标. 根据电磁铁设计与安装经验,E型电磁铁具备良好的空间结构,高度符合准零刚度磁悬浮隔振平台的设计需求,因此,电磁铁采用的是图3所示的E型结构. 同时,考虑到电磁铁会面临不同的振动环境和发热问题,电磁铁的铁芯和衔铁采用矽钢片叠片,型号为EI-180,电磁铁的线圈采用电阻较小的漆包铜圆导线,匝数为378匝,阻值为0.62 Ω.
永磁电磁混合作动器中永磁体装配在电磁铁铁芯上端,主要用来提供负刚度,减小或者平衡机械弹簧带给系统的正刚度,进而使系统的总刚度在平衡点附近达到准零刚度状态. 因此,永磁体采用的是具有高能量密度、大矫顽力的钕铁硼材料,牌号为N35,具体参数见表1.
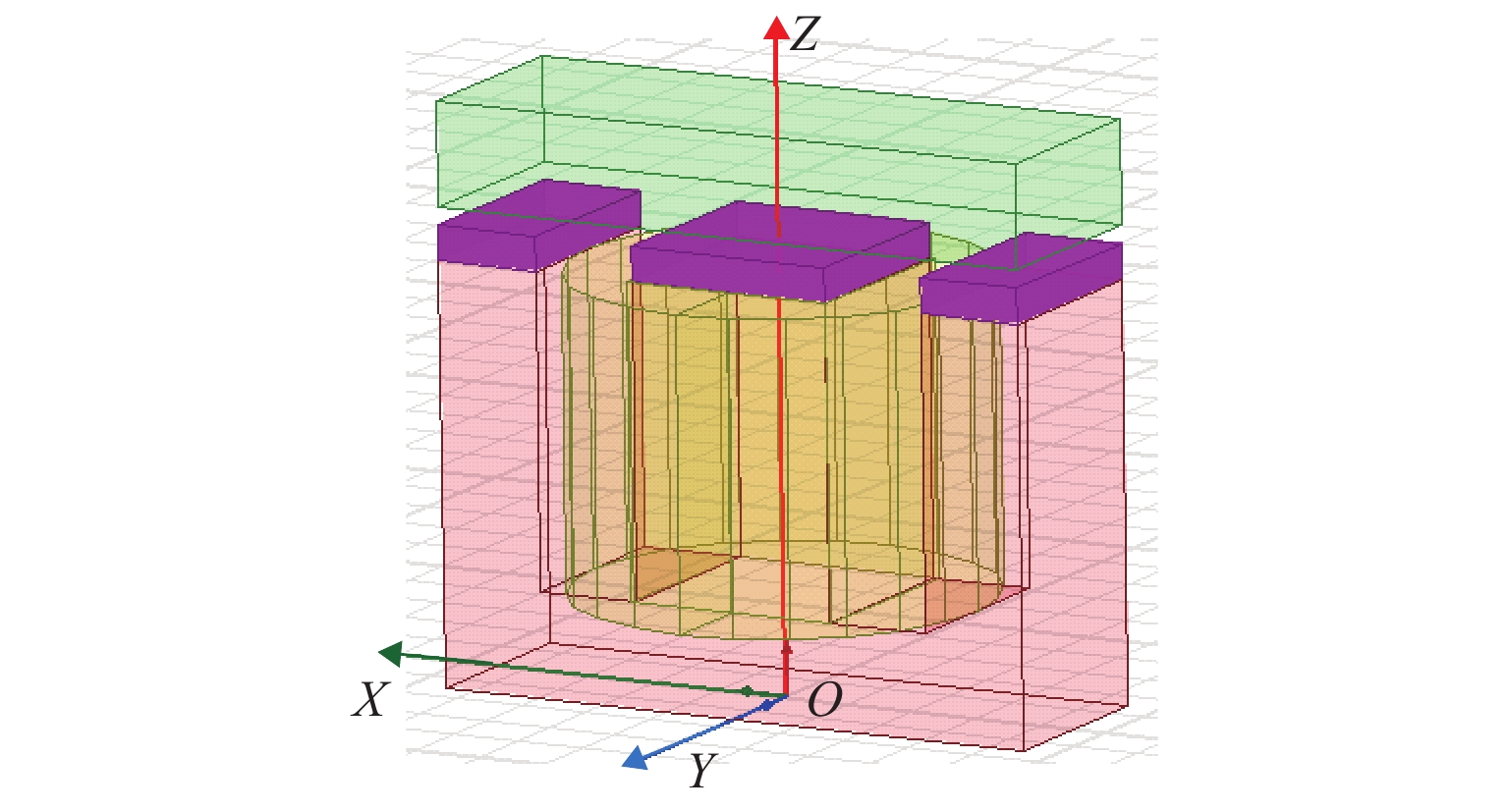
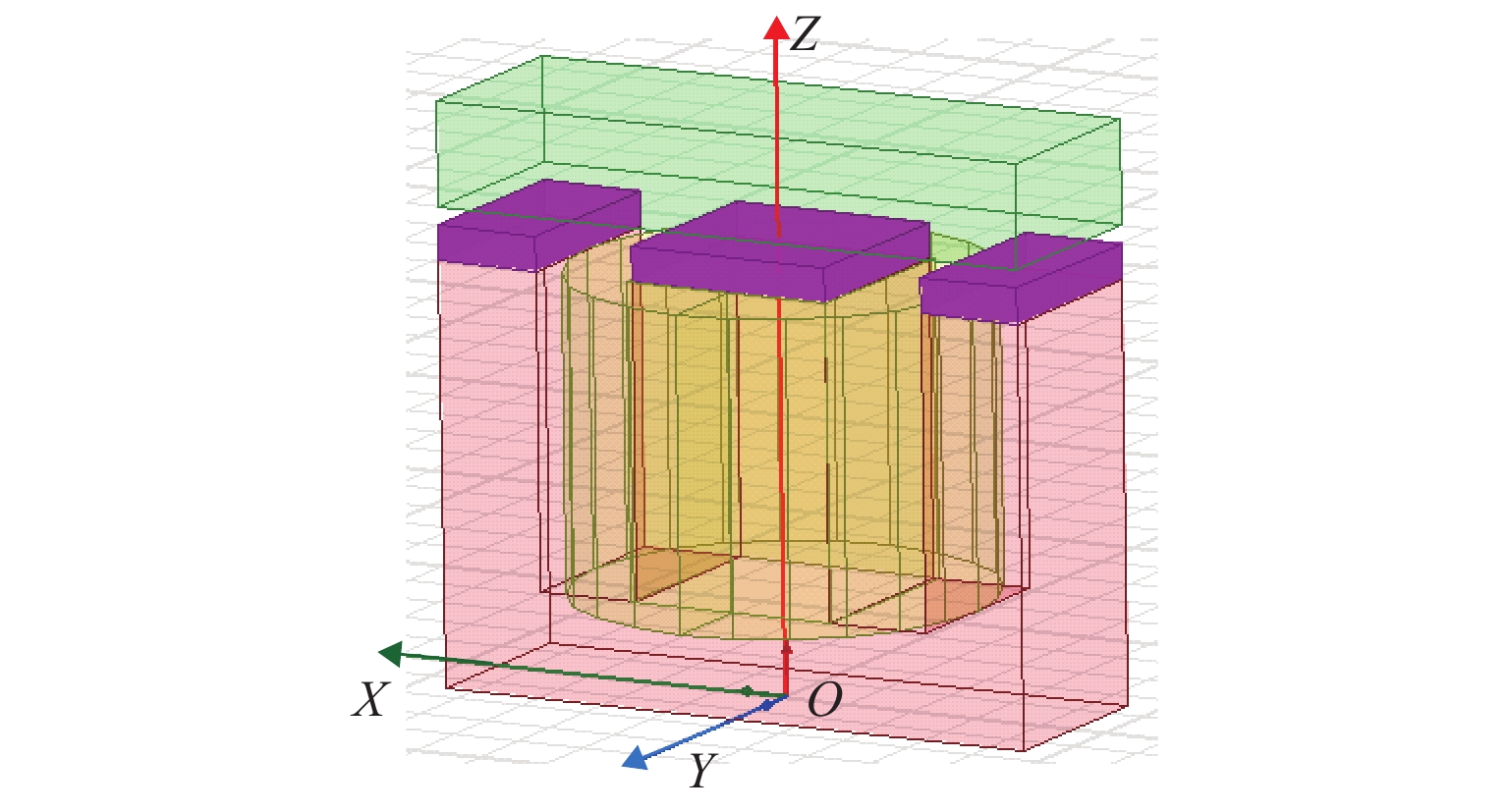
表 1 永磁体具体参数Table 1. Detailed parameters of permanent magnet参数名称 参数符号 参数值 剩余磁感应强度/T Br 1.2 矫顽力/(kA•m−1) Hc 896 相对磁导率 μr 1.05 永磁电磁混合作动器中永磁体产生的吸力大小不仅与悬浮间隙有关,还与永磁体的厚度直接相关. 本文通过Maxwell软件建立三维有限元模型,如图4所示,并利用有限元分析法对永磁体产生的电磁吸力进行数值计算与分析.
永磁电磁混合作动器在平衡位置的悬浮间隙为10.0 mm,当通过的电流为0时,分别对永磁体在不同厚度条件下产生的电磁吸力进行数值分析与计算,计算结果如表2所示.
表 2 永磁体在工作点附近产生的电磁吸力Table 2. Electromagnetic attraction generated by permanent magnet near working pointN 永磁体
厚度/mm悬浮间隙/mm 9.5 10.0 10.5 7 465.1 430.4 399.0 8 532.5 493.9 459.3 9 595.4 553.1 515.6 10 652.2 608.9 567.8 11 705.5 658.7 615.3 12 753.2 704.2 659.3 13 797.1 747.0 699.9 当永磁体的厚度为10 mm时,产生的电磁吸力就能够满足隔振平台的设计需求. 永磁体主要用来提供负刚度,减小或者平衡机械弹簧带给系统的正刚度,因此,永磁体在工作点附件的刚度应该大体为−86.461 N/mm. 在工作点附近,通过9.5 mm悬浮间隙下电磁吸力与10.5 mm悬浮间隙下电磁吸力差值就可以计算出永磁体提供的负刚度,具体为−84.400 N/mm.
此时,系统总刚度为2.061 N/mm,在平衡点附近的正负刚度大致相抵,总刚度趋于0,基本达到了准零刚度状态.
2. 基于模糊PID算法的振动主动控制
为了能够动态调节准零刚度磁悬浮隔振平台的刚度和阻尼,达到更好的隔振效果,需要研究永磁电磁混合作动器的动态特性,建立磁悬浮隔振平台的系统模型,并依据模型特性设计标称控制器,针对外部振动进行主动控制.
2.1 磁悬浮隔振平台的系统建模
为了描述磁悬浮隔振平台的电磁动态特性和动力学关系,需要建立相应的数学模型. 实际建模过程中,为了降低微分方程阶次,降低求解难度,忽略了漏磁和边缘效应,认为永磁电磁混合磁场的强度分布均匀[15]. 根据永磁电磁混合磁场理论和欧姆定律,永磁电磁混合作动器的等效磁路满足如下关系:
{Ni+Hczm−Rm1Φ1−Rm2Φ2+Hczm=0,Ni+Hczm−Rm1Φ1−Rm3Φ3+Hczm=0, (1) 式中:N为线圈匝数;i为电磁铁电流;zm为永磁铁的厚度; 磁路的磁通量;Φ1、Φ2、Φ3分别为E型电磁铁中间、左、右两侧磁路的磁通量; Rm1、Rm2、Rm3分别为中间、左侧、右侧气隙和永磁体的总磁阻.
其中,Φ1满足
Φ1=2Φ2=(Ni+2Hczm)μ0μrs12(zm+zμr), (2) 式中:μ0为真空磁导率的相对磁导率;s1为中部磁极面积;z为悬浮间隙.
电磁铁为感性元件,其电压u与电流的关系式为
u=Ri+N2μ0μrs12(zμr+zm)didt−N(Ni+2Hczm)μ0μ2rs12(zμr+zm)2dzdt, (3) 式中:R为电阻;t为时间.
永磁电磁混合作动器产生的磁力为
Fm=Φ21μ0s1+Φ22μ0s2+Φ23μ0s3=(Ni+2Hczm)2μ0μ2rs12(zμr+zm)2, (4) 式中:s2为左侧磁极面积;s3为右侧磁极面积.
为了求解方便,永磁电磁混合作动器产生的磁力需要转换成式(5)形式.
Fm=α(βi+1)2(z+λ)2, (5) 式中:α=2μ0s1(Hczm)2;β=N(2Hczm)−1;λ=zmμ−1r.
外部激励y1引发被隔振对象在竖直方向上产生振动,经过机械弹簧和永磁电磁混合作动器的隔离后,被隔振对象所受振动为x1.
以垂直向上为正方向,被隔振对象的动力学方程可以表示为
md2x1dt2=ks(y1−x1+Δl)+c(dy1dt−dx1dt)−mg−Fm, (6) 式中:ks和c分别为弹簧的刚度和阻尼;Δl为机械弹簧在工作点附近的压缩量;m为被隔振对象质量.
2.2 标称控制器的设计
磁悬浮隔振系统模型中存在平方项等非线性环节,通过求解非线性微分方程组来解析系统非常困难,但磁悬浮隔振系统工作点稳定,工作区间集中在工作点附近,并且不存在本质的非线性环节,因此,可以通过线性分析的方法来解析非线性系统的动态特性.
未施加外部激励时,永磁电磁混合作动器的悬浮间隙为z0. 因此,外部振动下的悬浮间隙z1满足:
z1=z0−y1+x1. (7) 综上,取状态变量\boldsymbol{X}=[{X_{1}}\;\;\;{X_{2}}\;\;\;{X_{3}}]=[{x_{1}}\;\;\;\dot {x_{1}}\;\;\;i],线性化后的系统模型为
\left\{ \begin{array}{lllll} {{\dot X}_1} = {X_2}\\ {{\dot X}_2} = \left( {\dfrac{{{k_{\rm{s}}}}}{m} - \dfrac{{2\alpha {{\left( {\beta {i_0} + 1} \right)}^2}}}{{m{{\left( {{{\textit{z}}_0} + \lambda } \right)}^3}}}} \right)\left( {y_1 - {X_1}} \right)+ \\ \quad \dfrac{{c\left( {\dot y_1 - {X_2}} \right)}}{m} - \dfrac{{2\alpha \beta \left( {\beta {i_0} + 1} \right)}}{{m{{\left( {{{\textit{z}}_0} + \lambda } \right)}^2}}}{X_3}\text{,}\\ {{\dot X}_3} = \dfrac{{2\left( {{{\textit{z}}_0}{\mu _{\rm{r}}} + {{\textit{z}}_{\rm{m}}}} \right)}}{{{N^2}{\mu _0}{\mu _{\rm{r}}}{s_1}}}\left( {u - R{X_3}} \right)\text{,} \end{array} \right. (8) 式中:i0为工作点电流.
系统输入{\boldsymbol{U}}=[ \begin{array}{lll}y_{1} & \dot{y}_{1}& u\end{array} ],系统的状态空间表达式为
\begin{split} & {\boldsymbol{\dot {X} }= \left[ {\begin{array}{*{20}{c}} 0&1&0\\ { - \dfrac{{{k_{\rm{s}}}}}{m} + \dfrac{{2\alpha {{(\beta {i_0} + 1)}^2}}}{{m{{({{\textit{z}}_0} + \lambda )}^3}}}}&{ - \dfrac{c}{m}}&{ - \dfrac{{2\alpha \beta (\beta {i_0} + 1)}}{{m{{({{\textit{z}}_0} + \lambda )}^2}}}}\\ 0&0&{ - \dfrac{{2({{\textit{z}}_0}{\mu _{\rm{r}}} + {{\textit{z}}_{\rm{m}}})}}{{{N^2}{\mu _0}{\mu _{\rm{r}}}{s_1}}}R} \end{array}} \right]\boldsymbol{X}}+\\ & { \left[ {\begin{array}{*{20}{c}} 0&0&0\\ {\dfrac{{{k_{\rm{s}}}}}{m} - \dfrac{{2\alpha {{(\beta {u_0} + 1)}^2}}}{{m{{({{\textit{z}}_0} + \lambda )}^3}}}}&{\dfrac{c}{m}}&0\\ 0&0&{\dfrac{{2({{\textit{z}}_0}{\mu _{\rm{r}}} + {{\textit{z}}_{\rm{m}}})}}{{{N^2}{\mu _0}{\mu _{\rm{r}}}{s_1}}}} \end{array}} \right]\boldsymbol{U}}, \end{split} (9) \boldsymbol{Y} = \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0 \end{array}} \right]\boldsymbol{X}, (10) 式中:Y为系统输出.
根据Hartman-Grobman定理,系统特征多项式不满足Hurwitz稳定性判据,系统是不稳定的. 但是,系统的能控矩阵的秩为3,磁悬浮隔振系统能够实现完全可控.
为了实现磁悬浮隔振系统的稳定可控,需要设计相应的控制律. 本文基于串级控制的思想,内环为电流环,外环为位置环,位置环的设计采用经典的PID控制算法[14]. 当电磁铁工作在平衡位置时,其电感只在极小范围内变化,描述电磁铁电压和电流关系的传递函数为
{G_{{i}}}(s) = \frac{{i}}{{u}} = \frac{{1/R}}{{\dfrac{{{N^2}{\mu _0}{\mu _{\rm{r}}}{s_1}s}}{{2R({{\textit{z}}_0}{\mu _{\rm{r}}} + {{\textit{z}}_{\rm{m}}})}} + 1}}\text{,} (11) 式中:s为复频率.
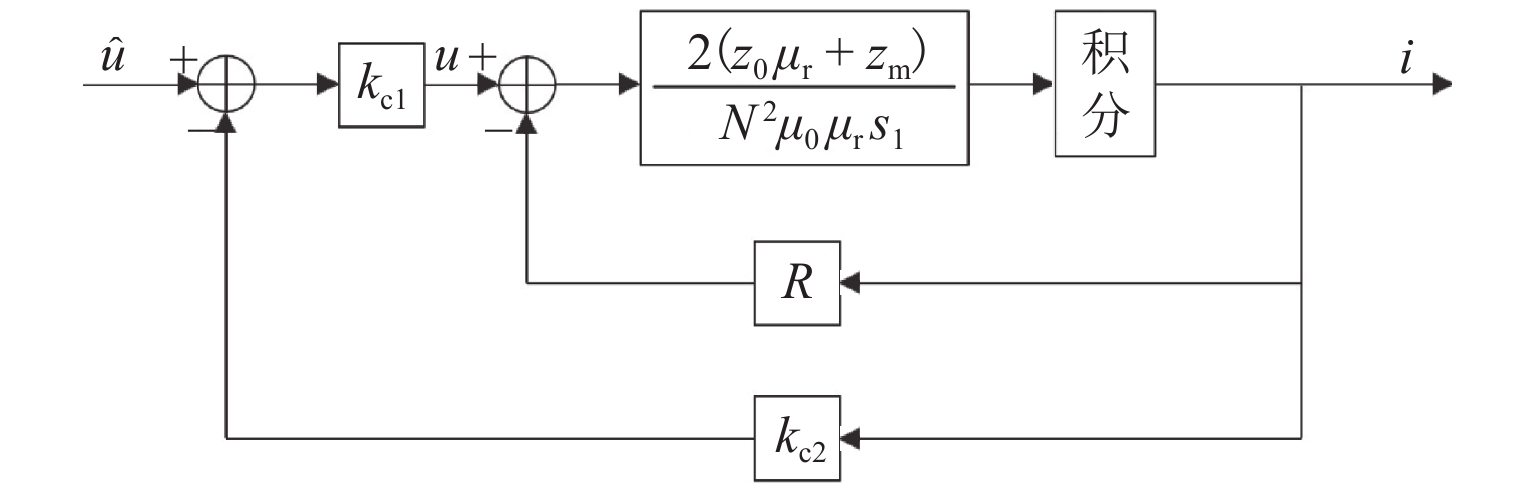
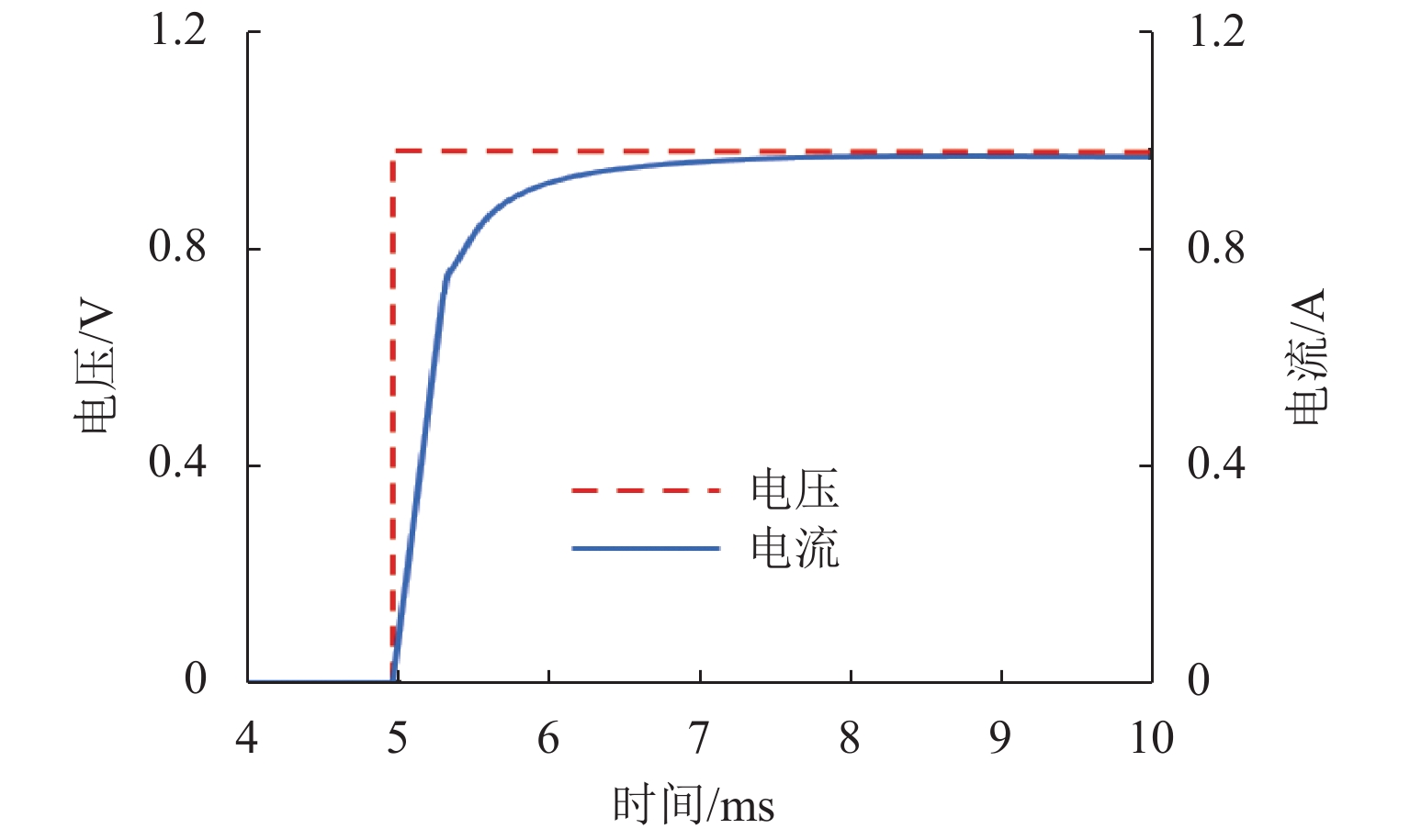
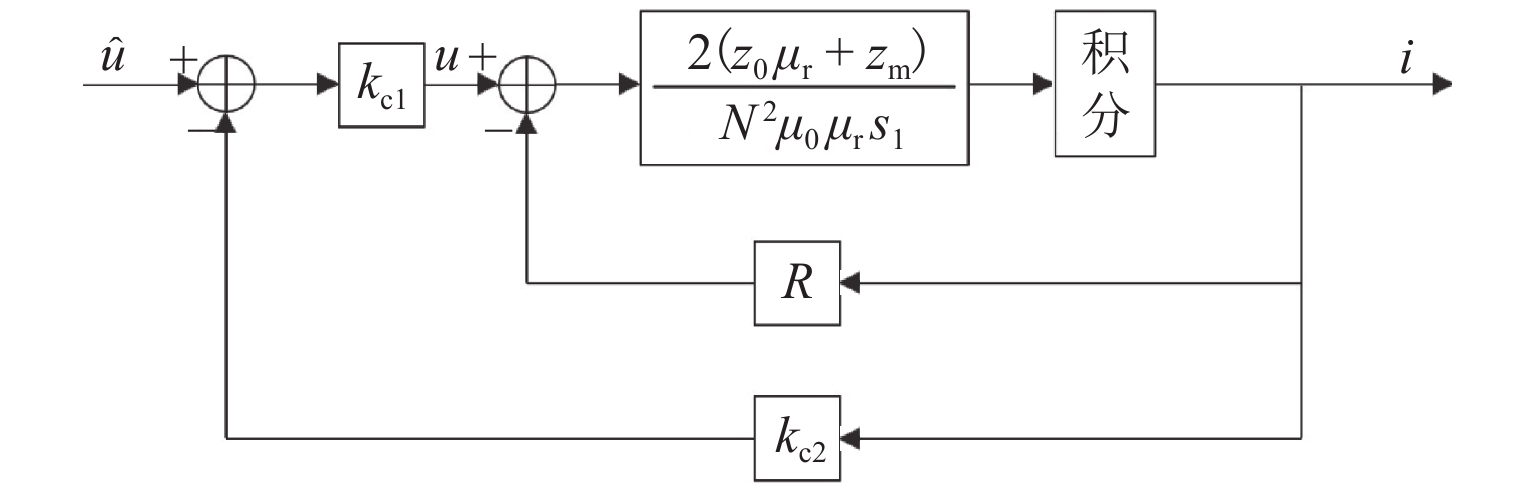
电磁铁电压和电流的传递函数表明,电磁铁是一个典型的惯性环节,输出电流的响应速度严重滞后于输入电压的变化速度. 电磁铁响应时间太长,无法满足系统的响应速度要求,为此,在控制算法的设计中引入了电流环,见图5. 图中: k_{\mathrm{c}1} 为前置放大系数; {k}_{\mathrm{c}2} 为负反馈系数; \hat u 为电流环前的输入电压.
则直接作用于电磁铁上的电压为
u = {k_{{\rm{c1}}}}(\hat u - {k_{{\rm{c2}}}}i)\text{.} (12) 当输入电压为单位阶跃信号时,引入电流环后的响应曲线如图6所示.
引入电流环后,输出电流能够快速跟踪输入电压的变化,同时在系统的频带内,电压与电流的比例系数近似等于1. 系统的阶次由3阶降为2阶. 电流环设计完成后,位置环的设计采用PID控制算法,如式(13).
\hat u = {K_{\rm{P}}}e + {K_{\rm{I}}}\mathop \int \nolimits_0^t e{\rm{d}}t + {K_{\rm{D}}}\frac{{{\rm{d}}e}}{{{\rm{d}}t}}\text{,} (13) 式中:K_{{\rm{P}}}为比例系数;K_{{\rm{I}}}为积分系数;K_{{\rm{D}}}为微分系数; e 为误差.
在磁悬浮隔振系统中,误差 e 为被隔振对象在垂直方向的变形量,即{x},初始值 x_{0}=0 ,因此,偏差 e=-x ,此时,最终的控制律为
u = {k_{{\rm{c1}}}}\left( { - \left( {{K_{\rm{P}}}x + {K_{\rm{I}}}\mathop \int \nolimits_0^t x{\rm{d}}t + {K_{\rm{D}}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}}} \right) - {k_{{\rm{c2}}}}i} \right) \text{.} (14) 综上,控制律设计完成后带入到磁悬浮隔振系统中,则满足
\begin{split} & m\dfrac{{{{\rm{d}}^2}x_1}}{{{\rm{d}}{t^2}}} = \left( {{k_{\rm{s}}} - \dfrac{{2\alpha {{(\beta {u_0} + 1)}^2}}}{{{{({{\textit{z}}_0} + \lambda )}^3}}}} \right)(y_1 - x_1) + c\left( {\dot y_1 - \dot x_1} \right)+ \\ & \dfrac{{2\alpha \beta (\beta {u_0} + 1)}}{{m{{({{\textit{z}}_0} + \lambda )}^2}}}\left( {{K_{\rm{P}}}x_1 + {K_{\rm{I}}}\mathop \int \nolimits_0^t x_1{\rm{d}}t + {K_{\rm{D}}}\frac{{{\rm{d}}x_1}}{{{\rm{d}}t}}} \right)\text{.} \end{split} (15) 此时,磁悬浮隔振系统的等效刚度\tilde k 和等效阻尼\tilde c 分别为
\left\{ \begin{array}{l} \tilde k = {k_{\rm{s}}} - \dfrac{{2\alpha {{(\beta {u_0} + 1)}^2}}}{{{{({{\textit{z}}_0} + \lambda )}^3}}} - \dfrac{{2\alpha \beta {K_{\rm{P}}}(\beta {u_0} + 1)}}{{m{{({{\textit{z}}_0} + \lambda )}^2}}} \text{,}\\ \tilde c = c - \dfrac{{2\alpha \beta {K_{\rm{D}}}(\beta {u_0} + 1)}}{{m{{\left( {{{\textit{z}}_0} + \lambda } \right)}^2}}} . \end{array}\right. (16) 因此,通过调整K_{{\rm{P}}}、K_{{\rm{I}}}、K_{{\rm{D}}} 3个参数可实现系统的刚度和阻尼的动态调整,也可以通过调节电压的方向来控制刚度和阻尼的增加或者减少的方向,从而实现更好的隔振效果. 但是,磁悬浮隔振系统的工作环境较为恶劣,外部振动复杂多变,传统的PID控制器难以满足系统全过程、多频段减振需求.
2.3 基于模糊PID算法的振动主动控制
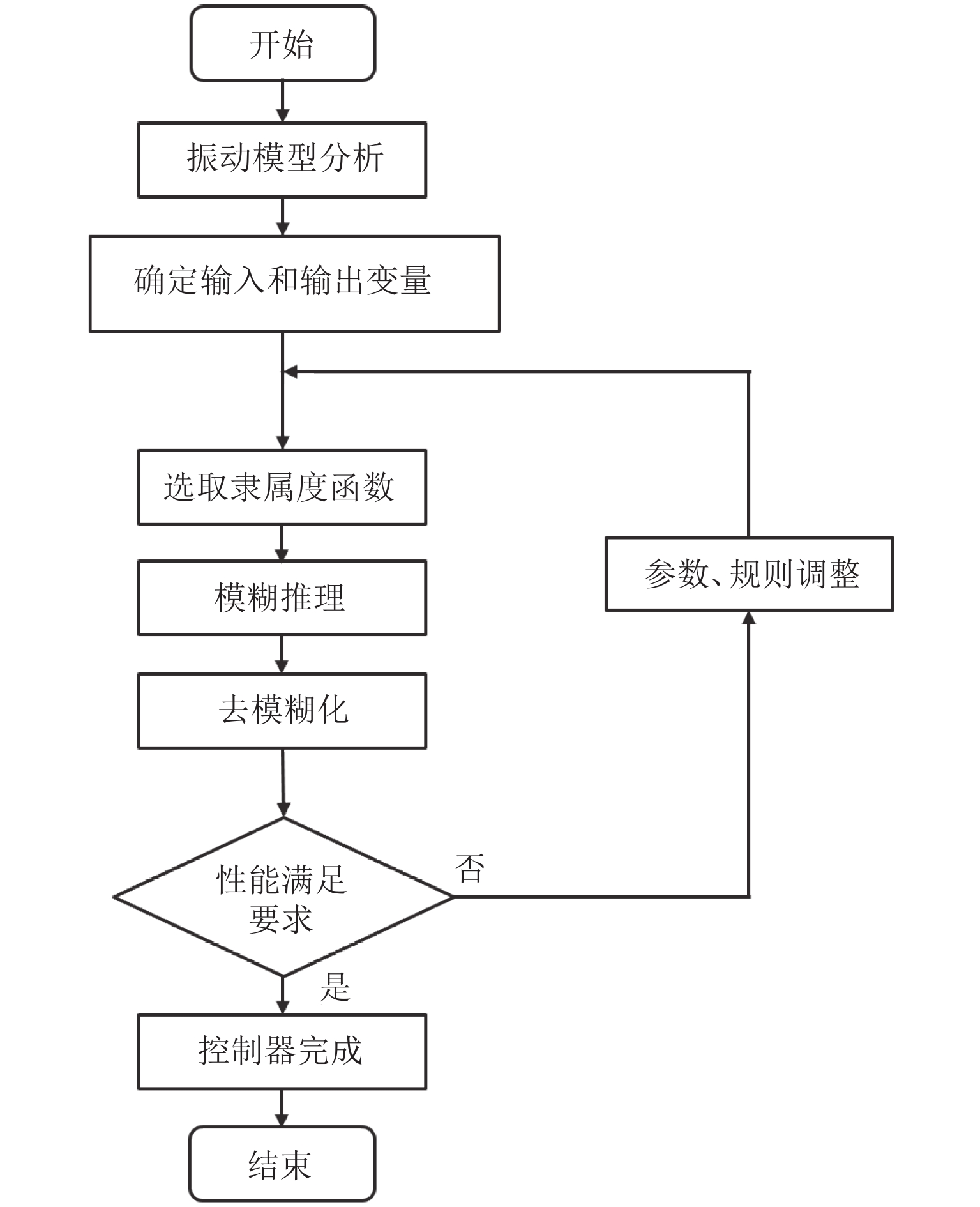
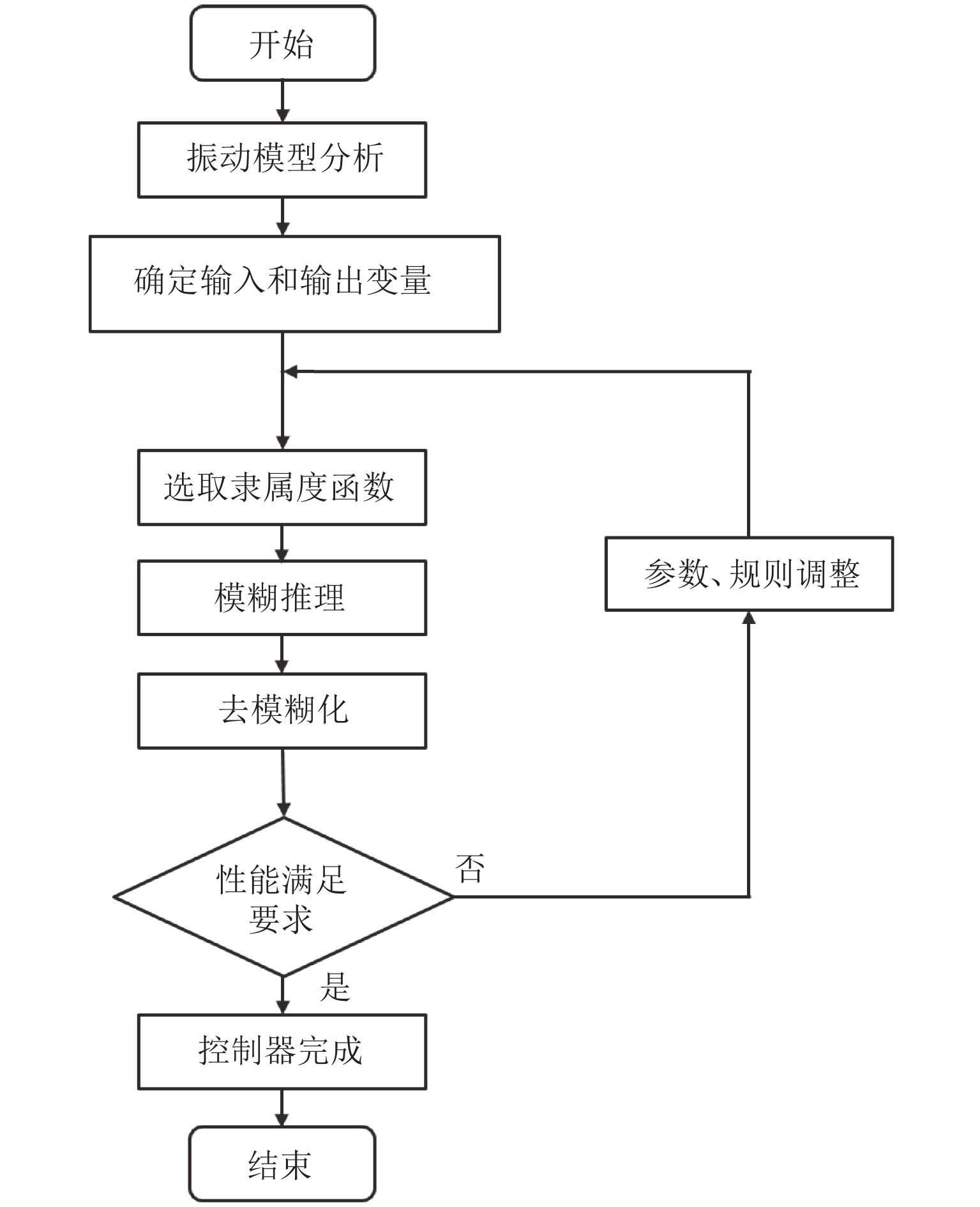
为满足系统全过程、多频段的减振需求,本文设计基于模糊PID算法的振动主动控制策略,完成对现有标称控制器的动态调整与控制参数优化,流程如图7.
基于模糊PID算法的设计原理将误差 e 和误差的变化率δ作为输入,利用调试经验建立规则库,通过模糊规则和去模糊化实时自动更新K_{{\rm{P}}}、K_{{\rm{I}}}、K_{{\rm{D}}}的修正值\Delta K_{{\rm{P}}}、\Delta K_{{\rm{I}}}、\Delta K_{{\rm{D}}}[16].
1) 确定输入和输出变量
分别确定输入输出变量误差 e 、误差变化率 \delta 、控制器输出量\Delta K_{{\rm{P}}}、\Delta K_{{\rm{I}}}和\Delta K_{{\rm{D}}}的取值范围,建立与模糊论域的映射关系. 表3为建立的模糊控制器的参数.
表 3 模糊控制器参数Table 3. Parameters of fuzzy controller模糊变量 基本论域 模糊论域 映射系数 e [−0.0025,0.0025] [−1,1] 400 \delta [−0.05,0.05] [−1,1] 20 \Delta K_{{\rm{P}}} [−5000,5000] [−1,1] 0.0002 \Delta K_{{\rm{I}}} [−10,10] [−1,1] 0.1 \Delta K_{{\rm{D}}} [−50,50] [−1,1] 0.02 2) 选取隶属函数
输入输出变量的大小一般以“大”“中”“小”3个等级进行划分,同时考虑正负方向和零状态,输入输出变量可以划分为7个等级. 因此,输入输出变量的模糊子集为 {正大(PB),正中(PM),正小(PS),零状态(ZE),负小(NS),负中(NM),负大(NB)}. 将输入输出变量模糊化,利用高斯型隶属函数计算输入输出的隶属度[17].
3) 模糊推理
模糊推理过程是基于系统模糊规则进行的,而系统模糊规则的建立基于振动特性规律.
参数K_{{\rm{P}}}主要用于调节整个隔振系统的刚度,刚度与振动误差直接相关,同时也决定隔振系统的调节速度. 因此,修正值\Delta K_{{\rm{P}}}的整定规则如表4.
表 4 \Delta K_{{\rm{P}}}整定规则Table 4. Setting rules of \Delta K_{{\rm{P}}}e δ NB NM NS ZE PS PM PB NB NB NB NM NM NM ZE ZE NM NB NM NM NM NS ZE PS NS NM NM NS NS ZE PS PS ZE NM NS NS ZE PS PS PM PS NS NS ZE PS PS PM PM PM NS ZE PS PM PM PM PB PB ZE ZE PM PM PM PB PB 由于可能存在积分累积,因此,对\Delta K_{{\rm{I}}}进行整定的过程中,如果控制量与设定值偏差较大,取消积分,如果控制量接近给定值,引入积分,从而提高控制精度. 因此,修正值\Delta K_{{\rm{I}}}的整定规则如表5.
表 5 \Delta K_{{\rm{I}}}整定规则Table 5. Setting rules of \Delta K_{{\rm{I}}}e δ NB NM NS ZE PS PM PB NB ZE ZE ZE ZE ZE ZE ZE NM ZE ZE ZE ZE ZE ZE ZE NS PS PS PS PS PS PS PS ZE PS PS PS PS PS PS PS PS PS PS PS PS PS PS PS PM ZE ZE ZE ZE ZE ZE ZE PB ZE ZE ZE ZE ZE ZE ZE 参数K_{{\rm{D}}}主要用于调节整个隔振系统的阻尼,增大阻尼能够快速将消耗外部振动带来的能量,抑制系统的振荡. 因此,修正值\Delta K_{{\rm{D}}}的整定规则如表6.
表 6 \Delta K_{{\rm{D}}}整定规则Table 6. Setting rules of \Delta K_{{\rm{D}}}e δ NB NM NS ZE PS PM PB NB NB NB PM PM PS ZE ZE NM NB NB PM PS PS ZE ZE NS NB NM PS PS ZE NS NS ZE NM NS PS ZE NS NS NM PS NS NS ZE NS NS NM NB PM ZE ZE NS NS NM NB NB PB ZE ZE NS NM NM NB NB 4) 去模糊化
常用的去模糊化的方法有最大隶属度法和加权平均法[18]. 加权平均法是通过一个参数计算出多个隶属度,把隶属度作为权重系数乘以该隶属度的值. 较之于最大隶属度法,加权平均法输出更为平滑,更易于系统的稳定. 因此在去模糊化时,本文采取了加权平均法,如式(17).
{m_0} = \frac{{ \displaystyle\sum\limits_{l = 1}^n {{\mu _{\rm{c}}}\left( {{m_l}} \right){m_l}} }}{{ \displaystyle\sum\limits_{l = 1}^n {{\mu _{\rm{c}}}\left( {{m_l}} \right)} }}\text{,} (17) 式中: m_{0} 为模糊控制器经加权计算后输出的模糊论域中的值; m_{l} 为输出模糊量论域中的值;\mu_{{\rm{c}}}\left(m_{l}\right)为隶属度.
输出变量的模糊论域值经过逆映射后就能变成实际输出\Delta K_{{\rm{P}}}、\Delta K_{{\rm{I}}}、\Delta K_{{\rm{D}}},根据以上建立模糊PID规则,基于模糊PID的主动控制策略设计完成.
2.4 仿真验证
为检验模糊PID算法的实际效果,利用Simulink搭建磁悬浮隔振系统模型,采用幅值随机变化的方法模拟实际外部振动,将设计好的PID控制器与模糊PID控制器分别代入系统模型进行动态仿真. 外部振动频率分别为20、50、100、200、300 Hz和500 Hz,其结果如图8所示.
仿真结果表明,模糊PID算法在不同频率段的外部振动作用下均取得了比传统PID算法更好的隔振效果. 通过主动调节PID参数实现系统等效刚度和阻尼的动态调节,能够有效适应外部振动变化.
3. 准零刚度磁悬浮隔振平台的实现与测试
围绕准零刚度磁悬浮隔振平台的实现与测试,需要基于Speedgoat实时目标机开发振动主动控制系统,搭建隔振测试平台,开展隔振性能测试,以验证基于模糊PID控制策略的准零刚度磁悬浮隔振平台的隔振效果.
3.1 基于Speedgoat的主动振动控制系统
为实时测量被隔振对象的位移和加速度,准零刚度磁悬浮隔振平台需要安装位移传感器和加速度传感器. 考虑到位移传感器固定在被隔振对象上,而被隔振对象处于振动过程中,因此,位移传感器采用非接触式的TR81系列电涡流传感器,加速度传感器采用YA23型ICP高灵敏度加速度传感器.
控制器是主动振动控制系统的核心. 为了便于准零刚度磁悬浮隔振平台的现场调试,实时在线观测系统状态,提高调试效率,本文基于Speedgoat实时目标机开发振动主动控制系统,控制器根据传感器检测到的位移和加速度信息,经过上面设计的基于模糊PID主动控制策略的计算,改变电压和电流的大小和方向,进而改变永磁电磁混合作动器的磁场强度,动态调节隔振平台的刚度和阻尼,最终满足系统全过程、多频段的减振需求.
为提供外部振动条件,本文采用苏式DC-600-6型振动台作为外部振动源,搭建隔振测试平台,开展一系列的隔振性能测试.
3.2 隔振测试
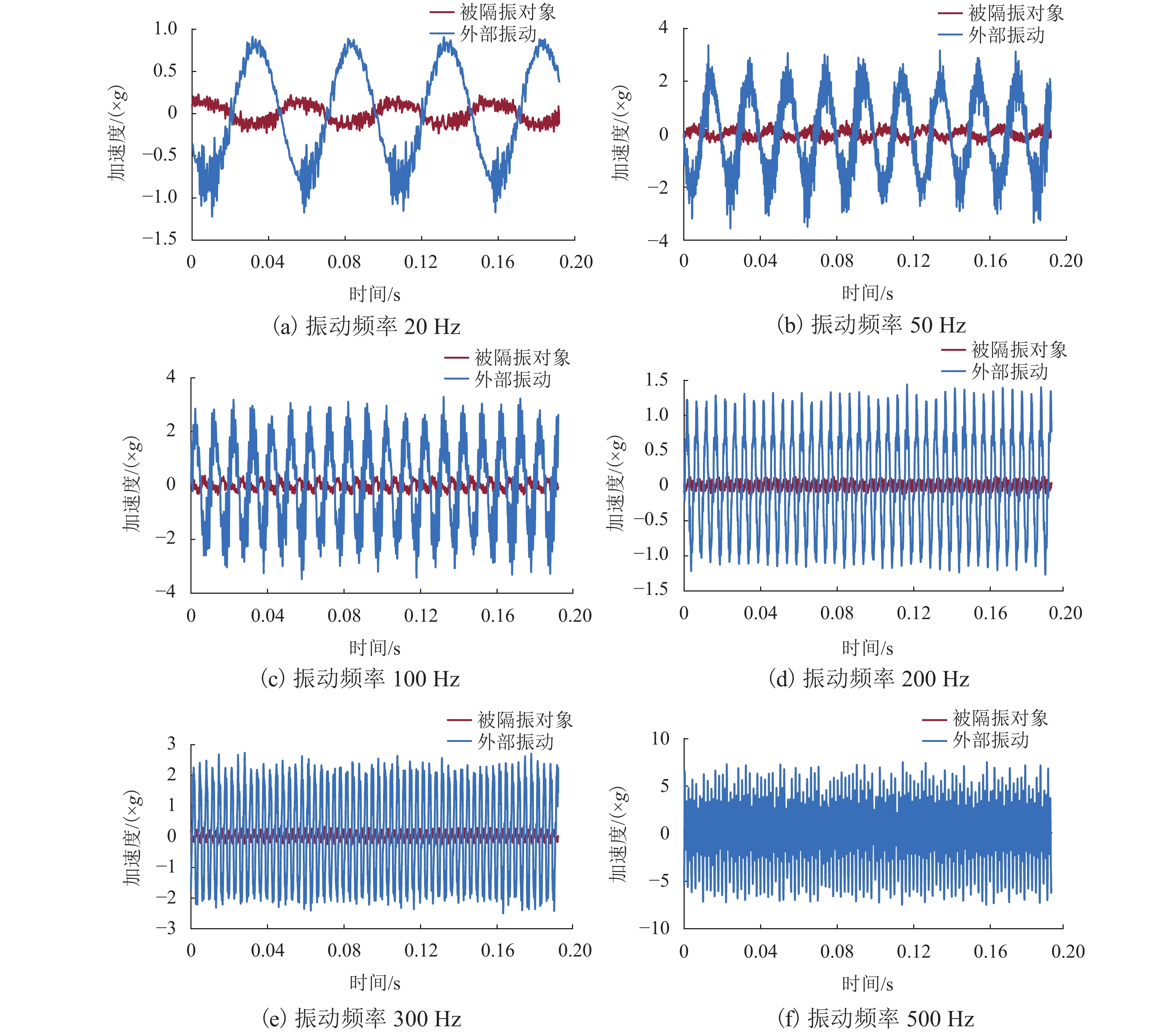
为开展隔振性能测试,试验中振动台分别设定振动频率为20、50、100、200、300 Hz和500 Hz、最大振幅为2.5 mm的伪正弦随机振动,准零刚度磁悬浮隔振平台的隔振效果如图9所示.
结果表明,本文设计的准零刚度磁悬浮隔振平台在不同频率段的外部振动作用下均取得了较好的隔振效果,实现了外部振动在多频段的强衰减.
为评估本文设计的准零刚度磁悬浮隔振平台的隔振能力,采用振级落差法计算系统的振动衰减率和振动传递率. 表7为准零刚度磁悬浮隔振平台在20、50、100、200、300 Hz和500 Hz频率下的振动衰减率和振动传递率.
表 7 振动衰减率和振动传递率Table 7. Vibration attenuation rate and vibration transmission rate振动频率/Hz 振动衰减率/% 振动传递率/dB 20 83.64 −15.72 50 90.55 −19.83 100 91.91 −21.84 200 92.60 −22.61 300 93.52 −23.77 500 95.35 −26.66 4. 结 论
本文以永磁电磁混合作动器为负刚度结构提出并设计了一种准零刚度的磁悬浮隔振平台,设计了基于模糊PID算法的振动主动控制策略,完成了系统等效刚度和阻尼的主动调节,基于Speedgoat实时目标机开发了振动主动控制系统,搭建了隔振测试平台,开展了一系列的隔振性能测试. 结果表明:外部振动频率在20~100 Hz频率段内,振动衰减大于80%;外部振动频率在100~500 Hz频率段内,振动衰减率大于90%. 基于模糊PID控制的准零刚度磁悬浮隔振平台在不同频率段的外部振动作用下均取得了较好的隔振效果,实现了外部振动在多频段的强衰减.
-
表 1 永磁体具体参数
Table 1. Detailed parameters of permanent magnet
参数名称 参数符号 参数值 剩余磁感应强度/T Br 1.2 矫顽力/(kA•m−1) Hc 896 相对磁导率 \mu_{{\rm{r}}} 1.05 表 2 永磁体在工作点附近产生的电磁吸力
Table 2. Electromagnetic attraction generated by permanent magnet near working point
N 永磁体
厚度/mm悬浮间隙/mm 9.5 10.0 10.5 7 465.1 430.4 399.0 8 532.5 493.9 459.3 9 595.4 553.1 515.6 10 652.2 608.9 567.8 11 705.5 658.7 615.3 12 753.2 704.2 659.3 13 797.1 747.0 699.9 表 3 模糊控制器参数
Table 3. Parameters of fuzzy controller
模糊变量 基本论域 模糊论域 映射系数 e [−0.0025,0.0025] [−1,1] 400 \delta [−0.05,0.05] [−1,1] 20 \Delta K_{{\rm{P}}} [−5000,5000] [−1,1] 0.0002 \Delta K_{{\rm{I}}} [−10,10] [−1,1] 0.1 \Delta K_{{\rm{D}}} [−50,50] [−1,1] 0.02 表 4 \Delta K_{{\rm{P}}}整定规则
Table 4. Setting rules of \Delta K_{{\rm{P}}}
e δ NB NM NS ZE PS PM PB NB NB NB NM NM NM ZE ZE NM NB NM NM NM NS ZE PS NS NM NM NS NS ZE PS PS ZE NM NS NS ZE PS PS PM PS NS NS ZE PS PS PM PM PM NS ZE PS PM PM PM PB PB ZE ZE PM PM PM PB PB 表 5 \Delta K_{{\rm{I}}}整定规则
Table 5. Setting rules of \Delta K_{{\rm{I}}}
e δ NB NM NS ZE PS PM PB NB ZE ZE ZE ZE ZE ZE ZE NM ZE ZE ZE ZE ZE ZE ZE NS PS PS PS PS PS PS PS ZE PS PS PS PS PS PS PS PS PS PS PS PS PS PS PS PM ZE ZE ZE ZE ZE ZE ZE PB ZE ZE ZE ZE ZE ZE ZE 表 6 \Delta K_{{\rm{D}}}整定规则
Table 6. Setting rules of \Delta K_{{\rm{D}}}
e δ NB NM NS ZE PS PM PB NB NB NB PM PM PS ZE ZE NM NB NB PM PS PS ZE ZE NS NB NM PS PS ZE NS NS ZE NM NS PS ZE NS NS NM PS NS NS ZE NS NS NM NB PM ZE ZE NS NS NM NB NB PB ZE ZE NS NM NM NB NB 表 7 振动衰减率和振动传递率
Table 7. Vibration attenuation rate and vibration transmission rate
振动频率/Hz 振动衰减率/% 振动传递率/dB 20 83.64 −15.72 50 90.55 −19.83 100 91.91 −21.84 200 92.60 −22.61 300 93.52 −23.77 500 95.35 −26.66 -
[1] ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273. doi: 10.1016/j.jsv.2009.11.001 [2] REN C, YANG D, QIN H. Mechanical performance of multidirectional buckling-based negative stiffness metamaterials: an analytical and numerical study[J]. Materials, 2018, 11(7): 1078.1-1078.19. [3] 张磊. 电磁主动隔振系统建模与控制方法研究[D]. 武汉: 武汉大学, 2020. [4] YAN B, YU N, WU C Y. A state-of-the-art review on low-frequency nonlinear vibration isolation with electromagnetic mechanisms[J]. Applied Mathematics and Mechanics, 2022, 43(7): 1045-1062. doi: 10.1007/s10483-022-2868-5 [5] ZHANG F, SHAO S B, TIAN Z, et al. Active-passive hybrid vibration isolation with magnetic negative stiffness isolator based on Maxwell normal stress[J]. Mechanical Systems and Signal Processing, 2019, 123: 244-263. doi: 10.1016/j.ymssp.2019.01.022 [6] 沈铖武. 车载光电瞄准平台主被动隔振关键技术研究[D]. 北京: 中国科学院大学, 2021. [7] 黄翠翠,李晓龙,杨洋,等. 基于自抗扰技术的机械-电磁悬浮复合隔振控制[J]. 西南交通大学学报,2022,57(3): 582-587,617. doi: 10.3969/j.issn.0258-2724.20210850HUANG Cuicui, LI Xiaolong, YANG Yang, et al. Mechanical-electromagnetic suspension compound vibration isolation control based on active disturbance rejection technology[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 582-587,617. doi: 10.3969/j.issn.0258-2724.20210850 [8] CARRELLA A, BRENNAN M, KOVACIC I, et al. On the force transmissibility of a vibration isolator with quasi-zero stiffness[J]. Journal of Sound and Vibration, 2009, 322(4): 707-717. [9] 苏攀,吴杰长,刘树勇,等. 弹簧-电磁力准零刚度隔振器研究[J]. 海军工程大学学报,2018,30(5): 36-41.SU Pan, WU Jiechang, LIU Shuyong, et al. Spring-electromagnetic force vibration isolator with quasi-zero-stiffness[J]. Journal of Naval University of Engineering, 2018, 30(5): 36-41. [10] 江友亮. 磁气混合准零刚度隔振系统设计与控制研究[D]. 武汉: 武汉理工大学, 2019. [11] XU J W, YANG X F, LI W, et al. Research on semi-active vibration isolation system based on electromagnetic spring[J]. Mechanics & Industry, 2020, 21(1): 101.1-101.12. [12] ZHANG L, ZHUAN X T. An experimental study of an electromagnetic isolator system with active control[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 61(3): 329-340. doi: 10.3233/JAE-180112 [13] 邹圣楠,刘畅,邓舒同,等. 基于混合式磁浮平台的解耦及控制分析[J]. 西南交通大学学报,2022,57(3): 40-548.ZOU Shengnan, LIU Chang, DENG Shutong, et al. Decoupling and control stability analysis based on hybrid repulsion maglev platform[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 40-548. [14] HU Y F, CHEN C H, WU H C, et al. Study on structural optimization design and cascade PID control of maglev actuator for active vibration isolation system[J]. Journal of Vibration and Control, 2018, 24(10): 1829-1847. doi: 10.1177/1077546317714939 [15] SUN Y G, XU J Q, WU H, et al. Deep learning based semi-supervised control for vertical security of maglev vehicle with guaranteed bounded airgap[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(7): 4431-4442. doi: 10.1109/TITS.2020.3045319 [16] MITRA P, DEY C, MUDI R K. Fuzzy rule-based set point weighting for fuzzy PID controller[J]. SN Applied Sciences, 2021, 3(6): 1-34. [17] YANG T, SUN N, FANG Y C. Adaptive fuzzy control for a class of MIMO underactuated systems with plant uncertainties and actuator deadzones: design and experiments[J]. IEEE Transactions on Cybernetics, 2022, 52(8): 8213-8226. doi: 10.1109/TCYB.2021.3050475 [18] WANG H Q, LIU P X, ZHAO X D, et al. Adaptive fuzzy finite-time control of nonlinear systems with actuator faults[J]. IEEE Transactions on Cybernetics, 2019, 50(5): 1786-1797. 期刊类型引用(8)
1. 段振云, 刘洋, 孙凤, 史策, 徐方超, 金俊杰, 张晓友, 陈熙. 磁悬浮直驱式无油涡旋压缩机模糊PID控制研究. 西南交通大学学报. 2025(04)  本站查看
本站查看2. 唐晓轩, 杜国伟, 孙喆, 赵雷. HTR-PM主氦风机转子系统响应分析与载荷优化. 西南交通大学学报. 2025(04)  本站查看
本站查看3. 铁世萃,王花兰. 考虑不同载荷的准零刚度运输隔振系统设计. 包装工程. 2025(05): 221-227 .  百度学术
百度学术4. 李汞,李逸健,田仁聪,翁德庆. 有色金属矿山横切割头掘进机械残余振动控制方法. 机械设计与制造工程. 2024(05): 51-55 .  百度学术
百度学术5. 张明,李洪涛,崔浩东,孙凤,徐方超,张磊. 一种电磁式高静-低动刚度隔振系统建模与特性分析. 西南交通大学学报. 2024(04): 858-866 .  本站查看
本站查看6. 颜枫,窦硕,陈骝. 准零刚度磁悬浮隔振平台主动混合控制系统设计. 计算机测量与控制. 2024(08): 222-227 .  百度学术
百度学术7. 孟祥瑞,王常虹,钟佳朋,夏红伟. 一种应用于精密隔振平台的双曲线磁通磁轴承设计. 中国惯性技术学报. 2024(10): 1025-1034+1042 .  百度学术
百度学术8. 杨焕峥,崔业梅,徐玲. 基于BSO算法及MBD开发的磁悬浮PID控制系统. 制造业自动化. 2023(11): 133-136 .  百度学术
百度学术其他类型引用(4)
-






 下载:
下载:








 下载:
下载:




 百度学术
百度学术