Correction of Magnetic Force of Hybrid Electromagnet Based on Magnetic Flux Leakage Compensation
-
摘要:
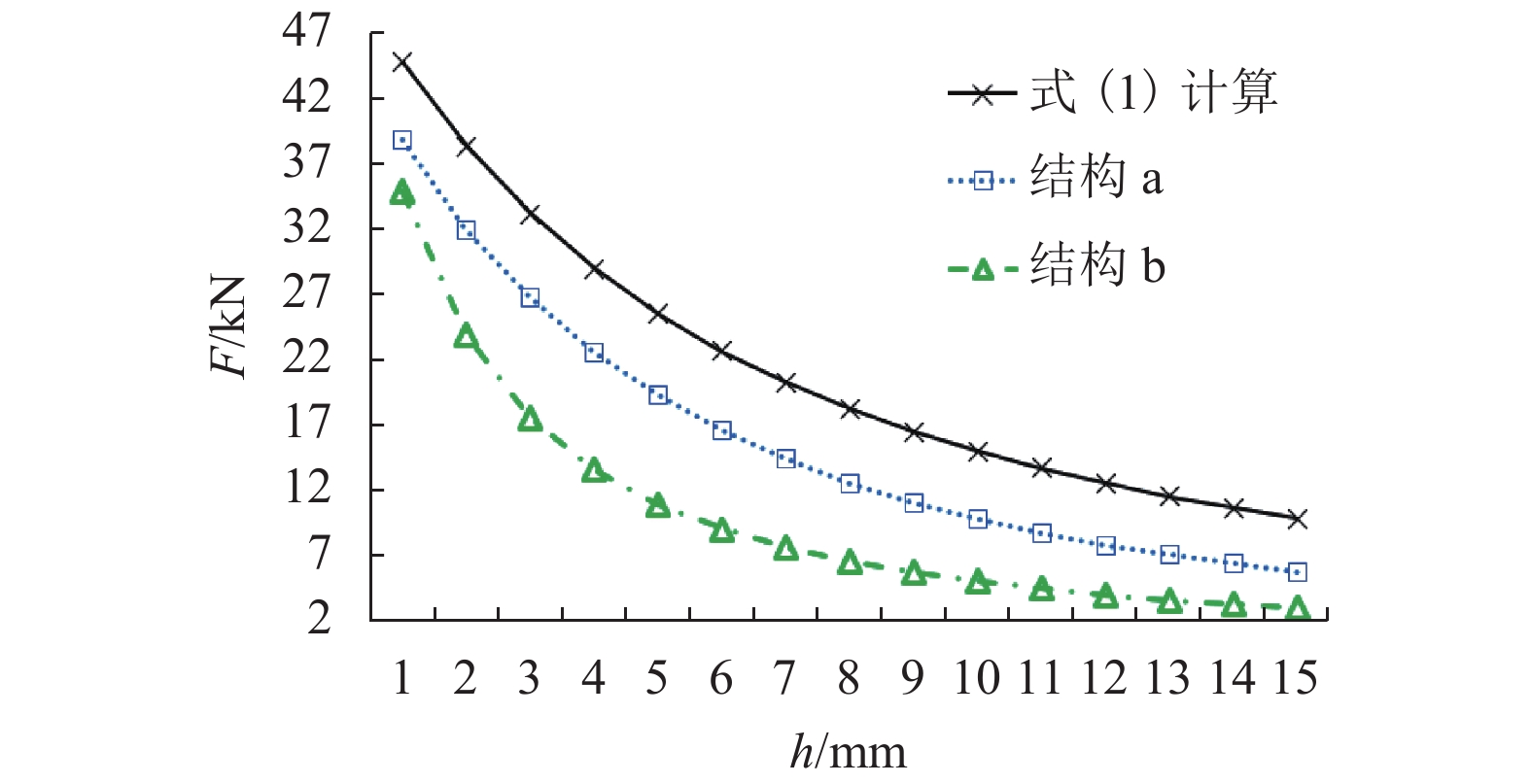
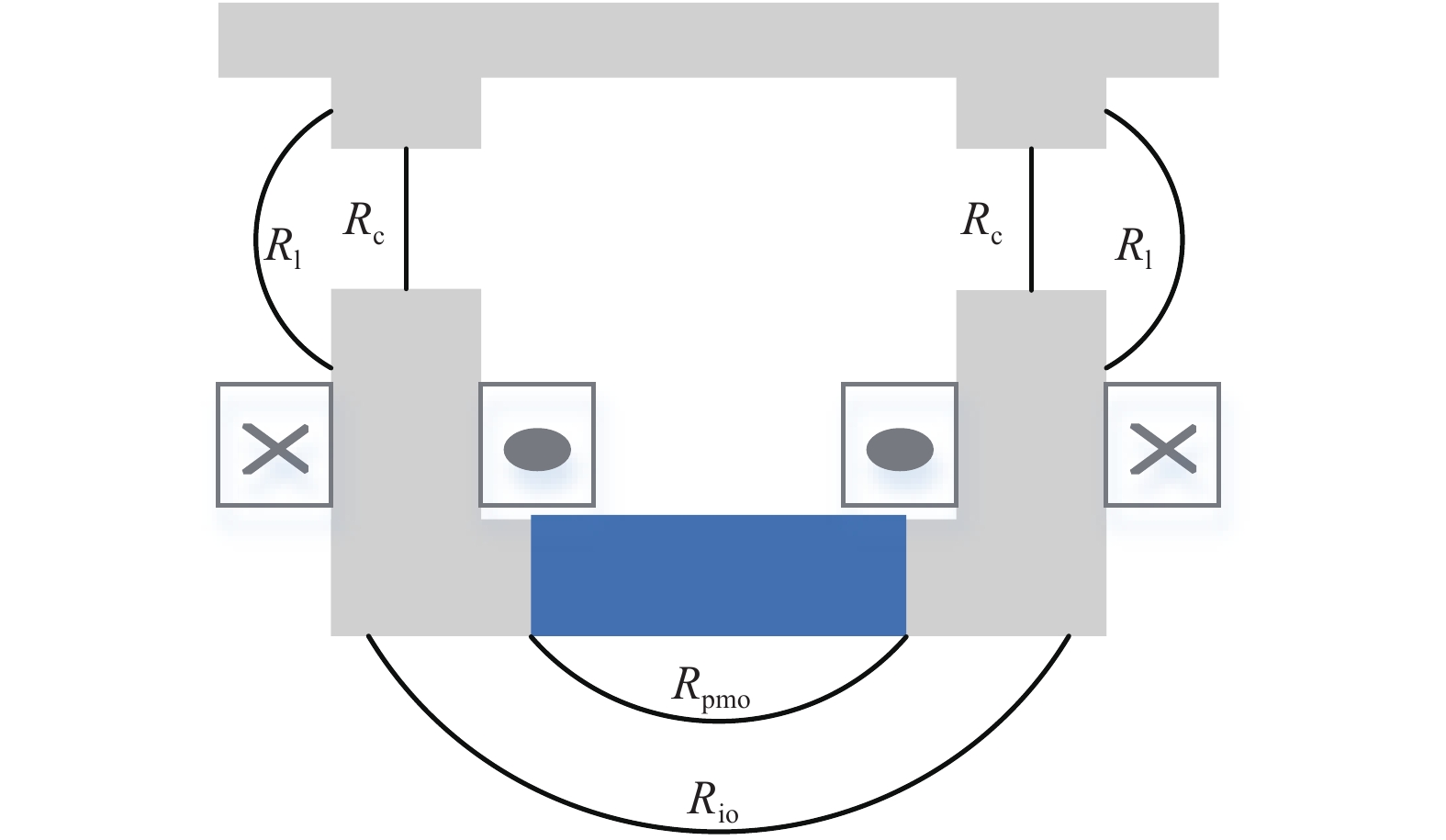
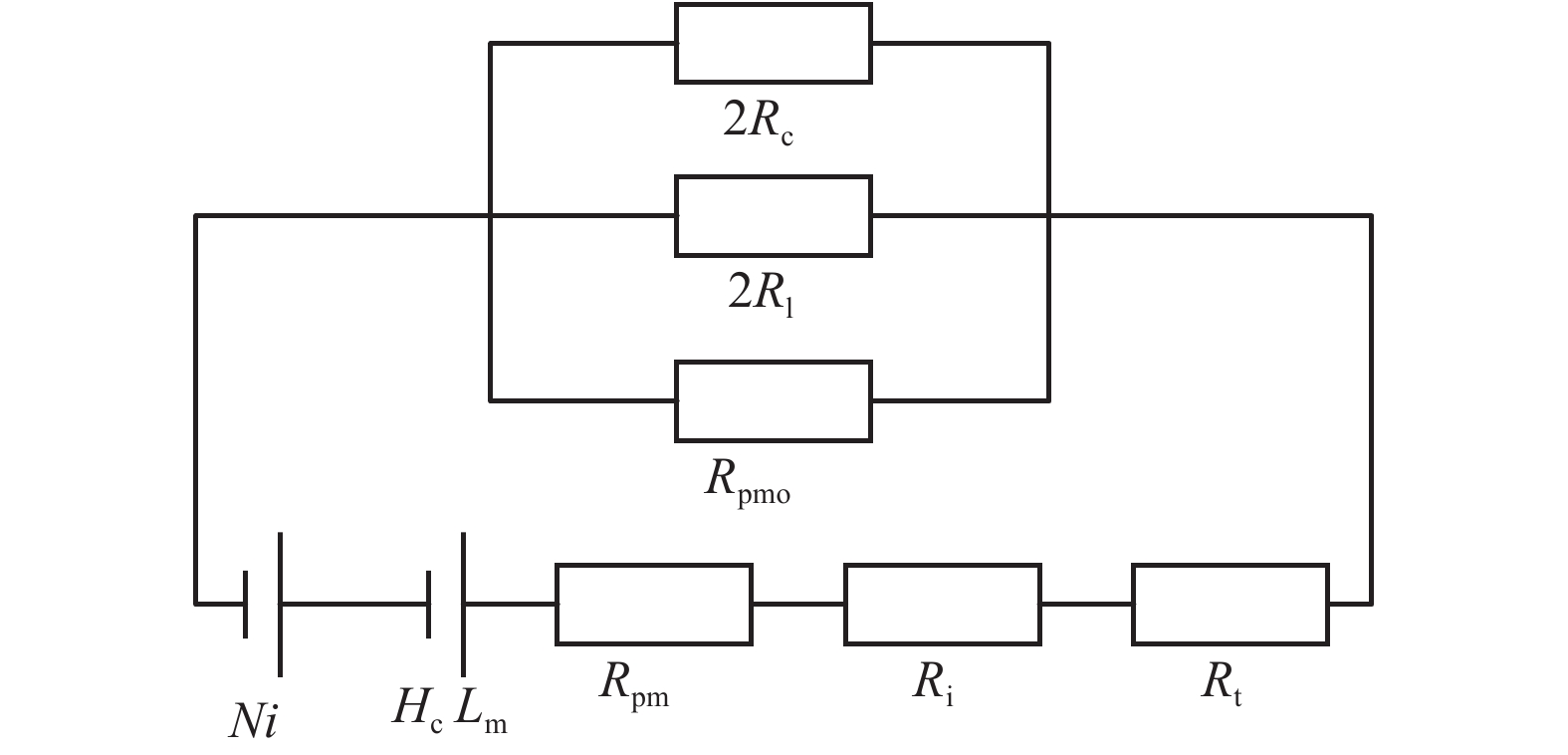
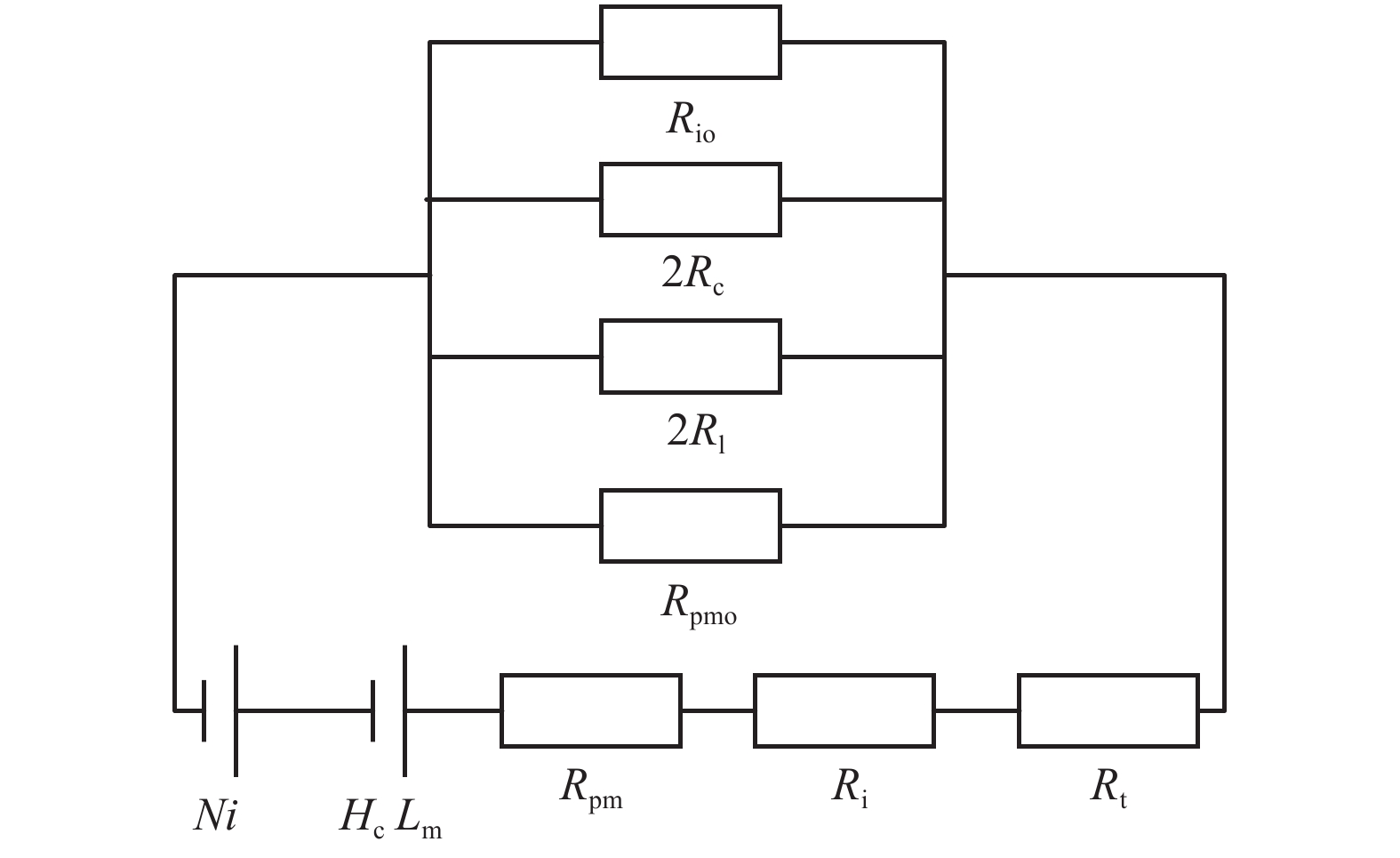
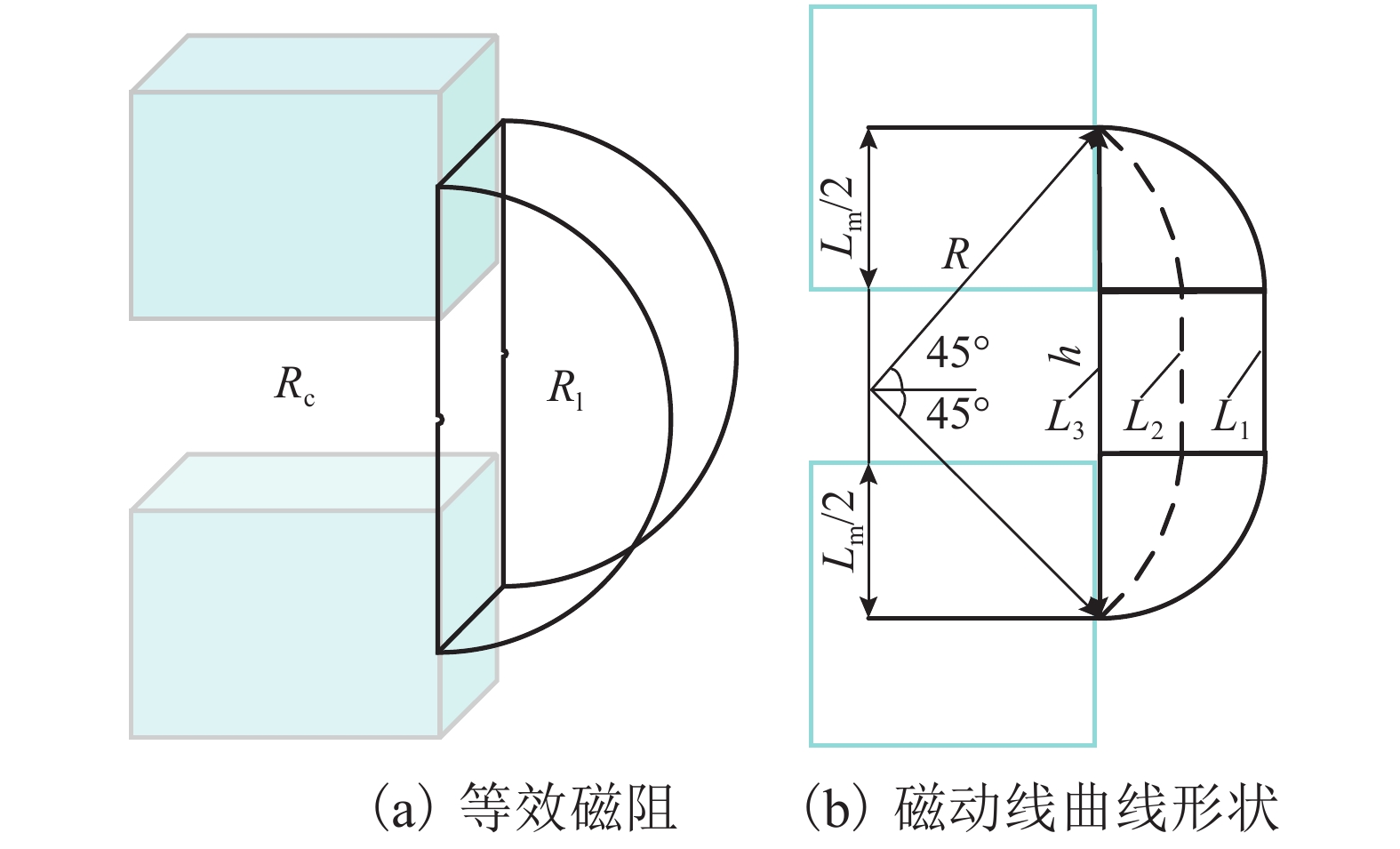
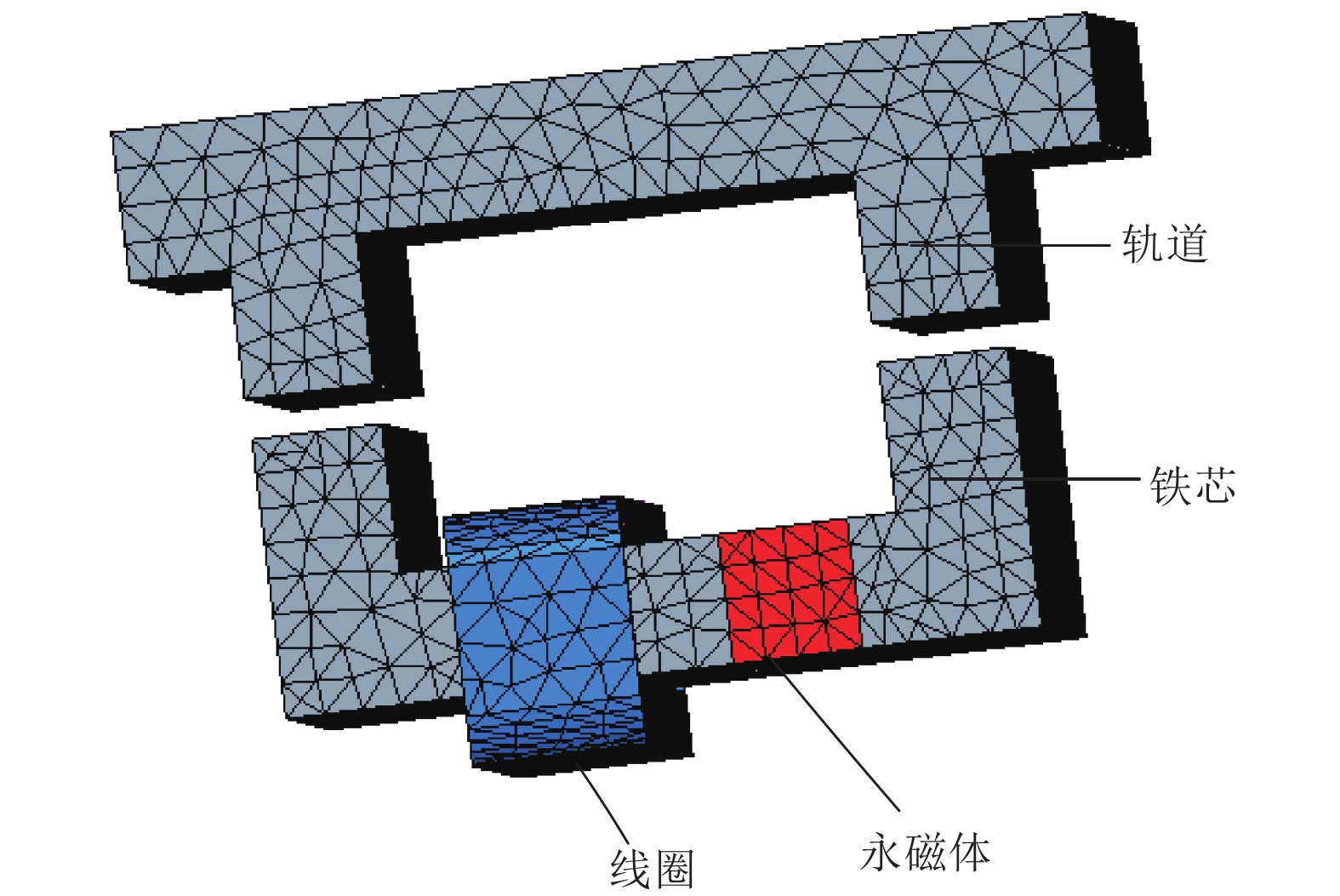
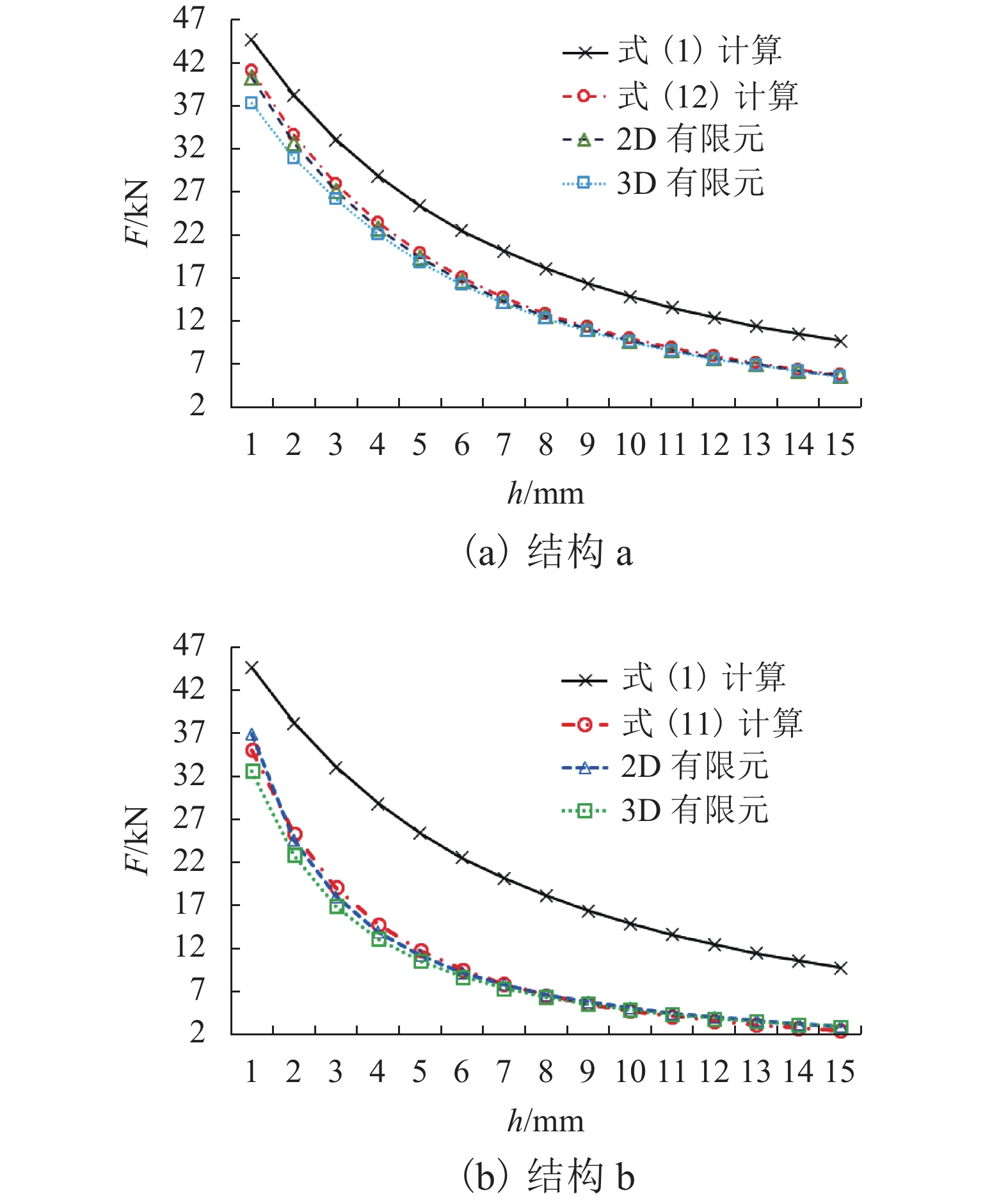
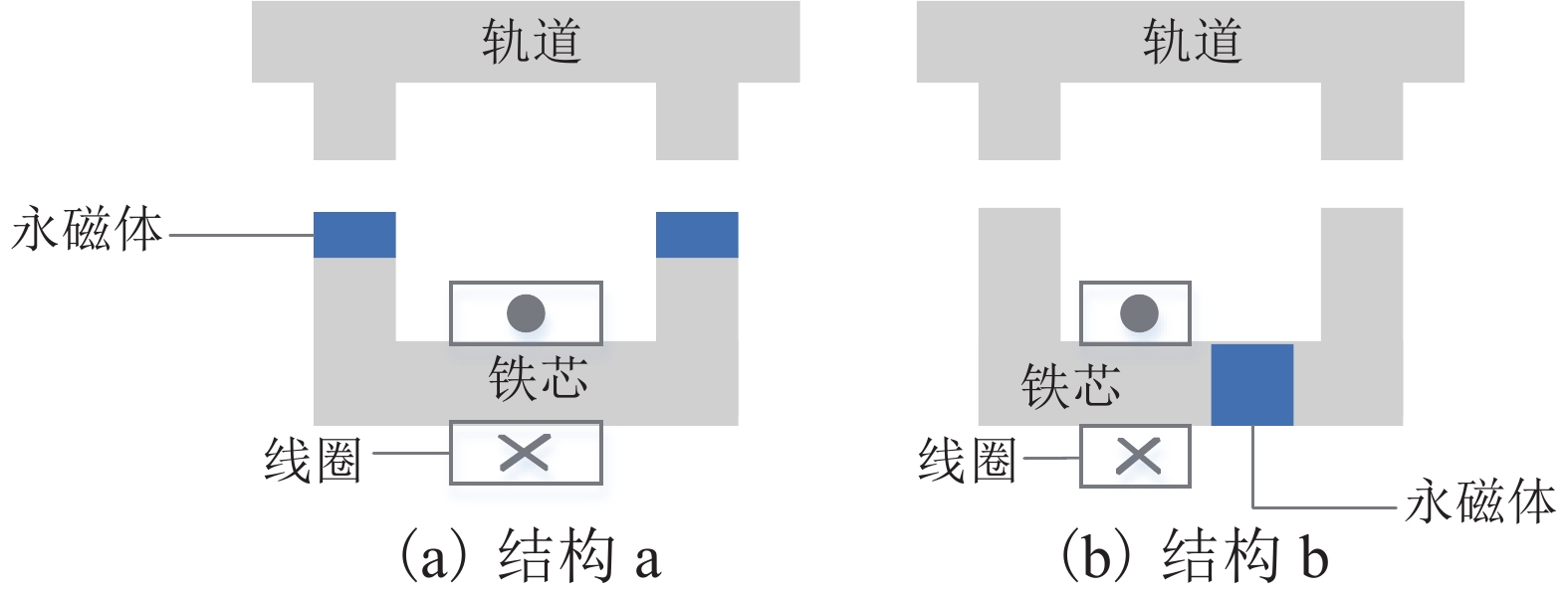
电磁永磁混合磁铁的悬浮磁力具有强非线性特点，与磁铁结构密切相关，而现有混合磁铁磁力解析计算公式忽略了磁路漏磁等因素影响，在实际计算中存在较大误差. 针对这一问题，建立了两种常用混合磁铁结构的磁路模型，分析了边缘磁通分布、磁路漏磁对磁铁工作磁路的影响，推导了两种混合磁铁的磁路方程及相关磁阻，提出了一种新的混合磁铁磁力修正计算方法，最终通过有限元分析对两种结构的混合磁铁磁力进行了验证. 研究结果表明：由于悬浮气隙较大，电磁永磁混合磁铁在电磁力计算中漏磁影响不能忽略；采用本文磁力修正公式计算，两种混合结构电磁力误差分别降低为3.8%和8.3%.
Abstract:The suspension magnetic force of electro-permanent magnets features strong nonlinearity, which is closely related to the magnet structure. The existing analytical calculation formula for magnetic force of the hybrid magnet ignores the influence of magnetic circuit leakage and some other factors, consequently resulting in big errors in actual calculations. To solve this problem, two common hybrid magnetic circuit models are established to analyze the influence of edge magnetic flux distribution and magnetic circuit leakage on the working magnetic circuit of the magnet. On this basis, the magnetic circuit equations and related reluctance of the two hybrid magnets are deduced, and a corrected calculation method of the hybrid ferromagnetic force is put forward. Finally, the corrected magnetic force of the hybrid magnets with the two structures is verified by finite element analysis. The results show that due to the large suspension air gap, the influence of magnetic flux leakage of an electro-permanent magnet cannot be ignored in the calculation of electromagnetic force. Using the magnetic force correction formula proposed in this paper, the electromagnetic force errors of magnets with the above two hybrid structures are reduced to 3.8% and 8.3%, respectively.
-
图 2 有限元电磁力计算结果
Figure 2. Calculated results of magnetic force by finite element method
-
[1] TZENG Y K, TSIH C W. Optimal design of the electromagnetic levitation with permanent and electro magnets[J]. IEEE Transactions on Magnetics, 1994, 30(6): 4731-4733. [2] TZENG Y K, TSIH C W. A novel compensating approach for self-sensing maglev system with controlled-PM electromagnets[J]. IEEE Transactions on Magnetics, 1995, 31(6): 4208-4210. [3] CHO H W, HAN H S, LEE J M, et al. Design considerations of EM-PM hybrid levitation and propulsion device for magnetically levitated vehicle[J]. IEEE Transactions on Magnetics, 2009, 45(1): 4632-4635. [4] 王莉. 混合EMS磁悬浮系统研究[D]. 成都: 西南交通大学, 2006. [5] MORISHITA M, AZUKIZAWA T, KANDA S. A new maglev system for magnetically levitated carrier system[J]. IEEE Transactions on Vehicular Technology, 1989, 38(4): 230-236. doi: 10.1109/25.45486 [6] 徐正国. 电磁永磁混合悬浮磁悬浮模型车控制方案的研究[D]. 北京: 中国科学院电工研究所, 2005. [7] 刘佳兴. 磁悬浮系统的滑模控制研究[D]. 哈尔滨: 哈尔滨理工大学, 2020. [8] 李云钢,陈树文,陈慧星. 基于超稳定性的混合磁浮系统控制器设计[J]. 控制工程,2010,17(2): 158-161. doi: 10.3969/j.issn.1671-7848.2010.02.009LI Yungang, CHEN Shuwen, CHEN Huixing. Controller design of hybrid maglev systems based on hyper-stability[J]. Control Engineering of China, 2010, 17(2): 158-161. doi: 10.3969/j.issn.1671-7848.2010.02.009 [9] 李卫东,王玮崧,王新屏. 磁悬浮列车简捷鲁棒控制与仿真研究[J]. 电子测量技术,2021,44(2): 56-60.LI Weidong, WANG Weisong, WANG Xinping. Research on simple and robust control and simulation of maglev train[J]. Electronic Measurement Technology, 2021, 44(2): 56-60. [10] WAI R, YAO J, LEE J. Design of back stepping fuzzy-neural-network control for hybrid maglev transportation system[C]//7th International Conference on Advanced Computational Intelligence. Wuxi: IEEE, 2015, 38-43 [11] WAI R J, CHEN M W, YAO J X. Observer-based adaptive fuzzy-neural-network control for hybrid maglev transportation system[J]. Neurocomputing, 2016, 175: 10-24. doi: 10.1016/j.neucom.2015.10.006 [12] 陈贵荣,刘少克,郝阿明. 中低速磁浮列车用混合电磁铁设计分析[J]. 都市快轨交通,2013,26(3): 73-76. doi: 10.3969/j.issn.1672-6073.2013.03.019CHEN Guirong, LIU Shaoke, HAO Aming. Design and analysis of the hybrid electromagnet for medium-low-speed maglev trains[J]. Urban Rapid Rail Transit, 2013, 26(3): 73-76. doi: 10.3969/j.issn.1672-6073.2013.03.019 [13] LIU S K, AN B, LIU S K, et al. Characteristic research of electromagnetic force for mixing suspension electromagnet used in low-speed maglev train[J]. Iet Electric Power Applications, 2015, 9(3): 223-228. doi: 10.1049/iet-epa.2013.0414 [14] 金森,刘国清,余思儒,等. 基于不等宽结构的混合型悬浮装置的研究[J]. 机车电传动,2016(5): 32-34.JIN Sen, LIU Guoqing, YU Siru, et al. Hybrid suspension system based on the unequal width structure[J]. Electric Drive for Locomotives, 2016(5): 32-34. [15] 李强, 唐敬虎, 孙凤, 等. 可变磁路式永磁悬浮系统的防跌落防吸附控制[J]. 仪器仪表学报, 2019, 40(3): 246-254.LI Qiang, TANG Jinghu, SUN Feng, et al. Anti-fall and anti-adsorption control of permanent magnetismlevitation system with flux path control[J]. Chinese Journal of Scientific Instrument, 2019, 40(3): 246-254. [16] 李云钢,闫宇壮,程虎. 混合EMS型磁浮列车的悬浮磁铁设计与分析[J]. 国防科技大学学报,2006,28(5): 94-98. doi: 10.3969/j.issn.1001-2486.2006.05.019LI Yungang, YAN Yuzhuang, CHENG Hu. Design and analysis of the hybrid magnet in ems maglev vehicles[J]. Journal of National University of Defense Technology, 2006, 28(5): 94-98. doi: 10.3969/j.issn.1001-2486.2006.05.019 [17] SAFAEI F, SURATGAR A A, AFSHAR A, et al. Characteristics optimization of the maglev train hybrid suspension system using genetic algorithm[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 1163-1170. doi: 10.1109/TEC.2014.2388155 [18] ZHANG Z, SHANG C, SHE L, et al. Structural optimal design of a permanent-electro magnetic suspension magnet for middle-low-speed maglev trains[J]. IET Electrical Systems in Transportation, 2011, 1(2): 61-68. doi: 10.1049/iet-est.2010.0018 [19] 张志洲,佘龙华,张玲玲,等. 考虑多约束条件的磁浮列车节能型永磁电磁磁铁优化设计[J]. 机械工程学报,2012,48(2): 146-152. doi: 10.3901/JME.2012.02.146ZHANG Zhizhou, SHE Longhua, ZHANG Lingling, et al. Optimal design of energy-saving permanent-electro magnet for maglev train with multi-restricted conditions[J]. Journal of Mechanical Engineering, 2012, 48(2): 146-152. doi: 10.3901/JME.2012.02.146 [20] SONG X, ZHANG K L, LIU G Q, et al. Optimal design of a for middle-low-speed maglev[J]. Open Physics, 2018, 16(1): 168-173. doi: 10.1515/phys-2018-0024 [21] 郭忠君. 中低速磁浮列车用混合悬浮电磁铁的电磁特性分析[D]. 长沙: 国防科学技术大学, 2008. [22] 甘淘利,宋春生,丁成苗. 混合磁悬浮隔振平台径向磁力模型研究[J]. 数字制造科学,2020,18(2): 143-147.GAN Taoli, SONG Chunsheng, DING Chengmiao. Research on radial magnetism model of hybrid maglev vibration isolating platform[J]. Digital Manufacture Science, 2020, 18(2): 143-147. [23] 罗华军,李文龙,方心宇,等. 混合EMS磁悬浮系统的悬浮力分析[J]. 低温与超导,2021,49(9): 21-25.LUO Huajun, LI Wenlong, FANG Xinyu, et al. Suspension force analysis of a hybrid EMS maglev system[J]. Cryogenics & Superconductivity, 2021, 49(9): 21-25. [24] 刘少克. 磁浮列车用悬浮电磁铁温度场三维建模与仿真[J]. 系统仿真学报,2013,25(5): 1118-1122.LIU Shaoke. 3D Modeling and simulation of temperature field for suspension electromagnet of maglev vehicle[J]. Journal of System Simulation, 2013, 25(5): 1118-1122. [25] JIAN L N, XU G Q, MI C C, et al. Analytical method for magnetic field calculation in a low-speed permanent-magnet harmonic machine[J]. IEEE Transactions on Energy Conversion, 2011, 26(3): 862-870. doi: 10.1109/TEC.2011.2140373 [26] 林其壬, 赵佑民. 磁路设计原理[M]. 北京: 机械工业出版社, 1987. -
下载:
点击查看大图
计量
- 文章访问数: 252
- HTML全文浏览量: 100
- PDF下载量: 13
- 被引次数: 0