Traffic Equilibrium Model of Reliable Network Based on Bounded Rationality
-
摘要:
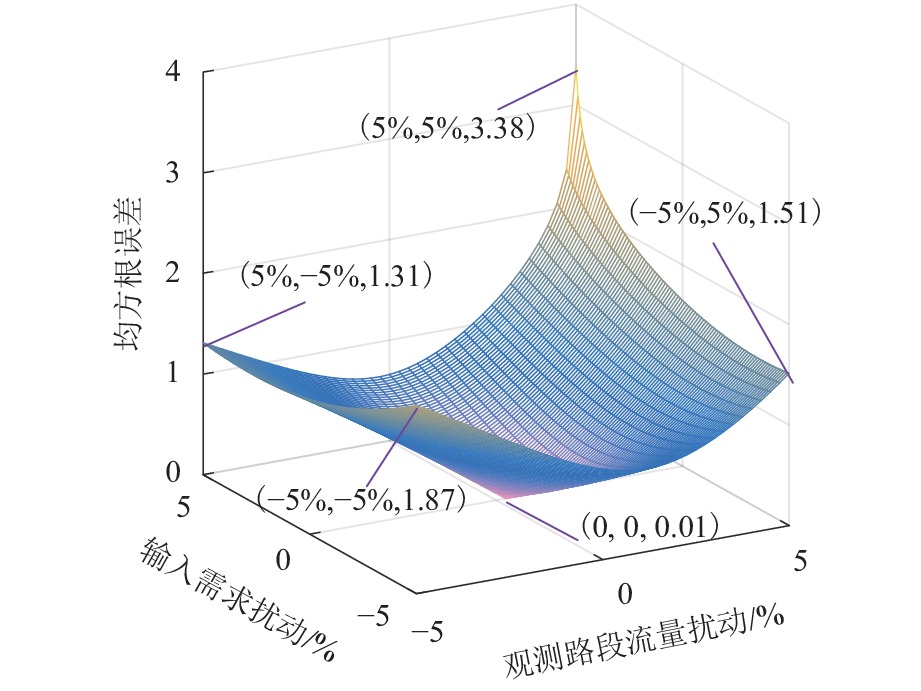
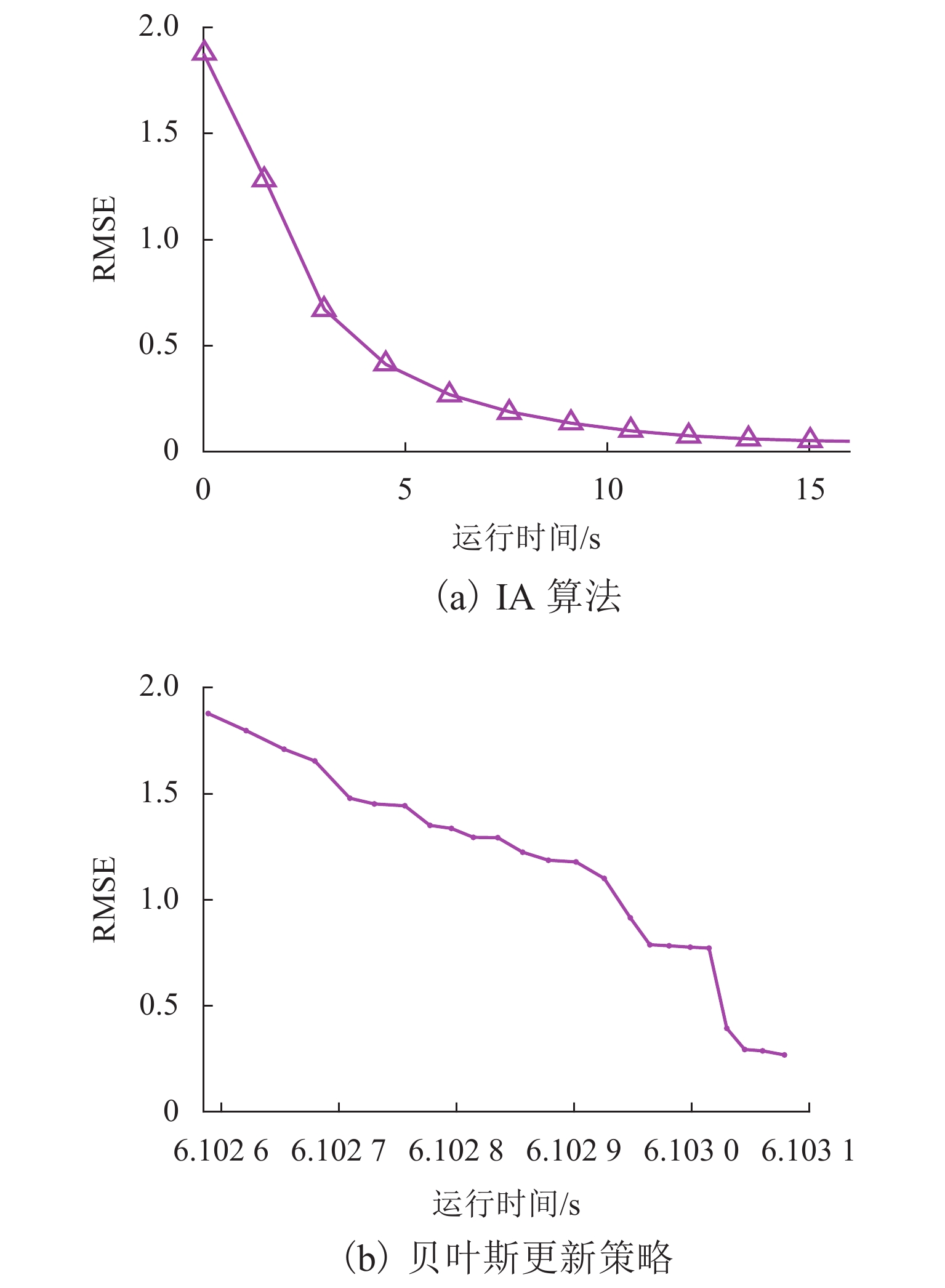
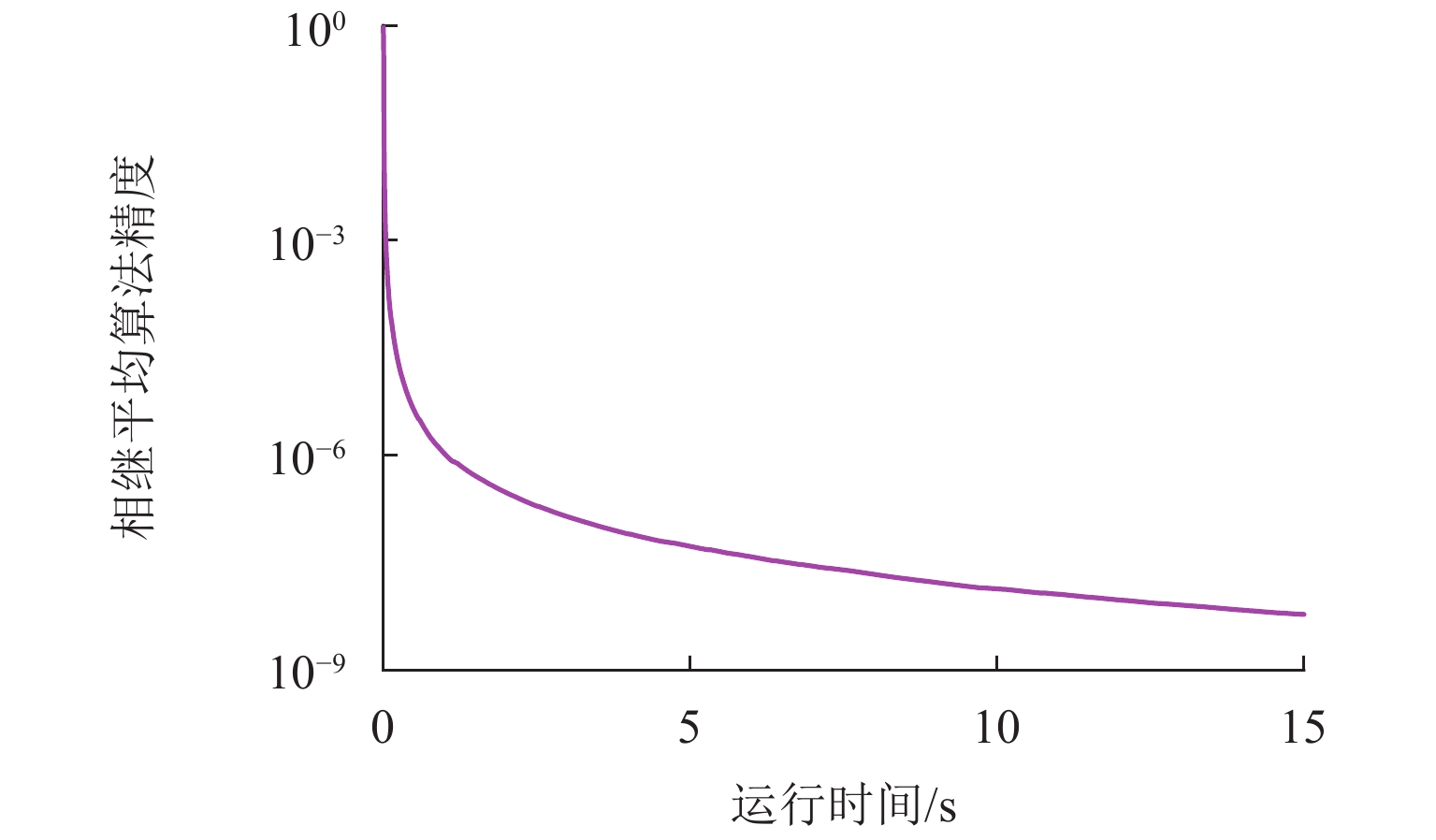
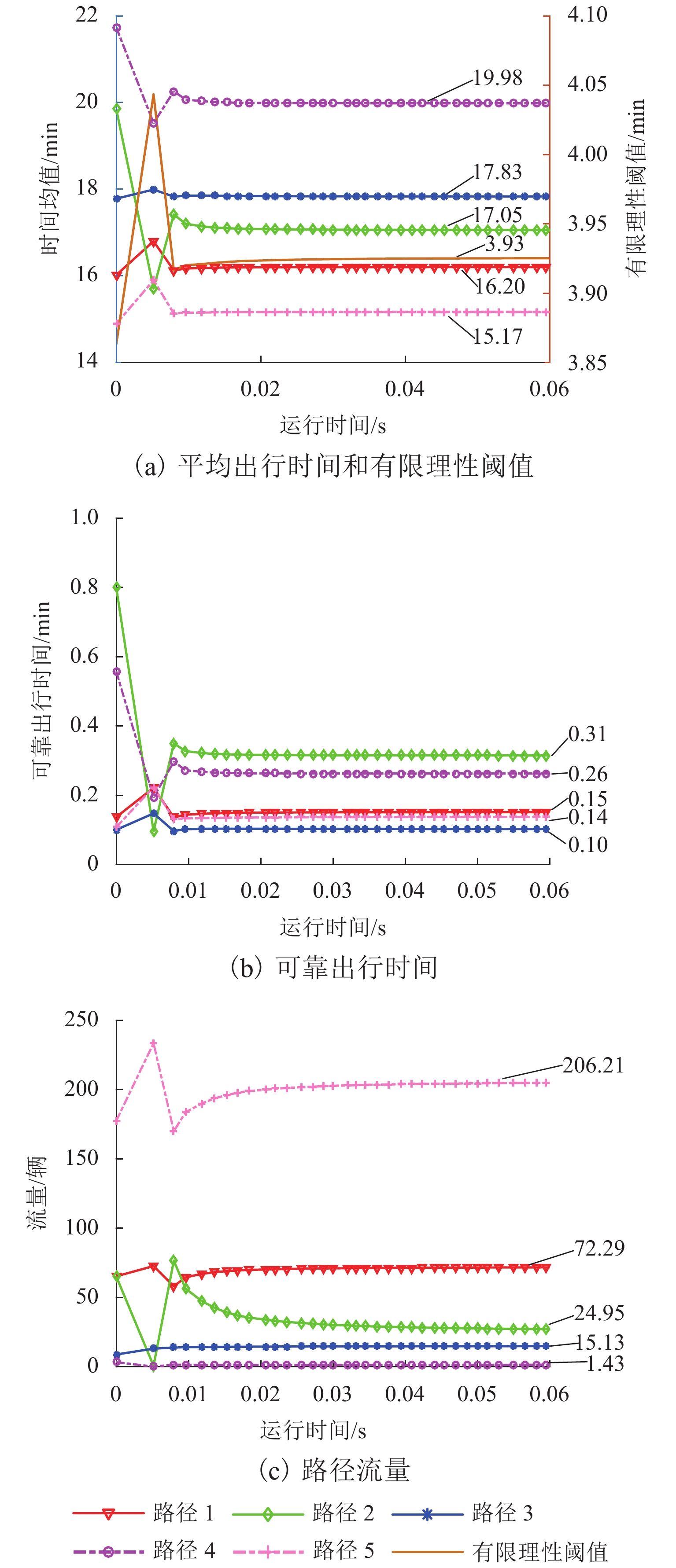
为探索交通系统不确定性和出行者心理感知差异对出行路径选择行为的影响，将路网可靠性和有限理性融入出行者的路径选择决策中，提出双目标交通网络均衡模型. 为应对模型多解问题，建立出行可靠性和有限理性下的贝叶斯随机用户均衡模型，运用贝叶斯统计和双层规划框架估计权重系数，采用变分不等式刻画交通均衡模型；分别设计迭代算法（iterative algorithm，IA）和相继平均算法（method of successive average，MSA）求解贝叶斯权重系数估计和变分不等式交通网络均衡模型. 算例表明：随着观测变量和输入变量扰动变小，估计参数的均方根误差逐步减小；IA在运行15 s后均方根误差达到0.05，MSA在1 s内收敛精度达到10−6；变分不等式均衡模型可以同时反映出行者的风险态度和有限理性决策过程.
Abstract:To explore the influence of the uncertainties of traffic systems and travelers’ perception differences on route choice behavior, the bi-objective traffic network equilibrium model is proposed by introducing the network reliability and bounded rationality into travelers’ route choice decision process. To solve multiple solutions of bi-objective user equilibrium model, the Bayesian stochastic user equilibrium model considering travel time reliability and bounded rationality is built, where the Bayesian statistics and bi-level program framework are used to estimate the weight coefficients, and the variational inequality is adopted to build the traffic equilibrium model. The iterative algorithm (IA) and the method of successive average (MSA) are used for the Bayesian estimation model of weight coefficient and variational inequality traffic network equilibrium model, respectively. Case studies show that, the root mean square error (RMSE) of the estimated parameter is decreasing with the increasing of disturbances of observed data and input variable; RMSE reaches to 0.05 after running IA for 15 s, and the convergence accuracy of MSA reaches 10−6 within 1 s; the variational inequality equilibrium model explores traveler’s risk preference and bounded rational decision process.
-
Key words:
- traffic engineering /
- traffic equilibrium /
- reliability /
- bounded rationality /
- Bayesian
-
图 3 估计权重的RMSE随观测路段流量和输入需求扰动的影响
Figure 3. RMSE of estimated weights with different disturbances of observed flows and input ODs
图 6 平均出行时间、有限理性阈值、可靠出行时间和路径流量演化过程
Figure 6. Evolution processes of mean travel time, boundedly rational threshold, reliable travel time, and traffic flow
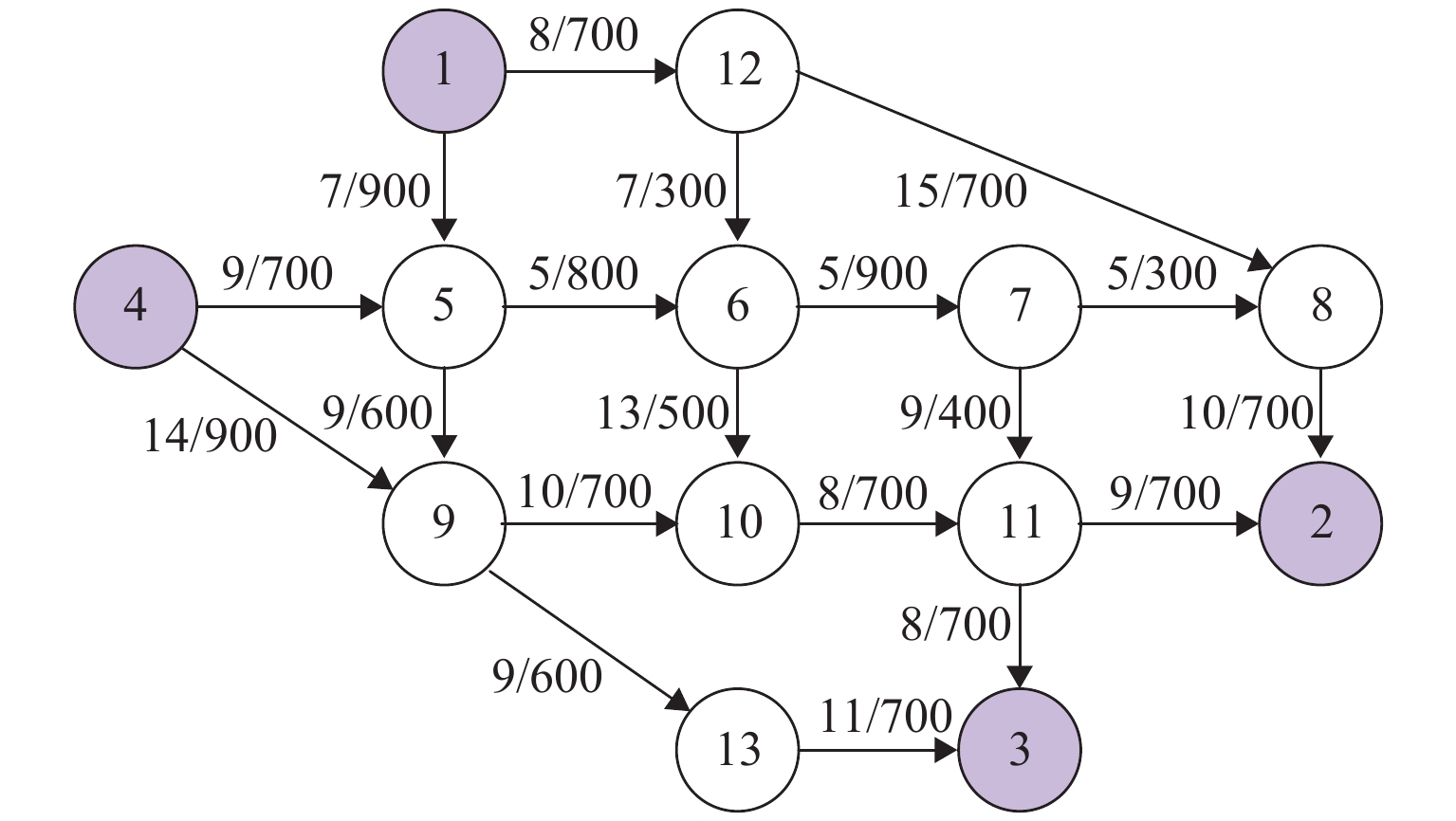
表 1 算例1的模型均衡解
Table 1. Equilibrium results of proposed model for case 1
OD 路径 时间均值/min 有限理
性阈值/min权重
系数可靠出
行时间/min感知多目标出行阻抗均值/min 流量/辆 1—2 1—12—8—2 35.94 7.69 2.00 0.52 44.67 368.24 1—5—6—7—8—2 38.36 0.70 47.45 23.02 1—5—6—7—11—2 40.35 0.72 49.48 3.02 1—5—6—10—11—2 43.77 0.25 51.96 0.25 1—5—9—10—11—2 44.41 0.20 52.50 0.15 1—12—6—7—8—2 40.04 0.66 49.05 4.65 1—12—6—7—11—2 42.04 0.67 51.07 0.61 1—12—6—10—11—2 45.46 0.07 53.29 0.07 1—3 1—5—6—7—11—3 39.58 8.20 1.50 0.72 48.86 327.15 1—5—6—10—11—3 43.01 0.26 51.60 21.28 1—5—9—10—11—3 43.65 0.21 52.17 12.07 1—12—6—7—11—3 41.27 0.68 50.49 64.53 1—12—6—10—11—3 44.69 0.10 53.04 5.04 1—5—9—13—3 39.85 0.46 48.74 369.93 4—2 4—5—6—7—8—2 39.66 8.21 2.50 0.67 49.55 302.33 4—5—6—7—11—2 41.66 0.69 51.60 39.21 4—5—6—10—11—2 45.08 0.18 53.74 4.66 4—9—10—11—2 41.41 0.05 49.75 250.74 4—5—9—10—11—2 45.72 0.09 54.16 3.05 4—3 4—5—6—7—11—3 40.89 7.82 3.00 0.70 50.81 1.40 4—5—6—10—11—3 44.31 0.19 52.70 0.21 4—5—9—10—11—3 44.95 0.11 53.10 0.14 4—9—13—3 36.84 0.42 45.92 184.53 4—5—9—13—3 41.15 0.42 50.23 2.43 4—9—10—11—3 40.64 0.08 48.70 11.30 
下载: 导出CSV
-
[1] 刘志伟,刘建荣,邓卫. 考虑潜在类别的市内机动化出行行为模型[J]. 西南交通大学学报,2021,56(1): 131-137.LIU Zhiwei, LIU Jianrong, DENG Wei. Inclusion of latent class in behavior model of motorized travel in city[J]. Journal of Southwest Jiaotong University, 2021, 56(1): 131-137. [2] LIU W, LI X W, ZHANG F N, et al. Interactive travel choices and traffic forecast in a doubly dynamical system with user inertia and information provision[J]. Transportation Research Part C: Emerging Technologies, 2017, 85: 711-731. doi: 10.1016/j.trc.2017.10.021 [3] WU L X, HUANG Z X, WANG Y L, et al. A dynamic evolution model of disequilibrium network traffic flow with quantity regulation of congestion[J]. Journal of Traffic and Transportation Engineering, 2018, 18(3): 167-179. [4] DE MORAES RAMOS G, MAI T E, DAAMEN W, et al. Route choice behaviour and travel information in a congested network: static and dynamic recursive models[J]. Transportation Research Part C: Emerging Technologies, 2020, 114: 681-693. doi: 10.1016/j.trc.2020.02.014 [5] ZHU S J, LEVINSON D. Do people use the shortest path? An empirical test of Wardrop’s first principle[J]. PLoS One, 2015, 10(8): 0134322.1-0134322.22. [6] FAYYAZ M, BLIEMER M C J, BECK M J, et al. Stated choices and simulated experiences: differences in the value of travel time and reliability[J]. Transportation Research Part C: Emerging Technologies, 2021, 128: 103145.1-103145.19. [7] WATLING D. User equilibrium traffic network assignment with stochastic travel times and late arrival penalty[J]. European Journal of Operational Research, 2006, 175(3): 1539-1556. doi: 10.1016/j.ejor.2005.02.039 [8] ZHU Z, XIONG C F, CHEN X Q, et al. Integrating mesoscopic dynamic traffic assignment with agent-based travel behavior models for cumulative land development impact analysis[J]. Transportation Research Part C: Emerging Technologies, 2018, 93: 446-462. doi: 10.1016/j.trc.2018.06.011 [9] ZHANG Y F, KHANI A. An algorithm for reliable shortest path problem with travel time correlations[J]. Transportation Research Part B: Methodological, 2019, 121: 92-113. doi: 10.1016/j.trb.2018.12.011 [10] XU X D, CHEN A, ZHOU Z, et al. A multi-class mean-excess traffic equilibrium model with elastic demand[J]. Journal of Advanced Transportation, 2014, 48(3): 203-222. doi: 10.1002/atr.205 [11] SUN C, CHENG L, ZHU S L, et al. Multiclass stochastic user equilibrium model with elastic demand[J]. Transportation Research Record: Journal of the Transportation Research Board, 2015, 2497(1): 1-11. doi: 10.3141/2497-01 [12] DI X, LIU H X. Boundedly rational route choice behavior: a review of models and methodologies[J]. Transportation Research Part B: Methodological, 2016, 85: 142-179. doi: 10.1016/j.trb.2016.01.002 [13] 赵传林,黄海军. 基于满意准则的有限理性用户均衡流量分配性质研究[J]. 系统工程理论与实践,2014,34(12): 3073-3078. doi: 10.12011/1000-6788(2014)12-3073ZHAO Chuanlin, HUANG Haijun. Properties of boundedly rational user equilibrium under satisficing rule in traffic assignment problem[J]. Systems Engineering—Theory & Practice, 2014, 34(12): 3073-3078. doi: 10.12011/1000-6788(2014)12-3073 [14] 张新洁,关宏志,赵磊,等. 有限理性视野下出行者出行方式选择分层Logit模型研究[J]. 交通运输系统工程与信息,2018,18(6): 110-116. doi: 10.16097/j.cnki.1009-6744.2018.06.016ZHANG Xinjie, GUAN Hongzhi, ZHAO Lei, et al. Nested logit model on travel mode choice under boundebly rational view[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(6): 110-116. doi: 10.16097/j.cnki.1009-6744.2018.06.016 [15] GONZÁLEZ RAMÍREZ H, LECLERCQ L, CHIABAUT N, et al. Travel time and bounded rationality in travellers’ route choice behaviour: a computer route choice experiment[J]. Travel Behaviour and Society, 2021, 22: 59-83. doi: 10.1016/j.tbs.2020.06.011 [16] SUN C, LI M H, CHENG L, et al. Boundedly rational user equilibrium with restricted unused routes[J]. Discrete Dynamics in Nature and Society, 2016, 2016: 9848916.1-9848916.11. [17] WANG D, LIAO F X, GAO Z Y, et al. Tolerance-based strategies for extending the column generation algorithm to the bounded rational dynamic user equilibrium problem[J]. Transportation Research Part B: Methodological, 2019, 119: 102-121. doi: 10.1016/j.trb.2018.11.008 [18] YU H, ZHU S L, YANG J, et al. A Bayesian method for dynamic origin−destination demand estimation synthesizing multiple sources of data[J]. Sensors, 2021, 21(15): 4971.1-4971.20. [19] LEBLANC L J. Mathematical programming algorithms for large scale network equilibrium and network design problems[D]. Evanston: Northwestern University, 1973 -
下载:
点击查看大图
计量
- 文章访问数: 493
- HTML全文浏览量: 190
- PDF下载量: 37
- 被引次数: 0