随着城市更新速度加快，交通拥塞问题日益凸显. 尤其在早、晚高峰时间更为严重，严重制约城市绿色化、低碳化发展. 对城市常发性、广泛性等交通拥塞进行溯源，快速、准确地识别出交通拥塞源参数（交通量、位置），对有效优化交通管控方案具有重要意义.

目前，国内外学者对交通拥塞控制及改进模型算法进行了大量研究. Zhang等^[1]提出了基于深度学习的交通拥堵预测模型；Pi等^[2]对区域进行划分并分析不同交通拥堵模式和成因；Chen等^[3]提出一种面向弹性的评估方法，以评估交通状态，并有效识别了交通拥堵扩散的临界阈值；Zhu等^[4]使用基于神经网络嵌入的新型注意力机制，用于城市交通拥塞点过程模拟；Chen等 ^[5]提出一种新的交通拥堵传播模型（SIS-CP）并基于希尔伯特黄变换（Hilbert-Huang transform）变换确定链路的交通状态，以此分析交通拥堵传播模式；陈美林等^[6]通过提取交通拥堵事件特征，确定时空范围以明确拥堵传播方向；石敏等^[7]提出一种空洞-稠密神经网络模型用于城市交通拥堵预测，并进行了有效性验证；曾筠程等^[8]提出了具备学习城市交通拥堵时空间特征的DGC-LSTM （directed graph convolution-long short term memory）预测模型；周辉宇等^[9]提出基于时空关联规则挖掘算法的传导模型，用于预测交通拥堵；梁军等^[10]提出DAGCRN （dual adaptive graph convolution recurrent network）来解决城市路网的交通拥堵问题；马庆禄等^[11]提出混合交通流时空演化模型，探究交通拥堵传播的内在规律和模型有效性；孙超等^[12]提出考虑交通系统不确定性的双目标交通网络均衡模型，刻画出行者的风险态度和有限理性决策过程.

然而，真实的城市交通拥塞异常繁杂，不同的交通拥塞源参数可能形成不同程度的交通拥塞，如常发性、节点性等交通拥塞源点. 通常交通拥塞源的扩散交通量和位置未知，具有一定隐蔽性，往往无法提前获取交通拥塞源的位置、源强等信息. 而上述研究主要以城市交通拥塞的预测和时空间特征分析为主，未考虑不同交通拥塞场景下不同目标函数选择对交通拥塞源反演的影响. 因此，本文基于贵阳市2021年1—6月的交通数据，确定贵阳市的交通拥塞点，并对高斯烟羽模型进行适应性改进，建立城市交通拥塞扩散传播模型，对3种启发式优化算法进行对比，确定选用人群搜索算法（SOA）作为“单点源”参数反演优化算法. 在此基础上，分析3种（单、两、三）不同交通拥塞源参数数量对5种典型目标函数的反演结果. 从高估率、准确性和稳定性3个维度，系统分析5种典型目标函数在不同源参数数量下的性能差异. 本研究有助于解决不同目标函数的性能差异问题，可为多种不同交通拥塞情形下的参数信息准确评估提供参考.

1.   模拟-优化方法

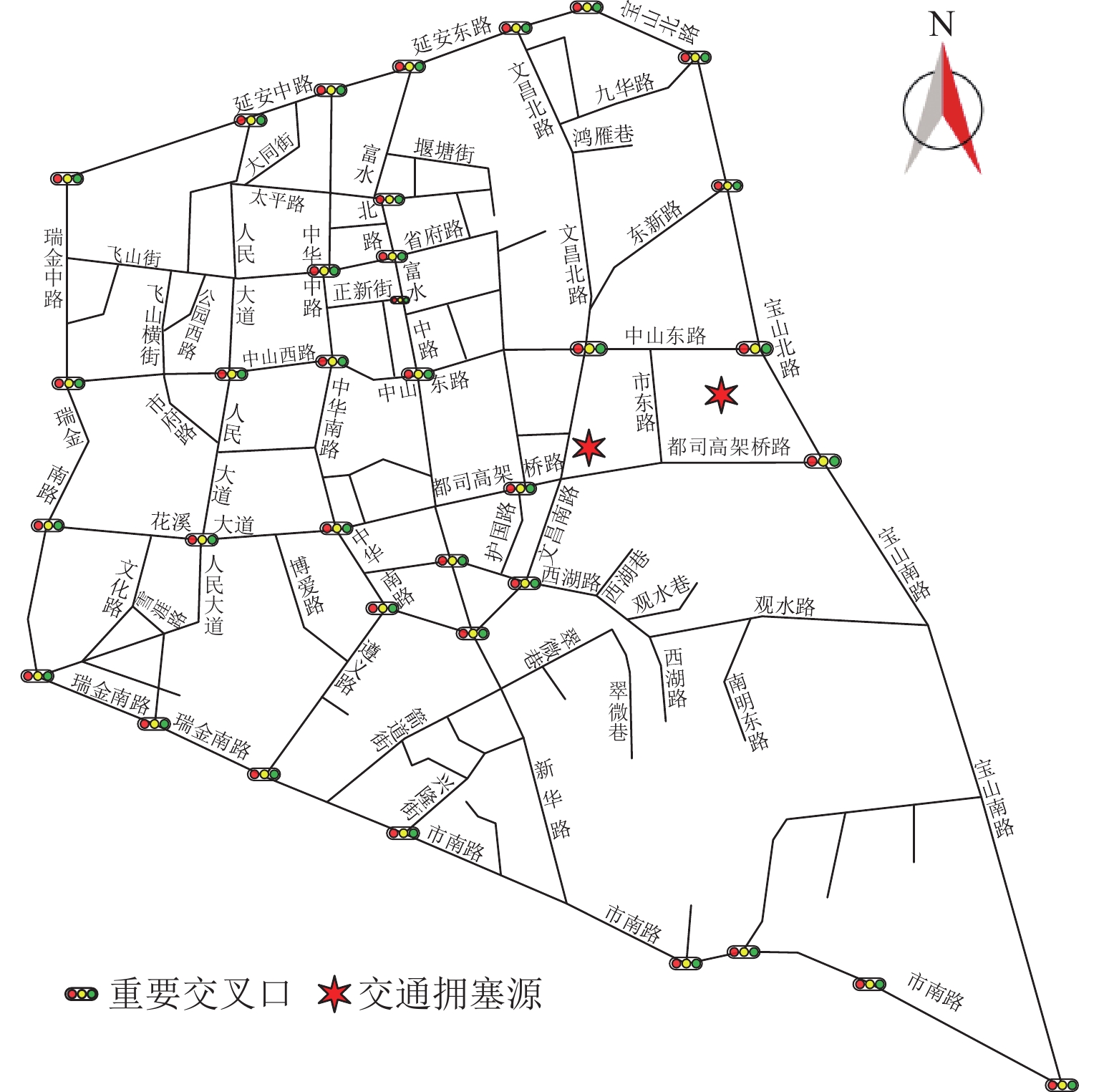
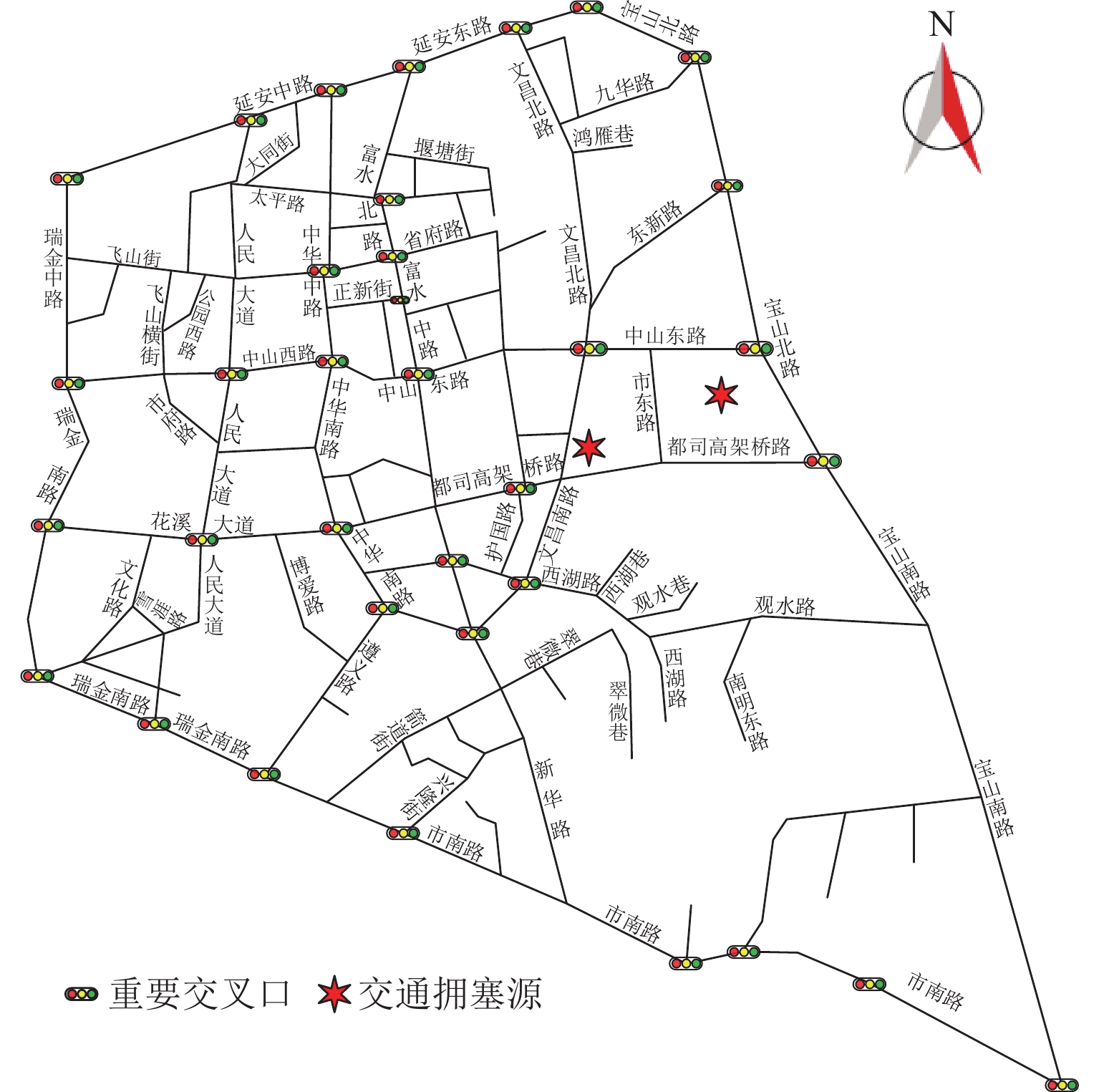
本文基于开放街区地图（OSM）获取的贵阳市城市路网矢量数据、Python爬取的交通流数据（交通量、延误时间等）、实地调查数据（校核车道数、数据差异点处理等）标注贵阳市的部分城市交通拥塞源点，交通拥塞源点主要考虑2021年1—6月常发性、短时性、大流量的关键性节点，重点包括医院、学校、商业中心等，研究区域内主要有2个交通拥塞源，其基本参数取值如表1所示. 本文选取的研究区域以住宅为主，占到80%以上，另外为商业中心、医院等. 研究区域的交通拥塞点位置如图1所示.

表  1  交通拥塞源基本参数取值

Table  1.  Basic parameter values of traffic congestion source

交通拥塞源编号	所在位置紧邻标志性建筑	道路名称	道路等级	车道数	区域平均行车速度/ （km·h−1）	进口道断面平均速度/ （km·h−1）	出口道断面平均速度/ （km·h−1）	饱和度
1	贵州省人民 医院	中山东路（北侧）	主干路	双向 6 车道	29.87	15.34	47.92	0.819
		都司高架桥路（南侧）	主干路	双向 6 车道	29.43	13.85	45.58	0.895
		市东路（西侧）	支路	双向 2 车道	20.28	8.73	24.32	0.889
		宝山南路（东侧）	城市快速路	双向 8 车道 + 潮汐车道	40.85	22.94	58.14	0.831
2	亨特城市 广场	中山东路（北侧）	主干路	双向 6 车道	29.87	14.79	48.35	0.819
		都司高架桥路（南侧）	主干路	双向 6 车道	29.43	13.19	46.39	0.895
		文昌南路（西侧）	次干路	单向 4 车道	27.86	11.37	43.21	0.908
		市东路（东侧）	支路	双向 2 车道	20.28	8.73	24.32	0.889

下载: 导出CSV 

| 显示表格

图  1  交通拥塞点区域位置

Figure  1.  Location of traffic congestion areas

下载: 全尺寸图片 幻灯片

2.   研究方法

2.1   基于高斯烟羽模型的城市交通拥塞扩散传播模型

城市道路网络结构中突发性、大交通量的“单点源”尽管不是严重的突发交通拥塞源，却在城市交通中最为常见. “单点源”的交通量扩散到城市路网结构中，对区域城市交通拥塞的破坏非常严重. 因此，有必要对易导致交通拥塞发生的“单点源”进行有效识别，降低交通拥塞发生的可能性，为管理者提供决策依据.

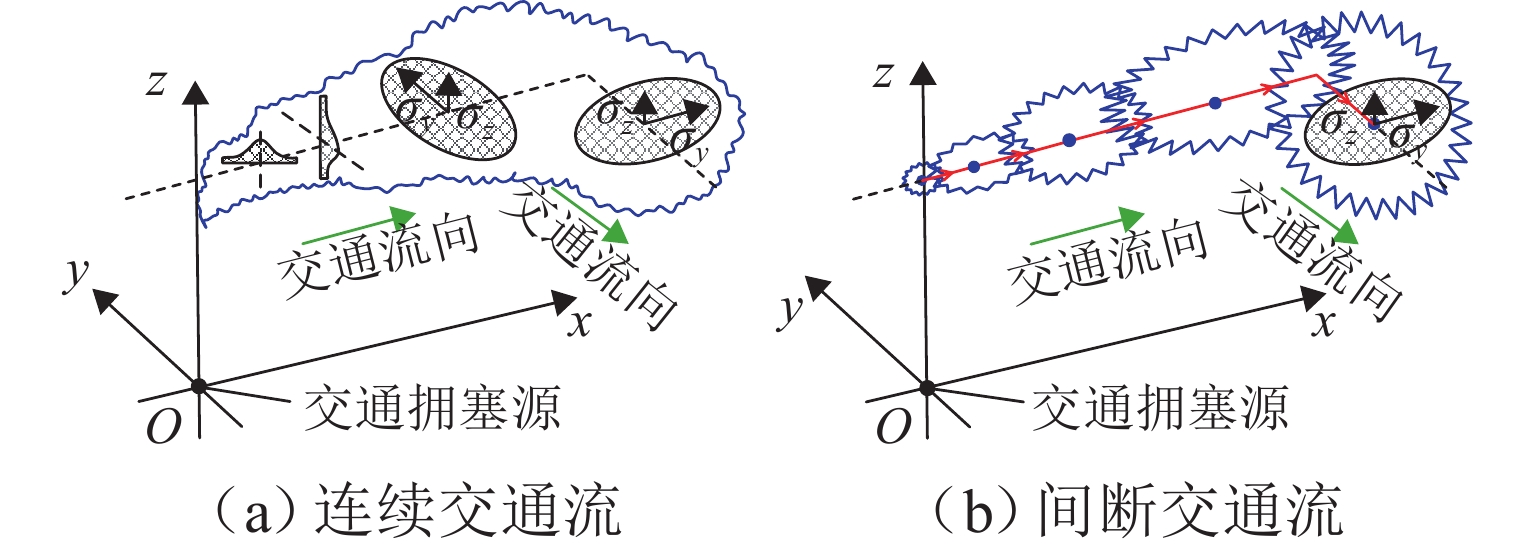
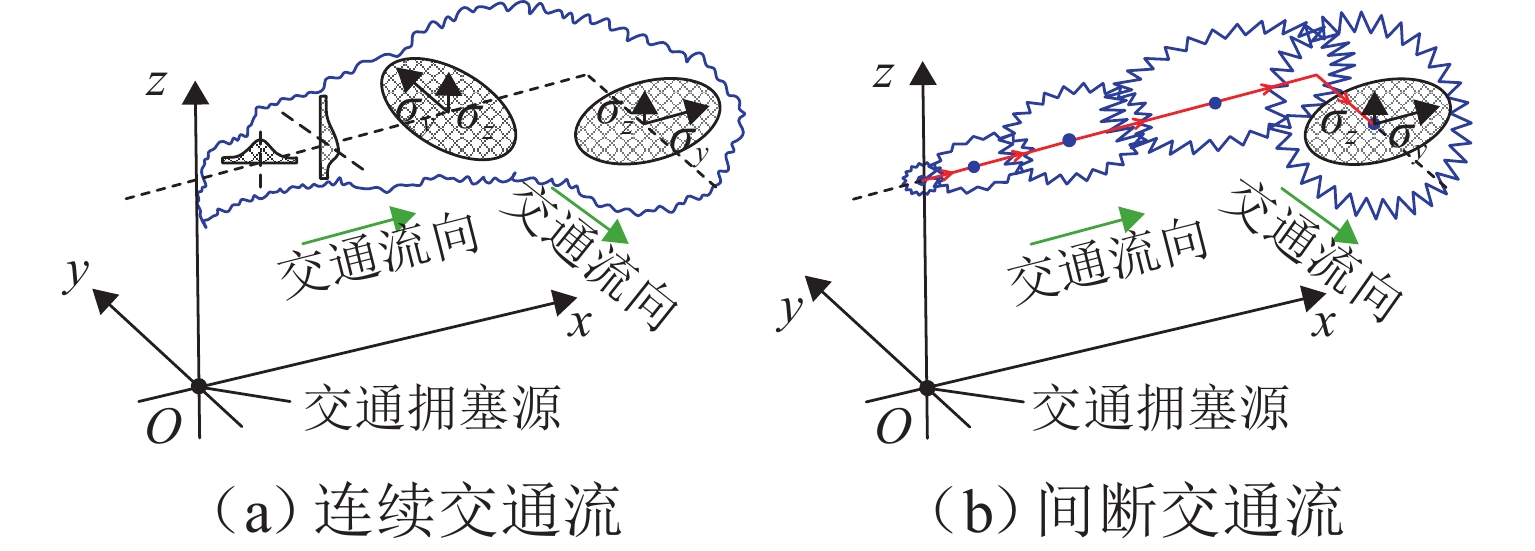
交通拥塞通常会在短时间内产生集聚效应，逐渐在路网结构中蔓延，最终演变成具有区域性和广泛性的城市交通拥塞区域. 近年来，高斯烟羽模型被广泛用于大气污染研究，火力发电会造成局部环境的大气污染，排放的污染物可视为一定时间内连续的高烟囱与环境污染点，而城市交通拥塞“单点源”也是一段时间内扩散的连续性交通流. 因此，研究高峰小时交通量的扩散及时空分布，可以选择高斯烟羽模型，以科学评估城市交通拥塞发生扩散后对周边区域的影响. 城市交通拥塞高斯烟羽模型结构如图2所示，图中：$ {\sigma _y} $、$ {\sigma _{\textit{z}}} $分别为横向和垂直扩散参数.

图  2  城市交通拥塞高斯烟羽模型结构示意

Figure  2.  Structure of Gaussian plume model for urban traffic congestion

下载: 全尺寸图片 幻灯片

根据大气污染的相关理论，假设影响交通拥塞扩散的因素在一定时间内相对恒定，城市交通拥塞扩散符合高斯分布，源强是一系列间断性或连续性的交通流，且城市交通拥塞参数在扩散过程中不会发生任何变化. 因此，可以将城市交通拥塞在城市路网中的扩散形态类比成大气污染高斯烟羽形式. 在有限条件下，交通拥塞源高斯烟羽扩散模型的一般形式^[13]为

式中：$ C\left( {x,y,{\textit{z}}} \right) $为点（$ x, y , {\textit{z}} $）处的气体扩散浓度；$ Q $为毒气源释放速率，g/s；$ u $为平均风速，m/s；$ {x_0} $、$ {y_0} $、$ {{\textit{z}}_0} $分别为毒气源二维平面的横坐标、纵坐标和释放高度，m.

城市交通拥塞在城市道路二维平面网络结构中进行^[14]，将式（1）变形为

式中：$ x_{\mathrm{c}} $、$ y_{\mathrm{c}} $分别为空间点距“单点源”的纵向、横向距离，m；$ h $为时间，s；$ C_{\mathrm{c}}\left( {x_{\mathrm{c}},y_{\mathrm{c}},h} \right) $为城市道路单位面积内的车辆数，即单位面积交通密度，辆/m²；$ Q_{\mathrm{c}} $为“单点源”的交通流量，辆/h；$ u_{\mathrm{c}} $为平均行车速度，km/h；$ \sigma_{\mathrm{c}y} $为“单点源”的横向扩散系数；y_co为二维平面的原点横向坐标，通常取值为0.

2.2   基于多种启发式算法比较的性能最优算法确定

近年来，启发式算法因数据依赖度低、高效等优点被广泛用于溯源问题. 本研究通过3种算法进行对比，选出寻优性能最好的算法作为源参数反演算法.

2.2.1   遗传算法（GA）

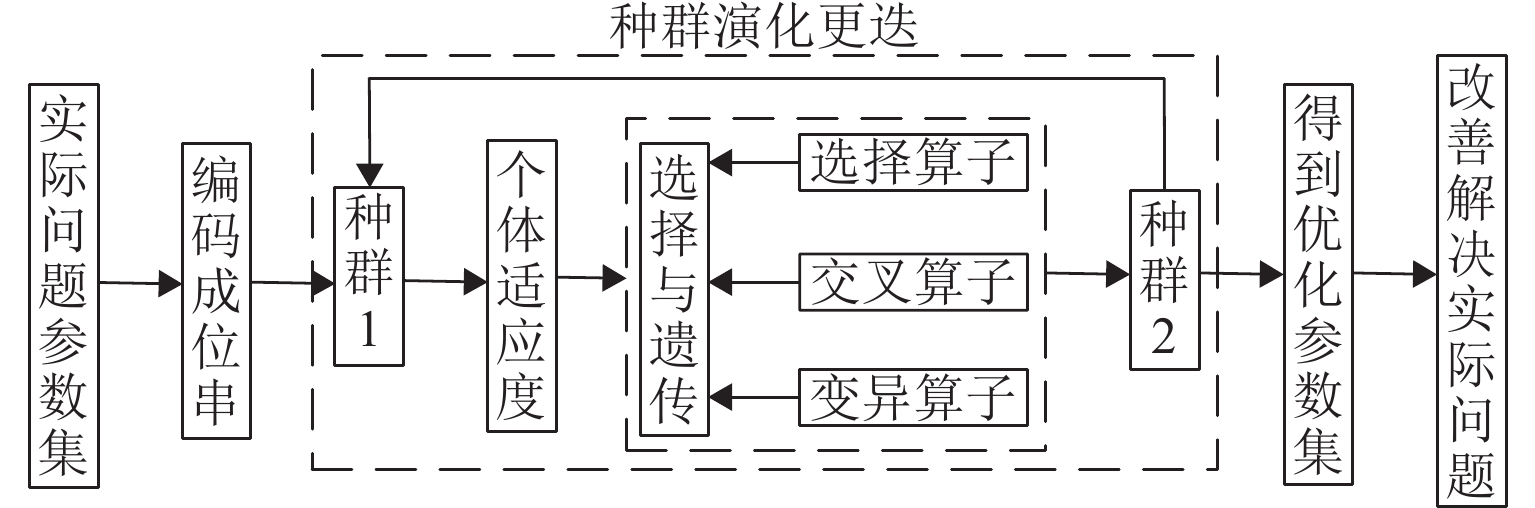
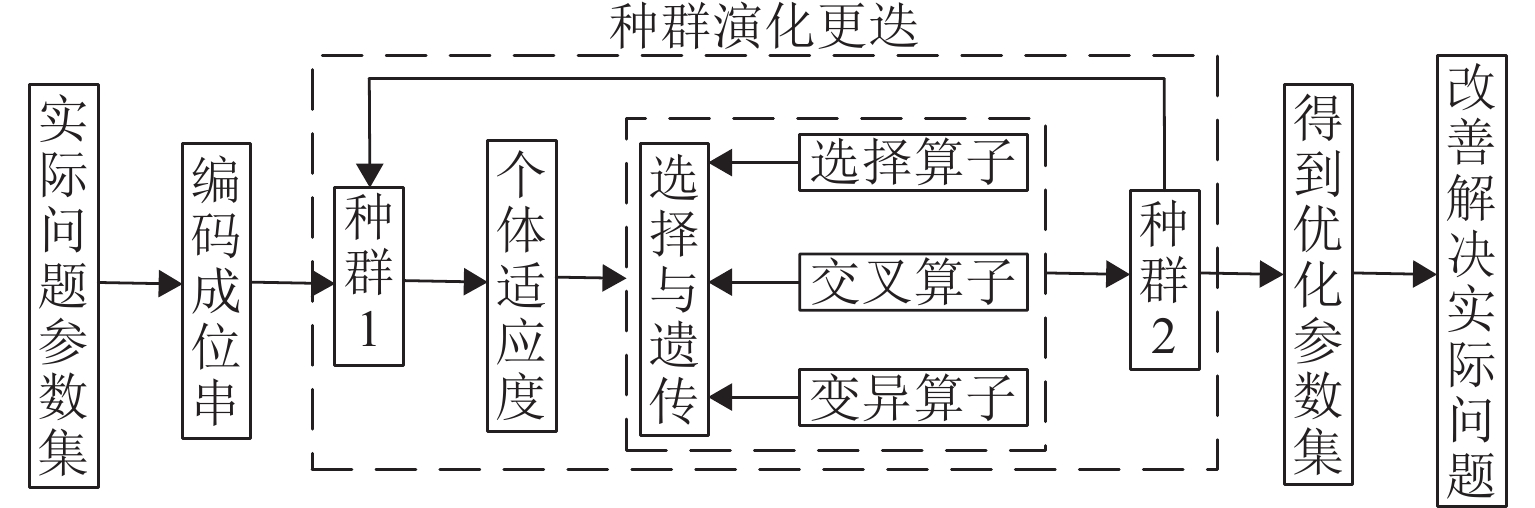
遗传算法是模拟自然进化过程发展来的启发式优化算法. 从一个固定规模的种群出发，计算个体适应度，经过选择、交叉、变异操作形成新的种群，最终使得种群进化到具有更高的适应环境程度，并进行不断繁衍，求得近似最优解. 算法流程如图3所示.

图  3  遗传算法流程

Figure  3.  genetic algorithm process

下载: 全尺寸图片 幻灯片

2.2.2   粒子群算法（PSO）

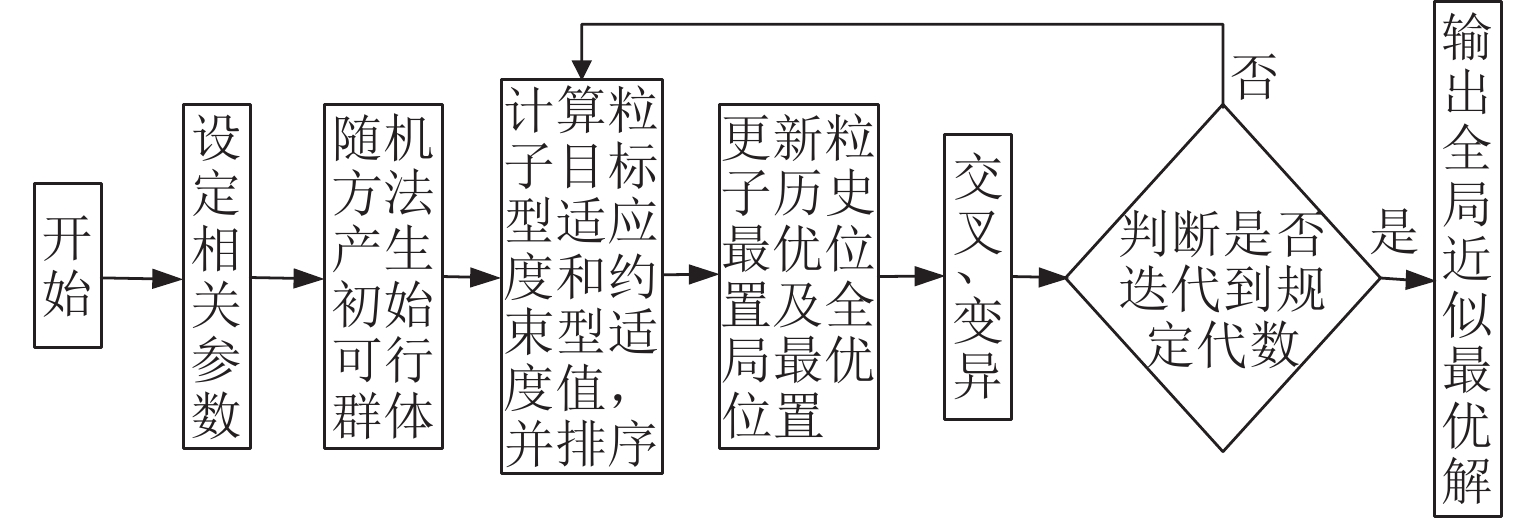
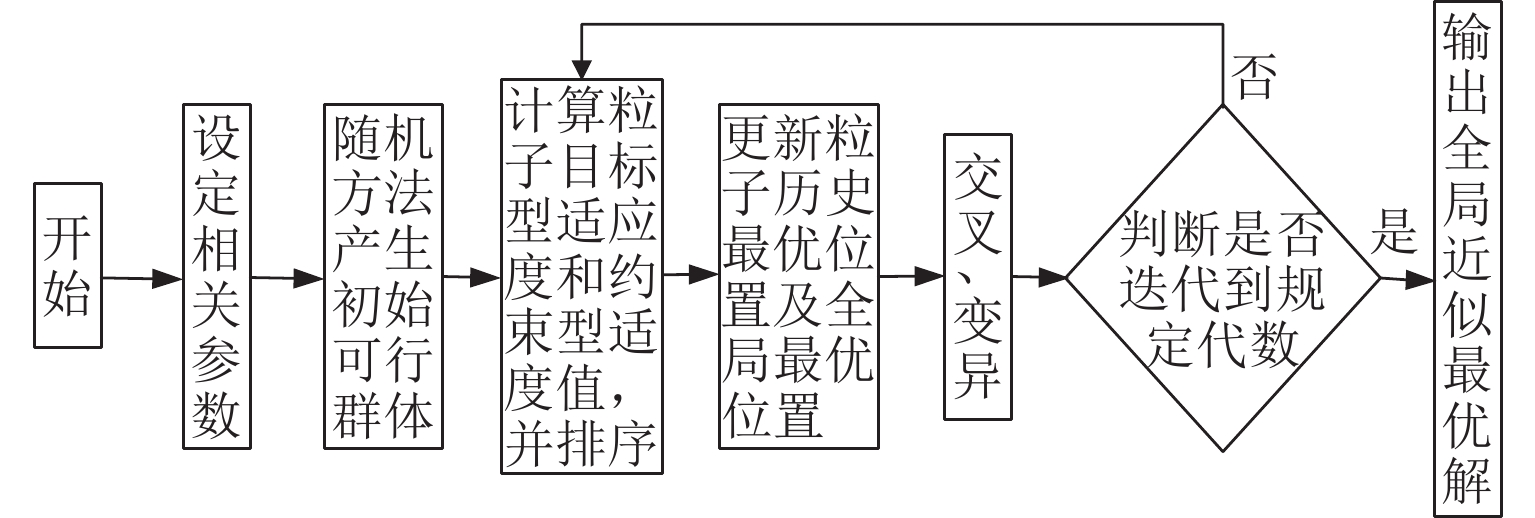
PSO的思路来自自然界中鸟类捕食过程，通过群体协作不断更新迭代信息，以找到问题的近似最优解，如图4所示. 单个粒子$ {\boldsymbol{X}}_{i}=(x_{i, 1}, x_{i, 2}, \cdots, x_{i, d}, \cdots , x_{i, D} ) $通过极值$ (p_{{\mathrm{best}},i,d},g_{{\mathrm{best}},d}) $实现速度和位置的更新，其中，x_i,d为第$ i $个粒子的第$ d $维变量，$ p_{{\mathrm{best}},i,d} $为第$ i $个粒子极值的第$ d $维变量，$ g_{{\mathrm{best}},d} $为子代全局极值的第$ d $维变量. 速度、位置见式（3）、（4）.

图  4  PSO算法流程

Figure  4.  PSO algorithm process

下载: 全尺寸图片 幻灯片

式中：$ v_{k,i,d} $、$ x_{k,i,d} $分别为第$ k $次迭代第$ i $个粒子第$ d $维变量的速度、位置；$ {r_1} $、$ {r_2} $为介于0～1的随机数；$ {c_1} $、$ {c_2} $为学习因子；$ {w_k} $为惯性权重，$ w_k=w_0-w_1k/K $，$ {w_0} $、$ {w_1} $为初始权重值，$ K $为总迭代次数.

适应度表示个体对环境的适应程度，通过约束函数求解适应度，如式（5）.

式中：$ F\mathrm{_{sc}} $(·)为约束性适应度函数；$ {F}_{{\mathrm{c}}} $(·)为约束条件的约束函数；$ {s_i} $为约束条件的权重，$ 0 \leqslant {s_i} \leqslant 1 $；$ m $为约束函数个数.

2.2.3   人群搜索算法（SOA）

人群搜索算法（SOA）通过模拟人对不同位置的响应和不确定性推理，以确定步长、方向，实现问题求解.

搜索方向的相关计算式为

式中：$ d_{pq}(t) $为第t次迭代第p个搜寻个体在第q维搜索空间的搜索方向；$ d_{\mathrm{ego},pq}(t) $、$ d_{\mathrm{alt},pq}(t) $、$ d_{\mathrm{pro},pq}(t) $分别为第$ p $个搜寻个体第q维的利己方向、利他方向和预动方向；$ w $为惯性权值；$ {\varphi _1} $、$ {\varphi _2} $为取值范围为$ \left[ {0,1} \right] $的随机数；$ p_{\mathrm{best},p} $，$ g_{\mathrm{best},p} $分别为第p个搜寻个体找到的最佳位置和所在邻域集体的历史最佳位置；$ \mathrm{sign} $(·)为sign函数转换；$ x_p\left(t\right) $为第t次迭代第p个搜寻个体的位置；$ x_p\left(t_1\right) $、$ x_p(t_2)\text{ } $为$ \{x_p(t-2),x_p(t-1), x_p(t)\} $中2个相邻的最佳位置.

搜索步长的计算，如式（7）所示.

式中：$ {x_{\min }} $、$ {x_{\max }} $分别为同一种群中最小和最大函数值的位置；$ {t_{\max }} $为最大迭代次数；$ u_{pq} $、$\alpha_{pq} $、$\delta_{pq} $分别为第p个个体第q维搜索空间的隶属度、搜索步长和高斯隶属度函数参数.

在式（6）～（7）的基础上通过式（8）进行位置更新.

式中：$x_{pq}(t) $为第t次迭代第p个个体第q维的搜索位置.

2.3   基于性能最优算法的源参数反演模型构建

通过目标函数来评估算法的优化性能，构建下列5种目标函数.

1） 基于单位面积交通密度偏差平方和的目标函数$ O_{{\mathrm{F}}_1} $为

式中：$ N $为交通观测点总数，$ {C_n} $为高斯烟羽扩散模型在第$ n $个点的单位面积交通密度计算值；$ {O_n} $为第$ n $个点的实际观测值.

2） 基于对数变换形式的单位面积交通密度均方根误差的目标函数$ O_{{\mathrm{F}}_2} $为

式中：$ l $为常数，用于保证$ l{C_n} $、$ l{O_n} $均大于1.

3） 基于相关系数的目标函数$ O_{{\mathrm{F}}_3} $，

式中：$ C $为高斯烟羽扩散模型的模拟单位面积交通密度，$ O $为观测单位面积的交通密度，$ {\sigma _C} $、$ {\sigma _O} $（$ \overline C $、$ \overline O $）分别为$ C $、$ O $的标准差（平均值）.

4） 基于单位面积交通密度的标准化均方根误差的目标函数$ O_{{\mathrm{F}}_4} $为

5） 复合目标函数

基于线性加权将上述4种函数转变为复合目标函数$O_{{\mathrm{F}}_5} $，权重都设为1/4，如式（14）所示.

在仅反演“单点源”交通流量$ Q_{\mathrm{c}} $情形下，即单参数反馈情形下，位置信息$ \left( {x,y} \right) $已知，优化模型及约束条件如式（14）所示.

式中：$O_{\mathrm{F}_b} $(·)为第b种目标函数形式，b=1, 2, …, 5.

在两参数反演情形下，“单点源”的交通流量$ Q_{\mathrm{c}} $、位置$ x $或$ y $是未知的，此时构建的优化模型及约束条件如式（15）～（16）所示.

在三参数反演情形下，“单点源”的交通流量$ Q_{\mathrm{c}} $和位置$ \left( {x,y} \right) $未知，此时构建的优化模型及约束条件如式（17）所示.

2.4   基于源参数反演模型的对比结果评估方法

反演源参数的过程如图5所示. 若反演结果比实际结果较高，将更有利于制定实际城市交通拥塞控制方案. 将反演模型计算结果值比实际值高的定义为高估情况，其在所有计算方案中的比值定义为高估率. 通过相对偏差绝对值实现对模型反演源强和位置的准确性评估，通过变异系数实现对同一个算法不同目标函数的变异情况分析，如式（18）～式（22）所示.

图  5  反演源参数的过程

Figure  5.  Inversion process of source parameters

下载: 全尺寸图片 幻灯片

式中：$ {M_{{\mathrm{over}}}} $为源强反演结果高于真实值的实验次数；$ {M_{{\mathrm{all}}}} $为总实验次数；$ {P_{{\text{over}}}} $为$ {M_{{\mathrm{over}}}} $占$ {M_{{\mathrm{all}}}} $的比重；$ e_{\mathrm{ARD}} $为源强反演相对偏差的绝对值；$ {N_{{\text{ARD,50}}}} $为$ {e_{{\mathrm{ARD}}}} $小于50%的实验次数；$ {P_{{\text{ARD,50}}}} $为$ {N_{{\text{ARD,50}}}} $占$ M\mathrm{_{all}} $的比重；$ {e_{{\mathrm{AD}}}} $为反演位置偏差的绝对值，用于表征不同目标函数源参数反演结果的准确性；$ {e_{{\mathrm{CV}}}} $为变异系数，用于评估不同目标函数在反演中的稳定性，变异系数越小，稳定性越强；$ e_{Q_{\mathrm{c}},{\textit{z}}} $、$ r_{Q_{\mathrm{c}},{\textit{z}}} $分别为“单点源”在扩散方案$ {\textit{z}} $中交通流量的计算值和真实值，辆/h；$ {e_{L,{\textit{z}}}} $、$ {r_{L,{\textit{z}}}} $分别为“单点源”在扩散方案$ {\textit{z}}$下位置$ L $的计算值和真实值，m；$ u_{Q_{\mathrm{c}},L} $、$ a_{Q_{\mathrm{c}},L} $分别为反演结果的偏差标准差和偏差平均值.

3.   结果分析

3.1   3种优化算法性能对比

通过Griewank、Schaffer和Rastrigin 3种经典函数对算法进行测试对比，函数表达式、搜索范围、变化情况等具体参考文献[15]. 各算法的优化结果如表2所示.

表  2  各测试函数优化结果

Table  2.  Optimization results for each test function

评价指标		GA				PSO				SOA
		Griewank	Schaffer	Rastrigin		Griewank	Schaffer	Rastrigin		Griewank	Schaffer	Rastrigin
平均最优值		1.25 × 10−2	7.52 × 10−1	1.85 × 10−4		1.32 × 10−1	2.67 × 10−4	1.59 × 10−1		8.53 × 10−3	3.89 × 10−6	6.12 × 10−6
标准差		1.19 × 10−2	2.31	3.57 × 10−4		6.74 × 10−2	3.12 × 10−4	3.79 × 10−1		3.43 × 10−3	4.21 × 10−6	6.21 × 10−6
最大值		5.34 × 10−2	8.97	2.34 × 10−3		3.26 × 10−1	1.74 × 10−3	1.21		2.45 × 10−2	2.16 × 10−5	4.46 × 10−5
最小值		9.26 × 10−4	7.69 × 10−7	0.89 × 10−7		1.06 × 10−2	7.08 × 10−7	3.85 × 10−6		1.86 × 10−3	4.32 × 10−8	7.96 × 10−8

下载: 导出CSV 

| 显示表格

实验参数设置如下：GA中种群数量为100个，最大迭代次数为100次，交叉概率为0.8，变异概率为0.05；PSO中粒子群规模为100个，$ K $为100，$ {w_k} $为1.5，$ {c_1} $为1.6，$ {c_2} $为1.8；SOA中种群数量为100个，$ w $为0.8，t_max为100次.

通过3种经典函数的优化结果对3种算法的性能进行评估. 在平均最优值方面，针对函数Rastrigin，SOA、GA、PSO的值分别为6.12 × 10⁻⁶、1.85 × 10⁻⁴、1.59 × 10⁻¹，表明SOA更容易跳出局部最优解，其多适用于一系列间断性交通流或连续性交通流的商场、医院等点源参数反演中，可以更容易找到全局最优解；在标准差方面，针对函数Schaffer，GA的值最大，为2.31，表明GA求解全局最优解的精度最低，而SOA为4.21 × 10⁻⁶，表明SOA求解全局最优解的精度最高；同样地，在求解模型的最大值和最小值方面，SOA的函数值明显优于GA、PSO. 综上可以得出，SOA算法在跳出局部最优解和求解全局最优解的精度2个方面高于PSO算法，PSO算法又高于GA算法. SOA算法对各函数进行优化，其结果敛散性较高、相对稳定，因此，选用SOA作为“单点源”参数反演优化算法.

3.2   单参数反演情形

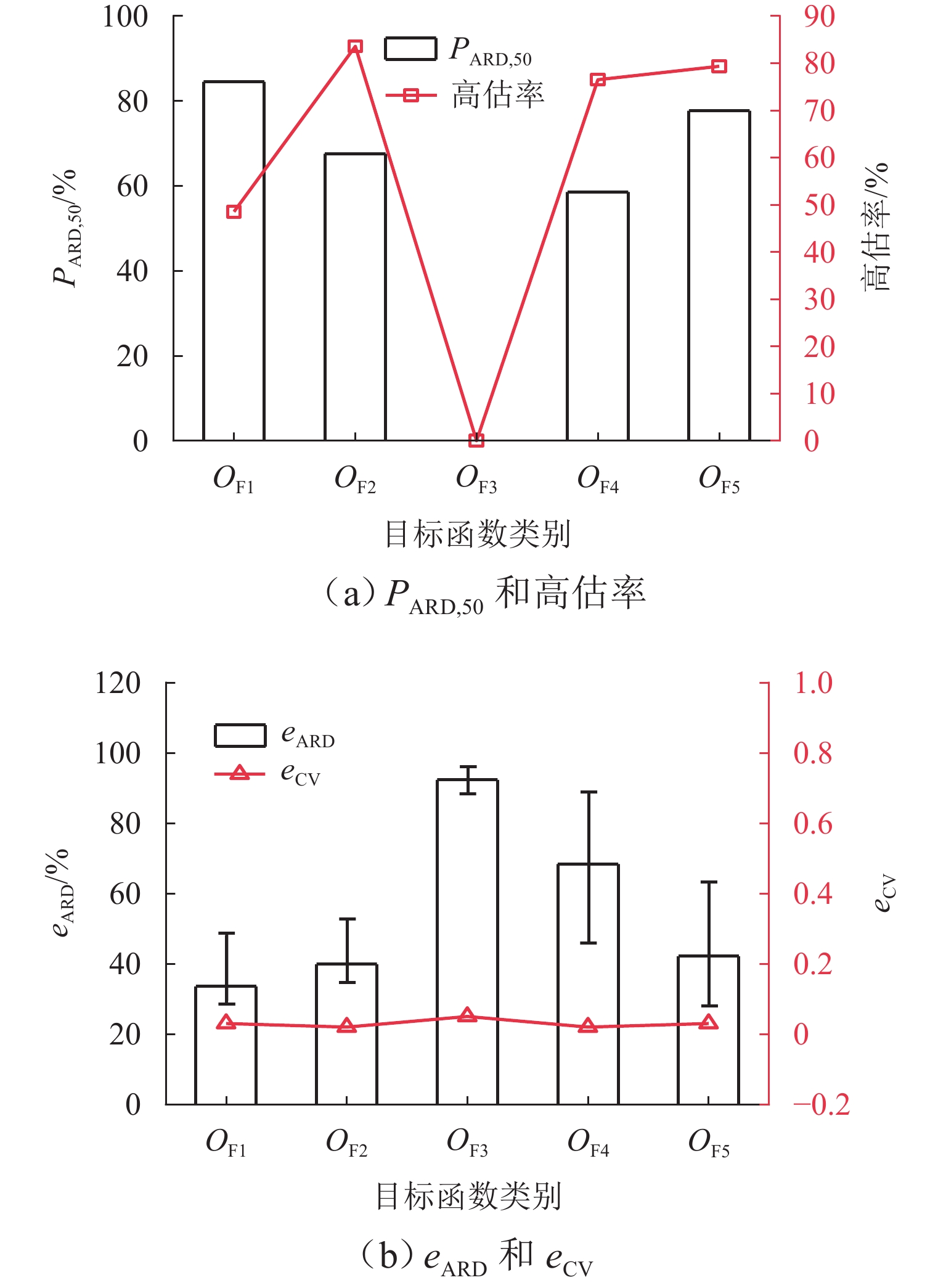
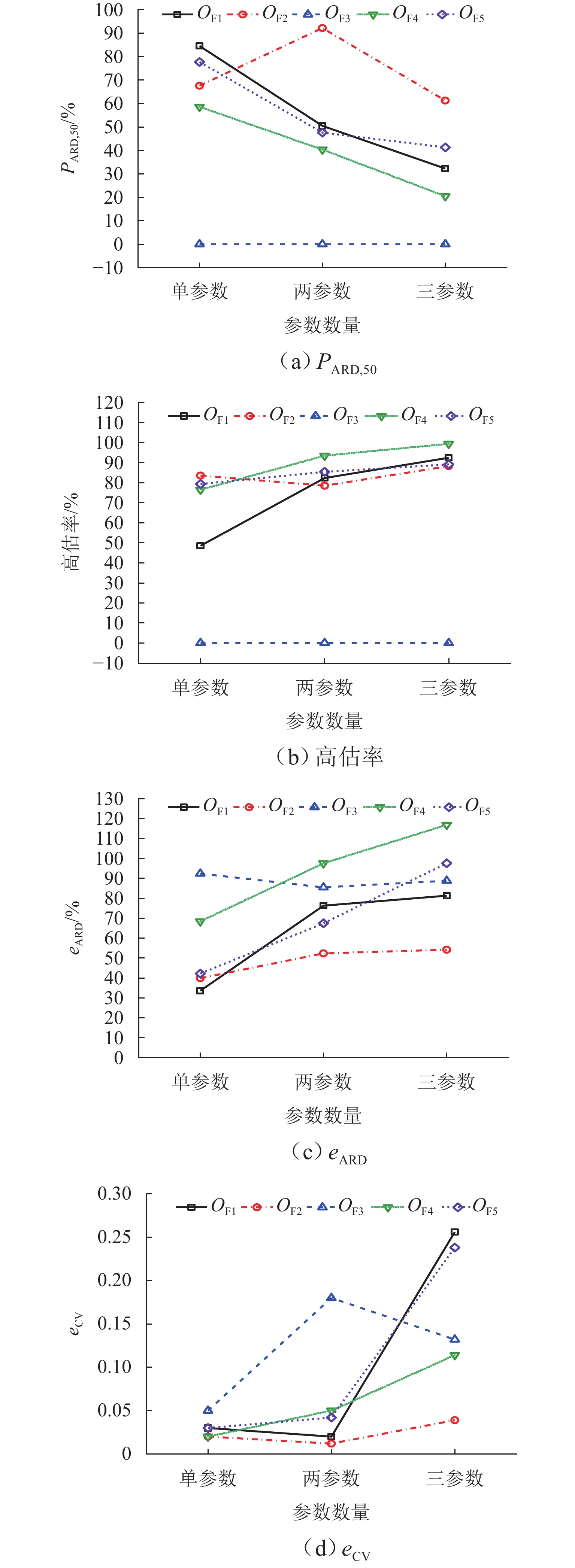
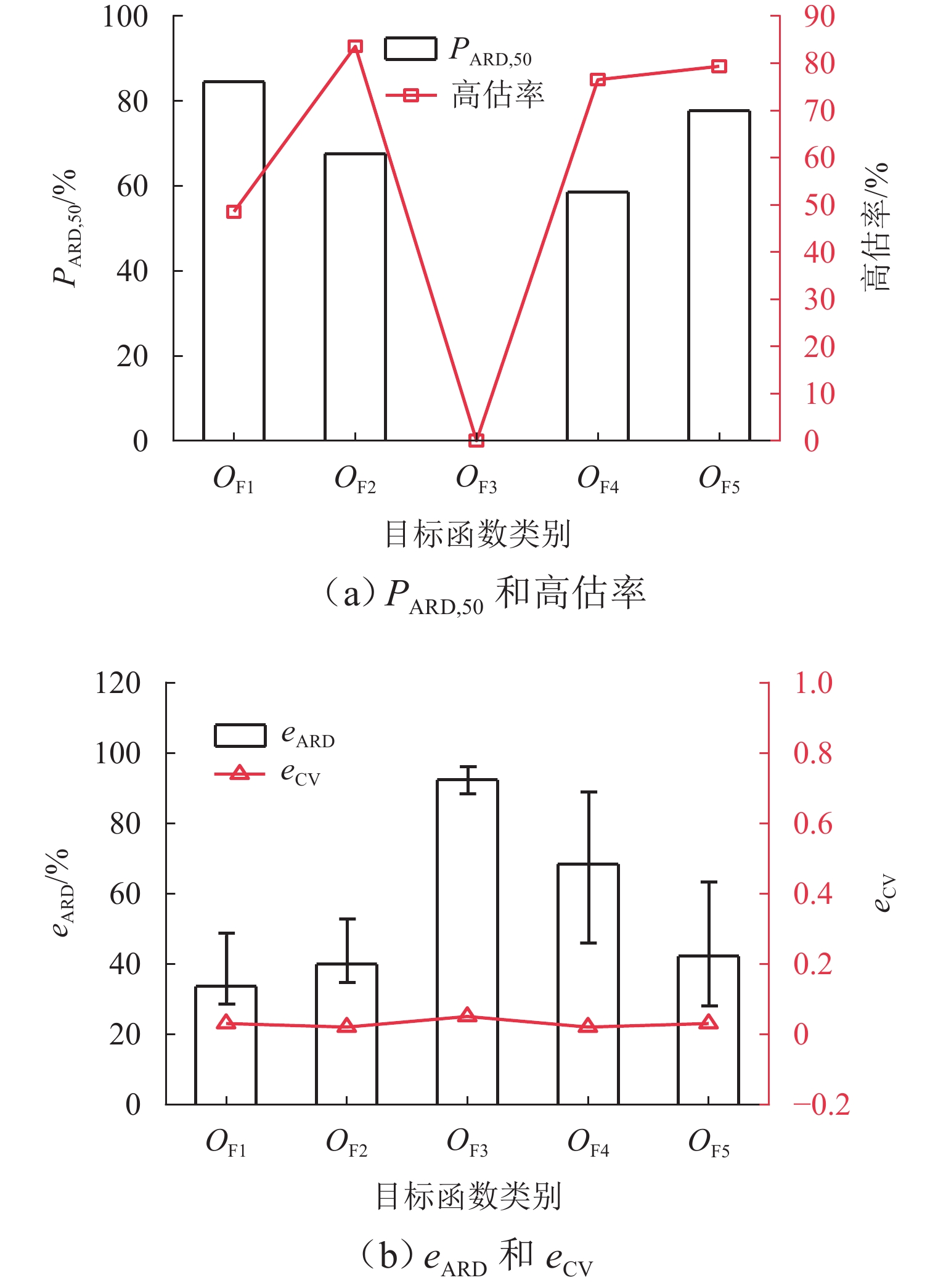
不同目标函数的偏差较大，如图6所示. $ O_{{\mathrm{F}}_2} $的高估率最大，为83.56%；$ O_{{\mathrm{F}}_4} $、$ O_{{\mathrm{F}}_5} $相差不大，均为78.00%左右；$ O_{{\mathrm{F}}_1} $为48.52%，由此可见，使用目标函数$ O_{{\mathrm{F}}_2} $的高估情况较好. 通过$ {P_{{\text{ARD,50}}}} $，e_ARD评估反演结果的准确性，目标函数$ O_{{\mathrm{F}}_1} $准确性最好，$ {P_{{\text{ARD,50}}}} $为84.52%，e_ARD的置信区间为38.38% ± 9.94%；目标函数$ O_{{\mathrm{F}}_3} $准确性最低，$ {P_{{\text{ARD,50}}}} $为0，e_ARD的置信区间为91.88% ± 4.44%. 各目标函数的稳定性均较好，$ e_{\mathrm{CV}} $<0.100. 在单参数的e_ARD目标函数$ O_{{\mathrm{F}}_1} $最低，稳定性较好.

图  6  单参数情形下源强反演对比

Figure  6.  Comparison of source intensity inversions in one-parameter case

下载: 全尺寸图片 幻灯片

3.3   两参数反演情形

3.3.1   源强反演性能分析

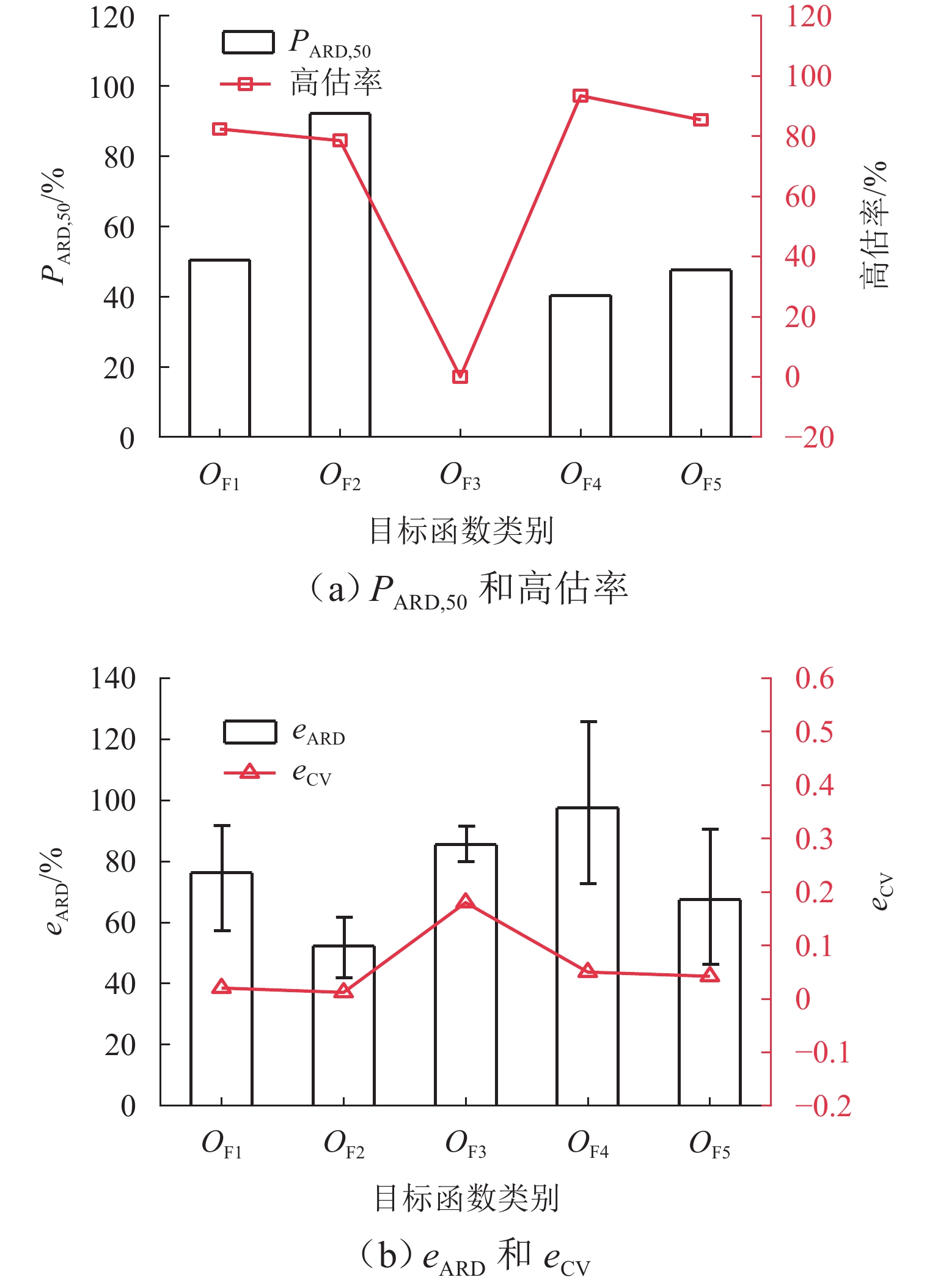
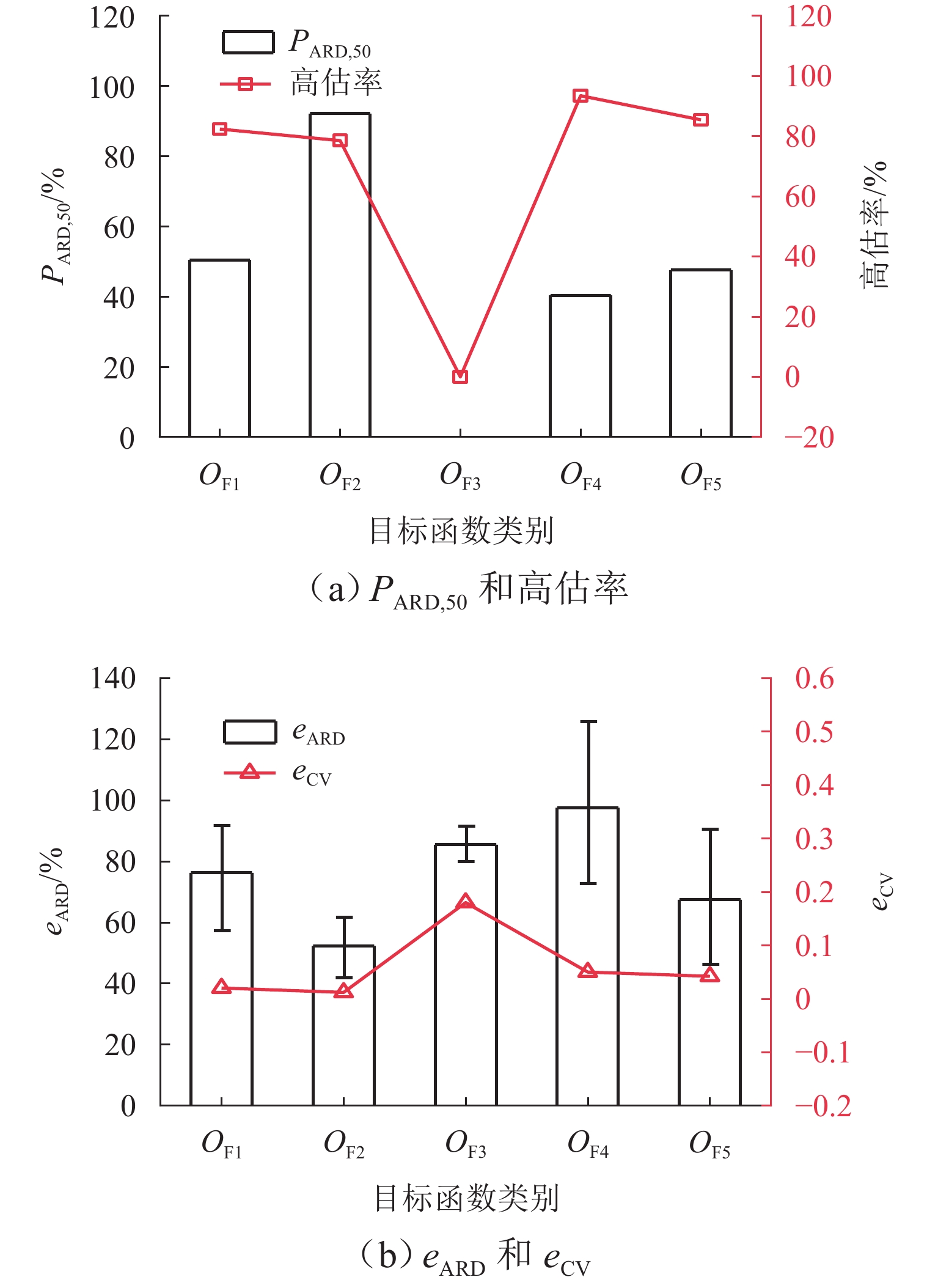
图7展示两参数情形下源强反演的对结果. 目标函数$ O_{{\mathrm{F}}_4} $的高估情况较好，高估率最大，为93.45%. 目标函数$ O_{{\mathrm{F}}_2} $准确性最高，$ {P_{{\text{ARD,50}}}} $为92.16%，且e_ARD的置信区间为51.42% ± 9.84%；其次为$ O_{{\mathrm{F}}_1} $，e_ARD的置信区间为68.78% ± 22.46%；$ O_{{\mathrm{F}}_4} $的高估率最大，e_ARD的置信区间为99.42% ± 27.08%，因此，在两参数反演情形下，$ O_{{\mathrm{F}}_2} $目标函数最优. 除$ O_{{\mathrm{F}}_3} $外，其余各目标函数的稳定性均较好，e_CV<0.100. 在两参数反演情形下，目标函数$ O_{{\mathrm{F}}_2} $反演结果准确且稳定，这可能是由于$ O_{{\mathrm{F}}_2} $弱化了城市交通拥塞点源参数反演结果的极值影响.

图  7  两参数情形下源强反演对比

Figure  7.  Comparison of source intensity inversions in two-parameter case

下载: 全尺寸图片 幻灯片

3.3.2   位置反演性能分析

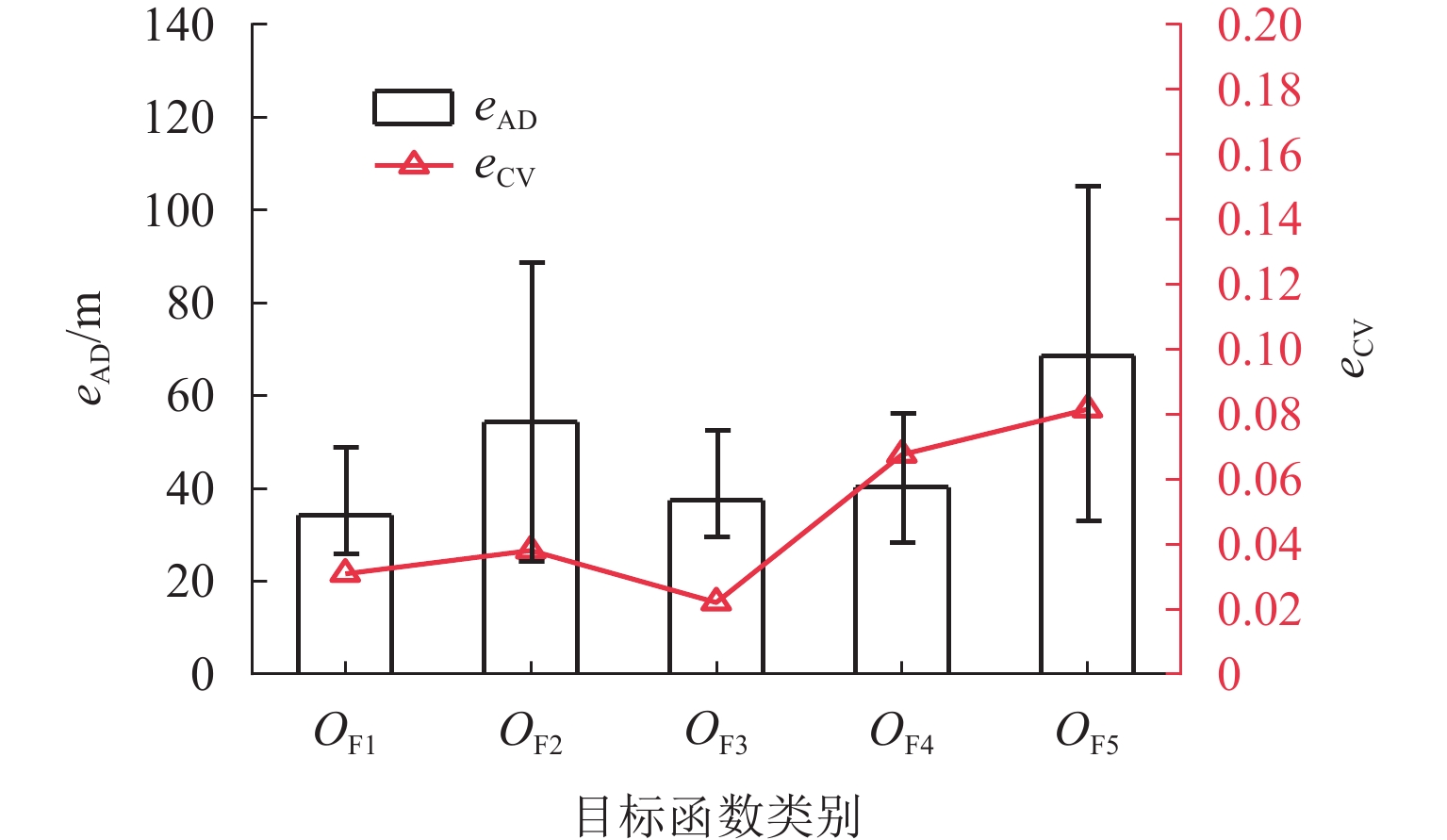
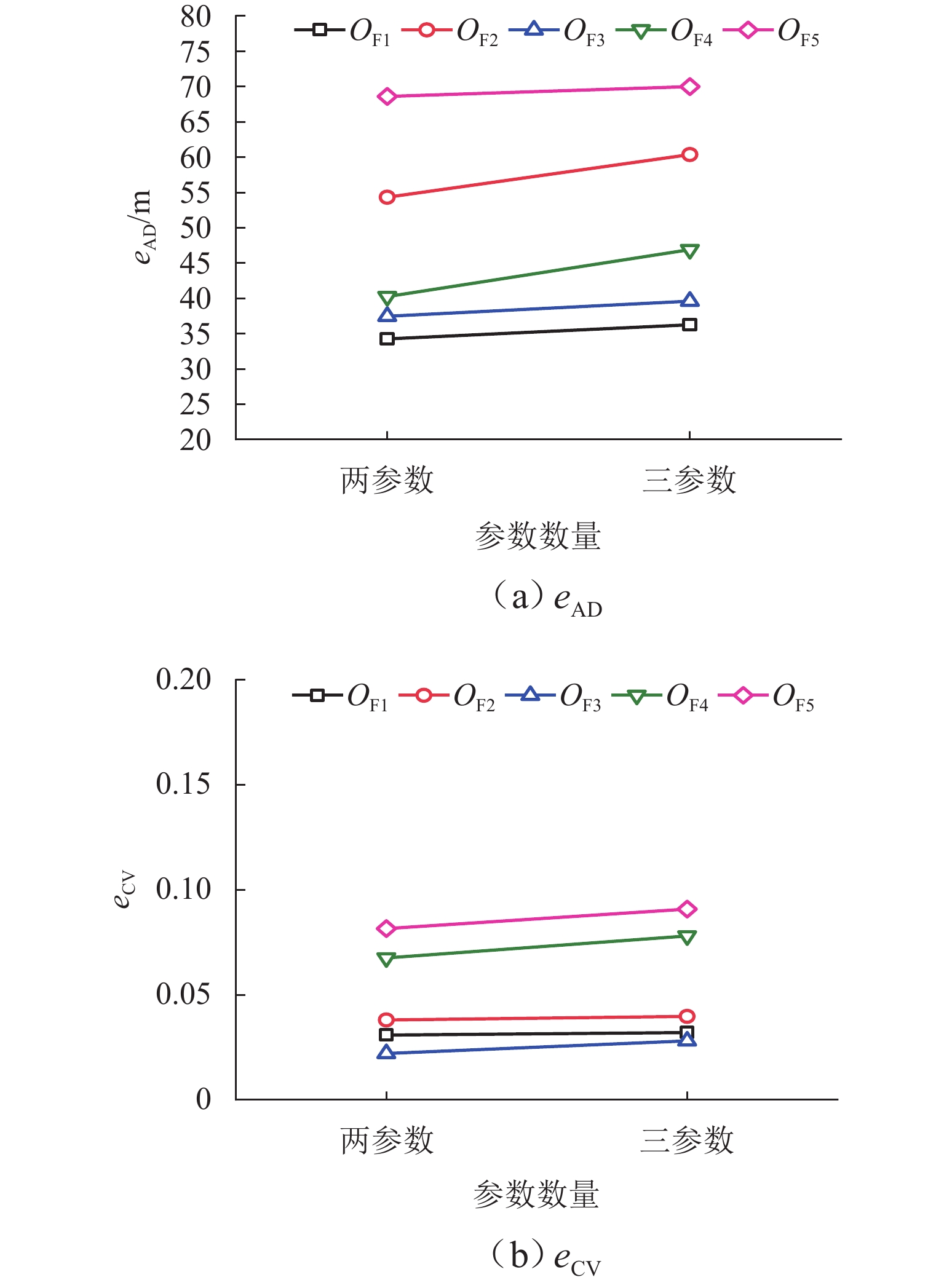
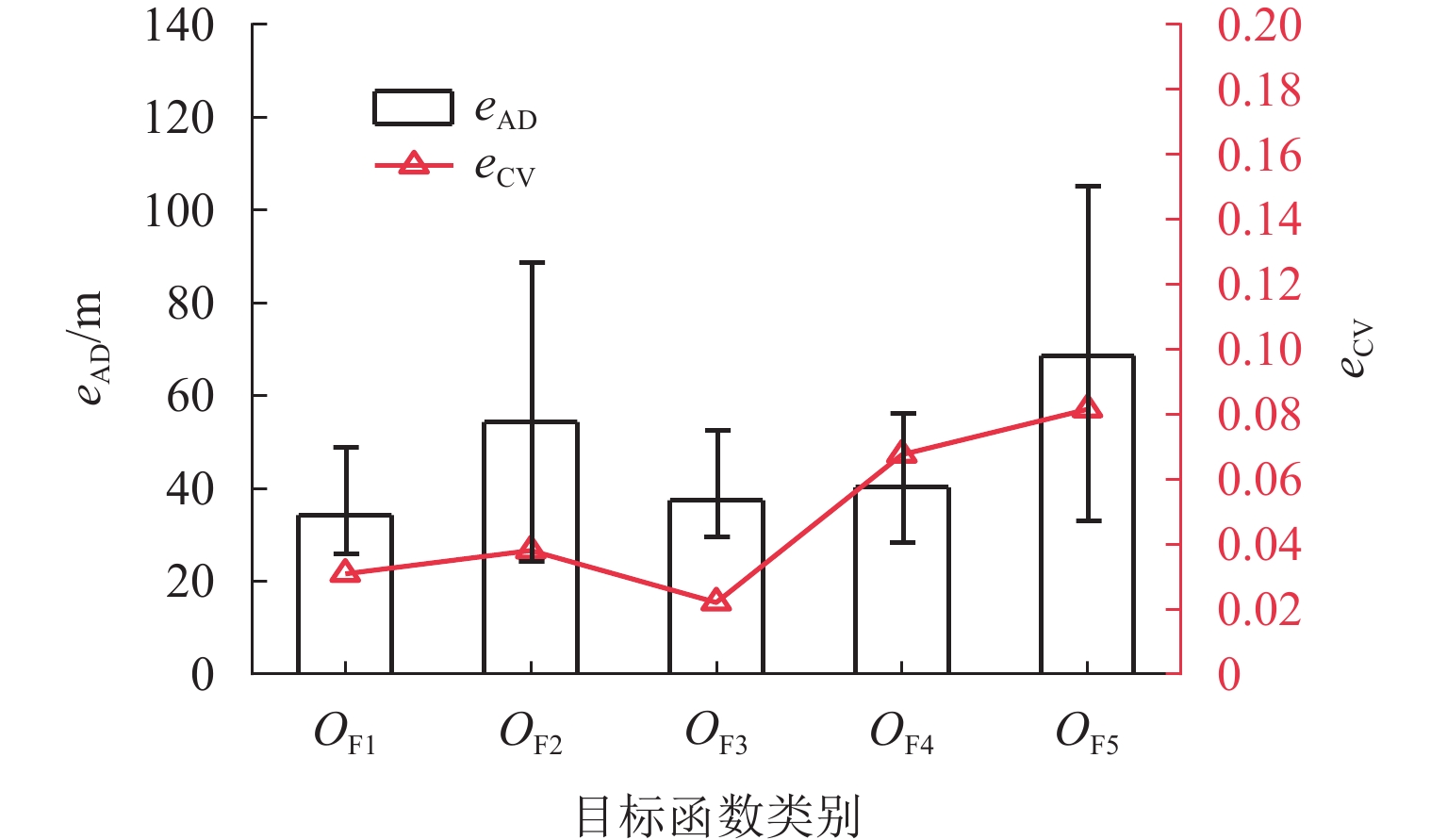
由图8可以看出两参数情形下，不同目标函数差异明显. 通过e_AD、e_CV评估反演结果的准确性和稳定性. 根据e_AD，目标函数$ O_{{\mathrm{F}}_1} $的值最小，置信区间为37.22 m ± 10.64 m；$ O_{{\mathrm{F}}_3} $次之，置信区间为41.82 m ± 11.36 m；$ O_{{\mathrm{F}}_5} $最大，置信区间为69.76 m ± 35.57 m. 目标函数$ O_{{\mathrm{F}}_1} $准确性略高于$ O_{{\mathrm{F}}_3} $，在目标函数中表现最好. 各目标函数变异系数均低于0.100，$ O_{{\mathrm{F}}_3} $最低，为0.022. 在两参数反演情形下，目标函数$ O_{{\mathrm{F}}_1} $准确性最好，$ O_{{\mathrm{F}}_3} $的稳定性最强，$ O_{{\mathrm{F}}_5} $稳定性最差.

图  8  两参数情形下位置反演对比

Figure  8.  Comparison of position inversions in two-parameter case

下载: 全尺寸图片 幻灯片

3.4   三参数反演情形

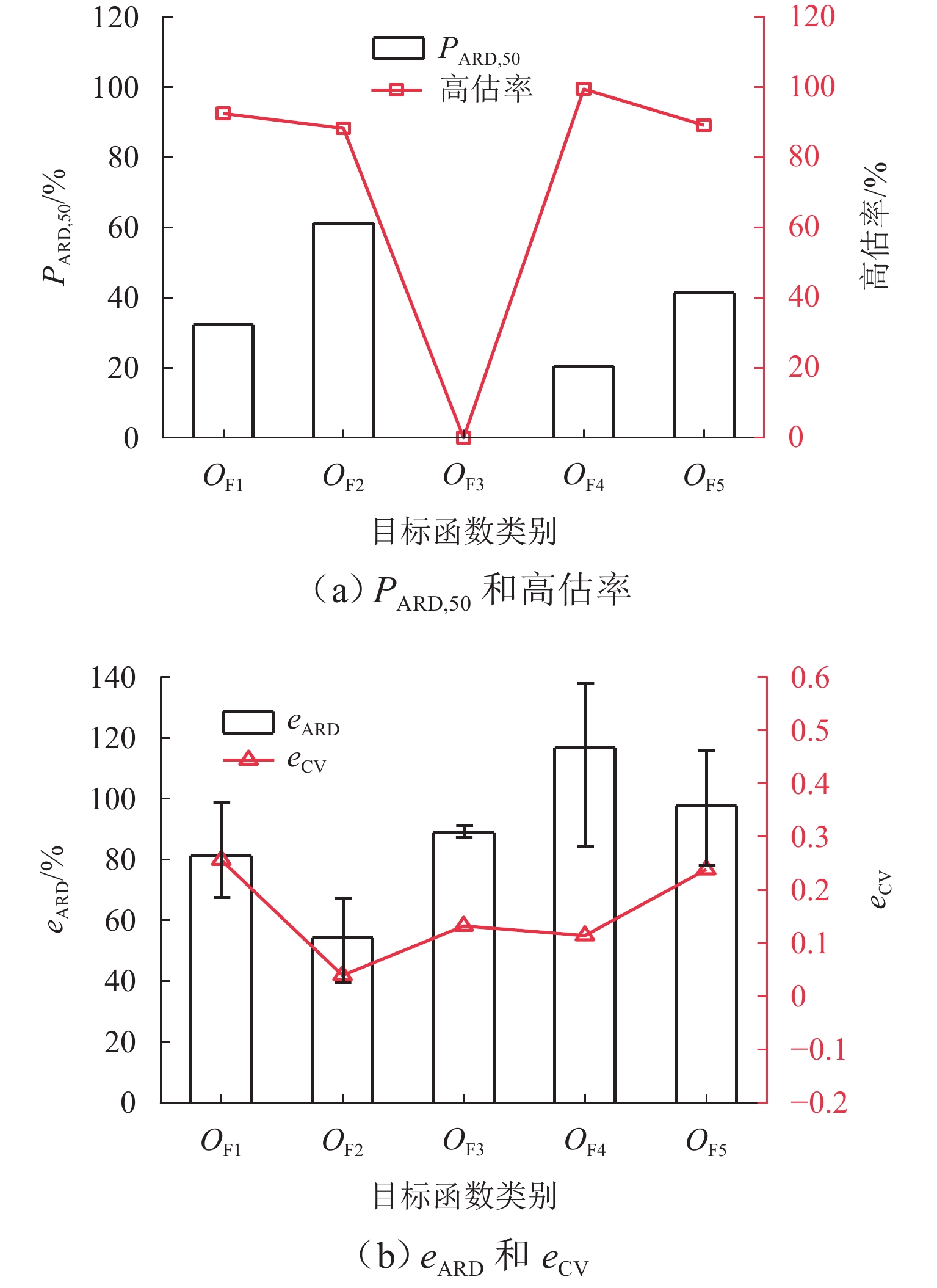
3.4.1   源强反演性能分析

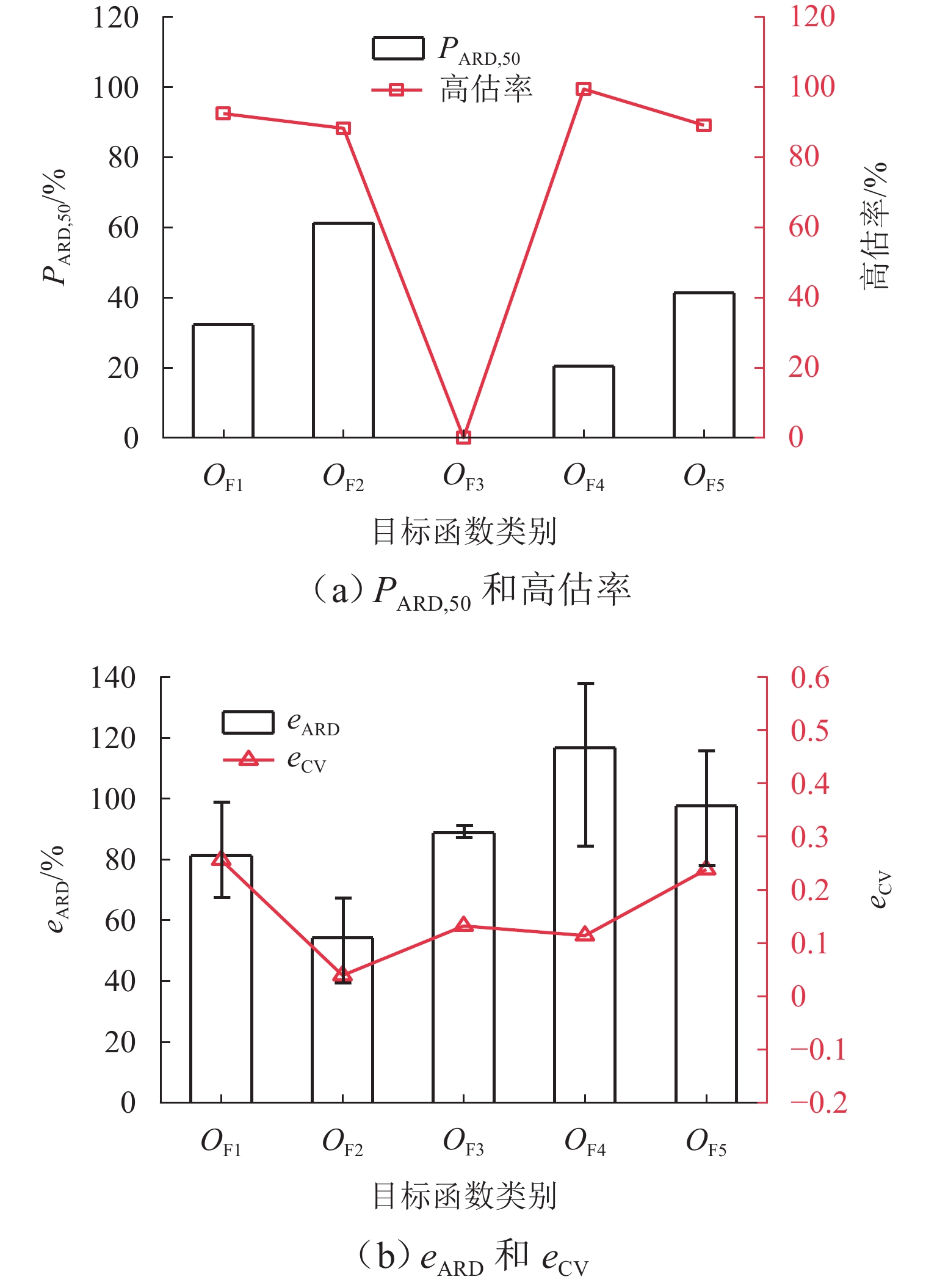
由图9可以看出，目标函数$ O_{{\mathrm{F}}_4} $高估情况最好，高估率为99.45%. 目标函数$ O_{{\mathrm{F}}_2} $准确性最好，$ {P_{{\text{ARD,50}}}} $为61.24%，且e_ARD的置信区间为53.85% ± 14.40%，其次为$ O_{{\mathrm{F}}_1} $，置信区间为83.50% ± 15.96%，最高为$ O_{{\mathrm{F}}_4} $，置信区间为110.41% ± 27.29%. 因此，在三参数反演情形下，目标函数$ O_{{\mathrm{F}}_2} $最优. 除$ O_{{\mathrm{F}}_2} $外，其余各目标函数稳定性均较差，e_CV>0.100. 目标函数$ O_{{\mathrm{F}}_2} $明显优于其他目标函数，这与两参数反演情形结论相互对应，可见当城市交通拥塞源的参数较多时，反演结果更准确，适用于单点源城市交通拥塞复杂的场景.

图  9  三参数情形下源强反演对比

Figure  9.  Comparison of source intensity inversions in three-parameter case

下载: 全尺寸图片 幻灯片

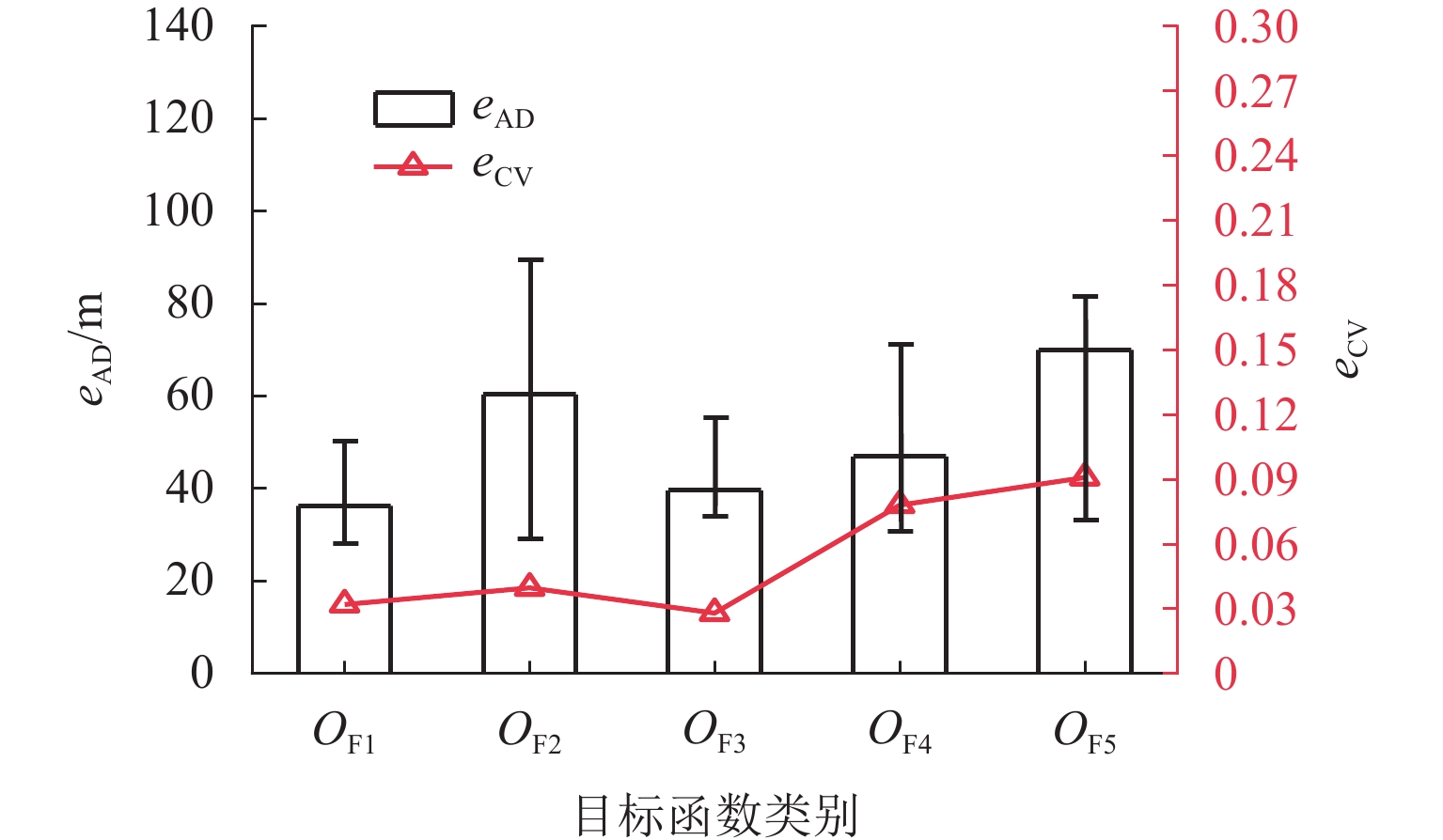
3.4.2   位置反演性能分析

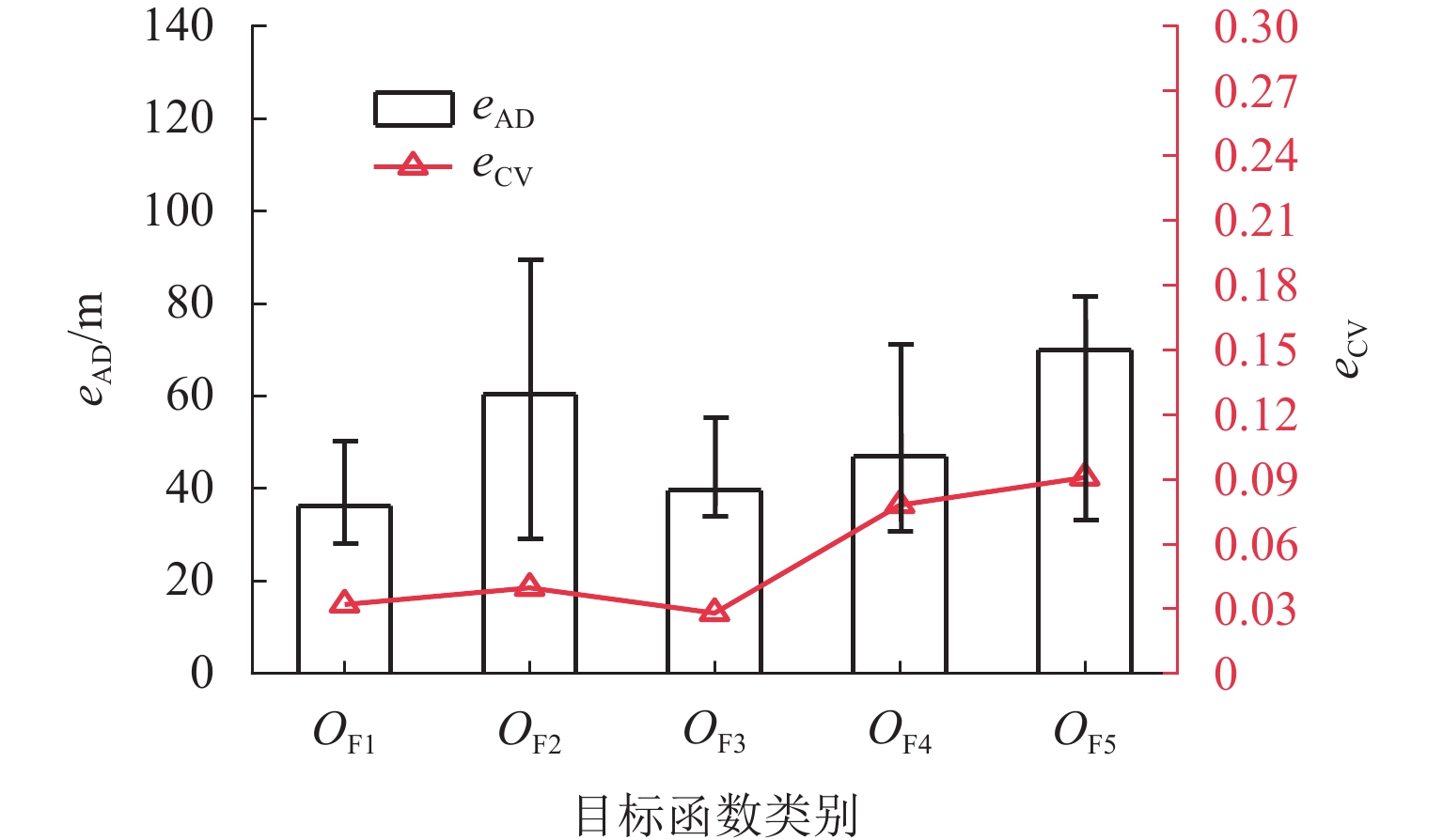
由图10可以看出，三参数情形下，不同目标函数差异明显. 根据e_AD，目标函数$ O_{{\mathrm{F}}_1} $的值最小，置信区间为（38.64 ± 10.95） m；$ O_{{\mathrm{F}}_3} $次之，置信区间为（45.05 ± 10.20） m；$ O_{{\mathrm{F}}_2} $最大，置信区间为（59.01 ± 29.43） m. 目标函数$ O_{{\mathrm{F}}_1} $准确性略高于$ O_{{\mathrm{F}}_3} $，在目标函数中表现最好. 各目标函数变异系数均e_CV低于0.100，$ O_{{\mathrm{F}}_3} $最低为0.028. 在三参数反演情形下，稳定性最强，$ O_{{\mathrm{F}}_5} $稳定性最差，这与两参数反演情形结论相互对应.

图  10  三参数情形下位置反演对比

Figure  10.  Comparison of position inversions in three-parameter case

下载: 全尺寸图片 幻灯片

3.5   不同目标函数源强反演参数对比

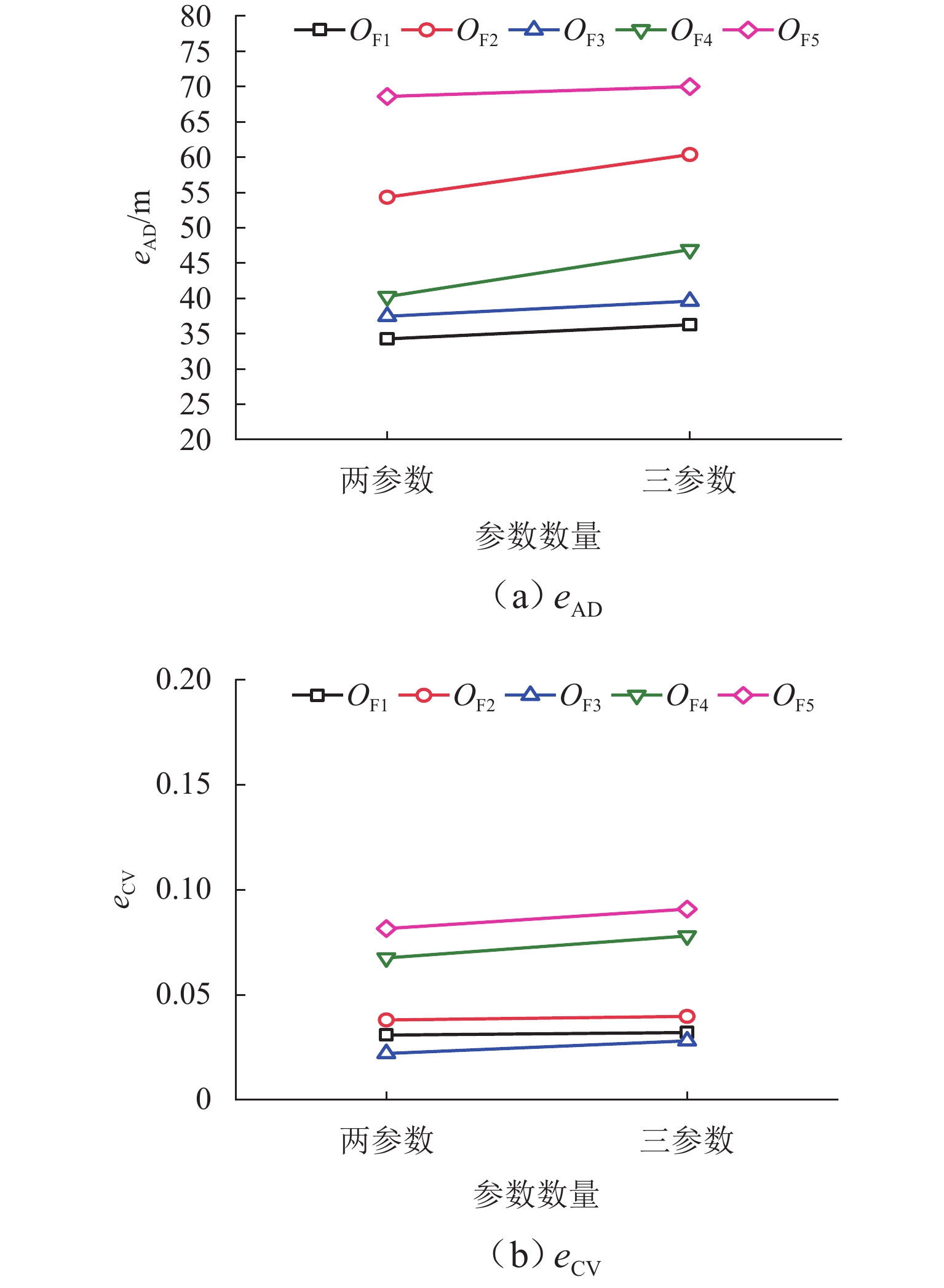
由图11可以看出，参数数量越多，目标函数$ O_{{\mathrm{F}}_2} $的$ {P_{{\text{ARD,50}}}} $和e_ARD更好，$ O_{{\mathrm{F}}_2} $、$ O_{{\mathrm{F}}_3} $的高估率变化影响较小. 目标函数$ O_{{\mathrm{F}}_3} $性能较差，可能由于受到相关性系数函数本身结构的影响. 目标函数$ O_{{\mathrm{F}}_2} $反演性能最为稳定，一直在较低变异水平.

图  11  源强反演性能对比

Figure  11.  Comparison of source intensity inversion performance

下载: 全尺寸图片 幻灯片

3.6   不同目标函数位置反演参数对比

由图12可以看出，反演参数数量越多，目标函数$ O_{{\mathrm{F}}_2} $准确性越高，$ O_{{\mathrm{F}}_1} $、$ O_{{\mathrm{F}}_3} $的e_AD变化较小，目标函数$ O_{{\mathrm{F}}_1} $准确性最好，且始终处于较低变异水平，适用于城市交通拥塞“单点源”在高峰小时内的交通稳定扩散阶段，此时各参数变化微小.

图  12  位置反演性能对比

Figure  12.  Comparison of position inversion performance

下载: 全尺寸图片 幻灯片

4.   结　论

本文得到的主要结论如下：

1） 将城市交通拥塞扩散传播类比为大气污染物传播，构建基于高斯烟羽模型的城市交通拥塞传播模型，可以更好地实现对城市交通拥塞传播的内在规律研究.

2） 通过Griewank、Schaffer和Rastrigin 3种经典函数通过对3种求解模型的启发式算法进行对比，最终综合确定SOA作为“单点源”参数反演优化算法.

3） 通过构建5种目标函数评估SOA的优化性能. 仅反演“单点源”交通流量$ Q_{\mathrm{c}} $的情形（单参数）下，目标函数$ O_{{\mathrm{F}}_2} $更优.

4） 从准确性来看，在单参数反演源强情形下，目标函数$ O_{{\mathrm{F}}_1} $最优，但在两参数、三参数情形下，目标函数$ O_{{\mathrm{F}}_2} $更优. 在两、三参数位置反演情形下，目标函数$ O_{{\mathrm{F}}_1} $准确性最高.

5） 从稳定性出发，在单参数反演源强情形下，各目标函数的稳定性均较好，e_CV<0.100. 但在两参数情形下，除$ O_{{\mathrm{F}}_3} $外，其余各目标函数的稳定性均较好；在三参数情形下，除$ O_{{\mathrm{F}}_2} $外，各目标函数的稳定性均较差，其中$ O_{{\mathrm{F}}_1} $稳定性最差（e_CV=0.256）. 在两、三参数位置反演情形下；目标函数$ O_{{\mathrm{F}}_3} $的稳定性最强，目标函数$ O_{{\mathrm{F}}_5} $稳定性最差.