Development and Prediction of Ruts in Airport Asphalt Pavement Based on Full-Scale Test
-
摘要:
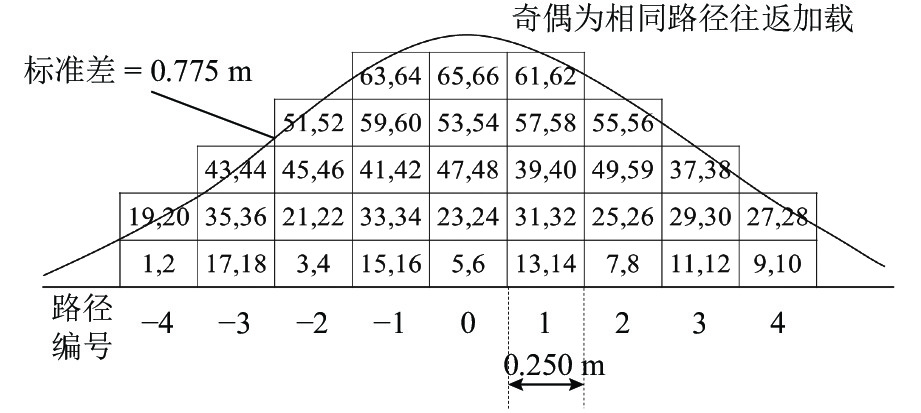
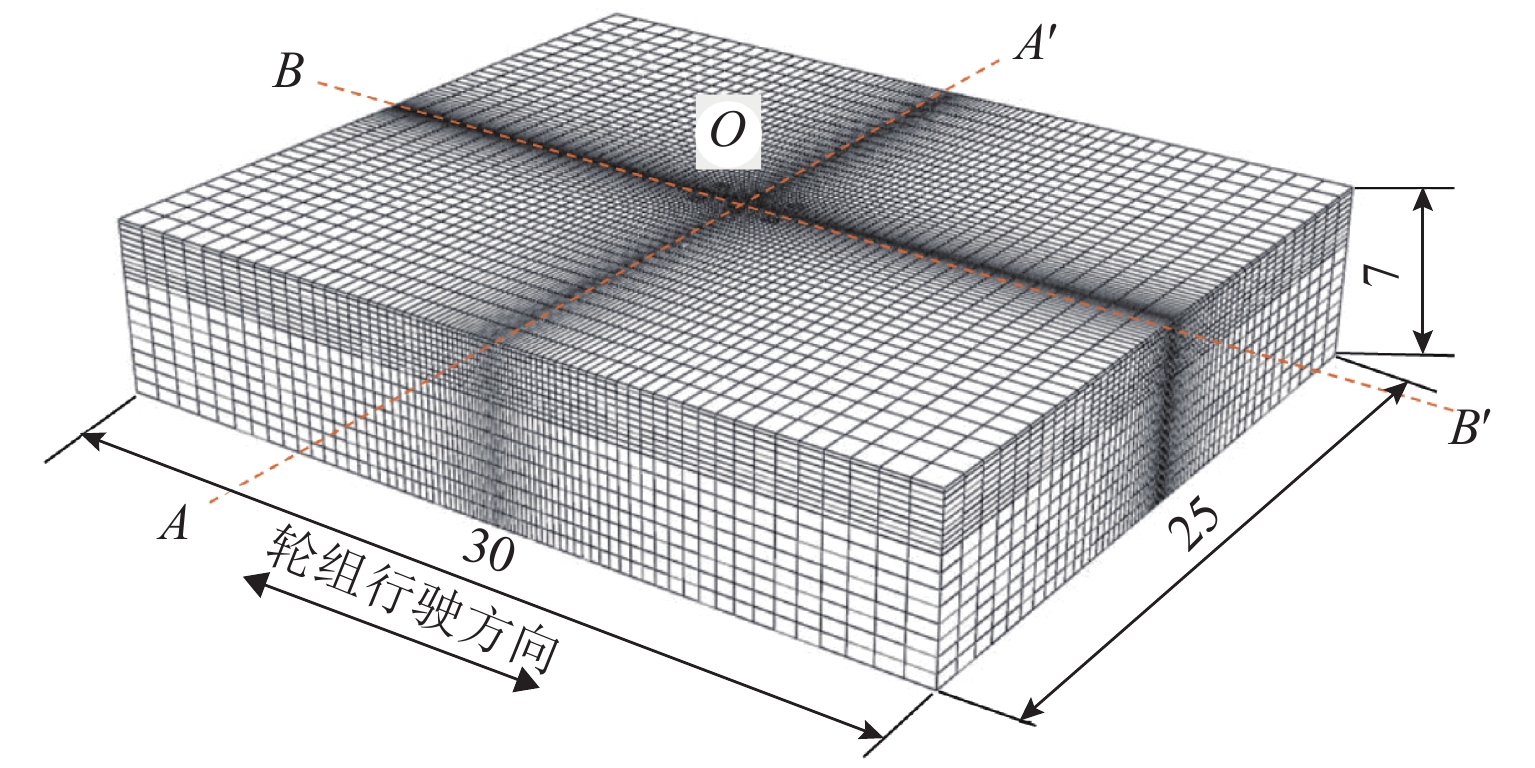
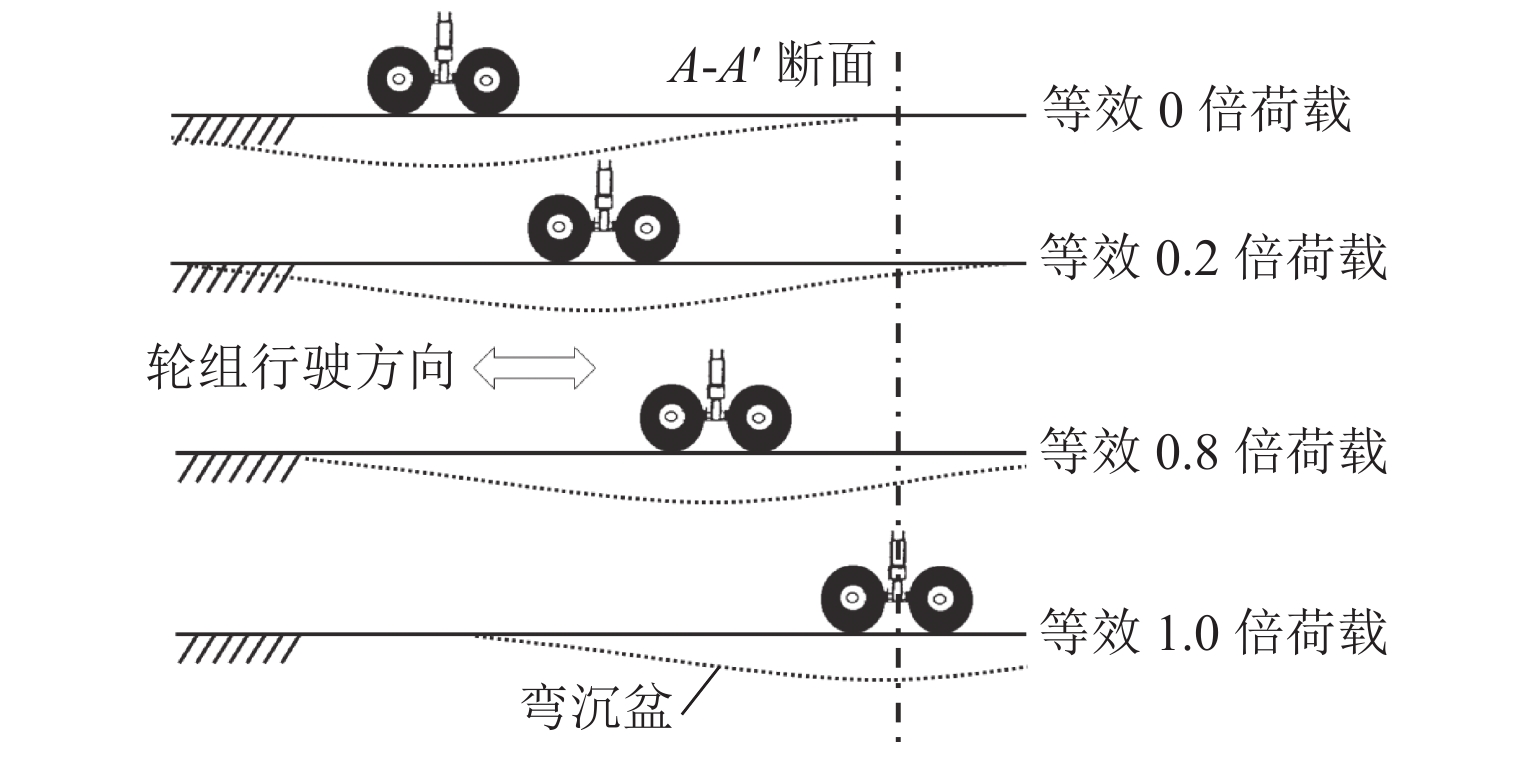
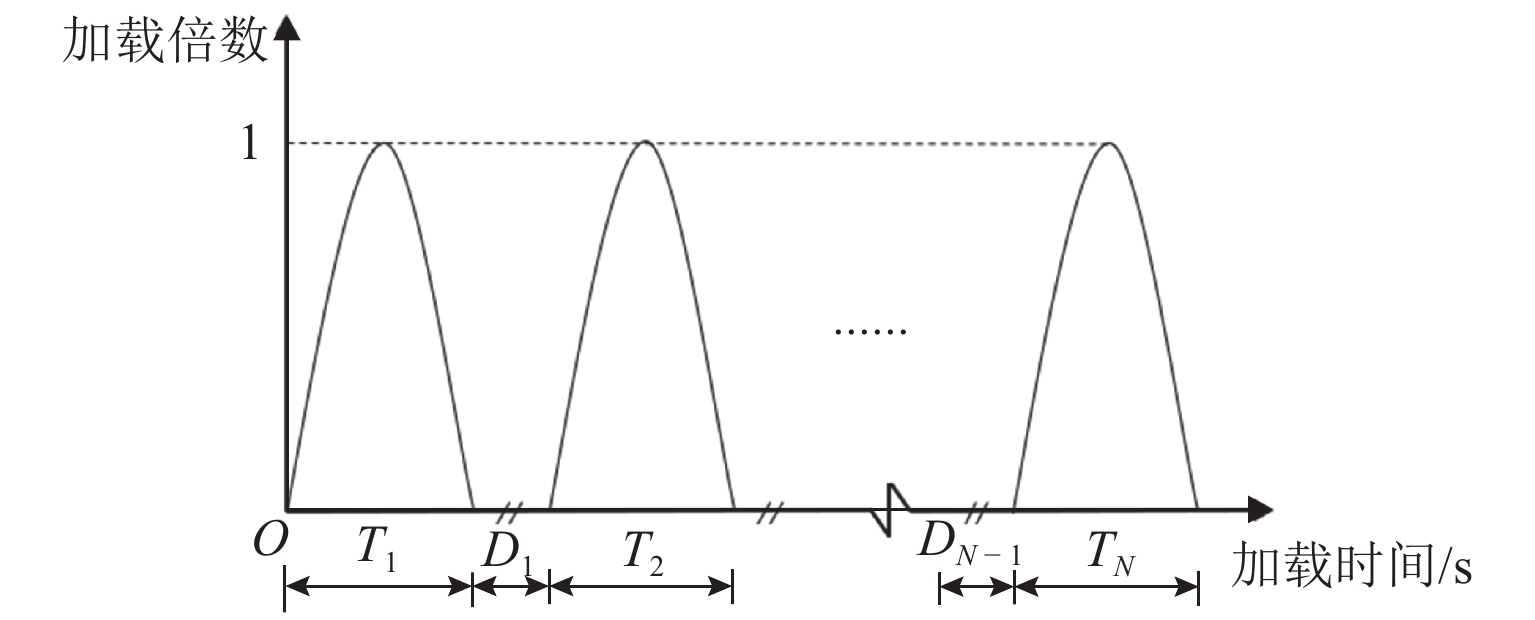
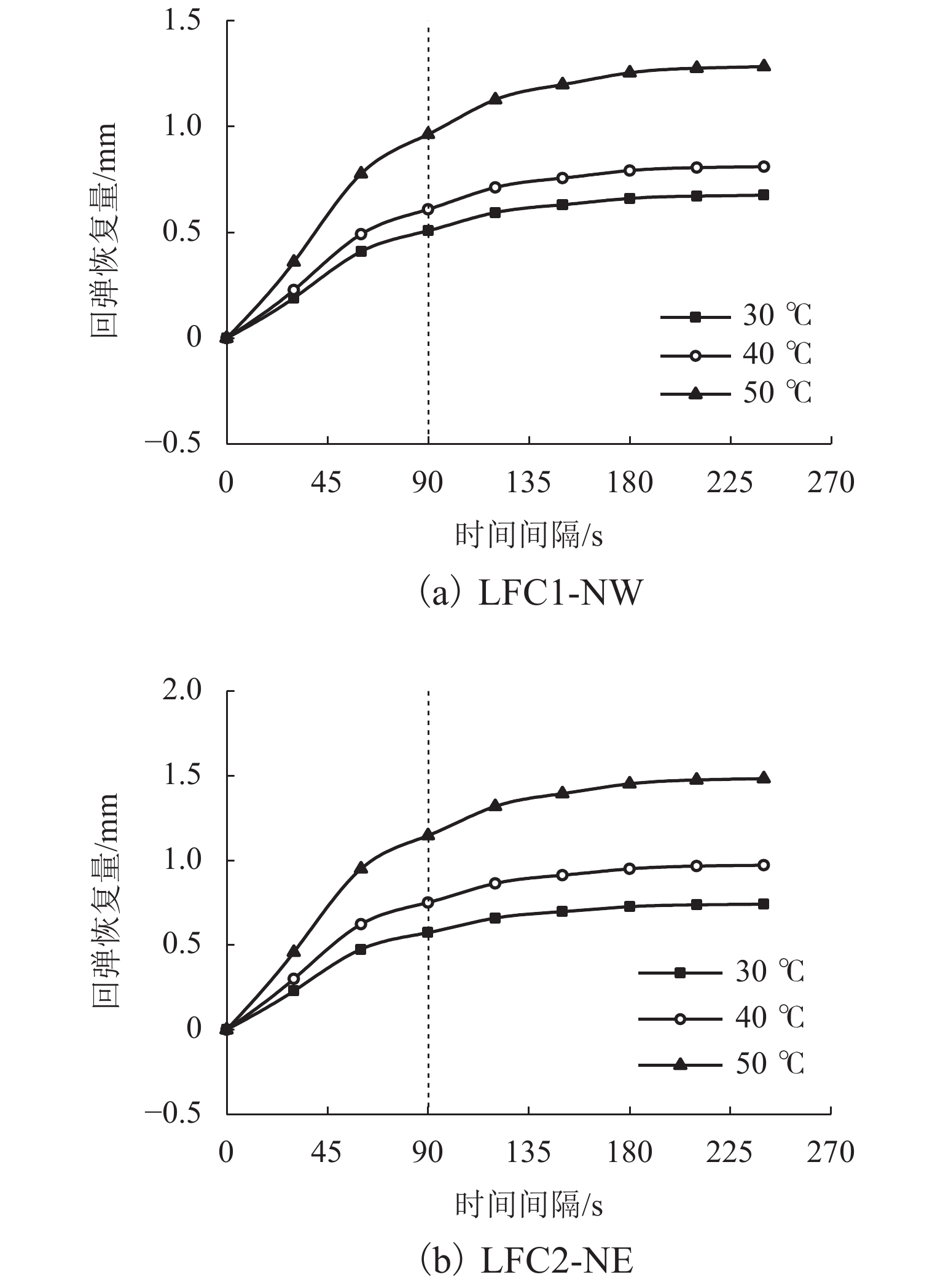
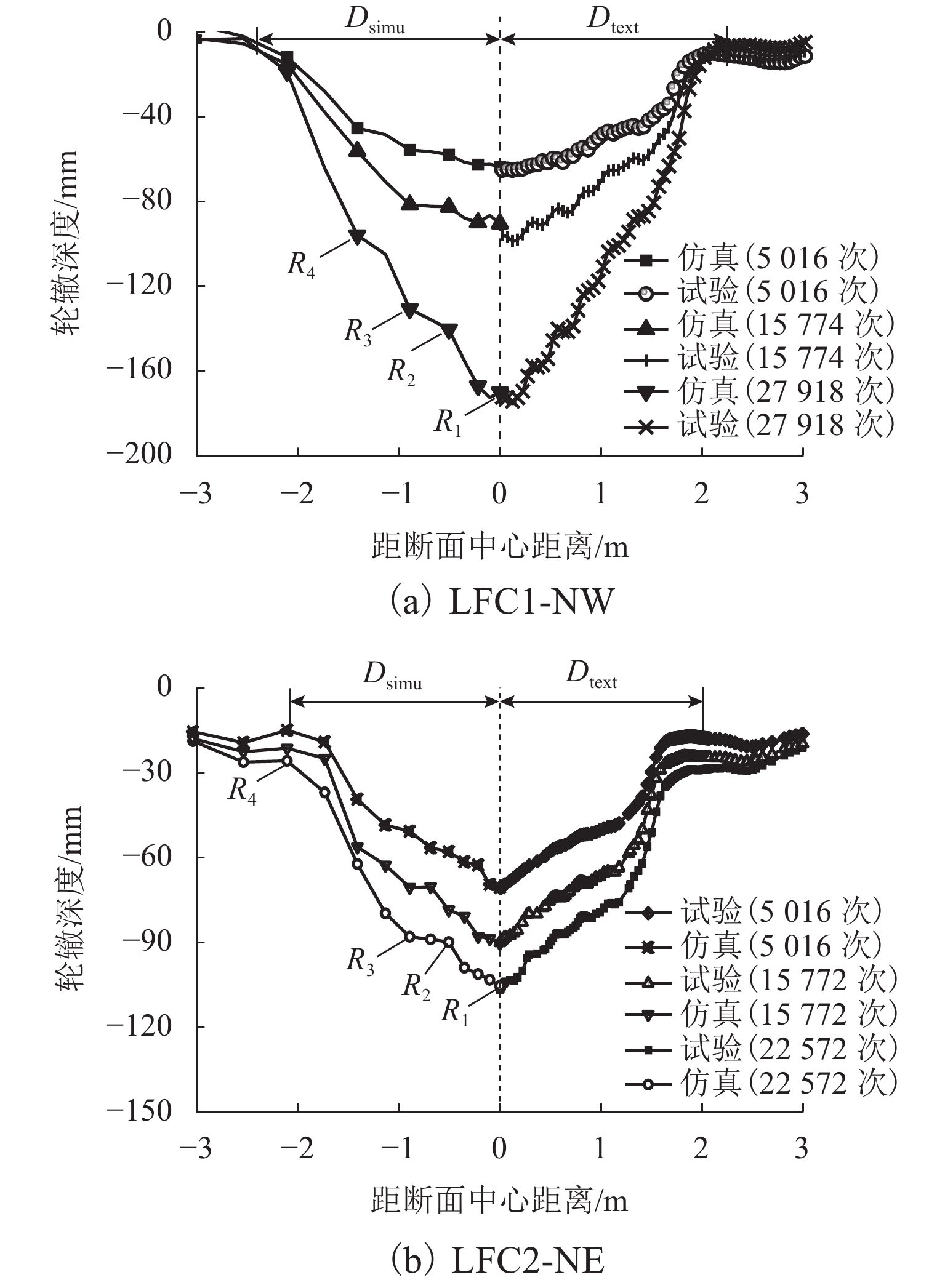
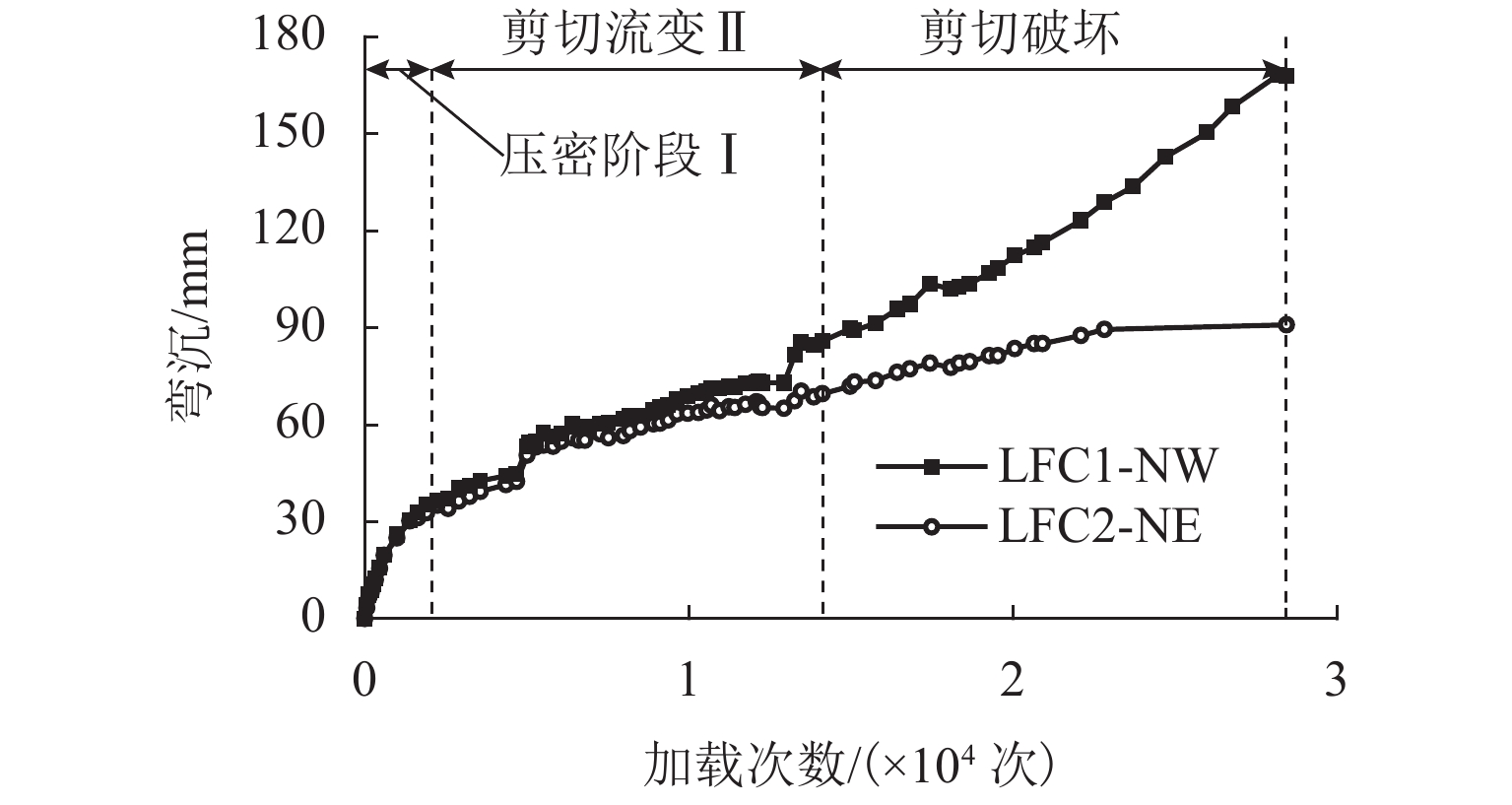
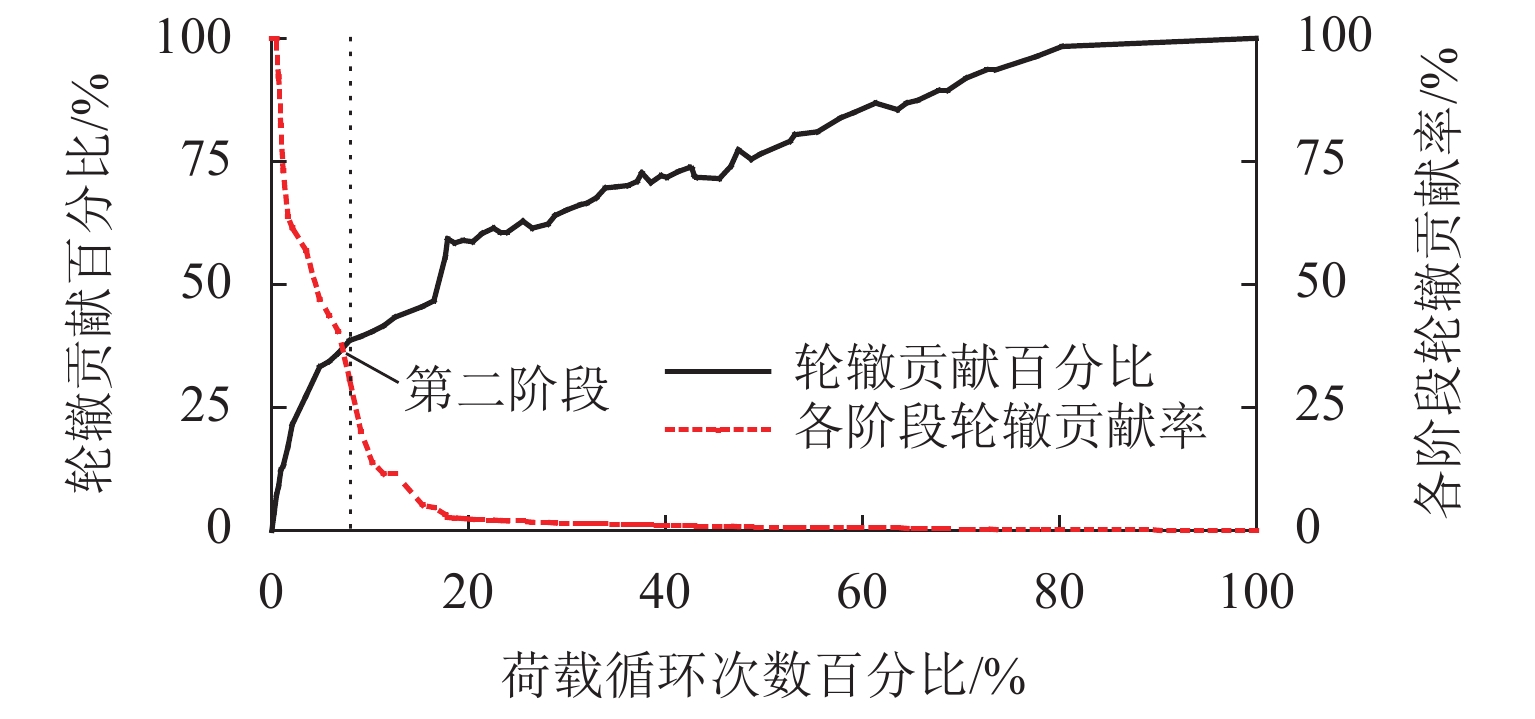
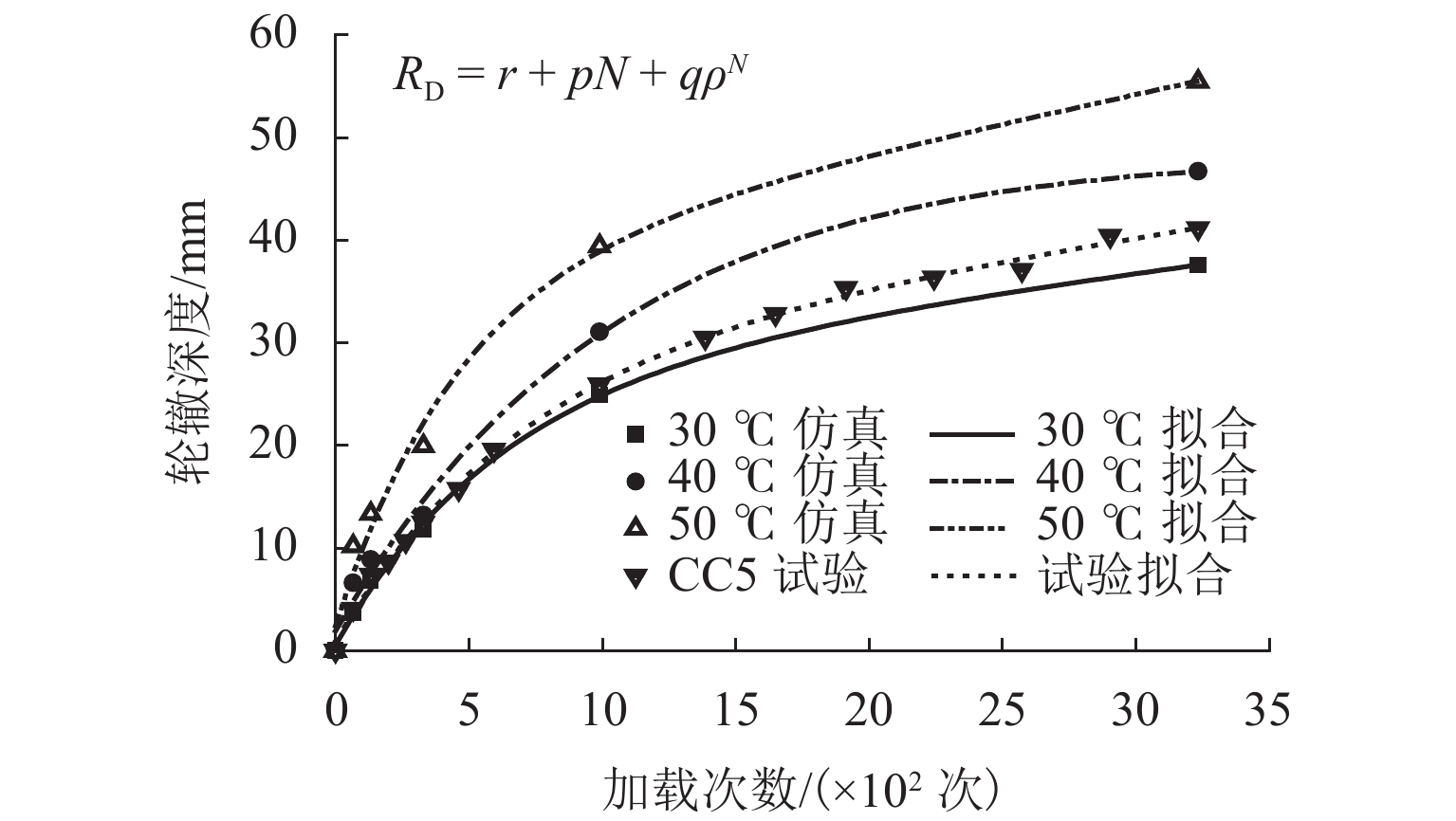
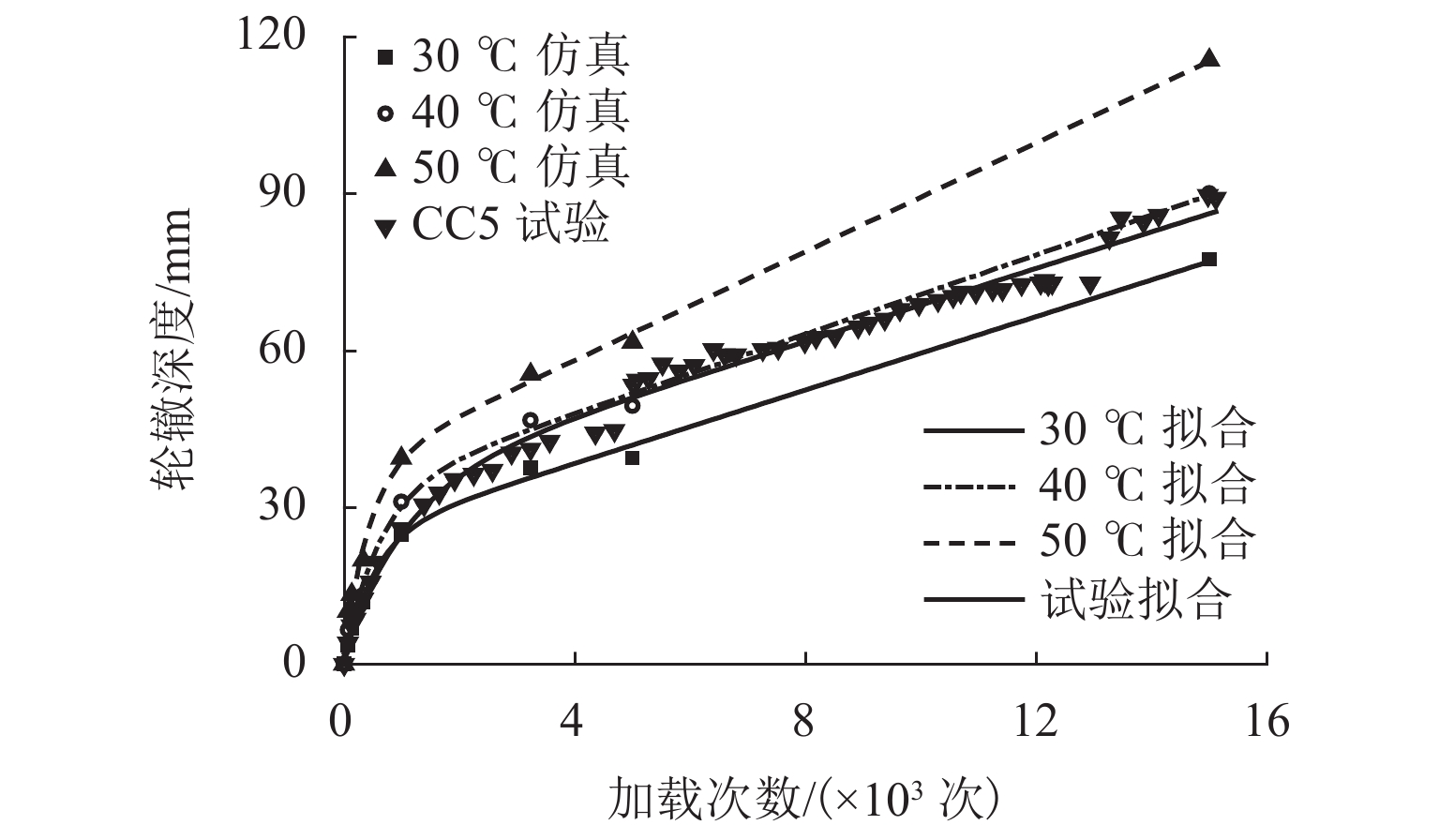
轮辙是引起沥青道面过早破坏的重要因素，飞机地面滑行渠化交通显著，由轮辙病害引起的道面平整度与舒适性问题突出. 为此，建立飞机轮组-地基-沥青道面结构体系仿真分析模型，提出适应轮组荷载特征的等效循环加载方式，依托NAPTF （National Airport Pavement Test Facility）足尺沥青道面轮辙试验，验证仿真结果的适用性与可靠性，并开展加载时间间隔与环境温度等多因素分析. 研究结果表明：考虑轮载作用横向偏移效应，轮辙总宽度达到轮组宽度的3倍，轮辙断面曲线有多处转折点与以往单一凹陷面特征明显不同；循环加载时间间隔对轮辙发展影响显著，经过150 s间隔后沥青面层回弹变形趋于稳定，可兼顾分析效率需要；前10%循环加载次数对轮辙变形的贡献超过40.4%，可基于初始轮辙建立指数型轮辙发展预测公式，对循环加载全过程拟合度高于96.4%，轮辙分析效率有明显提高.
Abstract:Ruts can be one of the key reasons for early damage of asphalt pavement. Due to the channelized traffic characteristics of aircraft taxiing, the evenness and comfort of airport pavement are notably affected by rut damage. In this paper, a simulation analysis model of aircraft landing gears-foundation-asphalt pavement system is established. An equivalent cyclical loading process is proposed according to the loading characteristic of landing gears. The feasibility and reliability of the simulation model are verified by the rut test result of full-scale asphalt pavement conducted by National Airport Pavement Test Facility (NAPTF). Factors such as the loading interval and environment temperature are then analyzed. The results show that due to lateral shift effect of landing gear load, the total width of the ruts reaches 3 times the width of the landing gears, and the rut section curve has many turning points, which is obviously different from those of the previous single concave surface. The cyclical loading interval has a remarkable influence on rut development. The rebound deformation of the asphalt surface course becomes stable after a loading interval of 150 s, which can meet the requirement of analysis efficiency. Since the first 10% number of cyclical loading contributes more than 40.4% of overall rut deformation, an exponential rut deformation prediction formula is derived based on initial ruts. The goodness of fit result during the whole cyclical loading process is over 96.4%, and the efficiency of rut analysis is dramatically increased.
-
Key words:
- road engineering /
- pavement ruts /
- asphalt pavement /
- rut test /
- loading waveform /
- cyclic loading
-
随着基础设施建设的推进，公路与铁路工程建设中为了保证线路的顺直，越来越多的隧道衬砌结构工程穿行大型滑坡区域，形成滑坡-隧道相互作用、相互影响的工程特征[1]，隧道衬砌结构势必会承受滑坡推力作用，当滑坡作用力足够大时，隧道衬砌结构会产生相应变形或破坏.
目前，国内外对这种滑坡-隧道相互作用的特征及机理投入了较多关注，主要表现在三方面，一是对滑坡-隧道相互作用模型体系进行了总结与归纳，如吴红刚等[2]从滑面与隧道相处位置出发，建立了以平行体系、正交体系和斜交体系为核心的较为完备的受力变形模式；张鲁新等[3]分析了滑坡与隧道变形特征并提出五种地质结构模型；陈小云等[4]对于正交体系下隧道与滑带相交力学模型进行了研究. 二是采用多种手段研究了滑坡作用下隧道衬砌结构受力机理以及滑坡-隧道相互作用机理，如陶志平[5]采用室内模型试验方法，分析了滑坡地段隧道的变形机理，研究了隧道围岩和隧道衬砌压力的变化规律；毛坚强等[6]运用接触面来模拟滑面，应用有限元算法分析了滑坡-隧道间的相互作用机理以及隧道的受力变形规律；陈刚[7]分别讨论了隧道开挖和降雨作用对滑坡体变形的影响；王旭[8]结合具体的工程实例，考虑隧道与滑面相对位置关系变化，计算了边坡的安全系数和隧道衬砌结构变形. 同时，国外一部分学者[9-14]确定了隧道在滑坡应力作用下的变形机理，并采用现代传感、监测新技术对滑坡-隧道模型进行研究. 另一部分学者[15-19]通过二维和三维数值模拟方法探讨隧道开挖诱发深部滑坡问题及隧道-滑坡相互作用机理. 特别地，Chiu等[20]通过隧道衬砌变形情况来反应滑坡作用下隧道所受作用力. 第三方面是滑坡-隧道治理措施上开展了卓有成效的研究，如杜升涛[21]通过选用抗滑桩支挡和排水工程综合治理的方案治理襄渝线赵家塘隧道滑坡；陶志平等[22]采用抗滑桩来治理滑坡地段隧道的变形问题；郑颖人等[23]以重庆某高速公路隧道出口段的滑坡治理工程为背景，采用有限元强度折减法研究了滑动面位置与抗滑桩位置和桩间距的关系. 总体来说，目前治理方式一般应用滑坡治理措施和隧道加固措施的原则，主要采用预应力锚索和抗滑桩等来治理滑坡，围岩注浆和增强隧道衬砌等方式来加固隧道，如赣龙铁路马蹄径隧道[24]和相田二号隧道[25]等. 虽然以上研究得了一定的成果，但所有研究主要依托于某一具体滑坡-隧道相互作用案例开展相关滑坡稳定性、隧道变形机理或治理措施相关的研究，还没有出现专门探讨滑坡滑带角度变化对隧道衬砌结构受力变化及对衬砌结构影响的相关研究.
因此，本文采用室内模型试验、数值模拟的方法，探讨针对不同滑带角度条件滑坡作用对隧道衬砌结构受力的影响，得到滑坡作用下偏压隧道衬砌受力[26]变化规律，这对于弥补滑坡-隧道相互作用研究的不足，更加清楚的掌握滑坡作用下隧道衬砌结构受力的变化有一定的现实意义.
1. 滑坡隧道室内模型试验设计
1.1 滑坡隧道工程实例
通过分析国内多个典型滑坡-隧道特征[1, 4, 26-28]可以得出，滑坡滑动带的倾角基本在0°～50°，破坏点基本位于拱脚处. 因此，以下研究主要以大（同）准（格尔）铁路K20南坪隧道为研究原型，考虑不同滑带角度作用下隧道衬砌结构受力变化特征及变化规律. 大（同）准（格尔）铁路K20南坪隧道洞顶回填区为宽缓平台，平台高程为1 205～1 207 m，宽43～77 m. 其地形、岩性结构剖面如图1. 其滑带与隧道夹角约为10°.
南坪隧道受滑坡影响变形较为严重，裂缝多位于拱壁墙边，以纵向为主最长达28 m. 在16～18避车间变形最大实测最大累计变形达24 mm （2016年1月14日—2016年5月1日），工务段实测最大累计变形达77 mm （2015年3月14日— 4月13日）. 避车洞墙边位移过大，导致水沟挤压变形：K20 + 082～K20 + 058段水沟被挤压扭曲，隧道表面混凝土面层产生脱落现象，位移量达28 cm；K20 + 41～K20 + 58段水沟受挤压，盖板鼓起，位移量达6 cm，在与滑带相交处产生了较大的局部剪切变形.
1.2 模型试验相似比
以南坪滑坡隧道为原型，几何比设为1∶100，将重要的滑坡体参数容重γ、黏聚力c、内摩擦角φ根据相似材料进行配比，隧道衬砌弹性模量E以及泊松比μ按照一定的比例进行配置. 按照相似比理论，各变量对应的相似比为CL=100，Cγ=1，Cμ=Cc=Cφ=1，Cσ=CE= 100，其中L为几何尺寸，σ为应力.
1.3 模型试验设计与制作
根据几何相似比，试验模型长2.5 m，宽0.5 m，高0.9 m，如图2. 滑带厚度为3.0 cm，滑动区为滑动面的角度分别设为0°、10°、20°、30°、40°、50°. 滑带材料采用黏性土加少量石膏，滑体由砾石粉粒分层压实组成，使其参数满足相似比要求. 滑床采用中等风化碎石同少量黏土石灰混合、夯实，以减少实验时不必要的沉降变形. 试验材料参数如表1.
表 1 模型试验材料力学参数Table 1. Mechanical parameters of model materials名称 密度 ρ/
（kg•m−3）E/MPa c/kPa φ/（°） 滑坡体 1 900 18.65 27.79 25.35 滑带 1 800 9.36 15.82 15.63 滑床 2 200 23.72 54.24 54.32 隧道衬砌 2 100 289.61 236.65 61.71 在滑体内部放置一长0.5 m、厚1.0 cm的石膏材料隧道. 模型隧道按照模型尺寸订做模具，模具材料为2.0 cm厚的PVC塑料板，并用螺杆穿起拼装为整体，隧道衬砌内模由两块弧形钢板拼成. 模具组装前，先在模具内铺设间距12.0 mm钢丝网，用螺杆拼接，采用石膏∶水＝2∶1比例进行隧道整体浇筑，形成模型试验用隧道结构.
模型试验按滑带角度0°、10°、20°、30°、40°、50° 分别制作相应模型进行试验，即一种滑带角度模型试验完成后，重新制作模型，进行下一种滑带角度模型试验.
1.4 测点布置
滑坡体表面设置位移计监测加载过程中位移变形情况（如图2）. 为了能够详细掌握不同滑带角度作用下隧道衬砌结构应力变化，内外分别布置20个应变片测点（N1～N20、W1～W20），如图3（a）所示. 在隧道横截面布置10个粘贴应变花的测点（J1～J10）监测隧道衬砌受剪情况（图3（b））. 微型压力盒（1～7）布置在隧道衬砌的外侧，用以监测隧道衬砌受到的滑坡推力或压力变化（图3（c））. 同时，为得到隧道衬砌结构上竖向压应力值，采用应变片的方法采集数据，应变片黏贴位置与图3（c）一致（图中未画出）.
1.5 加载方案
根据滑坡隧道演化规律，采用多级加载. 详细的装载方案见表2. 荷载施加在滑坡隧道模型的后缘. 在第一阶段，施加的荷载为500 N，保持20 min. 第二阶段施加1 000 N的荷载，并保持40 min. 从第三阶段到第六阶段，在20 min的时间间隔内平稳地增加了荷载，然后保持40 min，这一过程一直持续到滑坡模型破坏失效.
表 2 模型试验加载方案Table 2. Loading scheme in model test滑带角度/（°） 荷载/kN 加载时
间/min维持时
间/min0、10、20、30、40、50 0.5 10 20 1.0 10 20 5.0 20 40 10.0 20 40 15.0 20 40 20.0 30 40 25.0 30 40 1.6 试验结束标准
经过多次预试验及参考已有模型试验成果，模型试验结束标准选为坡体从隧道顶部滑出，同时加载测力计数值下降，此时判定为模型破坏、失效. 除坡体位移监测外，其他监测元件数据采用测力计为最大值时的监测值作为最终计算数据.
2. 模型试验结果与分析
2.1 模型试验破坏特征
依次开展了滑带角度为0°、10°、20°、30°、40°、50° 的滑坡隧道模型试验. 试验结束后，坡体产生两条裂缝，滑坡产生较大位移，隧道顶部的坡体（坡脚处）基本滑移出模型槽. 隧道顶部坡体表层位移监测点的位移如图4. 随着加载时间的推移，位移逐渐增长，滑带角度为0° 时，模型破坏时位移达到160 mm，滑带角度为50° 时，模型破坏时位移约10 mm. 可以看出：滑带角度越小，坡体变形越大，滑带角度越大，坡体变形越小. 另外，在模型加载初始阶段，滑带小角度变形增长最快，有突然增大过程，但滑带角度达到30° 以后，坡体位移初始阶段增长较慢. 同时，在滑坡推力作用下，隧道衬砌结构产生一定程度的变形，并且隧道衬砌结构相对于原位置产生了一定的位移，0° 时隧道所产生的位移最大约为10 mm，30° 时产生约4 mm的变形，50° 时几乎未产生位移. 可以得到，随着滑带角度的增大，在相同滑坡推力作用下，隧道的变形逐渐减小.
图 4 不同滑带角度条件下坡体位移Figure 4. Displacements of slope with various angles of sliding zone2.2 隧道衬砌结构受力特征
1） 弯矩与剪应力特征
根据图3中隧道衬砌结构上的应变片等测试元件，按照一定的关系式可以计算不同滑带角度下作用于隧道衬砌结构上的应力与弯矩值，如表3.
表 3 不同滑带角度下隧道弯矩与剪应力值Table 3. Bending and shear stress values of tunnel under different angles of sliding zone滑带角度/（°） 弯矩/（kN•m） 剪力/kN 0 
10 
20 
30 
40 
50 
从表3中可以看出：对于隧道衬砌结构上所受弯矩，滑带角度0° 时弯矩最大值为463 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为201 kN•m，左右两侧弯矩相差2.3倍，两侧受力不均，形成典型偏压隧道. 滑带角度30° 时，弯矩最大值为178 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为65 kN•m，左右两侧弯矩相差2.7倍. 当滑带角度50° 时，弯矩最大值为87 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为27 kN•m，左右两侧弯矩相差3.2倍. 可见，弯矩在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受弯矩越小.
对于隧道衬砌结构上所受剪力，基本与弯矩规律类似. 滑带角度 0° 时剪力最大值为20.3 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为18.5 kN. 滑带角度30° 时，剪力最大值为16.8 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为5.7 kN. 当滑带角度50° 时，剪力最大值为7.3 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为2.9 kN. 可见，剪力在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受剪力越小，被剪切破坏的可能性减小.
2） 土压力特征
由压力盒的监测数据计算得到滑坡推力作用在隧道衬砌结构上的土压力，如表4. 可以看出：作用在隧道衬砌结构上的土压力在靠山侧大于另一侧1～2倍，拱脚处大于拱肩、拱顶处的土压力，沿着隧道衬砌结构截面分布出现出左右不均的偏压现象. 由于滑带的作用，靠山侧拱脚处土压力值最大，在滑带角度为0° 时，土压力为16.4 kPa，30° 时，土压力为9.6 kPa，50° 时，土压力为7.4 kPa，仅为滑带角度为0° 时的0.45倍，可见随着滑带角度逐渐增大，作用在拱脚处的土压力逐渐减小.
表 4 不同滑带角度下隧道土压力值Table 4. Distribution of earth pressure on tunnel under different angles of sliding zone滑带角度/（°） 土压力分布/kPa 0 
10 
20 
30 
40 
50 
3） 偏压应力比
将同样埋深情况下隧道衬砌结构左右侧洞壁上对应点的竖向应力比值定义为偏压应力比[26]. 为了全面掌握不同滑带角度作用下的偏压应力比，布置了如图3（c）所示的7个隧道衬砌结构竖向压应力分析点.
如图3（c），对于其中顶部和底部应力比，底部采用点4、5的平均值. 分别对应拱顶（点1），左右拱肩（点2、7），拱脚（点3、6）以及拱底（点4、5）. 按照拱肩（点2、7）偏压应力比Δ1，以及拱脚（点3、6）偏压应力比Δ2进行计算分析.
Δ1=σ2σ7, (1) Δ2=σ3σ6, (2) 式中：σ2、σ7和σ3、σ6分别为隧道衬砌结构监测点测得左右拱肩（点2、7）和拱脚（点3、6）应力值.
由监测元件数据换算，并根据式（1）、（2）得到表5的数值，可以得出：在拱肩位置，当滑带角度为0° 时偏压应力比为1.17，滑带角度为30° 时，偏压应力比为1.07，50° 时，偏压应力比1.01. 可见，随着滑带角度的增大，偏压应力比逐渐减小，即随着滑带角度的增大，在拱肩位置处隧道衬砌拱结构左右应力差越来越小，越来越趋于平衡拱. 在拱脚位置，当滑带角度0° 时偏压应力比为1.08，滑带角度为30°时，偏压应力比为1.29，50° 时，偏压应力比1.87. 可见，随着滑带角度的增大，偏压应力比逐渐增大，即随着滑带角度的增大，在拱脚位置处隧道衬砌拱结构左右所受应力差越来越大，趋向于偏压隧道.
表 5 模型试验下不同滑带角度隧道衬砌偏压应力比Table 5. Bias stress ratio at different sliding angles in model test滑带角度/（°） Δ1 Δ2 0 1.17 1.08 10 1.09 1.25 20 1.04 1.27 30 1.07 1.29 40 1.02 1.54 50 1.01 1.87 3. 隧道衬砌结构受力数值模拟
3.1 模型建立
根据大准铁路南坪隧道原型结构，采用有限单元法进行不同滑带角度作用下隧道衬砌结构受力分析，数值模拟中所用模型参数如表1. 模拟中设置了桩与土、隧道结构与土之间的接触单元[29-31]，材料参数中桩接触单位极限剪切力0.99 N/m，法向刚度系数0.99 kN；隧道接触单元主应力刚度模量2.45 MPa，剪切刚度模量0.245 MPa，摩擦角36°.
分别采用 0°、10°、20°、30°、40°、50°，6种滑带角度条件进行模拟分析，分析模型如图5（限于篇幅，其他未列出）.
3.2 模拟结果分析
如图6所示为 30° 滑带角度滑坡推力作用下隧道衬砌结构位移变形（其他滑带角度作用下隧道位移云图规律类似，仅位移值不同），当滑带角度为 0° 时最大变形量为121 mm，滑带角度为30° 时最大变形为59.8 mm，滑带角度为 50° 时最大变形为0.2 mm，最大变形位置均发生在靠山侧的拱脚处. 可见，随着滑带角度的增大，隧道衬砌结构变形逐渐减小，这与模型试验得出的位移规律基本一致，仅在变形量数值上略有差别.
图7为数值模拟所得隧道衬砌结构所受弯矩（其他滑带角度作用下隧道弯矩云图规律类似，仅弯矩值不同）. 与模型试验所得规律基本一致，最大弯矩值分布在靠山侧的拱脚处，当滑带角度为 0° 时最大弯矩量为487.90 kN•m，滑带角度为30° 时最大弯矩为187.00 kN•m，滑带角度为50° 时最大弯矩为89.03 kN•m. 同样地，随着滑带角度的增大，隧道衬砌结构所受弯矩逐渐减小. 在滑坡推力作用下，隧道衬砌结构拱左右受力不均，存在偏压现象.
3.3 数值模拟与模型试验对比分析
数值模拟中设置如图3的监测点，得到隧道衬砌结构上7个监测点的应力值，并根据式（1）、（2）计算出偏压应力比，如表6，与模型试验中的监测数值进行比较，数值上接近，反映出的规律一致，在拱肩位置处，随着滑带角度的增长，拱左右两侧所受竖向应力差逐渐减少，趋于平衡拱，在拱脚位置处，由于滑坡推力的作用，随着滑带角度的增大，拱左右两侧的竖向应力值越来越大，更趋于偏压隧道.
表 6 数值模拟下不同滑带角度隧道衬砌偏压应力比Table 6. Bias stress ratios in numerical simulation滑带角度/（°） Δ1 Δ2 0 1.21 0.98 10 1.20 1.22 20 1.14 1.25 30 1.11 1.48 40 1.09 1.83 50 1.06 2.34 4. 结 论
以大准铁路K20南坪隧道为例，采用室内模型试验、数值模拟手段，开展了不同滑带角度的滑坡作用下隧道衬砌结构受力特征相关研究，得到如下结论：
1） 穿越滑坡区的隧道由于滑坡推力的作用，隧道衬砌结构容易产生变形或破坏.
2） 滑坡滑带角度的不同，对隧道衬砌结构的力学作用也不同. 对于隧道衬砌结构上所受弯矩与剪应力，在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受弯矩与剪应力越小. 作用在隧道衬砌结构上的土压力在靠山侧大于另一侧1～2倍，拱脚处大于拱肩、拱顶处的土压力，沿着隧道衬砌结构截面分布出现出左右不均的偏压现象，随着滑带角度逐渐增大，作用在拱脚处的土压力逐渐减小.
3） 计算得到隧道衬砌结构上不同位置处的竖向压应力，并计算出其左右两侧的偏压应力比，得出在拱肩位置，随着滑带角度的增大，隧道衬砌拱结构左右应力差越来越小，越来越趋于平衡拱. 在拱脚位置，随着滑带角度的增大，偏压应力比逐渐增大，隧道衬砌拱结构左右两侧所受应力差越来越大，趋向于偏压隧道.
在实际工程中，对于穿行大型滑坡区域的隧道，在设计过程中可在隧道衬砌结构拱脚处加强设置，同时采用抗滑桩等滑坡支挡措施抵御滑坡推力的作用.
-
图 2 加载路径横向分布与加载顺序
Figure 2. Translational distribution of wheel track and loading sequence
图 6 回弹变形随加载时间间隔变化曲线
Figure 6. Variation curves of rebound deformation versus loading interval
图 9 轮辙增长率及各阶段贡献率曲线
Figure 9. Curves of rutting growth ratio and contribution rate at different stages
图 11 不同温度下的轮辙公式预测结果
Figure 11. Predication results of rutting formula under different temperatures
表 1 道面结构层组成
Table 1. Consisting of pavement structure
结构层 材料编号 结构层厚度/mm LFC1-NW LFC2-NE 沥青混凝土面层 P-401 127.0 127.0 密级配碎石基层 P-209 203.0 203.0 碎石底基层 P-154 863.6 965.2 低强度土基 DPC 762.0 762.0 注：道面各结构层厚度由FAARFIELD软件计算. 
下载: 导出CSV
表 2 循环加载参数
Table 2. Parameters of accumulative loading
轮载等级/kN 累积作用次数/次 226.75 0～7920 263.03 7921～13038 294.78 13039～18612 317.51 18613～27918
下载: 导出CSV
表 3 加载测试车参数
Table 3. Parameters of loading vehicle
性能指标 参数取值 轮印宽度/cm 30.5 轮印长度/cm 53.3 机轮数量/个 6 轮胎胎压/kPa 1670 横向轮隙宽度/cm 106.5 纵向轮隙长度/cm 91.7
下载: 导出CSV
温度/℃ 瞬态模量/
MPa泊松比 f n m 20 870 0.25 6.54 × 10−11 0.937 −0.592 30 620 0.30 3.33 × 10−9 0.862 −0.587 40 554 0.35 1.45 × 10−8 0.792 −0.577 50 530 0.40 1.39 × 10−6 0.414 −0.525 注：f、n、m均为蠕变模型参数，均采用国际单位1，无量纲.
下载: 导出CSV
材料类型 弹性模量/MPa 泊松比 密级配碎石基层 518 0.35 碎石底基层 276 0.35
下载: 导出CSV
表 6 轮辙曲线特征点结果
Table 6. Results at feature points of rutting curve
mm 特征点 断面中心距 轮辙深度 试验 仿真 试验 仿真 R1 0.025 0 −172.4 −170.2 R2 0.500 −0.505 −150.4 −140.4 R3 0.899 −0.892 −121.8 −130.9 R4 −1.125 −1.133 −101.9 −105.0
下载: 导出CSV
表 7 不同温度下公式系数
Table 7. Fomula coefficients under different temperatures
温度/℃ r p q ρ 30 24.359 0.0035 24.077 0.998 40 32.832 0.0038 31.471 0.998 50 37.349 0.0052 35.033 0.997 CC5 试验 30.481 0.0033 29.570 0.998
下载: 导出CSV
-
[1] 刘文, 凌建明, 赵鸿铎. 民用机场沥青混凝土道面设计方法综述[J]. 中国民航学院学报, 2006, 24(4): 43-47, 64.LIU Wen, LING Jianming, ZHAO Hongduo. Review and analysis of design methods for asphalt concrete airport pavement[J]. Journal of Civel Aviation University of China, 2006, 24(4): 43-47, 64. [2] WHITE G. State of the art: asphalt for airport pavement surfacing[J]. International Journal of Pavement Research and Technology, 2018, 11(1): 77-98. doi: 10.1016/j.ijprt.2017.07.008 [3] PASINDU H R, FWA T F, ONG G P. Analytical evaluation of aircraft operational risks from runway rutting[J]. International Journal of Pavement Engineering, 2015, 17(9/10): 810-817. [4] 王海朋. 飞机多轮荷载作用下沥青道面高温变形叠加效应研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. [5] 朱杰涛. 基于平整度劣化条件下机场复合道面力学性能研究[D]. 天津: 中国民航大学, 2018. [6] 叶丛. 基于HVS加速加载试验的柔性基层沥青路面车辙预估研究[D]. 西安: 西安建筑科技大学, 2018. [7] 张霞,黄刚,刘昭,等. 热、光、水耦合老化条件对温拌沥青性能的影响[J]. 公路交通科技,2019,36(7): 10-19.ZHANG Xia, HUANG Gang, LIU Zhao, et al. Influence of coupled aging condition of heat, light and water on performance of warm mix asphalt[J]. Journal of Highway and Transportation Research and Development, 2019, 36(7): 10-19. [8] 朱天明. 基于加速加载试验的沥青路面车辙发展规律研究与数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2014. [9] 张宏,游庆龙,马靖莲. 新一代大型飞机荷载作用下沥青道面多轮叠加效应研究[J]. 公路交通科技,2015,32(10): 1-5,13. doi: 10.3969/j.issn.1002-0268.2015.10.001ZHANG Hong, YOU Qinglong, MA Jinglian. Multiple wheel gear load interaction effect of new generation large aircraft on airfield asphalt pavement[J]. Journal of Highway and Transportation Research and Development, 2015, 32(10): 1-5,13. doi: 10.3969/j.issn.1002-0268.2015.10.001 [10] ABDULLAH G M S. 3D finite element modeling to predict the foamed sulfur asphalt marl soil mixes rutting behavior[J]. Ain Shams Engineering Journal, 2019, 10(4): 661-668. doi: 10.1016/j.asej.2019.03.005 [11] 冉武平,邹益强,孔二春. 基于加速加载的SMA沥青道面轮辙特性分析[J]. 公路工程,2016,41(4): 6-11. doi: 10.3969/j.issn.1674-0610.2016.04.002RAN Wuping, ZOU Yiqiang, KONG Erchun. Analysis of the SMA asphalt pavement rutting characteristics based on accelerated pavement testing[J]. Highway Engineering, 2016, 41(4): 6-11. doi: 10.3969/j.issn.1674-0610.2016.04.002 [12] WANG Y, LU Y J, SI C D, et al. Finite element analysis for rutting prediction of asphalt concrete pavement under moving wheel load[J]. International Journal of Simulation Modeling, 2017, 16(2): 229-240. doi: 10.2507/IJSIMM16(2)4.374 [13] ZHENG M L, HAN L L, WANG C T, et al. Simulation of permanent deformation in high-modulus asphalt pavement with sloped and horizontally curved alignment[J]. Applied Sciences, 2017, 7(4): 331. doi: 10.3390/app7040331 [14] 张兰峰. 连续变温沥青路面车辙变形数值模拟[J]. 公路交通科技,2018,35(2): 15-24.ZHANG Lanfeng. Numerical simulation of rutting deformation of asphalt pavement at continuous variable temperature[J]. Journal of Highway and Transportation Research and Development, 2018, 35(2): 15-24. [15] WANG Y J. Analysis of asphalt pavement mechanical behaviour by using a tire-pavement coupling model[J]. International Journal of Simulation Modelling, 2018, 17(2): 245-256. doi: 10.2507/IJSIMM17(2)423 [16] WANG X W, GU X Y, NI F J, et al. Rutting resistance of porous asphalt mixture under coupled conditions of high temperature and rainfall[J]. Construction and Building Materials, 2018, 174: 293-301. doi: 10.1016/j.conbuildmat.2018.04.104 [17] KIM S M, DARABI M K, LITTLE D N, et al. Effect of the realistic tire contact pressure on the rutting performance of asphaltic concrete pavements[J]. KSCE Journal of Civil Engineering, 2018, 22(6): 2138-2146. doi: 10.1007/s12205-018-4846-1 [18] 李喜,王选仓,房娜仁,等. 基于温度与荷载实际耦合的沥青路面车辙预估[J]. 长安大学学报(自然科学版),2018,38(5): 67-75.LI Xi, WANG Xuancang, FANG Naren, et al. Rutting prediction of asphalt pavement based on actual coupling of temperature and load[J]. Journal of Chang’an University (Natural Science Edition), 2018, 38(5): 67-75. [19] 郑秉乾,马松林,李新凯. 美国联邦航空管理局机场道面试验中心足尺试验介绍[J]. 中外公路,2009,29(3): 98-100.ZHENG Bingqian, MA Songlin, LI Xinkai. Introduction to the full-scale test at National Airport Pavement Test Facility[J]. Journal of China & Foreign Highway, 2009, 29(3): 98-100. [20] 张鑫. 基于延长寿命的跑道结构参数优化研究[D]. 天津: 中国民航大学, 2018. [21] FAA Airport Technology Research & Development Branch. National airport pavement test facility [EB/OL]. (2020.04.12)[2021.07.16]. http://www.airporttech.tc.faa.gov/naptf. [22] 中国民用航空局. 民用机场沥青混凝土道面设计规范: MH 5010—2017[S]. 北京: 中国民航出版社, 2017. [23] 董倩. 基于飞机滑行刚性道面位移场的跑道承载力研究[D]. 天津: 中国民航大学, 2013. [24] 游庆龙,凌建明,袁捷,等. 适应大型飞机的沥青道面结构有限元模型[J]. 交通运输工程学报,2012,12(2): 18-23. doi: 10.3969/j.issn.1671-1637.2012.02.003YOU Qinglong, LING Jianming, YUAN Jie, et al. Finite element model of flexible airport pavement structure for large aircraft[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 18-23. doi: 10.3969/j.issn.1671-1637.2012.02.003 [25] 孙钦刚. 机场沥青道面转弯区温度场耦合作用轮辙形成规律分析[D]. 广汉: 中国民航大学, 2015. [26] 边际. 基于混合交通分析的机场柔性基层沥青道面轮辙控制研究[D]. 上海: 同济大学, 2008. [27] 骆妍. 基于有限元法的沥青路面车辙分析[D]. 石家庄: 石家庄铁道大学, 2015. [28] 中国民用航空局. 民用机场道面评价管理技术规范: MH/T 5024—2019 [S]. 北京: 中国民航出版社, 2019. [29] JAVILLA B, MO L T, HAO F, et al. Significance of initial rutting in prediction of rutting development and characterization of asphalt mixtures[J]. Construction and Building Materials, 2017, 153: 157-164. doi: 10.1016/j.conbuildmat.2017.07.007 期刊类型引用(3)
1. 吴宇宏，聂勇，李素菊，王文，谷昌军. 西藏定日6.8级地震灾区冰湖分布、变化与危害冰湖识别. 冰川冻土. 2025(01): 187-198 . 
百度学术2. 刘瑾，车文越，钱卫，张化鹏，黄国娇，丁亮，何秀凤. 基于M序列的磁电法探测坝基渗漏试验研究. 西南交通大学学报. 2024(06): 1448-1456 . 
本站查看3. 王亚妮，刘德高，董千里，申国强. 渗流和溢流导致冰碛坝溃决的数值分析. 山西水利. 2023(05): 39-43+64 . 百度学术其他类型引用(1)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 492
- HTML全文浏览量: 184
- PDF下载量: 38
- 被引次数: 4