Experimental Study on Dam Foundation Leakage Detection by Magnetoelectric Method Based on M Sequence
-
摘要:
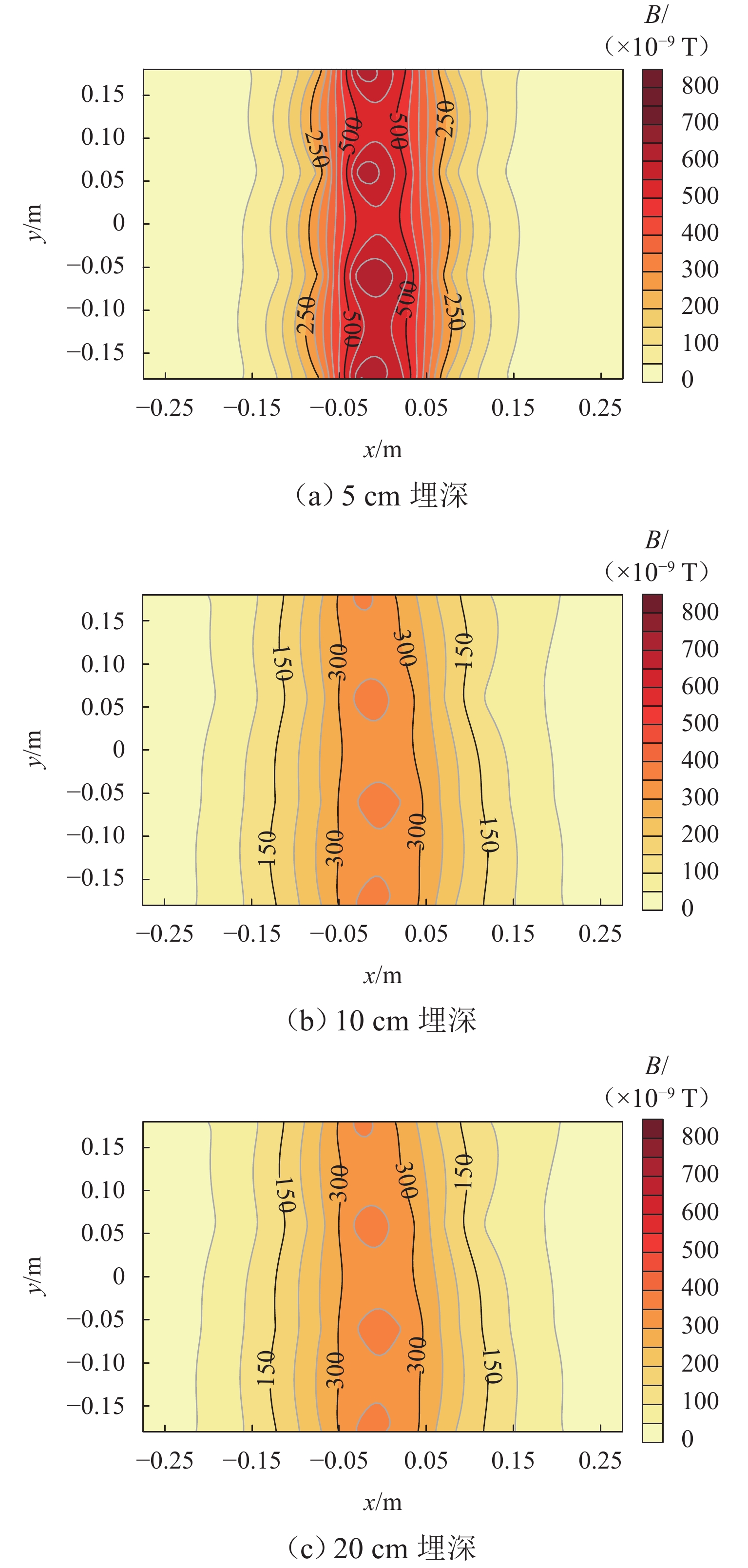
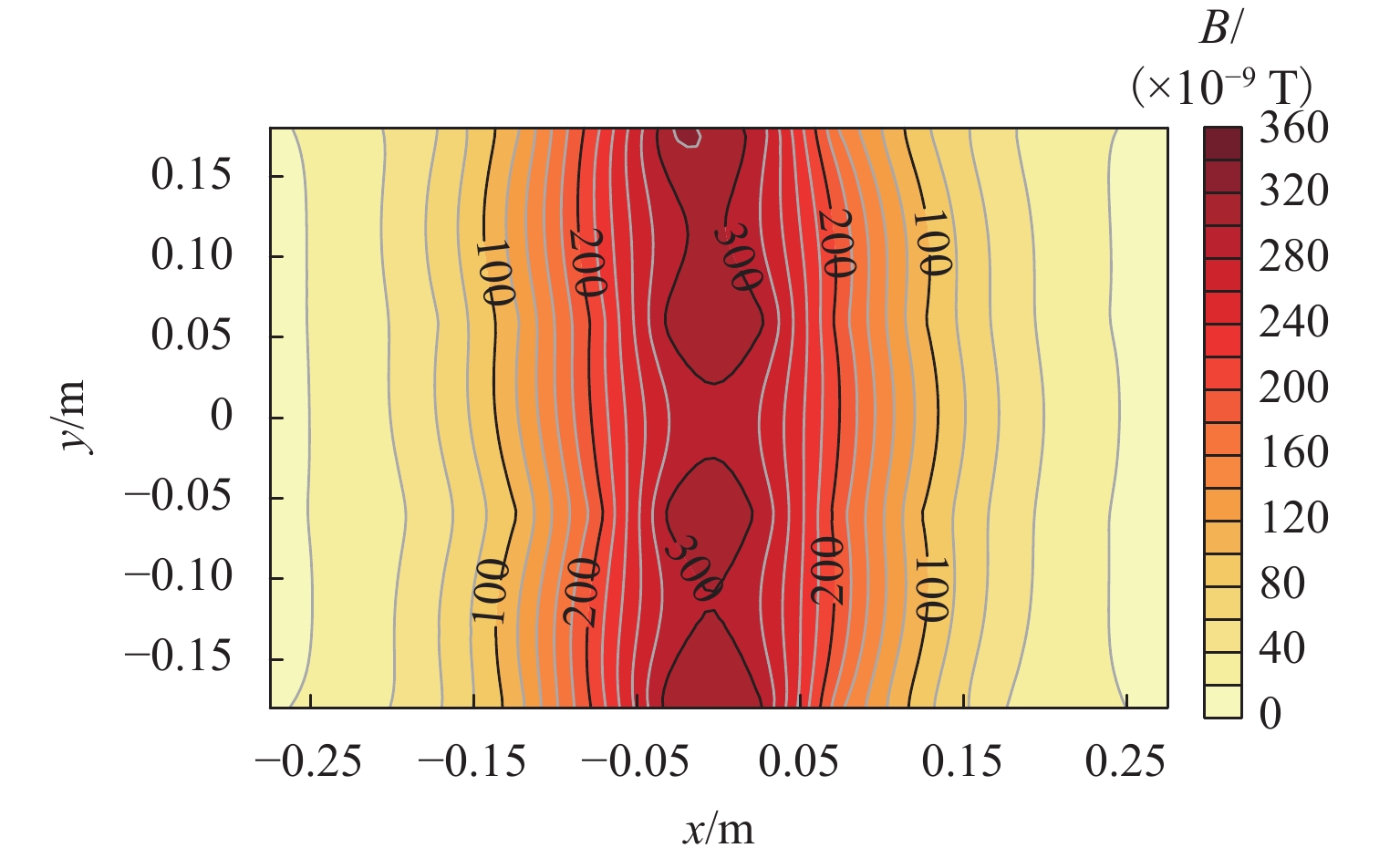
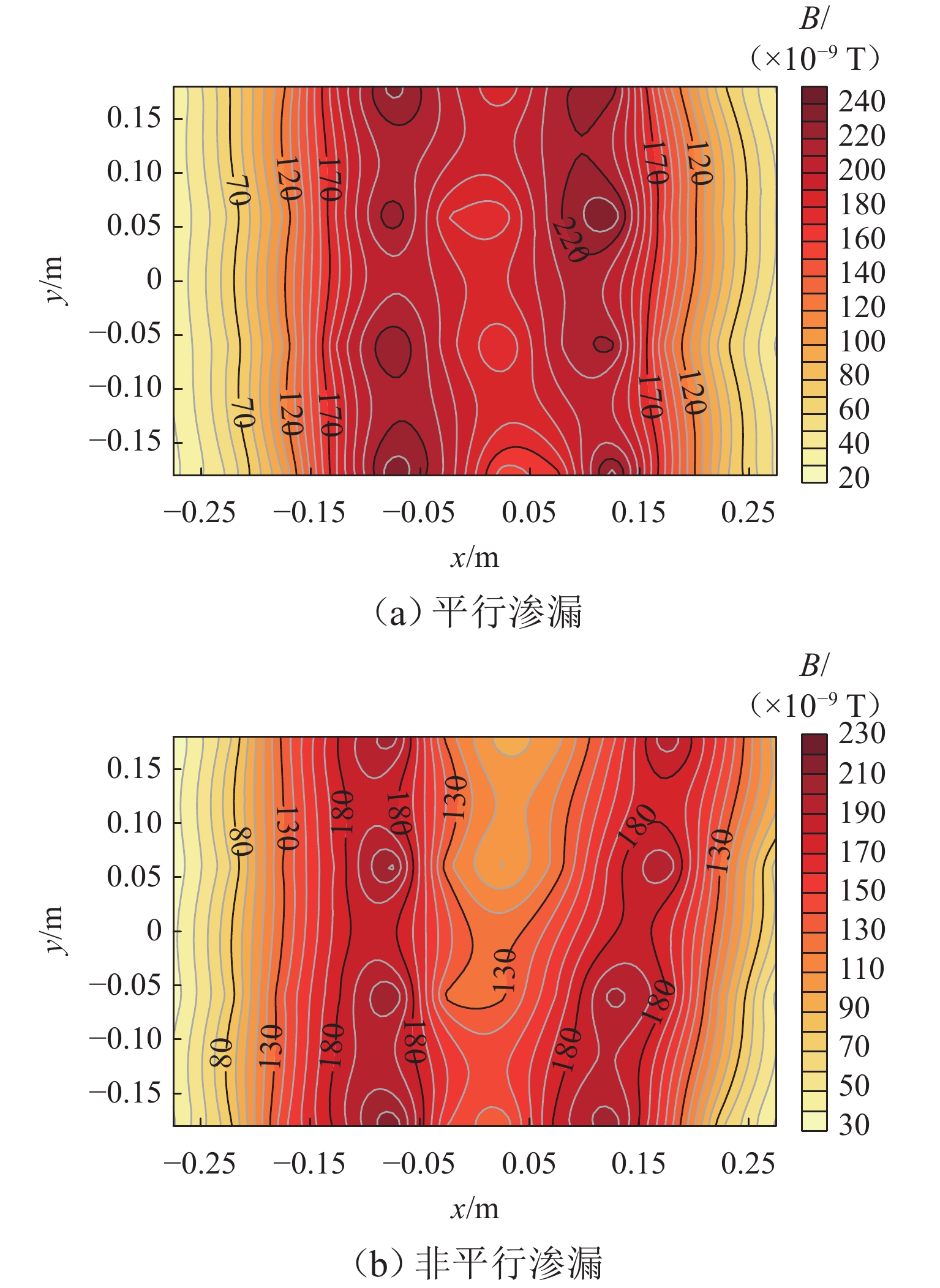
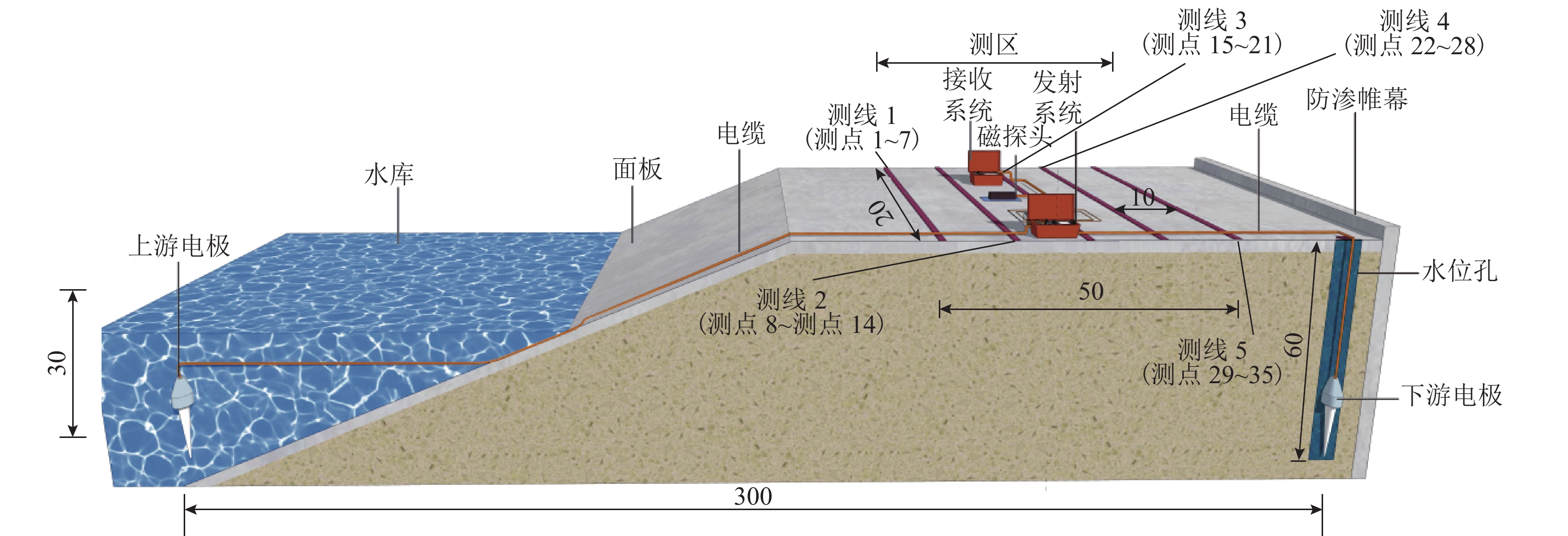
坝基渗漏问题是影响水库大坝整体安全的关键因素. 为有效、准确探测坝基渗漏,基于伪随机辨识原理,将M序列相关辨识的磁电法技术应用于堤坝渗漏探测. 首先,通过物理模型试验分析,获取不同渗漏深度下的磁感应强度分布、均方差及变异系数特征;然后,设计不同渗漏形态、高阻屏蔽层及渗漏通道数量条件,获取探测结果对倾斜通道、高阻屏蔽层以及多条渗漏通道的响应特征;最后,通过云南红石岩堰塞坝现场试验,分析该技术的可行性. 试验结果表明:在不同埋深条件下,磁感应强度最大值的变异系数均控制在2%以内;渗漏通道的倾斜引起磁感应强度沿渗漏方向缓慢降低,其磁场等值线图的脊线反映倾斜渗漏方向;高阻屏蔽层仅对磁感应强度产生影响,磁感应强度误差在10%~20%;多组渗漏通道会反映在磁场等值线图中异常场的多处集中分布;现场试验探测的渗流流向分别为NW300°、SW265°、W215°和NW305°.
Abstract:The dam foundation leakage problem has been a key factor affecting the overall safety of reservoir dams. To effectively and accurately detect dam foundation leakage, the magnetoelectric method based on M sequence correlation identification technology was applied to the dam leakage detection based on the pseudo-random identification principle. Firstly, the distribution of magnetic induction intensity, mean square error, and variation coefficient under various leakage depth conditions were characterized through the analysis of physical model experiments. Then, various leakage forms, high-resistance shielding layers, and leakage channel numbers were designed, so as to obtain the response characteristics of the detection results to the inclined channel, high-resistance shielding layer, and multiple leakage channels. Finally, the field test of Hongshiyan Dam in Yunnan Province was conducted to study the feasibility of this technology. The results show that under different burial depth conditions, the variation coefficients of maximum magnetic induction intensity vary within 2%. Along the inclined leakage channel, the magnetic induction intensity decreases slowly, and the ridge direction of the magnetic field contour map can be considered as the inclined leakage direction. The magnetic induction intensity is affected by the high-resistance shielding layer and has an error between 10% and 20%. The multiple leakage channels can be reflected by the concentrative distribution of abnormal zones in magnetic field contour maps. The leakage directions are observed in the field test, containing NW300°, SW265°, W215°, and NW305°, respectively.
-
Key words:
- leakage identification /
- M sequence /
- magnetoelectric method /
- dam foundation leakage /
- soil bin test
-
五螺箍是一种新型组合式螺旋箍筋,其构造方式为中间一个大螺箍,四角为四个小螺箍. 相比传统的单螺箍圆形柱,四个小螺箍可以约束四个角落的混凝土,使得螺旋箍筋可以适用于矩形截面. 五螺箍为机械自动化生产,相对于传统箍筋有更高的效率[1]. 目前,五螺箍的应用与研究主要在中国台湾,且设计与研究参照了文献[2].
国内外学者对单螺箍约束混凝土开展了大量的理论与试验研究,而多螺箍约束混凝土的研究较少. Mohamed等[3]通过试验对复合箍筋柱进行了参数分析,主要研究了配箍形式和体积配箍率对试件力学性能的影响. Mander等[4]通过对大量约束混凝土柱试件进行轴心受压试验,得到一套约束混凝土的本构模型. Assa等[5-6]对一系列螺旋箍筋柱试件进行实验,得到螺旋箍筋约束混凝土的本构关系. 过镇海等[7-8]进行方形箍约束混凝土在反复荷载下的应力-应变全曲线试验研究,试验得出试件强度和延性与体积配箍率呈正相关关系. 唐琼等[9]基于多螺箍筋试验数据建立有限元模型,分析受力机理提出轴压承载力计算公式. 史庆轩等[10]通过多根不同配箍形式的方形截面柱进行轴压试验,并对其延性与强度进行影响因素分析. 翁正强等[11]对多个五螺箍短柱进行了轴压试验,研究了三个不同系列小螺箍直径对柱整体力学性能的影响. 郑亮[12]通过试验研究了方钢管混凝土和配螺旋箍筋方钢管混凝土短柱的力学性能,并且对短柱承载力计算方法进行理论研究. 傅明月[13]对五螺箍混凝土柱进行了轴心受压与偏心受压试验,发现螺旋箍筋能明显地提高柱的承载能力和延性性能. Liang等[14]进行9根足尺多螺旋箍筋约束方形短柱的试验,发现减小螺旋间距可以明显提高柱的轴压承载力和延性.
由于目前对五螺箍柱轴压承载力计算式的研究鲜有报道,因此,有必要对其力学性能进行进一步研究,以提出适用于五螺箍柱的轴压承载力计算式. 本文利用ABAQUS软件,首先,基于试验模型建立有限元模型,并将有限元分析结果与已有的试验结果进行对比分析,以验证有限元模型分析结果的准确性. 接着,基于材料用量相等的原则,创建4种不同配箍形式的矩形截面柱,并进行力学性能对比分析. 最后,对五螺箍柱轴压承载力进行影响因素分析,提出基于体积配箍率的轴压承载力计算式.
1. 有限元分析模型
1.1 混凝土的本构关系
混凝土本构模型采用有限元软件ABAQUS中内置的塑性损伤模型,损伤因子按文献[15]公式计算. 因Mander模型[14]对不同箍筋的作用形式有不同的计算式,故本构关系采用Mander模型[14],模型的具体表达如下:
fcc=fcc1xrr−1+xr, (1) x=εcεcc, (2) εcc=εc0[1+5(fcc1fc0−1)], (3) r=EcEc−Esec, (4) Ec=5000√fcc, (5) Esec=fcc1εcc, (6) fcc1=fc0(−1.254+2.254√1+7.94f11fc0−2f11fc0), (7) f11=12Keρsfyh, (8) Ke=1−s2ds1−ρcc, (9) 式(1) ~ (9)中:
fcc 为混凝土应力;εc 为混凝土应变;fcc1 为约束混凝土的峰值应力;εcc 为约束混凝土的峰值应变;fyh 为箍筋屈服强度;s 为箍筋间净间距;ds 为约束箍筋的直径;fc0 为混凝土轴心抗压强度标准值;εc0 为非约束混凝土的峰值应变,通常取0.002;Ec 为非约束混凝土弹性模型;Esec 为约束混凝土割线模量;f11 为侧向约束力,对于未约束混凝土f11 = 0;Ke 为有效约束系数;ρs 为体积配箍率;ρcc 为纵筋配筋率.1.2 采用的钢筋本构
钢筋采用理想弹塑性模型,具体表达形式为
{σs=Esεs,εs⩽εy,σs=Fy,εs>εy, (10) 式中:
Es 、Fy 分别为钢筋的弹性模量和屈服强度;εs 为钢筋应变;εy 为钢筋屈服应变;σs 为钢筋应力.1.3 有限元模型验证
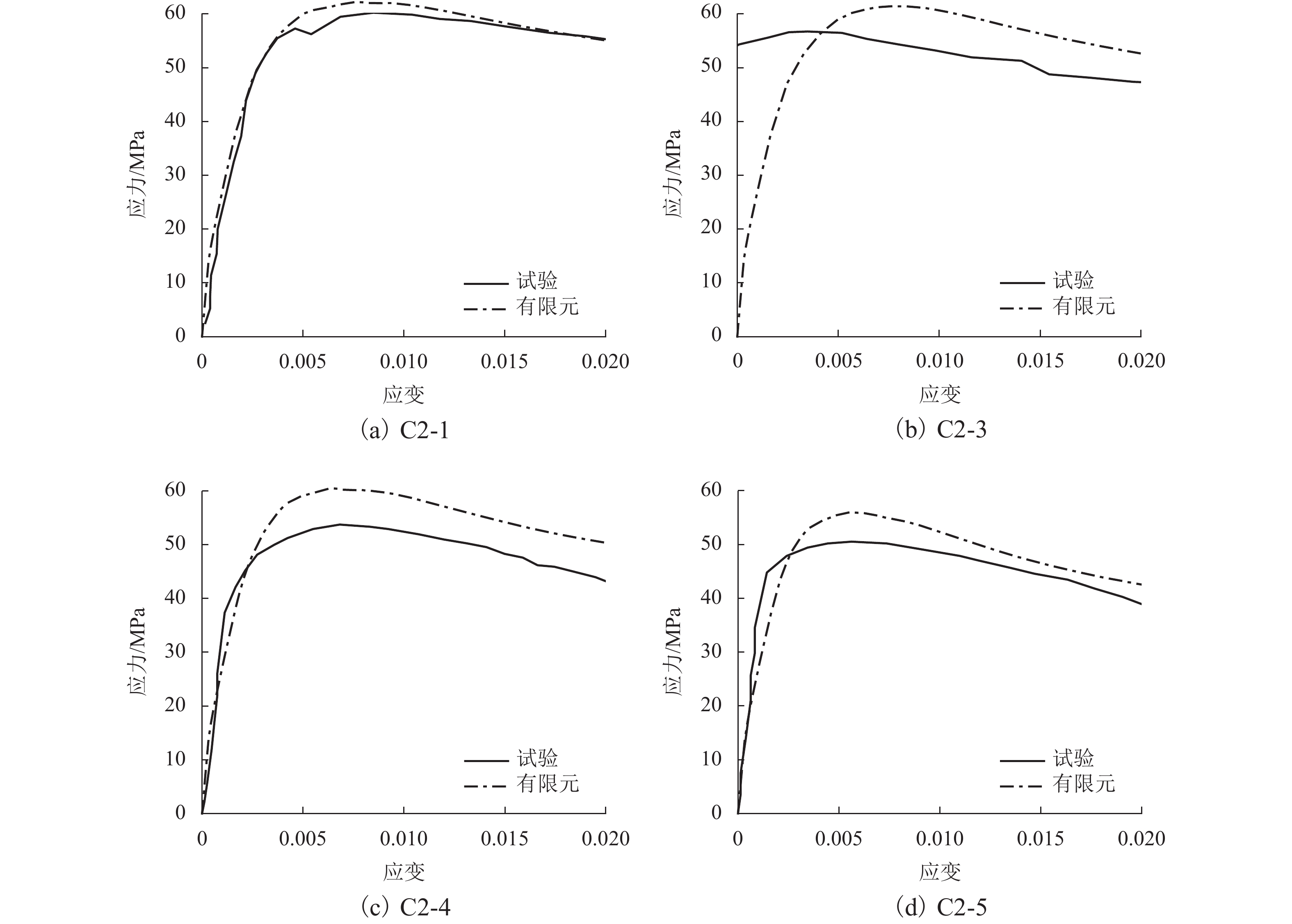
采用位移协调分离式来分析模型. 混凝土采用C3D8R单元,钢筋采用T3D2单元. 对钢筋和混凝土之间的连接,采用Embedded region进行两者的自由度耦合,不考虑钢筋和混凝土之间的连接滑移. 为了使柱体的边界约束条件接近实际受力情况,在柱体上、下两端采用铰接连接方式,并在柱顶进行位移加载. 本文选取文献[16]中的试件C2-1、C2-3、C2-4和C2-5,用有限元软件ABAQUS建模进行分析. 4根短柱的试验设计参数以及试验和有限元分析结果如表1所示. 图1为各试件试验和有限元分析的应力-应变曲线图.
表 1 试验和有限元计算结果对比Table 1. Comparison of experiment and finite element calculation results试件编号 材料强度/MPa 钢筋配置/mm 轴压承载力/kN 混凝土 纵筋 大螺箍 小螺箍 纵筋 大螺箍 小螺箍 试验值 模拟值 误差/% C2-1 39.4 420 280 280 D25 D13@50 D13@50 21670 22378 3.26 C2-3 40.3 D16@70 D13@70 20411 22109 8.32 C2-4 40.3 D13@60 D13@60 19336 21749 12.47 C2-5 39.4 D10@50 D10@50 18181 20128 10.70 从表1可以看出:轴压承载力的模拟结果稍微高于试验结果,轴压承载力最大误差为12.47%,最小误差为3.26%,平均误差仅为8.68%,可以说明有限元模拟得到的轴压承载力与试验结果比较接近. 从图1可以看出:有限元模拟结果和试验结果吻合较好.
2. 配箍形式对峰值荷载和延性的影响分析
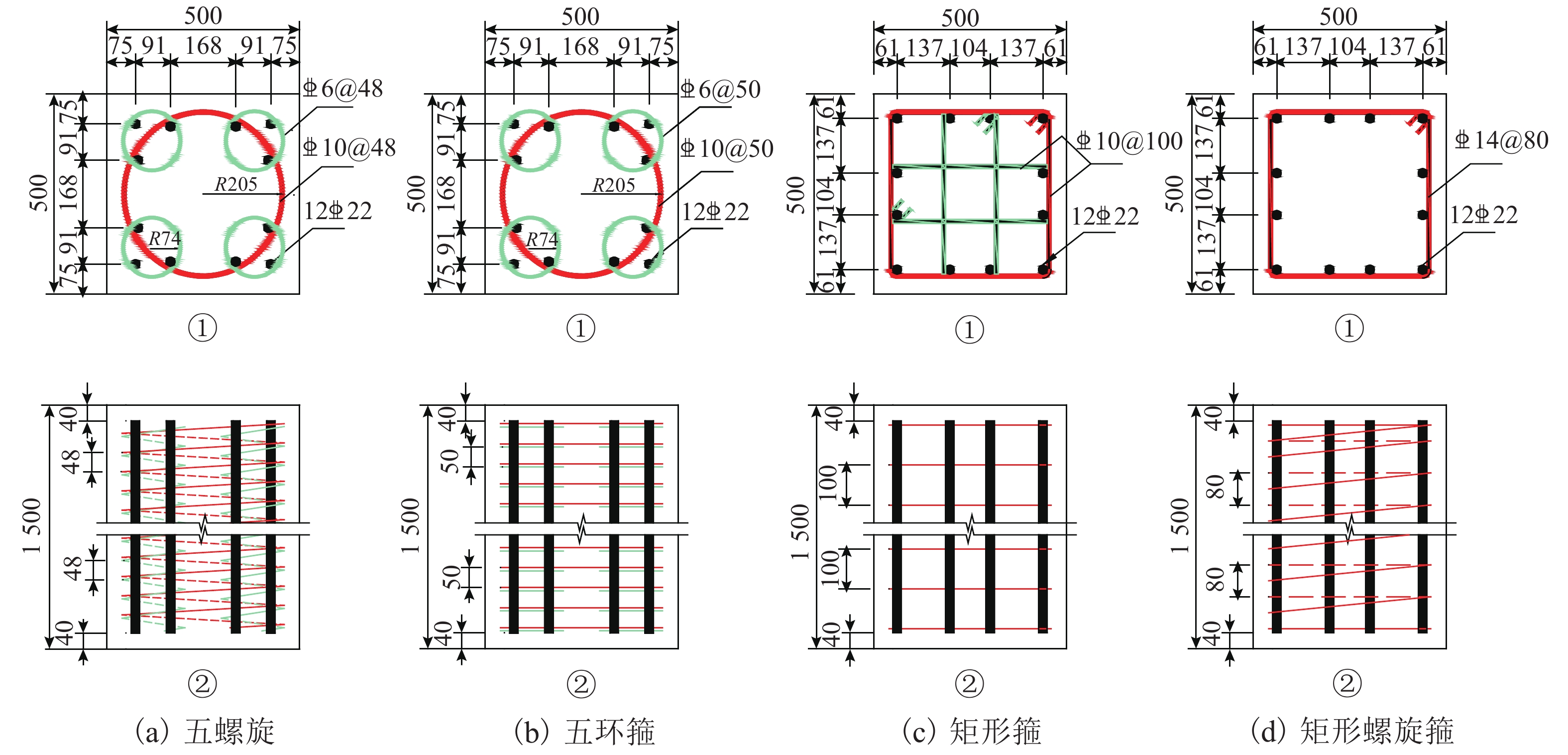
基于材料用量相等的原则,考虑混凝土强度等级和配箍形式对钢筋混凝土柱受压性能的影响,设计了混凝土强度等级从C25 ~ C50的6组钢筋混凝土柱分析模型,每组都包括五螺箍、五环箍、矩形箍、矩形螺旋箍4种配箍形式,各配箍形式模型的几何参数和材料构成如图2所示. 为尽可能符合实际情况,柱高取1.5 m,即反弯点处截取一半楼层高度. 五螺箍、五环箍、矩形箍、矩形螺旋箍配箍形式的钢筋混凝土柱模型用钢量分别为1.10 × 107 、1.09 × 107 、 1.10 × 107、1.10 × 107 mm3,最大相差为0.5%,可视为材料用量相等. 4种配箍形式模型的纵筋配筋率为1.82%,满足轴心受压构件纵筋最小配筋率0.5%、最大配筋率5.0%的要求,箍筋强度均为280 MPa,纵筋强度均为400 MPa.
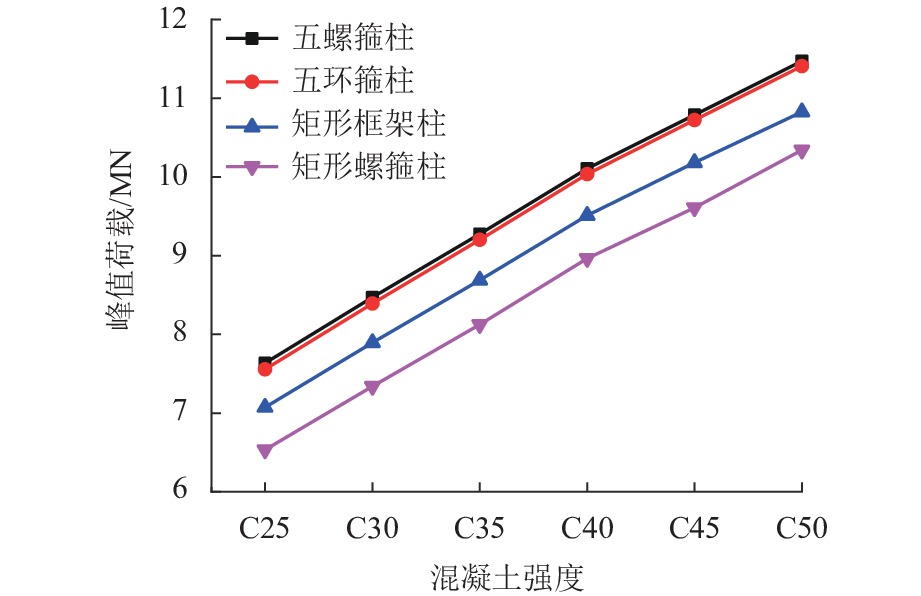
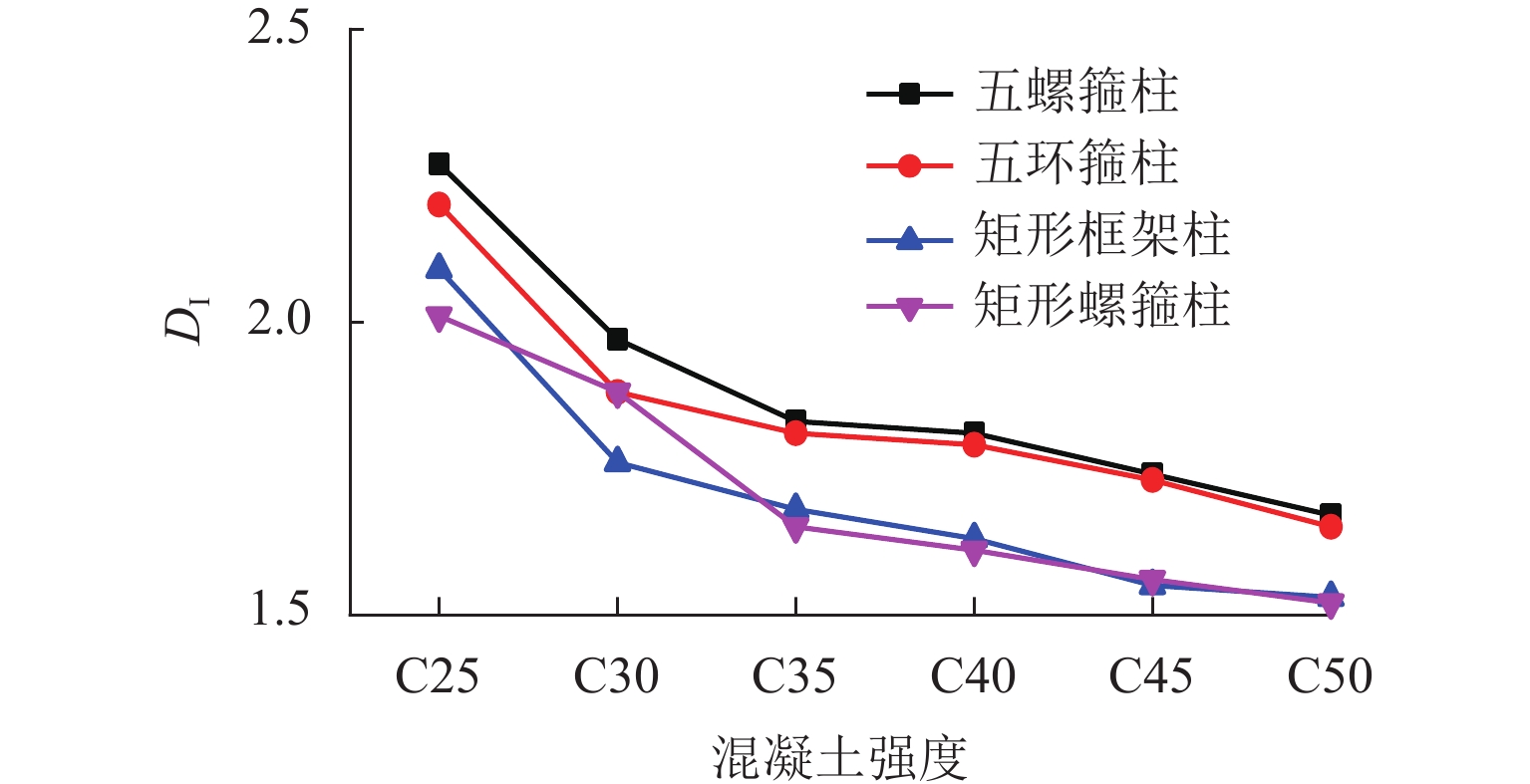
有限元分析结果如图3、4所示. 从图3中可以看出:五螺箍柱的峰值承载力较其他3种柱都高. 为反映短柱的延性性能,采用已有的对延性定义的指标延性系数DI[17]来表示,如式(11)所示.
DI=u85/u11, (11) 式中:
u11 为峰值荷载时的位移;u85 为峰值荷载下降到85%时的位移.从图4可以看出:五螺箍的延性优于其他3种柱,五螺箍较五环箍、矩形箍和矩形螺旋箍柱构件峰值承载力均值分别提高0.78%、6.70%和13.73%,延性系数均值分别提高2.00%、10.32%和10.41%,表明五螺箍柱具有较优的承载力及延性,这与文献[11]中的试验结论相符.
由于五螺箍柱的各性能指标均较优,有必要对五螺箍轴压承载力及延性进行影响因素分析,为提出五螺箍轴压承载力的计算式奠定基础. 本文按照《混凝土结构设计规范》(GB 50010—2010)[18] (以下均简称《混规》)的要求,设计了9个螺旋箍筋间距为40 ~ 80 mm (或
dcor/5 ,其中,dcor 为核心区混凝土的直径,可按螺旋箍筋内表面直径取值)的模型,其中,体积配箍率的计算式[11]为ρv=πDAsp1+4πdAsp2s5 Ach, (12) 式中:
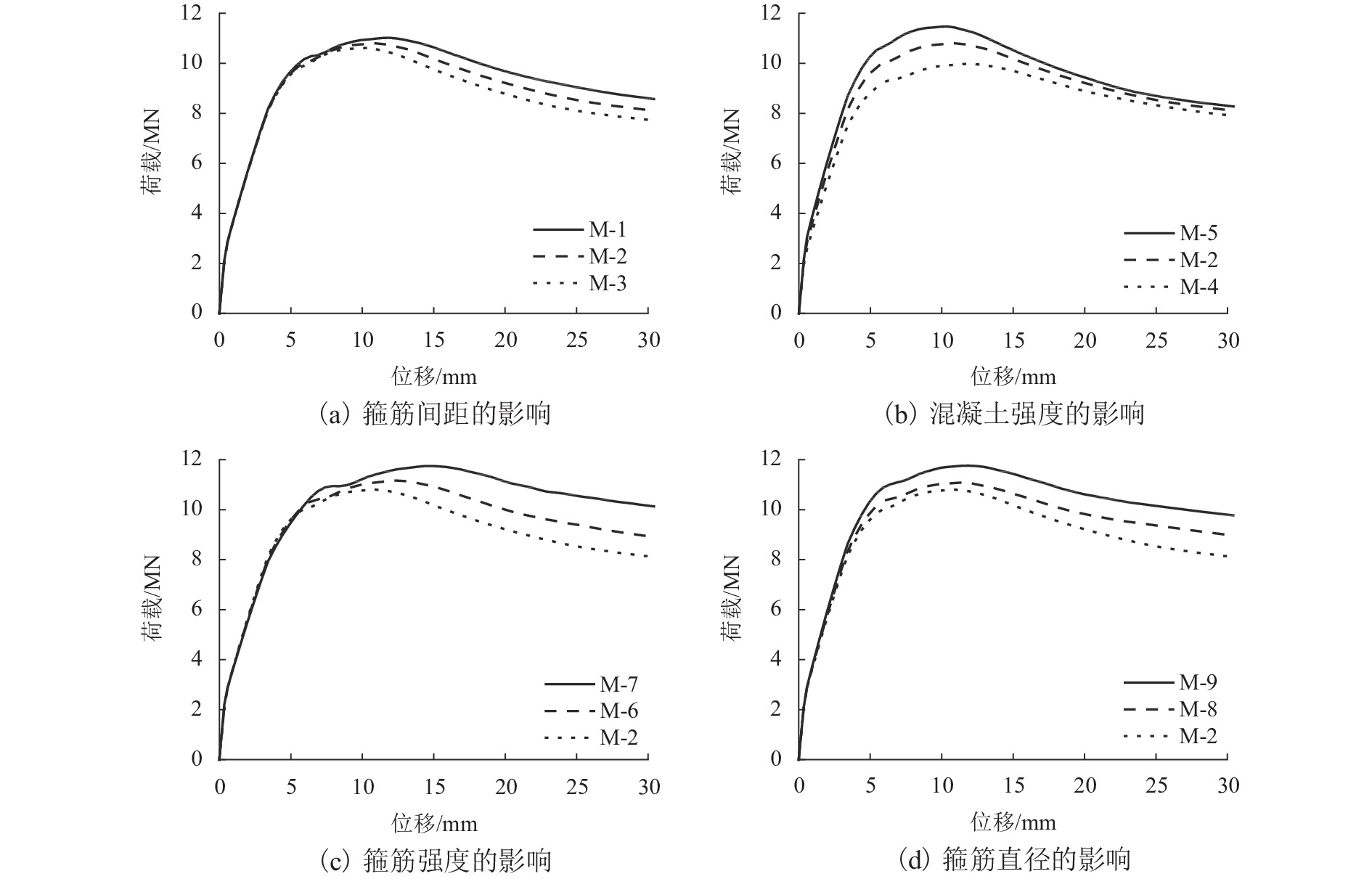
D、d 分别为大螺箍和小螺箍的直径;Asp1、Asp2 分别为大螺箍和小螺箍单根钢筋的截面面积;Ach 为五螺箍所约束的混凝土面积;s5 为五螺箍的间距.有限元分析结果如图5和表2所示. 图5(a)中模型M-1、M-2、M-3分别对应的箍筋间距为45、50、55 mm,可以看出:随着箍筋间距的减小,五螺箍柱的峰值荷载和延性系数都有提高,曲线下降段也更为平缓,延性更好. 图5(b)中模型M-4、M-2、M-5分别对应的混凝土强度为23.4、26.8、29.6 MPa,可以看出:随着混凝土强度的提高,五螺箍柱的峰值荷载有明显的提高,但延性系数减小,延性不能得到改善. 图5(c)中模型M-2、M-6、M-7对应的箍筋强度分别为335、400、500 MPa,可以看出:提高螺旋箍筋的强度,五螺箍柱的峰值承载力和延性系数有所提高,主要表现为箍筋的约束应力提高,约束效果更好,下降段曲线也更为平缓,延性得到了较大改善. 图5(d)中模型M-2、M-8、M-9对应的大(小)螺箍直径分别为10(6)、10(8)、12(8) mm,可以看出:随螺旋箍筋截面直径的增大,峰值荷载和延性系数随之提升,曲线下降段也更为平缓,五螺箍柱的轴压承载力和延性都有很大改善. 对比图5(a)和图5(d),箍筋间距的减小和箍筋直径的增大都是提高体积配箍率的方式,对五螺箍柱的影响结果相似,均能提高构件的峰值承载力和延性,有利于提高构件在考虑近场地震[19]等不利作用下结构构件极限变形能力. 故下文将基于体积配箍率研究五螺箍柱的轴压承载力计算式.
表 2 有限元模型主要参数Table 2. Main parameters of finite element models编号 螺旋箍筋
间距/mm螺旋箍筋
强度/MPa混凝土
强度/MPa大(小)螺箍
直径/mm体积配箍率/% 峰值荷载/kN DI M-1 45 335 26.8 10(6) 2.15 11020.60 1.84 M-2 50 335 26.8 10(6) 1.93 10779.40 1.78 M-3 55 335 26.8 10(6) 1.76 10613.50 1.76 M-4 50 335 23.4 10(6) 1.93 9979.90 1.97 M-5 50 335 29.6 10(6) 1.93 11472.50 1.75 M-6 50 400 26.8 10(6) 1.93 11163.90 1.94 M-7 50 500 26.8 10(6) 1.93 11744.80 2.16 M-8 50 335 26.8 10(8) 2.45 11078.90 2.13 M-9 50 335 26.8 12(8) 3.01 11756.80 2.27 3. 轴压承载力计算
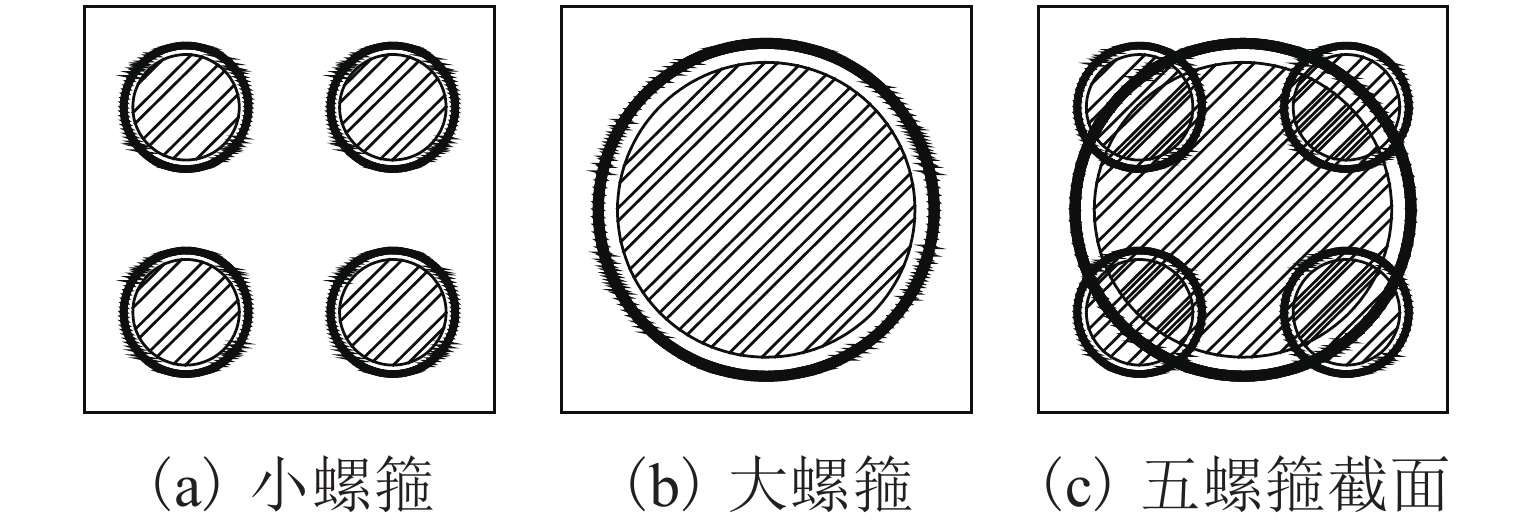
五螺箍柱的轴压承载力主要由以下4部分组成:混凝土抗压承载力、纵筋抗压承载力、大螺箍和小螺箍分别对核心区混凝土的约束效应而产生的承载力. 本文主要研究大、小螺箍通过对混凝土约束产生的承载力. 不同的配箍形式产生的约束效果不同,相对于矩形箍,圆形箍具有整体变形小,应力分布均匀及有效约束面积大等优点. 五螺箍柱中,大螺旋箍筋主要约束了柱中部的混凝土,小螺旋箍筋主要约束了柱四个角落的混凝土,二者相互弥补各自的弱约束区,较好地约束了整个截面. 螺旋箍筋有效约束区如图6所示,其中阴影部分表示有效约束区.
由于大、小螺箍的约束部位不同,故计算时应分别计算两者提供的约束作用力. 螺旋箍筋的有效约束面积[4]为
Ac=πd2cor4(1−s2dcor)2, (13) 式中:
s 为螺旋箍筋的间距.《混规》[18]关于约束混凝土的轴心抗压强度为
fc*=fc+βσr, (14) 式中:
σr 为核心混凝土受到的径向压应力值,如式(15);fc 为混凝土抗压强度设计值;对于约束混凝土,取β = 4 .σr=2fyAsssdcor, (15) 式中:
fy 为螺旋箍筋的抗拉屈服强度;Ass 为单根螺旋箍筋的截面面积.在Hobbs[20]的研究中有
f∗c=fc+3.7(σrfc)0.86fc. (16) 根据叠加理论,基于《混规》[18]的五螺箍轴压承载力为
Nu1=0.9[fcAcor+8Ass1s1dcor1fy1Ac1+4×8Ass2S2dcor2fy2Ac2+fy3As1], (17) 式中:
Ass1 和Ass2 分别为单根大、小螺旋箍筋的截面面积;fy1 和fy2 分别为大、小螺旋箍筋的屈服强度;s1 与s2 分别为大、小螺旋箍筋的间距;dcor1 和dcor2 分别为大、小螺旋箍筋包围的核心区混凝土直径;Acor 为混凝土核心区面积;fy3 为纵筋抗压强度;As1 为纵筋面积;Ac1、Ac2 分别为大、小螺旋箍筋的有效约束面积.根据叠加理论,基于Hobbs[20]修正后的五螺箍轴压承载力为
Nu2=0.9[fcAcor+3.7fcAc1(2fy1Ass1s1dcor1fc)0.86+3.7fcAc2(2fy2Ass2s2dcor2fc)0.86×4+fy3As1]. (18) 文献[11]提出的五螺箍轴压承载力为
Nu3=0.85fc0Acc+fy3As1, (19) 式中:
Acc 为五螺箍所约束的混凝土面积.美国ACI规范[2]规定的短柱受压承载力为
Nu4=0.85[0.85fc0(Ac−As1)+fy3As1], (20) 式中:
Ac 为混凝土柱全断面积;方括号外的“0.85”表示结构抗力折减系数,方括号内的“0.85”表示尺寸效应对受压承载力的影响系数.由上文轴压承载力影响因素分析可知,材料的强度、箍筋的间距、箍筋的面积等都对五螺箍柱的承载力有影响,为简便起见,本文将这些因素统一考虑为体积配箍率
ρv ,这样就可以很大程度上减小承载力计算的复杂程度. 由于混凝土及纵筋所提供的竖向承载力计算较为明确,无需修正,本文重点修正螺旋箍筋对混凝土的约束作用. 将每个构件的轴压承载力减去混凝土和纵筋提供的竖向承载力,得到螺旋箍筋提供的竖向承载力N1 ,由此可以推出约束作用系数为ξ=N1/[fcfy(Ac1+4Ac2)]. (21) ξ 随ρv 的变化关系如图7所示,对两者进行线性关系拟合,结果可以看出两者大致成线性分布. 根据ξ 与ρv 的关系,参考《混规》[18]和Hobbs[20]修正按叠加理论计算的公式,本文提出五螺箍柱的轴压承载力为Nu5=0.9[fcAcor+fy3As1+fcfy(Ac1+4Ac2)(0.0019+0.076ρv)]. (22) 采用上述5个承载力计算式(即式(17)~(20)和式(22)),不考虑安全储备及折减系数,混凝土强度统一采用轴心抗压强度标准值,得到上述9个模型和4个试验[16]构件的轴压承载力,分别如表3和表4所示. 表中:
δ1 、δ2 、δ3 、δ4 和δ5 为5个承载力对应的相对误差.表 3 9个模型的轴压承载力计算Table 3. Axial compression bearing capacity calculation of nine models编号 模拟值 Nue/kN 计算值/kN 相对误差/% Nu1 Nu2 Nu3 Nu4 Nu5 δ1 δ2 δ3 δ4 δ5 M-1 11020.60 10024.25 10459.24 6543.56 7871.88 11039.23 −9.04 −5.09 −40.62 −28.57 0.17 M-2 10779.40 9601.01 10019.12 6543.56 7871.88 10675.10 −10.93 −7.05 −39.30 −26.97 −0.97 M-3 10613.50 9258.53 9656.58 6543.56 7871.88 10373.72 −12.77 −9.02 −38.35 −25.83 −2.26 M-4 9979.90 9001.25 9362.72 6002.76 7162.57 9610.15 −9.81 −6.18 −39.85 −28.23 −3.70 M-5 11472.50 10094.93 10555.22 6988.93 8456.03 11552.11 −12.01 −8.00 −39.08 −26.29 0.69 M-6 11163.90 10104.07 10515.16 6543.56 7871.88 11386.56 −9.49 −5.81 −41.39 −29.49 1.99 M-7 11744.80 10878.01 11257.04 6543.56 7871.88 12481.12 −7.38 −4.15 −44.29 −32.98 6.27 M-8 11078.90 10056.88 10453.68 6543.56 7871.88 11110.52 −9.22 −5.64 −40.94 −28.95 0.29 M-9 11756.80 10962.58 11334.17 6543.56 7871.88 11579.44 −6.76 −3.59 −44.34 −33.04 −1.51 绝对值均值 9.71 6.06 40.91 28.93 1.98 标准差 0.0197 0.0175 0.0215 0.0261 0.0195 由表3数据可知:计算值
Nu3 远远小于模拟值和试验值,原因是该式中混凝土的计算面积是五螺箍约束混凝土的面积,且混凝土抗压强度取的是轴心抗压强度标准值,而不是约束后的混凝土抗压强度值;计算值Nu4 相比模拟值和试验值误差较大,原因是计算式仅考虑了纵筋和混凝土提供的竖向抗压承载力,而忽略了螺旋箍筋对混凝土的约束作用;计算值Nu1 和Nu2 比较接近模拟值和试验值,两个计算式既考虑了混凝土和纵筋所提供的竖向抗压承载力,又考虑了箍筋对混凝土的约束效应;在分析范围内,本文提出的修正式的计算值Nu5 更加接近模拟值和试验值,与模拟值的误差均值为1.98%,与试验值的误差均值为2.83%,且标准差分别为0.0195和0.0216,总体上偏于安全. 用体积配箍率考虑箍筋的间距、箍筋的面积、螺箍直径等多因素使得承载力计算更加简便与精确,且具有很好的实用性.表 4 4个试验构件的轴压承载力Table 4. Axial compression bearing capacity calculation of four test members编号 试验值[16]/kN 计算值/kN 相对误差/% Nu1 Nu2 Nu3 Nu4 Nu5 δ1 δ2 δ3 δ4 δ5 C2-1 21672.00 20569.22 21094.45 12090.38 11518.40 22156.09 −5.09 −2.66 −44.21 −46.85 2.23 C2-2 20412.00 19005.14 19508.17 12291.21 11706.16 20390.35 −6.89 −4.43 −39.78 −42.65 −0.11 C2-4 19332.00 19334.76 19871.39 12291.21 11706.16 20319.01 0.01 2.79 −36.42 −39.45 5.11 C2-5 18181.00 17305.58 17781.27 12090.38 11518.40 18883.65 −4.82 −2.20 −33.50 −36.65 3.86 绝对值均值 4.20 3.02 38.48 41.40 2.83 标准差 0.029 4 0.009 7 0.046 0 0.043 9 0.021 6 4. 结 论
1) 建立与参考文献中试验模型一致的五螺箍短柱有限元模型进行对比分析,分析结果显示有限元模拟结果与试验结果误差较小,在可接受范围内,从而验证了该有限元模型的正确性.
2) 基于材料用量相等原则,对4种不同配箍形式的短柱进行对比分析,表明五螺箍柱承载力和延性均较优.
3) 对五螺箍柱进行影响因素分析,改变材料强度、螺箍间距、箍筋面积等均能改变五螺箍柱性能,提高配箍率可以明显改善五螺箍柱的延性及峰值承载力.
4) 在多个参数分析的基础上,提出了基于体积配箍率的五螺箍短柱轴压承载力计算方法,与各国规范式对比,该式更为简便且较为精确.
-
表 1 高精度磁电探测仪器性能指标
Table 1. Performance indexes of high-precision magnetoelectric detection instrument
项目 性能 发射功率/W 2000 发射电压/V 20 ~ 1200 发射电流/A 0.01~5.00 发射波形 M 序列 位宽/ms 100~ 2000 阶数/阶 4~12 频带宽度/Hz 0.01~50.00 同步方式 GPS 同步 工作温度/℃ −20~70 磁力仪精度/T 1 × 10−9 最大测深/m 1000 表 2 模型试验方案设置
Table 2. Scheme setting of model test
试验组 渗漏通道电阻率/
(Ω·m)通道埋深/cm 通道数量/个 渗漏通道
状态屏蔽层 2.5 Ω•m 土槽试验 2.5 5 1 平直 无 10 平直 20 平直 5 倾斜 高阻屏蔽层影响试验 2.5 10 1 平直 有 双渗漏土槽模型试验 2.5 10 2 平直,平行 无 平直,不平行 表 3 2.5 Ω•m模型试验均方差及变异系数
Table 3. Mean square errors and variation coefficients in 2.5 Ω•m model test
渗漏埋深/cm S/(×10−9 T) CV/% 5 2.78 0.41 10 3.16 0.94 20 3.32 1.93 表 4 渗漏磁感应强度最大值
Table 4. Maximum magnetic induction intensity of leakage
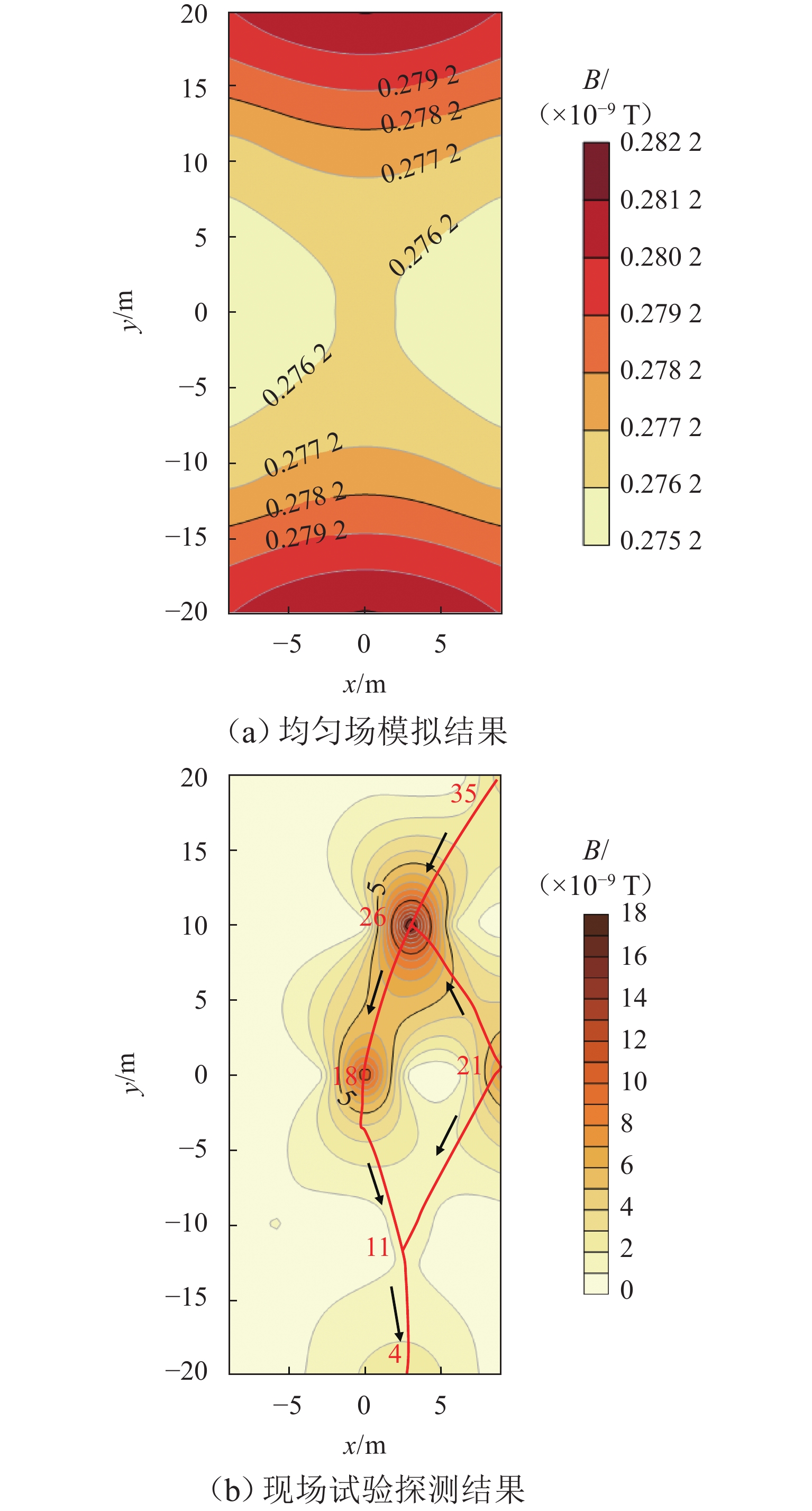
× 10−7 T 测线 测点 平行渗漏 非平行渗漏 1 5 2.38 2.19 9 2.36 2.07 2 17 2.30 2.11 21 2.23 2.04 3 29 2.28 2.13 33 2.39 1.98 4 41 2.35 2.06 45 2.26 1.99 表 5 磁感应强度极值大小及异常埋深
Table 5. Extreme values of magnetic induction intensity and abnormal burial depth
测点 B/(×10−9 T) 埋深/m 4 2.7 14.6 18 11.4 3.6 21 7.8 5.2 26 17.0 2.2 -
[1] 中华人民共和国水利部. 2021中国水利发展报告[M]. 北京:中国水利水电出版社,2021. [2] 张聪,姚令侃,黄艺丹,等. 地震共振涌浪作用下冰碛堰塞坝的漫顶溃决[J]. 西南交通大学学报,2021,56(3): 564-571.ZHANG Cong, YAO Lingkan, HUANG Yidan, et al. Overtopping failure of moraine dams under action of earthquake-induced resonant water surges[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 564-571. [3] 赵海鑫,姚令侃,黄艺丹,等. 地震与滑坡碎屑流引发堰塞湖涌浪动水压力研究[J]. 西南交通大学学报,2021,56(3): 558-563.ZHAO Haixin, YAO Lingkan, HUANG Yidan, et al. Hydrodynamic pressures study of barrier lake under coaction of earthquake and clastic flow landslide[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 558-563. [4] 杨雄兵. 某水库坝基渗漏规律与模式研究[D]. 兰州:兰州大学,2019. [5] 徐轶,谭政,位敏. 水库大坝渗漏常用探测技术及工程应用[J]. 中国水利,2021(4): 48-51. doi: 10.3969/j.issn.1000-1123.2021.04.025XU Yi, TAN Zheng, WEI Min. Typical leakage detection techniques and the application for reservoir dams[J]. China Water Resources, 2021(4): 48-51. doi: 10.3969/j.issn.1000-1123.2021.04.025 [6] 苏怀智,周仁练. 土石堤坝渗漏病险探测模式和方法研究进展[J]. 水利水电科技进展,2022,42(1): 1-10,39.SU Huaizhi, ZHOU Renlian. Research progress and prospect of earth-rockfill dam leakage detection modes and method[J]. Advances in Science and Technology of Water Resources, 2022, 42(1): 1-10,39. [7] 邹德兵,傅兴安,闵征辉. 磁电阻率法在水库渗漏探测中的应用[J]. 水利与建筑工程学报,2019,17(5): 148-152.ZOU Debing, FU Xing’an, MIN Zhenghui. Application of magnetometric resistivity method in reservoir leakage detection[J]. Journal of Water Resources and Architectural Engineering, 2019, 17(5): 148-152. [8] 徐磊,张建清,严俊,等. 磁电阻率法在平原水库渗漏探测中的试验研究[J]. 地球物理学进展,2021,36(5): 2222-2233. doi: 10.6038/pg2021EE0069XU Lei, ZHANG Jianqing, YAN Jun, et al. Experimental research of magnetic resistivity method in plain reservoir leakage detection[J]. Progress in Geophysics, 2021, 36(5): 2222-2233. doi: 10.6038/pg2021EE0069 [9] EDWARDS R N. The magnetometric resistivity method and its application to the mapping of a fault[J]. Canadian Journal of Earth Sciences, 1974, 11(8): 1136-1156. doi: 10.1139/e74-108 [10] HOWLAND-ROSE A W, LINFORD G, PITCHER D H, et al. Some recent magnetic induced-polarization developments—part I: theory[J]. Geophysics, 1980, 45(1): 37-54. doi: 10.1190/1.1441038 [11] PAI D, EDWARDS R N. Programme MMR2DFD: finite difference modeling of MMR anomlales[J]. Reports in Applied Geophysics, 1983, 25(4): 1453-1456. [12] OPPLIGER G L. Three-dimensional terrain corrections for mise-á-la-masse and magnetometric resistivity surveys[J]. Exploration Geophysics, 1984, 15(3): 194-195. [13] NABIGHIAN M N, OPPLIGER G L, EDWARDS R N, et al. Cross-hole magnetometric resistivity (MMR)[J]. Geophysics, 1984, 49(8): 1313-1326. doi: 10.1190/1.1441758 [14] CUNNINGHAM A B. Some alternate vibrator signals[J]. Geophysics, 1979, 44(12): 1901-1921. doi: 10.1190/1.1440947 [15] 柴治媛. 可控震源伪随机扫描方法与地震响应的数值模拟[D]. 长春: 吉林大学,2007. [16] 张群英,方广有. 伪随机序列编码脉冲信号在探地雷达中的应用研究[J]. 电子与信息学报,2011,33(2): 424-428.ZHANG Qunying, FANG Guangyou. The study of pseudo random sequence’s application to GPR[J]. Journal of Electronics & Information Technology, 2011, 33(2): 424-428. [17] 齐彦福,殷长春,王若,等. 多通道瞬变电磁m序列全时正演模拟与反演[J]. 地球物理学报,2015,58(7): 2566-2577. doi: 10.6038/cjg20150731QI Yanfu, YIN Changchun, WANG Ruo, et al. Multi-transient EM full-time forward modeling and inversion of m-sequences[J]. Chinese Journal of Geophysics, 2015, 58(7): 2566-2577. doi: 10.6038/cjg20150731 [18] 王显祥,底青云,王妙月,等. 基于m伪随机序列的电磁法抗噪能力分析[J]. 地球物理学报,2016,59(5): 1861-1874. doi: 10.6038/cjg20160529WANG Xianxiang, DI Qingyun, WANG Miaoyue, et al. A study on the noise immunity of electromagnetic methods based on m pseudo-random sequence[J]. Chinese Journal of Geophysics, 2016, 59(5): 1861-1874. doi: 10.6038/cjg20160529 [19] 颜廷杰,王赛昕,马一行,等. 人文干扰对电法勘探的影响及应对措施[J]. 矿产勘查,2016,7(4): 634-639. doi: 10.3969/j.issn.1674-7801.2016.04.016YAN Tingjie, WANG Saixin, MA Yixing, et al. Influence of human interference on application of electrical prospecting and corresponding anti-interference measures[J]. Mineral Exploration, 2016, 7(4): 634-639. doi: 10.3969/j.issn.1674-7801.2016.04.016 [20] 王洪波. KGR-1B抗干扰电法仪在石墨矿地区的运用[J]. 煤炭与化工,2018,41(4): 79-82.WANG Hongbo. Application of KGR-1B anti-jamming electro-detecting in graphite ore deposit[J]. Coal and Chemical Industry, 2018, 41(4): 79-82. [21] 李巧灵,雷晓东,李晨. 抗干扰编码电法在通州深部岩溶发育区地质构造探测中的应用[J]. 工程勘察,2018,46(2): 71-78.LI Qiaoling, LEI Xiaodong, LI Chen. Application of a coded electrical method with anti-interference ability to detect geological structures in Tongzhou karst areas[J]. Geotechnical Investigation & Surveying, 2018, 46(2): 71-78. [22] 罗先中,李达为,彭芳苹,等. 抗干扰编码电法仪的实现及应用[J]. 地球物理学进展,2014,29(2): 944-951. doi: 10.6038/pg20140263LUO Xianzhong, LI Dawei, PENG Fangping, et al. Implementation and applications of an coded electrical instrument with anti-interference ability[J]. Progress in Geophysics, 2014, 29(2): 944-951. doi: 10.6038/pg20140263 -







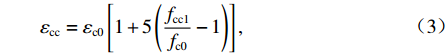



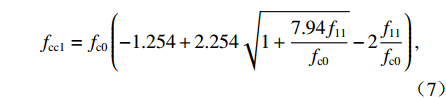


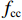
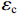
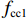
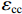
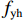
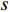
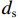
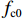
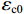
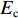
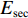
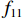
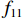
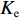
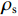
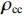
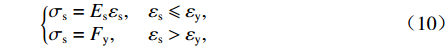
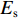
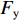
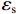
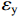
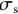
 下载:
下载:





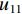
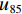
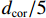
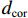
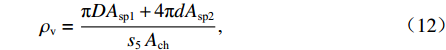
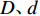
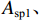
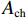
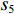


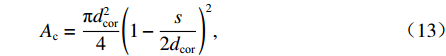
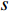


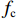
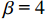

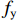
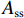
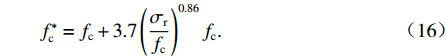
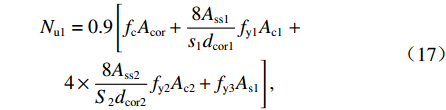
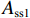
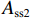
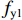
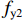
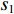
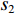
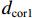

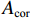
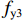
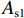
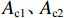
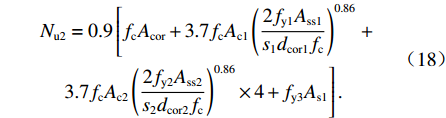
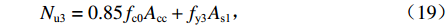
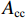
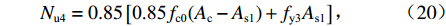
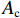
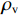
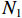
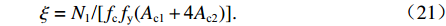
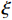
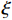
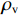
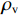

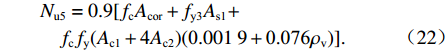
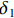
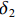
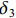
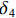
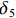
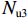
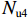
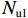
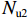
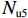
 下载:
下载: