Uneven Wear of Running Wheel Tires of Straddle Monorail Train
-
摘要:
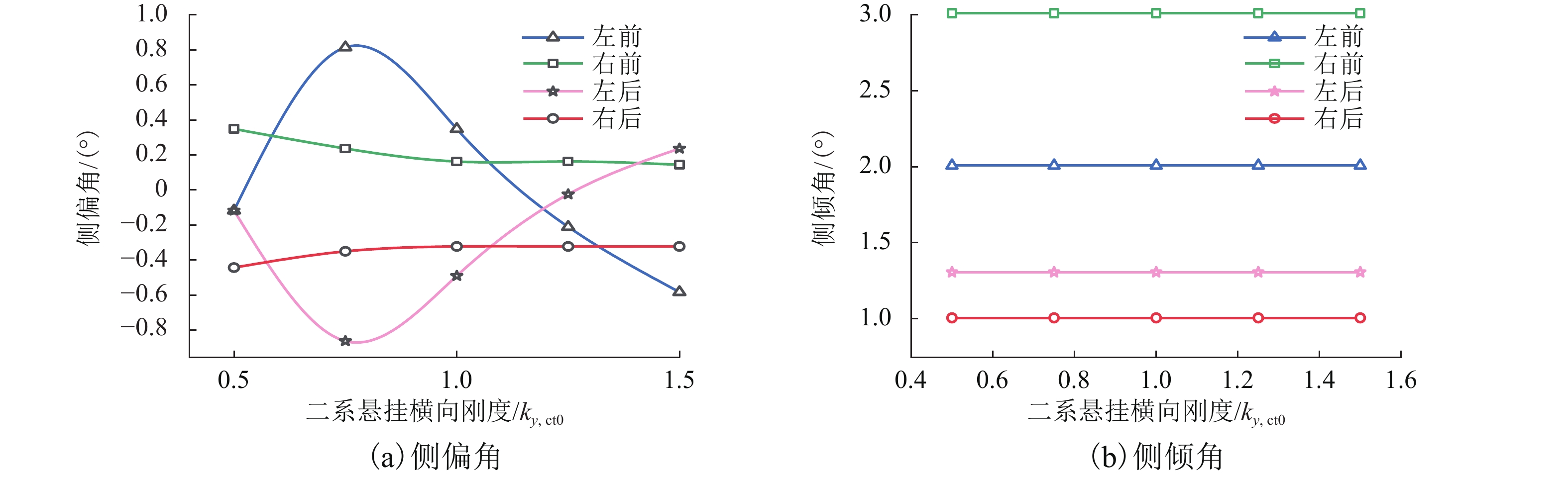
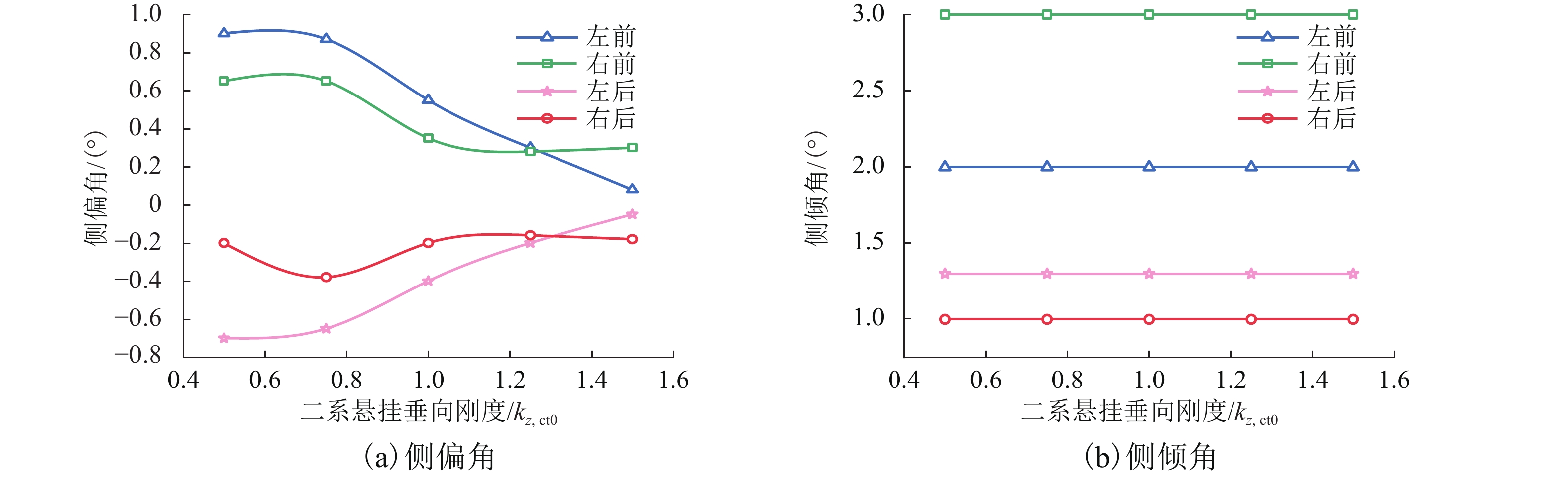
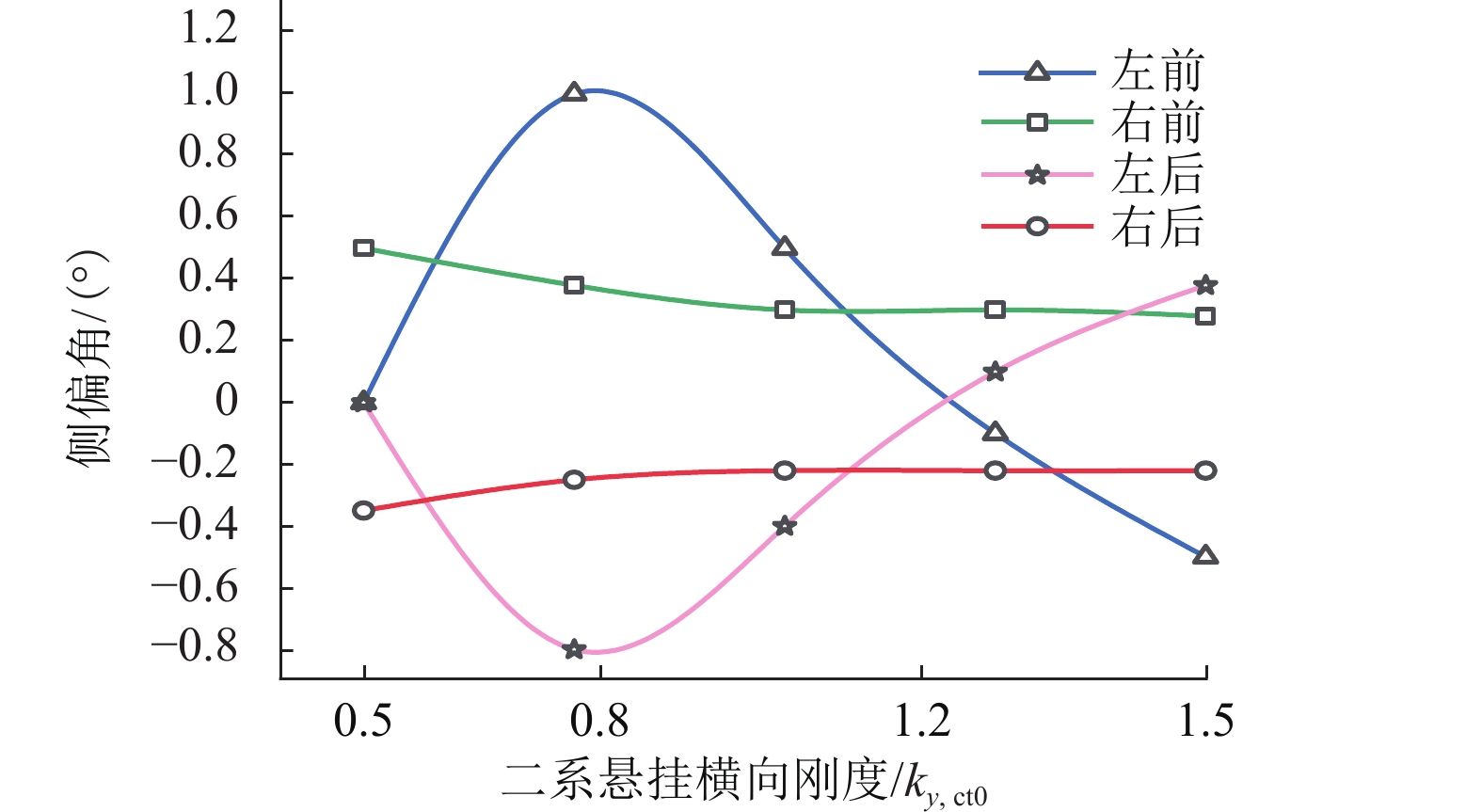
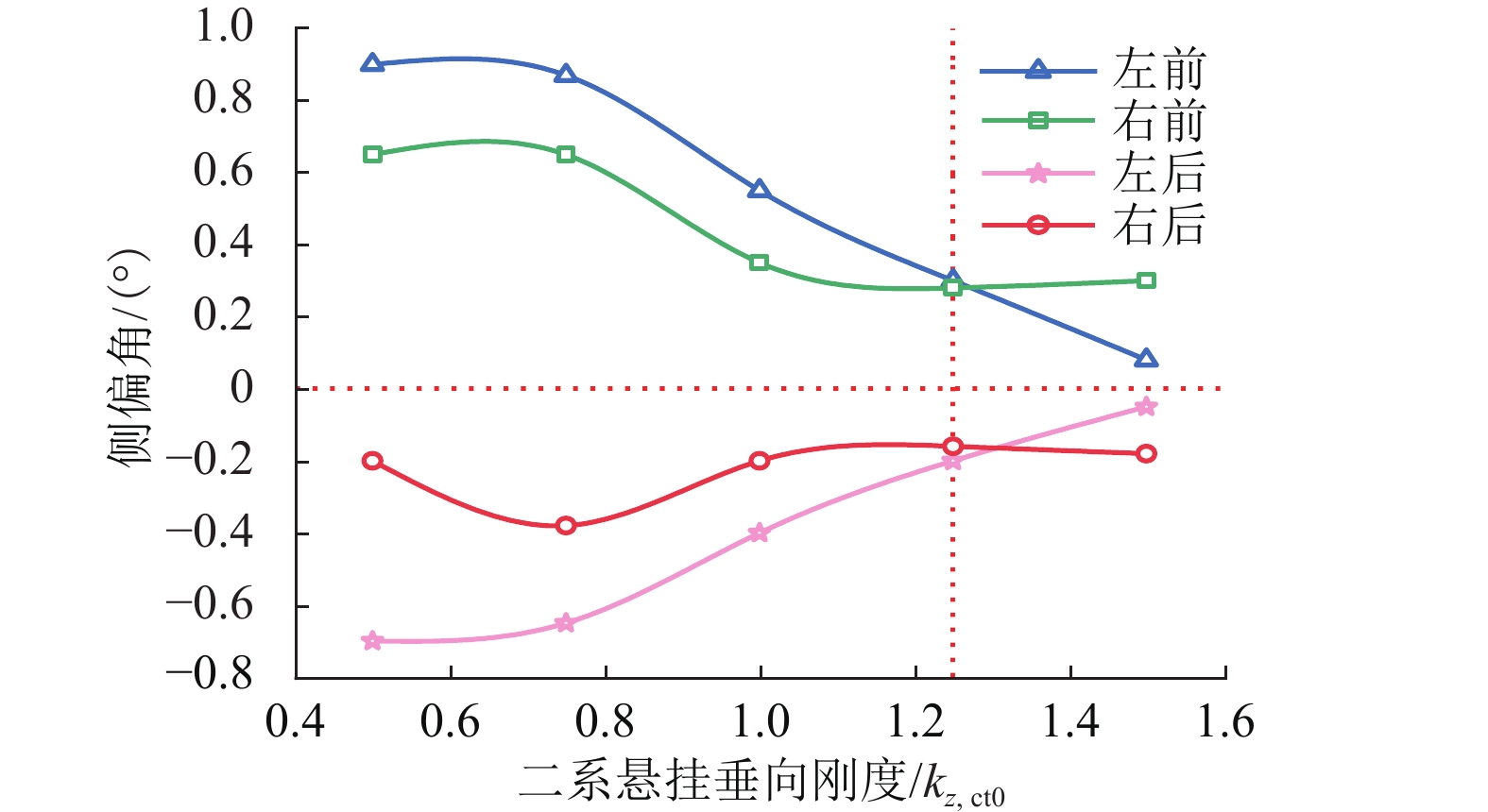
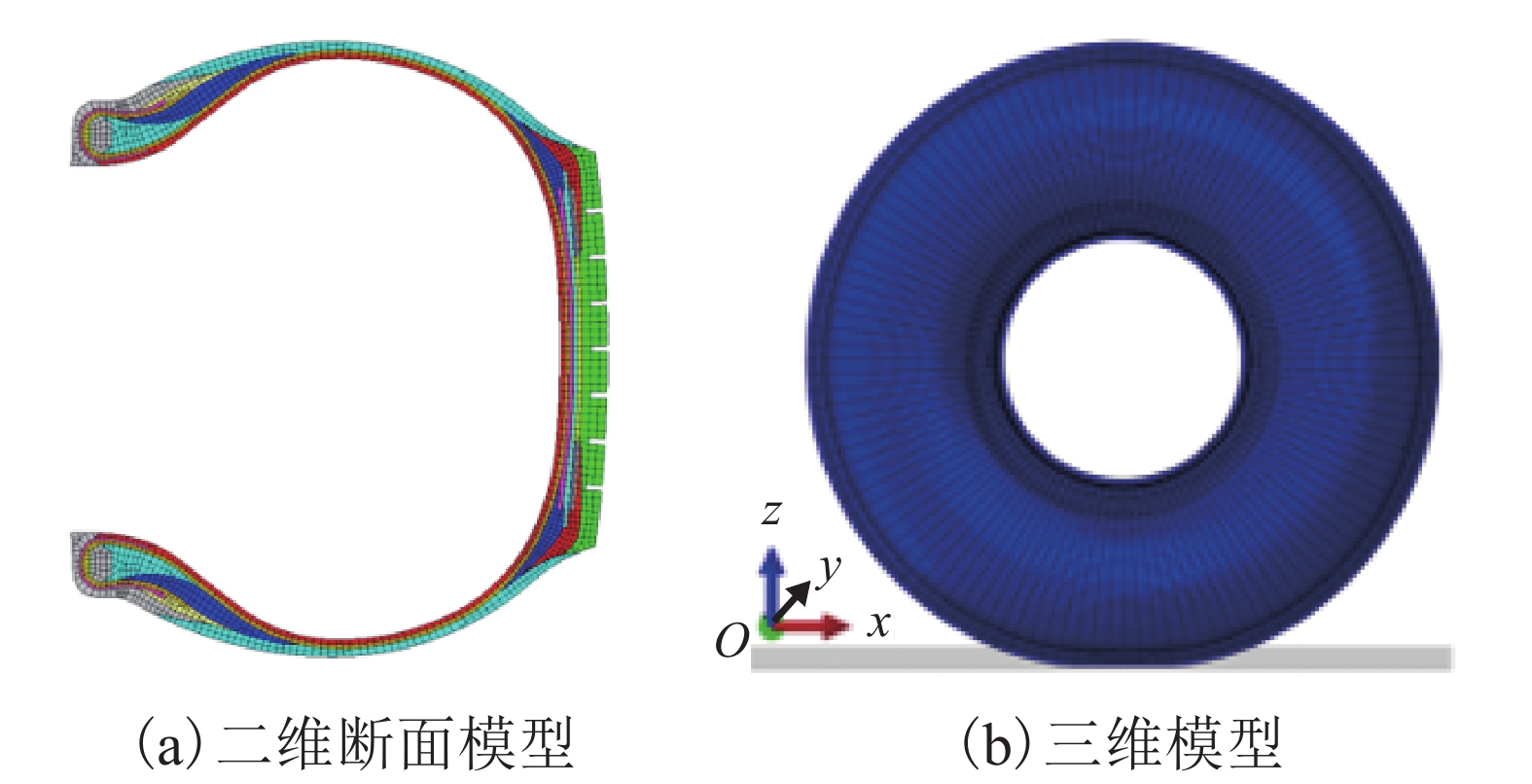
为了优化跨座式单轨列车走行轮轮胎不均匀磨损性能，在运行工况分析基础上建立了走行轮轮胎有限元模型；结合走行轮磨损特性评价指标，建立了一套新的走行轮磨损间接评价方法，该方法以侧偏角和侧倾角为设计变量，通过探索走行轮轮胎侧偏角、侧倾角及其组合对走行轮轮胎磨损与不均匀磨损的影响对车辆二系悬挂参数进行优化，减轻走行轮轮胎磨损. 研究结果表明：优选前，转向架（以前转向架为例）中前、后排走行轮轮胎侧偏角分别为0.5°、0.3°、−0.4°、−0.2°；优选后，转向架中前、后走行轮轮胎侧偏角为0.2°、0.2°、−0.2°、−0.2°；车辆结构参数中二系悬挂横向刚度、垂向刚度对走行轮各轮胎不均匀磨损的影响较大，且选取合适的参数值在一定程度上能够减轻走行轮各轮胎不均匀磨损.
Abstract:Aiming at investigating the correlation between the parameters of a vehicle’s secondary suspension structure and the uneven wear of the running wheel tires, the goal of optimization was to improve the uneven wear performance of the running wheel tires and the design variables are the vehicle’s secondary suspension parameters. An indirect method of evaluating the running wheel wear was established from the analysis of a finite element model and by combining with evaluation indexes of the running wheel wear characteristics. This method minimizes the running wheel tire wear by exploring the effects of the slip angle and roll angle of the running wheel tires and their combination on the wear and uneven wear of the running wheel tires, and by optimizing the vehicle’s secondary suspension parameters. The results show that before optimization, the slip angles of the front and rear running wheels of the bogie (where the former bogie is taken as an example) are 0.5°, 0.3°, −0.4°, and −0.2°, respectively, and that the slip angles of the rear running wheel tires are 0.2°, 0.2°, −0.2°, and −0.2°, respectively. Among the vehicle structural parameters, the lateral stiffness of the secondary suspension and the vertical stiffness of the secondary suspension strongly affect the uneven wear of the running wheel tires, which can be reduced to a certain extent by selecting appropriate parameter values.
-
Key words:
- finite element model /
- secondary suspension /
- uneven wear /
- slip angle /
- roll angle
-
图 2 走行轮轮胎有限元模型验证
Figure 2. Validation of finite element model of the running wheel tire
图 5 纯侧偏工况下走行轮轮胎磨损量及其偏度值
Figure 5. Wear mass loss and its skewness of the running wheel tire with slip angle
图 6 纯侧倾工况下走行轮轮胎磨损量及其偏度值
Figure 6. Wear mass loss and its skewness of the running wheel tire with roll angle
图 7 二系悬挂纵向刚度对侧偏角、侧倾角的影响
Figure 7. Influence of longitudinal stiffness of secondary suspension on the slip angle and roll angle
图 8 二系悬挂横向刚度对侧偏角、侧倾角的影响
Figure 8. Influence of lateral stiffness of secondary suspension on the slip angle and roll angle
图 9 二系悬挂垂向刚度对侧偏角、侧倾角的影响
Figure 9. Influence of vertical stiffness of secondary suspension on the slip angle and roll angle
图 10 二系悬挂横向刚度参数优选
Figure 10. Parameter optimization of lateral stiffness of secondary suspension
图 11 二系悬挂垂向刚度参数优选
Figure 11. Parameter optimization of vertical stiffness of secondary suspension
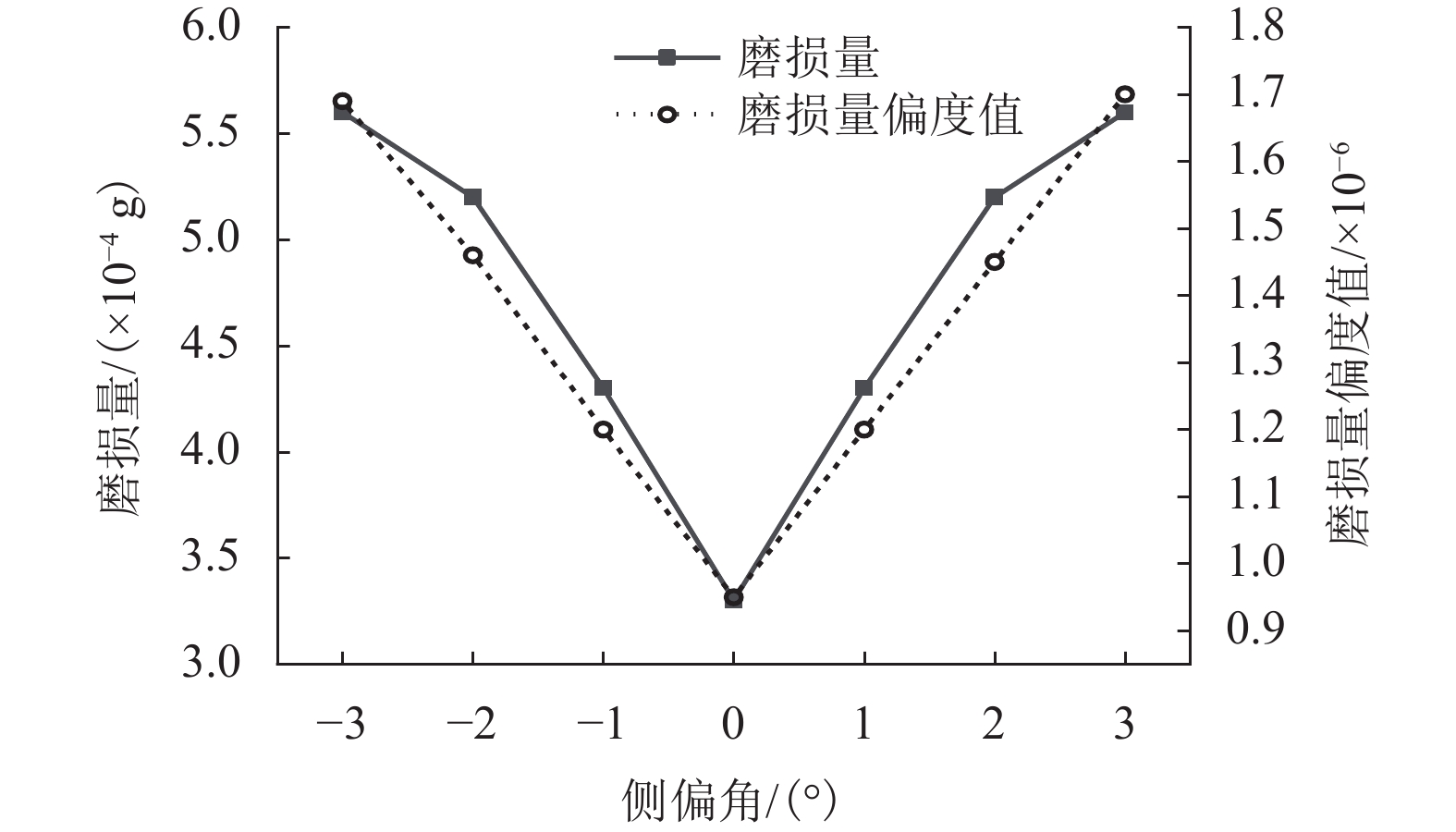
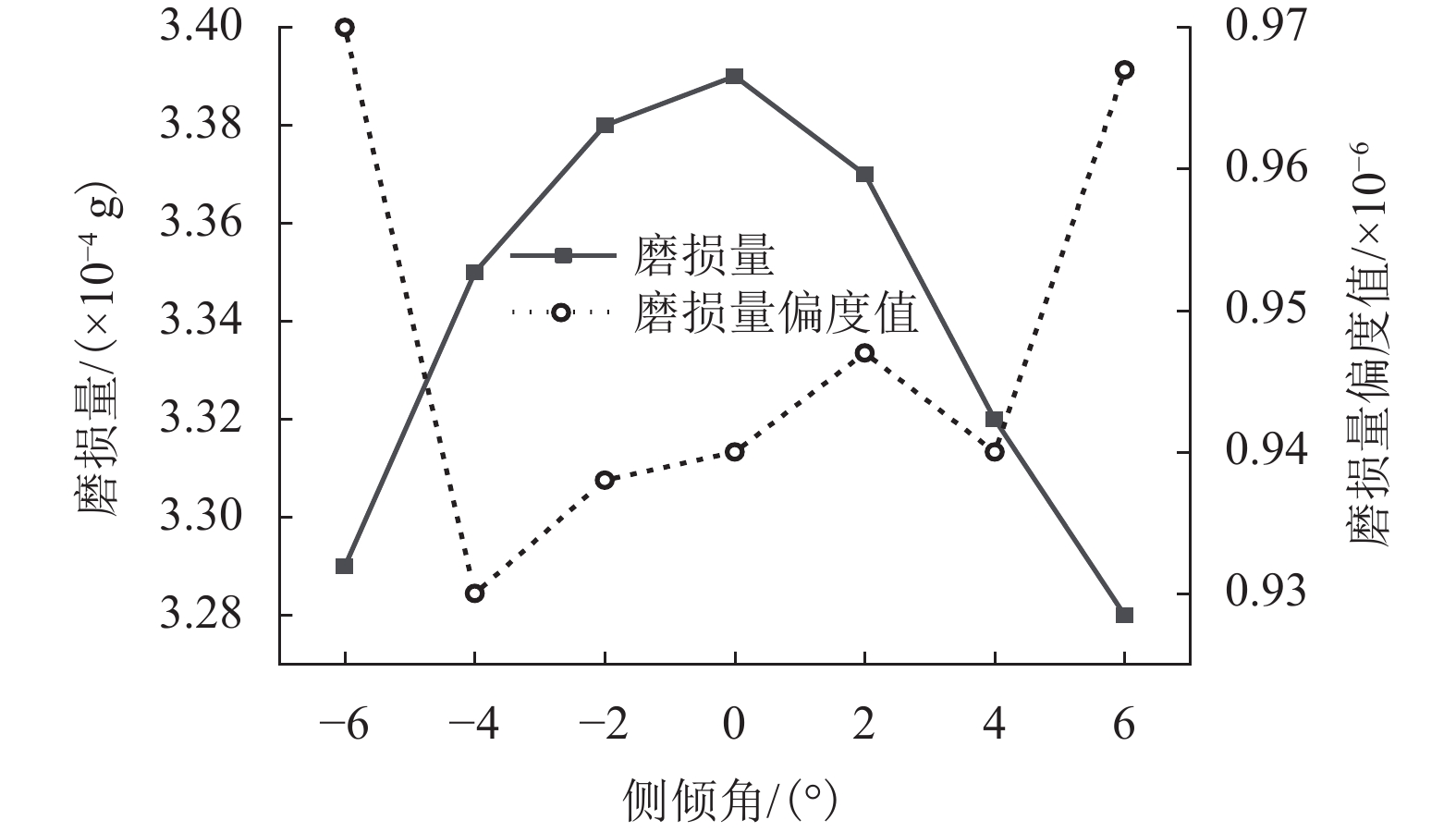
表 1 不同侧偏角、侧倾角组合下轮胎磨损量
Table 1. Wear of walking wheel tire with different slip angles and roll angles
× 10−4 g 侧倾角/（°） 侧偏角/（°） −3.0 −2.0 −1.0 0 1.0 2.0 3.0 −6.0 5.29 4.80 4.12 3.29 4.28 5.17 5.67 −4.0 5.53 5.07 4.24 3.35 4.34 5.25 5.70 −2.0 5.71 5.20 4.30 3.38 4.38 5.23 5.71 0 5.82 5.22 4.32 3.39 4.36 5.22 5.81 2.0 5.86 5.24 4.52 3.37 4.31 5.20 5.62 4.0 5.72 5.18 4.29 3.32 4.25 5.06 5.42 6.0 5.70 5.11 4.23 3.28 4.13 4.86 5.16 
下载: 导出CSV
-
[1] 贺观. 重庆单轨车走行轮胎胎面磨损分析研究与对策[J]. 城市轨道交通研究,2010,13(6): 63-67. doi: 10.3969/j.issn.1007-869X.2010.06.017HE Guan. Analysis and countermeasures for tire tread wear of Chongqing monorail vehicles[J]. Urban Rail Transit Research, 2010, 13(6): 63-67. doi: 10.3969/j.issn.1007-869X.2010.06.017 [2] 任利惠,周劲松,沈钢. 跨座式独轨车辆动力学模型及仿真[J]. 中国铁道科学,2004,25(5): 26-32. doi: 10.3321/j.issn:1001-4632.2004.05.005REN Lihui, ZHOU Jinsong, SHEN Gang. Dynamic model and simulation of straddle monorail vehicle[J]. China Railway Science, 2004, 25(5): 26-32. doi: 10.3321/j.issn:1001-4632.2004.05.005 [3] 赵树恩,罗宝良,李玉玲. 考虑轮胎非线性特性的单轨车辆平稳性研究[J]. 重庆交通大学学报(自然科学版),2018,37(8): 119-126. doi: 10.3969/j.issn.1674-0696.2018.08.20ZHAO Shuen, LUO Baoliang, LI Yuling. Study on the stability of monorail vehicle considering the nonlinear characteristics of tire[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2018, 37(8): 119-126. doi: 10.3969/j.issn.1674-0696.2018.08.20 [4] 文孝霞,杜子学,左长永,等. 曲线工况下跨座式单轨走行轮侧偏刚度对轮胎磨损的影响[J]. 交通运输工程学报,2014,14(2): 41-48. doi: 10.3969/j.issn.1671-1637.2014.02.008WEN Xiaoxia, DU Zixue, ZUO Changyong, et al. Effect of sideslip stiffness of straddle monorail running wheel on tire wear under curve condition[J]. Journal of Traffic and Transportation Engineering, 2014, 14(2): 41-48. doi: 10.3969/j.issn.1671-1637.2014.02.008 [5] 申震. 基于跨座式单轨走行轮轮胎偏磨研究的车辆动力学参数影响分析[D]. 重庆: 重庆交通大学, 2015. [6] MACIEL G, BARBOSA R S. Monorail vehicle model to study influence of tyre modelling on overall dynamics[J]. International Journal of Heavy Vehicle Systems, 2016, 23(4): 317-332. doi: 10.1504/IJHVS.2016.079270 [7] 王国林,郑州,张松,等. 跨座式单轨列车走行轮胎磨损控制方法研究[J]. 机械工程学报,2018,54(6): 78-85. doi: 10.3901/JME.2018.06.078WANG Guolin, ZHEN Zhou, ZHANG Song, et al. Research on control method of running tire wear of straddle monorail train[J]. Journal of Mechanical Engineering, 2018, 54(6): 78-85. doi: 10.3901/JME.2018.06.078 [8] 郑州. 跨座式单轨列车走行轮胎偏磨损机理及控制方法研究[D]. 镇江: 江苏大学, 2017. [9] 王国林,王晨,张建,等. 基于有限元分析的轮胎磨损性能优化[J]. 汽车工程,2009,31(9): 867-870. doi: 10.3321/j.issn:1000-680X.2009.09.016WANG Guolin, WANG Chen, ZHANG Jian, et al. Tire wear performance optimization based on finite element analysis[J]. Automotive Engineering, 2009, 31(9): 867-870. doi: 10.3321/j.issn:1000-680X.2009.09.016 [10] 王晨,王国林,张建,等. 子午线轮胎性能的多目标优化研究[J]. 武汉理工大学学报,2010,32(10): 69-72,103. doi: 10.3963/j.issn.1671-4431.2010.10.016WANG Chen, WANG Guolin, ZHANG Jian, et al. A study on multi-objective optimization of the performance of meridian tire[J]. Journal of Wuhan University of Technology, 2010, 32(10): 69-72,103. doi: 10.3963/j.issn.1671-4431.2010.10.016 [11] 林波. 基于灵敏度分析的子午线轮胎疲劳性能优化[D]. 镇江: 江苏大学, 2008. [12] 葛金虎. 基于有限元的轮胎磨损性能优化[D]. 镇江: 江苏大学, 2008. [13] 陈芳. 基于rebar单元的载重子午胎有限元分析[D]. 镇江: 江苏大学, 2007. [14] 揭琳锋. 基于复合材料理论的轮胎帘线受力模型及测试技术研究[D] . 镇江: 江苏大学, 2007. [15] 梁晖. 跨座式单轨列车走行踏面优化设计研究[D]. 镇江: 江苏大学, 2019. [16] GROSCH K A. The relation between the friction and visco-elastic properties of rubber[J]. Proceedings of the Royal Society of London, 1963, 274(1356): 21-39. [17] HEINRICH G, M, KLÜPPEL, VILGIS T A. Evaluation of self-affine surfaces and their implication for frictional dynamics as illustrated with a Rouse material[J]. Computational and Theoretical Polymer Science, 2000, 10(1/2): 53-61. doi: 10.1016/S1089-3156(99)00033-1 [18] 赵大毅. 跨座式单轨车辆走行轮轮胎偏磨损数值分析[D]. 重庆: 重庆交通大学, 2015. [19] 余志生. 汽车理论[M]. 修订本. 北京: 机械工业出版社, 1989. -
下载:
点击查看大图
计量
- 文章访问数: 326
- HTML全文浏览量: 205
- PDF下载量: 9
- 被引次数: 0