Hybrid Characteristics of Heterogeneous Traffic Flow in Intelligent Network
-
摘要:
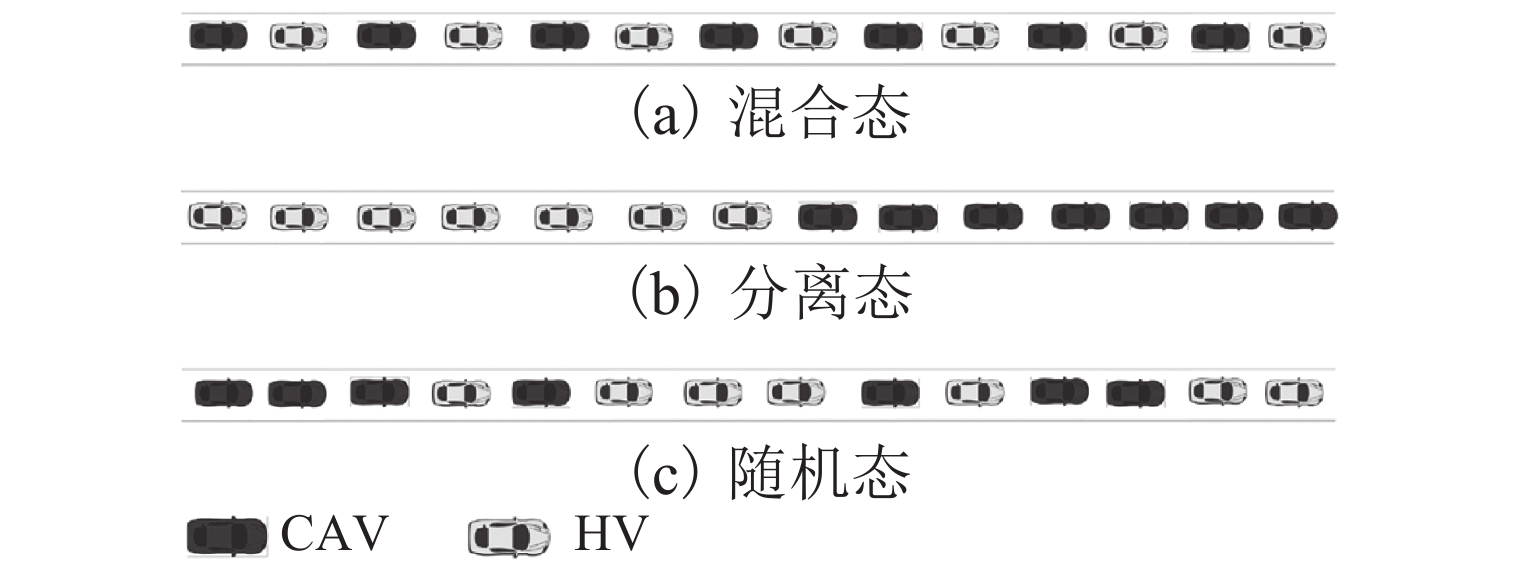
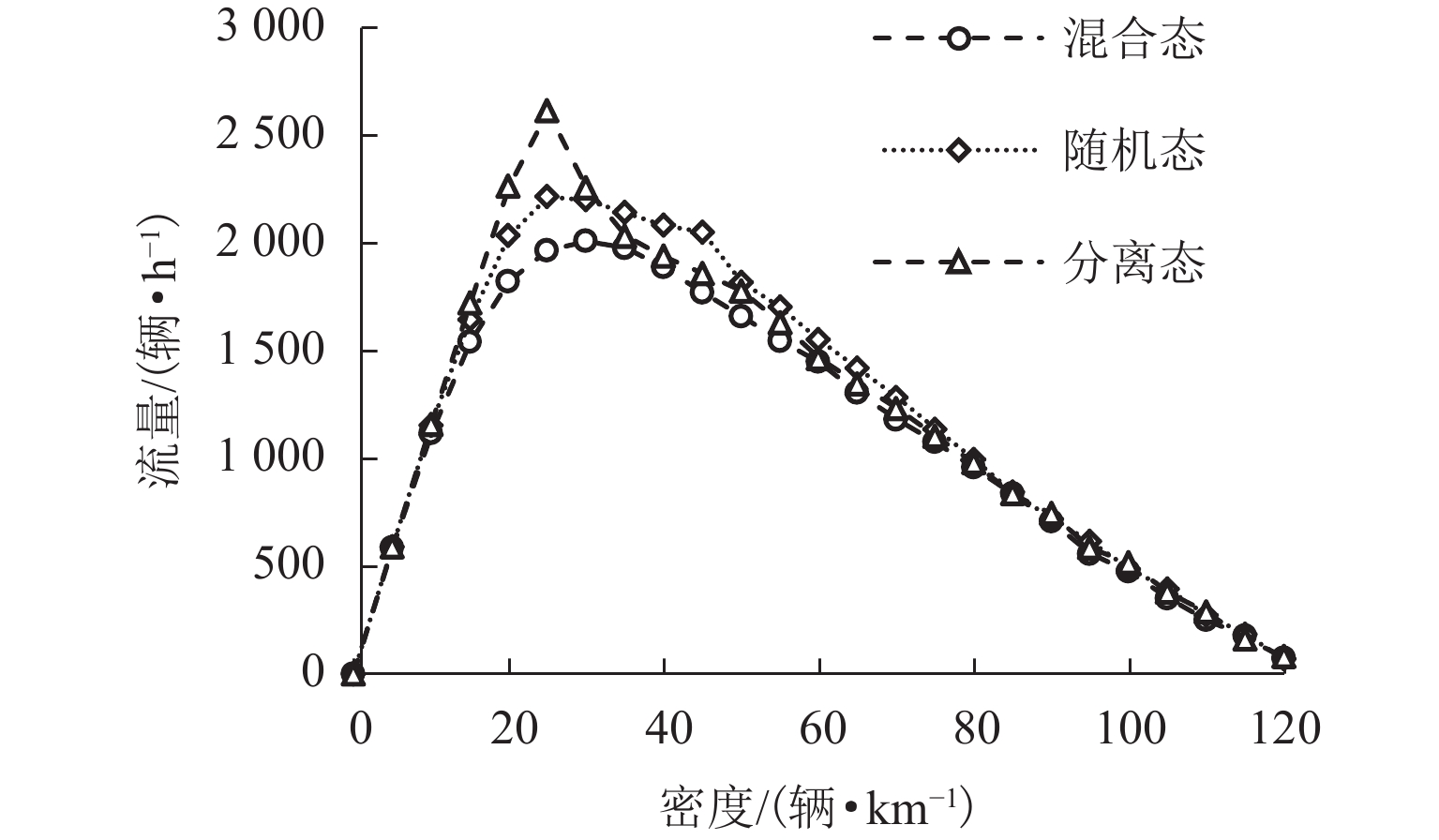
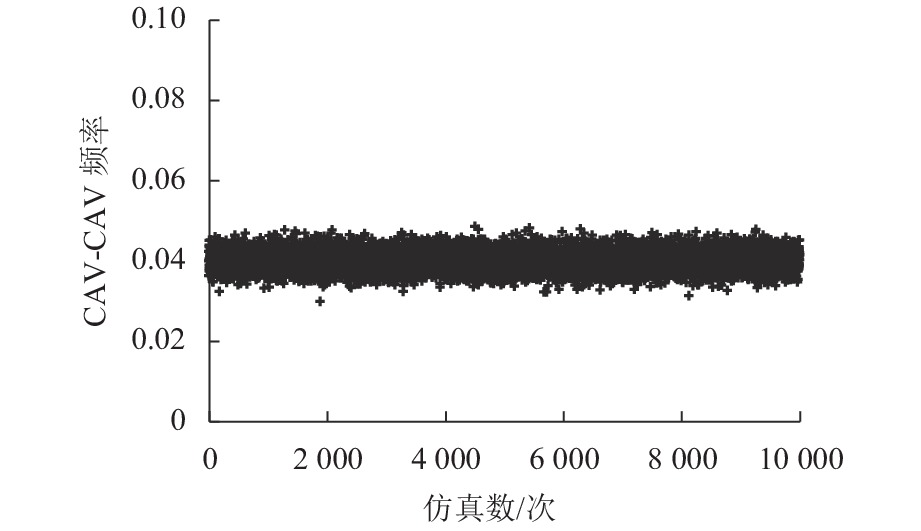
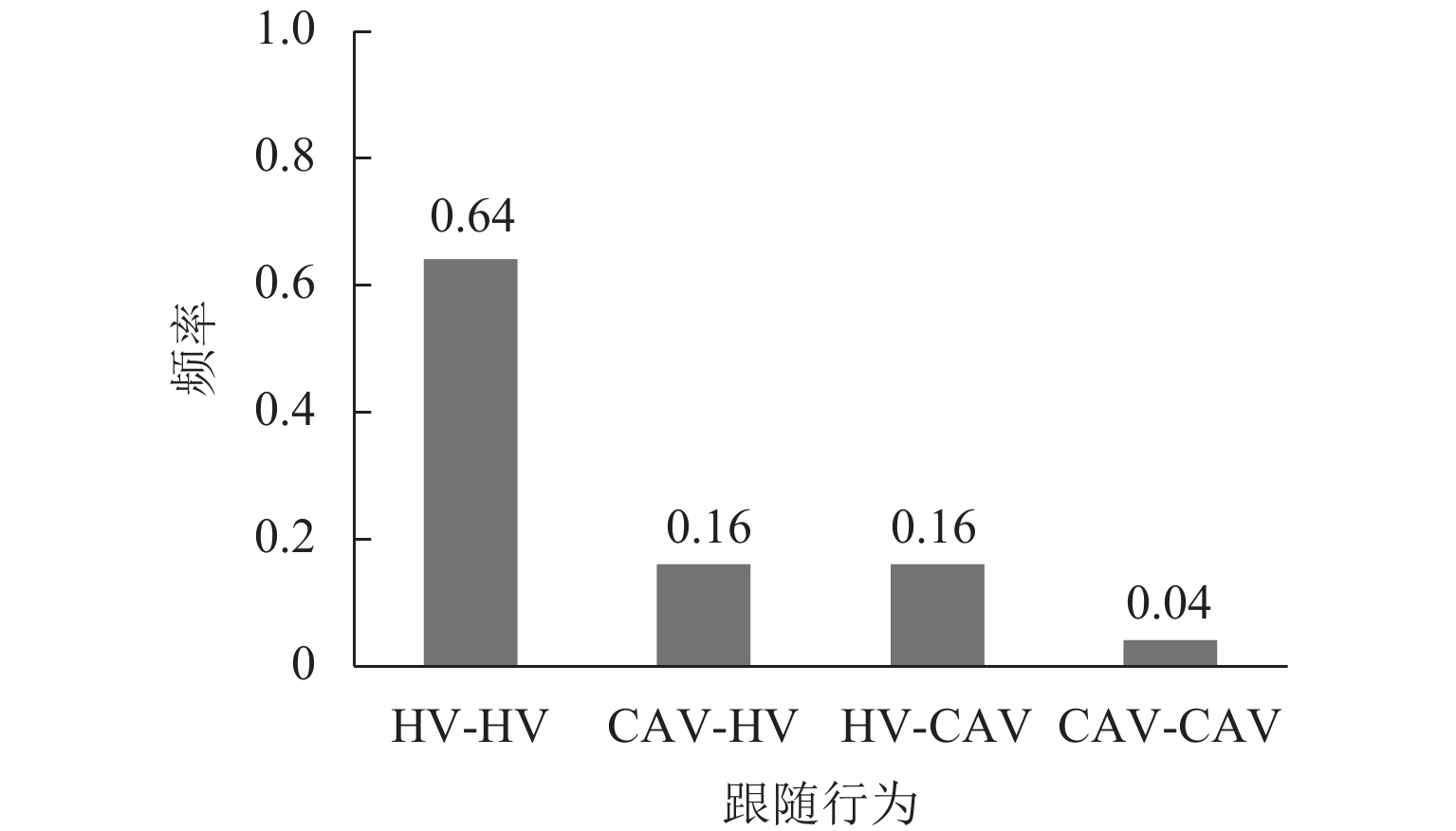
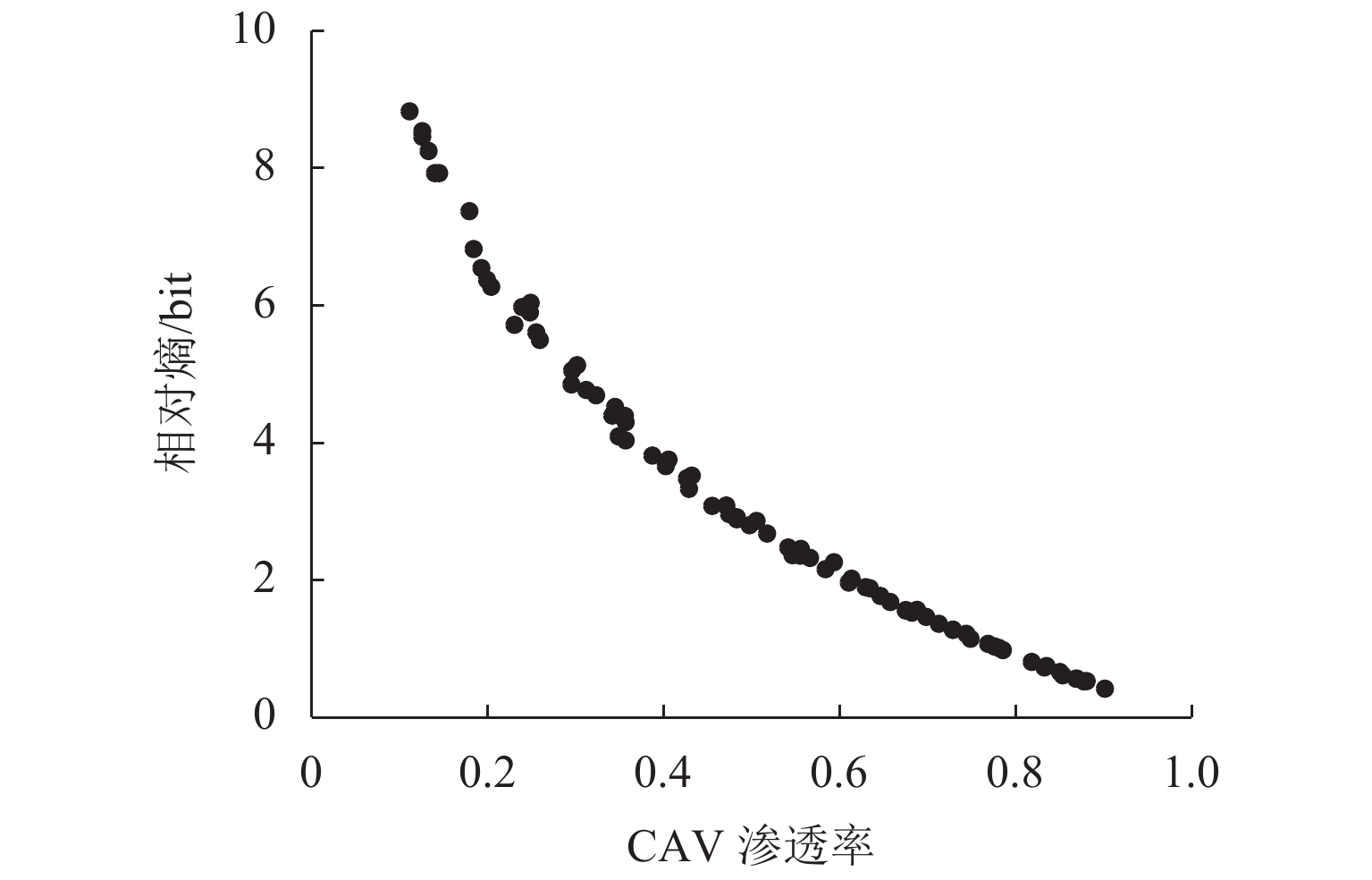
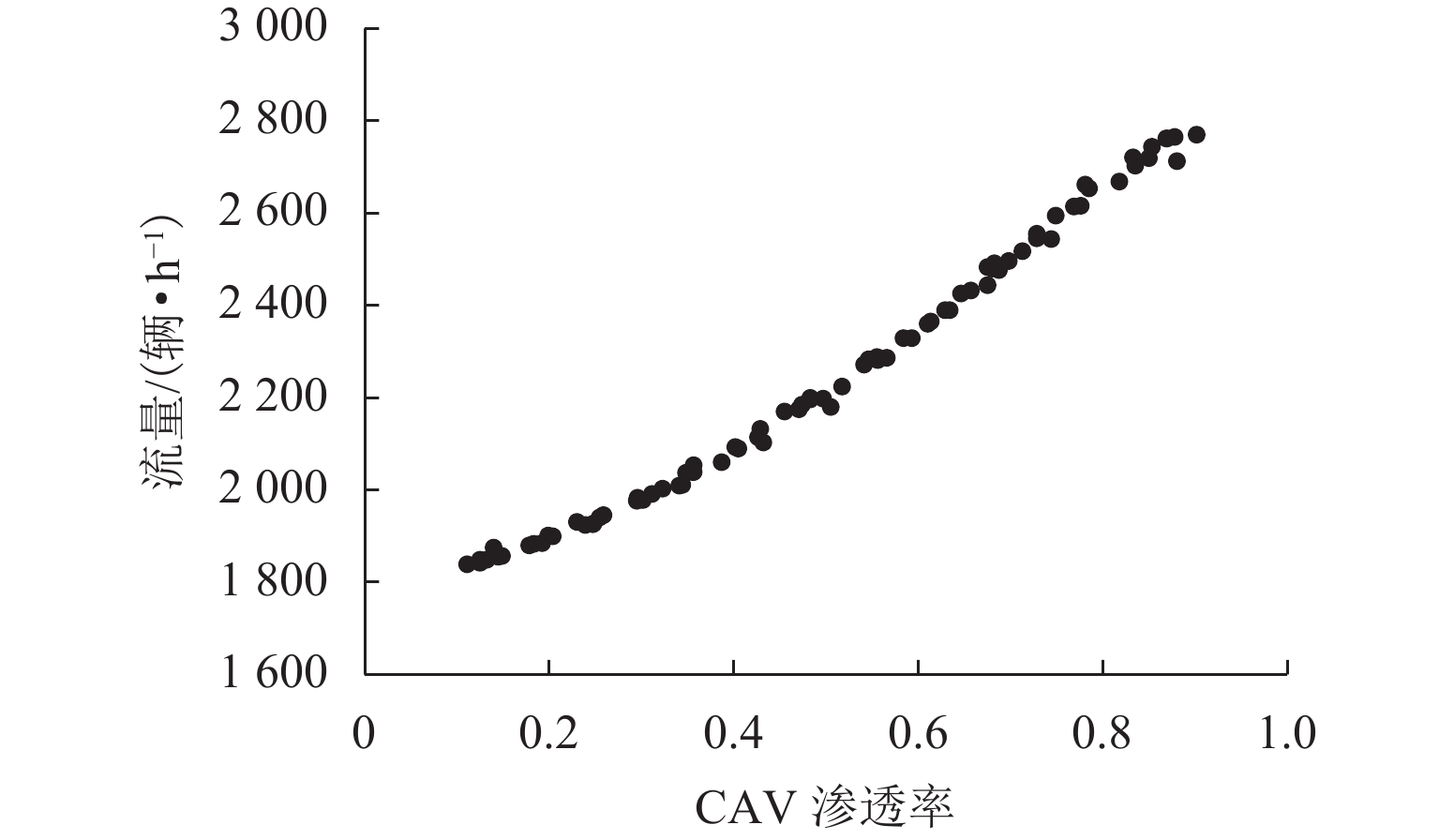
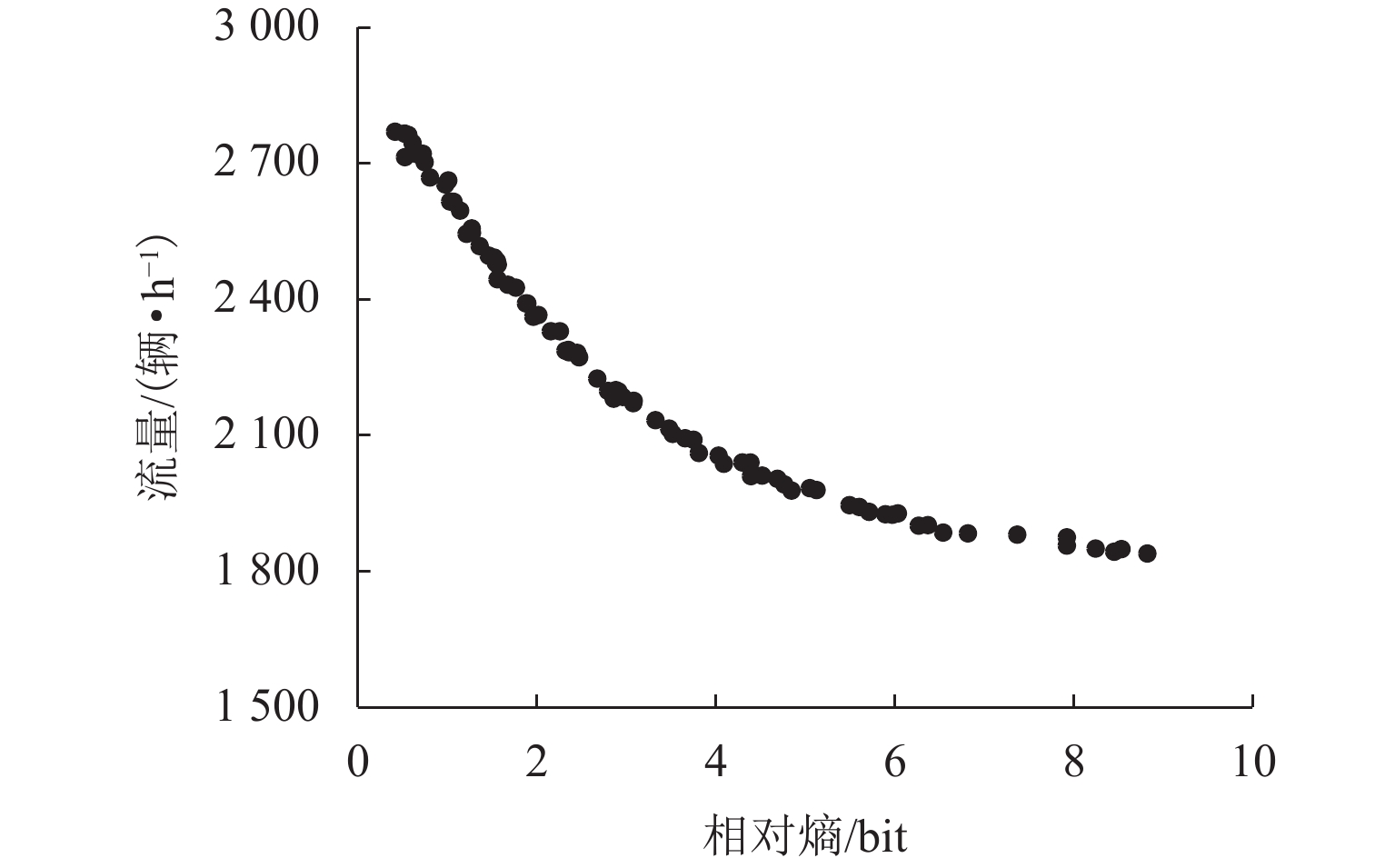
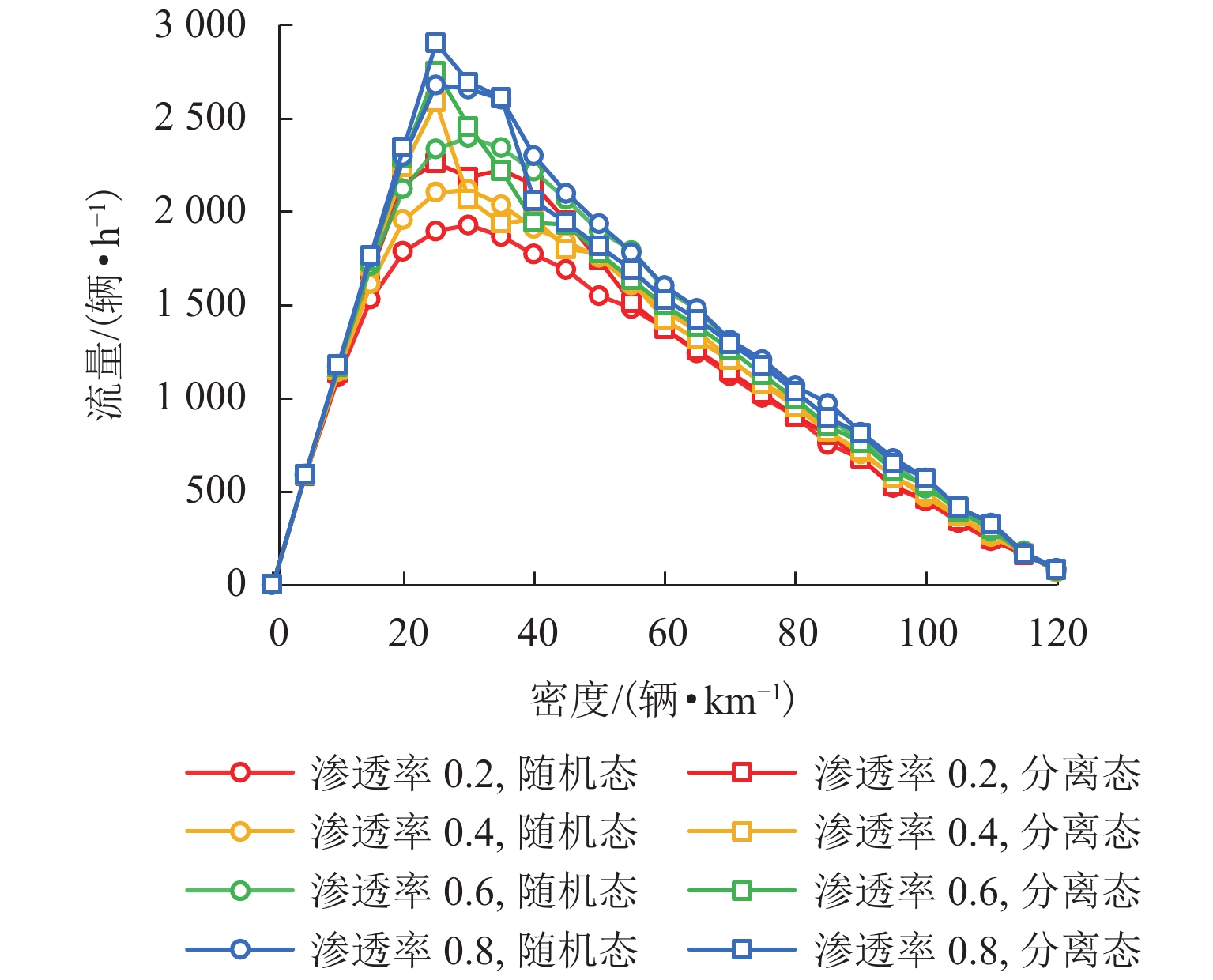
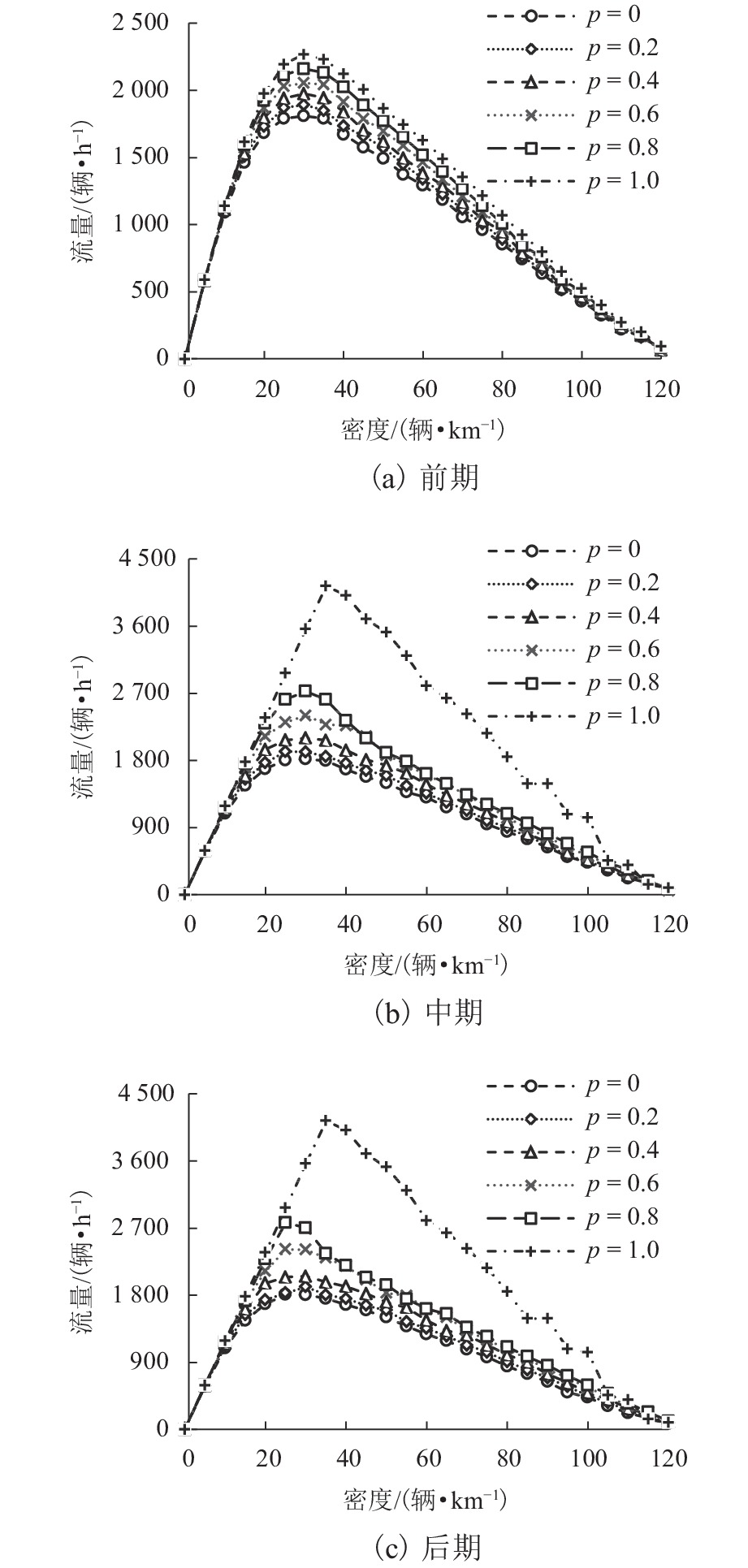
为研究车联网环境下异质交通流的演变规律,基于改进的NaSch模型,针对智能网联化程度的前期、中期和后期分别进行仿真实验,得到交通流基本图,并分析通行能力与网联车渗透率的内在联系;其次,通过马尔可夫链证明了网联车形成的有序排列能提高道路通行能力,随机仿真实验验证了理论推导的正确性;最后,引入考虑车辆排列方式的相对熵,从而定量描述异质车流的有序性,阐明了智能网联车辆(connected and autonomous vehicle,CAV)改善交通状况的本质原因. 研究结果表明:随着智能网联车渗透率的增加,通行能力增加,在智能网联化前期,渗透率的增加对通行能力提升较小,最高仅提升23.5%,中、后期通行能力最高能提升125.0%;在一定交通密度下,CAV渗透率与流量呈现正相关,相对熵与流量呈现负相关;智能网联车处于分离态时相对熵较小,分离态对随机混合的通行能力的提升随着CAV渗透率的增加而降低.
Abstract:To understand the evolutionary law of heterogeneous traffic flows in intelligent network, based on the improved NaSch model, the simulation experiments are conducted respectively for the early, middle and late stages of intelligent network connectivity, and the basic diagram of traffic flow is obtained via numerical simulation to analyze the intrinsic connection between the capacity and the penetration rate of connected vehicles. Through Markov chain, the orderly arrangement of connected vehicles is proved to improve the road capacity, and random simulation experiments verify the theoretical derivation. The relative entropy in terms of vehicle arrangement is introduced to quantify the order of heterogeneous traffic flow, and clarify the essence of the connected and autonomous vehicle (CAV) improving traffic conditions. The results show that: the capacity increases with the penetration of CAV; in the early stage, the increase of penetration has a little effect on the capacity improvement with the maximum of 23.5%, while in the middle and late stages, it improves the capacity by 125.0%; under certain traffic density, CAV penetration positively correlates with traffic, and the relative entropy negatively correlates with traffic; when CAVs are in a separated state, the relative entropy is low and the improvement in the randomly mixed capacity reduces with increasing CAV penetration .
-
表 1 IDM参数取值
Table 1. Values of IDM parameters
参数 取值 a/(m·s−2) 1 vf/(m·s−1) 33.3 $ s_{0} / \mathrm{m} $ 2 $ T/{\rm{s}} $ 1.6,1.1 b/(m·s−2) 2 L/m 6 表 2 通行能力提升程度
Table 2. Level of capacity improvement
% 异质阶段 渗透率 0.2 0.4 0.6 0.8 1.0 前期 2.9 6.9 11.1 15.7 23.5 中期 7.3 18.8 31.5 52.0 125.0 后期 2.7 12.0 32.0 55.0 125.0 表 3 随机态和分离态的通行能力及相对熵
Table 3. Capacity and relative entropy in random and separated states
渗透率 相对熵/bit 通行能力/(辆·h−1) 随机态 分离态 随机态 分离态 0.2 6.44 3.22 1974 2461 0.4 3.67 1.83 2162 2586 0.6 2.04 1.02 2240 2750 0.8 0.89 0.45 2745 2904 -
[1] 秦严严,王昊,王炜,等. 混有CACC车辆和ACC车辆的异质交通流基本图模型[J]. 中国公路学报,2017,30(10): 127-136. doi: 10.3969/j.issn.1001-7372.2017.10.016QIN Yanyan, WANG Hao, WANG Wei, et al. Fundamental diagram model of heterogeneous traffic flow mixed with cooperative adaptive cruise control vehicles and adaptive cruise control vehicles[J]. China Journal of Highway and Transport, 2017, 30(10): 127-136. doi: 10.3969/j.issn.1001-7372.2017.10.016 [2] NTOUSAKIS I A, NIKOLOS I K, PAPAGEORGIOU M. On microscopic modelling of adaptive cruise control systems[J]. Transportation Research Procedia, 2015, 6: 111-127. doi: 10.1016/j.trpro.2015.03.010 [3] TALEBPOUR A, MAHMASSANI H S. Influence of connected and autonomous vehicles on traffic flow stability and throughput[J]. Transportation Research Part C: Emerging Technologies, 2016, 71: 143-163. doi: 10.1016/j.trc.2016.07.007 [4] 秦严严,王昊,王炜,等. 混有协同自适应巡航控制车辆的异质交通流稳定性解析与基本图模型[J]. 物理学报,2017,66(9): 094502.1-094502.9. doi: 10.7498/aps.66.094502QIN Yanyan, WANG Hao, WANG Wei, et al. Stability analysis and fundamental diagram of heterogeneous traffic flow mixed with cooperative adaptive cruise control vehicles[J]. Acta Physica Sinica, 2017, 66(9): 094502.1-094502.9. doi: 10.7498/aps.66.094502 [5] 常鑫,李海舰,荣建,等. 混有智能网联车队的交通流基本图模型分析[J]. 东南大学学报(自然科学版),2020,50(4): 782-788. doi: 10.3969/j.issn.1001-0505.2020.04.024CHANG Xin, LI Haijian, RONG Jian, et al. Analysis on fundamental diagram model for mixed traffic flow with connected vehicle platoons[J]. Journal of Southeast University (Natural Science Edition), 2020, 50(4): 782-788. doi: 10.3969/j.issn.1001-0505.2020.04.024 [6] 常鑫,李海舰,荣建,等. 混有网联车队的高速公路通行能力分析[J]. 华南理工大学学报(自然科学版),2020,48(4): 142-148.CHANG Xin, LI Haijian, RONG Jian, et al. Analysis of capacity for mixed traffic flow with connected vehicle platoon on freeway[J]. Journal of South China University of Technology (Natural Science Edition), 2020, 48(4): 142-148. [7] 马丽娜. 基于元胞自动机的自动驾驶—手动驾驶交通流特性研究[D]. 成都: 西南交通大学, 2017. [8] MILANÉS V, SHLADOVER S E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data[J]. Transportation Research Part C:Emerging Technologies, 2014, 48: 285-300. doi: 10.1016/j.trc.2014.09.001 [9] TREIBER M, HENNECKE A, HELBING D. Congested traffic states in empirical observations and microscopic simulations[J]. Physical Review E:Statistical, Nonlinear, and Soft Matter Physics, 2000, 62(2): 1805-1824. doi: 10.1103/PhysRevE.62.1805 [10] CREMER M, LUDWIG J. A fast simulation model for traffic flow on the basis of Boolean operations[J]. Mathematics and Computers in Simulation, 1986, 28(4): 297-303. doi: 10.1016/0378-4754(86)90051-0 [11] NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J]. Journal de Physique Ⅰ, 1992, 2(12): 2221-2229. doi: 10.1051/jp2:1992262 [12] 敬明,邓卫,季彦婕,等. 更新步长和元胞尺寸对元胞自动机模型的影响[J]. 吉林大学学报(工学版),2013,43(2): 310-316.JING Ming, DENG Wei, JI Yanjie, et al. Influences of time step and cell size on cellular automaton model[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(2): 310-316. [13] 李烨,王炜,邢璐,等. 自动巡航与可变限速协同控制对高速公路基本路段通行效率的改善[J]. 吉林大学学报(工学版),2017,47(5): 1420-1425.LI Ye, WANG Wei, XING Lu, et al. Improving traffic efficiency of highway by integration of adaptive cruise control and variable speed limit control[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(5): 1420-1425. [14] YE L H, YAMAMOTO T. Evaluating the impact of connected and autonomous vehicles on traffic safety[J]. Physica A:Statistical Mechanics and Its Applications, 2019, 526: 121009.1-121009.12. [15] 叶丽萍,翁小雄,刘芹. 结合改进跟驰模型的交通流元胞自动机模型[J]. 公路交通科技,2014,31(7): 115-120,128. doi: 10.3969/j.issn.1002-0268.2014.07.019YE Liping, WENG Xiaoxiong, LIU Qin. Cellular automata model of traffic flow combined with improved car-following model[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 115-120,128. doi: 10.3969/j.issn.1002-0268.2014.07.019 [16] GHIASI A, HUSSAIN O, QIAN Z, et al. A mixed traffic capacity analysis and lane management model for connected automated vehicles:a Markov chain method[J]. Transportation Research Part B:Methodological, 2017, 106: 266-292. doi: 10.1016/j.trb.2017.09.022 [17] 邹乐强. 马尔可夫链模型及其应用[J]. 科技创新导报,2020,17(11): 97-98. [18] 朱福元. 熵与信息论[J]. 自然杂志,1992,14(3): 187-188. [19] 周思,柳祖鹏,陈玲娟,等. 路段上集群智能网联汽车的车队形成机制[J]. 公路,2021,66(2): 210-215.ZHOU Si, LIU Zupeng, CHEN Lingjuan, et al. Platoon formation mechanism of collective connected autonomous vehicles on road[J]. Highway, 2021, 66(2): 210-215. [20] 李松,贺国光,张晓利. 一种基于交通熵的交通流无序度量方法[J]. 公路交通科技,2007,24(11): 92-95. doi: 10.3969/j.issn.1002-0268.2007.11.021LI Song, HE Guoguang, ZHANG Xiaoli. A measuring method for disorder motion in traffic flow based on traffic entropy[J]. Journal of Highway and Transportation Research and Development, 2007, 24(11): 92-95. doi: 10.3969/j.issn.1002-0268.2007.11.021 [21] LIU Z P, XU C X, CHEN L J, et al. Dynamic traffic flow entropy calculation based on vehicle spacing[J]. IOP Conference Series:Earth and Environmental Science, 2019, 252(5): 052073.1-052073.6. -




 下载:
下载: