异质流网联车的不同换道集聚策略

吴德华; 彭锐; 陈荣峰

doi:10.3969/j.issn.0258-2724.20211035

异质流网联车的不同换道集聚策略

doi: 10.3969/j.issn.0258-2724.20211035

福州大学土木工程学院，福建福州 350108

基金项目: 福建省自然科学基金（2016J01230）

详细信息

通讯作者:
吴德华（1978—），男，副教授，博士，研究方向为智能交通，E-mail：610706517@qq.com

中图分类号: U268.6
计量
- 文章访问数: 536
- HTML全文浏览量: 297
- PDF下载量: 43
- 被引次数: 4
出版历程
- 收稿日期: 2021-12-12
- 修回日期: 2022-06-30
- 网络出版日期: 2023-01-18
- 刊出日期: 2022-07-12

Hybrid Characteristics of Heterogeneous Traffic Flow Under Different Aggregating Lane-Change Strategies in Intelligent Network

College of Civil Engineering, Fuzhou University, Fuzhou 350108, China

Funds: QIN Yanyan, WANG Hao, WANG Wei, et al. Stability analysis and fundamental diagram of heterogeneous traffic flow mixed with cooperative adaptive cruise control vehicles[J]. Acta Physica Sinica, 2017, 66(9): 257-265.

摘要

摘要:
为研究车联网环境下异质交通流的演变规律，首先，引入相对熵定量描述异质流的有序性，并分析有序性与智能网联车（connected and autonomous vehicle，CAV）市场渗透率、协同自适应巡航控制（cooperative adaptive cruise control，CACC）队列数之间的内在联系，推导得出智能网联车渗透率的增加及队列数的减少可以提升异质流的有序性；其次，提出了保守型集聚（conservative aggregation，CSA）、激进型集聚（radical aggregation，RDA）两种改进的智能网联车集聚换道策略，并通过元胞自动机仿真实验，从通行能力、相对熵和平均队列长度等方面比较了无集聚（no aggregation，NOA）、常规集聚（conventional aggregation，CVA）、CSA、RDA 4种换道策略的优劣；最后，在CSA换道策略中分析了不同最小队列规模限制对于通行能力的影响. 研究结果表明：在双车道环境下，采取集聚换道策略能使智能网联车形成CACC队列，使异质流趋于“有序”，在20～95辆/km密度范围内提升通行能力；相比NOA换道策略，CSA、RDA换道策略分别最大提升道路通行能力12.6%、14.0%，但当智能网联车市场渗透率为0.8时，RDA换道策略导致最大通行能力反而降低25.8%；根据相对熵对异质流中智能网联车辆集聚程度的定量描述，NOA、CVA、CSA、RDA 4种换道策略对智能网联的集聚能力依次递增；在CSA换道策略中，CACC最小队列规模取4辆时道路通行效率达到最佳.
- 智能交通 /
- 异质交通流 /
- 元胞自动机 /
- 智能网联车 /
- 换道策略 /
- 相对熵
Abstract:
In order to study the evolution rule of heterogeneous traffic flow under the background of IOV （internet of vehicles）, the concept of relative entropy in introduced to quantitatively describe the orderliness of heterogeneous flow, and analyze the inner link among orderliness, market penetration rate of CAV （connected and autonomous vehicle）and the number of queues for CACC (cooperative adaptive cruise control). Then, it is deduced that the increase on the market penetration rate of CAV and decrease on the number of queues can improve the orderliness of heterogeneous flow. Second, two improved lane change strategies for CAVs are proposed, namely, conservative aggregation (CSA) and radical aggregation (RDA). Through the simulation test of cellular automata, the advantages and disadvantages of no aggregation (NOA), conventional aggregation (CVA), CSA, and RDA are compared in terms of traffic capacity, relative entropy and average queue length. Finally, the effect of different limits of minimum queue size on traffic capacity is analyzed with the lane change strategy of CSA. The results show that the use of lane change strategy can prompt the CACC collaborative queue in CAV and orderly heterogeneous flow. It improves traffic capacity in the density range from 20 to 95 veh/km. Compared with the NOA strategy, the CSA strategy increases the traffic capacity by 12.6%, and the RDA strategy by 14.0%. However, when the market penetration rate of CAV is 0.8, the maximum traffic capacity of the RDA strategy is reduced by 25.8%. According to the quantitative description of relative entropy for the aggregation degree of CAV in heterogeneous flow, four lane change strategies (NOA, CVA, CSA and RDA) increases the aggregation degree of CAV in turn. In the CSA strategy, when the minimum queue size of CACC takes 4 vehicles, the efficiency of traffic capacity is the optimal.
- intelligent transportation /
- heterogeneous traffic flow /
- cellular automaton /
- connected and autonomous vehicle /
- lane change strategy /
- relative entropy

HTML全文

我国高速铁路以其高速、平稳等优点深受广大旅客的青睐，但随着高速列车运营里程逐渐增加，轮轨接触关系逐步恶化，高铁线路上频繁地出现了复杂多样且严重的钢轨波磨，即沿着线路方向发生在钢轨表面可见的形似波浪状的钢轨磨损现象^[1]. 这不仅会降低整车和轨道结构系统的工作寿命，还会引起较大的振动噪声，甚至严重威胁行车安全^[2].

由于高铁线路条件的复杂性及波磨的多样性，尚无统一的理论来解释钢轨波磨的根本成因. 目前，国内外学者主要围绕由于钢轨本身存在的初始不平顺引起的系统反馈振动^[3]和由于轮轨系统的固有振动特性引起的系统自激振动^[4-5]这两种观点，对高速铁路上的钢轨波磨开展了大量研究. Wang等^[6]建立高铁轮对-轨道耦合滚动模型，采用瞬态有限元方法研究轨道超高对钢轨波磨发展的影响，同时进行扣件参数化分析；王立乾等^[7]介绍了高速铁路波磨的特点，并指出目前波磨理论的局限性，分析钢轨结构的材质对波磨的影响；Correa等^[8]研究了4种高速轨道结构下的钢轨波磨，在考虑动态特性下分析并比较不同轨道结构对钢轨波磨发展的影响；司道林等^[9]建立高速铁路车辆-轨道仿真模型，分析车辆的悬挂参数及扣件参数对高速铁路钢轨波磨磨耗的影响；姜子清等^[10]通过现场测试和动力学计算，研究轨道结构的动力响应，并以此探究钢轨波磨整治的深度限值；Cui等^[11]分析了轨道结构上通过不同的车型对高速铁路钢轨波磨的影响，从动态角度探究了钢轨波磨的成因；吴波文^[12]研究高铁轮轨和制动摩擦耦合作用对摩擦自激振动的影响，提出高速列车制动时轮轨和制动系统摩擦自激振动耦合是导致钢轨波磨的主要原因；崔晓璐等^[13]进一步建立高速列车动/拖车轮对-钢轨-制动系统的有限元模型，研究制动方式对钢轨波磨的影响，发现在拖车的轮轨摩擦和制动摩擦耦合作用的摩擦自激振动更容易诱导钢轨波磨.

上述研究大多从车辆和轨道结构等单一方面研究高铁线路全局的钢轨波磨，而针对线路某特定局部区段，尤其是钢轨波磨高发的制动区段，结合较为完整的制动结构和轨道结构方面研究钢轨波磨抑制的相对较少. 本文通过对京广高速铁路钢轨波磨发生区段的现场调查，发现列车制动区段是钢轨波磨的高发区段，钢轨波磨更加严重且同时出现在左、右两条钢轨上^[11].

结合前期研究发现，轮轨粘滑和制动滚滑耦合作用导致的轮对-轨道-制动系统的摩擦自激振动是诱导高速列车制动区段钢轨波磨的主要成因^[11,14]. 在制动结构方面，学者们主要探究了制动织构对摩擦噪声的影响，并没有研究其对钢轨波磨的影响. 在轨道结构方面，学者们只研究了扣件单参数对钢轨波磨的影响，考虑多扣件参数共同作用的研究较少. 因此，本文基于摩擦自激振动理论^[15-16]，构建较为完整的包含轨道结构和制动结构的轮对-轨道-制动系统的有限元模型，从制动结构和轨道结构两方面探究高速列车制动区段钢轨波磨的抑制方法. 最后，探究多扣件参数对钢轨波磨的影响，寻求抑制钢轨波磨的扣件参数最优解.

1. 现场调研及数值仿真

1.1 钢轨波磨的现场调研

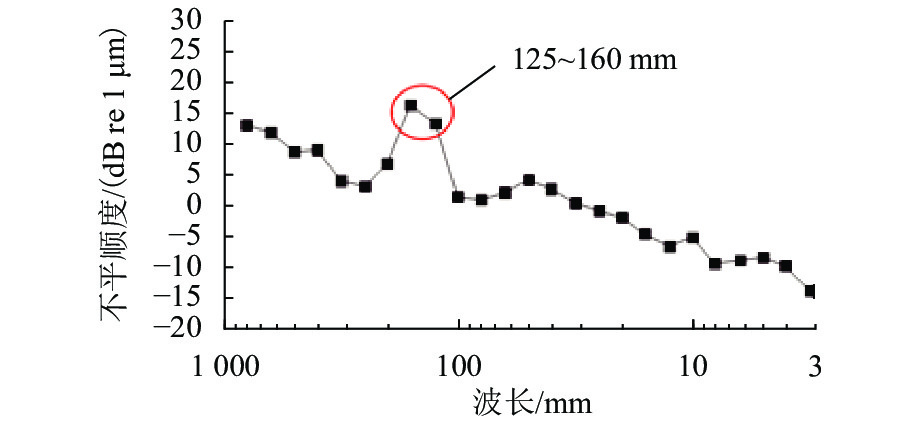
通过现场调研，使用钢轨表面不平顺测试小车，采集了高速列车制动区段的钢轨表面的波磨数据. 对采集的数据进行1/3倍频程的频谱特性分析，从而确定该制动区段钢轨波磨的主波长，钢轨波磨频谱特性分析如图1所示. 通过现场调查和数据分析，可以发现该制动区段钢轨波磨的主要波长为125～160 mm.

图 1 制动区段钢轨波磨现场调查分析

Figure 1. On-site investigation and analysis of rail corrugation on braking section

下载: 全尺寸图片幻灯片

1.2 CRH3高速列车轮对-轨道-制动系统接触模型

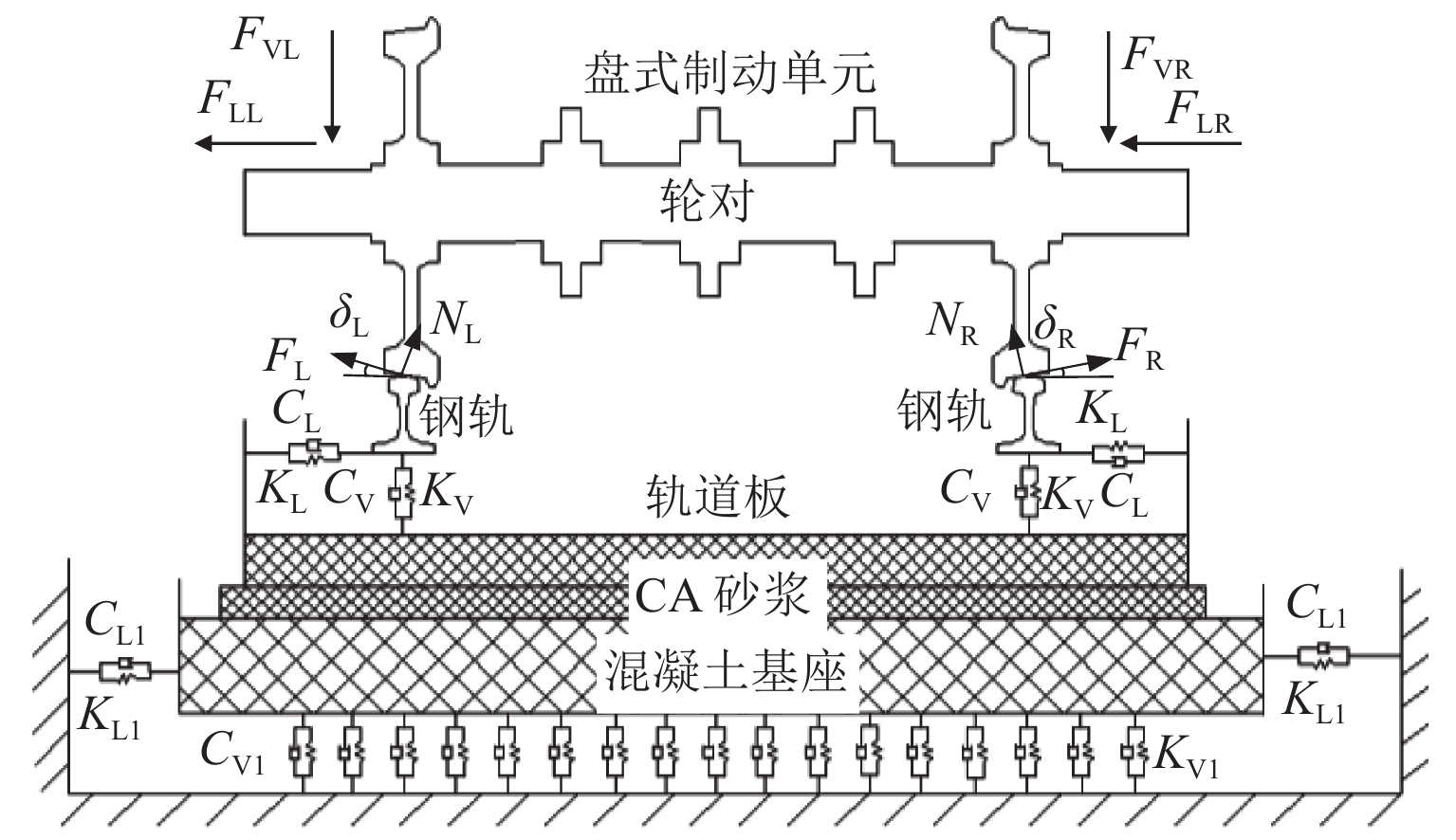
通过现场调研，得到CRH3高速列车轮对-轨道-制动系统的接触模型^{[17- 18]}，如图2所示. 用等效弹簧阻尼单元表示扣件的连接作用，K_V和K_L分别为钢轨与轨道板间的垂向刚度和横向刚度，C_V和C_L分别为垂向阻尼和横向阻尼，K_V1和K_L1分别为混凝土基座接地的垂向刚度和横向刚度，C_V1和C_L1分别为垂向阻尼和横向阻尼. 在直线制动区段，F_LL和F_LR为轮对左右两端所受的横向悬挂力，忽略不计，F_VL和F_VR为轮对两端所受的垂向悬挂力，N_L、N_R分别为左、右轮轨间的法向接触力，F_L、F_R分别为左、右轮轨接触的横向蠕滑力，δ_L和δ_R为轮轨接触角.

图 2 CRH3高速列车轮对-轨道-制动系统的接触模型

Figure 2. Contact model of wheelset–track–brake system of CRH3 high-speed train

下载: 全尺寸图片幻灯片

1.3 CRH3高速列车轮对-轨道-制动系统有限元模型

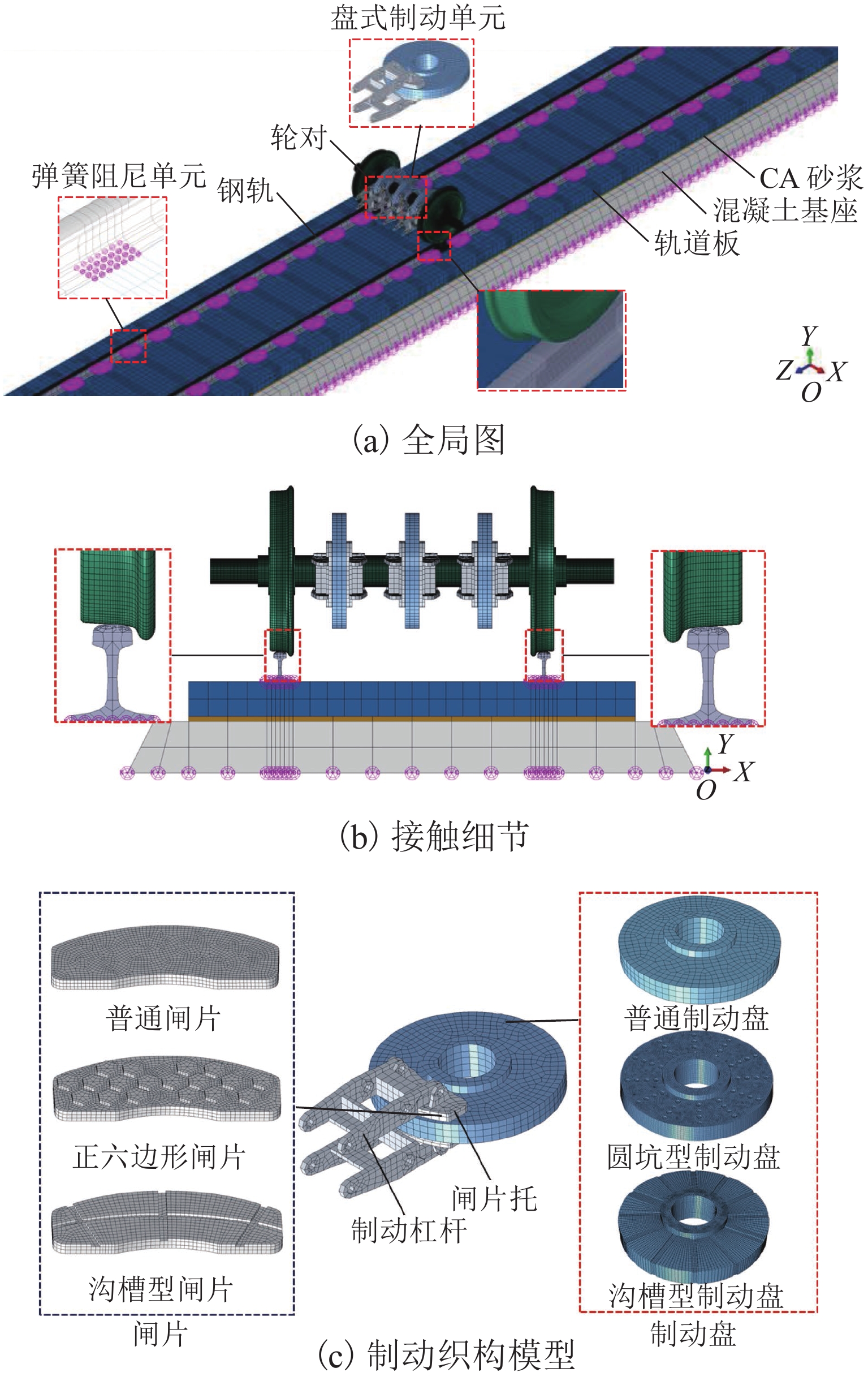
建立高速列车轮对-轨道-制动系统有限元模型如图3所示，该模型包括了轮轨子系统和制动子系统，轮轨子系统包括钢轨、拖车轮对和完整的轨道支撑结构. 其中，车轮的名义滚动圆直径920 mm，采用LM_A磨耗型踏面，空心车轴. 钢轨轨距为1435 mm，为降低钢轨两端约束产生的边界效应，钢轨总长取30扣件跨距，并将两端进行固定约束. 扣件采用等效弹簧阻尼单元模拟，其间距取650 mm^[19]. 整个模型的材料参数和连接参数分别如表1和表2所示^[11-12]，高速铁路多为直线段或大半径曲线段^[11]，故设置左、右轮轨接触状态相同，并对轮轨接触区域进行网格细化，在分析过程中设置轮轨间纵向的相对滑移来体现轮轨子系统的粘滑作用，轮轨间接触摩擦系数设置为0.3，车速取300 km/h^[11]，车轴两端的横向悬挂力很小，忽略不计，垂向悬挂力大小为75 kN^[20].

图 3 CRH3高速列车轮对-轨道-制动系统有限元模型

Figure 3. Finite element model of wheelset–track–brake system of CRH3 high-speed train

下载: 全尺寸图片幻灯片

表 1 有限元模型材料参数

Table 1. Material parameters of finite element model

部件参数	密度/（k•gm⁻³）	弹性模量/MPa	泊松比
轮对	7800	210000	0.30
钢轨	7800	210000	0.30
制动盘	7300	207000	0.30
制动闸片	2500	8100	0.30
闸片托	5600	100000	0.30
制动杠杆	7000	190000	0.30
轨道板	2400	29500	0.25
CA 砂浆层	2600	32500	0.20
混凝土底座	2400	22500	0.20

下载: 导出CSV

| 显示表格

表 2 有限元模型连接参数

Table 2. Connection parameters of finite element model

方向	扣件刚度/ （MN·m⁻¹）	扣件阻尼/ （kN·s·m⁻¹）	地基支撑刚度/（MN·m⁻¹）	地基支撑阻尼/（kN·s·m⁻¹）
垂向	50	30	190	30
横向	28	20
纵向	28	20

下载: 导出CSV

| 显示表格

当高速列车制动时，由制动气缸产生的压力推动制动夹钳并使其抱紧制动盘，产生闸片与制动盘间的摩擦力，实现制动^[18]. 根据制动原理，建立CRH3高速列车拖车轮对简化的制动子系统有限元模型，如图3（c）所示，该模型由制动盘、制动闸片、闸片托和制动杠杆组合而成. 其中，制动盘与车轴间采用固定连接，制动盘与制动闸片间为摩擦接触，摩擦系数为0.4^[12]；闸片托与制动闸片采用固定连接，闸片托与制动杠杆之间设为无摩擦接触；制动杠杆上、下支点间以及闸片托和制动杠杆间使用铰链连接并约束；制动时，制动压力施加在制动杠杆的自由端，大小为10 kN^[18]，轮对设置初始滚动的预定义场，体现制动子系统的滚滑作用. 在高速列车中，常见闸片织构以不同形状和分布的凹坑和槽形为主^[21]，制动盘织构主要有具有不同宽度的发散型沟槽织构和不同直径与间距的发散型圆坑织构^[22]. 闸片分别为普通型闸片、六边形闸片和沟槽型闸片，制动盘分别为普通型制动盘、圆坑型制动盘和沟槽型制动盘.

1.4 复特征值分析法

本文基于摩擦自激振动理论，采用复特征值法^[4]展开系列研究. 根据机械振动理论建立系统的运动方程为

${\boldsymbol{M}}\ddot {\boldsymbol{x}} + {\boldsymbol{C}}\dot {\boldsymbol{x}} + {\boldsymbol{Kx}} = {\boldsymbol{q}} ,$

(1)

式中：M、C和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵，其结构矩阵为正定；q为作用在系统的广义外力向量； $\ddot{{\boldsymbol{x}}}$ 、 $\dot{{\boldsymbol{x}}}$ 和x分别为系统在平衡位置附近的振动加速度、振动速度及位移.

轮轨间接触的摩擦力视为主要的振动激励来源，即

${\boldsymbol{q}} = \mu {\boldsymbol{K}}_{\rm{f}}{\boldsymbol{x}} ,$

(2)

式中：K_f为接触刚度矩阵；μ为轮轨摩擦系数.

将式（2）带入式（1）得

${\boldsymbol{M}}\ddot {\boldsymbol{x}} + {\boldsymbol{C}}\dot {\boldsymbol{x}} + ({\boldsymbol{K}} - \mu {\boldsymbol{K}}_{\rm{f}}){\boldsymbol{x}} = {\boldsymbol{0}} .$

(3)

K−μK_f为系统整体刚度矩阵，是不对称矩阵，因此，该系统会出现不稳定的振动.

式（3）的特征方程为

$[{\lambda ^2}{\boldsymbol{M}} + \lambda {\boldsymbol{C}} + ({\boldsymbol{K}} - \mu {\boldsymbol{K}}_{\rm{f}})]{\boldsymbol{\varphi}} = {\boldsymbol{0}} ,$

(4)

式中：λ和 ${\boldsymbol{\varphi}}$ 分别为原系统的特征值及特征向量.

由于K−μK_f为不对称矩阵，用子空间投影法求解，即将原始特征系统投影至无阻尼、对称系统的特征向量所跨的线性子空间中，转化为求解对称广义特征问题. 在无摩擦和阻尼的情况下，式（4）简化为

$(\lambda _{\rm{t}}^2{\boldsymbol{M}} + {\boldsymbol{K}}){{\boldsymbol{\varphi}} _{\rm{t}}} = {\boldsymbol{0}} ,$

(5)

式中：λ_t和 ${\boldsymbol{\varphi}}$ _t分别为简化系统的特征值和特征向量，二者采用有限元中的迭代法提取得到.

使用简化后的解将原始系统所有结构矩阵投到简化特征向量的子空间, 有

$\left\{ \begin{aligned} {{\boldsymbol{M}}^*} = {[{{\boldsymbol{\varphi}} _{\text{t}}}]^{\rm{T}}}{\boldsymbol{M}}[{{\boldsymbol{\varphi}} _{\rm{t}}}], \\ {{\boldsymbol{C}}^*} = {[{{\boldsymbol{\varphi}} _{\rm{t}}}]^{\rm{T}}}{\boldsymbol{M}}[{{\boldsymbol{\varphi}} _{\rm{t}}}],\;\\ {{\boldsymbol{K}}^*} = {[{{\boldsymbol{\varphi}} _{\rm{t}}}]^{\rm{T}}}{\boldsymbol{M}}[{{\boldsymbol{\varphi}} _{\rm{t}}}],\\ \end{aligned} \right.$

(6)

式中： $[{{\boldsymbol{\varphi}} _{\rm{t}}}]$ 为由简化特征向量 ${{\boldsymbol{\varphi}} _{\rm{t}}}$ 组成的变换矩阵, 余同； ${{\boldsymbol{M}}^*}$ 、 ${{\boldsymbol{C}}^*}$ 和 ${{\boldsymbol{K}}^*}$ 为由特征值 $\lambda_{\rm{t}}$ 构成的质量、刚度和阻尼的对角阵.

原始系统在结构矩阵模态子空间的运动方程为

${{\boldsymbol{M}}^*}\ddot {\boldsymbol{y}} + {{\boldsymbol{C}}^*}\dot {\boldsymbol{y}} + {{\boldsymbol{K}}^*}{\boldsymbol{y}} = {\boldsymbol{0}} ,$

(7)

式中：y为模态坐标向量，与x关系为 ${\boldsymbol{x}}=[{{\boldsymbol{\varphi}} _{\rm{t}}}]{\boldsymbol{y}}$ .

得到式（7）的特征方程为

$(\lambda _{\rm{p}}^2{{\boldsymbol{M}}^*}{\boldsymbol{y}} + {\lambda _{\rm{p}}}{{\boldsymbol{C}}^*}{\boldsymbol{y}} + {{\boldsymbol{K}}^*}){{\boldsymbol{\varphi}} _{\rm{p}}} = {\boldsymbol{0}} ,$

(8)

式中： $\lambda_{\rm{p}}$ 和 ${{\boldsymbol{\varphi}} _{\rm{p}}}$ 分别为投影系统的特征值和特征向量.

将 $\lambda_{\rm{p}}$ 和 ${{\boldsymbol{\varphi}} _{\rm{p}}}$ 还原到原始空间可得到原始系统的特征向量及特征值.

原始系统的通解由单个特征模态叠加得到，即

${\boldsymbol{x}}(t) = \sum\limits_{i = 1}^n {{{\boldsymbol{\varphi}} _i}} \exp ({\alpha _i} + {\rm{j}}{w_i})t ,$

(9)

式中：t为时间； ${{\boldsymbol{\varphi}} _{i}}$ 为第i阶复特征向量；α_i和w_i分别为第i阶复特征值λ_i的实部和虚部.

由式（9）知，当α_i > 0时，运动方程的通解呈发散状态，即系统容易发生不稳定振动，且α_i越大，不稳定振动的可能性越大；w_i表示不稳定振动的频率. 本文综合考虑轮轨系统和制动系统的耦合作用，通过复特征值法研究整个系统的摩擦自激振动特性，进而探究钢轨波磨的抑制方法.

2. 结果与讨论

2.1 轮对-轨道-制动系统摩擦自激振动特性分析

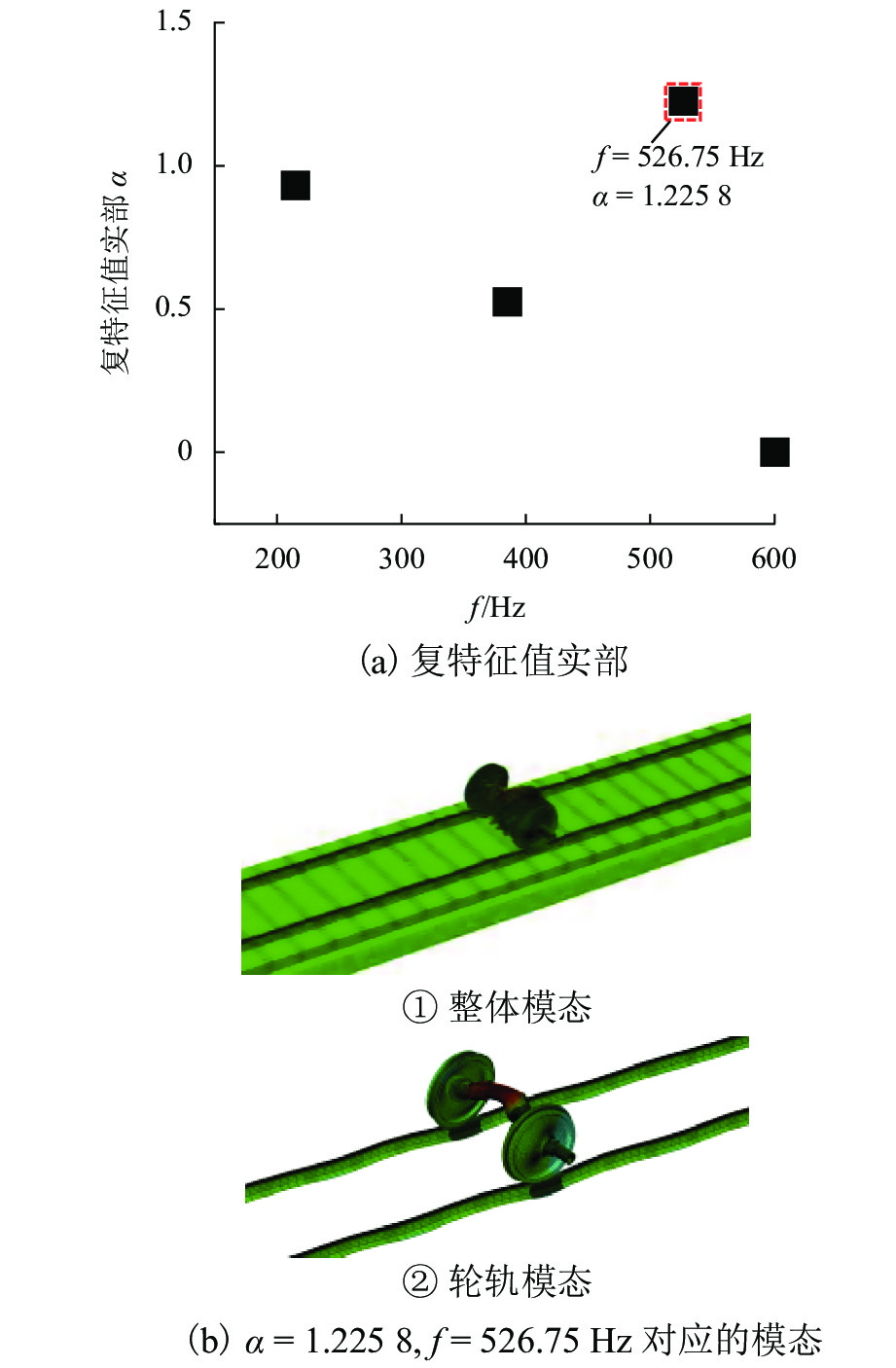
由于在高速铁路制动区段存在轮轨粘滑和制动滚滑的现象，本文基于摩擦自激振动理论在考虑了制动区段时轮轨子系统和制动子系统的耦合作用下，采用复特征值法探究轮对-轨道-制动系统的摩擦自激振动特性，如图4所示. 轮对-轨道-制动系统出现了4个实部大于0的摩擦自激振动，实部最大为1.2258，对应摩擦自激振动频率f = 526.75 Hz，模态中对应的左、右钢轨上均发生摩擦自激振动，在此频率下，系统发生摩擦自激振动的可能性最大. 根据波长与频率的关系式可知，诱导该制动区段现场钢轨波磨的频率为520.83～666.67 Hz，526.75 Hz的自激振动频率与现场诱导钢轨波磨的特征频率接近，说明可能是轮轨和制动摩擦自激振动的耦合作用诱导了制动区段的钢轨波磨.

图 4 轮对-轨道-制动系统摩擦自激振动实部分布及模态

Figure 4. Real part distribution and modes of frictional self-excited vibration in wheelset–track–brake system

下载: 全尺寸图片幻灯片

2.2 不同制动表面织构对轮对-轨道-制动系统摩擦自激振动的影响

根据前期研究^[23-24]，具有一定表面织构的闸片或制动盘能打断闸片与制动盘间的滚滑作用，进而一定程度抑制闸片和制动盘耦合系统的摩擦自激振动. 本节研究具有不同表面织构的闸片或制动盘下高速列车轮对-轨道-制动系统的摩擦自激振动特性. 通过复特征值分析，得到不同表面织构下整个系统的摩擦自激振动的实部分布和制动子系统的接触应力如图5所示. 由图可知：在5种不同制动结构下，整个系统发生摩擦自激振动的主要频率平均集中在525.0 Hz左右，普通型、沟槽型闸片、正六边形闸片、沟槽型制动盘和圆坑型制动盘的复特征值实部分别为1.22580、0.28388、0.42684、0.71094和0.77230；相比于普通型，其他4种织构的复特征值实部均减小，且沟槽型闸片的实部最小，同时, 比较具有表面织构的闸片和制动盘的闸片上最大接触压力发现，沟槽型闸片的最大接触压力最小. 综上所述，具有一定表面织构的闸片或制动盘能够一定程度抑制轮对-轨道-制动系统的摩擦自激振动，从而抑制钢轨波磨，其中，沟槽型闸片的抑制效果相对最佳.

图 5 不同表面织构下轮对-轨道-制动系统摩擦自激振动实部分布及闸片接触应力

Figure 5. Real part distribution of frictional self-excited vibration of wheelset–track–brake system and contact stress of brake pads under different surface textures

下载: 全尺寸图片幻灯片

2.3 扣件参数对轮对-轨道-制动系统摩擦自激振动的影响

2.3.1 扣件刚度对摩擦自激振动的影响规律

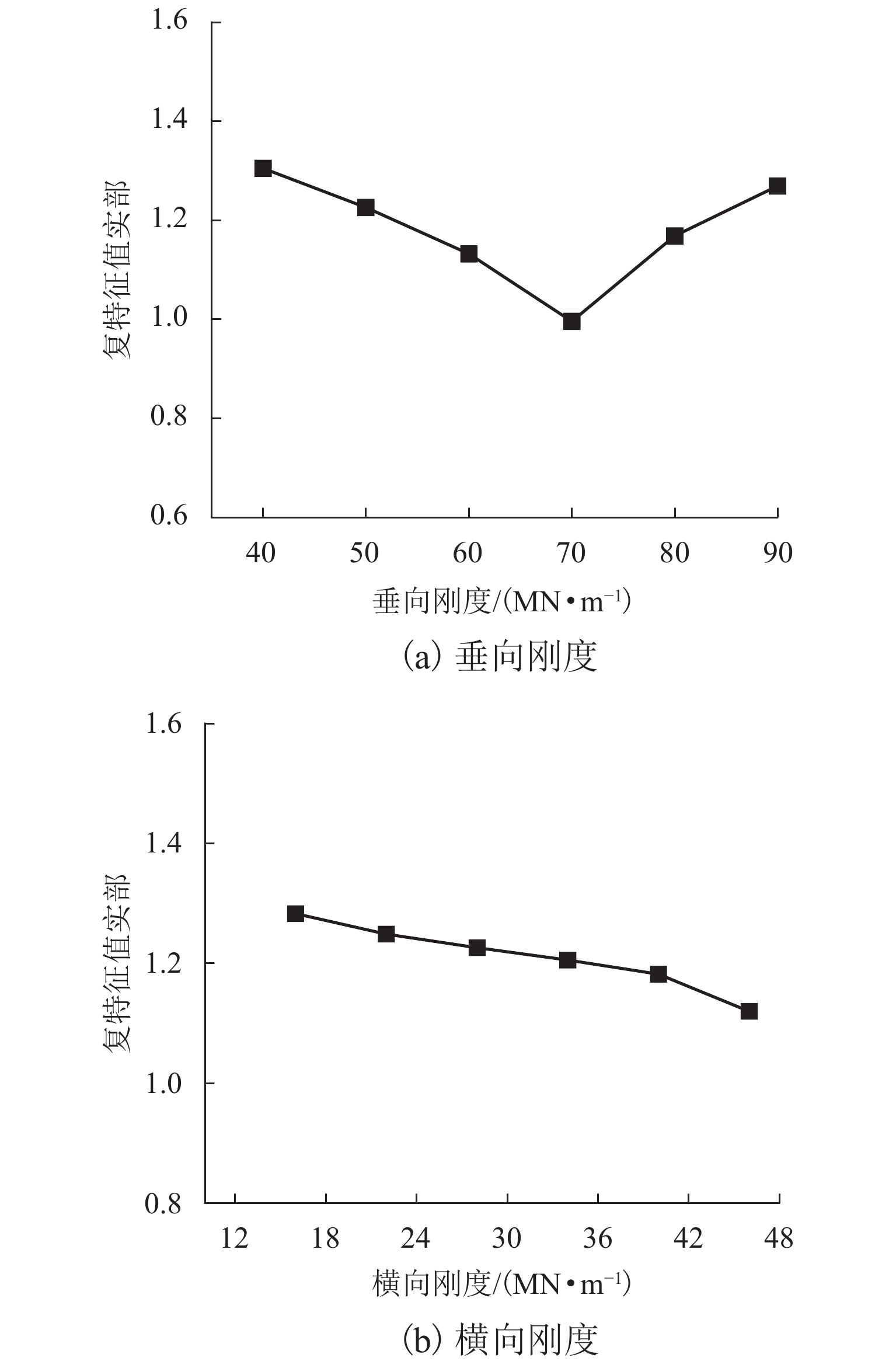
扣件作为轨道系统的中间联结件，不仅将钢轨紧扣在轨枕上，还在列车运行中起减振降噪的作用^[25]. 本节研究扣件垂向刚度和横向刚度对轮对-轨道-制动系统摩擦自激振动的影响. 扣件刚度分别取K_V = 40～90 MN/m，间隔为10 MN/m，K_L = 16～46 MN/m，间隔为6 MN/m.

通过复特征值法分析，得到扣件刚度对整个系统摩擦自激振动的影响规律如图6所示. 对于不同的垂向刚度和横向刚度，整个系统可能发生摩擦自激振动的主要频率变化很小，其大小为525～530 Hz. 由图6（a）可知，随着扣件的垂向刚度增大，最可能发生摩擦自激振动的复特征值实部先减小后增大，当垂向刚度为70 MN/m时，复特征值实部最小，为0.995 96. 由此说明扣件垂向刚度过小或过大都不利于抑制整个系统的摩擦自激振动，当取垂向刚度为70 MN/m时，可以最大限度减弱整个系统的摩擦自激振动，进而抑制制动区段钢轨波磨. 由图6（b）可知，随横向刚度的增大，复特征值实部有逐渐减小的趋势，说明随着横向刚度的增大，轮对-轨道-制动系统发生摩擦自激振动的可能性会逐渐降低，进而可以抑制高速列车制动区段钢轨波磨.

图 6 扣件刚度对整个系统摩擦自激振动的影响

Figure 6. Influence of fastener stiffness on frictional self-excited vibration of overall system

下载: 全尺寸图片幻灯片

2.3.2 扣件阻尼对摩擦自激振动的影响规律

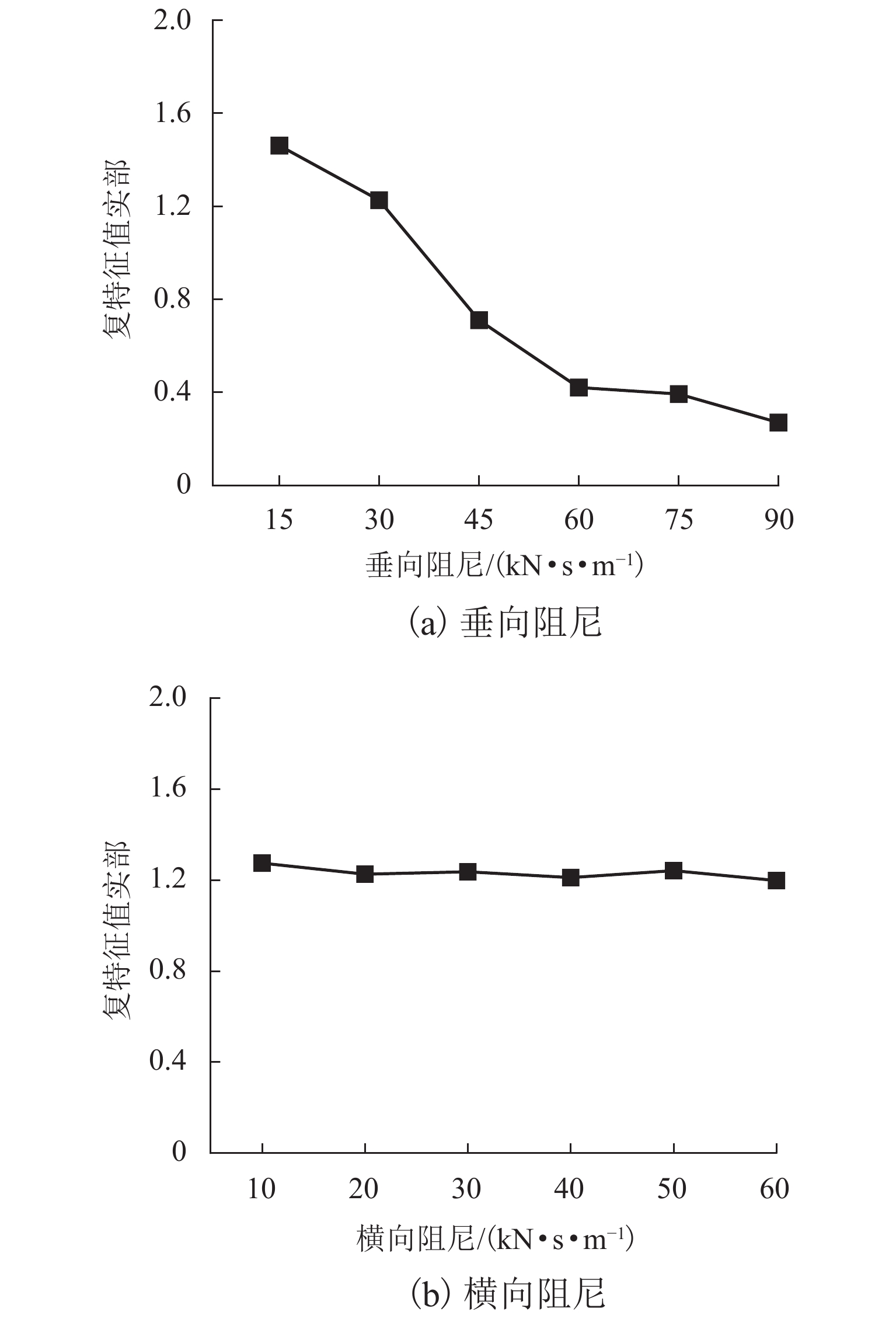
高速铁路扣件阻尼作用主要体现在橡胶材质的轨枕垫上，有一定的减振作用^[25]. 本节研究了扣件阻尼对轮对-轨道-制动系统摩擦自激振动的影响规律. 扣件阻尼的取值分别为C_V = 15～90 kN·s/m，取值间隔15 kN·s/m，C_L = 10～60 kN·s/m，间隔10 kN·s/m.

扣件阻尼对整个系统摩擦自激振动影响如图7所示. 由图可知，随着扣件垂向阻尼增大，复特征值实部有逐渐减小的趋势，说明发生摩擦自激振动的可能性逐渐降低，所以，在一定范围适当地增加扣件的垂向阻尼能减弱轮对-轨道-制动系统的摩擦自激振动，进而抑制高速列车制动区段的钢轨波磨；随着扣件横向阻尼增大，复特征值实部基本无明显的变化，说明横向阻尼对整个系统摩擦自激振动的影响很小，即对高速列车制动区段的钢轨波磨的影响很小.

图 7 扣件阻尼对整个系统摩擦自激振动的影响规律

Figure 7. Influence of fastener damping on frictional self-excited vibration of overall system

下载: 全尺寸图片幻灯片

2.3.3 扣件多参数影响优化分析

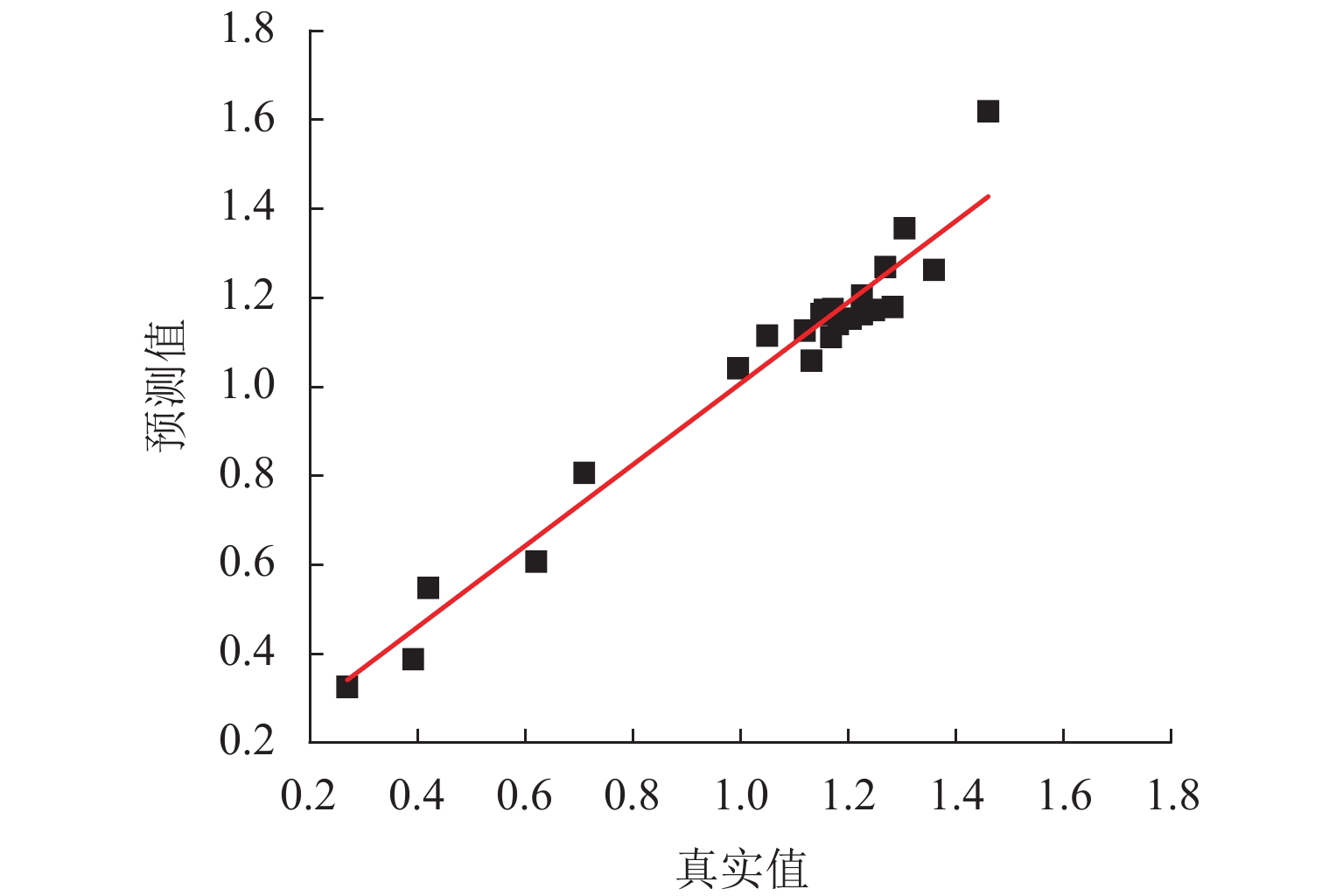
上节通过控制变量法分别研究了扣件的垂向刚度、横向刚度、垂向阻尼和横向阻尼作为单一变量对轮对-轨道-制动系统摩擦自激振动的影响规律. 为进一步研究扣件参数同时变化时对整个系统摩擦自激振动的影响规律，先采用最小二乘法对4组结果进行多参数拟合^[26]，再根据其拟合方程采用粒子群算法对扣件参数求最优解，从而得到参数共同影响下能抑制高速列车制动区间钢轨波磨的优化解. 首先，采用最小二乘法对扣件的4个参数进行单一拟合，所选用的拟合方程如式（10）、（11）所示. 通过拟合得到的单参数拟合方程如式（12）所示. 采用最小二乘法进行单参数拟合方程的多元回归误差分析，如图8所示，由图可知，拟合方程的预测值与复特征值实部的吻合性较好.

图 8 多元回归方程误差分析

Figure 8. Error analysis of multiple regression equation

下载: 全尺寸图片幻灯片

$a = \sum\limits_{b = 0}^{15} {{\beta _b}} \prod\limits_{j = 1}^4 {x_{j,{\rm{f}}}^{{i_j}}},$

(10)

$b = {2^3}{i_1} + {2^2}{i_2} + 2{i_3} + {i_4},\quad i_j = 0,1,$

(11)

式中：x₁～x₄分别为扣件垂向刚度、扣件横向刚度、扣件横向阻尼和垂向阻尼；β_b为回归方程中多项式的未知系数.

$\left\{ \begin{aligned} &x_{1,{\rm{f}}} = 0.877\;2x_1^2 - 0.946\;8{x_1} + 1.335 ,\\ &x_{2,{\rm{f}}} = - 0.063\;48x_2^2 - 0.084\;65{x_2} + 1.276 ,\\ &x_{3,{\rm{f}}} = - 0.051\;91{x_3} + 1.257, \\ &x_{4,{\rm{f}}} = 1.156x_4^2 - 2.373{x_4} + 1.496. \end{aligned} \right.$

(12)

式中：x_1,f～x_4,f分别为x₁～x₄经过一元拟合后得到的变量.

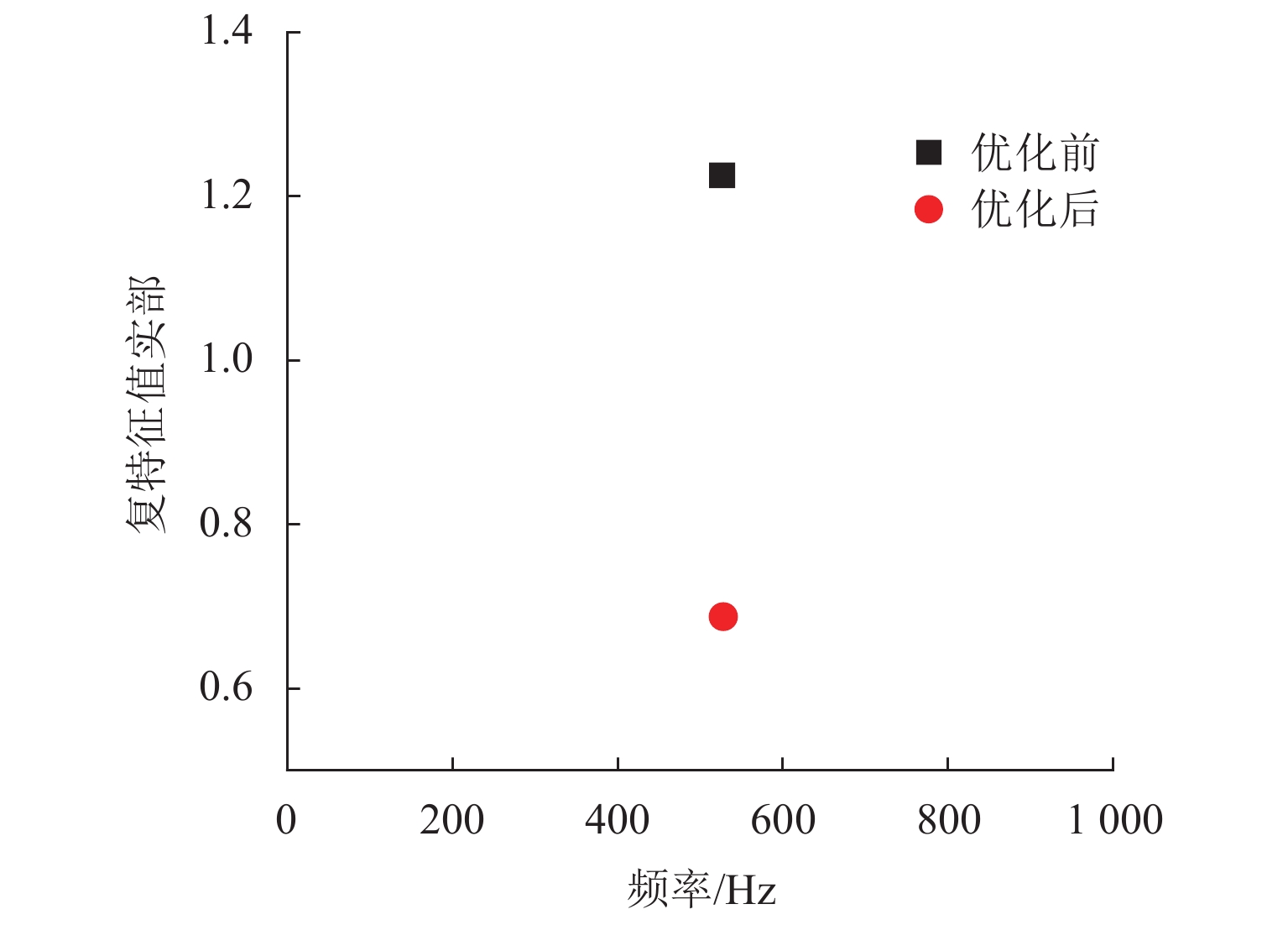
然后，采用粒子群算法对上述的拟合方程求解复特征值实部最小时x₁～x₄的取值，粒子位置的取值区间为 [0, 1]，粒子初始速度为 [−1，1]. 最后通过优化得到拟合方程的局部最优解为x₁=0.51, x₂=1, x₃=0.261, x₄=0.98，即扣件的垂向刚度为65.5 MN/m，横向刚度为46.0 MN/m，横向阻尼为23.5 kN·s/m和垂向阻尼为84.0 kN·s/m. 为进一步验证粒子群算法优化后的结果，将优化的4个值代入有限元进行复特征值分析，优化前、后的结果如图9所示，优化后的复特征值实部为0.687 49，比优化前的1.22580 明显减小，说明该组优化后的扣件参数达到了一定的优化效果，可以减弱轮对-轨道-制动系统的摩擦自激振动，进而能够有效地抑制高速列车制动区段的钢轨波磨.

图 9 优化前、后复特征值实部结果对比

Figure 9. Comparison of real part results of complex eigenvalues before and after optimization

下载: 全尺寸图片幻灯片

3. 结　论

根据现场调查，高速列车制动区段钢轨波磨频发且比较严重. 本文基于摩擦自激振动诱导钢轨波磨的观点，建立了高速列车轮对-轨道-制动系统的有限元模型，分别研究了制动表面织构和扣件参数对整个系统摩擦自激振动特性的影响；使用最小二乘法对扣件参数进行多参数拟合，并采用粒子群算法求得抑制相应钢轨波磨的扣件参数的最优解, 从而得到高速列车制动区段钢轨波磨的有效抑制方法. 综上所述，本文的研究结论如下：

1）高速列车在制动区段时，轮对-轨道-制动系统最可能发生摩擦自激振动的频率为526.75 Hz，此频率与现场诱导钢轨波磨的频率相符合，可能是轮轨系统和制动系统摩擦耦合产生整个系统的摩擦自激振动导致了钢轨波磨.

2）从制动结构角度，采用具有表面织构的制动闸片或制动盘能抑制轮对-轨道-制动系统的摩擦自激振动，进而抑制高速列车制动区段的钢轨波磨，且沟槽型闸片的抑制效果更佳.

3）从轨道结构角度，当扣件垂向刚度65.5 MN/m，横向刚度46.0 MN/m，垂向阻尼84.0 kN·s/m，横向阻尼23.5 kN·s/m时, 能减弱轮对-轨道-制动系统的摩擦自激振动，从而有效抑制高速列车制动区段的钢轨波磨.

致谢：轨道交通基础设施性能检测与保障国家重点实验室开放课题（HJGZ2021115）.

图 1 CAV排列方式

Figure 1. Arrangement of CAV

下载: 全尺寸图片幻灯片

图 2 CVA控制算法流程

Figure 2. Flowchart of CVA control algorithm

下载: 全尺寸图片幻灯片

图 3 CAV换道示意

Figure 3. CAV lane change

下载: 全尺寸图片幻灯片

图 4 CSA控制算法流程

Figure 4. Flowchart of CSA control algorithm

下载: 全尺寸图片幻灯片

图 5 RDA控制算法流程

Figure 5. Flowchart of RDA control algorithm

下载: 全尺寸图片幻灯片

图 6 不同渗透率下流量与密度关系

Figure 6. Relationship between flow and density under different penetration rates

下载: 全尺寸图片幻灯片

图 7 最大通行能力

Figure 7. Maximum capacity

下载: 全尺寸图片幻灯片

图 8 不同换道策略下相对熵

Figure 8. Relative entropy under each lane change strategy

下载: 全尺寸图片幻灯片

图 9 不同策略下的队列规模

Figure 9. Queue sizes under different strategies

下载: 全尺寸图片幻灯片

图 10 两车道密度差

Figure 10. Density difference between two lanes

下载: 全尺寸图片幻灯片

图 11 规模限制与最大流量关系

Figure 11. Relationship between size limit and maximum flow

下载: 全尺寸图片幻灯片

表 1 仿真参数值

Table 1. Simulation parameter value

参数	取值
${a / \rm{ {(m {\text{•} } {s^{ - 2} } })} }$	1
${{{v_{\rm{f}}}}/ {({\rm{m}}}} {\text{•}} {{\rm{s}}^{ - {\text{1}}}})$	33.3
${{{v_{{\rm{max}}}}} / {({\rm{m}}}} {\text{•}} {{\rm{s}}^{ - {\text{1}}}})$	33.3
${{{d_0}} / {\rm{m}}}$	2
${{{t_0}} /{\rm{ s}}}$	1.6 （CAV）, 1.1 （HV）
${b / {({\rm{m}}}} {\text{•}}{{\rm{s}}^{ - 2}})$	2
${{{b_{{\rm{max}}}}}/ {({\rm{m}}}} {\text{•}} {{\rm{s}}^{ - 2}})$	6
${l / {\rm{m}}}$	6
${{{D_{\rm{R}}}} / {\rm{m}}}$	300
${k_{\rm{p}}}$	0.45
${k_{\rm{d}}}$	0.25
${t_{\rm{c}}}$	0.6
$\lambda$	0.5
S_min/辆	3.0

下载: 导出CSV

表 2 最大通行能力提升程度

Table 2. Maximum capacity improvement %

集聚策略	p = 0.2	p = 0.4	p = 0.6	p = 0.8
CVA	2.1	6.7	1.2	0.4
CSA	10.4	12.6	5.1	3.3
RDA	12.3	14.0	9.7	−25.8

下载: 导出CSV

参考文献(18)

[1]	GHIASI A, HUSSAIN O, QIAN Z, et al. A mixed traffic capacity analysis and lane management model for connected automated vehicles: a Markov chain method[J]. Transportation Research Part B: Methodological, 2017, 106: 266-292. doi: 10.1016/j.trb.2017.09.022
[2]	MILANÉS V, SHLADOVER S E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data[J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 285-300. doi: 10.1016/j.trc.2014.09.001
[3]	CHEN D J, AHN S, CHITTURI M, et al. Towards vehicle automation: roadway capacity formulation for traffic mixed with regular and automated vehicles[J]. Transportation Research Part B: Methodological, 2017, 100: 196-221. doi: 10.1016/j.trb.2017.01.017
[4]	VRANKEN T, SLIWA B, WIETFELD C, et al. Adapting a cellular automata model to describe heterogeneous traffic with human-driven, automated, and communicating automated vehicles[J]. Physica A: Statistical Mechanics and Its Applications, 2021, 570: 125792.1-125792.17.
[5]	LAI J T, HU J, CUI L, et al. A generic simulation platform for cooperative adaptive cruise control under partially connected and automated environment[J]. Transportation Research Part C: Emerging Technologies, 2020, 121: 102874.1-102874.24.
[6]	YE L H, YAMAMOTO T. Impact of dedicated lanes for connected and autonomous vehicle on traffic flow throughput[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 512: 588-597. doi: 10.1016/j.physa.2018.08.083
[7]	PAPADOULIS A, QUDDUS M, IMPRIALOU M. Evaluating the safety impact of connected and autonomous vehicles on motorways[J]. Accident Analysis & Prevention, 2019, 124: 12-22.
[8]	ZHONG Z J, LEE J. The effectiveness of managed lane strategies for the near-term deployment of cooperative adaptive cruise control[J]. Transportation Research Part A: Policy and Practice, 2019, 129: 257-270. doi: 10.1016/j.tra.2019.08.015
[9]	梁军,杨程灿,王文飒,等. 自动驾驶车辆混行集聚MAS控制模型[J]. 中国公路学报,2021,34(6): 172-183. LIANG Jun, YANG Chengcan, WANG Wensa, et al. Agglomeration control model based on multi-agents for autonomous vehicles in mixed traffic environment[J]. China Journal of Highway and Transport, 2021, 34(6): 172-183.
[10]	吴德华,彭锐,林熙玲. 智能网联异质交通流混合特性[J]. 西南交通大学学报,2022,57(4): 761-768. WU Dehua, PENG Rui, LIN Xilin. Hybrid characteristics of heterogeneous traffic flow in intelligent network[J]. Journal of Southwest Jiaotong University, 2022, 57(4): 761-768.
[11]	秦严严,王昊,王炜,等. 混有CACC车辆和ACC车辆的异质交通流基本图模型[J]. 中国公路学报,2017,30(10): 127-136. doi: 10.3969/j.issn.1001-7372.2017.10.016 QIN Yanyan, WANG Hao, WANG Wei, et al. Fundamental diagram model of heterogeneous traffic flow mixed with cooperative adaptive cruise control vehicles and adaptive cruise control vehicles[J]. China Journal of Highway and Transport, 2017, 30(10): 127-136. doi: 10.3969/j.issn.1001-7372.2017.10.016
[12]	周思,柳祖鹏,陈玲娟,等. 路段上集群智能网联汽车的车队形成机制[J]. 公路,2021,66(2): 210-215. ZHOU Si, LIU Zupeng, CHEN Lingjuan, et al. Platoon formation mechanism of collective connected autonomous vehicles on road[J]. Highway, 2021, 66(2): 210-215.
[13]	李松,贺国光,张晓利. 一种基于交通熵的交通流无序度量方法[J]. 公路交通科技,2007,24(11): 92-95. doi: 10.3969/j.issn.1002-0268.2007.11.021 LI Song, HE Guoguang, ZHANG Xiaoli. A measuring method for disorder motion in traffic flow based on traffic entropy[J]. Journal of Highway and Transportation Research and Development, 2007, 24(11): 92-95. doi: 10.3969/j.issn.1002-0268.2007.11.021
[14]	LIU Z P, XU C X, CHEN L J, et al. Dynamic traffic flow entropy calculation based on vehicle spacing[J]. IOP Conference Series: Earth and Environmental Science, 2019, 252: 052073.1-052073.6.
[15]	ZHOU Y J, ZHU H B, GUO M M, et al. Impact of CACC vehicles’ cooperative driving strategy on mixed four-lane highway traffic flow[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 540: 122721.1-122721.13.
[16]	董长印,王昊,王炜,等. 混入智能车的下匝道瓶颈路段交通流建模与仿真分析[J]. 物理学报,2018,67(14): 179-193. doi: 10.7498/aps.67.20172752 DONG Changyin, WANG Hao, WANG Wei, et al. Hybrid traffic flow model for intelligent vehicles exiting to off-ramp[J]. Acta Physica Sinica, 2018, 67(14): 179-193. doi: 10.7498/aps.67.20172752
[17]	TALEBPOUR A, MAHMASSANI H S, HAMDAR S H. Effect of information availability on stability of traffic flow: percolation theory approach[J]. Transportation Research Part B: Methodological, 2018, 117: 624-638. doi: 10.1016/j.trb.2017.09.005
[18]	秦严严,王昊,王炜,等. 混有协同自适应巡航控制车辆的异质交通流稳定性解析与基本图模型[J]. 物理学报,2017,66(9): 257-265. doi: 10.7498/aps.66.094502 QIN Yanyan, WANG Hao, WANG Wei, et al. Stability analysis and fundamental diagram of heterogeneous traffic flow mixed with cooperative adaptive cruise control vehicles[J]. Acta Physica Sinica, 2017, 66(9): 257-265. doi: 10.7498/aps.66.094502

施引文献

期刊类型引用(3)

1.	崔晓璐，彭双千，徐佳，钟建科，祁亚运. 钢轨波磨区段科隆蛋扣件弹条断裂机理. 西南交通大学学报. 2025(01): 205-213 . 本站查看
2.	周世祺，崔晓璐，杨冰. 高速铁路钢轨波磨高发区段弹条断裂机理研究. 振动与冲击. 2023(23): 267-275 . 百度学术
3.	崔晓璐，卜涵，徐晓天，尹越，徐佳，杨红娟. 高速铁路车轮多边形和钢轨波磨相关性及影响. 振动.测试与诊断. 2025(01): 45-50+199 . 百度学术