考虑尖轨变截面廓形的轮轨接触与磨耗分析

陈雨; 安博洋; 潘自立; 莫宏愿; 王平; 方嘉晟; 钱瑶; 徐井芒

doi:10.3969/j.issn.0258-2724.20210040

考虑尖轨变截面廓形的轮轨接触与磨耗分析

doi: 10.3969/j.issn.0258-2724.20210040

陈雨^{1, 2,},
安博洋^{1, 2, ,},
潘自立³,
莫宏愿³,
王平^{1, 2},
方嘉晟^{1, 2},
钱瑶^{1, 2},
徐井芒^{1, 2}

1.
西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031
2.
西南交通大学土木工程学院，四川成都 610031
3.
中铁二院工程集团有限责任公司，四川成都 610031

基金项目: 国家自然科学基金（U1734207, 51978586, 51908474）；四川省重点研发计划（2019YFG0460）；中央高校基本科研业务费（2682020CX67）；中铁二院工程集团有限责任公司科技开发计划（KNSQ202054)

详细信息

作者简介:
陈雨（1997—），女，博士研究生，研究方向轮轨关系与轮轨损伤分析，E-mail：291035338@qq.com

通讯作者:
安博洋（1988—），男，讲师，博士，研究方向轮轨接触动力学与伤损，E-mail：anboyang@swjtu.edu.cn

中图分类号: U211.5
计量
- 文章访问数: 438
- HTML全文浏览量: 147
- PDF下载量: 53
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-19
- 修回日期: 2021-04-05
- 网络出版日期: 2022-07-15
- 刊出日期: 2021-04-08

Analysis of Wheel-Rail Contact and Wear Considering Variable Cross-Sections of Switch Rail

CHEN Yu^{1, 2
,},
AN Boyang^{1, 2
, ,},
PAN Zili³,
MO Hongyuan³,
WANG Ping^{1, 2},
FANG Jiasheng^{1, 2},
QIAN Yao^{1, 2},
XU Jingmang^{1, 2}

1.
MOE Key Laboratory of High-Speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
3.
China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China

摘要

摘要:
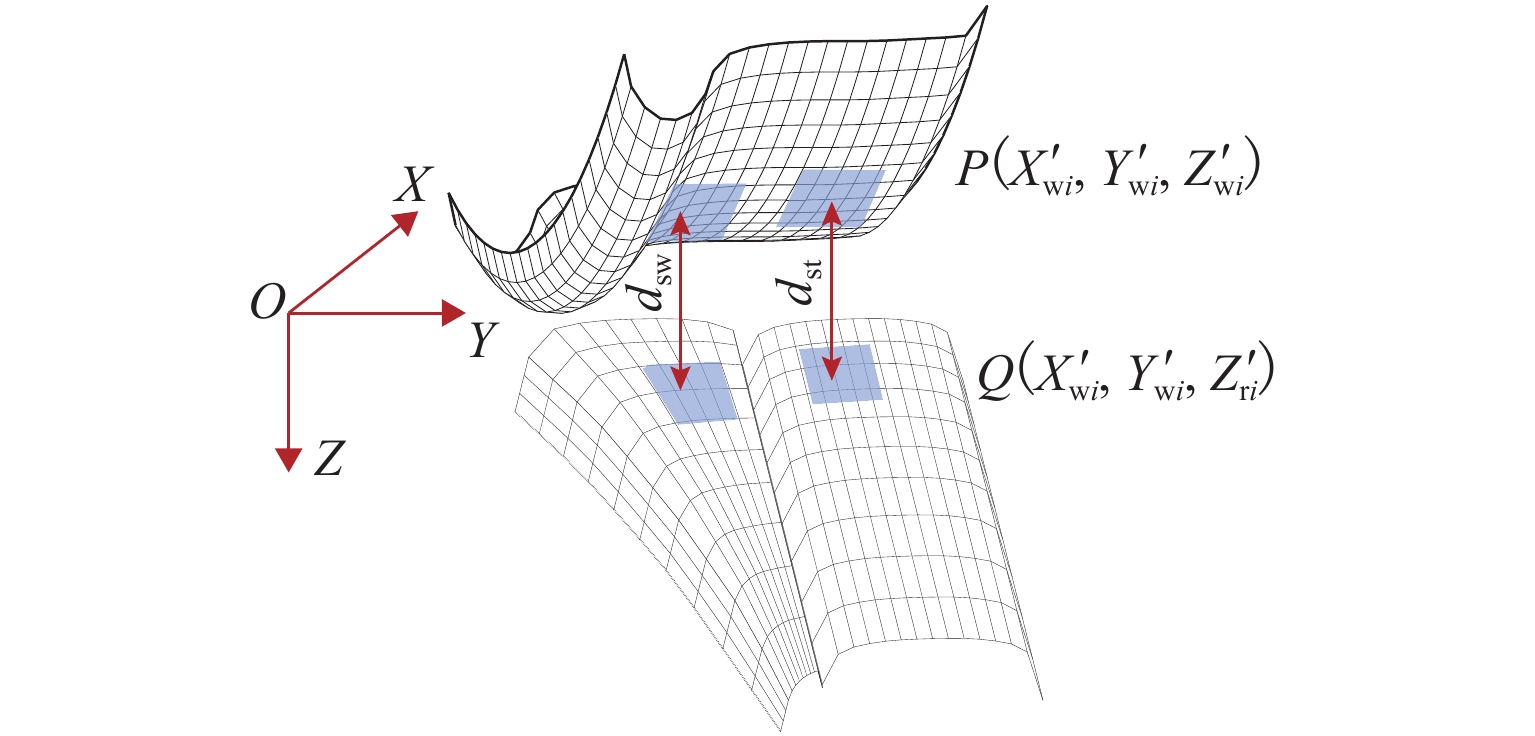
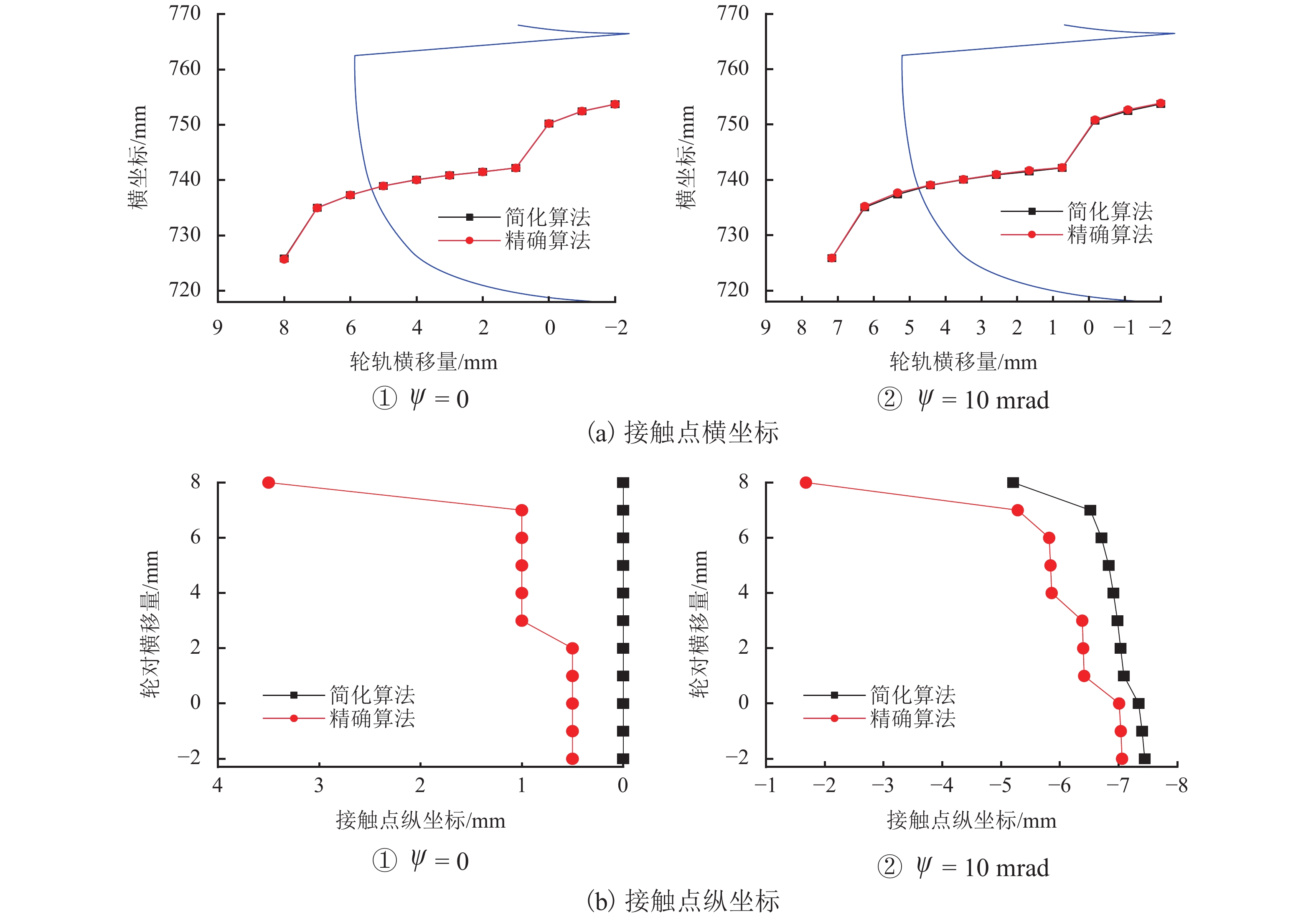
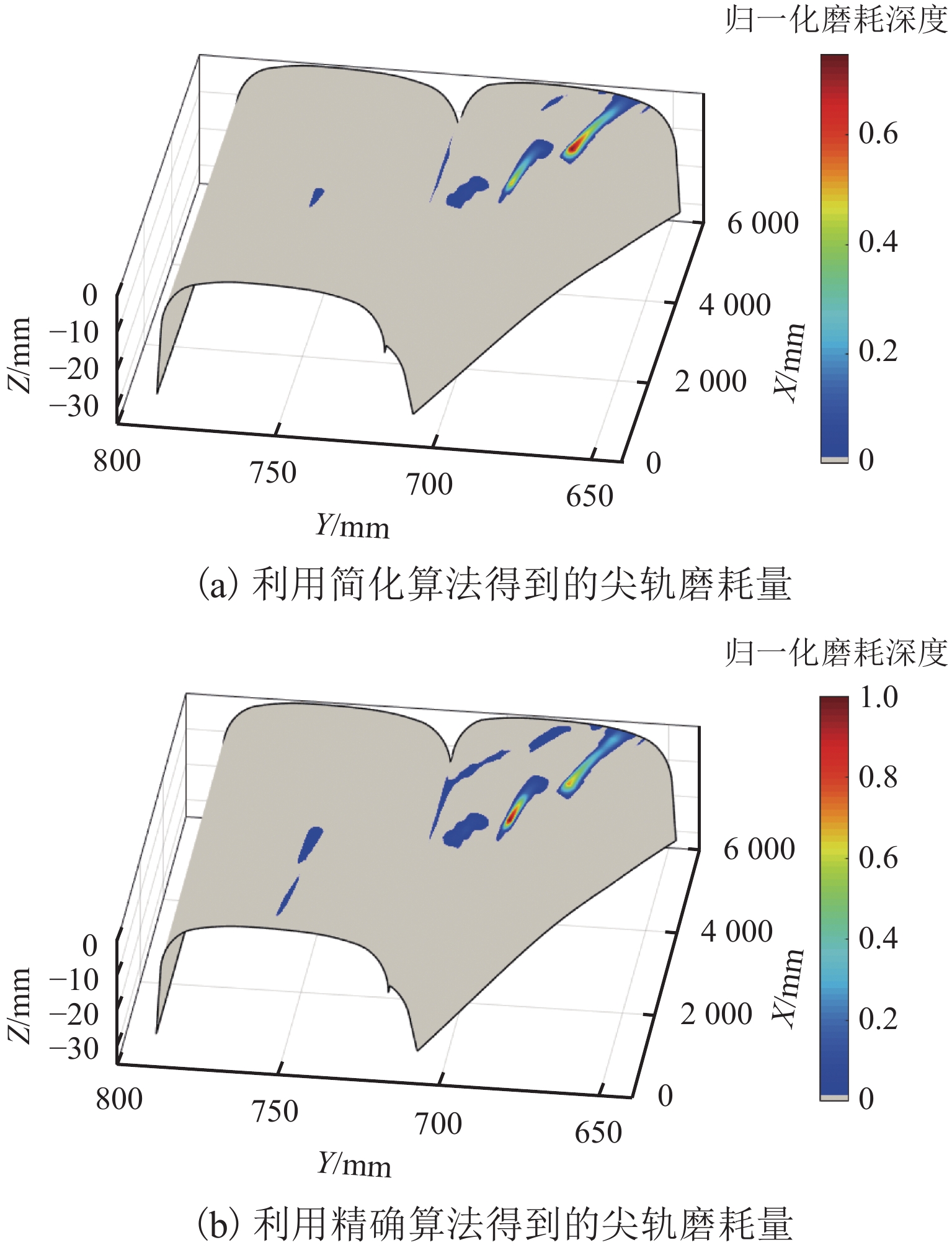
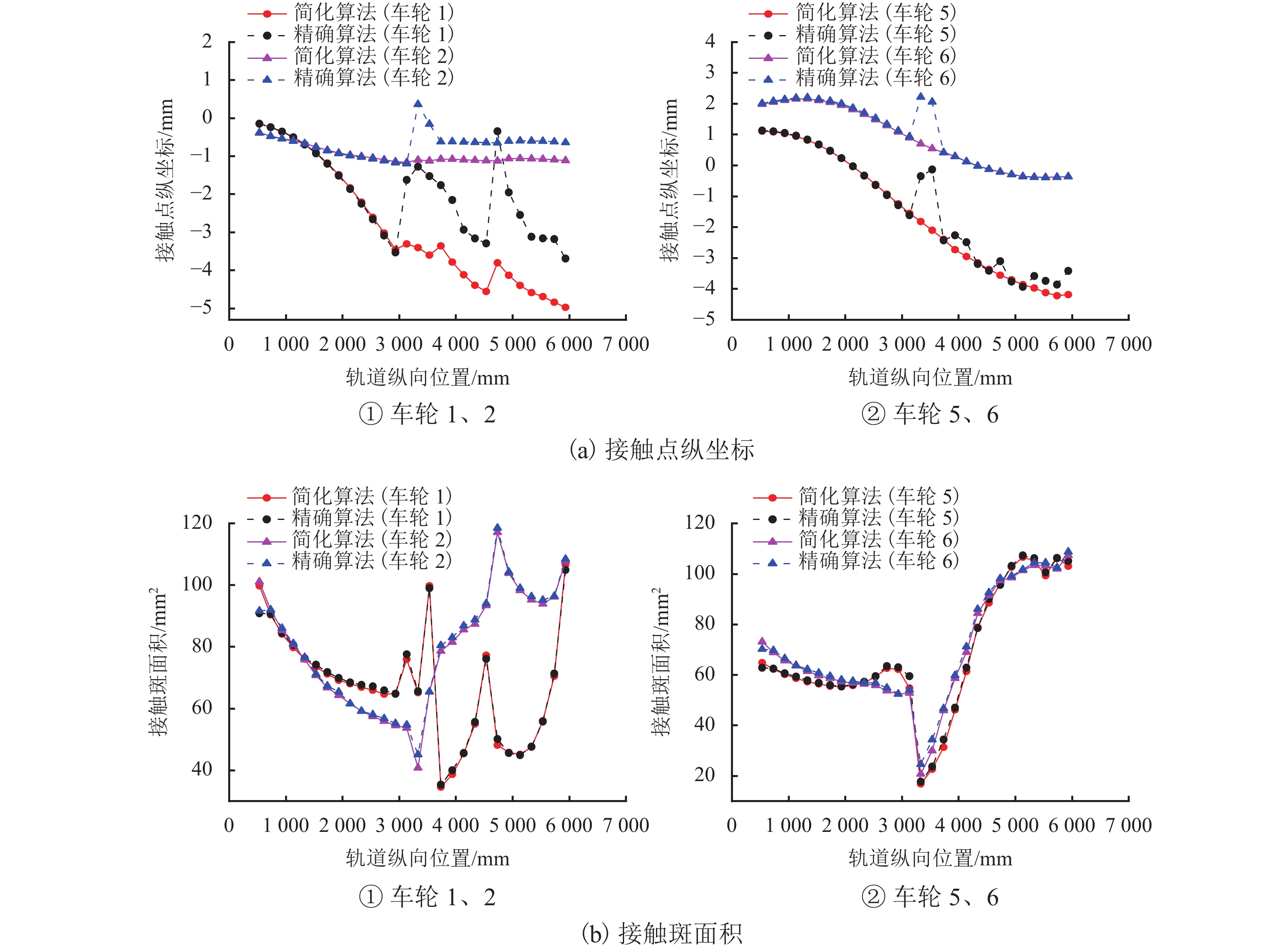
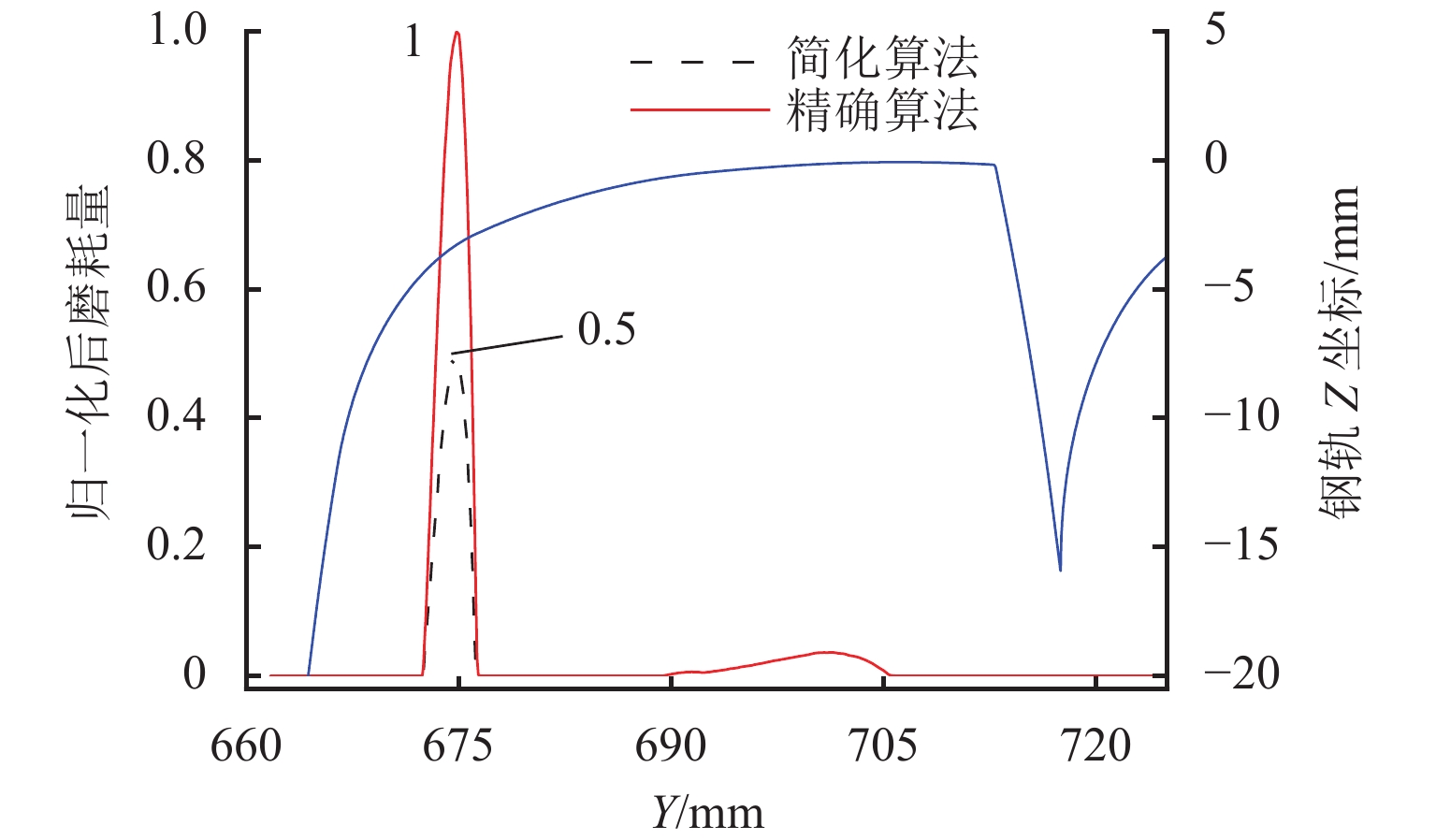
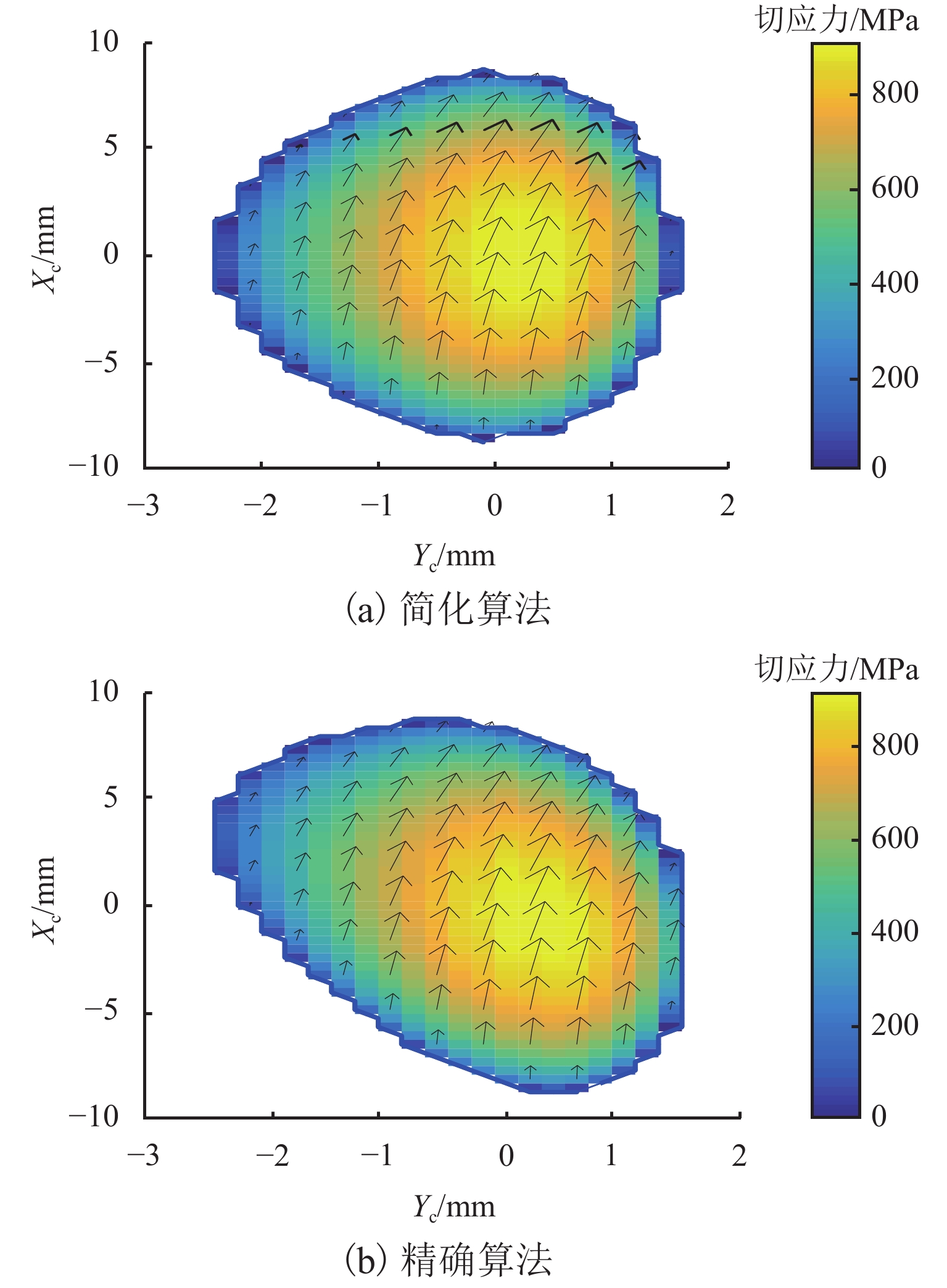
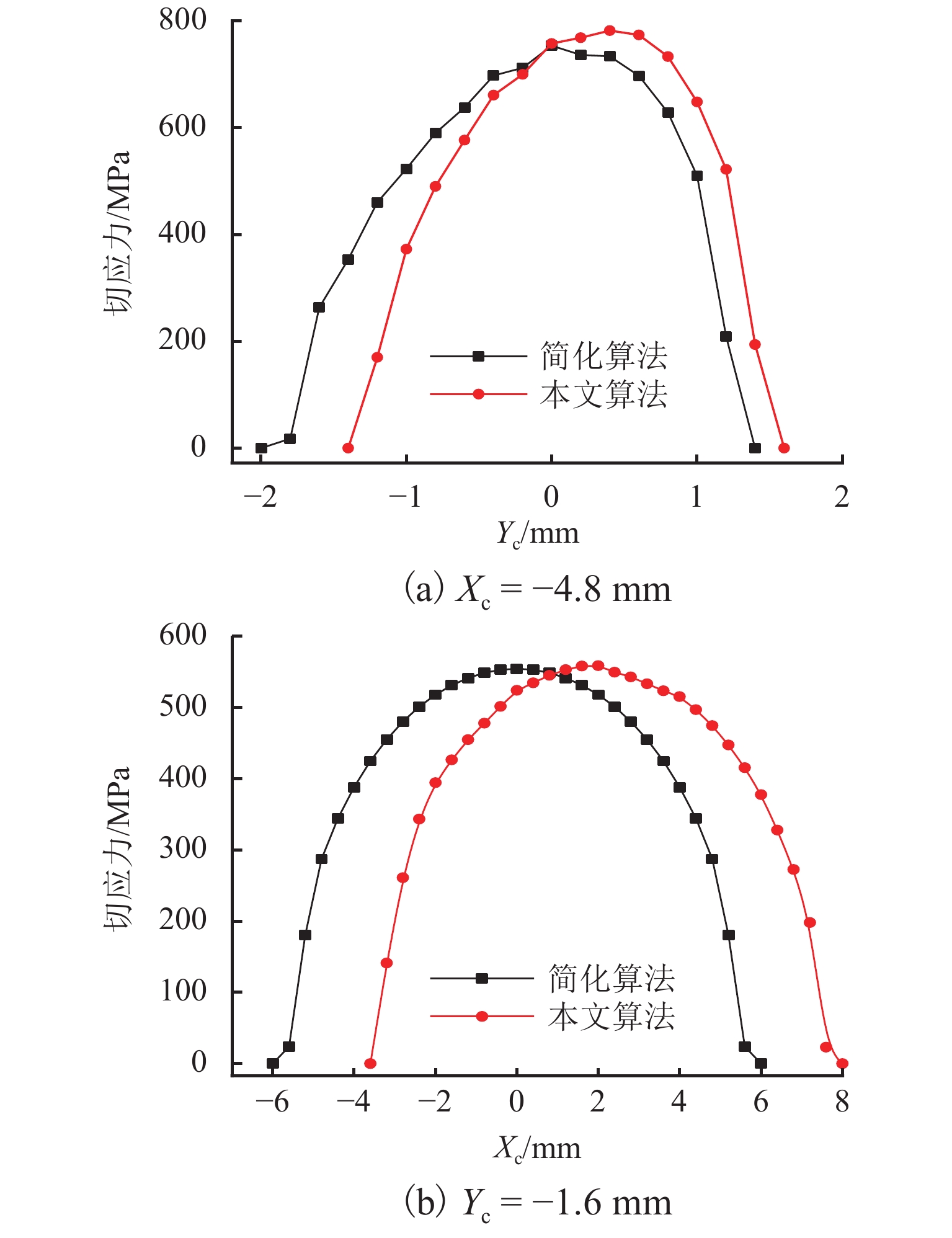
为研究尖轨变截面对曲尖轨轮轨接触行为和磨耗分布的影响，提出了一种适用于道岔区的三维非对称接触几何算法，该算法可计算车轮与曲尖轨间的真实法向间隙. 使用SIMPACK建立车辆-道岔多体动力学模型，获得仿真结果；利用考虑变截面的接触模型与英国谢菲尔大学提出的USFD磨耗模型计算曲尖轨磨耗. 研究结果表明：1）以S1002CN车轮与12号道岔曲尖轨为例，轮对摇头角与尖轨变截面均会引起轮轨法向间隙沿接触斑纵向非对称分布，从而导致接触斑形状与应力沿接触斑纵向非对称分布；当摇头角为10 mrad，横移量为7.5 mm时，本文算法得到的接触斑面积比未考虑尖轨变截面和摇头角的简化算法所得结果大9.2%. 2）以CRH3型车与12号曲尖轨道岔为研究对象，简化算法得到的最大磨耗深度为本文算法所得结果的0.75倍.
- 铁路道岔 /
- 尖轨磨耗 /
- 轮轨接触 /
- 变截面 /
- 摇头角
Abstract:
To investigate the influence of variable switch rail cross-sections on wheel-rail contact behaviors and the wear distribution of the curved switch rail, a three dimensional (3D) asymmetric contact geometry method for the turnout area was proposed, which could calculate the real normal gap between the wheel and curved switch rail. The vehicle-turnout multi-body dynamics model was initially built by SIMPACK to obtain simulated results. And then the wear depth of the curved switch rail was calculated by the contact model considering variable cross-sections and the USFD wear model proposed by University of Sheffield. The results show that: 1) Taking the S1002CN wheel profile and No. 12 curved switch rail for examples, both the wheel-set yaw angle and variable cross-sections result in the asymmetric distribution of wheel-rail normal gap along the longitudinal direction within the contact patch. Therefore, the normal gap causes the contact patch shape and stress distribution asymmetric along the longitudinal direction within the contact patch. When the wheel-set yaw angle is 10 mrad and the lateral displacement is 7.5 mm, the area of contact patch obtained by the proposed method is 9.2% larger than that solved by the simplified method without considering the variable cross-sections and yaw angle. 2) Taking the CRH3 vehicle and No.12 curved switch blades as the research objects, the maximum wear depth calculated by the simplified method is 0.75 times as large as that according to the proposed method.
- railway turnout /
- switch rail wear /
- wheel-rail contact /
- variable cross-sections /
- yaw angle

HTML全文

图 1 接触点局部坐标

Figure 1. Wheel-rail contact coordinate system

下载: 全尺寸图片幻灯片

图 2 精确算法求解轮轨接触点示意

Figure 2. Schematic diagram of the exact method for determining the wheel-rail contact point

下载: 全尺寸图片幻灯片

图 3 不同横移量下的接触点位置

Figure 3. Positions of the contact points under different lateral displacements

下载: 全尺寸图片幻灯片

图 4 接触斑轮廓对比

Figure 4. Comparison of contact patch contour

下载: 全尺寸图片幻灯片

图 5 横移量为7.5 mm时接触斑内法向应力

Figure 5. Pressure distribution within contact patch at a lateral displacement of 7.5 mm

下载: 全尺寸图片幻灯片

图 6 尖轨磨耗量分布

Figure 6. Distribution of wear depth on the switch panel

下载: 全尺寸图片幻灯片

图 7 不同车轮与曲尖轨接触时的接触点纵坐标与接触斑面积

Figure 7. Longitudinal coordinates of the contact point and contact areas between different wheelsets and the curved switch rail

下载: 全尺寸图片幻灯片

图 8 钢轨截面磨耗深度分布

Figure 8. Wear depth on the switch rail cross-section

下载: 全尺寸图片幻灯片

图 9 两种算法得到的切应力分布

Figure 9. Distribution of tangential stress solved by the two methods

下载: 全尺寸图片幻灯片

图 10 切应力沿Y_c和X_c方向分布

Figure 10. Distribution of tangential stress along Y_c-direction and X_c-direction

下载: 全尺寸图片幻灯片

参考文献(16)

[1]	王平,汪鑫,王源,等. 基于高铁轨道不平顺的车轮不圆顺识别模型[J]. 西南交通大学学报,2020,55(4): 681-687,678. doi: 10.3969/j.issn.0258-2724.20180283 WANG Ping, WANG Xin, WANG Yuan, et al. Polygonal wheel detection model based on track irregularity of high-speed railways[J]. Journal of Southwest Jiaotong University, 2020, 55(4): 681-687,678. doi: 10.3969/j.issn.0258-2724.20180283
[2]	蔡小培,谭希,郭亮武,等. 列车荷载下钢轨振动加速度的空间分布特征[J]. 西南交通大学学报,2018,53(3): 459-466. doi: 10.3969/j.issn.0258-2724.2018.03.005 CAI Xiaopei, TAN Xi, GUO Liangwu, et al. Spatial distribution characteristics of rail vibration acceleration under train load[J]. Journal of Southwest Jiaotong University, 2018, 53(3): 459-466. doi: 10.3969/j.issn.0258-2724.2018.03.005
[3]	GE X, LING L, GUO L R, et al. Dynamic derailment simulation of an empty wagon passing a turnout in the through route[J]. Vehicle System Dynamics, 2022,60(4): 1-22.
[4]	娄平,赵晨,宫凯伦. 组合荷载作用下CRTSⅢ型板式无砟轨道层间离缝影响分析[J]. 铁道科学与工程学报,2019,16(12): 2913-2920. LOU Ping, ZHAO Chen, GONG Kailun. Study on the influence of connection damage for CRTS Ⅲ slab ballastless track under combined loads[J]. Journal of Railway Science and Engineering, 2019, 16(12): 2913-2920.
[5]	AN B Y, MA D L, WANG P, et al. Assessing the fast non-Hertzian methods based on the simulation of wheel-rail rolling contact and wear distribution[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2020, 234(5): 524-537. doi: 10.1177/0954409719848592
[6]	LIU B B, BRUNI S, VOLLEBREGT E. A non-Hertzian method for solving wheel-rail normal contact problem taking into account the effect of yaw[J]. Vehicle System Dynamics, 2016, 54(9): 1226-1246. doi: 10.1080/00423114.2016.1196823
[7]	SUN Y, ZHAI W M, YE Y G, et al. A simplified model for solving wheel-rail non-Hertzian normal contact problem under the influence of yaw angle[J]. International Journal of Mechanical Sciences, 2020(174): 105554.1-105554.13. doi: 10.1016/j.ijmecsci.2020.105554
[8]	KALKER J J. Three-dimensional elastic bodies in rolling contact[M]. Dordrecht: Springer Netherlands, 1990.
[9]	杨新文,姚一鸣,周顺华,等. 基于修正的轮轨非Hertz接触的重载铁路曲线超高对钢轨磨耗的影响分析[J]. 机械工程学报,2018,54(4): 22-29. doi: 10.3901/JME.2018.04.022 YANG Xinwen, YAO Yiming, ZHOU Shunhua, et al. Influence of curve superelevation of heavy haul railway on rail wear based on revised wheel/rail non-hertz contact[J]. Journal of Mechanical Engineering, 2018, 54(4): 22-29. doi: 10.3901/JME.2018.04.022
[10]	马晓川,王平,王健,等. 高速铁路磨耗车轮与60 N钢轨静态接触分析[J]. 西南交通大学学报,2018,53(4): 741-747. doi: 10.3969/j.issn.0258-2724.2018.04.011 MA Xiaochuan, WANG Ping, WANG Jian, et al. Static contact analysis of worn-wheel profiles and 60 N rail of high-speed railway[J]. Journal of Southwest Jiaotong University, 2018, 53(4): 741-747. doi: 10.3969/j.issn.0258-2724.2018.04.011
[11]	王平,高天赐,汪鑫,等. 基于拟合平纵断面的铁路特大桥梁线路平顺性评估[J]. 西南交通大学学报,2020,55(2): 231-237,272. doi: 10.3969/j.issn.0258-2724.20180295 WANG Ping, GAO Tianci, WANG Xin, et al. Smoothness estimation of super-large bridges in railway line based on fitting railway plane and profile[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 231-237,272. doi: 10.3969/j.issn.0258-2724.20180295
[12]	王开文. 车轮接触点迹线及轮轨接触几何参数的计算[J]. 西南交通大学学报,1984,19(1): 89-99. WANG Kaiwen. The track of wheel contact points and the calculation of wheel/rail geometric contact parameters[J]. Journal of Southwest Jiaotong University, 1984, 19(1): 89-99.
[13]	陈嵘,方嘉晟,汪鑫,等. 车轮型面演变对高速道岔区轮轨接触行为影响分析[J]. 铁道学报,2019,41(5): 101-108. doi: 10.3969/j.issn.1001-8360.2019.05.012 CHEN Rong, FANG Jiasheng, WANG Xin, et al. Influence of wheel profile evolution on wheel-rail contact behavior in high-speed turnout area[J]. Journal of the China Railway Society, 2019, 41(5): 101-108. doi: 10.3969/j.issn.1001-8360.2019.05.012
[14]	任尊松,孙守光. 道岔区轮轨接触几何关系研究[J]. 工程力学,2008,25(11): 223-230. REN Zunsong, SUN Shouguang. Study on the wheel/ rail contact geometry relation of the turnout zone[J]. Engineering Mechanics, 2008, 25(11): 223-230.
[15]	BRAGHIN F, LEWIS R, DWYER-JOYCE R S, et al. A mathematical model to predict railway wheel profile evolution due to wear[J]. Wear, 2006, 261(11/12): 1253-1264.
[16]	XU J M, WANG P, WANG J, et al. Numerical analysis of the effect of track parameters on the wear of turnout rails in high-speed railways[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2018, 232(3): 709-721. doi: 10.1177/0954409716685188