Influence of Nose Rail Reconstruction Profile Parameters Based on B-Spline Curve
-
摘要:
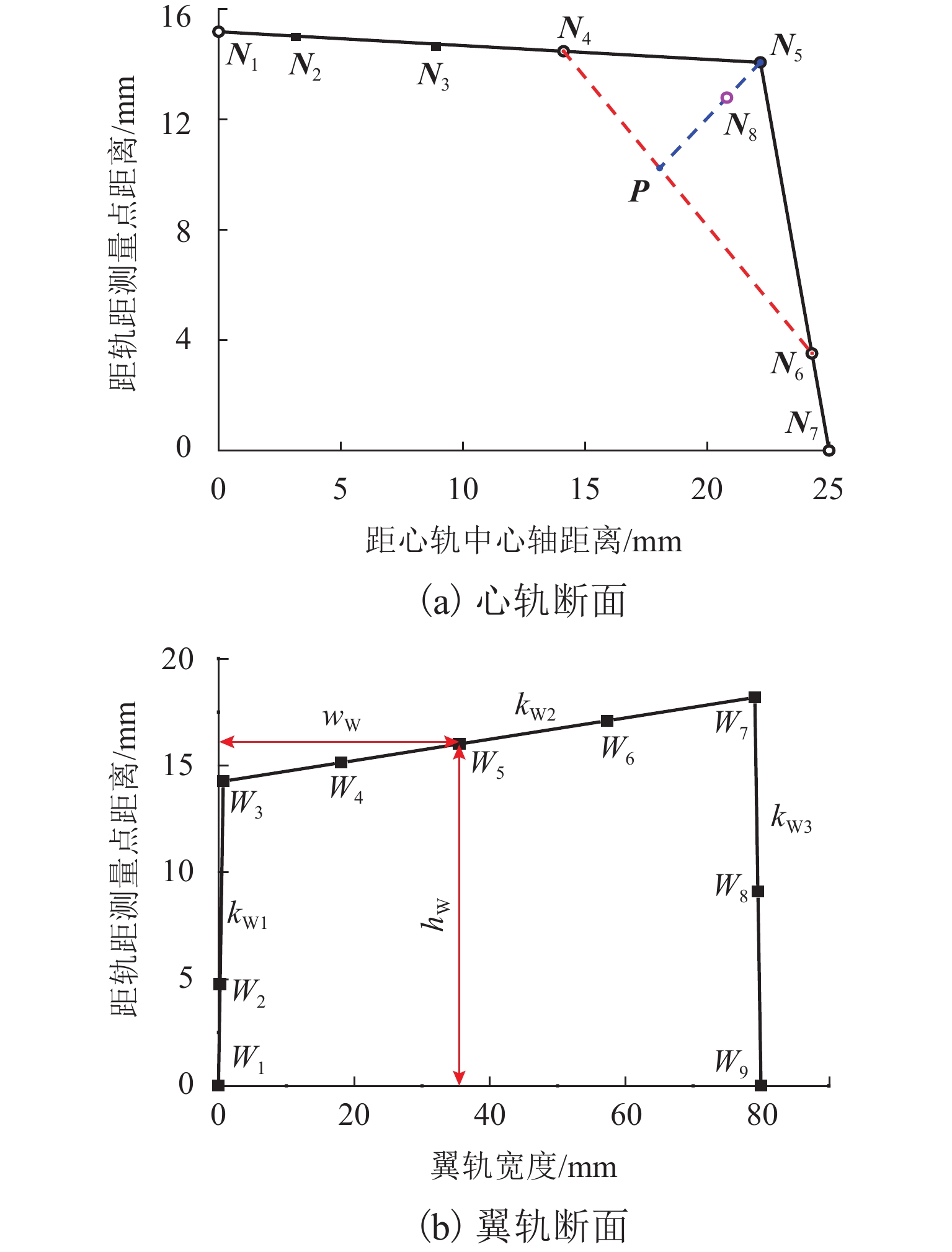
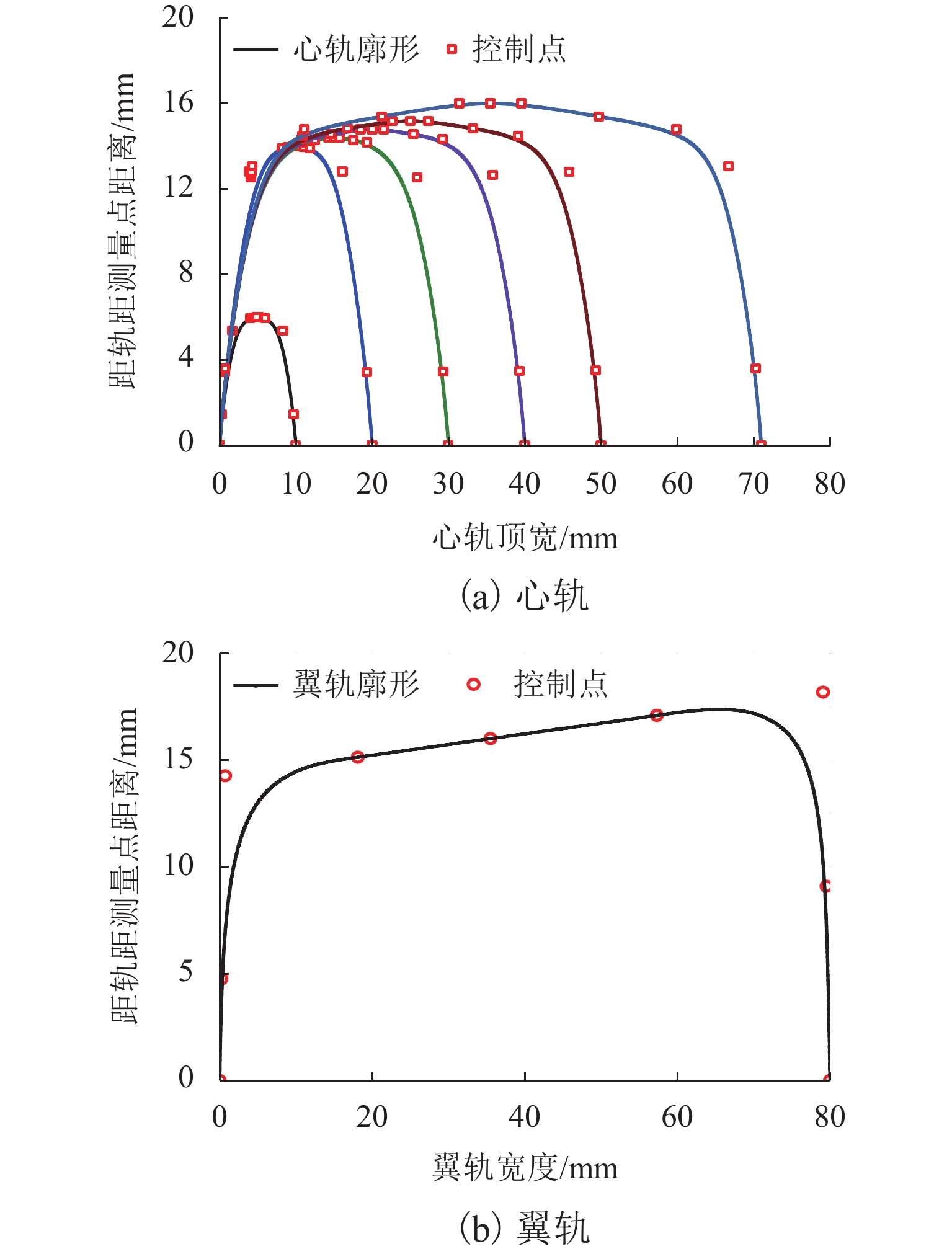
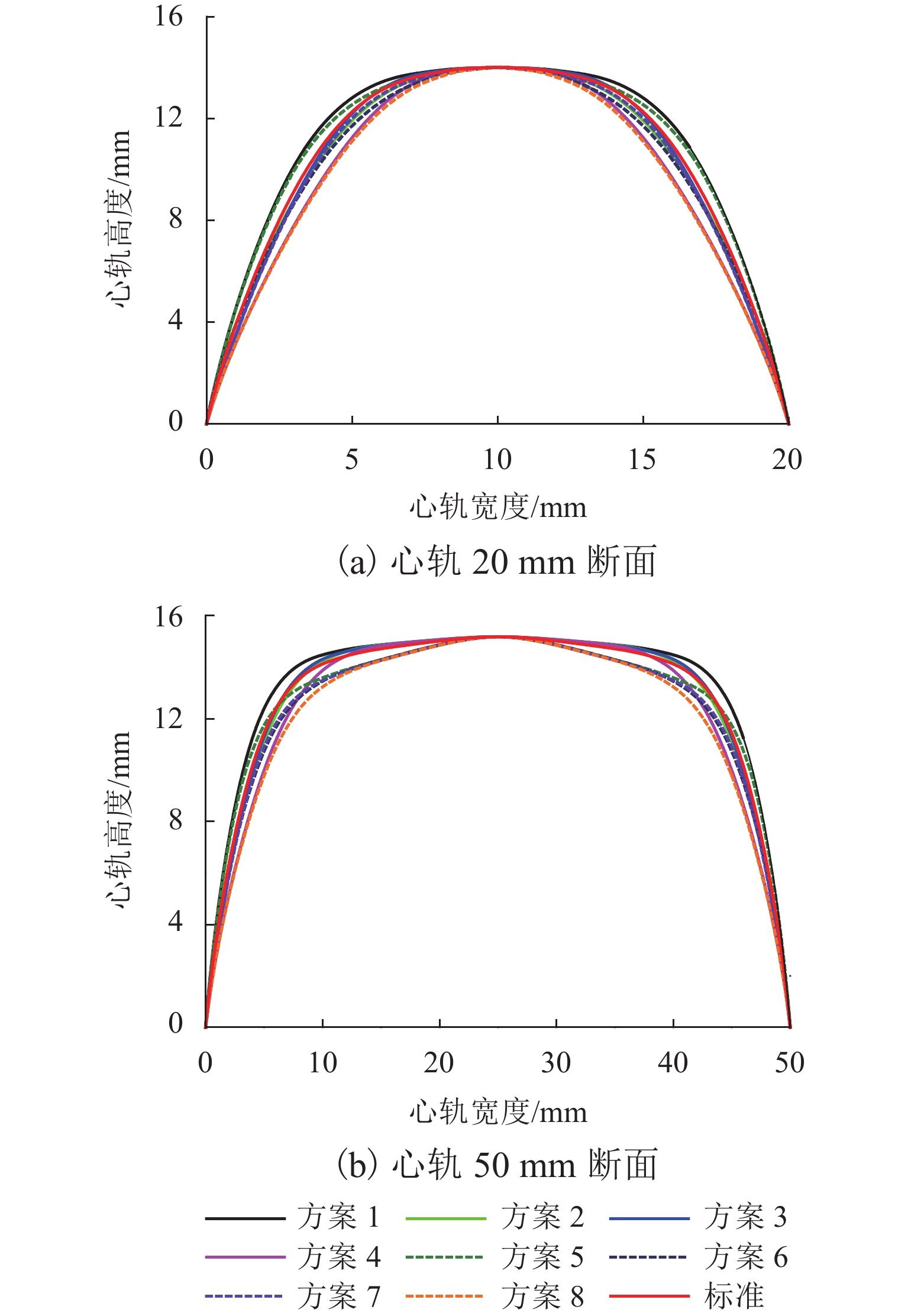
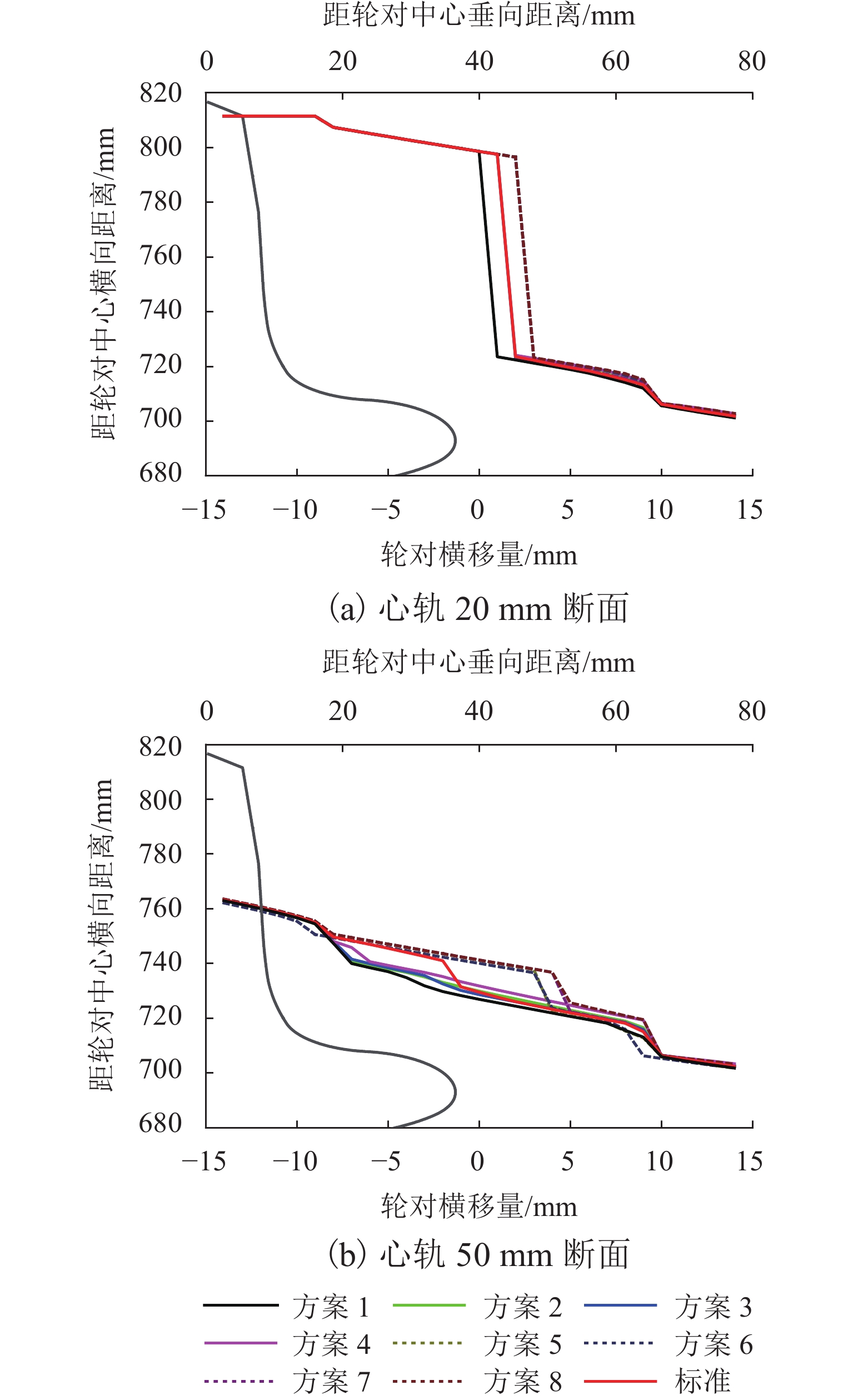
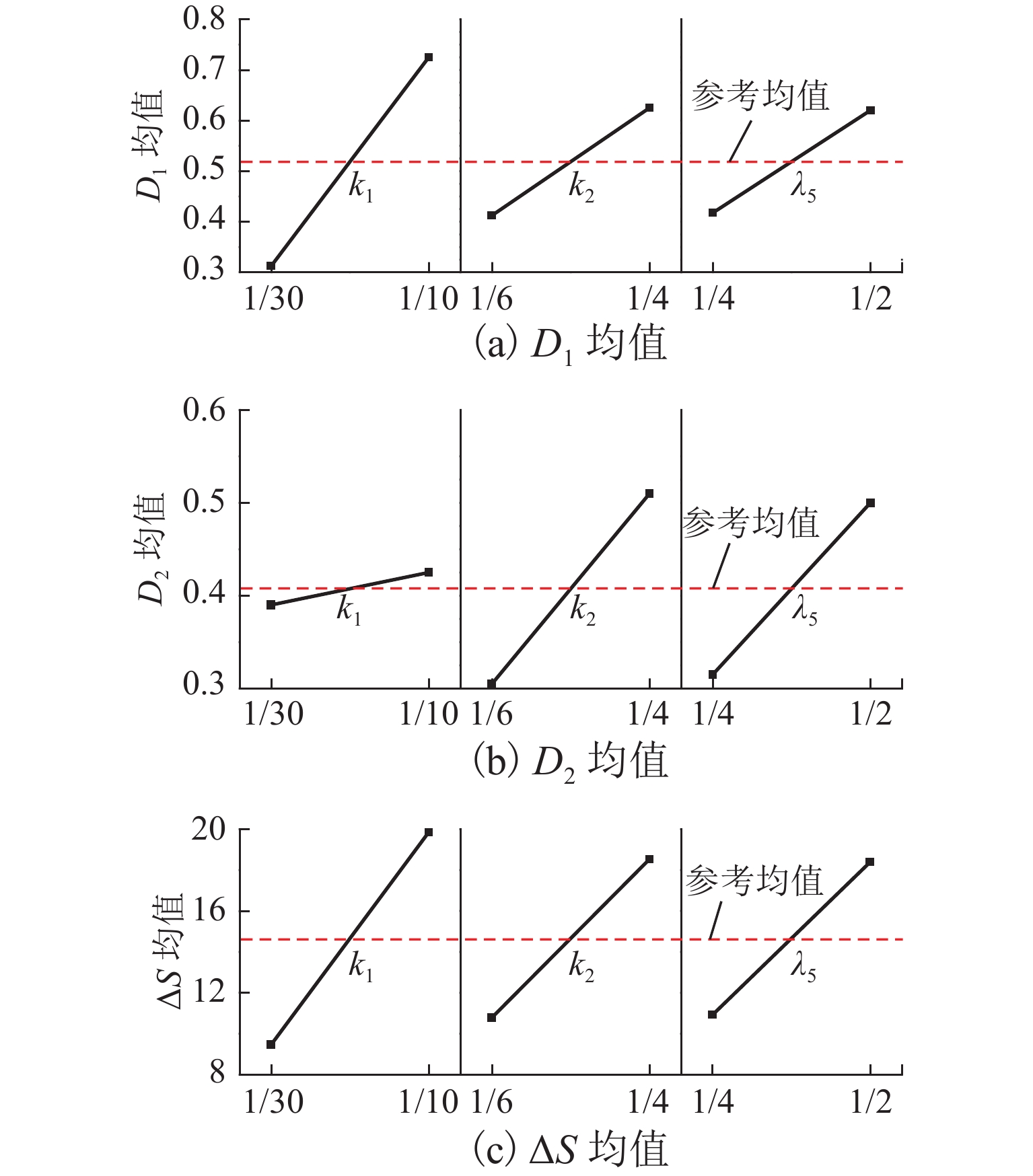
针对固定辙叉钢轨廓形不规则变化特点,基于B样条理论提出一种考虑固定辙叉钢轨断面廓形特征的参数化设计方法,并提出拟合钢轨廓形贴合度评价指标和关键控制参数对廓形贴合度影响权重指标;以60 kg/m钢轨12号固定辙叉为例,采用DOE (design of experiments)方法分析轨顶横坡、侧面纵坡和复合圆弧段比例系数对心轨轨头整体廓形、轨顶面廓形和侧面廓形的影响. 结果表明:1) 在心轨20 mm断面,轨顶横坡、侧面纵坡和复合圆弧段比例系数对心轨整体廓形变化的影响权重分别为21.08%、56.89%和22.02%,对心轨顶面廓形变化影响权重分别为8.42%、61.95%、29.63%;在心轨50 mm断面,各关键控制参数对心轨轨头整体廓形变化影响权重分别为55.9%、33.38%、10.72%;侧面纵坡对心轨20 mm和50 mm断面的侧面廓形变化影响权重分别为76.82%、66.04%. 2) 当心轨轨头宽度为20 mm时,侧面纵坡对各部分廓形变化影响均达到50%以上;随着心轨轨头宽度的增大,心轨轨顶横坡对整体廓形变化影响权重由21.8%增至55.9%,侧面纵坡和复合圆弧段比例系数影响权重则分别减小41.3%和51.3%.
Abstract:According to irregular changes in rail profiles in a fixed-nose crossing, a parametric design method was proposed based on the B-spline theory by considering the section characteristics of rail profiles in a fixed-nose crossing. In addition, the rail profile fitting evaluation indexes and the influence weights of key control parameters on the rail profile fitting were proposed. With No.12 turnout of fixed-nose crossing of 60 kg/m rail as an example, the design of experiment (DOE) was employed to analyze the influence of railhead slope, rail side slope, and proportion coefficient of composite circular arc on the changes in the full railhead profile, rail top profile, and rail side profile of the nose rail. The results show that 1) for nose rail with a section of 20 mm, the influence weights of railhead slope, rail side slope, and proportion coefficient of composite circular arc on the full railhead profile change are 21.08%, 56.89%, and 22.02%, respectively, and the influence weights on the rail top profile change of the nose rail are 8.42%, 61.95%, and 29.63%, respectively. For nose rail with a section of 50 mm, the influence weights of the key control parameters on the full railhead profile change are 55.9%, 33.38%, and 10.72%, respectively. For nose rails with a section of 20 mm and 50 mm, the influence weights of the rail side slope on the rail side profile change are 76.82% and 66.04%, respectively. 2) When the nose railhead width is 20 mm, the influence of the rail side slope on the nose profiles is more than 50%. As the nose railhead width increases, the influence weight of railhead slope on full railhead profile gradually increases from 21.8% to 55.9%, while that of rail side profile and proportion coefficient of composite circular arc is reduced by 41.3% and 51.3%, respectively.
-
Key words:
- turnout /
- fixed-nose crossing /
- B-spline curve /
- rail profile /
- parametric design /
- design of experiments
-
《中国制造2025》战略的落地实施给制造业转型升级指明了方向. 作为一种重要的基础加工行业,金属切削制造业正逐步向智能化、柔性化的精益制造方向发展. 无人化的“熄灯工厂”新模式正在加速推广应用. 高端数控机床作为制造业的核心加工设备,切削加工质量指标(如:表面粗糙度)是影响加工生产效率的主要因素. 加工质量状态监测系统能够保证产品一致性,其推广运用不仅能够提升工厂效益,也能降低废品率,提升资源有效转换比,为国家“双碳”战略目标作出贡献.
近年来,随着工业大数据时代的转型升级以及深度学习技术的发展[1],采用数据驱动的有监督深度学习、边缘计算[2]以及机器视觉图像处理方法等专业技术相结合的工业监测手段得到广泛应用. 刀具[3]、丝杠[4-5]等部件作为数控切削加工的关键零件,其退化过程直接影响加工质量和生产安全. 而在线监测作为重要的监测手段,能够适配金属切削加工现场的复杂监测环境.
对于加工制造业,传统的离线监测与定期维修方式极大地影响了工厂的生产效率. 目前,在许多传统机械加工过程中,工件加工质量的判定是使用触针式表面粗糙度计或者白光干涉仪等设备进行测量. 这些监测方式虽然准确,但离线测量方式并不适用于工厂车间的大批量测试,且测试采样区窄小,需要多次测试. 间接测量方法则在批量测试上具有一定优势,其通过传感器或者机器视觉方法获取监测信号,通过特征提取与分析对切削加工过程和工件质量进行评估,具有在机安装方便、测试效率高等特点.
目前有少量国外研究者对采用传统传感器监测信号的粗糙度间接监测方法进行了研究. Papandrea等[6]研究了基于声发射信号的硬车削加工过程的粗糙度识别与监测方法. Plaza等[7]研究了基于振动监测信号和奇异谱分析方法的粗糙度监测方法. Tangjitsitcharoen等[8]基于切削力信号特征,研究了球头刀铣削加工过程的粗糙度监测方法. 然而,考虑到实际加工过程振动、切削力、声发射等时序信号对安装位置的敏感性以及昂贵的信号采集与处理设备的局限性,直接观测加工表面纹理的监测方法是另一种可探索的监测手段. Rifai等[9]对卷积神经网络在铣削、车削粗糙度识别任务的可行性进行了研究. 然而,其研究缺乏针对在机监测模型的实时性和数据分布特性的优化.
本文基于此,提出了一种改进型轻量级卷积网络,采用代价敏感损失提升在不平衡数据上训练的鲁棒性. 基于铣削纹理图像的监测算法能够实现工件粗糙度的快速识别. 此外,提出模型对低质量现场数据的类间不平衡特性和环境噪声干扰具有较强鲁棒性.
1. 轻量级卷积模型
研究新一代基于深度学习、边缘计算的在线监测技术对数控加工中心等高端制造设备的生产效率提升和加工质量控制具有重要意义. 其相比传统机器学习方法的手工特征选择与设计,过程得到简化.
自2012年AlexNet[10]首个深度卷积网络在大规模图像数据集取得突破性进展后,残差网络[11]等研究避免了卷积网络结构训练过程易出现的梯度弥散现象,使得训练大型神经网络模型成为现实. 而轻量级卷积结构(如:基于可分离卷积的MobileNet[12],结构见图1)的发展为基于边缘计算的工业监测提供了基础. ImageNet数据集[10]为模型预训练提供了支持.
2. 立铣粗糙度在线监测模型
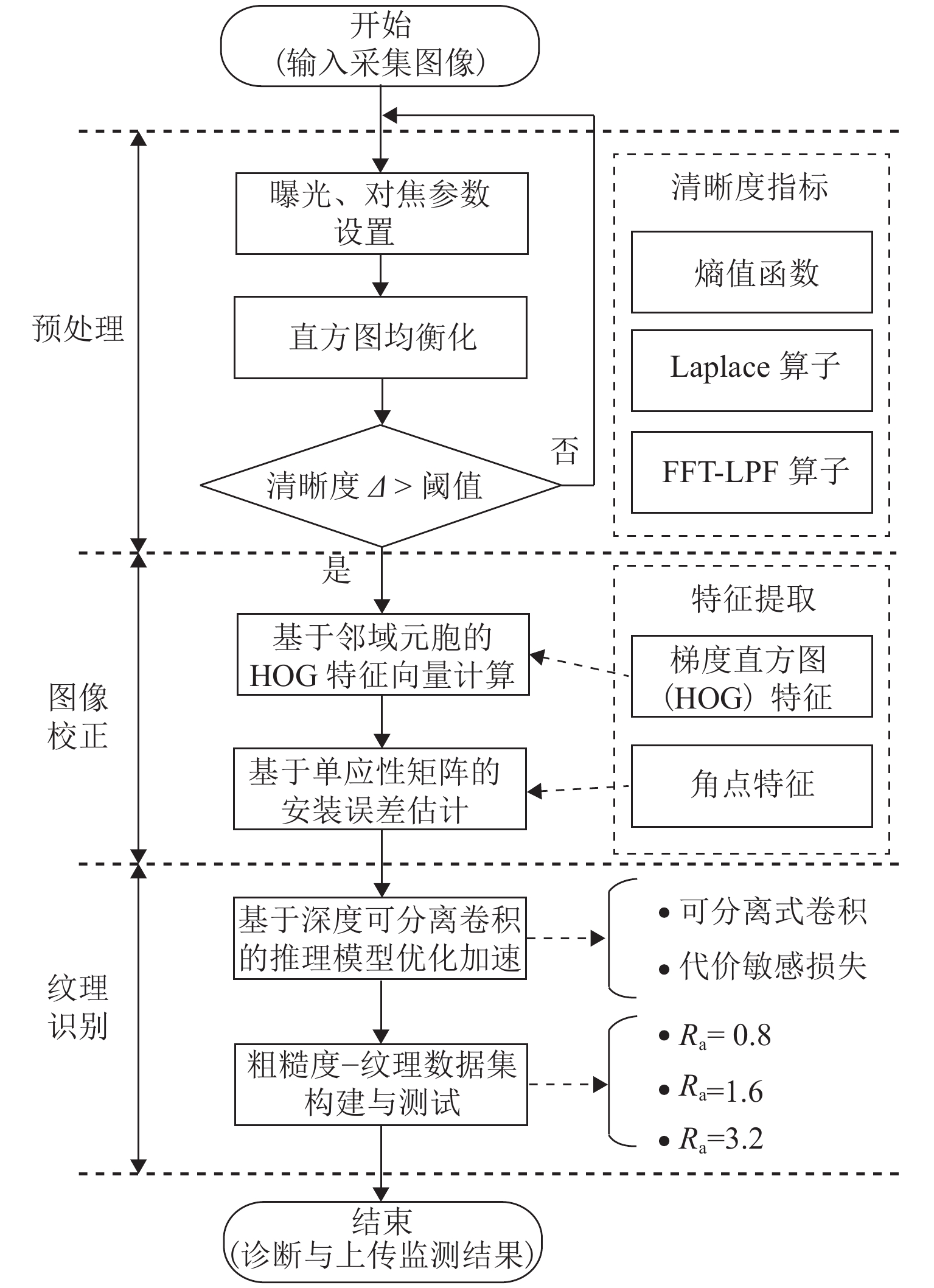
铣削粗糙度在线监测模型示意如图2. 算法具体包括图像预处理、图像校正、纹理识别. 图中:FFT-LPF算子为傅里叶频域变换后低通滤波处理算子,Ra为粗糙度值.
首先,对采集原始图像预处理. 具体包括2个步骤,即采用直方图均衡化方法增强图像、基于纹理图像的清晰度评价判断并采集大于设定阈值的样本,清晰度评价指标包括拉普拉斯(Laplace)算子、FFT-LPF算子2种,阈值(thresh)根据不同工况适当调整.
然后,图像校正模块实现了一种基于匹配点信息对比的位姿校正方法. 基于方向HOG特征的工件区域(目标区域)检测算子对工件区域进行检测;并基于单应性矩阵位姿估计方法,对相机安装偏差进行校正,实现对校正后工件纹理图样的采集与数据集制作.
最后,设计了一种轻量级卷积网络结构,采用代价敏感的交叉熵损失函数模型能够稳定、鲁棒地实现对不同粗糙度刀具加工表面的图样进行纹理特征提取与识别. 下面将进一步阐述各模块的功能实现.
2.1 图像预处理
图像预处理是保证原始图像数据质量的必要手段,而合理的曝光、对焦参数能够实现高质量成像.
2.1.1 直方图均衡化
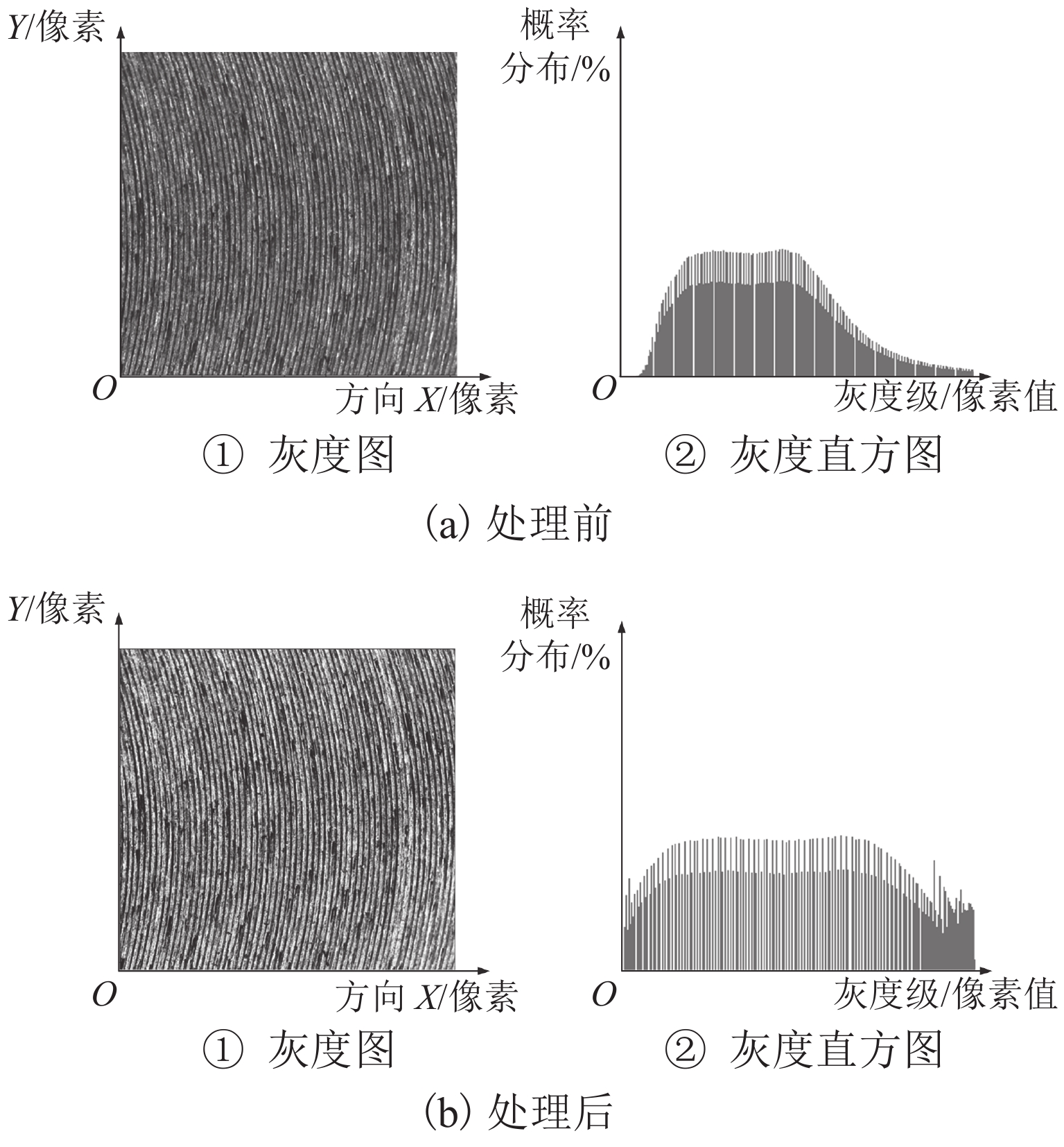
灰度直方图描述了灰度分布情况. 对于尺寸为M(长) × N(宽)的工件纹理灰度图像,其灰度直方图为
p(rm)=nm/(M×N),rm∈[0,255], (1) 式中:p(rm)为灰度级rm在图像中的概率分布,nm为灰度值统计.
扩展灰度分布动态范围能够改善局部亮度分布. 对于图像的直方图均衡化过程,可以描述为一个线性变换过程T(rm),如式(2).
T(rm)=(255−1)K∑rm=0p(rm), (2) 式中:K为目标灰阶值.
图3(a)、(b)为纹理图像经过标准化后,采用直方图均衡化处理前后差异比较.
2.1.2 清晰度评价
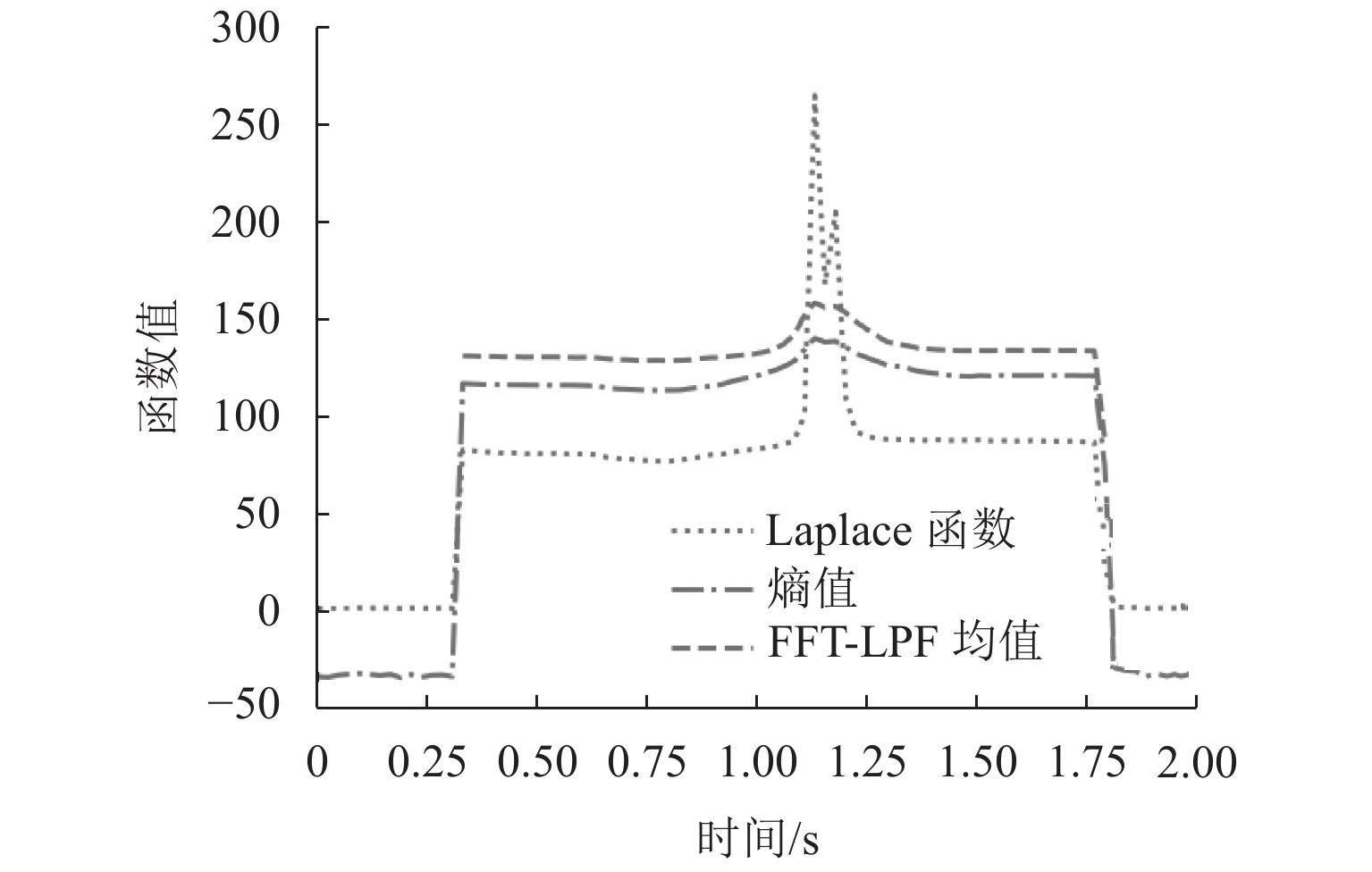
无参考图像质量评价采用清晰度指标来对采集图像优劣进行评判. 常用的清晰度评价指标包括:Laplace函数、熵值函数和FFT-LPF均值函数.
图像空间频域信息描述了纹理图像在长、宽方向上的变化剧烈程度. 类似于Laplace变换的高通低阻特性,通过FFT-LPF,能够表征纹理图像中纹理色块变化程度(轮廓、角点). 其中,二维离散傅里叶变换得到的空间频域成分为
F(k,l)=M−1∑m=0N−1∑n=0f(m,n)e−2πn(kmM+lnN), (3) 式中: m、n为离散时域变量,k、l为离散频域变量,f(m,n)为图像空间域矩阵像素值.
对于任意F(k,l),可通过将空间频域与相应的基函数相乘并将结果相加得到. 通过高通低阻滤波后,将图像信息从空间频域恢复到空间域,变换过程表示为
f(m,n)=1N2M−1∑k=0N−1∑l=0F(k,l)e2πn(kmM+lnN). (4) 2.2 图像校正
采集得到的纹理图像,需要进一步通过校正方法,减小其安装误差带来的特征扰动的影响. 为实现在线数据采集,设计了一种快速图像校正方案. 首先,基于改进的低感度参数设置的HOG算子,检测并识别工件目标区域,并通过单应性矩阵方法对相机安装误差进行校正.
2.2.1 基于HOG算子的目标区域检测
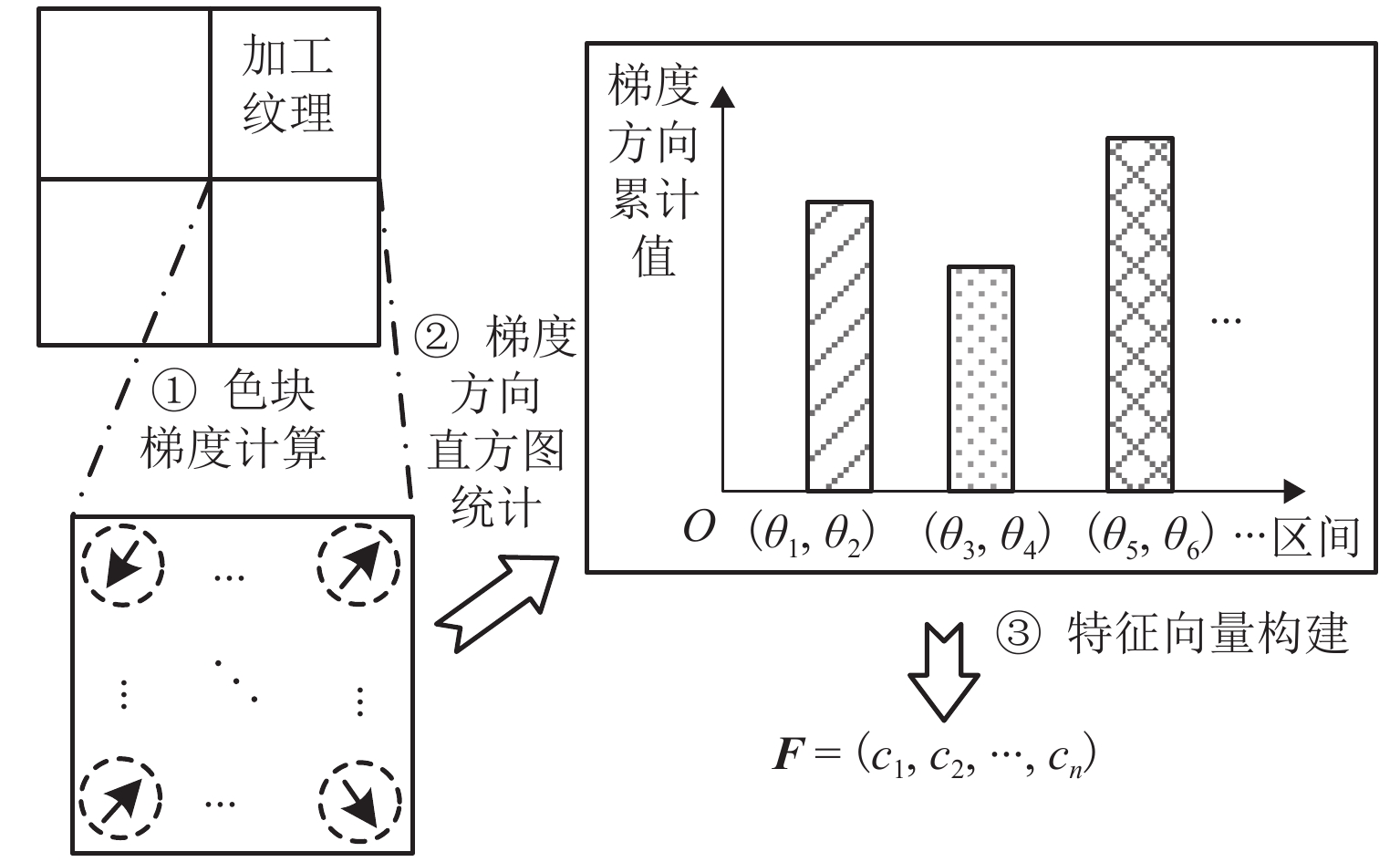
如图4所示,根据不同划分区间(θ1,θ2)、(θ3,θ4)、(θ5,θ6)、⋯⋯得到梯度方向信息,将局部图像信息的梯度统计编码为特征向量F. 通过基于特征的智能算法(支持向量机)方法,即可实现对目标区域的提取.
其中,色块梯度的方向描述了图像某一方向灰度阶变化快慢. 当图像局部色块存在边缘等纹理信息时,体现为较大某一方向上的梯度值较大. 对于图像长(M)、宽(N)方向上的梯度Gm和Gn分别为
[GmGn]=[∂f(m,n)∂m∂f(m,n)∂n]. (5) 则梯度幅值为√G2m+G2n,梯度方向θ=arctan(Gn/Gm).
对于灰度阶纹理图像矩阵,宽度方向梯度:∂f(•)/∂m=f(m+1,n)−f(m,n),长度方向梯度:∂f(•)/∂n=f(m,n+1)−f(m,n).
获得色块梯度信息后,通过直方图信息统计、特征向量构建,输入智能模型后即可实现对关键区域的识别.
2.2.2 考虑安装误差的在线图像校正
通过尺度不变特征变换(SIFT)算子识别不同批次采集图像的特征点,与标准安装距离下的测试进行比较,求解单应性矩阵,实现图像安装误差的校正.
根据尺度不变特征变换(SIFT)算子获取的标准图像与在线监测纹理图像之间的匹配点对(xi,x∗i)xi∈P1,x∗i∈P2,i=1,2,⋯,即可计算标准图像到在线监测图像之间的投影变换. 单应性矩阵即根据2D匹配点之间变换关系的估计,使得对于xi∈P1,x∗i∈P2投影空间内的点对匹配误差最小.
尺度归一化后的单应性矩阵通过点检测与匹配得到的多个已知点对,即可求解出单应性矩阵估计值. 图5为图像间的点对算法匹配的结果.
由于实际匹配过程难免出现误匹配,使得投影变换ft估计不准确. 采用随机采样一致性(RANSAC)方法,能够有效滤除一定误匹配点对,从而计算得到相对较优的单应性矩阵估计值.
2.3 基于代价敏感损失与可分离卷积的识别模型
铣削纹理提供了丰富的切削质量监测信息. 按照纹理特征提取特点,常用的工件加工表面纹理特征可分为一阶统计算子(如灰度阶直方图)、多阶统计学算子(如灰度共生矩阵算子[13]、Voronoi多边形[14])以及空间频域特征[15-16]. 这些纹理识别算子为粗糙度识别提供了大量可用特征[17-18]. 但这些特征却难以全面和完备表征多工况情形下的工件表面纹理特性.
深度学习方法借助其较强的高维非线性表征能力,能够较好解决这一问题. 基于代价敏感损失的深度卷积网络,进一步解决了存在类间不平衡现象的低质量数据的模型训练问题. 并且在准确性上,模型通过充分训练,与经典深度卷积模型在高质量数据训练情形下效果相当.
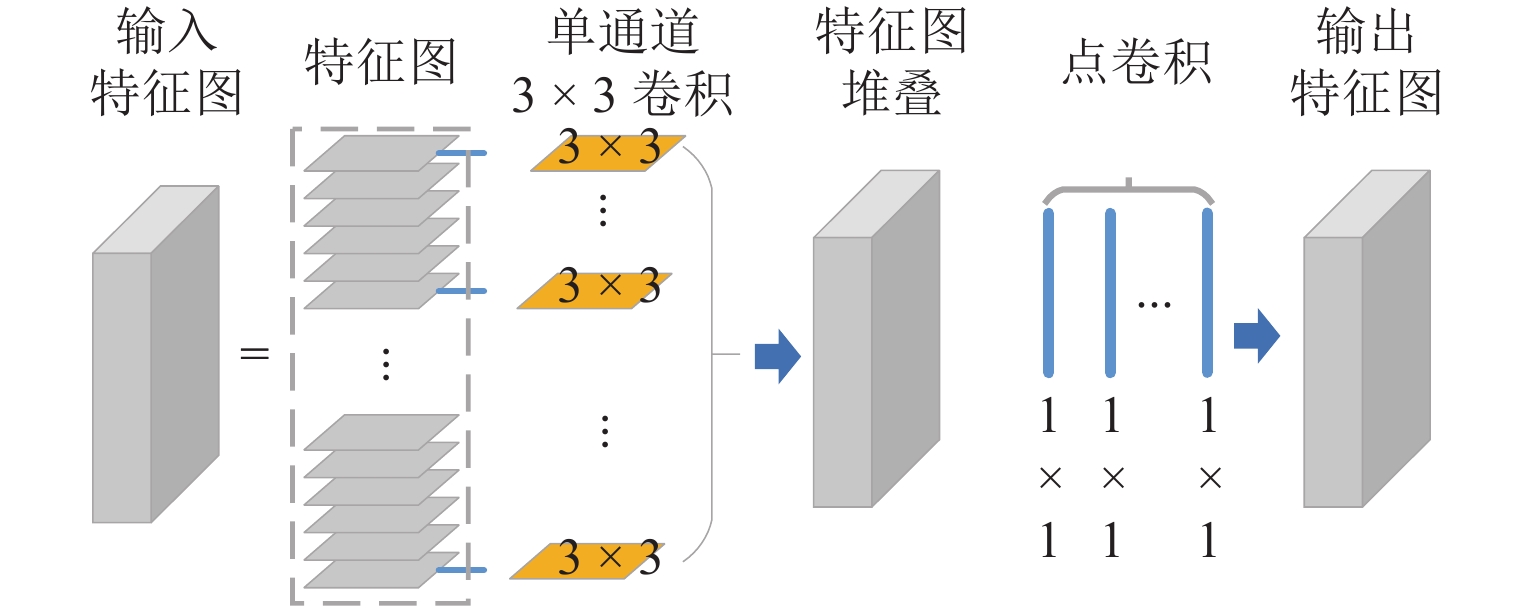
此外,通过在普通卷积网络模型中替换部分标准卷积为深度可分离卷积,可以提升模型的推理速度. 深度可分离卷积包括两个部分:逐点卷积和逐通道卷积. 在逐通道卷积中,单个卷积核只实现输入特征图(FM)的一个通道的卷积运算. 在完成逐通道卷积后,叠加得到中间特征层后再对其做点卷积运算,得到输出FM. 其具体计算步骤如下:
步骤1 逐通道卷积:采用一个尺寸为kc×kc×1的卷积核,对一个尺寸为Hi×Wi×c1的输入FM的每个通道进行卷积操作,得到尺寸为Hm×Wm×c1的中间特征图;
步骤2 逐点卷积:采用c2个尺寸为1×1×c1尺寸的卷积核对中间特征图作点卷积操作,得到尺寸为Ho×Wo×c2的输出FM.
对于单个深度可分离卷积,其通过逐通道卷积和点卷积两个分解操作得到了采用c2个尺寸为kc×kc×c1的卷积核做普通卷积的相同输出FM,而其乘法运算次数得到大幅度降低. 假设两种卷积方法的卷积核共移动了Nk×Nk次,以乘法运算量作为量化指标,则两种计算方法效率比值可表示为
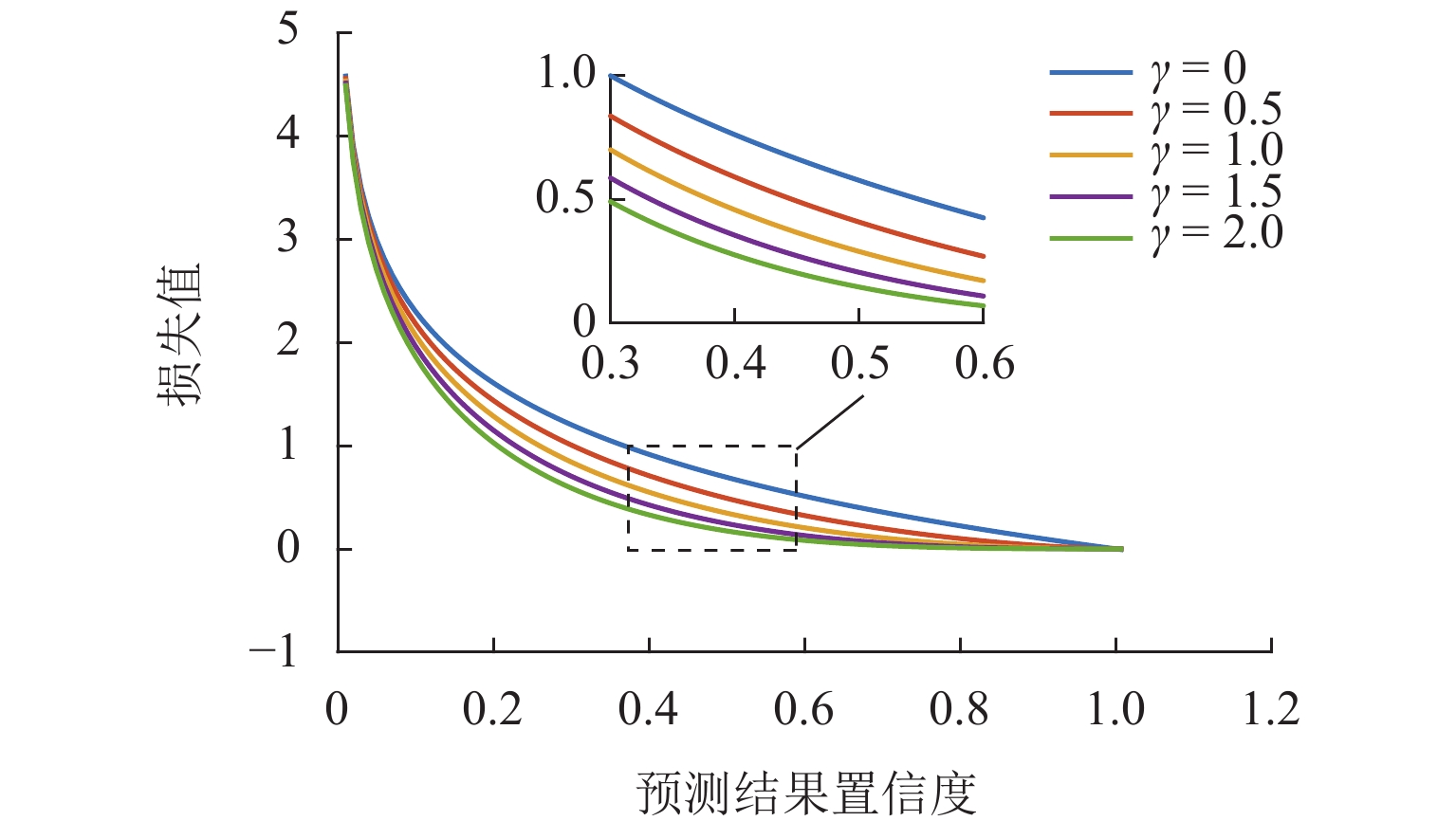
RDS−C=c1k2cNk2+c2c1N2kc2k2cc1Nk2=1c2+1k2c. (6) 图6可视化了多代价敏感损失不同调制因子(γ)下损失值与预测结果置信度之间的关系. 普通交叉熵损失函数难以训练样本数量少的类别中难区分的样本. 而代价敏感损失通过调整不同类权值,控制模型对各类的训练损失,能够较好解决这一问题.
3. 提出算法验证与分析
3.1 铣削纹理采集与监测实验
本实验所用的加工纹理数据包括粗糙度对比样块以及切削加工实验的工件数据. 实验所获得的工件不同倍率、粗糙度的加工纹理数据如图7所示. 铣削实验采集了整体式立铣刀(C1)和方肩立铣刀(C2)不同工况下的纹理图像,并采用触针式粗糙度仪进行了测量与图像标注,如图8所示.
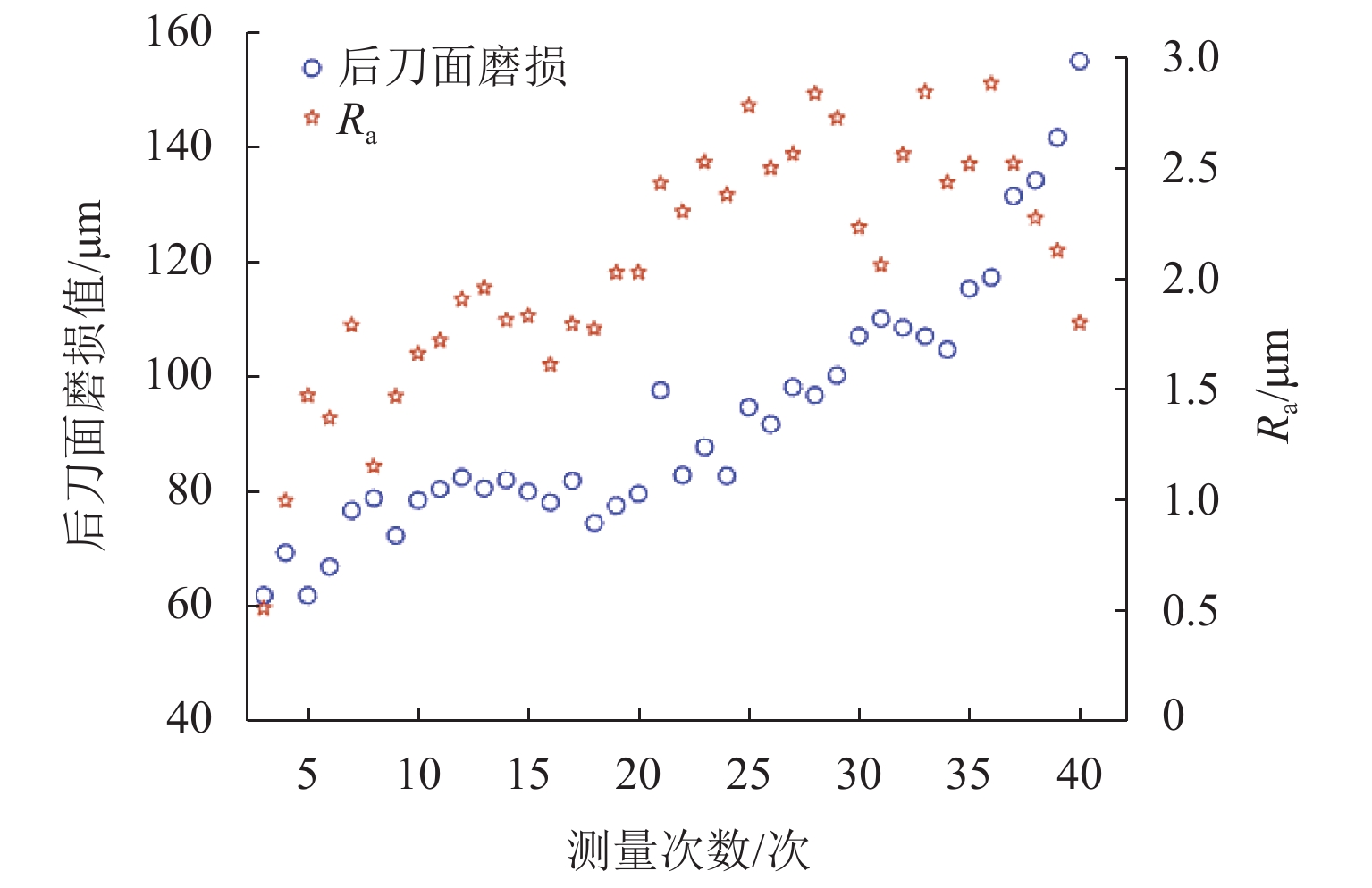
在刀具磨损退化监测实验中,采集了3种工况设置下,刀具进展性磨损下的工件表面粗糙度情况. 工况参数设置如表1所示,C1刀具的测量值如图9所示. 据工件生产加工的工艺的范围要求,将数据划分为符合要求的A类和不符合要求的B类. 划分方式为指标Ra在3次测量中两次小于或等于2的划分为A类,大于则为B类.
表 1 监测实验工况设置明细Table 1. Details of monitoring experiment工况 主轴转速/
(r·min−1)进给速度/
(mm·min−1)切削深度/mm 刀具
类型机床
型号1 3000 200 1 C1 KVC650 2 4000 200 1 C2 KVC650 3 2000 200 0.5 C2 VMC850 3.2 纹理在线采集与校正
图10为几种不同清晰度评价阈值设置方式得到的纹理数据采集比较. 在采集过程中光源持续照明时间为2 s. 镜头和相机以恒定速度完成对焦过程.
相比于Laplace函数计算方法,熵值和FFT-LPF均值方法调焦过程指标变化波动较少,有利于对焦过程的快速调整. 但熵值方法敏感性过低,难以收敛到最佳点. 因而,选用FFT-LPF均值方法折中敏感性与单调性的优势,适合在线监测.
3.3 纹理识别实验分析
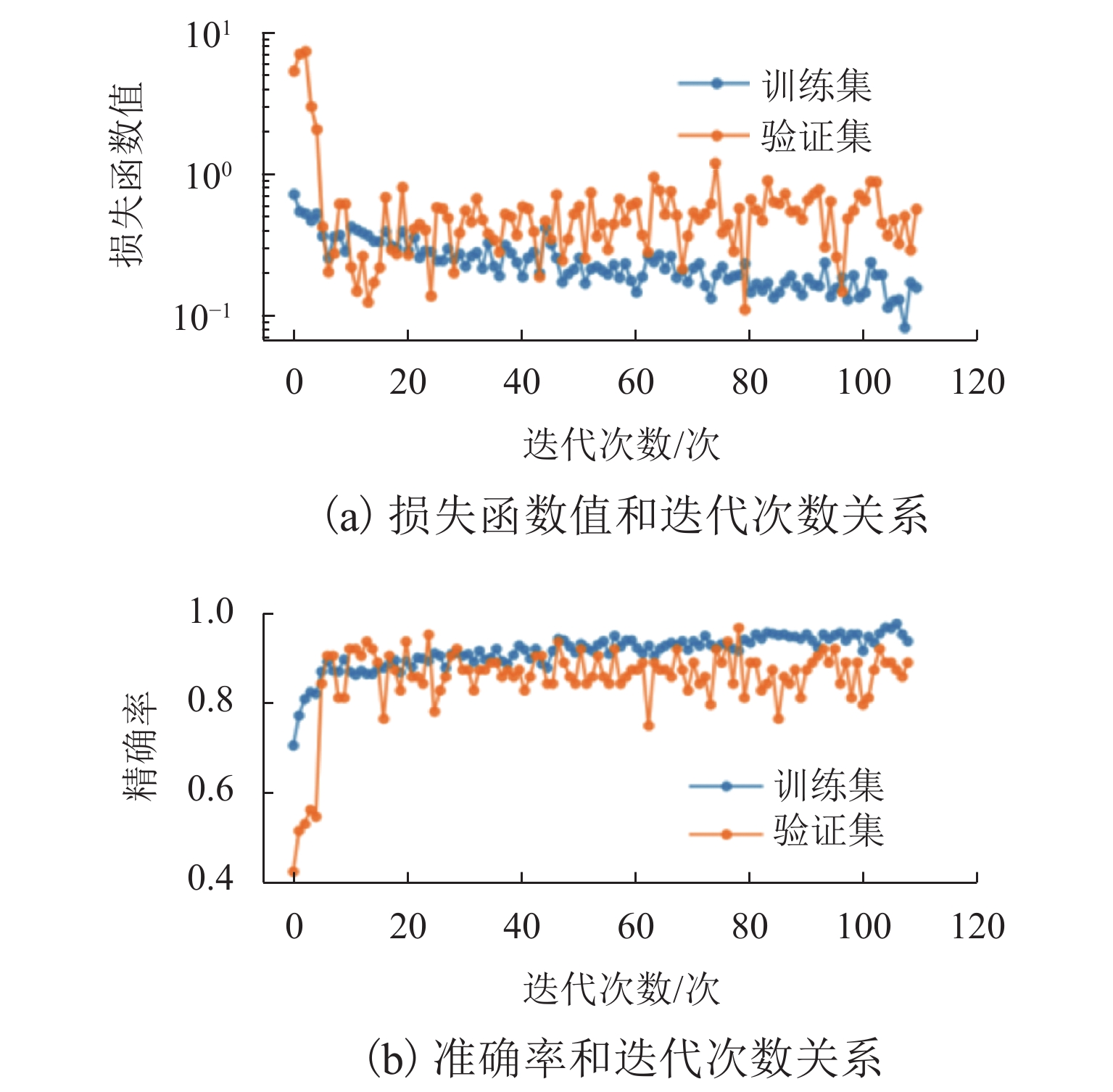
深度可分离的代价敏感深度卷积网络在训练过程的可视化如图11所示. 可以看到,在训练初期,模型训练集损失值下降过程存在轻微波动,收敛效果相比基于标准卷积的神经网络稍差. 但可以观察到,由于DP (dropout)层以及全局最大池化层的正则化项作用,损失逐渐趋于稳定.
表2所示为深度可分离卷积结构的消融实验结果, 表中,α为可分离卷积结构在模型中替代标准卷积结构的比率. 可以观察到,采用深度可分离卷积结构能够在模型精度损失较小情况下有效提升模型的推理速度.
表 2 可分离卷积结构的消融实验结果Table 2. Ablation experiment for separable convolution模型结构 推理速度/ms 准确率/% 普通卷积 33.7 77.6 可分离卷积(α=0.2) 25.2 75.7 可分离卷积 2(α=0.3) 25.1 72.1 如表3所示为采用普通交叉熵损失和代价敏感损失函数的模型在不同参数设置下的精准率(P)和召回率(R)的比较结果. 其中:工况1下的刀具失效模式为剧烈磨损,磨损各个阶段持续时间相对较为均匀(数据类间比率为1∶1.2);由于工况2与工况1的数据分布情况类似,不做附加比较;工况3下刀具失效模式为崩刃,各个阶段持续时间上具有差异,类间不均衡比率较大(数据类间比率为1∶3.1). 可以观察到代价敏感损失有效提升了模型存在显著类间不均衡情况(工况3)下的识别准确性.
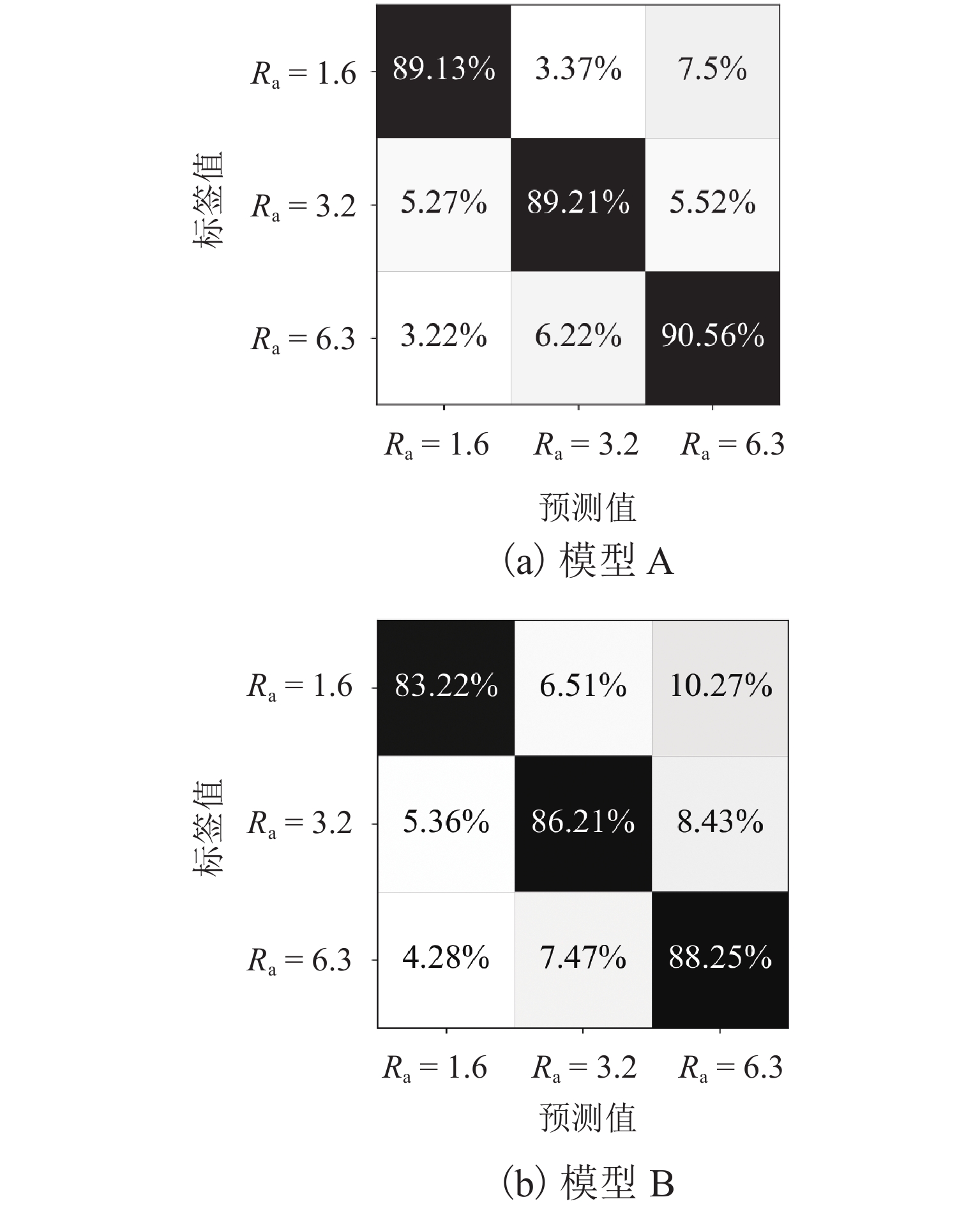
表 3 普通交叉熵损失和代价敏感损失函数测试结果Table 3. Test results of standard cross-entropy and cost-sensitive loss% 损失函数 精准率 召回率 工况 1 工况 3 工况 1 工况 3 普通交叉熵 79.1 77.5 80.2 78.3 代价敏感损失 78.7 79.9 80.6 80.3 图12所示的基于对比实验的混淆矩阵测试与可视化结果说明了深度卷积模型采用代价敏感损失函数的必要性. 模型A采用代价敏感损失函数,模型B采用普通交叉熵损失函数. 可以观察到,采用代价敏感损失的模型具有更小的类间差异.
为验证提出方法相比手工特征的优势,表4给出了最终模型与GLCM (gray level co-occurence matrix) + SVM (支持向量机类算法)方法的比较结果. GLCM + SVM和GLCM + RF (随机森林算法)方法采用4种典型的灰度共生矩阵纹理特征[19]分别作为支持向量机和随机森林模型的数据输入. 支持向量机方法测试了Linear核函数和RBF核函数. 并给出了P、R和识别速度的比较,计算如式(7)、(8).
表 4 模型性能评估测试Table 4. Model performance evaluation方法 P/% R/% 计算时间/(s·帧−1) GLCM + SVM (RBF) 73.7 65.3 0.208 GLCM + SVM (linear) 73.2 65.5 0.208 GLCM + RF 73.4 65.1 0.208 提出方法 81.6 86.2 0.150 P=Ntp/(Ntp+Nfp)×100%, (7) R=Ntp/(Ntp+Nfn)×100%, (8) 式中:Ntp为真阳性数量,Nfp为假阳性数量,Nfn为假阴性数量.
可以观察到:RF和SVM在计算时间上基本不具备差异性,这是由于算法主要耗时在纹理图像的灰度共生矩阵特征计算上. 其中,采用不同核函数的高斯核(RBF)、线性核(linear)以及RF决策部分的350张图像计算耗时分别为7.50、7.98、1.99 ms,相对于特征计算过程其耗时几乎可以忽略. 而提出模型在考虑模型加载时间的情况下,仍然能够达到0.150 s/帧的实时计算性能.
4. 结 论
本文针对加工表面粗糙度在机监测问题提出了基于代价敏感损失函数与轻量级卷积的深度学习模型的铣削加工粗糙度识别方法. 对于铣削纹理采集的自动校正、对焦算子进行了探究. 考虑已加工表面纹理信息的轻量级卷积网络能够适配在机监测的实时计算需求;而代价敏感损失函数能够有效提升轻量级模型在数据分布波动情形下的鲁棒性,缩短调试周期.
SIFT算子在铣削纹理图像匹配上具有较好的性能. 并通过消融实验,验证了提出模型所采用的代价敏感损失函数与可分离卷积网络结构方法用于在机监测的优越性. 算法在工件纹理图像数据上进行粗糙度识别实验,结果验证了提出方法的准确性和高效性,相比传统的手工特征智能方法,准确率和运算速度提升明显. 在收敛性上,相比于普通卷积神经网络,模型收敛较快,但过早收敛也容易陷入局部最佳点,或者出现过拟合现象等,该方面仍有待进一步研究.
-
表 1 DOE全阶乘方案设计
Table 1. DOE full factorial scheme design
方案 k1 k2 λ5 方案 1 1/30 1/6 1/4 方案 2 1/30 1/6 1/2 方案 3 1/30 1/4 1/4 方案 4 1/30 1/4 1/2 方案 5 1/10 1/6 1/4 方案 6 1/10 1/6 1/2 方案 7 1/10 1/4 1/4 方案 8 1/10 1/4 1/2 标准 1/20 1/5 1/3 -
[1] 高原,王平,陈嵘,等. 重载铁路固定辙叉区轮轨瞬态滚动接触行为分析[J]. 铁道学报,2020,42(6): 35-43.GAO Yuan, WANG Ping, CHEN Rong, et al. Analysis of 3D transient wheel-rail rolling contact behavior for fixed frog in heavy haul railways[J]. Journal of the China Railway Society, 2020, 42(6): 35-43. [2] 杨新文,张昭,孟玮,等. 道岔区固定辙叉心轨垂磨对轮轨动态接触的影响[J]. 同济大学学报(自然科学版),2020,48(11): 1595-1604.YANG Xinwen, ZHANG Zhao, MENG Wei, et al. Effect of vertical wear of unmovable frog nose rail on dynamical wheel-rail contact in turnout zone[J]. Journal of Tongji University (Natural Science), 2020, 48(11): 1595-1604. [3] MA Y W, MASHAL A A, MARKINE V L. Modelling and experimental validation of dynamic impact in 1: 9 railway crossing panel[J]. Tribology International, 2018, 118: 208-226. doi: 10.1016/j.triboint.2017.09.036 [4] WIEDORN J, DAVES W, OSSBERGER U, et al. Simplified explicit finite element model for the impact of a wheel on a crossing-Validation and parameter study[J]. Tribology International, 2017, 111: 254-264. doi: 10.1016/j.triboint.2017.03.023 [5] SKRYPNYK R, NIELSEN J C O, EKH M, et al. Metamodelling of wheel-rail normal contact in railway crossings with elasto-plastic material behaviour[J]. Engineering With Computers, 2019, 35(1): 139-155. doi: 10.1007/s00366-018-0589-3 [6] 于淼,张军,鹿广清,等. 重载货车作用下固定辙叉心轨磨耗分析[J]. 铁道学报,2014,36(7): 30-35.YU Miao, ZHANG Jun, LU Guangqing, et al. Analysis on wear of unmovable frog nose rail under the action of heavy-haul freight car[J]. Journal of the China Railway Society, 2014, 36(7): 30-35. [7] 王树国,葛晶,司道林,等. 固定辙叉查照间隔及心轨加宽研究[J]. 中国铁道科学,2014,35(1): 7-12.WANG Shuguo, GE Jing, SI Daolin, et al. Study on guard check gauge of fixed frog and design on widening nose rail[J]. China Railway Science, 2014, 35(1): 7-12. [8] 徐井芒,王平. 基于轮轨廓型的固定辙叉优化设计方法[J]. 中国铁道科学,2014,35(2): 1-6.XU Jingmang, WANG Ping. Optimization design method for rigid frog based on wheel/rail profile type[J]. China Railway Science, 2014, 35(2): 1-6. [9] 徐井芒,郑兆光,赖军,等. 轨道参数对高速道岔轮轨接触行为的影响[J]. 西南交通大学学报,2022,57(5): 990-999.XU Jingmang, ZHENG Zhaoguang, LAI Jun, et al. Influence of track parameters on wheel/rail contact behavior of high-speed turnout[J]. Journal of Southwest Jiaotong University, 2022, 57(5): 990-999. [10] 曹洋,王平. 固定辙叉心轨轨顶降低值优化[J]. 西南交通大学学报,2015,50(6): 1067-1073.CAO Yang, WANG Ping. Optimization of nose depth for rigid frog[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1067-1073. [11] 沈钢,汪徐江. 固定辙叉区心轨轨顶降低值优化设计方法[J]. 同济大学学报(自然科学版),2020,48(11): 1605-1611.SHEN Gang, WANG Xujiang. An optimization method for height of nose rail at turnout crossing[J]. Journal of Tongji University (Natural Science), 2020, 48(11): 1605-1611. [12] 张鹏飞,朱旭东,雷晓燕. 提速道岔辙叉翼轨的加高值方案优化[J]. 西南交通大学学报,2021,56(3): 602-610.ZHANG Pengfei, ZHU Xudong, LEI Xiaoyan. Optimization of wing rail lifting value for rigid frog of speed-up turnout[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 602-610. [13] WAN C, MARKINE V L, SHEVTSOV I Y. Improvement of vehicle−turnout interaction by optimising the shape of crossing nose[J]. Vehicle System Dynamics, 2014, 52(11): 1517-1540. doi: 10.1080/00423114.2014.944870 [14] WAN C, MARKINE V L, SHEVTSOV I. Optimisation of the elastic track properties of turnout crossings[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail and Rapid Transit, 2016, 230(2): 360-373. doi: 10.1177/0954409714542478 [15] 铁道部第三设计院. 道岔设计手册[M]. 北京: 人民铁道出版社, 1975: 413-503. [16] 韩江,江本赤,夏链,等. 基于轮廓关键点的B样条曲线拟合算法[J]. 应用数学和力学,2015,36(4): 423-431.HAN Jiang, JIANG Benchi, XIA Lian, et al. A B-spline curve fitting algorithm based on contour key points[J]. Applied Mathematics and Mechanics, 2015, 36(4): 423-431. [17] YANG Y, QIU W S, ZENG W, et al. A prediction method of rail grinding profile using non-uniform rational B-spline curves and Kriging model[J]. Journal of Central South University, 2018, 25(1): 230-240. doi: 10.1007/s11771-018-3732-9 [18] 温士明. 地铁线路小半径曲线钢轨打磨廓形研究[D]. 成都: 西南交通大学, 2018: 11-25. [19] 刘建桥. 地铁曲线轨道钢轨廓型优化研究[D]. 成都: 西南交通大学, 2019: 24-29. [20] 唐彦玲,吴磊,董勇,等. 重载铁路曲线钢轨廓形多目标优化设计[J]. 机械,2020,47(12): 1-9.TANG Yanling, WU Lei, DONG Yong, et al. Multi-objective optimization design of rail profiles on curve tracks of heavy haul railway[J]. Machinery, 2020, 47(12): 1-9. [21] 王亮,向伟彬,刘宏达,等. 小半径曲线钢轨非对称打磨目标型面优化[J]. 机械科学与技术,2021,40(6): 949-954.WANG Liang, XIANG Weibin, LIU Hongda, et al. Target profile optimization of asymmetrical grinding for rail with sharp-radius curve[J]. Mechanical Science and Technology for Aerospace Engineering, 2021, 40(6): 949-954. [22] 林凤涛,吴涛,杨洋,等. 高速铁路辙叉区钢轨打磨廓形设计方法[J]. 交通运输工程学报,2021,21(6): 124-135.LIN Fengtao, WU Tao, YANG Yang, et al. Design method of rail grinding profile in frog area of high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2021, 21(6): 124-135. [23] 史振帅. 基于NURBS曲面拟合的道岔打磨廓形研究[D]. 南昌: 华东交通大学, 2021: 22-27. [24] 陈雨,安博洋,潘自立,等. 考虑尖轨变截面廓形的轮轨接触与磨耗分析[J]. 西南交通大学学报,2022,57(6): 1250-1258.CHEN Yu, AN Boyang, PAN Zili, et al. Analysis of wheel-rail contact and wear considering variable cross-sections of switch rail[J]. Journal of Southwest Jiaotong University, 2022, 57(6): 1250-1258. [25] 王璞,王树国,赵振华,等. 基于改善轮轨共形度的60 kg/m钢轨廓形优化[J]. 西南交通大学学报,2022,57(6): 1233-1238.WANG Pu, WANG Shuguo, ZHAO Zhenhua, et al. Optimization of 60 kg/m rail profile based on improving wheel-rail conformal degree[J]. Journal of Southwest Jiaotong University, 2022, 57(6): 1233-1238. -






 下载:
下载:











 下载:
下载: