Fatigue Characteristic of High-Frequency Vibration for CRTS Ⅱ Track Slab
-
摘要:
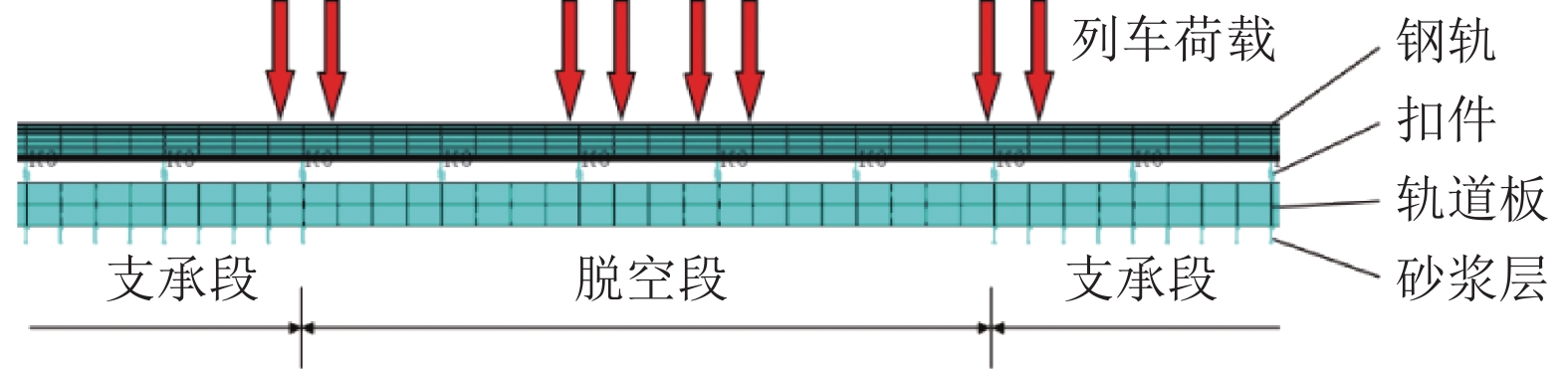
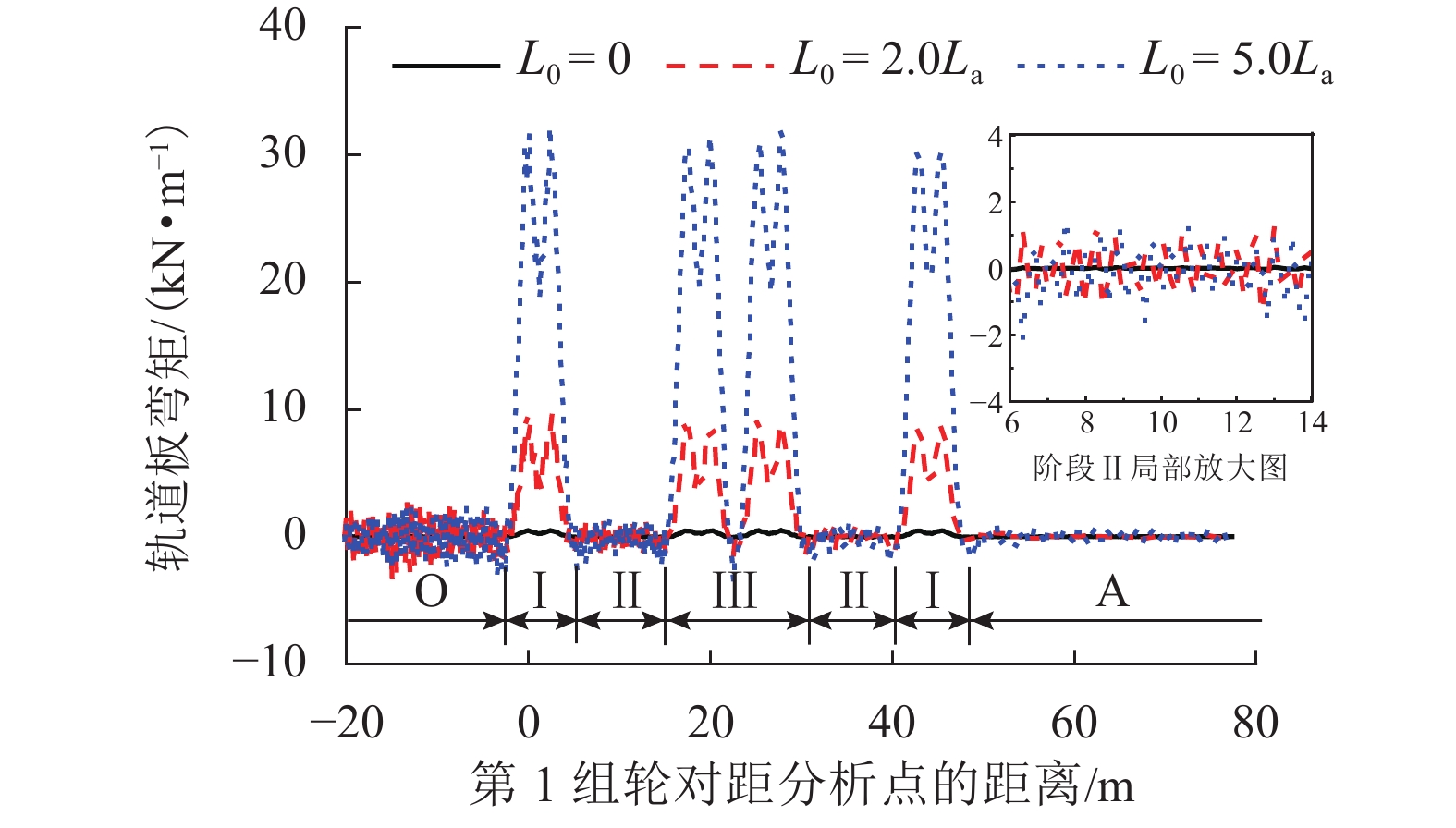
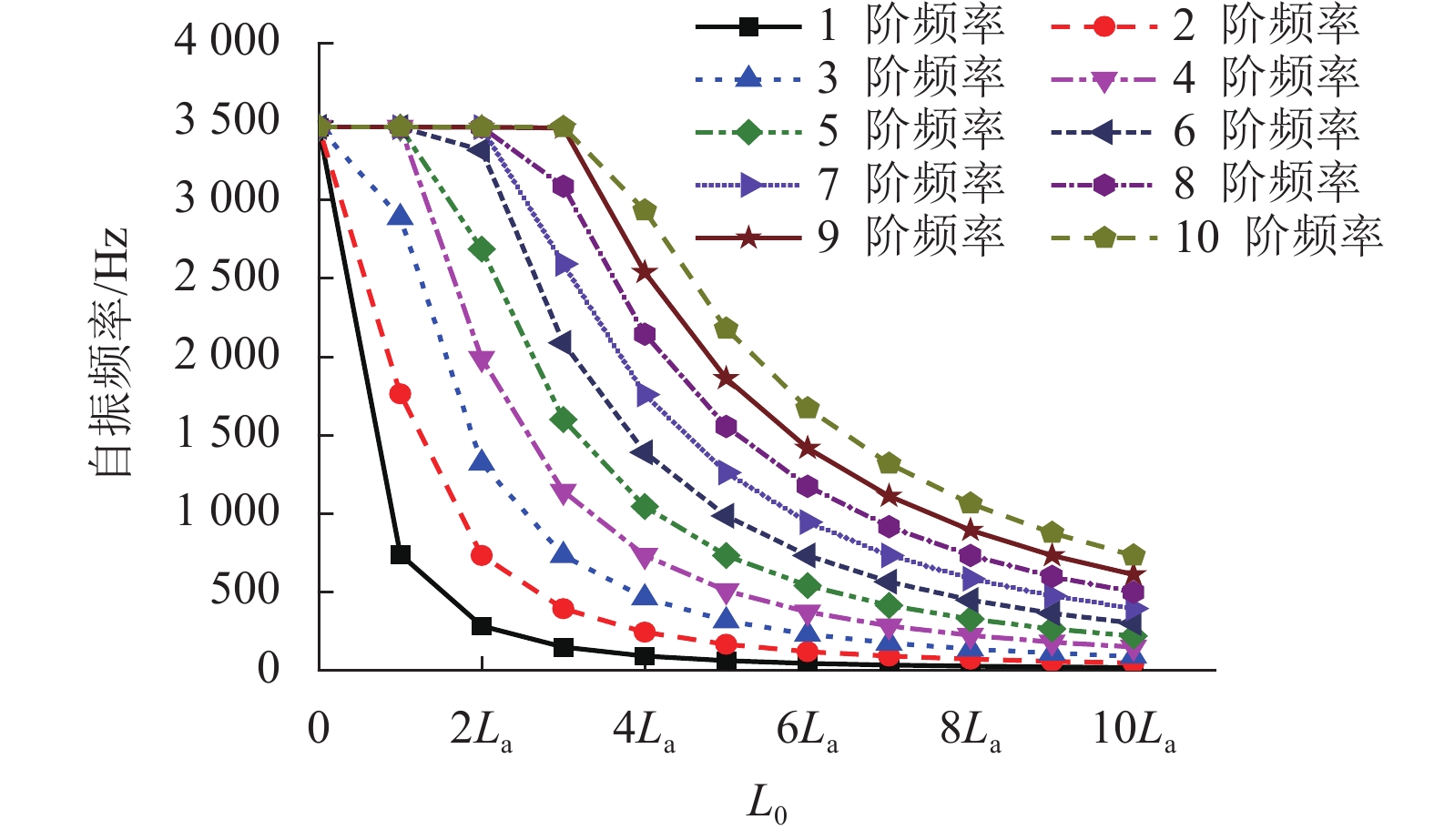
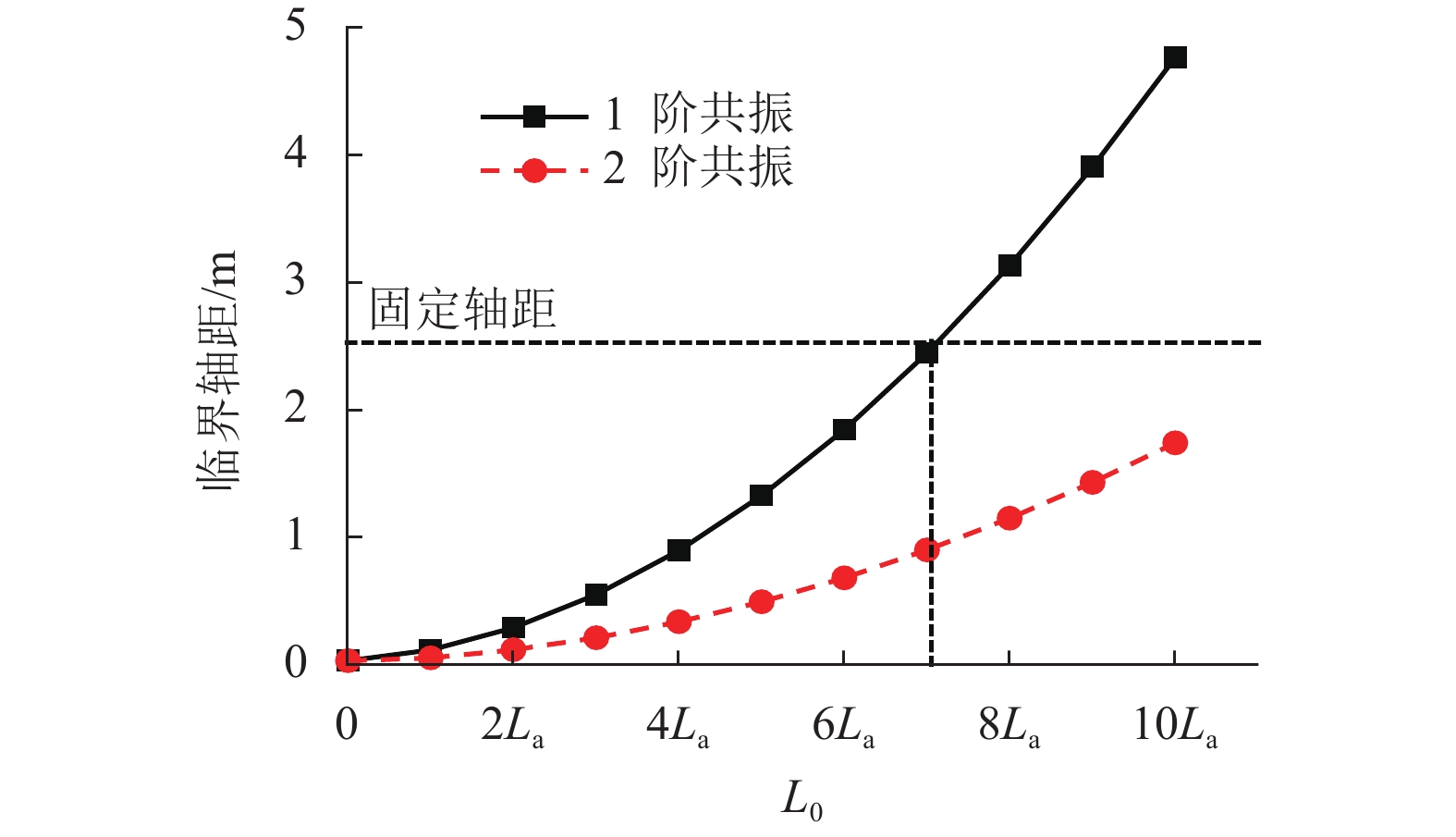
列车轮载作用会引发轨道板的高频自振效应. 为分析高频荷载下CRTS Ⅱ型轨道板的疲劳特性以及板体自振效应对疲劳寿命的影响程度，基于现有的疲劳损伤准则，探究轮对作用间隙阶段轨道板自振影响下的疲劳特性. 对脱空长度影响下轨道板的疲劳寿命进行预测，并与仅考虑荷载作用次数的结果进行对比. 结果表明：轨道结构完好时，列车轮载引发轨道板伤损的可能性较小；若列车行车速度为360 km/h，列车轮载在引发轨道板共振前即发生板底开裂；轨道结构完好时，列车轮载引发的板体自振效应对轨道板疲劳损伤影响程度最大，此时列车轮载对轨道板产生约1.8倍的疲劳荷载当量；当轨道板脱空长度大于2.0倍枕距后，可忽略板体自振对疲劳损伤的影响；轨道板的脱空长度大于3.2倍枕距后，现场无砟轨道难以维持60 a的使用寿命.
-
关键词:
- 无砟轨道 /
- CRTS Ⅱ型轨道板 /
- 疲劳特性 /
- 板体自振 /
- 局部脱空
Abstract:The effect of the wheel load could cause the self-vibration effect of high frequency for the track slab. To analyze the fatigue characteristic of CRTS Ⅱ track slab under high-frequency load and the effect of the self-vibration of the track slab on its fatigue life, the fatigue characteristics of the track slab under the influence of this self-vibration during the interval in the wheelset was explored on the basis of existing fatigue damage criteria. The fatigue life of the track slab was predicted with reference to the effect of the de-bonding length, and the results obtained were compared with the results obtained when only the number of load actions was considered. Results show that, the possibility of damage to the track slab caused by the train wheel load is reduced when the track structure is intact. The bottom of the track slab would crack before resonance triggering occurred if the train speed was 360 km/h. When the track structure is intact, the self-vibration effect in the track slab caused by the wheel load has its greatest impact on the fatigue damage to the track slab, and the wheel load produces approximately 1.8 times the equivalent fatigue load to the track slab. The effect of the self-vibration effect in the track slab on the fatigue damage could be ignored when the slab de-bonding length is more than twice the distance between sleepers. When de-bonding length of the track slab is more than 3.2 times the distance between sleepers, it becomes difficult for the ballastless track on-site to maintain its expected 60-year service life.
-
行为决策是智能网联汽车实现自动控制的重要组成[1-6]，也是该领域的研究热点. 车辆通过信号交叉口时，其行为会受到信号灯和周围车辆的影响，如果不能准确预判通行条件，得到的决策结果会导致通行效率低、闯红灯甚至引发交通事故.
目前，智能网联汽车领域有关车辆通过信号交叉口的研究，主要关注简单交通环境下的辅助驾驶速度规划，研究目的大多为降低排放和燃油消耗[7-12]，或者提高通行效率[13-16]，涉及到的车辆行为是一些基本规则. 在行为决策层面，现有的智能网联汽车将一般道路场景的决策方法应用到信号交叉口，也有少部分学者专门研究在信号交叉口这种特殊复杂场景下的行为决策，只考虑信号灯影响时，Park等[17]根据信号、车速、交叉口大小和车辆与停车线的距离构建了简单的停止/通过决策算法；Zhou等[18]提出了基于强化学习的跟驰模型来获取合适的驾驶行为；Liu等[19]基于行驶规则，在各种转向条件下构建了不同信号灯色时的决策流程图；苏冲等[20]将动作序列划分为不同的行为状态，建立了各种工况下的状态迁移图. 考虑周围车辆影响时，学者们主要解决各方向车辆之间的冲突，在机器学习、运筹优化等方面进行探索，Gadepally等[21]利用隐马尔可夫模型从连续的滤波中观测中估计驾驶员行为，为行为决策提供有效依据；Beaucorps等[22]根据人类驾驶员的录音数据建立有其他车辆存在场景下的无信号交叉口和环形路决策算法；杜明博[23]提出基于有限状态机的驾驶场景转换模型，构建基于ID3决策树的驾驶行为决策模型；de Campos等[24]量化每辆车为避免潜在碰撞而配置的自由度，用成本函数和局部约束条件解决车辆之间的协调问题；Alonso等[25]根据靠近交叉口车辆的状态信息构建车辆优先通行图结构，以此来解决不同方向车辆之间的冲突；宋威龙等[26]设计了基于模糊逻辑的驾驶员类型判别模型，根据其他车辆的行驶意图和驾驶员激进程度建立了决策规则；Makarem等[27]提出了一种分散式模型预测控制方法，对具有预定路径的车辆引入线性二次最优控制器，加入线性约束来避免碰撞.
从以上回顾可以发现，无论是否在车联网环境下，现有智能车辆在信号交叉口的控制研究主要集中在速度控制层面，在行为决策层面只有很少的研究，鲜有对通行决策策略的研究，考虑的行驶环境也非常单一，没有把周围车辆的干扰纳入考虑范围，特别是前车对智能网联汽车的行驶空间有显著影响[28-29]. 如果不考虑前车状态，只考虑自身状态和信号灯，会使车辆在判断通过/不通过问题上有局限性，容易产生两难区. 鉴于此，本文关注的是车联网环境下智能网联汽车在信号交叉口的行为决策问题，为了让车辆准确控制运动，从微观交通流的本质出发，基于信号时间信息，利用Gipps跟驰理论预测前方车辆的状态和判断自身通过条件，同时加入换道行为来寻求更优的决策结果，从而构建一种智能网联汽车直行通过信号交叉口的决策模型.
1. 信号交叉口行为决策模型
1.1 信号交叉口行为决策流程
当前车路协同技术还未成熟，本文研究的交通环境是非协同控制的车联网环境，通过交叉口的智能网联主车辆SV （subject vehicle）只能通过车联网获取信号信息和其他车辆的位置、速度等，并根据信号灯色和时间、前车行驶意图做出相应的决策. 考虑一般情况，将信号灯情况分为绿灯（倒计时未出现）、黄灯、红灯、绿灯倒计时，只要车辆在可识别到信号灯范围内，就启动决策；当识别到的是红灯或黄灯，则做出停车的决策；当识别到的是绿灯（倒计时未出现），则继续按照跟驰状态行驶；当识别到的是绿灯倒计时，则识别自身在当前车道是领头车还是跟随车，并结合前车行驶意图判断能否在绿灯结束前通过停止线，若不能通过，则根据换道时间模型判断换道后能否通过，再做出相应的决策. 车辆的行为决策流程如图1所示.
1.2 前方车辆状态预测模型
预测前方车辆未来的状态，本质就是判断车辆是否能够在绿灯倒计时间内通过停止线，这取决于车辆在倒计时间内走过的距离和倒计时间结束时的位置. 在交叉口，车辆为了追求高效行驶，都保持在跟驰状态，本文采用Gipps跟驰模型[30]来表征前后车行驶状态的相互影响.
1.2.1 Gipps跟驰模型
Gipps跟驰模型属于安全距离模型，其基本思想是寻找一个特定的跟驰距离，当前车紧急刹车时，如果后车与前车的跟驰距离小于该特定距离，就有可能发生碰撞. 在交叉口，根据为避免与其前车（车辆n-1）发生追尾所需保证的安全距离，可以得到跟驰车（车辆n）行驶的安全速度，如式（1）.
vn(t+T)=−bnT/2+{[b2n(T/2)2+bn[2(xn−1(t)−sn−1−xn(t))−vn(t)T+v2n−1(t)/bn−1]}1/2, (1) 式中：T为车辆n的反应时间；bn为车辆n的最大制动减速度；sn车辆n的效用尺寸，其值等于车身长度；vn(t)为车辆n的速度；xn(t)为车辆n沿行驶方向的位置；t为时间.
Gipps跟驰模型根据运动学推导，具有明确的物理意义，能较好地体现出行驶速度因素在跟驰过程中的影响，可以真实地模拟车辆之间的跟随行为，在交通仿真中有着广泛应用，如英国交通部的SISTM模型、美国的CARSIM模型等，是交通流理论的核心内容之一.
1.2.2 车辆状态预测
以反应时间作为车辆决策间隔，领头车是位置最靠近交叉口停止线的车辆，将领头车编号为PV1，其行为不受其他车辆的影响. 通过Gipps跟驰模型，可以计算出跟驰车辆在反应时间后的速度，再结合初始的速度和位置可以得到车辆在反应时间后的位置. 求得领头车经过每个反应时间后的速度和位置后，则可以通过递推方法依次求得其后的所有跟随车辆在每个反应时间后的速度和位置.
按照与交叉口距离从小到大的顺序对所有车辆进行编号，依次为PV1, PV2, ···, PVn, 用vP,1, vP,2, ···, vP,n分别表示其速度，xP,1, xP,2, ···, xP,n分别表示其沿行驶方向的位置. 设所有车辆在初始时刻t0的位置为xP,1(t0), xP,2(t0), ···, xP, n(t0)，速度为vP,1(t0), vP,2(t0), ···, vP,n(t0)，从初始时刻开始的第k （k = 1, 2, ···）个反应时间后的车辆状态如下：
1） 当n = 1时，
{xP,1(t0+kT)=xP,1(t0)+kvP,1(t0)T,vP,1(t0+kT)=vP,1(t0); (2) 2） 当n > 1时，
{vP,n(t0+kT)=−bnT/2+{[b2n(T/2)2+bn[2(xP,n−1(t0+(k−1)T)−sn−1−xP,n(t0+(k−1)T))−vP,n(t0+(k−1)T)T+v2P,n−1(t0+(k−1)T)/bn−1]}1/2,xP,n(t0+kT)=xP,n(t0+(k−1)T)+(vP,n(t0+kT)+vP,n(t0+(k−1)T))T/2. (3) 1.3 不换道通过交叉口条件
车辆SV通过车联网获取到信号灯信息后，首先需要判断能否在当前车道通过交叉口，根据其前方是否有车辆，可将SV分为领头车和跟随车.
1.3.1 SV为领头车
当SV为领头车，其行驶行为不受其他车辆的影响，设SV在当前位置为xP,S(t0)，速度为vP,S(t0)，可以计算出SV先匀加速行驶，后匀速行驶到绿灯结束时刻的位置：
xP,S(t0+tg(t0))=xP,S(t0)+ v2lim−v2P,S(t0)2amax+ (tg(t0)−vlim−vP,S(t0)amax)vlim, (4) 式中：等号右边第2项为车辆SV匀加速行驶的距离；第3项为按最大限速值匀速行驶的距离；tg(t0)为当前绿灯剩余时长；vlim为道路最大限速值；amax为车辆的最大舒适加速度.
设xstop为停止线位置，可得到车辆SV在绿灯结束时刻与停止线的位置差为
ΔxP,S=xstop−xP,S(t0+tg(t0)). (5) 1.3.2 SV为跟随车
当SV为跟随车，其行为决策结果受到前方车辆行为的影响，假设SV在未来按照Gipps跟驰模型行驶，那么可以用该模型描述其行驶状态并进行预测. 车辆SV每隔一个反应时间进行一次决策，可以得到车辆走完剩余绿灯时间需要进行h次决策，如式（6）.
h=tg(t0)/tg(t0)TT. (6) 根据式(2)和式(3)，可以得到当前车道中车辆SV之前的每辆车在绿灯信号结束时刻的位置为xP,n(t0 + hT)，车辆SV在绿灯信号结束时刻的位置为xP,S(t0 + hT)，如图2 （图中x、y分别为车辆的纵向、横向位置），根据车辆位置和交叉口停止线位置，可以判断每辆车是否能够在绿灯结束时通过停止线.
ΔxP,n=xstop−xP,n(t0+hT). (7) 式中：ΔxP,n为第n辆车在绿灯结束时刻与停止线的位置差.
SV在绿灯结束时刻与停止线的位置差
$\Delta {x_{{\rm{P,S}}}}$ 也可由式（7）计算得出. 根据SV为领头车和跟随车的两种情况分别判断，若$\Delta {x_{{\rm{P,S}}}} > 0$ ，则SV在绿灯结束时刻不能通过停止线；如果$\Delta {x_{{\rm{P,S}}}} \leqslant 0$ ，则SV在绿灯结束时刻能够通过停止线.1.4 换道通过交叉口条件
1.4.1 SV换道时间模型
当SV不能在当前车道通过时，可以寻求相邻车道的换道通行方案，在对换道策略进行评估时，最主要的考虑因素就是换道带来的时间损失，故以下分析换道过程的时间计算方法，SV换道的运动过程如图3所示.
参考Yang等[31]的研究，将车辆的换道轨迹描述为多项式曲线，假设车辆换道开始时的横纵向位置均为0、导航角处于水平状态、车辆在换道结束时的纵横向位置分别为xf和yf，以此来计算SV换道执行时间. SV换道执行时间为换道行驶的路程与平均速度的比值，如式（8）.
tS=lˉv=2∫xf0√1+y12dxv0+vf, (8) 式中：
y1=6yfx2fx−6yfx3fx2, (9) xf=5√4A/B, (10) {A=ω(6v2fyf/amax,S)2，B=(1−ω)/xmax,f， (11) vf=m∑i=1vL,i/m， (12) 式中：
${\bar v}$ 为SV在换道过程中的平均速度，取值为初始速度v0与目标速度vf的平均值；vf为SV在换道结束时的目标速度，取值为目标车道前面车辆的初始速度，若目标车道无前车，则取值为初始速度提升15%后的值；l为换道行驶的路程；amax,S为车辆在所有不同换道轨迹下产生的最大法向加速度；xmax,f为车辆在所有换道轨迹下完成换道需要的最大纵向位移；vL,i为目标车道前面的第i辆车在当前的速度；m为目标车道的前车数量；ω为协调经济性和舒适性的权重.1.4.2 目标车道前车通过条件判断
若目标车道的前车数量太多，会导致：1） SV没有换道空间，即车辆不能从当前位置开始换道；2） SV换道后通过停止线的概率减小. 所以，本文认为如果目标车道上远离交叉口的最后一辆车位置在与SV平行的道路横向截面之后，则目标车道前车不能通过停止线；如果该车在与SV平行的道路横向截面之前，则目标车道有前车；如果目标车道上与SV平行的的道路横向截面之前没有车辆，则目标车道无前车.
在换道过程中，目标车道前车保持为跟驰行驶状态，对其进行编号，依次为LV1, LV2, ···, LVm. 与前述计算当前车道的车辆状态相同的思路，可以得到目标车道前面的车辆在绿灯结束时刻与停止线的位置差为
ΔxL,m=xstop−xL,m(t0+hT). (13) 式中：xL,m(t0 + hT)为目标车道前面的车辆LVm在绿灯结束时刻的位置.
1.4.3 SV换道后通过条件判断
有了换道时间后，可以计算出换道过程经历的反应时间个数为h1=tS/T，从而得到SV在换道结束时刻的速度和位置如式（14）.
{vL,S(t0+h1T)=vf,xL,S(t0+h1T)=xP,S(t0)+xf. (14) SV换道结束后，后续阶段的通过条件判断和前述在当前车道的方法类似，从SV换道结束后的状态开始计算，如果目标车道没有前车，SV可以加速行驶，可以根据式（4）计算其在绿灯结束时刻的位置；如果目标车道有前车，SV只能跟随前车行驶，可以根据式（3）计算其在绿灯结束时刻的位置，最后得到SV在绿灯结束时刻与停止线的位置差ΔxL,S. 如果
$\Delta {x_{{\rm{L,S}}}} > 0$ ，则SV换道后在绿灯结束时刻不能通过停止线；如果$\Delta {x_{{\rm{L,S}}}} \leqslant 0$ ，则SV换道后在绿灯结束时刻可以通过停止线.2. 仿真分析
2.1 仿真方案
给定所有车辆当前的状态数据（车辆位置、速度）、车辆固定属性（最大舒适加速度、最大制动减速度）、道路属性（最大限速值、车道宽度、交叉口停止线位置、绿灯倒计时间），可以模拟出SV在剩余绿灯时间内的行驶过程. 本文考虑一般情况，场景设置为SV前方有车辆，相邻车道前方有车辆，通过配置车辆位置和当前绿灯剩余时间参数来构建不同的交通环境，以此来评估模型的决策能力，分析车辆的行为决策过程和速度变化.
2.2 模型评价
搭建不同的场景来评价模型的决策能力，设置两个不同绿灯倒计时间10.0 s和14.0 s的场景，分别为场景1和场景2，在两个场景中道路限速值为60 km/h，停车线位置为300 m，最大舒适加速度为2 m/s2，最大制动减速度为3 m/s2. 在其他设置都相同的条件下，使用基于规则的现有决策模型和本文决策模型分别仿真车辆的运行，得到车辆行驶过程中的决策结果，两个场景如图4、图5所示.
在场景1下，由对比可知：在车辆靠近信号交叉口的前阶段，现有模型和本文模型都做出减速停车的决策，说明本文模型具有和现有模型一致的基本决策能力，在后阶段越来越靠近停止线时，在现有模型做出减速停车决策的情况下，本文模型做出直行跟驰的决策，即前者决策出不能通过交叉口，而后者预测出可以通过，说明本文模型能捕获到微小的交通状态变化，有使得决策结果更加精确的优势，从而提高车辆的通过效率. 在场景2中，增加了绿灯倒计时间长度，车辆使用本文模型的决策结果就一直为直行跟驰，这也符合绿灯时间越长，车辆通过交叉口概率越大的交通规律，说明本文模型能应用到实际的车辆运行控制中.
2.3 行为决策影响因素分析
2.3.1 当前绿灯剩余时间
将当前绿灯剩余时间作为变化量，分别以20.0，19.0，···，1.0 s的剩余时间来构建场景，场景的主要参数设置见表1.
表 1 不同绿灯剩余时间的场景输入Table 1. Scene input information for different green light countdown time输入信息 数值 输入信息 数值 停止线位置/m 300 SV当前位置/m 171 道路最大限速值/（km•h−1） 60 SV当前速度/（km•h−1） 29 最大舒适加速度/（m•s−2） 2 当前车道头车位置/m 200 最大制动减速度/（m•s−2） 3 相邻车道头车位置/m 290 选取3个典型决策过程和速度变化结果如图6所示，当前绿灯剩余时间较短时，SV既不能在当前车道通过也不能换道，每次决策只能是停车；当前绿灯剩余时间在10.0 s和13.0 s之间时，SV在前阶段计算出不能在当前车道通过停止线，故做出了换道决策，换道之后的阶段做出了直行加速决策；当前绿灯剩余时间较长时，SV就一直做出直行跟驰决策. 综合以上分析，绿灯剩余时间每增加一个单位，SV在当前绿灯周期通过交叉口的概率可提升20%，车辆面对不同的当前绿灯剩余时间时做出的决策有较大差异.
图 6 不同绿灯剩余时间的决策过程和速度变化Figure 6. Decision-making process and speed change of different remaining time of green light2.3.2 当前车道车辆位置
将当前车道车辆位置作为变化量，设置当前车道前车和车辆SV的不同位置来构建场景，场景的主要参数设置见表2.
选取3个典型决策过程和速度变化结果如图7所示，当前车道车辆与停止线的距离大于220 m时，SV不能在绿灯倒计时间内通过，故一直做出减速停车的决策；当头车位置在160～220 m时，SV在前阶段有换道的决策，换道之后的阶段做出了直行加速的决策；当前车道车辆与停止线的距离小于160 m时，SV可以在当前车道通过停止线，故一直做出直行跟驰的决策. 由此可知，不同的前车和SV自身位置得到的决策结果有较大差异.
表 2 不同当前车道车辆位置的场景输入Table 2. Scene input information for different vehicle positions in current lane输入信息 数值 输入信息 数值 当前绿灯剩余时间/s 11 最大制动减速度/
（m•s−2）3 停止线位置/m 300 SV当前速度/（km•h−1） 29 道路最大限速值/（km•h−1） 60 当前车道头车位置 最大舒适加速度/（m•s−2） 2 相邻车道头车位置/m 290 
图 7 不同当前车道车辆位置的决策过程和速度变化Figure 7. Decision process and speed change of different vehicle positions in current lane3. 结 论
1） 本文以周围车辆对智能网联汽车的影响为研究重点，以行驶时间和行驶路程作为通行条件计算依据，建立智能网联汽车在信号交叉口的行为决策方法，让其利用前车状态对执行各种行为的条件进行了超前判断，并得到准确的决策结果.
2） 仿真结果表明，决策模型可以使车辆根据车联网获取的信号倒计时间、车辆位置和速度状态，对交叉口停止线附近车辆的通过、停车和换道行为之间做出准确的选择，解决了前车不确定行为带来的决策困难问题，对智能网联汽车的实际控制具有指导意义.
3） 本研究考虑了车辆直行时的情况，当车辆有转向需求时，不同车道上车辆的状态和其他进口道车辆的冲突对决策也具有不可忽略的影响，未来研究关注的是车辆在交叉口有不同转向需求时的行为决策问题.
-
图 4 局部脱空影响下轨道板自振频率
Figure 4. Natural frequencies of track slab under the effect of partial de-bonding
图 6 不同脱空长度下轨道板疲劳寿命值
Figure 6. Fatigue lifes of track slab with different de-bonding lengths
表 1 主要计算参数
Table 1. Main calculation parameters
部件 项目 取值 钢轨 弹性模量/Pa 2.06 × 1011 惯性矩/m4 7.745 × 10−3 密度/（kg•m−3） 7850 泊松比 0.30 扣件刚度/（N•m−1） 6.0 × 107 轨道板 弹性模量/Pa 3.55 × 1010 密度/（kg•m−3） 2400 泊松比 0.20 宽度（厚度）/m 2.55 （0.20） CA砂浆 弹性模量/Pa 7.0 × 109 厚度/m 0.03 单向受压刚度/（N•m−2） 5.95 × 1011 
下载: 导出CSV
-
[1] 刘笑凯,刘学毅,肖杰灵,等. 温度作用下纵连式无砟轨道垂向稳定性研究[J]. 西南交通大学学报,2018,53(5): 921-927, 944. doi: 10.3969/j.issn.0258-2724.2018.05.007LIU Xiaokai, LIU Xueyi, XIAO Jieling, et al. Vertical stability of longitudinal continuous ballastless track under temperature variation[J]. Journal of Southwest Jiaotong University, 2018, 53(5): 921-927, 944. doi: 10.3969/j.issn.0258-2724.2018.05.007 [2] 张鹏飞,桂昊,雷晓燕. CRTS Ⅱ型板断裂条件下桥上无缝线路伸缩力特性[J]. 西南交通大学学报,2020,55(5): 1036-1043.ZHANG Pengfei, GUI Hao, LEI Xiaoyan. Expansion-constriction force characteristics of continuously rails on bridge under fracture condition of CRTS Ⅱ track slab welded[J]. Journal of Southwest Jiaotong University, 2020, 55(5): 1036-1043. [3] LICHTBERGER B. Track compendium: formation, permanent way, maintenance, economics[M]. Hamburg: Eurail Press, 2005. [4] 李培刚. CRTS Ⅱ型板式轨道层间损伤及其影响研究[D]. 成都: 西南交通大学, 2015: 18-19. [5] 宋玉普,王怀亮,贾金青. 混凝土的多轴疲劳性能[J]. 建筑结构学报,2008,29(增刊1): 260-265.SONG Yupu, WANG Huailiang, JIA Jinqing. Behavior of concrete under multi-axial fatigue loading[J]. Journal of Building Structures, 2008, 29(S1): 260-265. [6] 王怀亮,宋玉普. 定侧压混凝土双轴疲劳破坏准则研究[J]. 土木工程学报,2010,43(10): 1-7.WANG Huailiang, SONG Yupu. Criterion of concrete fatigue failure under biaxial fatigue stress and constant confining stress[J]. China Civil Engineering Journal, 2010, 43(10): 1-7. [7] 冯秀峰,宋玉普,朱美春. 随机变幅疲劳荷载下预应力混凝土梁疲劳寿命的试验研究[J]. 土木工程学报,2006,39(9): 32-38. doi: 10.3321/j.issn:1000-131X.2006.09.005FENG Xiufeng, SONG Yupu, ZHU Meichun. An experimental study on the fatigue life of prestressed concrete beams under random-amplitude fatigue loading[J]. China Civil Engineering Journal, 2006, 39(9): 32-38. doi: 10.3321/j.issn:1000-131X.2006.09.005 [8] CORNELISSEN H A W, REINHARDT H W. Uniaxial tensile fatigue failure of concrete under constant- amplitude and programme loading[J]. Magazine of Concrete Research, 1984, 129(36): 216-227. [9] DOBROMIL P, JAN C, RADOMIR P. Material model for finite element modelling of fatigue crack growth in concrete[J]. Procedia Engineering, 2010, 2(1): 203-212. doi: 10.1016/j.proeng.2010.03.022 [10] 刘学毅, 赵坪锐, 杨荣山. 客运专线无砟轨道设计理论与方法[M]. 成都: 西南交通大学出版社, 2010. [11] 徐庆元,林青腾,方子匀,等. 桥上纵连板式无砟轨道疲劳应力谱的理论研究[J]. 西南交通大学学报,2018,53(5): 906-912. doi: 10.3969/j.issn.0258-2724.2018.05.005XU Qingyuan, LIN Qingteng, FANG Ziyun, et al. Theoretical study on fatigue stress spectrum of longitudinal connected slab track on bridge[J]. Journal of Southwest Jiaotong University, 2018, 53(5): 906-912. doi: 10.3969/j.issn.0258-2724.2018.05.005 [12] 徐庆元,林青腾,方子匀,等. 组合荷载下桥上纵连板式无砟轨道疲劳特性[J]. 中国铁道科学,2017,38(6): 37-46. doi: 10.3969/j.issn.1001-4632.2017.06.06XU Qingyuan, LIN Qingteng, FANG Ziyun, et al. Fatigue characteristics of longitudinally connected slab ballastless track on bridge under combined load[J]. China Railway Science, 2017, 38(6): 37-46. doi: 10.3969/j.issn.1001-4632.2017.06.06 [13] POVEDA E, YU R C, LANCHA J C, et al. A numerical study on the fatigue life design of concrete slabs for railway tracks[J]. Engineering Structures, 2015, 100: 455-467. doi: 10.1016/j.engstruct.2015.06.037 [14] TARIFA M, ZHANG X X, RUIZ G, et al. Full-scale fatigue tests of precast reinforced concrete slabs for railway tracks[J]. Engineering Structures, 2015, 100: 610-621. doi: 10.1016/j.engstruct.2015.06.016 [15] KONINGS P. A study on the lifetime aspects of the RHEDA 2000 track system [D]. Delft: Delft University of Technology, 2005. [16] 刘学毅,刘丹,赵坪锐,等. CRTS Ⅲ型板式无砟轨道疲劳性能试验研究[J]. 铁道工程学报,2016,33(11): 51-56,112. doi: 10.3969/j.issn.1006-2106.2016.11.010LIU Xueyi, LIU Dan, ZHAO Pingrui, et al. Experimental research on the fatigue behavior test of CRTS Ⅲ slab track[J]. Journal of Railway Engineering Society, 2016, 33(11): 51-56,112. doi: 10.3969/j.issn.1006-2106.2016.11.010 [17] 童明娜,卢朝辉,赵衍刚,等. CRTS Ⅱ型无砟轨道板疲劳时变可靠度研究[J]. 铁道学报,2020,42(10): 92-100. doi: 10.3969/j.issn.1001-8360.2020.10.013TONG Mingna, LU Zhaohui, ZHAO Yangang, et al. Time-dependent fatigue reliability evaluation of CRTS Ⅱ ballastless track slab[J]. Journal of the China Railway Society, 2020, 42(10): 92-100. doi: 10.3969/j.issn.1001-8360.2020.10.013 [18] CHAPELEAU X, SEDRAN T, COTTINEAU L M, et al. Study of ballastless track structure monitoring by distributed optical fiber sensors on a real-scale mockup in laboratory[J]. Engineering Structures, 2013, 56: 1751-1757. doi: 10.1016/j.engstruct.2013.07.005 [19] 王青,卫军,董荣珍,等. CRTS Ⅱ板式无砟轨道结构的疲劳力学性能分析[J]. 铁道工程学报,2014,31(5): 41-47. doi: 10.3969/j.issn.1006-2106.2014.05.008WANG Qing, WEI Jun, DONG Rongzhen, et al. Fatigue behavior analysis of CRTS Ⅱ slab ballastless track structure[J]. Journal of Railway Engineering Society, 2014, 31(5): 41-47. doi: 10.3969/j.issn.1006-2106.2014.05.008 [20] 曹伟,宋玉普,刘海成. 混凝土三轴变幅拉-压疲劳性能试验研究[J]. 工程力学,2006,23(3): 111-117. doi: 10.3969/j.issn.1000-4750.2006.03.020CAO Wei, SONG Yupu, LIU Haicheng. Fatigue properties of plain concrete under triaxial variable-amplitude tension-compression cyclic loading[J]. Engineering Mechanics, 2006, 23(3): 111-117. doi: 10.3969/j.issn.1000-4750.2006.03.020 [21] TEPFERS R, KUTTI T. Fatigue strength of plain,ordinary and lightweight concrete[J]. Journal of the American Concrete Institute, 1979, 76(5): 635-652. [22] 徐庆元,张泽,陈效平,等. 桥上CRTS Ⅱ型板式无砟轨道混凝土疲劳寿命预测模型试验研究[J]. 铁道科学与工程学报,2017,14(8): 1565-1570. doi: 10.3969/j.issn.1672-7029.2017.08.001XU Qingyuan, ZHANG Ze, CHEN Xiaoping, et al. Experimental study on fatigue life prediction model of concrete of CRTS Ⅱ slab track on bridge[J]. Journal of Railway Science and Engineering, 2017, 14(8): 1565-1570. doi: 10.3969/j.issn.1672-7029.2017.08.001 [23] 祝志文,黄炎,文鹏翔,等. 随机车流下钢-UHPC组合正交异性桥面疲劳性能研究[J]. 中国公路学报,2017,30(3): 200-209. doi: 10.3969/j.issn.1001-7372.2017.03.022ZHU Zhiwen, HUANG Yan, WEN Pengxiang, et al. Investigation on fatigue performance of orthotropic bridge deck with steel-UHPC composite system under random traffic flows[J]. China Journal of Highway and Transport, 2017, 30(3): 200-209. doi: 10.3969/j.issn.1001-7372.2017.03.022 期刊类型引用(5)
1. 杨荣山，仪皓楠，康维新，曹世豪. 疲劳荷载作用下无砟轨道混凝土钙溶蚀特性. 铁道学报. 2025(02): 160-171 . 
百度学术2. 彭语堂，曹鹏，周雄，肖祺滨，陈科，宋奎，唐现琼. 司机操纵模式对岸桥起重机小车轨道疲劳寿命的影响研究. 湘潭大学学报(自然科学版). 2024(02): 72-80 . 百度学术3. 鲁佩林，王凯. 城际铁路“桥建合一”车站车致振动特性及舒适度评价研究. 建筑技术. 2024(S1): 123-127 . 百度学术4. 徐磊，余志武. 铁路列车-轨道-基础结构动力相互作用统一分析PartⅡ：混凝土车致疲劳损伤与空时演化. 铁道科学与工程学报. 2023(02): 385-392 . 百度学术5. 何橼，吴兴文，邹洪伟，池茂儒. 动车组轴装撒砂装置随机振动疲劳研究. 机车电传动. 2022(05): 64-71 . 百度学术其他类型引用(7)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 502
- HTML全文浏览量: 243
- PDF下载量: 18
- 被引次数: 12