Optimization on Railway Empty Wagon Allocation Based on Robust Connecting Time
-
摘要:
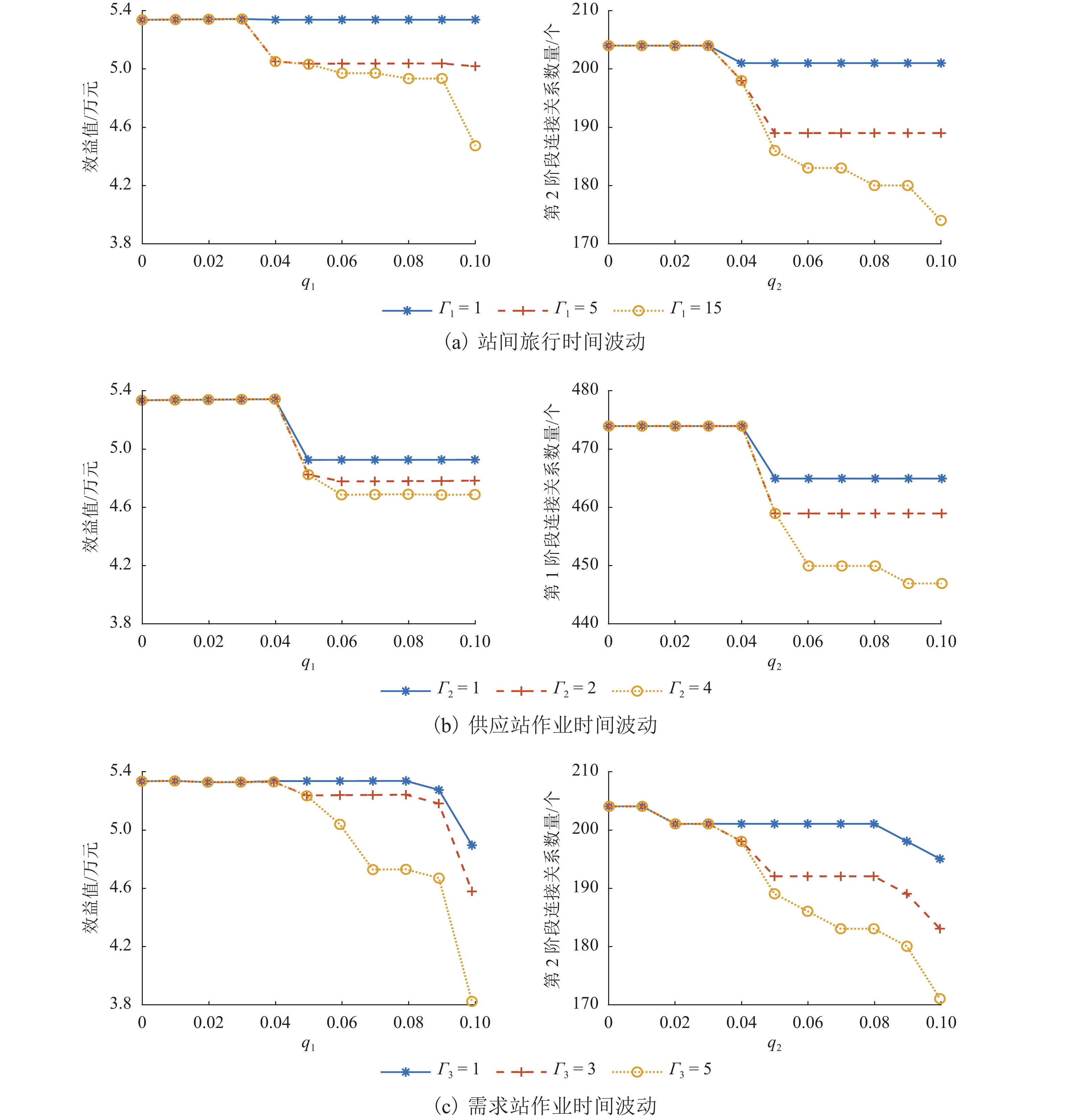
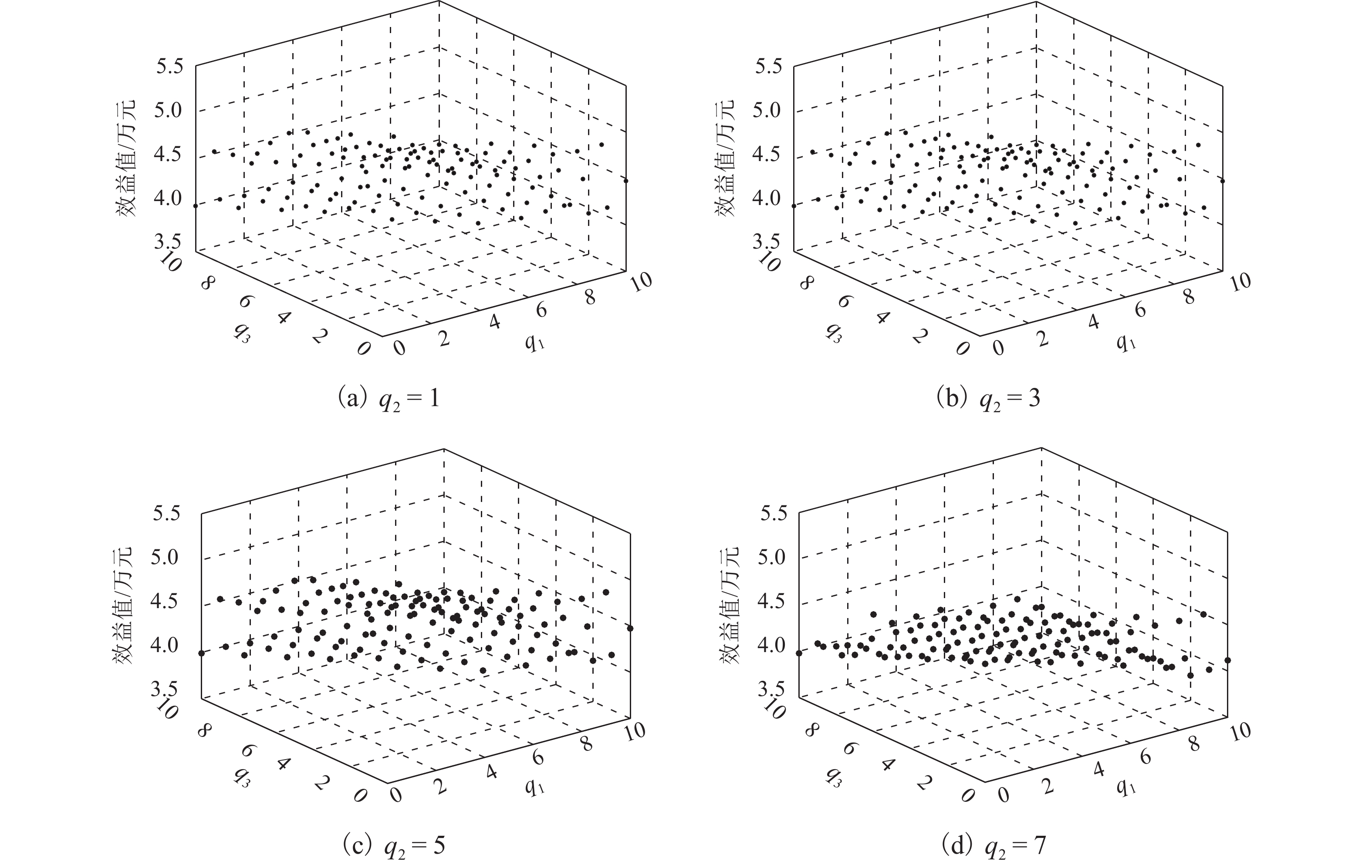
空车调运是铁路运输的关键环节,其方案具有一定的鲁棒性,可以避免车站技术作业时间以及站间旅行时间等不确定因素对调运方案实施的影响. 基于固定的车站技术作业时间和站间旅行时间,提出了空车供应站到达列车与发出列车、空车供应站发出列车与空车需求站发出列车间的空车接续时间关系判别方法. 以空车调运收益最大化为目标,建立了确定情形下考虑车种替代的空车调运模型,在此基础上,引入波动率描述车站技术作业时间和站间旅行时间的不确定性,并通过设置波动下限调整模型的鲁棒性,建立了不确定情形下的空车调运鲁棒优化模型;结合模型性质,以车流关系变化为依据,设计了鲁棒优化模型的快速求解算法,将非线性优化问题转化为易求解的鲁棒等价模型. 结果表明:求得的空车调运方案可以得出列车间的空车配流和车种替代情况,不确定因素的波动率和波动下限会影响空车调运方案的效益值,绝对鲁棒下站间旅行时间、供应站技术作业时间和需求站技术作业时间3个不确定因素导致方案效益值较确定模型分别下降了16.2%、12.1%和28.1%.
Abstract:Empty wagon allocation is the key link in railway transportation. The scheme of empty wagon allocation should have robustness to avoid the influence of uncertain factors. Based on the fixed technical operation time of stations and travel time between stations, the connection time relationships between arrival and departure trainsin supply stations, and between departure trainsin supply stations and in demand stations are identified. To maximize the revenue of empty wagon allocation, an empty wagon allocation model involving vehicle type substitution is established. On this basis, the fluctuation rate is introduced to describe the uncertainty due to the technical operation time of stations and travel time between stations, and the lower limit of fluctuation is set to adjust the model robustness. A robust optimization model is established for empty wagon allocation under uncertain conditions. Combined with model properties, a fast algorithm for solving the robust optimization model is designed in terms of the change of traffic flow relationship, and the nonlinear problem is transformed into a robust equivalent model that is easy to solve. The results show the empty wagon allocation scheme can accurately obtain the empty wagon flow and vehicle type substitution, and the fluctuation rate and lower limit of uncertain factors affect the revenue of the scheme. Under absolute robustness, compared with the certain model, the revenue of the scheme is decreased by 16.2%, 12.1% and 28.1%, respectively, due to the uncertain factors, including the travel time between stations, technical operation time of supply stations and technical operation time of demand stations.
-
Key words:
- empty wagon allocation /
- robust optimization /
- connecting time /
- multi-factor uncertainty
-
表 1 供应站列车到达时刻及空车产生数量
Table 1. Time of train arrival and number of empty wagons produced in supply stations
供应站 产生空车的到达列车编号 1 2 3 4 1 7,5,7,5 412,3,5,5 −439,5,5,5 −100,5,3,5 2 −35,3,5,7 450,3,10,2 −465,7,5,3 −50,5,8,3 3 −367,5,6,5 −497,5,5,5 200,3,4,5 4 −436,5,5,2 −356,5,2,5 80,6,4,5 注:以逗号为分隔的各项依次为列车到达时间/min、平车数目/辆、棚车数目/辆、敞车数目/辆. 表 2 供应站列车最晚编组时刻及最大空车挂运数量
Table 2. Train marshalling time limit and maximum number of empty wagons in supply stations
供应站 可挂运空车的发出列车编号 1 2 3 4 5 1 222,1,10 627,3,15 −224,5,15 300,2,10 150,4,15 2 203,1,10 693,3,15 −217,5,15 0,2,15 500,4,10 3 −138,2,10 −268,4,10 400,1,10 800,3,10 500,5,10 4 −326,2,15 −246,4,15 200,1,10 400,3,10 340,5,10 注:以逗号为分隔的各项依次为最晚编组时间/min、发往需求站编号、最大空箱挂运数目/辆. 表 3 需求站列车最晚编组时刻及所需空车数量
Table 3. Train marshalling time limit and number of empty trains required in demand stations
列车
序号需求站编号 1 2 3 4 5 1 660,2,6,2 280,5,2,10 1160,5,8,2 260,2,6,1 400,2,8,2 2 780,5,5,2 560,6,8,5 1400,6,5,2 920,8,5,5 800,10,2,2 注:以逗号为分隔的各项依次为最晚编组时间/min、平车数目/辆、棚车数目/辆、敞车数目/辆. 表 4 站间空车输送费用及名义旅行时间
Table 4. Empty wagon transportation cost and nominal travel time between stations
供
应
站需求站编号 1 2 3 4 5 1 200,3.3 157,2.3 285,4.6 322,4.8 420,5.9 2 174,3.4 79,1.2 202,3.3 288,4.1 406,5.5 3 298,4.0 172,3.4 186,2.8 193,4.1 204,3.4 4 363,5.5 338,6.2 248,4.9 210,3.5 209,3.1 注:以逗号为分隔的各项依次为空车输送费用/(元•箱)−1、名义旅行时间/h. 表 5 车站参数数据
Table 5. Station parameter data
站点编号 需求站 供应站 pj/(元•箱−1) tj/min cj /(元•h−1) ti/min ci /(元•h−1) 1 673 231 3 205 2 2 485 205 5 225 4 3 598 246 6 218 6 4 659 271 2 105 2 5 805 257 3 表 6 供应站发出列车的空车来源
Table 6. Empty wagon source of trains leaving from supply stations
供应站编号 列车发出序号 1 2 3 4 5 1 (1,4);(1,6);0 (2,3):0;(2,2) (3,5);(3,5);(3,5) 0;0;0 (4,2);(4,3);(4,1) 2 (1,3);(1,5);(1,2) (2,3);(2,10);(2,2) 0;(3,1);0 (3,7);(3,4);(3,3) 0;0;0 3 0;(1,1);[(1,5),(2,4)] (2,4);(2,5);(2,1) 0;0;0 (1,5);(1,3);0 0;0;0 4 (1,5);(1,5);(1,2) (2,4);(2,2);(2,5) 0;0;(3,2) 0;0;0 [(2,1),(3,6)];(3,2);(3,1) 注:以分号分割的各项依次对应的车型为平车、棚车、敞车; [ ]内为相同车型的空车来源集;( )内各项依次表示到达列车序号、提供空车数量/辆. 以“(1,4);(1,6);0”为例,供应站1发出的第1列列车中,挂运空车的来源为:第1列到达列车提供4辆平车;第1列到达列车提供6辆棚车;该列车中不包含敞车. 表 7 需求站发出列车空车来源
Table 7. Empty wagon source of trains leaving from demand station
需求站编号 列车发出序号 1 2 1 (2,1,2);(1,1,6);(2,1,2) [(1,1,4),(2,1,1)];(2,1,5);(4,3,2) 2 [(2,4,1),(4,1,4)];(4,1,2);[(2,4,3),(3,1,5),(4,1,2)] (2,4,6);[(2,4,4),(3,1,1),(4,1,3)];[(3,1,4),(4,1,1)] 3 [(1,2,2),(2,2,3)];(2,2,8);(1,2,2) [(1,2,1),(3,4,5)];[(2,2,2),(3,4,3)];(2,2,2) 4 (4,2,2);[(3,2,5),(4,2,1)];(3,2,1) [(1,5,2),(3,2,4),(4,2,2)];[(1,5,4),(4,2,1)];(4,2,5) 5 (1,3,2);[(1,3,7),(2,3,1)];(1,3,2) [(1,3,3),(4,5,7)];(4,5,2);[(1,3,1),(4,5,1)] 注:以分号分割的各项依次对应的车型为平车、棚车、敞车; [ ]内为相同车型的空车来源集合;( )内各项依次表示供应站编号、供应站发出列车序号、空车数量/辆. 以“[(1,1,4),(2,1,1)];(2,1,5);(4,3,2)”为例,需求站1发出的第2列列车中,其装车空箱的来源为:供应站1发出的第1列车提供4辆平车,供应站2发出的第1列车提供1辆平车;供应站2发出的第1列车提供5辆棚车;供应站4发出的第3列车提供2辆敞车. -
[1] 王龙,马建军,林柏梁,等. 全路空车动态调配及路网分界口排空流量测算方法[J]. 铁道学报,2015,37(6): 1-9. doi: 10.3969/j.issn.1001-8360.2015.06.001WANG Long, MA Jianjun, LIN Boliang, et al. Dynamic empty car distribution for the whole rail system and calculation for empty car flow discharged over network boundaries[J]. Journal of the China Railway Society, 2015, 37(6): 1-9. doi: 10.3969/j.issn.1001-8360.2015.06.001 [2] 张红斌,董宝田,孙远运. 基于能力约束的多车种空车动态调整方法[J]. 北京交通大学学报,2016,40(6): 50-56.ZHANG Hongbin, DONG Baotian, SUN Yuanyuan. Multi-type empty car dynamic distribution method based on capacity constraints[J]. Journal of Beijing Jiaotong University, 2016, 40(6): 50-56. [3] 陈胜波,何世伟,刘星材,等. “实货制”下铁路空车动态调配两阶段优化模型与算法研究[J]. 铁道学报,2015,37(5): 1-8. doi: 10.3969/j.issn.1001-8360.2015.05.001CHEN Shengbo, HE Shiwei, LIU Xingcai, et al. Study on two-phase optimization models and algorithms for empty railcar dynamic distribution based on "real freight system"[J]. Journal of the China Railway Society, 2015, 37(5): 1-8. doi: 10.3969/j.issn.1001-8360.2015.05.001 [4] 邹华鹏. 基于车流波动的车流组织优化及空车调配问题研究[D]. 长沙: 中南大学, 2014. [5] 赵策. 动态随机铁路空车调配问题模型及算法[D]. 北京: 北京交通大学, 2015. [6] 段刚,陈莉,李引珍,等. 基于鲁棒软时间窗的铁路集装箱空箱调运优化研究[J]. 铁道学报,2015,37(9): 8-16.DUAN Gang, CHEN Li, LI Yinzhen, et al. Optimization on railway empty container allocation with robust soft time window[J]. Journal of the China Railway Society, 2015, 37(9): 8-16. [7] 潘兰蓉. 铁路空车调整协同优化模型的改进研究[D]. 成都: 西南交通大学, 2017. [8] 宋晓东. 铁路空车调配多目标优化模型研究[D]. 长沙: 中南大学, 2009. [9] HE J L, HUANG Y F, CHANG D F. Simulation-based heuristic method for container supply chain network optimization[J]. Advanced Engineering Informatics, 2015, 29(3): 339-354. [10] HAO C L, YUE Y X. Optimization on combination of transport routes and modes on dynamic programming for a container multimodal transport system[J]. Procedia Engineering, 2016, 137: 383-388. [11] BERTSIMAS D, SIM M. The price of robustness[J]. Operations Research, 2004, 52(1): 35-53. -




 下载:
下载: