Failure Mechanism of Flood Damage to Jinsha River Bridge at Zhubalong
-
摘要:
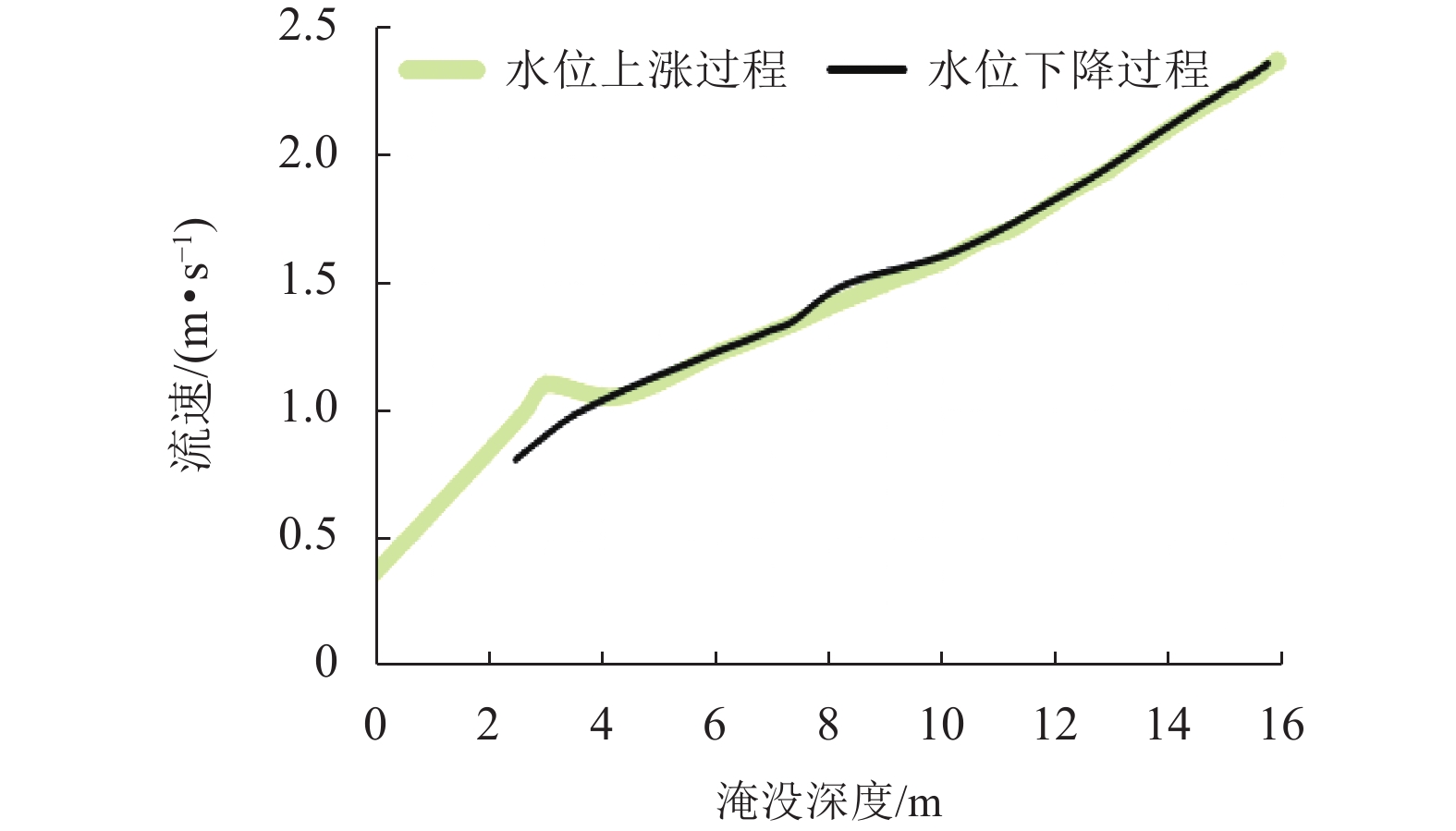
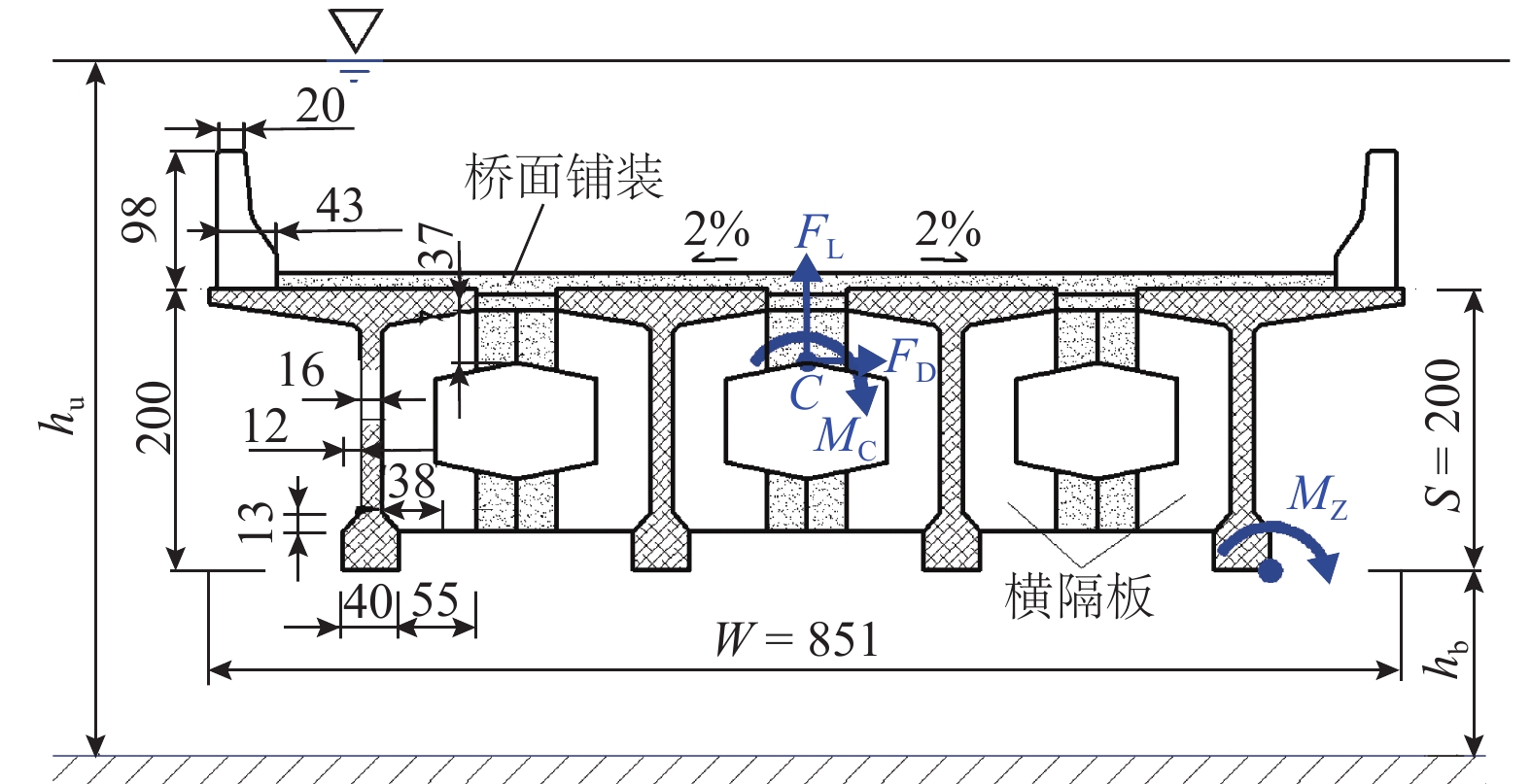
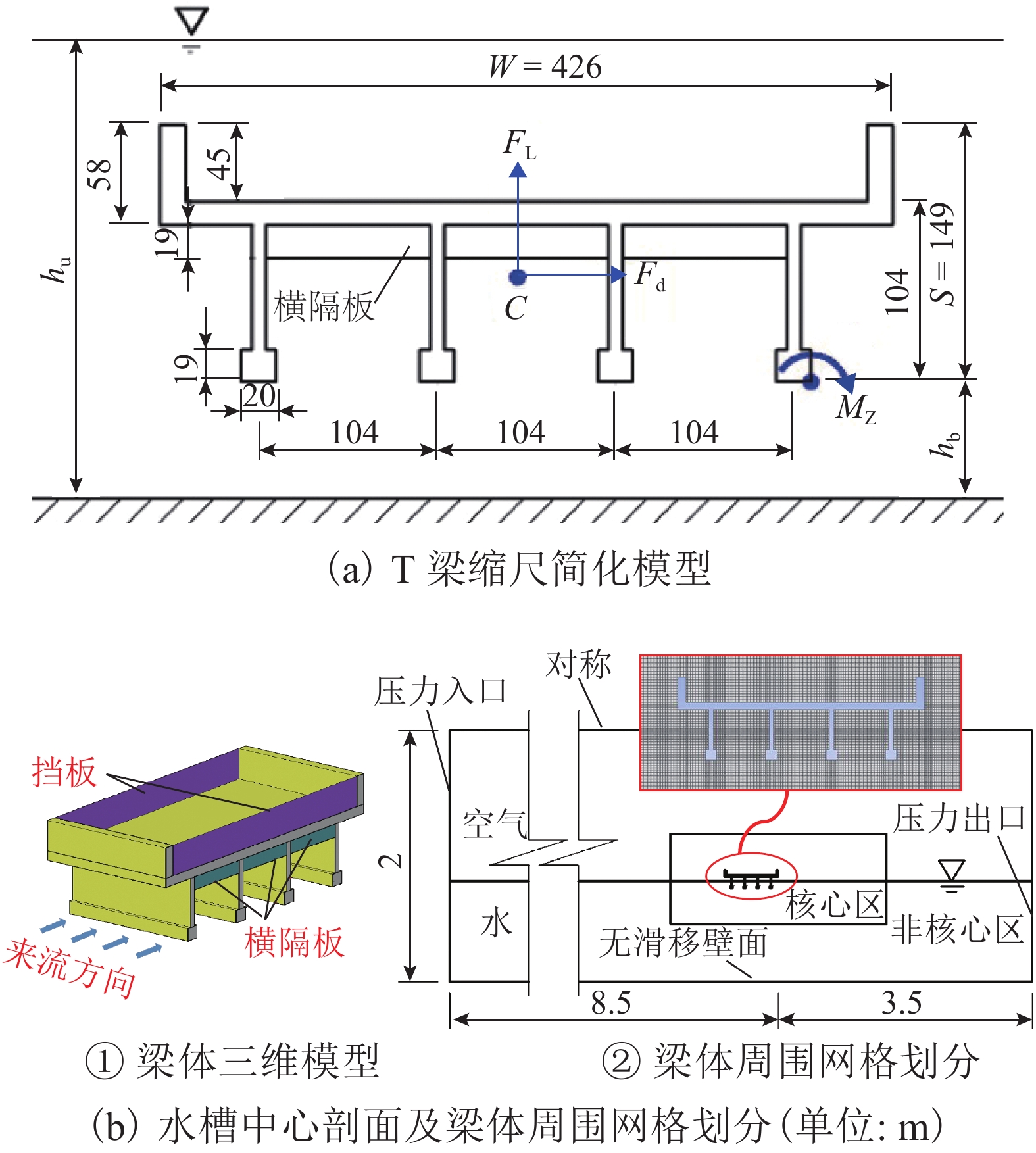
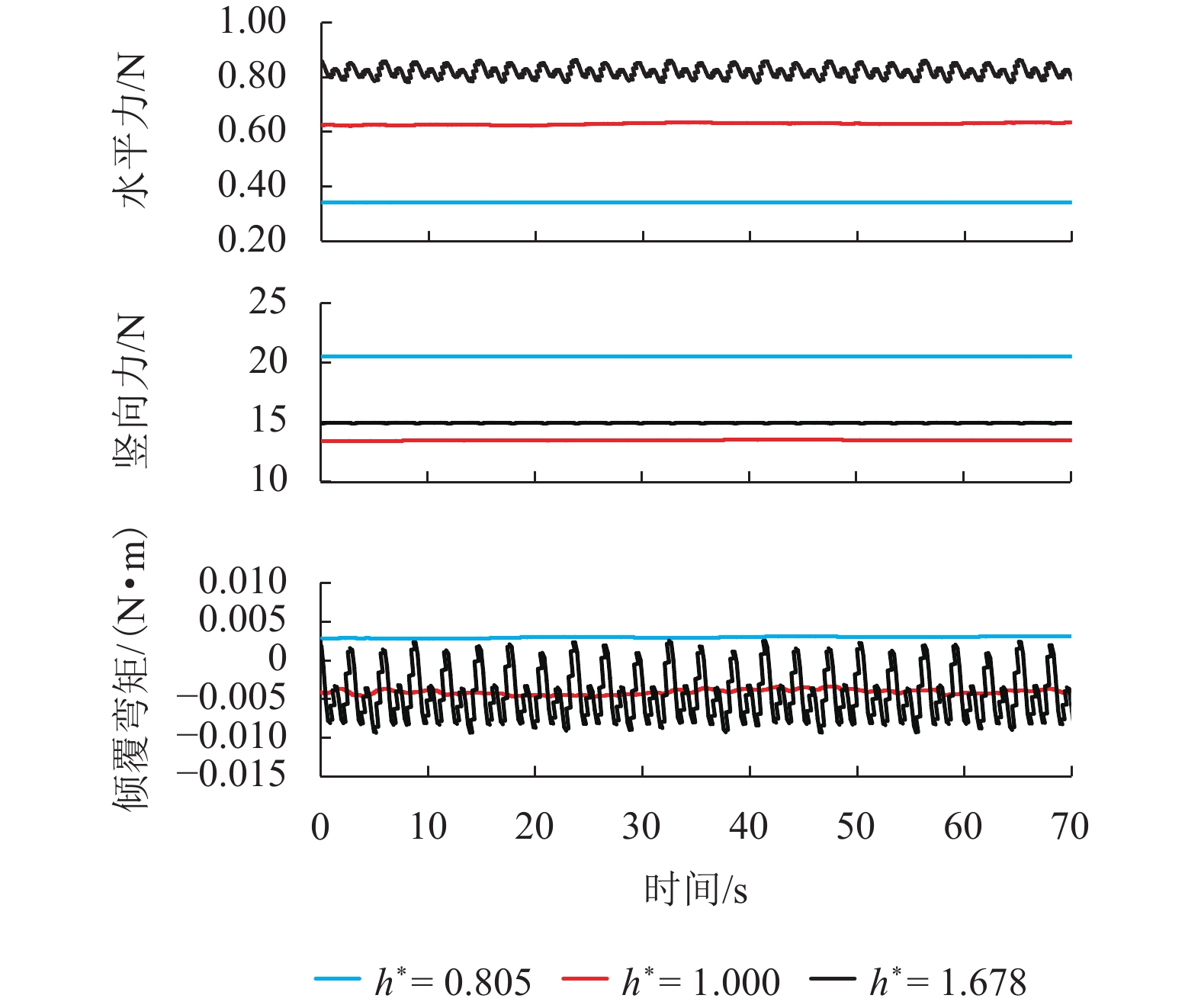
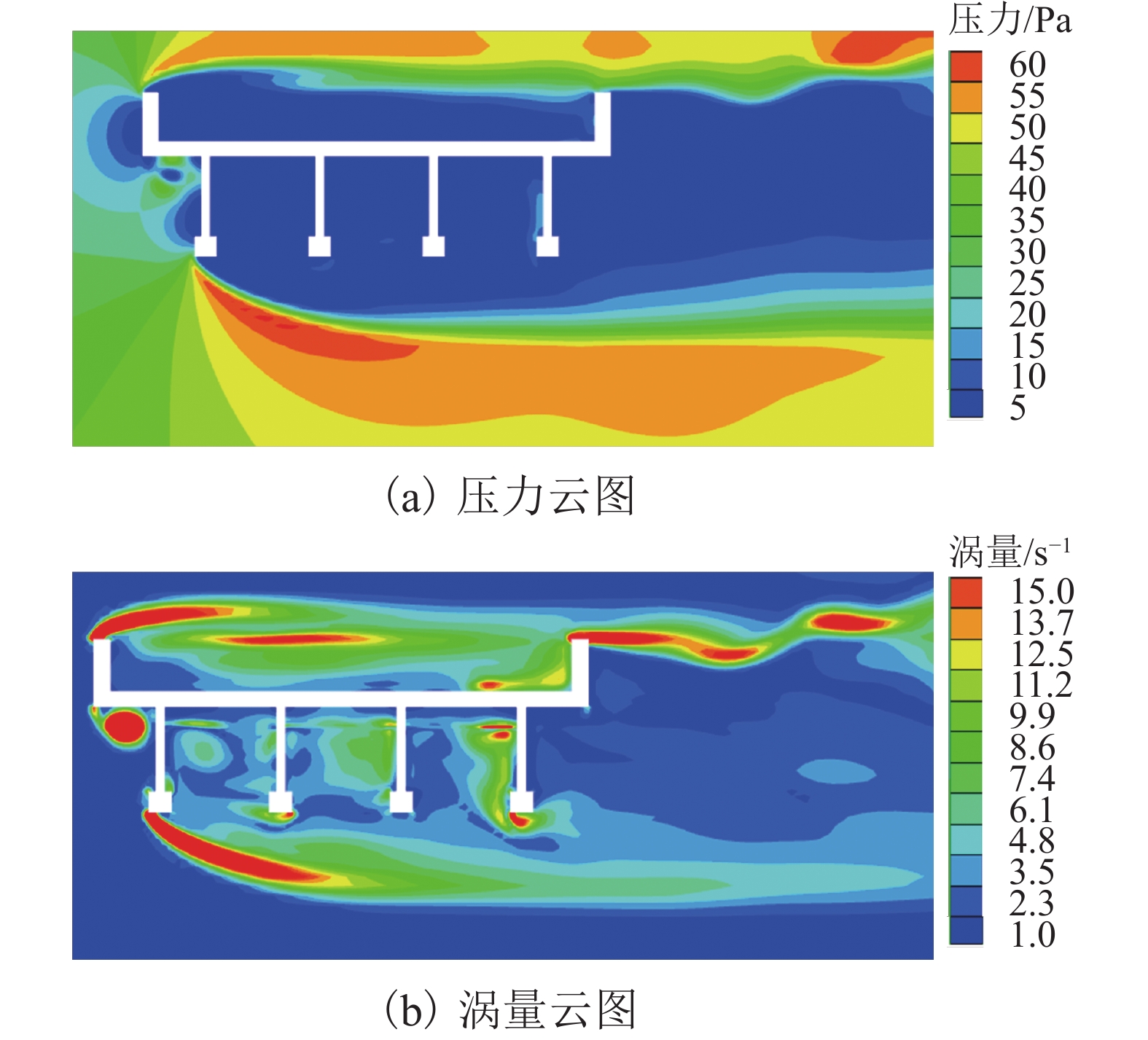
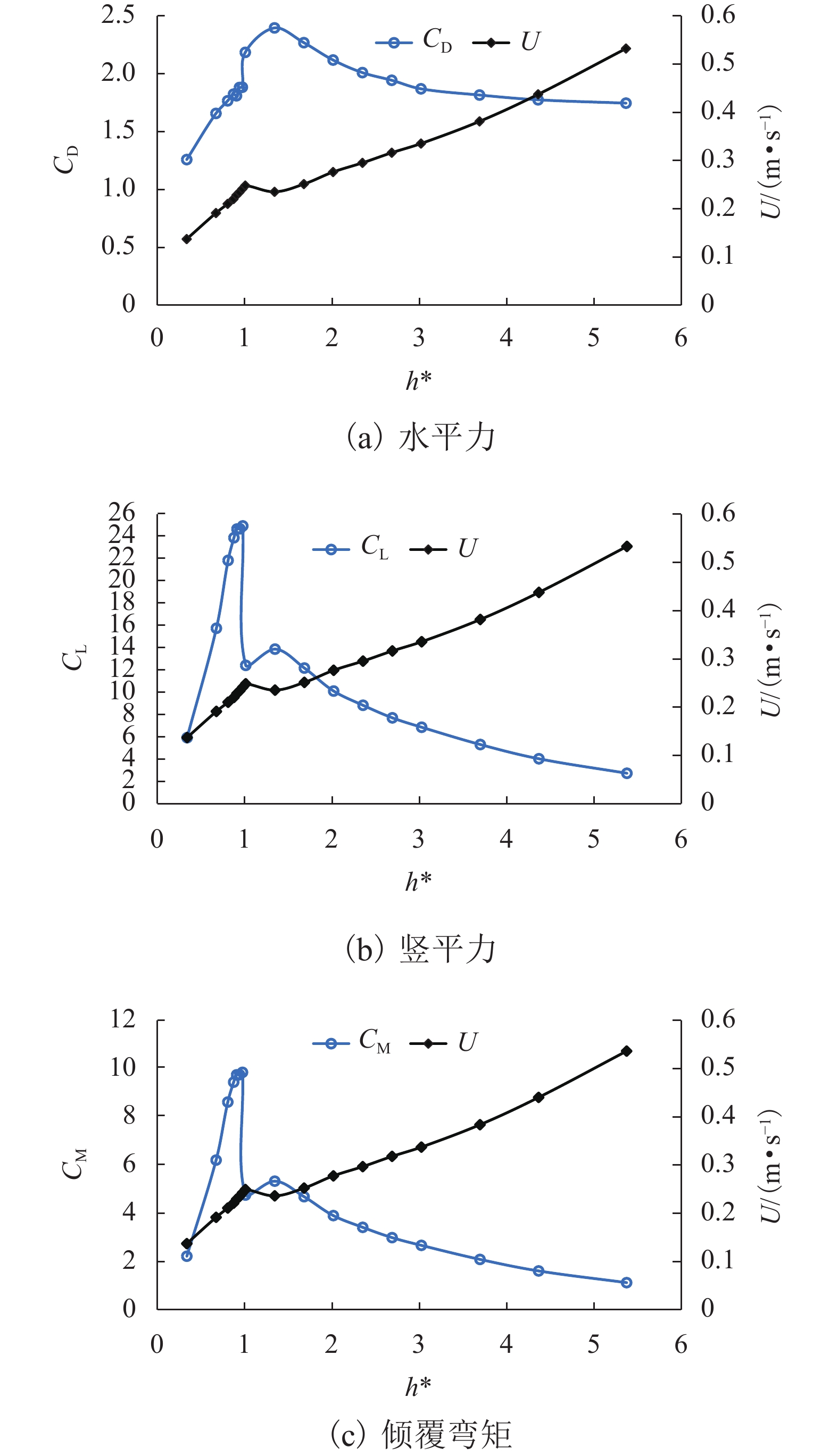
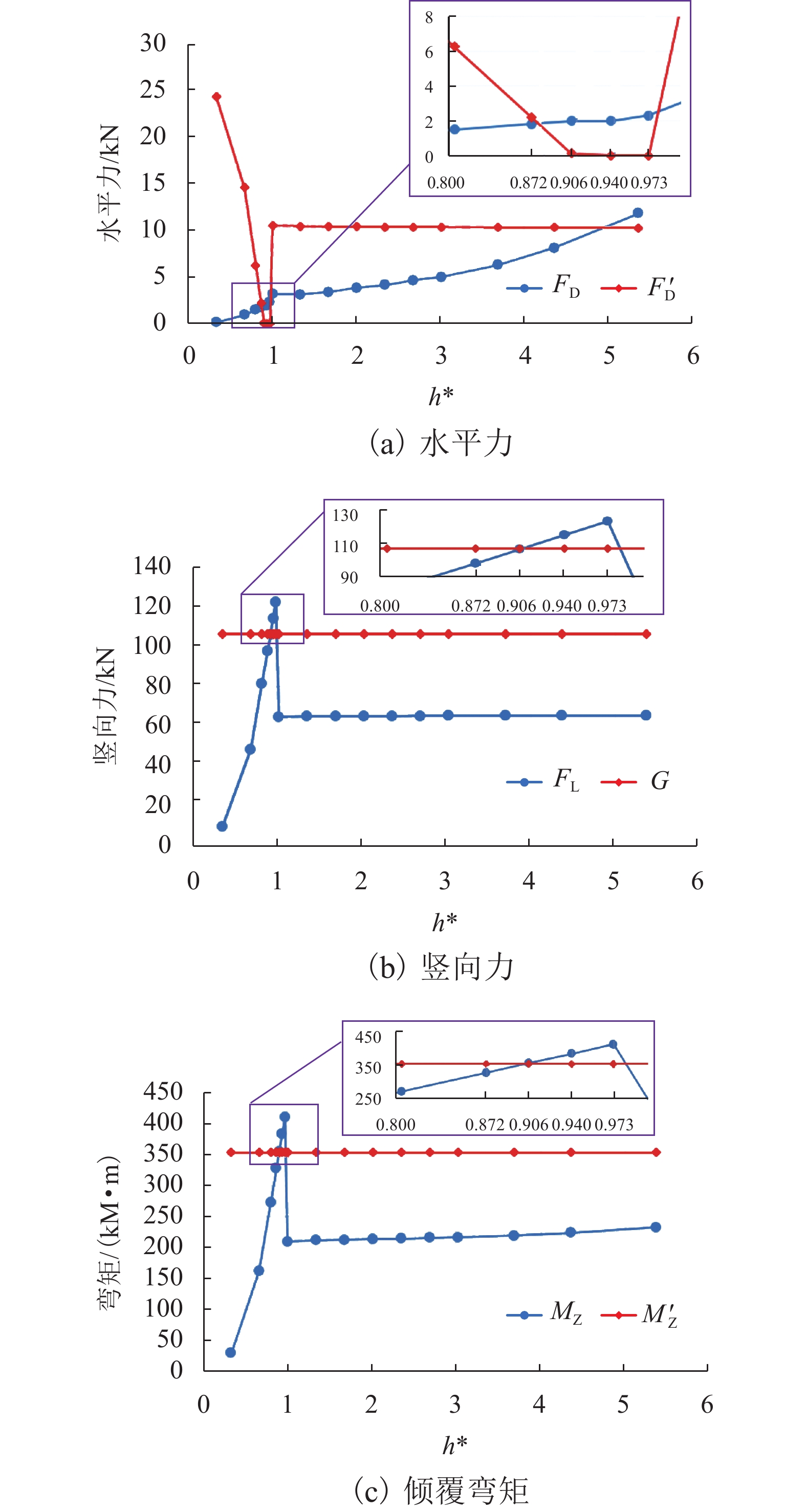
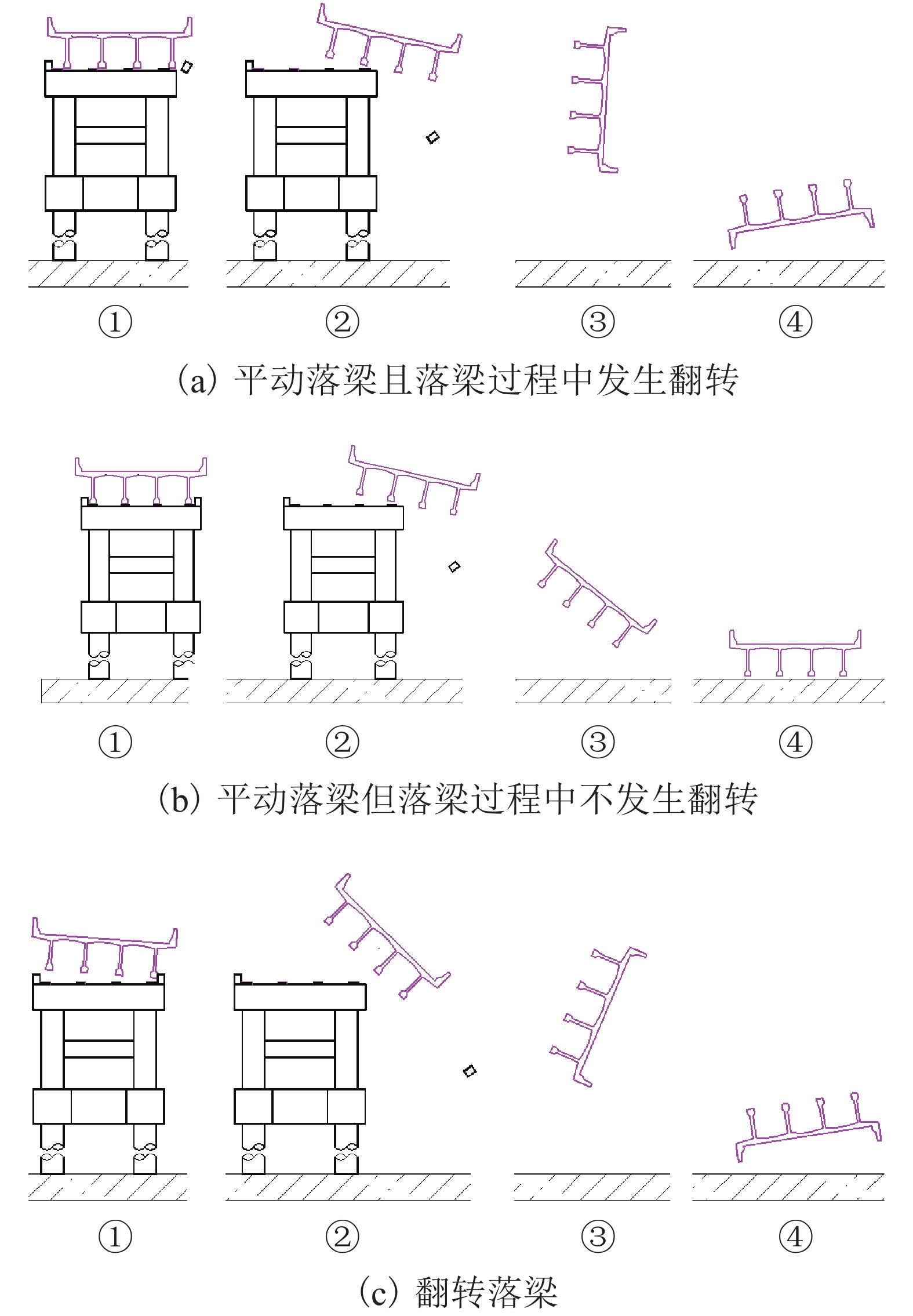
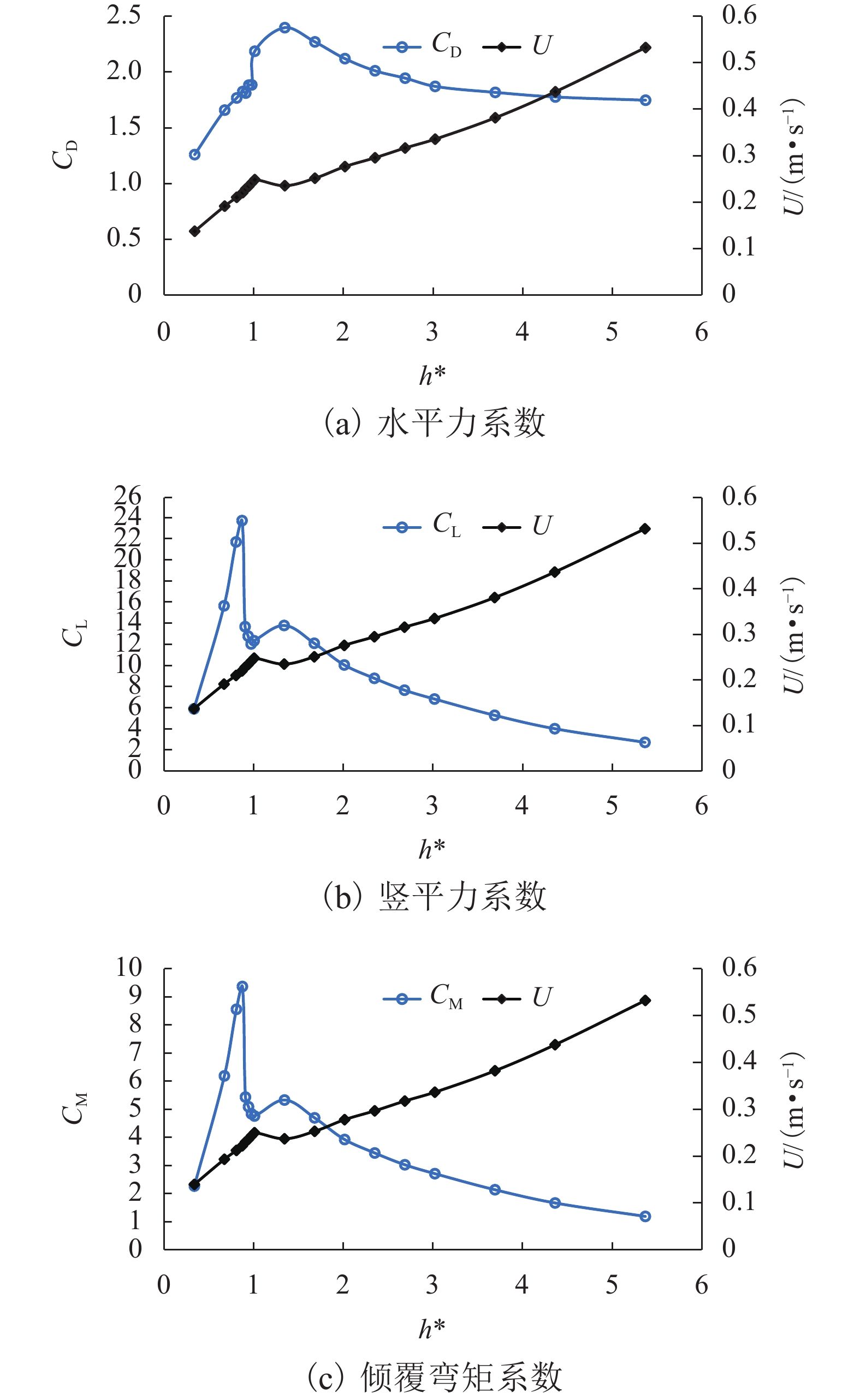
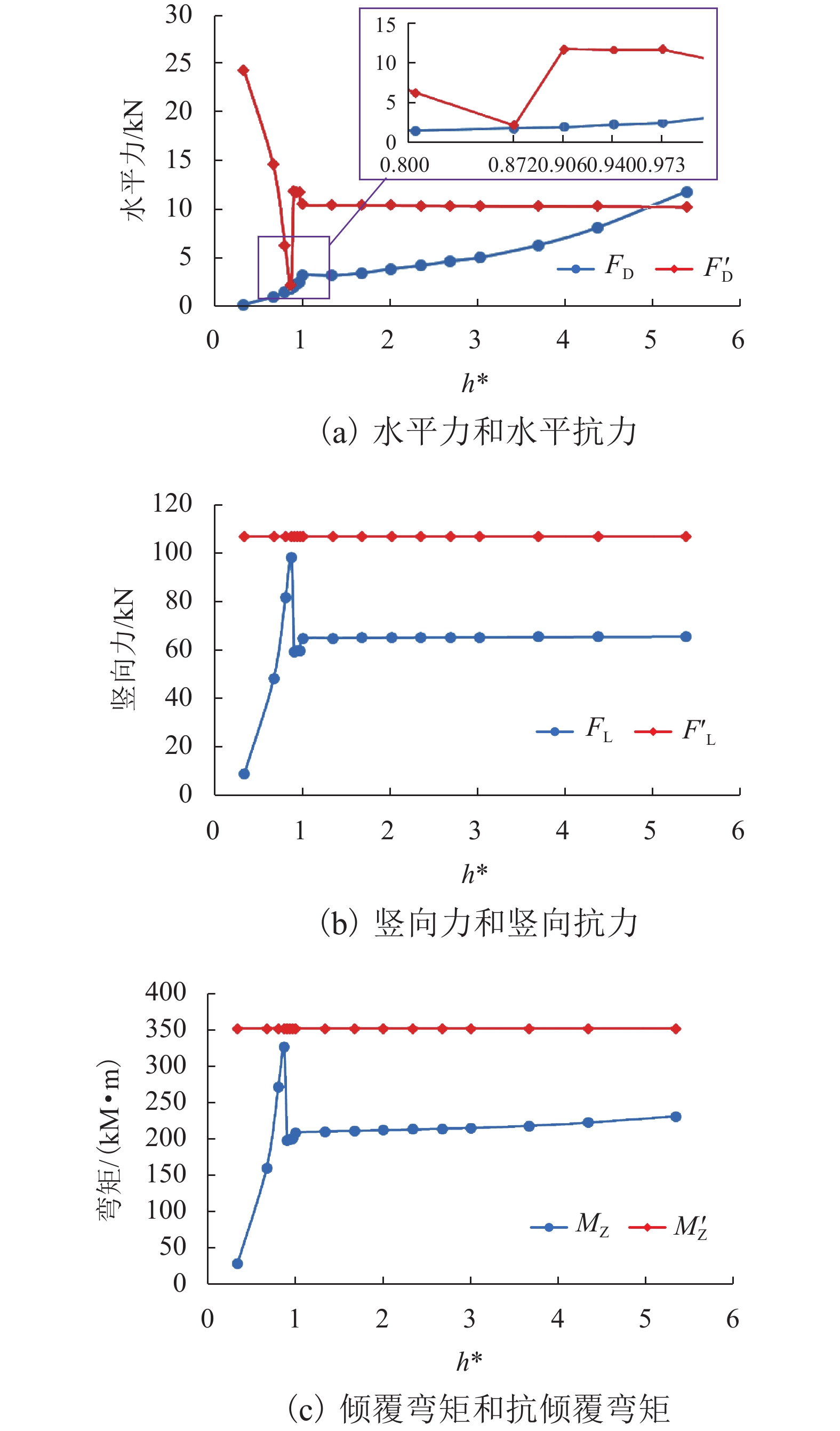
为了研究竹巴龙金沙江大桥的破坏机理，基于泄洪实测数据，并考虑T梁底部横隔板腔室中裹挟空气的影响，建立了该桥1∶20缩尺数值仿真模型，对洪水作用下简支T梁桥上部结构洪水作用力特征、流场特征和破坏机理开展了深入研究. 研究结果表明：当淹没率不超过1.342时，水平力系数随淹没率的增大而增大，当淹没率大于1.342时，水平力系数随淹没率的增大逐渐减小；在壅水翻越护栏前，竖向力和倾覆弯矩系数随着淹没率的增大而逐渐增大；当壅水翻越护栏后，竖向力和倾覆弯矩系数将急剧减小；在淹没率接近1.000时，上部结构发生破坏的风险最大；该桥破坏过程中首先发生了水平运动，随后大概率发生上浮和翻转，梁体运动导致挡块破坏，部分梁体在跌落中发生翻转；实心栏杆贡献了多达31%的水平力，裹挟空气对竖向力的贡献最高达到18%，实心栏杆和裹挟空气是引起该桥水毁破坏或加速该桥破坏的重要原因.
Abstract:To explore the failure mechanism of Jinsha River Bridge at Zhubalong, a 1∶20 scaled numerical simulation model of the bridge was built with the measured field data in flood discharge, while the influence of air trapped in the diaphragm chamber at the bottom of T-beam is analyzed. The characteristics of flood force, flow field and failure mechanism of superstructure of the simply supported T-beam bridge under the effect of flood are studied in depth. Results show that when the submergence ratio is less than 1.342, the horizontal force coefficient increase with the ratio; when it is beyond 1.342, the coefficient decreases with the ratio. Before the backwater crosses the guardrail, the vertical force and overturning moment coefficient gradually increase with the submergence ratio. When it crosses the guardrail, the vertical force and overturning moment coefficient decrease sharply. When the submergence ratio is close to 1.000, the risk of the superstructure failure is the greatest. During the failure process of the bridge, horizontal movements occur first, and then there is a high probability that floating and overturning occur. The beam movement leads to the destruction of the link stopper, and part of the beam overturns in the falling. Solid railings contribute up to 31% of the horizontal force, and the contribution of entrapped air to the vertical force is up to 18%. Solid railings and entrapped air are important causes for flood damage or accelerating the bridge damage.
-
Key words:
- flood /
- beam bridge /
- failure analysis /
- entrapped air
-
图 1 白格堰塞湖泄洪冲毁竹巴龙金沙江大桥
Figure 1. Jinsha River Bridge at Zhubalong destroyed by discharge from Baige landslide dam
图 2 梁体淹没深度与断面平均流速
Figure 2. Submergence depth of beam body and average velocity at cross section
图 3 实桥T梁跨中断面（单位：cm）
Figure 3. Cross section at middle span of actual T-girder bridge (unit: cm)
图 5
$ {h}^{\mathrm{*}}= $ 0.805,1.000,1.678时水流力时程曲线Figure 5. Time histories of flow force for cases with
$ {\mathit{h}}^{\mathit{*}}= $ 0.805, 1.000 and 1.678
图 6 工况h* = 1.678中t = 1413.894 s时刻云图
Figure 6. Contour of case with h* = 1.678 at t = 1413.894 s
图 7 水流力系数随着淹没率
$ {h}^{\mathrm{*}} $ 的变化趋势（不考虑壅水漫顶）Figure 7. Variation trend of flow force coefficient with submergence ratio
$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping is not considered)
图 8 节段梁体洪水作用力和相应的抗力随
$ {h}^{\mathrm{*}} $ 变化趋势（不考虑壅水漫顶）Figure 8. Variation trend of flood force and resistance of segmental beam with submergence ratio
$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping is not considered)
图 11 水流力系数随着淹没率
$ {h}^{\mathrm{*}} $ 变化趋势（壅水漫顶）Figure 11. Variation of flow force coefficient with submergence ratio
$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping)
图 12 节段梁体作用力和相应的抗力随淹没率
$ {h}^{\mathrm{*}} $ 变化趋势（壅水漫顶）Figure 12. Variation of flood force and resistance of segmental beam with submergence ratio
$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping)表 1 CFD数值模拟计算工况
Table 1. Cases of CFD numerical simulation
工况 $ {h}^{*} $ 流速/(m•s−1) 工况 $ {h}^{*} $ 流速/(m•s−1) C1 0.336 0.136 C10 1.342 0.235 C2 0.671 0.190 C11 1.678 0.250 C3 0.805 0.212 C12 2.013 0.275 C4 0.872 0.223 C13 2.349 0.295 C5 0.889 0.226 C14 2.685 0.316 C6 0.906 0.229 C15 3.02 0.335 C7 0.940 0.235 C16 3.691 0.380 C8 0.973 0.242 C17 4.362 0.438 C9 1.007 0.248 C18 5.369 0.532 
下载: 导出CSV
表 2 网格划分精细程度对数值模拟计算精度和计算效率的影响
Table 2. Influence of grids generation accuracy on calculation precision and efficiency of numerical simulation
工况 y+ dcb/mm N/个 T/h CD CL 模型试验 1.250 −1.240 粗糙 60 3 413086 11 1.176 −1.259 中等 45 2 507650 23 1.224 −1.124 精细 30 1 701862 36 1.238 −1.157
下载: 导出CSV
-
[1] 郭俊峰. 凌汛期大跨径桥梁的安全性评价[D]. 武汉: 武汉理工大学, 2008. [2] WARDHANA K, HADIPRIONO F C. Analysis of recent bridge failures in the United States[J]. Journal of Performance of Constructed Facilities, 2003, 17(3): 144-150. doi: 10.1061/(ASCE)0887-3828(2003)17:3(144) [3] MELVILLE B W. Local scour at bridge abutments[J]. Journal of Hydraulic Engineering, 1992, 118(4): 615-631. doi: 10.1061/(ASCE)0733-9429(1992)118:4(615) [4] NAUDASCHER E, MEDLARZ H J. Hydrodynamic loading and backwater effect of partially submerged bridges[J]. Journal of Hydraulic Research, 1983, 21(3): 213-232. doi: 10.1080/00221688309499416 [5] 杨斌,赖立煌,黄启亮,等. 洪水对桥梁结构水平作用力的计算及试验研究[J]. 重庆交通学院学报,1996,15(2): 2-6.YANG Bin, LAI Lihuang, HUANG Qiliang, et al. Calculation and experiment study of horizontal applied force which floodwater acts on the bridge constructure[J]. Journal of Chongqing Jiaotong Institute, 1996, 15(2): 2-6. [6] 杨斌,郑银功,吴珷,等. 洪水期间板桥桥面水流阻力的计算[J]. 重庆交通学院学报,1996,15(3): 1-4,10.YANG Bin, ZHENG Yingong, WU Wu, et al. Calculation of stream drag of the flat bridge ’s surface during the flood[J]. Journal of Chongqing Jiaotong Institute, 1996, 15(3): 1-4,10. [7] 杨斌,郑银功,庹瑶,等. 洪水对桥梁结构的压力测试试验与桥梁安全分析[J]. 重庆交通学院学报,1997,16(1): 1-7.YANG Bin, ZHENG Yingong, TUO Yao, et al. Floodwater pressure testing and safety analysis of the bridge constructure[J]. Journal of Chongqing Jiaotong Institute, 1997, 16(1): 1-7. [8] 肖盛燮, 凌天清, 陈世民, 等. 公路与桥梁抗洪分析[M]. 北京: 人民交通出版社, 1999: 58-71 [9] 曹芳,肖盛燮. 洪水主流变异对桥梁结构的破坏分析及其防患[J]. 重庆交通学院学报,2006,25(6): 27-30.CAO Fang, XIAO Shengxie. The destruction analysis of bridge structures due to the mainstream variance of the flood and the corresponding preventive measures[J]. Journal of Chongqing Jiaotong Institute, 2006, 25(6): 27-30. [10] 张辉. 山洪、流冰对桥梁的破坏机理及计算模式研究[D]. 大连: 大连理工大学, 2001. [11] MALAVASI S, GUADAGNINI A. Hydrodynamic loading on river bridges[J]. Journal of Hydraulic Engineering, 2003, 129(11): 854-861. doi: 10.1061/(ASCE)0733-9429(2003)129:11(854) [12] KERENYI K, SOFU T, GUO J. Hydrodynamic forces on inundated bridge decks[R]. McLean: Turner-Fairbank Highway Research Center of Federal Highway Administration, United States Department of Transportation, 2009. [13] 邵鹏. 洪水作用下简支箱型梁桥结构安全性研究[D]. 重庆: 重庆大学, 2015. [14] 庄一舟,徐亮,任卫岗,等. 整体式桥台无缝桥梁抗洪性能分析[J]. 福州大学学报(自然科学版),2016,44(7): 472-479,486.ZHUANG Yizhou, XU Liang, REN Weigang, et al. Research on flooding-resistant performance of integral abutment jointless bridge[J]. Journal of Fuzhou University (Natural Science Edition), 2016, 44(7): 472-479,486. [15] 吴安杰,杨万理,赵雷. 洪水对桥墩的瞬间冲击效应[J]. 公路交通科技,2018,35(6): 67-73.WU Anjie, YANG Wanli, ZHAO Lei. Moment impact effect of flood on bridge pier[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 67-73. [16] 杨万理,吴承伟,朱权龙,等. 桥梁墩柱三维绕流特性精细化研究[J]. 西南交通大学学报,2020,55(1): 134-143. doi: 10.3969/j.issn.0258-2724.20180335YANG Wanli, WU Chengwei, ZHU Quanlong, et al. Refined study on 3D flow characteristics around bridge piers[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 134-143. doi: 10.3969/j.issn.0258-2724.20180335 [17] 金沙江白格堰塞湖洪峰过境水面高出桥面12米四川实现“零伤亡”. 人民网四川频道 [EB/OL]. （2018-11-15） [2020-10-11]. https://www.sohu.com/a/275586924_99960442 [18] NADERI N. Numerical simulation of hydrodynamic forces on bridge decks[D]. Delft: Delft University of Technology, 2018. [19] 吴龙旺. 中小跨度桥梁上部结构海啸作用力研究[D]. 成都: 西南交通大学, 2017. -
下载:
点击查看大图
计量
- 文章访问数: 401
- HTML全文浏览量: 240
- PDF下载量: 19
- 被引次数: 0