Simplified Prediction Method for PGA Amplification Factors Corrected by Site Conditions
-
摘要:
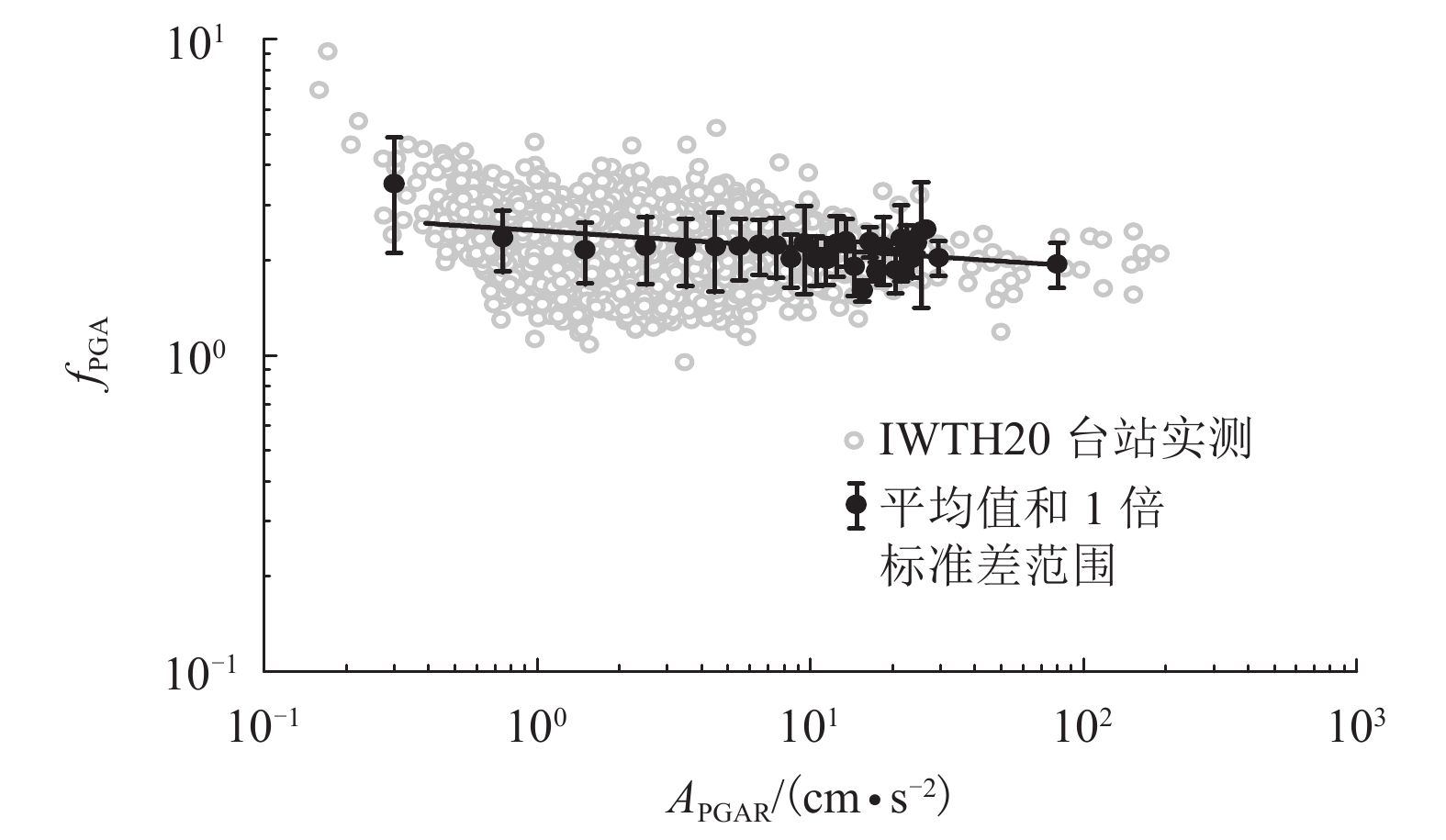
地表峰值加速度（peak ground-motion acceleration，PGA）是直观反映地震动强度的一个物理量，概念清晰且工程应用方便. 场地条件校正的PGA及其校正方法是特定工程抗震设计需要解决的问题. 为此，选取日本具有地表和井下记录KiK-net台网的32个台站及地震数据，通过对实测地震数据分析，提出了一种场地校正的PGA放大系数（
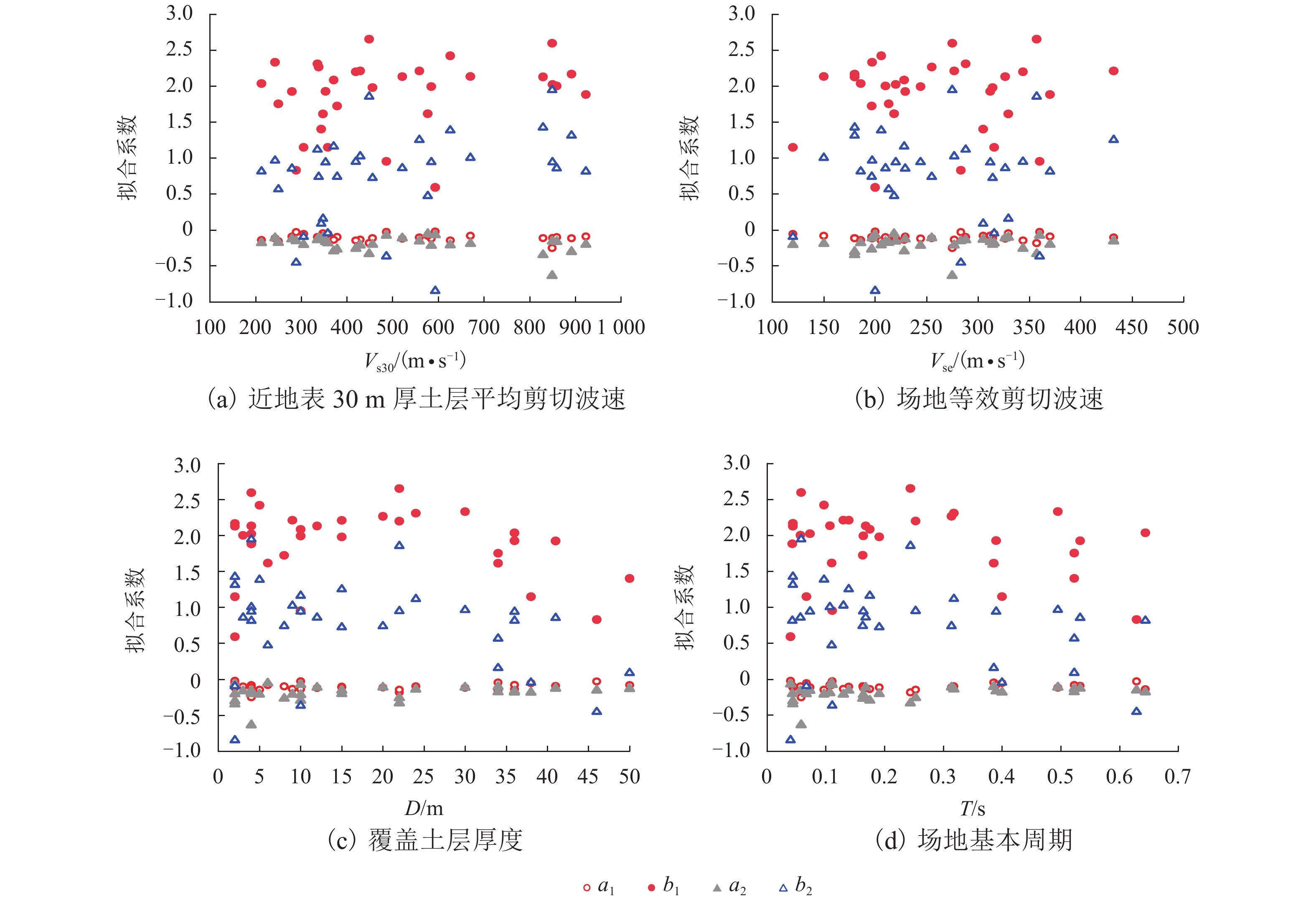
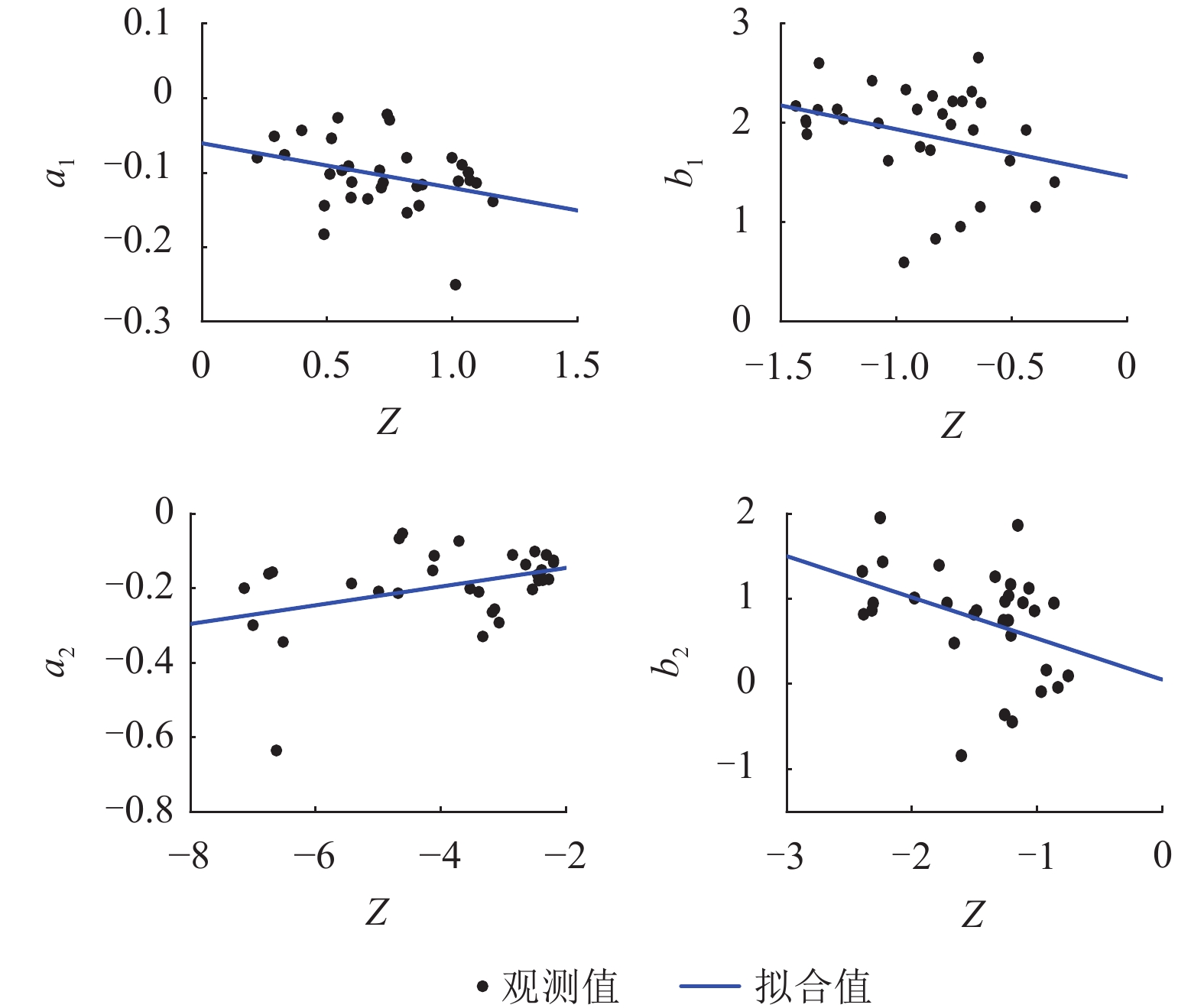
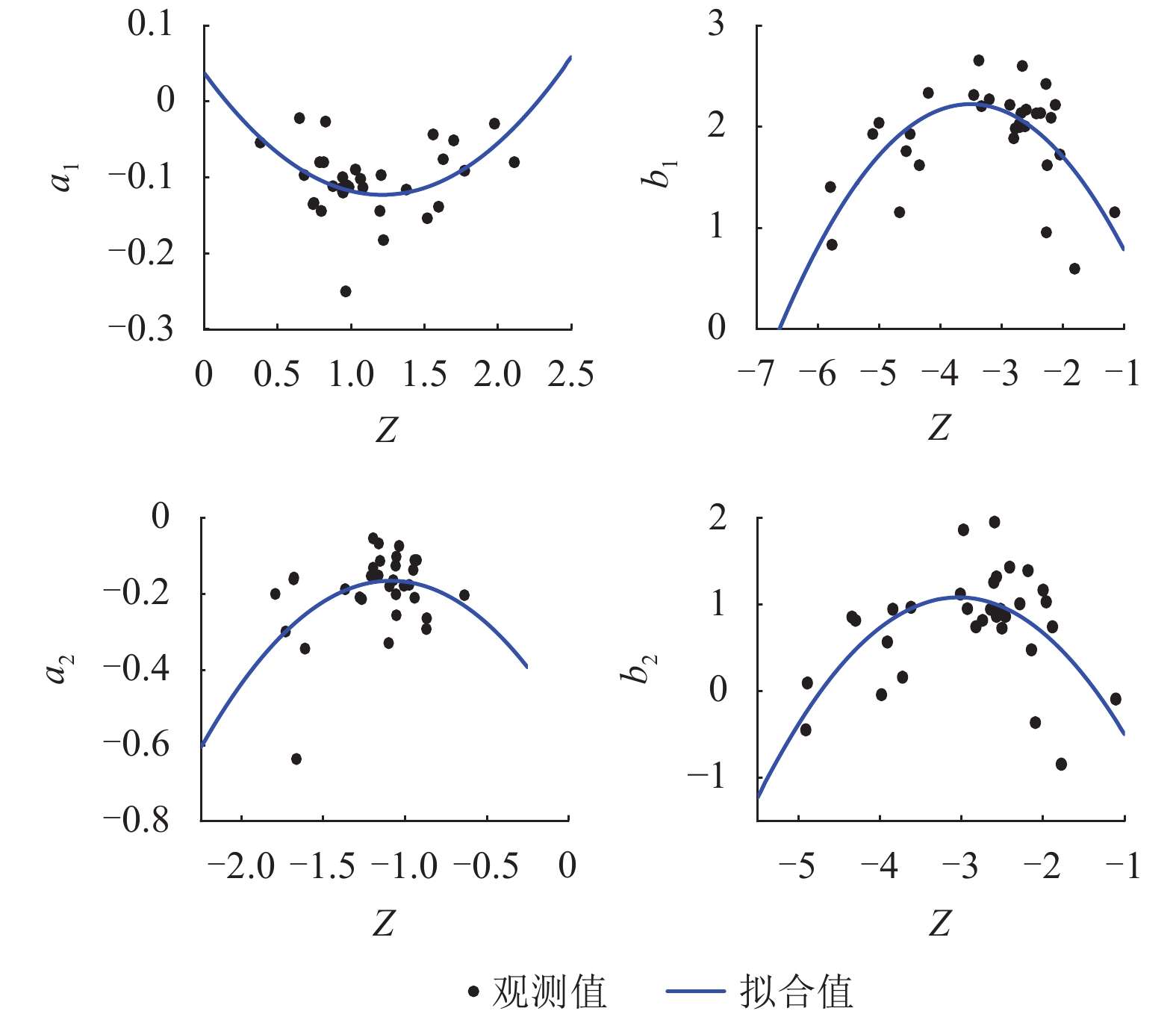
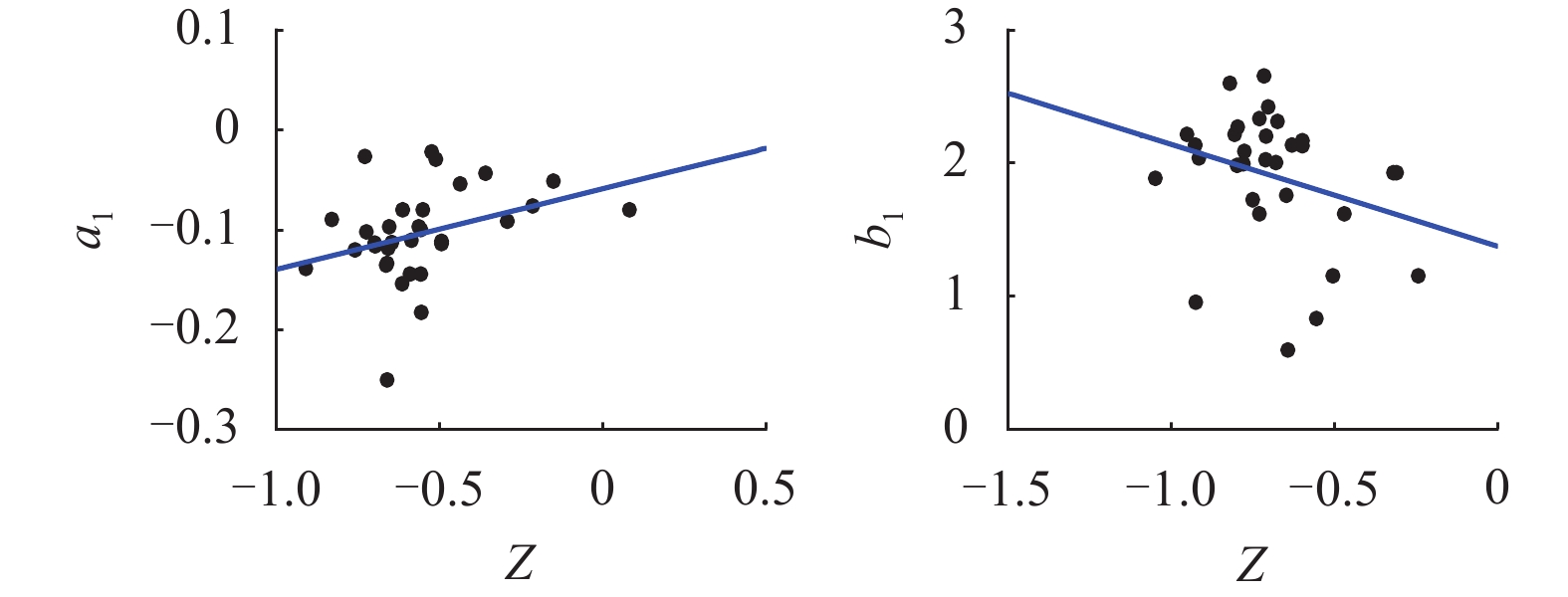
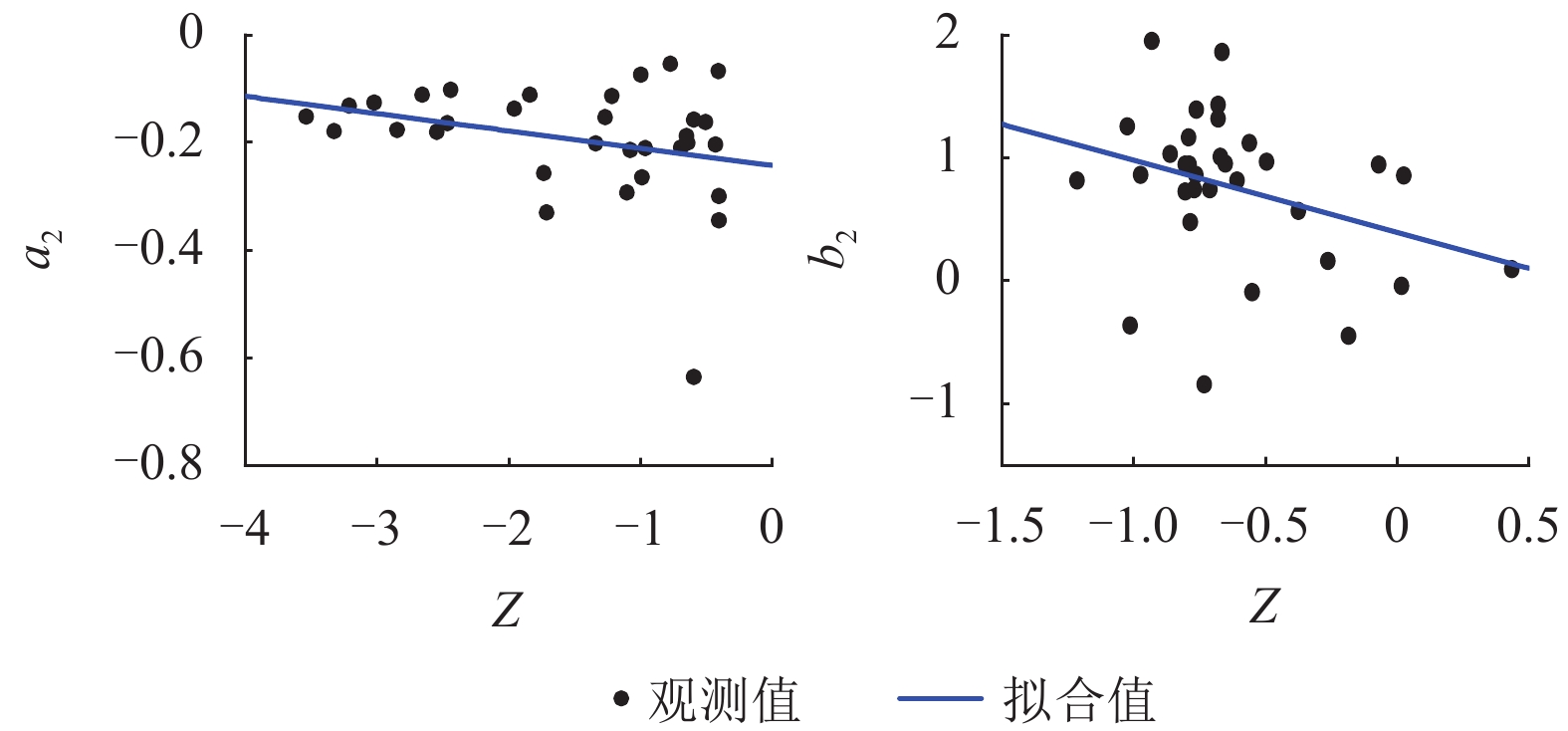
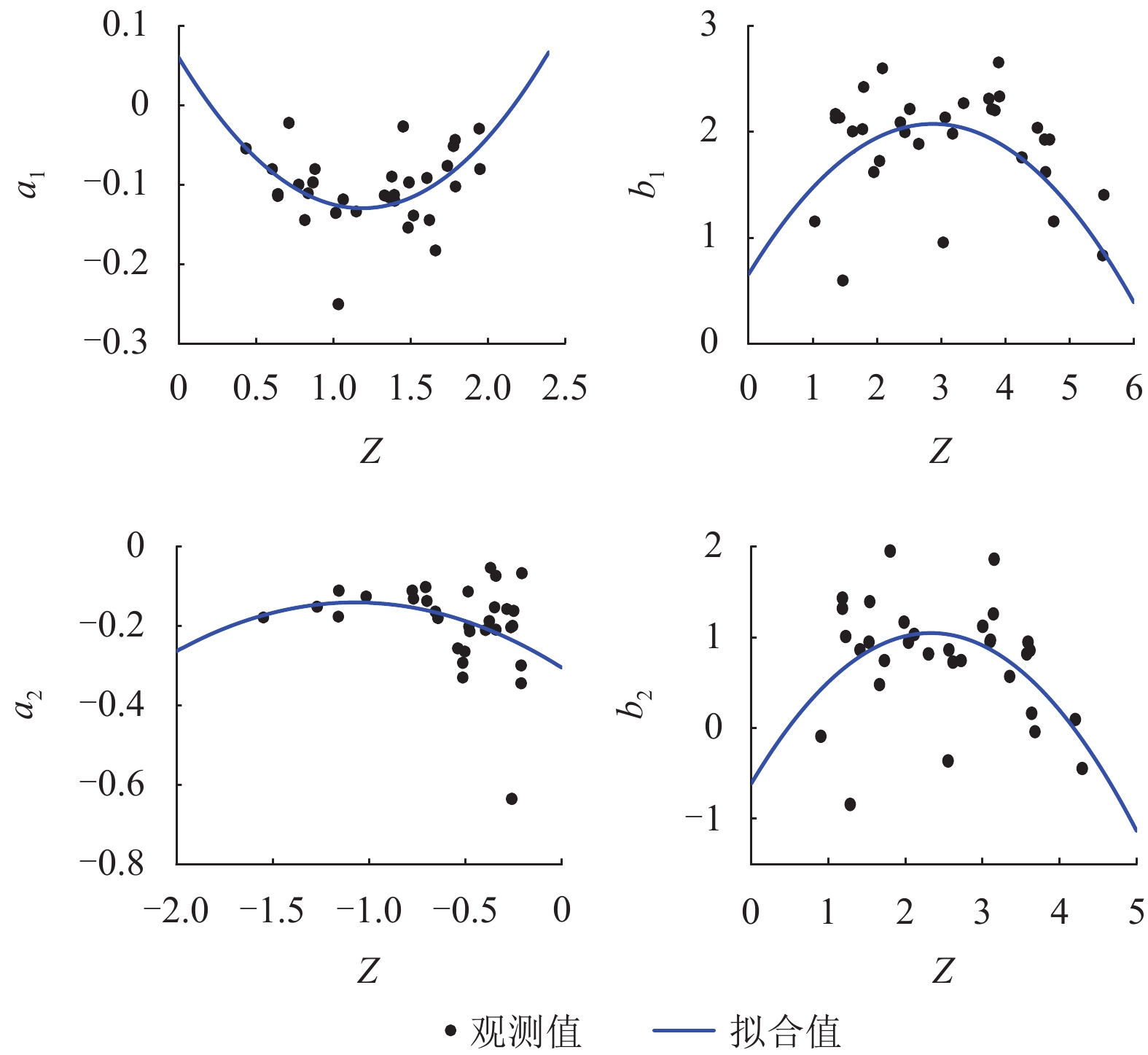
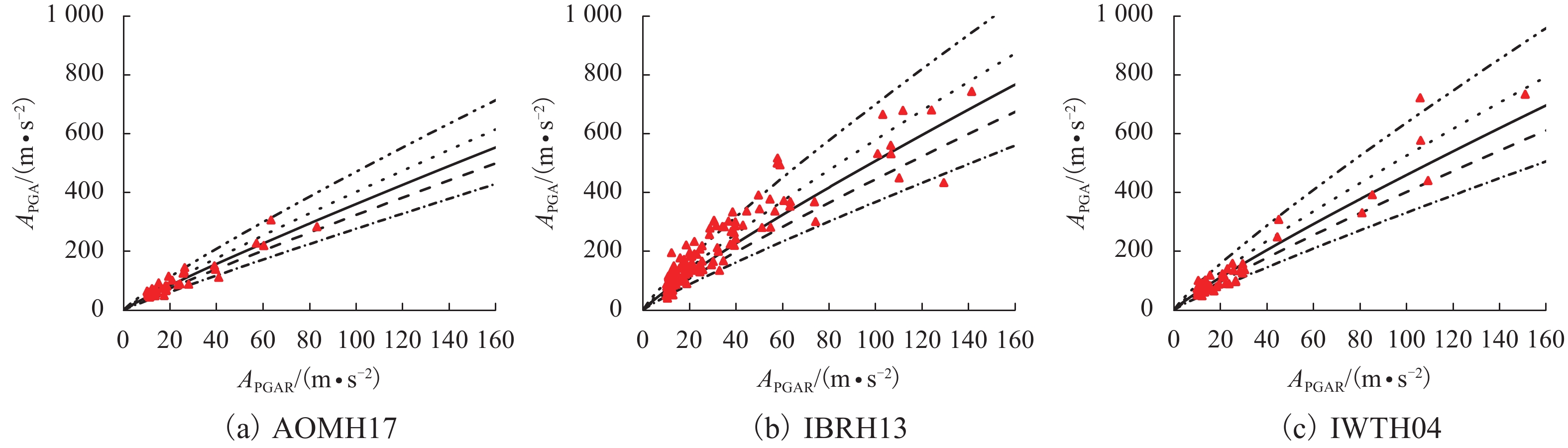
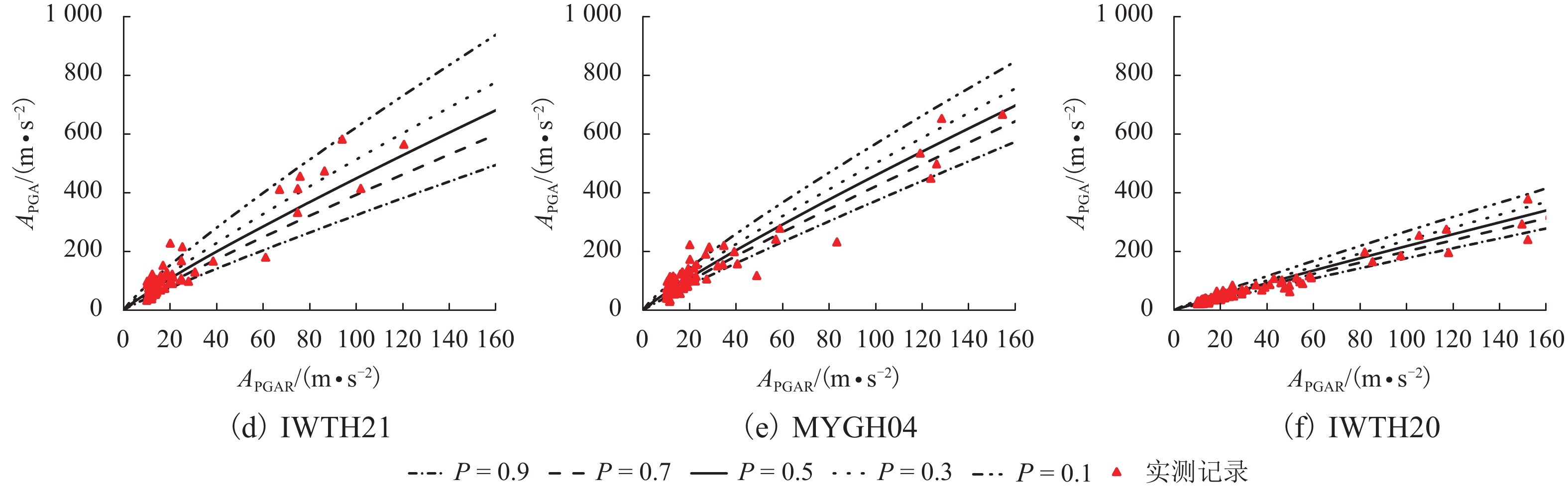
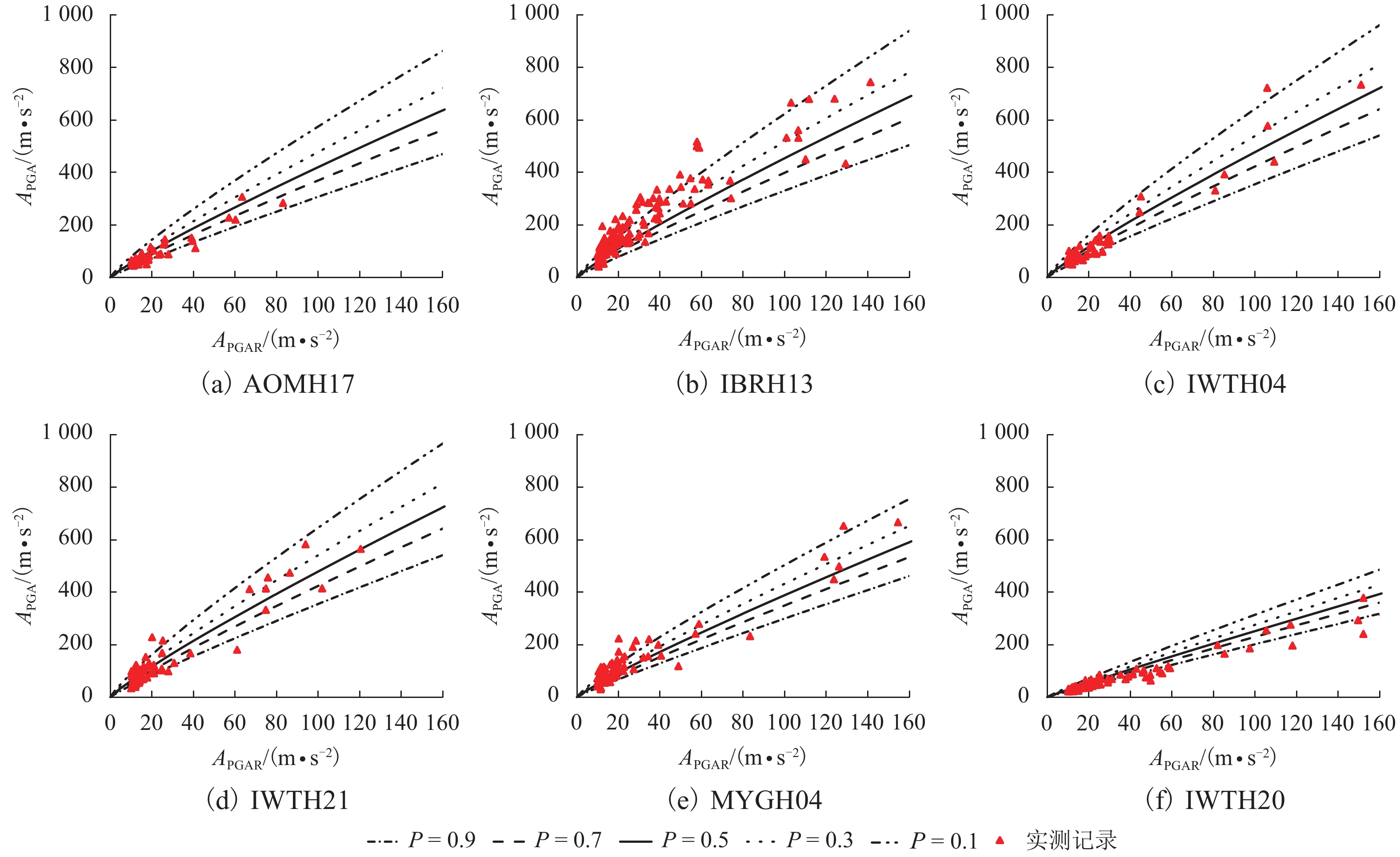
f PGA）的简化估计方法. 该方法通过数据回归给出f PGA概率密度函数参数与场地特征参数线性组合之间的线性和二次函数形式的拟合公式；并采用f PGA概率预测模型，提出了多超越概率水平地表PGA值的预测方法. 数据分析结果显示：场地f PGA具有随机不确定性，可以采用对数正态分布函数模拟，其概率密度函数的参数（均值和标准差）与单一场地特征参数相关性较小，但与场地特征参数的线性组合相关性较大. 模型预测值与实测数据吻合较好，验证了简化估计方法的可行性.Abstract:Peak ground-motion acceleration (PGA) directly reflects ground shaking intensity with the advantages in conceptual clarity and engineering application. Prediction of PGA, along with site condition correction, needs to be handled in site-specific seismic design. In this work, 32 stations and the earthquake data recorded are collected from the KiK-net strong motion array, Japan, so as to propose a simplified method to predict PGA amplification factors (
f PGA) corrected by site condition. Linear and quadratic empirical formulae of thef PGA possibility model parameters with respect to the combinations of site characteristic parameters are obtained via regression analysis. Using thef PGA model, ground surface PGA values, corrected by site conditions, can be predicted under different exceedance probability levels. Data analysis indicates thatf PGA is variable but can be simulated by a log-normally distributed function, of which mean and standard deviation are less correlated with a single site characteristic parameter but have good correlation with the linear combinations of the site characteristic parameters. The reasonable agreement between the predictions and records testifies the feasibility of the proposed method.-
Key words:
- seismic data /
- PGA amplification factor /
- site correction /
- simplified method /
- KiK-net
-
降雨是诱发边坡失稳的主要因素之一[1-3]，在我国，每年几乎均有降雨诱导的滑坡. 因此，降雨作用下边坡稳定性问题受到科研人员的广泛关注. 雨水诱导边坡失稳特征及过程对人们理解边坡破坏特征、提出合理的稳定性分析方法具有重要作用. 一些学者通过室内试验研究了边坡失稳的多种破坏特征[4-8]，结果表明，初始滑坡的时间主要取决于坡趾附近土体的饱和程度, 若坡趾附近土体接近饱和，不论其他部位饱和与否，土坡总会发生局部失稳破坏. 为了研究降雨诱导边坡失稳机制，人们从多角度解释相关物理现象. 已有研究表明，边坡失稳过程中产生了高孔隙水压力[4-5,9-10]，而有的研究也发现当高孔隙水压力出现时边坡并不一定会发生失稳破坏[11]. 含水率对非饱和土的抗剪强度有明显影响[12-13]. 研究表明，非饱和土强度随含水率增加呈现出非线性变化特性[12,14-15]. 综合分析表明含水率和孔隙水压力在边坡内的分布特征对边坡失稳机制的解释有重要作用. 通过文献调研发现，目前对于降雨停止后边坡内孔隙水压力、含水率的空间变化尚需深入研究，雨停后边坡的失稳特征及承载力变化尚涉及较少，而这方面的内容对于边坡稳定性设计有重要作用. 另外，基覆型边坡是一种下部为基岩、上部为松散堆积体的二元结构体，很多情况下基覆界面对边坡的失稳模式有重要影响，目前对此研究较少.
基于以上分析，本文以基覆型边坡为对象，但不以某具体工程边坡为对象，而是通过概化模型进行研究. 探讨降雨作用下边坡失稳特征及对应的机制，分析雨停后不同阶段边坡的承载力变化规律，为基覆型边坡工程设计提供理论支持. 实际工程的基覆型边坡的基覆界面形状各不一样，本文对基覆界面进行抽象概化处理，采用两段直线组合模拟典型工况.
1. 相似分析
基于量纲分析法，基覆型堆积体边坡在降雨作用下稳定性及承载力的主要相似准则可表述为
zH、α、β、θ1、θ2、cγH、ϕ、ν、k√gH、Irk、 H/(tIr) 、qγH ，边坡模型示意如图1所示. 其中：z/H为边坡某位置高程z与边坡高度H之比，即相对高程，表达了该点在边坡上所处的位置信息；β 为基覆型堆积体边坡坡角；α 为边坡顶面与水平面的夹角，θ1 为基覆界面上部倾角；θ2 为基覆界面下部倾角；c/(γH) 为边坡土体的黏聚力c与边坡土体所受自重应力之比，该参数最早由Tailor于1937提出[16]，称为稳定数(stability number)，该无量纲量与边坡失稳条件密切相关，γ 为土体重度；ϕ 为土体内摩擦角，表达了土颗粒间相对运动的难易程度；ν 为泊松比；k/√gH 可理解为无量纲渗透系数，k 为土体的渗透系数；Ir/k 为降雨强度Ir与渗透系数之比，表示降雨量与入渗量之间的相对大小；H/(tIr) 为无量纲降雨持续时间（t为降雨持续时间）；q/(γH) 为边坡顶部承载力q与自重应力之比.各物理量的相似关系如表1所示.
表 1 各物理量的相似关系Table 1. Similarity law of each physical quantity物理量 相似常数 物理量 相似常数 H CH c Cc=CγCH γ Cγ ϕ 1 g Cg ν 1 β 1 Ir CIr=C0.5HC0.5g α 1 k Ck=C0.5HC0.5g z CH t Ct=C0.5HC−0.5g θ1 1 q Cq=CγCH θ2 1 在试验过程中，γ与g保持不变，则有
Cγ =1，Cg =1. 由表1可知：与原型保持一致的物理量有γ、β 、α 、θ1、θ2、ϕ、ν ；q、H、z和c，模型比尺均为CH . 模型缩尺为C0.5H 的物理量为强雨强度、渗透系数和降雨时间，即上述物理量相对于原型边坡应缩小√CH .由上可见：物理量的模型比尺主要受边坡的几何比尺所控制，所以在一定条件下，该模型可以模拟多个原型边坡. 原型边坡的高度、土性等具有不确定性，因此，一个模型边坡模拟多个原型边坡是可能的. 综上所述，本文并不是模拟某一具体的边坡，而是一类边坡的概化模型.
2. 试验方案
试验装置由研究团队自制而成（见图2），主要由不锈钢框架与有机玻璃板构成，侧面为透明有机玻璃板，制作边坡的底板由不锈钢板构成，其上可铺设不同粗糙度的泡沫板以模拟基覆界面的粗糙程度. 本文主要采用较粗糙的泡沫板来模拟基覆界面的粗糙度. 模型箱几何尺寸为： 1.8 m（长） × 0.3 m（宽） × 1.2 m（高）. 试验采用喷头式降雨器进行人工模拟降雨. 降雨强度由水泵和出水阀门控制，并用雨量计测量降雨强度，其值Ir=21.96 mm/h，根据降雨等级的划分，此降雨强度为暴雨级别.
试验采用川西某地区砂土，在试验之前对该砂土进行干燥并配置成不同的质量含水率，对不同质量含水率的砂土进行非饱和强度试验，获得土体在不同质量含水率下的强度指标，如表2、图3、4所示.
表 2 不同质量含水率条件下的强度指标Table 2. Strength index under different water moistures质量含水率/% 饱和度/% c/kPa ϕ/ （°） 0 0 0 35.89 6 25.75 2.71 32.59 12 51.50 6.09 31.15 18 77.25 6.15 30.98 23 100.00 1.16 29.88 由图3、4可知：试验所用砂土表观黏聚力（此处黏聚力主要来自毛细水压力作用）随饱和度的增加先增大后减小；砂土的ϕ则随饱和度的增大而减小. 由于含水量的增加，砂土颗粒之间受到润滑作用摩擦力减小，因此内摩擦角呈减小趋势.
试验测得砂土饱和渗透系数为0.000 31 m/s，质量含水率5%的砂土密度约为1.590 g/cm3，对应的干密度为1.514 g/cm3，此含水率下砂土的最大干密度为1.851 g/cm3, 最小干密度为1.463 g/cm3. 试验用砂的粒径级配曲线如图4所示. 由图可知：d50=0.578 mm，为粗砂，有效粒径d10=0.178 mm，控制粒径d60=0.765 mm，d30=0.37 mm. 由上可知：不均匀系数Cu= 4.3，该土为较均匀土；曲率系数为1.002（大于1.000），该土级配连续.
图 3 砂土表观黏聚力和内摩擦角随饱和度变化曲线Figure 3. Variation of sand cohesion and sand internal with saturation本试验主要使用的仪器有含水率传感器和孔隙水压力传感器，其中，含水率传感器为美国Decagon公司EC-5土壤水分传感器，该传感器综合精度为1.0%；孔隙水压力传感器是成都泰斯特公司生产的电荷型传感器，传感器量程为10 kPa, 综合精度为0.1%，也即测量误差在10 Pa左右. 在箱体侧面设置条带状白砂和箱体侧壁的初始标识线，边坡变形后，条带白砂明显偏离初始标识线，采用摄像机拍摄图像，后期进行图像处理即可得到边坡的变形. 测量仪器布置如图5所示. 图中：P1~P6为孔隙水压力传感器，W1~W6为含水率传感器，对应的为测点1~5.
试验采用质量含水率为5%的砂土. 分层填筑边坡模型，每层的填筑厚度不超过5 cm，并进行逐层夯实. 夯实完成后，利用环刀测量土体密度以及含水率，从而得到干密度，然后将边坡夯实至预设的体积. 边坡填筑完毕后间隔24 h后开始降雨试验，降雨停止后开始边坡顶部加载试验. 最终填筑完成后的边坡相对密度为0.161，土体处于疏松状态.
本试验的主要目的是进行降雨条件下基覆型边坡失稳特征及极限承载力研究，分析边坡内孔隙水压力和含水率对其稳定性的影响. 试验工况共6组（见表3）. 基覆界面下部倾角为 14°, 上部倾角为52°.
表 3 边坡降雨试验设计Table 3. Design of slope rain test工况
编号降雨持续
时间/h降雨强度/
（mm•h–1）降雨
等级雨停后加
载时间/h1 4.5 21.96 暴雨 0 2 4.5 21.96 暴雨 5 3 4.5 21.96 暴雨 10 4 4.5 21.96 暴雨 20 5 4.5 21.96 暴雨 40 6 4.5 21.96 暴雨 无加载 表3中：工况6 在降雨中仅打开两个喷头，关闭坡脚上方降雨区3的喷头，目的是观察其降雨与否对坡脚破坏的影响.
针对表2中不同质量含水率的边坡土体可计算出对应的试验边坡模型的安全系数理论值，如表4所示. 由表可见，随着边坡土体质量含水率的增大，边坡安全系数也经历了先增大后减小的变化规律.
表 4 不同含水率下边坡安全系数理论值Table 4. Safety factor of slope under different water moistures质量含水率/% 饱和度/% 安全系数 0 0 < 0.10 6 25.75 1.80 12 51.50 3.70 18 77.25 4.20 23 100.00 0.85 3. 试验结果分析与讨论
3.1 边坡破坏典型特征
以工况1为例分析边坡破坏特征. 图6给出了降雨过程中边坡失稳的发展过程.
由图6可知：由于土体初始含水率较低，砂土的渗透速率大于降雨强度，所以边坡在降雨初期未出现坡面径流现象；随着降雨的发展，在t =36 min时，在坡脚处开始出现土体流动现象（图6（b）②），而出现这一现象的原因为在降雨过程中，边坡上部土体内孔隙水逐渐汇集至坡脚，导致坡脚处土体最先达到饱和而软化，同时也存在表面雨滴的冲刷作用使土体更易失稳；由于坡脚土体逐渐被雨水软化而发生破坏，边坡坡脚处出现局部脱落 （见图6（a）③和图6（b）③）；随着降雨的持续进行，土体脱落的范围逐渐增大，进而导致上方土体临空面加大，土体破坏后随即被雨水饱和软化而向下滑动，后方土体进一步被侵蚀，最终造成了一定深度和宽度的边坡破坏现象（图6（a）④、图6（b）④）.
在前5个工况中，边坡坡脚均在30 min左右呈现流动破坏，而工况6在降雨t = 56 min时才出现边坡坡脚流动破坏（见图7）. 如前所述，边坡坡脚土体的破坏主要是土体饱和软化导致的. 工况6少了土体表面的雨水冲刷作用，且土体内部雨水入渗作用削弱，进而出现了工况6坡脚土体流动破坏晚于其他工况的现象. 此外，在工况6中，土体局部脱落体积明显小于其他工况. 由此可知：在坡脚处降雨会加速坡脚土壤的破坏. 因此，在实际的边坡治理过程中，在坡脚处应当做好排水和加固措施.
3.2 降雨前后土体体积含水率与孔隙水压力变化规律
边坡土体含水率和孔隙水压力的变化对分析边坡失稳机制有重要作用. 图8和图9给出了降雨过程中边坡土体体积含水率和孔隙水压力随时间的变化. 图8表明：降雨初期，各传感器含水率均较稳定；随着降雨的持续进行，坡体下部体积含水率首先增长，这说明雨水会首先在坡脚附近积累，随着降雨的持续进行，边坡中部和上部体积含水率依次增长（图9）.
图 8 孔隙水压力与体积含水率随时间变化曲线Figure 8. Variations of pore water pressure and water content with time由体积含水率变化曲线可知：测点3、4、5号的体积含水率均小于饱和状态下的体积含水率，即未达到饱和状态；测点1、2、6号处均达到饱和，所以可以判定在降雨过程中，边坡内部水位线始终处于边坡中下部，表明降雨过程中随着雨水的不断入渗，雨水逐渐从各处汇至坡脚，边坡内部水位线逐渐由坡脚上升至边坡中部（图9）. 由此可见边坡坡脚处土体最先饱和，因此坡脚最先发生破坏（图6（b）②）.
降雨过程中，边坡表面体积含水率首先开始上升，随着降雨的进行而趋于稳定，随后土体内部体积含水率由外到里依次增加. 在雨水入渗至边坡坡脚处基覆界面之后，该区域土体的体积含水率开始增大，并达到饱和状态. 当坡脚基覆界面附近土体含水量达到饱和后，边坡中的水位开始逐渐上升，在降雨作用下由下至上各测点土体依次达到饱和. 由此也进一步解释了随着降雨的持续进行，边坡坡脚土体局部脱落范围不断增大的原因.
图 9 边坡内体积含水率不同时间的空间分布Figure 9. Spatial distribution of moisture content in slope at different time由图9（a）可知：雨停后土体含水率随即开始下降；边坡上部（W5、W4传感器处）所在土体体积含水率最先开始下降，最后稳定在17%左右；边坡下部表层土体（W6号传感器处）也很快开始下降，直至稳定在33%左右；与边坡上部及表层土体（W4、W5、W6号传感器位置）不同，边坡坡角及基覆界面处土体含水率下降缓慢. 由上可知：降雨停止过后，边坡土体内部水位线不断下降. 雨停后较长时间内，在基覆界面和坡脚处均存在残留水，所以测点1、2、3处土体体积含水率始终保持在饱和含水率附近，其体积含水率时程曲线变化较小，数值较为平稳.
图10为降雨过程中孔隙水压力随时间的变化. 由图8和图10表明：各测点孔隙水压力值在降雨初期基本没有变化；随着降雨的持续，边坡内各测点孔隙水压力值从外到里依次增加，并且边坡中下部孔隙水压力最先趋于稳定，并达到正峰值，表明降雨过程中边坡土体水位线由坡脚逐渐上升至边坡中部，这与前述结论一致，而边坡中上部孔隙水压力稳定峰值均为负值，表明降雨过程中边坡中上部土体在降雨过程中均始终处于水位线以上. 由此可见：边坡坡脚处孔隙水压力最先达到正值，从而使该处土体有效应力最先减小，也促使其最先破坏.
由图9（b）可以看出：各测点孔隙水压力数值都有所变化. 边坡上部土体（测点4、5号处）孔隙水压力迅速下降；边坡中下部土体孔隙水压力也呈现下降趋势，但与上部相比下降速率较为缓慢；而坡脚处孔隙水压力下降速率则非常缓慢.
从以上分析可见：降雨过程中边坡土体含水率与坡内孔隙水压力呈同方向变化，含水率增加，孔隙水压力增大，含水率稳定时孔隙水压力也稳定，含水率下降，孔隙水压力也相应下降，土体含水率与孔隙水压力几乎同步变化.
图 10 边坡内孔隙水压力不同时刻的空间分布Figure 10. Spatial distribution of pore water pressure in slope at different times3.3 边坡失稳机制分析
通过对边坡含水率、孔隙水压力分布和边坡失稳特征的分析，发现在降雨作用下边坡坡脚附近土体含水率和孔隙水压力增长最快，此处土体最先达到饱和，且孔隙水压力最高，饱和后随着降雨的进行，土体从塑态过渡到流态，土体几乎失去了强度，从而坡脚土体发生了破坏. 随着降雨持续进行，从坡脚至坡体中下部含水率和孔隙水压力逐渐升高，部分区域土体也达到饱和状态而发生失稳，因此出现了边坡失稳逐渐从坡脚向坡中发展的现象. 在降雨持续一定时间后，边坡内土体含水量将达到较高值，此时土体强度将较大幅度减小，整个边坡稳定性进一步降低，随着边坡坡脚土体的变形而失去承载力，最终整个边坡将发生整体失稳.
3.4 雨停后各工况边坡极限承载力及破坏模式
试验表明：经过4.5 h降雨后，边坡仅在坡脚处发生了局部破坏，并未发生整体破坏，边坡尚有较高地承载力，在其顶部能够承受一定大小的静荷载. 当降雨结束后的不同时间内，边坡所能承受的极限静荷载是否会发生变化，如有变化，其变化规律是怎样的，这对于实际工程有一定的指导意义. 基于此，本文探讨了降雨停止后边坡极限承载力的变化规律及其对应的破坏模式. 加载方式通过短时间内在边坡顶面分级施加静荷载来探讨边坡承载力的大小. 每级荷载大小控制在5 kg以内，前期用大值，临近破坏时用小值. 这样保证了每个工况加荷等级在10级以上，且能较好地控制误差. 由各工况试验现象可以看出，边坡在顶部静荷载作用下破坏模式可概括为整体滑移模式和局部滑移模式，如图11~13所示. 对工况1而言，在雨水浸泡及渗流作用下，降雨刚停止时边坡土体含水率高，孔隙水压力高，基质吸力小，边坡稳定性较弱，当坡顶的静荷载较小时，边坡滑移面出现在基覆界面附近（图13）. 从工况2~5可以发现，降雨停止后，边坡内部水体逐渐从坡脚流出，边坡土体含水率逐渐下降，孔隙水压力逐渐减小，基质吸力逐渐增大，从而土体抗剪强度有所提高，最终使得边坡破坏模式为局部滑移，即在中上部位置破坏面沿基覆界面滑动，在中下部位置破坏面沿坡体内部发展，最后在坡脚上部某一位置剪出.
图14给出了边坡极限荷载与雨停后时间的变化曲线. 从图可看出：降雨停止后，边坡所能承受的极限荷载先增大后减小，最后趋于稳定，表明边坡稳定性在降雨停止时刻最小，随时间增加，稳定性逐渐增大，在某一时刻达到最大，随时间进一步增大，边坡稳定性略有减小直至稳定不变. 该现象可根据前述砂土的强度指标随含水率的变化规律进行解释. 从图3可知：随着砂土含水率从饱和开始降低，其黏聚力经历了逐渐增大然后减小的规律，而内摩擦角呈缓慢减小趋势. 从边坡稳定性系数的理论分析结果（见表4）可知：其稳定性在边坡饱和时很低. 结合已有研究结果[17]，在含水率从饱和开始下降，砂土强度也经历了一个先增大后减小的过程. 因此当降雨停止一段时间后，砂土强度增大到最大值，边坡极限承载力最高. 其后含水率稳定，边坡极限承载力也稳定在一定值.
图 14 边坡顶部极限载荷随雨停后时间的变化Figure 14. Variation of ultimate load with time after rain stop4. 结 论
本文对降雨作用下基覆型边坡失稳特征及承载力进行了试验研究，得出了以下结论：
1） 降雨作用下边坡坡脚附近土体含水率增长最快，孔隙水压力最先达到正值，土体最先发生破坏. 随降雨的进行，边坡内水位逐步上升，边坡破坏位置逐步从坡脚向上发展.
2） 降雨停止后，边坡内土体含水率和孔隙水压力随即开始下降，而坡脚处含水率和孔隙水压力下降速率非常缓慢，雨停后相当长一段时间内仍保持较高数值. 边坡内土体含水率与孔隙水压力几乎保持同步变化.
3） 雨停后随着时间的推移，边坡所能承受的极限荷载呈增大—减小—稳定不变的变化趋势，即边坡稳定性在降雨停止时刻最小，随时间增加，稳定性逐渐增大，在某一时刻达到最大，随时间进一步增大，边坡稳定性略有减小直至稳定不变.
4） 雨停后基覆型边坡在顶部静荷载作用下破坏模式主要呈现两种模式，即整体滑移模式和局部滑移模式.
-
图 2 IWTH20台站实测fPGA随APGAR的分布
Figure 2. Distribution of fPGA from IWTH20 with respect to APGAR
图 3 拟合系数与场地特征参数的分布
Figure 3. Scattering of regressive coefficients with respect to site characteristic parameters
图 4 拟合系数和Z(Vs30, D, T)线性拟合曲线与实测数据对比
Figure 4. Regressive coefficients linearly predicted by Z(Vs30, D, T) compared with real data
图 5 拟合系数和Z(Vs30, D, T)二次函数拟合曲线与实测数据对比
Figure 5. Regressive coefficients quadratically predicted by Z(Vs30, D, T) compared with real data
图 6 拟合系数和Z(Vse, D, T)线性拟合曲线与实测数据对比
Figure 6. Regressive coefficients linearly predicted by Z(Vse, D, T) compared with real data
图 7 拟合系数和Z(Vse, D, T)二次函数拟合曲线与实测数据对比
Figure 7. Regressive coefficients quadratically predicted by Z(Vse, D, T) comparing with data
图 8 多概率水平下地表PGA预测值与实测数据对比（中间变量Z = C1Vs30 + C2D + C3T）
Figure 8. Prediction of surface PGA under different probability levels compared to observed data (Z = C1Vs30 + C2D + C3T)
图 9 多概率水平下地表PGA预测值与实测数据对比（中间变量Z = C1Vse + C2D + C3T）
Figure 9. Prediction of surface PGA under different probability levels compared to observed data (Z = C1Vse + C2D + C3T)
表 1 所选Kik-net台站场地特征参数
Table 1. Site characteristic parameters from KiK-net
台站 Vs30/(m•s−1) Vse/( m•s−1) D/m T/s 台站 Vs30/(m•s−1) Vse/( m•s−1) D/m T/s AOMH17 378.4 196.6 8 0.163 IWTH26 371.1 228.2 10 0.175 FKSH09 584.6 244.2 10 0.164 IWTH27 670.3 150.0 4 0.107 FKSH12 448.5 357.1 22 0.244 KMMH02 576.7 218.4 6 0.110 FKSH19 338.1 255.0 20 0.314 KMMH16 279.7 229.2 41 0.533 IBRH11 242.5 197.1 30 0.495 KSRH03 249.8 213.2 34 0.523 IBRH13 335.4 288.0 24 0.318 KSRH10 212.9 185.9 36 0.644 IBRH14 829.1 180.0 2 0.044 MYGH04 849.8 220.0 4 0.073 IBRH16 626.1 205.9 5 0.097 MYGH05 305.3 120.0 2 0.067 IBRH18 558.6 432.0 15 0.139 MYGH06 593.1 200.0 2 0.040 IWTH04 455.9 314.3 15 0.191 MYGH09 358.2 315.8 38 0.400 IWTH05 429.2 276.9 9 0.130 MYGH10 347.5 329.6 34 0.386 IWTH18 891.6 180.0 2 0.044 MYGH11 859.2 210.0 3 0.057 IWTH20 288.8 283.4 46 0.629 TCGH07 419.5 343.8 22 0.253 IWTH21 521.1 326.5 12 0.168 TCGH12 343.7 305.1 50 0.523 IWTH23 922.9 370.0 4 0.043 TCGH14 849.0 275.0 4 0.058 IWTH24 486.4 360.0 10 0.111 TKCH08 353.2 312.0 36 0.390 
下载: 导出CSV
表 2 选取台站拟合系数
Table 2. Regressive parameters for selected station sites
台站 a1 b1 a2 b2 台站 a1 b1 a2 b2 AOMH17 −0.098 1.724 −0.266 0.741 IWTH26 −0.136 2.085 −0.294 1.163 FKSH09 −0.119 1.994 −0.215 0.945 IWTH27 −0.081 2.134 −0.189 1.005 FKSH12 −0.183 2.654 −0.331 1.855 KMMH02 −0.081 1.617 −0.054 0.473 FKSH19 −0.114 2.266 −0.111 0.740 KMMH16 −0.092 1.924 −0.127 0.854 IBRH11 −0.117 2.332 −0.112 0.966 KSRH03 −0.155 1.754 −0.177 0.567 IBRH13 −0.098 2.311 −0.138 1.118 KSRH10 −0.139 2.036 −0.179 0.816 IBRH14 −0.112 2.128 −0.346 1.427 MYGH04 −0.111 2.023 −0.158 0.943 IBRH16 −0.145 2.421 −0.209 1.386 MYGH05 −0.055 1.149 −0.204 −0.094 IBRH18 −0.103 2.211 −0.154 1.253 MYGH06 −0.022 0.592 −0.068 −0.846 IWTH04 −0.113 1.980 −0.201 0.724 MYGH09 −0.052 1.149 −0.181 −0.046 IWTH05 −0.134 2.212 −0.211 1.026 MYGH10 −0.044 1.614 −0.102 0.157 IWTH18 −0.115 2.168 −0.301 1.314 MYGH11 −0.100 2.002 −0.162 0.859 IWTH20 −0.030 0.831 −0.152 −0.453 TCGH07 −0.145 2.200 −0.257 0.951 IWTH21 −0.120 2.133 −0.114 0.860 TCGH12 −0.081 1.402 −0.132 0.089 IWTH23 −0.090 1.884 −0.201 0.815 TCGH14 −0.251 2.596 −0.636 1.947 IWTH24 −0.027 0.954 −0.075 −0.365 TKCH08 −0.077 1.927 −0.165 0.941
下载: 导出CSV
表 3 Vs30、D和T参数组合Z情况下待定系数值
Table 3. Regressive coefficients corresponding to Z in combination of Vs30, D and T
函数类型 待定系数 拟合系数 a1 b1 a2 b2 线性函数 C1 0.001 −0.002 −0.008 −0.003 C2 −0.044 0.045 0.051 0.044 C3 3.905 −3.946 −3.946 −3.935 C4 −0.061 1.456 −0.096 0.049 C5 −0.060 −0.479 0.025 −0.483 二次函数 C1 0.001 −0.003 −0.002 −0.003 C2 0.031 −0.062 −0.003 −0.046 C3 0.409 −3.445 −0.788 −3.235 C4 0.038 −0.589 −0.550 −2.427 C5 −0.265 −1.603 −0.707 −2.311 C6 0.109 −0.228 −0.325 −0.381
下载: 导出CSV
表 4 Vse、D和T参数组合Z情况下待定系数值
Table 4. Regressive coefficients corresponding to Z in combination of Vse, D and T
函数类型 待定系数 拟合系数 a1 b1 a2 b2 线性函数 C1 −0.002 −0.003 −0.001 −0.004 C2 0.057 0.060 −0.017 0.071 C3 −3.932 −3.884 −3.922 −3.899 C4 −0.059 1.377 −0.243 0.393 C5 0.081 −0.764 −0.032 −0.587 二次函数 C1 0.004 0.006 −0.001 0.006 C2 0.007 0.043 0.028 0.021 C3 1.020 2.734 −3.786 2.767 C4 0.094 0.651 −0.305 −0.614 C5 −0.347 0.990 −0.306 1.424 C6 0.134 −0.172 −0.143 −0.306
下载: 导出CSV
表 5 不同方法中拟合系数的残差平方和
Table 5. Sum of squared residuals of regressive coefficients in different methods
中间变量 函数类型 拟合系数残差平方和 a1 b1 a2 b2 Z(Vs30, D, T) 线性函数 0.060 7.042 0.312 10.459 二次函数 0.054 4.364 0.296 7.734 Z(Vse, D, T) 线性函数 0.060 6.857 0.334 10.937 二次函数 0.051 5.672 0.328 9.708
下载: 导出CSV
-
[1] 李晰,何澜,李倩,等. 脉冲型地震动对CFST拱桥抗震性能的影响分析[J]. 西南交通大学学报,2019,54(4): 731-740. doi: 10.3969/j.issn.0258-2724.20180855LI Xi, HE Lan, LI Qian, et al. Effect of pule-like ground motion on seismic performance of concrete-filled steel tubular arch bridge[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 731-740. doi: 10.3969/j.issn.0258-2724.20180855 [2] 李小军. 地震动参数区划图场地条件影响调整[J]. 岩土工程学报,2013,35(S2): 21-29.LI Xiaojun. Adjustment of seismic ground motion parameters considering site effects in seismic zonation map[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 21-29. [3] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 中国地震动参数区划图: GB 18306—2015[S]. 北京: 中国标准出版社, 2016. [4] ANDREOTTI G, FAMÀ A, LAI C G. Hazard-dependent soil factors for site-specific elastic acceleration response spectra of Italian and European seismic building codes[J]. Bulletin of Earthquake Engineering, 2018, 16(12): 5769-5800. doi: 10.1007/s10518-018-0422-9 [5] 张红才,金星,李军,等. 地震预警系统研究及应用进展[J]. 地球物理学进展,2013,28(2): 706-719. doi: 10.6038/pg20130219ZHANG Hongcai, JIN Xing, LI Jun, et al. Progress of research and application of earthquake early warning system (EEWs)[J]. Progress in Geophysics, 2013, 28(2): 706-719. doi: 10.6038/pg20130219 [6] 俞言祥,汪素云. 青藏高原东北地区水平向基岩加速度峰值与反应谱衰减关系[J]. 地震学报,2004,26(6): 591-600. doi: 10.3321/j.issn:0253-3782.2004.06.004YU Yanxiang, WANG Suyun. Attenuation relations for horizontal peak ground acceleration and response spectrum in northeastern Tibetan Plateau region[J]. Acta Seismologica Sinica, 2004, 26(6): 591-600. doi: 10.3321/j.issn:0253-3782.2004.06.004 [7] BOORE D M, ATKINSON G M. Ground-motion prediction equations for the average horizontal com- ponent of PGA,PGV,and 5%-damped PSA at spectral periods between 0.01 s and 10.0 s[J]. Earthquake Spectra, 2008, 24(1): 99-138. doi: 10.1193/1.2830434 [8] DU K, DING B R, LUO H, et al. Relationship between peak ground acceleration,peak ground velocity,and macroseismic intensity in Western China[J]. Bulletin of the Seismological Society of America, 2019, 109(1): 284-297. doi: 10.1785/0120180216 [9] 陈龙伟,陈玉祥,袁晓铭. 基于强震数据的场地反应项分析及地震动参数预测[J]. 土木工程学报,2019,52(2): 97-105,117.CHEN Longwei, CHEN Yuxiang, YUAN Xiaoming. Site-term analysis and site-specific ground-motion parameters prediction based on strong motion data[J]. China Civil Engineering Journal, 2019, 52(2): 97-105,117. [10] FACCIOLI E, PAOLUCCI R, VANINI M. Evaluation of probabilistic site-specific seismic-hazard methods and associated uncertainties,with applications in the Po Plain,northern Italy[J]. Bulletin of the Seismological Society of America, 2015, 105(5): 2787-2807. doi: 10.1785/0120150051 [11] SHINGAKI Y, GOTO H, SAWADA S. Evaluation performance for site amplification factors:S-wave impedance vs. VS30[J]. Soils and Foundations, 2018, 58(4): 911-927. doi: 10.1016/j.sandf.2018.05.001 [12] TAVAKOLI H, SOLEIMANI KUTANAEI S. Evaluation of effect of soil characteristics on the seismic amplification factor using the neural network and reliability concept[J]. Arabian Journal of Geosciences, 2015, 8(6): 3881-3891. doi: 10.1007/s12517-014-1458-z [13] HASANCEBI N, ULUSAY R. Evaluation of site amplification and site period using different methods for an earthquake-prone settlement in Western Turkey[J]. Engineering Geology, 2006, 87(1/2): 85-104. [14] REGNIER J, BONILLA L F, BERTRAND E, et al. Influence of the VS profiles beyond 30 m depth on linear site effects:assessment from the KiK-net data[J]. Bulletin of the Seismological Society of America, 2014, 104(5): 2337-2348. doi: 10.1785/0120140018 [15] SANDıKKAYA M A, AKKAR S, BARD P Y. A probabilistic procedure to describe site amplification factors for seismic design codes[J]. Soil Dynamics and Earthquake Engineering, 2019, 126: 105068. doi: 10.1016/j.soildyn.2018.01.050 [16] 中国建筑科学研究院. 建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010. [17] 李瑞山,袁晓铭. 成层场地基本周期简化计算方法研究[J]. 岩土力学,2019,40(8): 3227-3235.LI Ruishan, YUAN Xiaoming. Simplified calculation method for the fundamental period of layered soil sites[J]. Rock and Soil Mechanics, 2019, 40(8): 3227-3235. [18] WANG Suyang, SHI Yang, JIANG Weiping, et al. Estimating site fundamental period from shear-wave velocity profile[J]. Bulletin of the Seismological Society of America, 2018, 108(6): 3431-3445. doi: 10.1785/0120180103 [19] 金井清. 工程地震学[M]. 常宝琦, 张虎男, 译. 北京: 地震出版社, 1987. [20] 唐川,陈龙伟. 场地校正的地表PGA放大系数概率模型研究[J]. 工程力学,2020,37(12): 99-113. doi: 10.6052/j.issn.1000-4750.2020.01.0023TANG Chuan, CHEN Longwei. Probability modelling of PGA amplification factors corrected by site condi- tions[J]. Engineering Mechanics, 2020, 37(12): 99-113. doi: 10.6052/j.issn.1000-4750.2020.01.0023 [21] BAZZURRO P. Nonlinear soil-site effects in probabilistic seismic-hazard analysis[J]. Bulletin of the Seismological Society of America, 2004, 94(6): 2110-2123. doi: 10.1785/0120030216 期刊类型引用(2)
1. 张妙芝，李楠，周运锋. 地震作用下锚固边坡的动力响应试验与数值分析. 自动化与仪器仪表. 2024(03): 67-71 . 
百度学术2. Zhang Panpan，Zhang Lei，Zhang Zhen. Seismic fragility analysis of clay-pile-pier systems considering the optimization of ground motion intensity measures. Earthquake Engineering and Engineering Vibration. 2023(04): 965-977 . 必应学术其他类型引用(6)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 576
- HTML全文浏览量: 349
- PDF下载量: 27
- 被引次数: 8