Testing Modeling Method for Safety Critical Function of High-Speed Railway Signal System
-
摘要:
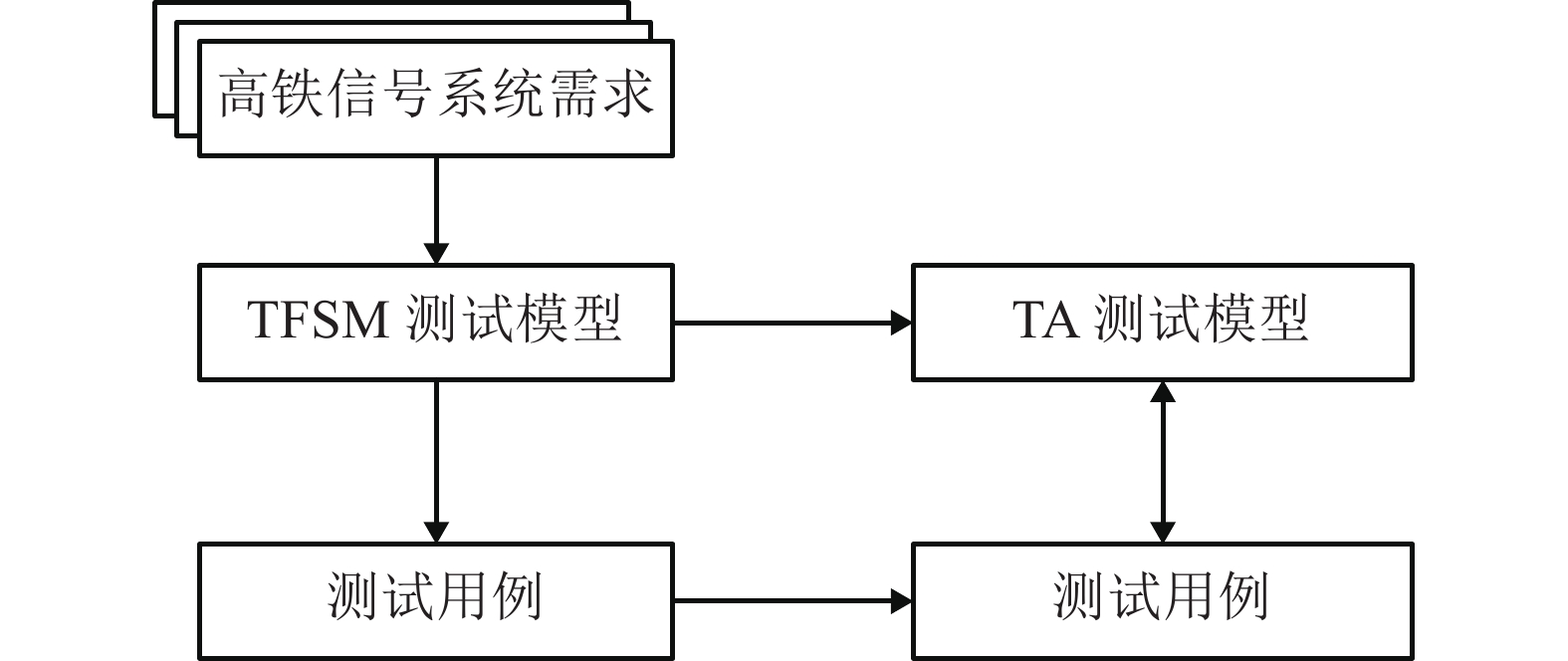
测试模型是高铁信号系统安全关键功能测试用例编制的重要基础，针对高铁信号系统安全关键功能测试建模过程中描述信号系统领域特征不够全面的问题，提出时间状态机测试建模理论和测试用例生成方法. 分析高铁信号系统测试建模的特点，提出信号系统安全关键功能测试模型的建模需求；以有限状态机理论为研究基础，结合功能逻辑和时钟约束提出时间状态机建模方法，采用Z规格说明语言给出时间状态机的形式化定义；将时间状态机转换为时间自动机，证明转换之间的一致性，并基于时间自动机的测试理论自动生成测试用例，再以计算机联锁系统中的道岔转换功能为例，建立时间状态机测试模型并生成测试用例. 最后，将两种方法生成的测试案例进行对比，结果表明：在功能逻辑方面，基于时间状态机建模方法生成的测试案例100% 地覆盖了基于时间自动机建模方法生成的测试案例，并新增了16条具有时钟约束的测试案例，能够满足高铁信号系统安全关键功能测试建模的需求.
Abstract:Testing model is an important basis to create the test cases of safety critical function of high-speed railway signal system. To solve the problem that the characteristics of signal system are not fully represented in the modeling process of safety critical function test of high-speed railway signal system, the modeling theory of timed finite state machine (TFSM) and test case generation method are proposed. The characteristics in the test modeling of high-speed railway signal system is analyzed, and the modeling requirements are put forward. Then, based on the theory of finite state machine, a modeling method of TFSM is proposed by utilizing functional logic and clock constraints, and its formal definition is established with Z notation. Further, the TFSM is transformed into timed automata, which can prove the consistency between them, and test cases are automatically generated with timed automata based testing theory. The switch conversion function of the computer interlocking system is used as an example to build the testing model of TFSM and generate the test cases. The result shows that compared with the test cases generated by timed automata, in terms of functional logic, the test cases generated by TFSM can fully cover those generated by timed automata, and add 16 more test cases with clock constraints, showing that TFSM can meet the testing modeling requirements for the safety critical function of high-speed railway signal system.
-
Key words:
- railway signal system /
- modeling method /
- timed finite state machine /
- Z notation /
- timed automata
-
动车所调车作业计划是根据动车所检修能力、场库布局形式、出入所时刻、作业项目等编制的动车所运用组织指导性文件. 它保证了动车组按时入所和上线运行，并在规定时间内利用各功能股道，实现检修、整备、调移等作业的高效协同进行. 随着我国高速铁路规模增大，上线运用动车组数量增加，传统人工编制的动车所调车作业计划存在很大的局限性，难以满足现实需求，如何自动化编制高质量的动车所调车作业计划成为动车组运用管理中亟须解决的问题.
国内外学者对动车所调车作业优化问题进行了大量研究，取得了较好成果. 王忠凯等[1]以减少关键检修线区的无效占用时间和降低调车路径费用为目标，基于动车组转线作业拓扑图，建立调车作业计划编制优化模型，采用改进蚁群算法进行求解；张惟皎等[2]考虑了存车线的列位占用，以提高存车线运用效率和减少调车走行距离为目标建立存车线运用优化模型，采用模拟退火法进行求解；王家喜等[3]考虑动车所的股道占用和进路占用冲突问题，以调车钩数最小为目标建模，并采用粒子群算法进行求解；郭小乐等[4]把动车组总延误时间最小作为优化目标，设计微进化算法进行模型的求解；Broek[5]提出了一种可自动构建分流计划的综合局部搜索方法，整合了动车组出入进路、作业任务、股道停放、列车路线，在交通规划软件和真实场景中的应用证明了该方法优于当时最先进的混合整数规划算法；Haahr等[6]首次将动车组调车优化问题和列车单元重组优化问题相结合，通过基于分枝切割的方法求解这一综合优化问题，并且对比了股道分配领域不同求解算法的性能，通过反例说明了传统最优化方法的启发式性质. 陈韬等[7]提出了将高速铁路枢纽站技术作业与动车所调车作业计划协同编制的思想，以作业效率最大化为优化目标构建模型，设计了一种基于并行禁忌搜索策略的混合算法进行求解. 韩宝明等[8]以最小化最晚完工时间为目标，建立动车所一级修灵活作业顺序的数学模型，考虑动车组作业先后顺序、单个动车组作业流程等条件，设计改进遗传算法进行求解.
综上，动车所调车作业计划编制可归结为一类多目标、多约束的大规模复杂优化问题，既有文献多是基于旅行商、多商品流等问题的思想，建立混合整数规划模型，采用启发式算法进行求解，有较好的效果，但针对某些具体场景的研究尚有不足. 一是部分研究忽略了调车作业进路安排，在较大规模案例中进路冲突问题将会凸显，可能降低解的质量；另一方面，既有研究较少考虑动车组的长短编之分和股道双列位占用对调车作业计划编制的影响. 本文基于我国动车所设施设备布局及动车组调车作业特点，考虑动车所股道两个列位的合理占用，建立调车作业计划编制优化模型，基于动车组可行路径生成和作业优先次序交换设计模拟退火算法，并采用某动车所实际运营数据对模型和算法进行验证.
1. 问题分析
1.1 动车所内动车组作业项目及特征
为提高动车所内动车组的检修整备效率，我国采用动车组一体化检修制度，作业项目包括：出所和入所、一级修和二级修、联合检查、镟轮和临修、吸污和洗车、存车和热备、解体和编组、转线等. 其中，一些作业具有前后衔接关系，例如一级修完成后需进行联合检查. 动车所进行作业有白班和夜班之分：夜班多为一级修，作业时间较短但作业动车组数量多；白班多为是二级修或临修与一级修结合，作业时间较长，但作业动车组数量少.
《铁路动车组运用维修规则》[9]规定动车组的检修作业原则上在其配属的动车所内进行. 因此，根据配属关系和作业项目可将入所作业的动车组分为三类：本所配属的需入库作业动车组、本所配属的不需入库作业动车组和非本所配属的动车组. 由于动车所库内检修线相对库外存车线数量较少，通常情况下需入库作业动车组在所有入所动车组中占比最大，对该类动车组进行合理作业安排，提高检修线的利用率，是动车所调车作业计划编制中的重点. 非本所配属的动车组作业较简单，通常只在存车线上过夜或进行吸污、上水作业.
1.2 动车所场库布局对调车作业的影响
动车所调车作业计划编制的影响因素较多，从动车所场库布局角度来看，动车所平面功能区域的布置会直接影响动车组的作业流程，进而影响调车作业计划的编制. 例如，场库布局为“检查库 + 库前场 + 存车场”的动车所，如图1（a）所示，动车组的检修整备流程一般为“入所→（存车）→洗车→吸污→检修→存车→出所”；场库布局为“检查库 + 存车场”的动车所，如图1（b）所示，动车组的检修整备流程一般为“入所→（存车）→检修（可含洗车、吸污）→存车→出所”. 动车所的股道类型和功能区域布置的多样性使动车组的作业次序较为灵活，如洗车和检修作业的先后次序可互换. 此外，对于兼具存车线功能的洗车线和镟修线，在股道后续占用不冲突的前提下，可安排已完成作业的动车组停放在该股道上以提高股道的利用率.
1.3 动车组编组状态和列位占用的影响
我国铁路动车组按编成辆数有短编动车组和长编动车组之分，按编组状态可分为短编动车组单编、短编动车组重联和长编动车组. 短编动车组在编组上具有灵活性，根据出入所呈现的不同编组状态，可划分为不同情形，如表1所示.
表 1 短编动车组编组状态Table 1. Marshalling state of short-form EMUs可能情形 动车组 入所编组状态 出所编组状态 情形 1 动车组 1 单编 单编 情形 2 动车组 2、3 重联 重联 情形 3 动车组 4 单编 重联 动车组 5 单编 情形 4 动车组 6、7 重联 单编 为满足长编和重联动车组的检修、整备、存车等作业需求，我国动车所股道的有效长均按照可以停放一列长编或重联动车组的标准而设计的. 事实上，动车所的每条股道均有两个列位，若设有分割信号，则可停放两列未重联的短编动车组；若无分割信号，则可以选择任一列位停放一列短编动车组. 重联动车组待解体、短编动车组待重联、空闲存车线数量较少时，均会出现两列短编动车组占用同一股道相邻两列位的情况. 由于该两列动车组的存放时间和作业项目可能存在差异，其调车作业次序及下阶段的股道占用情况会受到较大影响. 因此，编制动车所调车作业计划应考虑股道列位的合理占用，尽力避免进路冲突、存车线占用冲突等问题.
一方面，由于未重联短编动车组的出入所时刻、各作业完成时刻可能存在差异，若盲目地将两列未重联短编动车组停放在同一条股道，可能产生额外的转线，降低调车作业效率. 另一方面，动车所各功能区的股道数量固定，在动车组检修任务日益繁重的情况下，若实现短编动车组对股道两个列位的合理占用，且避免产生多余的转线和进路冲突，则能够提高股道的利用率，从而提高动车所的检修能力和调车作业效率.
1.4 关键技术问题描述
目前，我国动车组运用组织有以下特点：动车组通常在白天上线运行，日常的一级检修、洗车等一系列所内作业大多在夜间进行. 在白班计划中动车组的调车作业时间相对宽松，而对于作业较繁忙的夜班计划，动车组出入所时刻、空闲股道状态等对调车作业计划编制的限制更显著. 基于此，本文研究的动车所调车作业计划编制优化有以下两个关键技术问题：一是如何在动车组出入所时刻及作业项目不同的情况下，合理确定动车组调车作业的先后次序及股道占用的具体情况，保证动车组按时出入所并能完成所有作业；二是如何在编制调车作业计划时考虑实时的动车组编组状态和股道及其列位占用情况，从而合理利用股道及其列位以提高调车作业效率.
2. 模型建立
2.1 建模说明与假设
基于我国动车所的设施设备布局形式、动车所现行调车作业的特点及其计划编制实际情况，对本文模型建立做以下说明：
1） 针对单一类型动车所的调车作业计划编制问题进行建模，编制周期为一个班计划，即白班计划或夜班计划；
2） 在动车所内进行检修整备作业的动车组，从编组形式上包括短编动车组单编、短编动车组重联和长编动车组，从动车组配属上分为本所动车组和外所动车组；
3） 动车所内的进路包括入所进路、调车进路和出所进路；
4） 各动车组到达和出发时刻已知，即动车组在动车所内的停留总时间确定，必须在该时间内完成检修整备作业；
5） 本班计划开始时，可能存在上一班计划中入所但未出所的动车组；
6） 满足动车组转线所需的实际最大时间，所有动车组均采用相同的最小转线时间标准.
考虑到动车所调车作业的复杂性，为突出重点，降低模型复杂度及求解难度，做以下假设：
1） 动车所的检修班组的数量充足，每条检修线可同时进行检修作业；
2） 动车所的股道均带分割信号，即各股道都可停放两列短编动车组.
2.2 模型参数
模型主要参数定义和说明如下：
E为动车组集合，
E=EL∪ES=EW∪EO ，其中：EL 为短编动车组集合；ES 为长编动车组集合；EW 为本所动车组集合；EO 为外所动车组集合.e 为动车组索引，对于同一股道上先后紧邻作业的动车组，定义后行车组e 的前行车组为e′ ，∀e,e′∈E .D为动车所股道集合, 由检修线和其他股道两大部分组成，
D = DM∪DN = DM∪DS∪DW1∪DW2∪DX∪DI ，其中：DM 为检修线集合；DN 为除检测线外的其他股道集合；DS 为普通存车线集合；DW1 和DW2 分别为机洗线和人工洗车线集合；DX 和DI 分别为镟修线和临修线集合.d 为股道索引,∀d∈D ，特别地，用d1 和d2 表示股道的两个列位，d1,d2∈d .R为动车所内的进路集合，
R = RA∪RD∪RS ，其中：RA 为白日交路集合；RD 为夜晚交路集合；RS 为调车作业进路集合. r为进路索引，∀r∈R .Nr 为不同咽喉区域的平行进路数量.Ts 为转线作业的时间标准.τ 为同一进路上避免冲突的列车间隔时间.ter,s 、ter,f 分别为动车组e执行进路r的开始时刻、结束时刻.Pe 为动车组e的作业项目集合，p为作业项目索引，∀p∈Pe ，对于动车组e后紧邻两项作业，定义后项作业p的前项作业为p'，∀p′∈Pe′ .Ne 为常量，其值等于动车组e的作业项目数量.p=Ne 时表示最后的作业项目，p=1 时表示最开始的作业项目.Pd 为动车所股道d 可进行的作业项目集合.Tep 为动车组e执行作业项目p的时间标准.tedp,s 、tedp,f 分别为动车组e在股道d上执行作业项目p的开始时刻、结束时刻.te,a 、te,d 分别为动车组e的入所时刻、出所时刻.ts 、tf 分别为本班调车计划的开始时刻、结束时刻.Ted 为辅助变量，表示前行车组 e' 离开股道d后，该股道可供后行车组e作业的时间.θpp′ 为0-1辅助变量，动车组e 作业p和p' 需要转线取1，否则取0.yedr 为0-1辅助变量，股道d满足动车组e承担进路r的任务功能时时取1，否则取0.sedp 为0-1辅助变量，股道d满足动车组e执行作业p功能时取1，否则取0.cedp 为0-1决策变量，考虑约束动车组e能在股道d进行作业p时取1，否则取0.xedp 为0-1决策变量，动车组e执行在股道d进行作业p时取1，否则取0.2.3 优化模型
已知动车所班计划中需进行各项作业的动车组数量，通过减少动车组不必要的转线作业，降低调车进路发生时间冲突的几率，有利于提高动车所的调车作业效率. 采用本班计划内的动车所股道占用次数来衡量动车所的调车作业效率，以减少动车所股道占用次数作为优化目标，如式（1）所示.
min (1) 约束条件包括：
{t}_{edp,}{}_{\text{s}}\geqslant \mathrm{max}\left\{{t}_{\text{s}},{t}_{e,\text{a}}\right\}\text{ }\text{,}\quad\text{ }p=1, (2) {t}_{edp,\text{f}}\leqslant \mathrm{min}\left\{{t}_{\text{f}},{t}_{e,\text{d}}\right\}\text{ }\text{,}\quad p={N}_{e}, (3) {\text{|}}{t_{edp,{\text{f}}}} - {t_{edp,{\text{s}}}}| \geqslant {T_{ep}}{\text{ }}, (4) {t_{edp',{\rm{f}}}} + {\theta _{pp'}}{T_{\rm{s}}} \leqslant {t_{edp,{\rm{s}}}}{\text{ }}, (5) {\theta }_{p{p}^{\prime }}= \left\{ {\begin{array}{l}1, \quad {s}_{edp}=1\text{,}\;\;{s}_{ed{p}^{\prime }}=1,\\ 0, \quad 其他,\end{array}} \right. (6) \sum\limits_{d } {{s_{edp}}{x_{edp}}} \geqslant {\text{0 }}, (7) {s}_{edp}=\left\{ {\begin{array}{l}1\text{,}\quad {P}_{d}\cap {P}_{e}\ne \varnothing ,\\ 0,\quad {其他},\end{array}} \right. (8) {x_{e'dp'}}{t_{e'dp'{\rm{,s}}}} \leqslant {x_{edp}}{t_{edp,{\rm{f}}}}{\text{ }}, (9) {t_{e'r,{\rm{s}}}} \leqslant {t_{er,{\text{s}}}} + \tau {\text{ }}, (10) {t_{e'r{\rm{,f}}}} \leqslant {t_{er,{\rm{f}}}} + \tau {\text{ }}, (11) {c_{edp}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{T_{ed}} \geqslant {T_{ep}}},\\ {0,}&{{T_{ed}} < {T_{ep}}}, \end{array}} \right. (12) {T}_{ed}=\left\{ {\begin{array}{l}{t}_{\text{f}}-{t}_{{e}^{\prime },\text{a}}-{T}_{{\rm{s}}},\quad d\in {D}_{{\rm{N}}}\\ {t}_{\text{f}}-{t}_{{e}^{\prime }dp,\text{f}}-{T}_{{\rm{s}}},\quad d\in D,p\in \left\{\mathrm{1,2,\cdots},{N}_{p}-1\right\},\\ {t}_{\text{f}}-{t}_{{e}^{\prime },{d}}\text{}\text{,}\quad d\in {D}_{{\rm{N}}},\end{array}} \right. (13) \sum\limits_{e } {{y_{edr}}} \leqslant {N_{\rm{r}}}, (14) {y}_{edr}=\left\{ {\begin{array}{l}1\text{,}\quad {\theta }_{p{p}^{\prime }}=1,\;\; {c}_{edp}=1, \\ 0,\quad \text{其他},\end{array} } \right. (15) \sum\limits_{d } {{x_{edp}}} \leqslant 1, (16) \sum\limits_{e } {{x_{edp}}} \leqslant 2. (17) 式（2）、（3）表示动车组任一作业项目均应在本班时间内完成；式（4）表示动车组某项作业在股道上的停留时间不小于该作业的时间标准；式（5）、（6）为考虑动车组进行后项作业是否需要转线的前、后项作业的时间接续约束；式（7）、（8）表示动车组不同类型的作业必须在具备相应作业功能的股道上进行；式（9）为动车所某股道及其列位不发生占用时间冲突的约束；式（10）、（11）为考虑列车间隔时间的咽喉进路不发生占用时间冲突的约束；式（12）、（13）为动车组是否在某股道进行作业的决策约束；式（14）为动车组是否进行转线调车的决策约束；式（15）为平行进路数量约束；式（16）表示动车组某项作业时只占用一条股道；式（17）表示某股道在同一时刻最多停留两列动车组.
3. 算法设计
上述模型属于大规模的混合整数规划模型，约束条件较多且复杂. 在运输组织优化建模中，此类模型比较普遍，一般结合模型特点，采用启发式算法进行求解[10-11]. 模拟退火算法是一种经典的启发式算法，具有易于实现、鲁棒性高、计算过程简单等特点，被广泛用于求解复杂的非线性优化问题. 在结构设计上，根据实际情况和输入数据特点设置合适的状态函数和退火策略，符合本文模型的特点和求解需求.
本文模型中，当动车所的股道数目、动车组的数量、作业任务量增大，模型的求解难度会急剧上升. 求解得到的调车作业计划需确定每列动车组进行各项作业的起止时间和占用的股道，即反映各动车组在所内完成调车作业走行的全过程. 模型的求解过程分为以下3个阶段：
1） 生成单列动车组的检修整备可行路径.
2） 生成包含全部动车组可行路径的调车作业计划可行解.
3） 采用模拟退火算法在可行解中寻优.
3.1 模型的编码和可行解
动车所调车作业计划包含的信息涉及各动车组入所、检修整备、出所等作业过程和动车所各股道的占用情况，因此，本文分别对上述两种信息进行实数编码. 由于动车组调车作业时间标准通常为5 min的整数倍，按5 min的整数倍为单位时间，划分本班计划得到编码长度. 例如以15 min为一段进行编码，动车组编码片段如图2所示，0表示未进行检修整备作业，正整数表示作业项目类型（2、9分别为检修整备作业、转线），−1表示存车. 股道编码片段如图3所示，0表示股道空闲状态，3表示占用该股道的动车组序号为e3，−1表示某动车组转线时占用该股道. 模型求解完成后，解码两套编码得到完整的动车所调车作业计划方案.
根据某动车组入所时各股道的占用和剩余可作业时间状态对其各项作业的顺序、时间、股道占用作出合理安排，即得到该动车组的检修整备可行路径. 对于全部动车组，由于出入所时间不一，在动车所的实际停留时间也不同，为尽量避免无法生成调车作业计划可行解，应制订合理的动车组间进行检修整备作业的优先级顺序. 同时考虑将动车组按照作业项目先分类再生成可行解，在求解过程中不同分类的动车组仅与具有相应功能的股道集合双向匹配，有利于降低方案组合数量，提高求解速率.
本文中模型的可行解生成算法如下：
步骤1 输入各动车组入所、出所时刻、作业项目和编组状态，本班计划开始、结束时刻，各股道的功能和初始占用状态，各类型作业时间标准等；
步骤2 根据各动车组具体作业项目生成其合理作业顺序，并将全部动车组分为上文所述三类，根据各动车组在所实际停留时间从小到大排列生成检修作业初始优先级顺序；
步骤3 按照动车组检修作业优先级顺序选取一列动车组，根据股道当前列位占用状态和剩余可用作业时间等信息及各约束条件，对该动车组按照其作业项目顺序随机选取具有相应功能且空闲的股道进行检修整备作业，每项作业结束后更新该动车组和占用股道的时空状态；
步骤4 重复步骤3，遍历该动车组的作业项目，若能在其停留时间内完成全部的检修整备作业，则得到该动车组完整的个体编码，即生成该动车组的检修整备可行路径，否则该路径不可行；
步骤5 重复步骤4，遍历该班计划内的所有动车组，得到各动车组个体编码和各股道个体编码，若能在班计划时间内生成全部动车组的检修整备可行路径，则该解可行，若无法生成则表明产生了作业的时空冲突，应舍弃该不可行解；
步骤6 对于可行解，根据各动车组个体编码和各股道个体编码的信息，得到完整的动车所调车作业计划，计算该可行解的目标值；
步骤7 采用模拟退火算法产生随机扰动，得到新的动车组检修作业优先级顺序，重复步骤3 ～ 6，生成新的动车所调车作业计划可行解.
3.2 模拟退火算法寻优
在可行解中进行寻优的关键是邻域解的生成，对于动车所调车作业计划，一种邻域构造方法是随机交换可行解中两列动车组对股道的占用，但这种方法在作业动车组数量较多、问题求解规模较大时具有一定的盲目性，求解效率不高.
动车组检修优先级顺序对调车作业计划编制结果有影响，在实践中，当作业动车组数量较多时，按照动车组在所实际停留时间从小到大排列的动车组检修优先级顺序可能无法得到可行的调车作业计划. 例如图4（a）所示，图中：t1~t3为动车所入所时间，t4~t6 为完成调车作业后的出所时间；S1、S2和 M1分别表示机洗线、人工洗车线和运用检修线. 按该排序方式的动车组检修优先级顺序为e2，e1，e3，而e3无法按图中时间出所，原因是M1在e2检修前的可用检修时间被浪费. 将优先级顺序调整为e1，e2，e3时，e3可顺利完成检修整备，如图4（b）所示.
鉴于此，本文的邻域结构设计为：对初始可行解的动车组检修作业优先级排序，在非重联的短编动车组中随机选择两列，交换其在检修作业优先级顺序中的位置. 这种邻域结构有较好的随机扰动性能，有利于可行解的优化，同时能保证重联的短编动车组同步作业，有利于提高调车作业的效率. 本文的模拟退火算法采用线性降温方式，依据Metropolis接受准则接受新解，其他规则不再赘述. 完整的动车所调车作业计划编制优化模型的算法流程如图5所示.
图 5 动车所调车作业计划编制优化算法流程Figure 5. Flow chart of optimization algorithm for shunting operation plan of EMU depot4. 实例分析
4.1 数据准备
国内某尽端式动车所，采用“存车场 + 检查库”的场库布局，如图6所示，检查库设有4条检修线JC1～JC4，存车场设有12条股道，均可用于动车组存放，其中S1道为机洗线，S2道为人工洗车线，S11道为镟轮线，S12道为临修线，动车所内所有股道均带有分割信号，调车作业的平行进路为2条.
该动车所承担本所配属动车组的检修整备及部分外所动车组的过夜任务，进行各项作业的时间标准如表2所示.
表 2 动车组作业时间标准Table 2. EMU operating time standards作业名称 时间
标准/min备注 一级修 135 检修、洗车、吸污等作业同步进行，不需要转线 二级修 视检修项目而定 一级修试验 60 仅有电作业，在存车线上进行 联检 45 长编或重联动车组联检 30 短编动车组联检 镟轮 每辆车 60 需在镟轮线进行 临修 视维修项目
而定需在临修线进行 机洗 45 不在检查库进行的机洗作业 人工洗车 90 不在检查库进行的人工洗车作业 吸污 30 不在检查库进行的长编或重联动车组吸污 15 不在检查库进行的短编动车组吸污 解体 15 编组 30 转线 15 某个夜班（20：00—08：00）中需要进行检修整备作业的动车组的各项信息如表3所示，其中e1 ～ e12为本所配属动车组，e13 ～ e15为外所过夜动车组. “线存”“库存”表示本班开始时或结束时动车组在存车线或检修线上，本班开始时e1在S5道，e2、e3分别在S9道两列位. 作业项目中“检修”表示在检查库进行一级修及其他作业，“机洗”“人工洗车”“吸污”表示对应作业不在检查库进行.
4.2 求解与结果分析
采用Python语言在Spyder开发环境上实现优化模型的求解. 取初始温度100，降温速率0.98，终止温度为1，最大迭代次数500，同温迭代次数1，经多次测试，均能在4 s内求得该算例的最优解. 取其中一次求解结果，迭代收敛曲线如图7所示. 将求解结果进行整理，得到该算例的最优调车作业计划如表4所示.
表 3 作业动车组基本信息Table 3. Basic information of operating EMU动车组 到达
编组入所
时刻出所
时刻作业项目 e1 长编 线存 05：52 检修、联检 e2 重联 线存 库存 解体 e3 线存 05：09 解体、检修、联检 e4 重联 20：07 06：16 检修、联检 e5 20：07 06：16 检修、联检 e6 短编 20：32 线存 检修、联检 e7 长编 21：26 06：38 机洗、检修、联检 e8 短编 21：58 07：37 检修、镟轮（1 辆）、联检 e9 短编 23：24 06：51 检修、联检、人工洗车 e10 短编 23：59 线存 检修、联检 e11 短编 21：32 06：52 一级修试验 e12 长编 23：06 04：39 一级修试验 e13 短编 20：09 20：56 吸污 e14 重联 21：40 05：47 e15 21：40 05：47 在本例中，一级修作业时间15 min及转线时间15 min，动车组入库一级修用时约3 h，本班计划为12 h，检修线为4条，则不考虑检修线双列位占用时理论最大检修能力为16列. 本班计划实际入库检修的动车组为10列，且检修线JC4利用了双列位，从编制结果来看检修线的能力也有较多富余. 该动车所存车线为12条，占用存车线的动车组为15列，本算例中存车线恰好满足一股道一列车的停放需求，但当动车组数量增加或停留时间延长时，充分利用股道列位具有求解优势.
表 4 最优调车作业计划Table 4. Optimal shunting operation plan动车组 调车作业 e1 20：00 线存 S5，20：00—20：15 转线到 JC2， 20：15—22：30 JC2 检修，22：30—22：45 转线到 S9，22：45 之后 S9 联检并存车，05：52 出所 e2 20：00 线存 S9，20：00—20：15 转线到 JC4， 20：15—20：30 解体，20：30—08：00 库存 JC4 西 e3 20：00 线存 S9，20：00—20：15 转线到 JC4， 20：15—20：30解体，20：30—22：45 JC4 东检修，22：45—23：00 转线到 S5， 23：00 之后 S5 联检并存车，05：09 出所 e4 20：07 入所，经 S6 进入 JC1，20：30—22：45 JC1 检修，22：45—23：00 转线到 S7，23：00 之后 S7 联检并存车，06：16 出所 e5 20：07 入所，经S6进入JC1，20：30—22：45 JC1检修，22：45—23：00 转线到S7，23：00之后S7联检并存车，06：16 出所 e6 20：32 入所，经S10进入JC3西，20：45—23：00 JC3西检修，23：00—23：15 转线到S10西，23：15—08：00联检并存车 e7 21：26入所，进入S1，21：45—22：30 S1机洗作业，22：30—23：00 S1存车，23：00—23：15 转线到JC1，23：15—01：30 检修，01：30—01：45 转线到S4，01：45 之后S4联检并存车，06：38 出所 e8 21：58入所，进入S11，22：15—23：15 S11镟轮作业，23：15—23：30 转线到JC4东，23：30—01：45 JC4东检修作业，01：45—02：00 转线到S11，02：00 之后联检并存车，07：37 出所 e9 23：24 入所，经S2进入JC2，23：45—02：00 JC2检修，02：00—02：15 转线到S2，02：15—03：45 S2人工洗车， 03：45 之后S2存车，06：51 出所 e10 23：59入所，经S3进入JC3，00：15—02：30 JC3检修作业，02：30—02：45 转线到S3，02：45—08：00 联检并存车 e11 21：32 入所，进入S7，22：00—23：00 S7一级修试验，23：00 之后S7存车，06：52 出所 e12 23：06 入所，进入S8，23：30—00：30 S8一级修试验，00：30 之后S8存车，04：39 出所 e13 20：19 入所，进入S3，20：30—20：45 S3吸污作业，20：56 出所 e14 21：40 入所，进入S12存车，05：47 出所 e15 21：40 入所，进入S12存车，05：47 出所 在迭代过程中，股道占用次数最多为41次，其产生原因是为避免股道时空占用冲突，部分动车组进行了不必要的转线，最低为34次，对应的方案中没有动车组不必要的转线. 在需要入库作业的10列动车组中，有8列实现了入所后快速入库作业，对于检修线作业效率和利用率的提高有较好的效果. 可以看出，本文的模型和算法在求解动车所调车作业计划的有效性和实用性得到了一定提高.
5. 结 论
本文根据我国现行动车组运用管理和动车所调车作业的特点，在上线运用动车组数量增加的背景下，着眼于动车所调车作业效率和实际检修能力的提高，考虑动车所股道双列位的合理利用，建立调车作业计划编制优化模型，设计基于动车组作业优先次序的模拟退火算法进行求解，结合算例对其进行验证，得到如下结论：
1） 合理利用动车所股道双列位有利于提高股道利用率和动车所调车作业效率.
2） 合理的动车组作业优先次序能够提高调车作业计划的编制速率和质量.
针对不同类型的动车所，考虑调车作业白班计划和夜班计划的联合协调编制，是需要进一步研究的方向.
-
表 1 道岔子系统信号的含义
Table 1. Meaning of signals in the switch subsystem
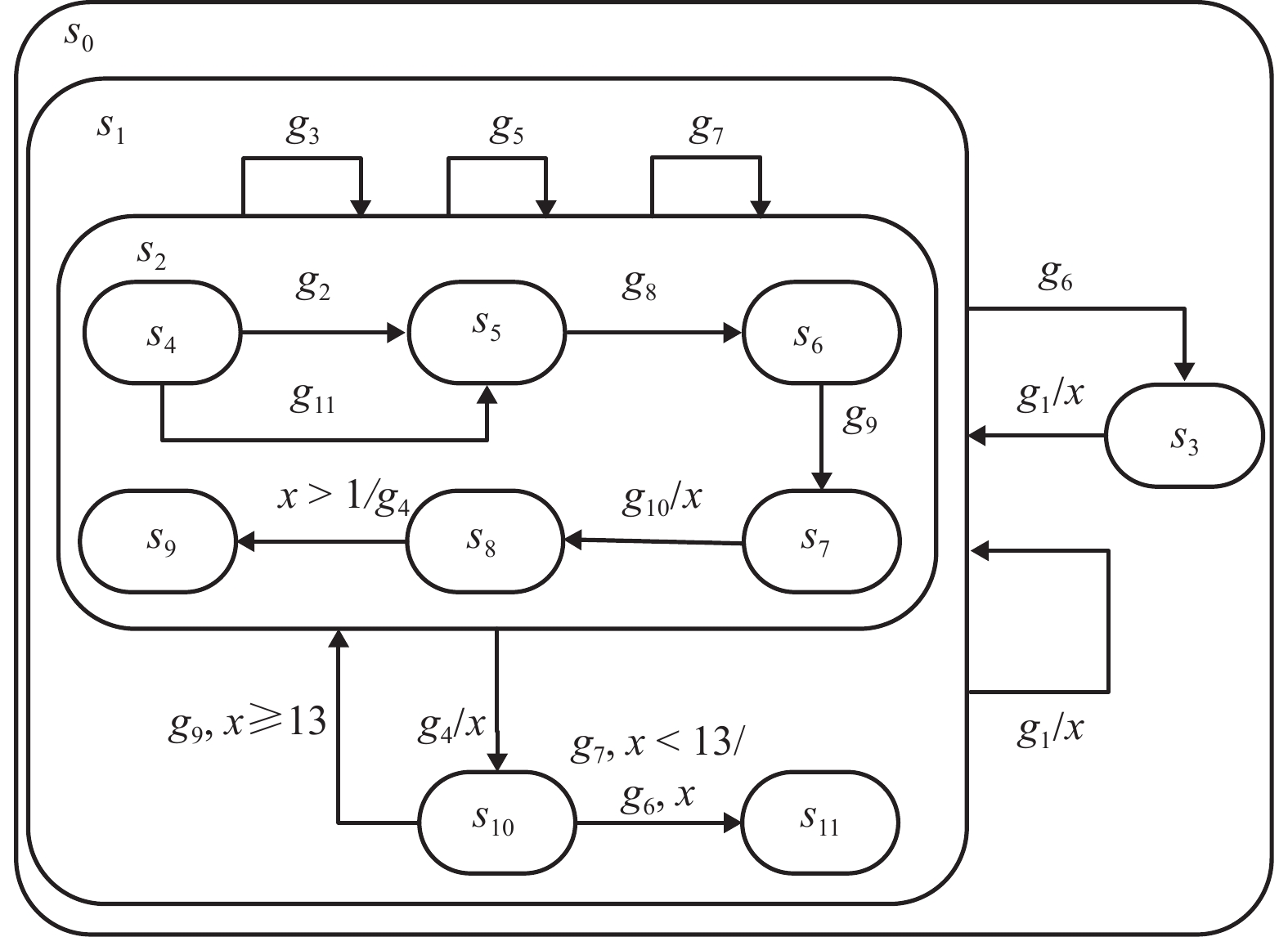
信号 含义 信号 含义 g1 反位请求 g2 定位需求 g3 正在转换 g4 请求转换 g5 道岔锁闭 g6 选排一致 g7 道岔定位 g8 道岔未锁闭 g9 道岔未在定位 g10 道岔未转换 g11 道岔定位操作 
下载: 导出CSV
表 2 DTFSM_SW测试用例统计
Table 2. Test case statistics of DTFSM_SW
覆盖准则 用例总数/个 时钟约束用例/个 NC 1 1 EC 28 8 EPC 32 8 CPC 52 16
下载: 导出CSV
表 3 DTFSM_SW与DTA_SW对比
Table 3. Comparison of DTFSM_SW and DTA_SW
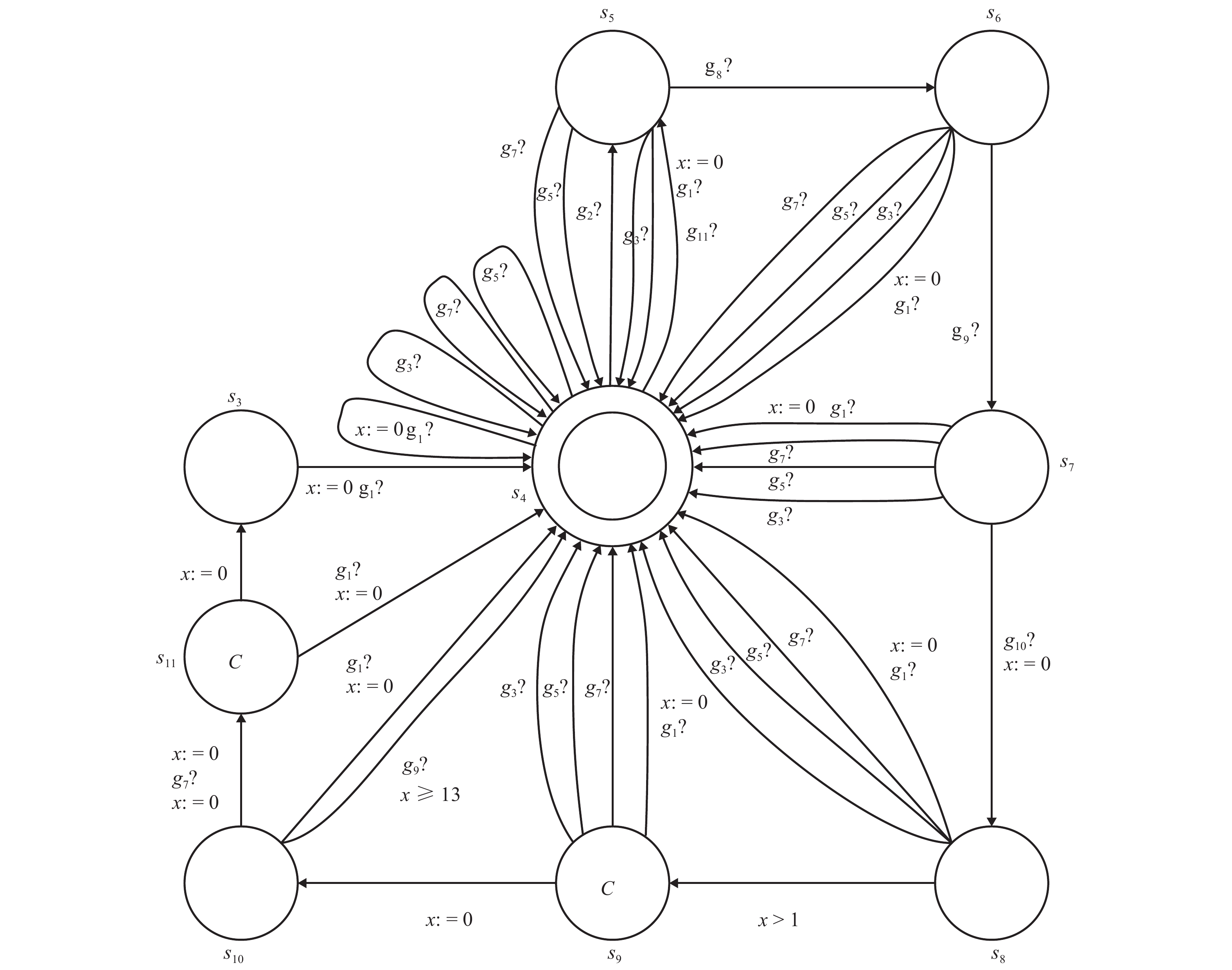
模型 状态/个 变迁/条 信号/个 DTFSM_SW 9 15 11 DTA_SW 9 37 11
下载: 导出CSV
表 4 不同建模方法生成的测试用例对比
Table 4. Comparison of test cases generated by different modeling methods
建模方法 功能逻辑
用例/个时钟约束
用例/条TFSM 36 16 Petri 36 0 UML Statechart 36 0
下载: 导出CSV
表 5 DTFSM_SW具有时钟约束的测试案例
Table 5. Test cases with clock constraints of DTFSM_SW
序号 时钟约束测试案例 序号 时钟约束测试案例 1 g2, g8, g9, g10, x＞1, g1 9 g2, g8, g9, g10, x＞1, g9, x≥13 2 g2, g8, g9, g10, x＞1, g3 10 g2, g8, g9, g10, x＞1, g1 3 g2, g8, g9, g10, x＞1, g5 11 g2, g8, g9, g10, x＞1, g7, x＜13, g1 4 g2, g8, g9, g10, x＞1, g7 12 g2, g8, g9, g10, x＞1, g7, x＜13, g1 5 g11, g8, g9, g10, x＞1, g1 13 g11, g8, g9, g10, x＞1, g9, x≥13 6 g11, g8, g9, g10, x＞1, g3 14 g11, g8, g9, g10, x＞1, g1 7 g11, g8, g9, g10, x＞1, g5 15 g11, g8, g9, g10, x＞1, g7, x＜13, g1 8 g11, g8, g9, g10, x＞1, g7 16 g11, g8, g9, g10, x＞1, g7, x＜13, s3, g1
下载: 导出CSV
-
[1] 上官伟,胡福威,袁敏,等. 基于弹复力效应的列控车载设备可靠性分析方法[J]. 铁道学报,2018,40(6): 75-82. doi: 10.3969/j.issn.1001-8360.2018.06.010SHANGGUAN Wei, HU Fuwei, YUAN Min, et al. Reliability analysis method for on-board equipment of train control system based on resilience effect[J]. Journal of the China Railway Society, 2018, 40(6): 75-82. doi: 10.3969/j.issn.1001-8360.2018.06.010 [2] 袁磊,吕继东,刘雨,等. 一种全覆盖的列控车载系统测试用例自动生成算法研究[J]. 铁道学报,2014,36(8): 55-62. doi: 10.3969/j.issn.1001-8360.2014.08.010YUAN Lei, LÜ Jidong, LIU Yu, et al. Research on model-based test case generation method of onboard subsystem in CTCS-3[J]. Journal of the China Railway Society, 2014, 36(8): 55-62. doi: 10.3969/j.issn.1001-8360.2014.08.010 [3] 吕继东,朱晓琳,李开成,等. 基于模型的CTCS-3级列控系统测试案例自动生成方法[J]. 西南交通大学学报,2015,50(5): 917-927. doi: 10.3969/j.issn.0258-2724.2015.05.023LYU Jidong, ZHU Xiaolin, LI Kaicheng, et al. Model-based test case automatic generation of CTCS-3 train control system[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 917-927. doi: 10.3969/j.issn.0258-2724.2015.05.023 [4] LI C L, LI K C, TANG T, et al. Model-based generation of safety test-cases for onboard systems[C]//2013 IEEE International Conference on Intelligent Rail Transportation Proceedings. Beijing: IEEE, 2013: 191-196. [5] 魏柏全. 基于TAIO变异分析的新型列控系统安全功能测试评价研究[D]. 北京: 北京交通大学, 2018. [6] CHEN Lijie, ZHAO Tianshi, SUN Chao, et al. Test case generation method based on colored Petri net for train control system[C]//2018 3rd International Conference on System Reliability and Safety (ICSRS). Barcelona: IEEE, 2018: 1-5. [7] 赵晓宇, 杨志杰, 吕旌阳. 基于有色Petri网的车载设备模式转换测试序列生成方法[J]. 中国铁道科学, 2017, 38(4): 115-123.ZHAO Xiaoyu, YANG Zhijie, LYU Jingyang, Test sequence generation method of mode transition for on-board equipment based on colored Petri net[J]. China Railway Science, 2017, 38(4): 115-123. [8] 曹雅鑫. 基于UML状态图的列控中心轨道电路编码功能测试用例生成方法研究[D]. 成都: 西南交通大学, 2017. [9] 王秀玄. 基于UML的列控中心改变运行方向功能测试用例生成方法研究[D]. 成都: 西南交通大学, 2016. [10] AMMANN P, OFFUTT J. Introduction[M]//Introduc- tion to Software Testing. Cambridge: Cambridge University Press, 2017: 3-24. [11] 梅林. 形式化联锁软件测试技术研究[D]. 兰州: 兰州交通大学, 2014. [12] 郭昊男. 新型列控系统车载ATP安全功能在线测试研究[D]. 北京: 北京交通大学, 2019. [13] 富德佶. 基于模型的CTCS-3列控系统互联互通测试自动分析方法研究[D]. 北京: 北京交通大学, 2015. [14] 谢林,杨扬. 基于模型的进路建立过程测试用例自动生成[J]. 铁道标准设计,2017,61(2): 109-116.XIE Lin, YANG Yang. Model-based automatic generation of test case of route establishment process[J]. Railway Standard Design, 2017, 61(2): 109-116. [15] HUANG Y S, CHUNG T H, CHEN C T. Modeling traffic signal control systems using timed colour Petri nets[C]//2005 IEEE International Conference on Systems, Man and Cybernetics. Waikoloa: IEEE, 2005: 1759-1764. [16] ZAID D H. Safecharts: a statecharts variant for safety-critical systems design[D]. Reading: University of Reading, 2005. [17] ANDRÉ C. Computing SyncCharts reactions[J]. Electronic Notes in Theoretical Computer Science, 2004, 88: 3-19. doi: 10.1016/j.entcs.2003.05.007 [18] 李耀. 铁路信号系统安全关键软件建模与分析方法[D]. 成都: 西南交通大学, 2018. [19] ZHANG Tao, HUANG Shaobin, HUANG Hongtao. An operational semantics for UML RT-statechart in model checking context[C]//2009 Fourth International Conference on Internet Computing for Science and Engineering. Harbin: IEEE, 2009: 12-18. [20] 铁道部科学技术司, 铁道部运输局. CTCS-3级列控系统测试案例(V3.0): 科技运[2009] 59号[S]. 北京: [出版者不详], 2009. [21] 铁道部科学技术司,铁道部运输局. CTCS-3级列控系统测试案例(V3.0):科技运[2009] 59号[S]. 北京: [出版者不详], 2009. doi: 10.3969/j.issn.0258-2724.2015.01.005LI Yao, CHEN Rongwu, GUO Jin, et al. Modeling and verification of TSSM-based CBTC zone controller for urban rail transit[J]. Journal of Southwest Jiaotong University, 2015, 50（1）: 27-35. doi: 10.3969/j.issn.0258-2724.2015.01.005 [22] 张曙光. CTCS-3级列控系统总体技术方案[M]. 北京: 中国铁道出版社, 2008. [23] 饶畅,李楠,张亚东,等. 铁路信号安全关键软件的组合测试序列集约简[J]. 西南交通大学学报,2020,55(3): 596-603. doi: 10.3969/j.issn.0258-2724.20190157RAO Chang, LI Nan, ZHANG Yadong, et al. Combinatorial test sequence set reduction approach for railway signaling safety-critical software[J]. Journal of Southwest Jiaotong University, 2020, 55(3): 596-603. doi: 10.3969/j.issn.0258-2724.20190157 [24] 吴彪. 基于EFSM的测试用例自动生成方法的研究[D]. 杭州: 浙江理工大学, 2016. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 429
- HTML全文浏览量: 309
- PDF下载量: 16
- 被引次数: 0