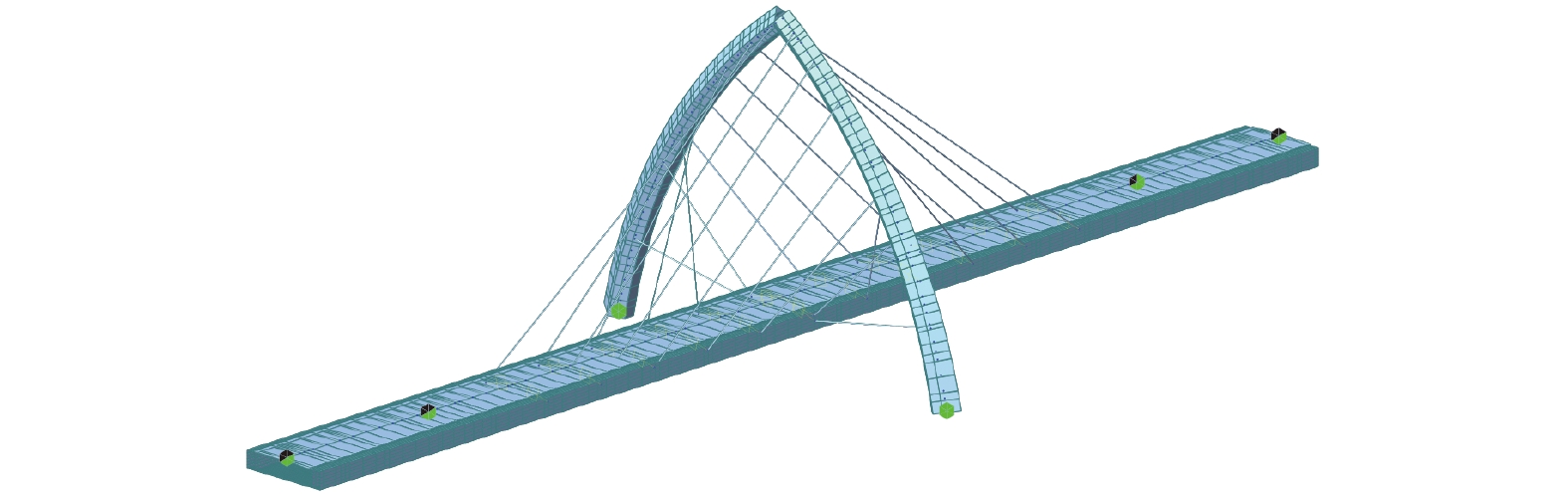
Optimization on Axis of Arch-Shaped Pylon for High-Speed Railway Cable-Stayed Bridge
-
摘要: 为解决高速铁路斜拉桥以小角度跨越既有交通线路、河流等时塔墩布置难题，引入拱塔结构，并基于不动点迭代方法及有限元计算对拱塔轴线线形的优化求解问题进行了分析. 在确定拱塔高度和跨度并拟定初始拱塔轴线的基础上，首先对拱塔结构进行受力平衡分析，建立拱塔线形优化非线性方程组；然后应用不动点迭代方法求解该非线性方程组，得到合理拱塔轴线的近似解，求解过程中通过有限元方法计算斜拉索的索力；最后以广汕铁路跨深汕高速拱塔斜拉桥为工程背景，分别优化得到恒载、恒载 + 单线列车竖向静活载、恒载 + 双线列车竖向静活载3种工况下合理拱塔轴线的近似解. 结果表明：3种不同的荷载工况下，线形优化后的拱塔弯矩最不利值相对优化前弯矩降低89.8%～94.8%；主力、主力 + 附加力荷载组合下，拱塔弯矩降低幅度介于64.6%～92.2%，拱塔应力由−172.6～−179.5 MPa降低至−74.0～−6.2 MPa，拟合轴线下拱塔正负挠度分别降低51.0%、33.8%.Abstract: In order to resolve the pylon layout difficulty for high speed railway cable-stayed bridges when the bridges span existing traffic lines, rivers and so on with small angles, the arch-shaped pylon was adopted and the optimization on axis of arch-shaped pylon was analyzed based on the fixed point iteration method and finite element analysis. Firstly, nonlinear equations for arch pylon optimization are established by analyzing the force balance of arch-shaped pylon based on that the height and span of the arch tower are determined and the initial axis is drawn up. Secondly, the non-linear equations are solved by the fixed point iteration method, and the approximate solution of the reasonable arch-shaped pylon axis is obtained, in which the cable-stayed cable force is calculated by the finite element method. Finally, taking the arch-shaped pylon cable-stayed bridge of Guangzhou–Shanwei High-Speed Railway spanning Shenzhen–Shantou Expressway as the engineering background, the approximate solutions of reasonable arch-shaped pylon axes are obtained under three typical load conditions, i.e., dead load, dead load combined with single-track train vertical static live load, and dead load combined with double-track train vertical static live load. The results show that under the three different load conditions, using the optimized arch-shaped pylon axes can reduce bending moments of arch-shaped pylons by 89.8% to 94.8%, compared with using the initial arch-shaped pylon axis; under the main force or both the main force and additional force, bending moments of optimized arch-shaped pylons are reduced by 64.6% to 92.2%, stresses of arch-shaped pylons are reduced from −172.6–−179.5 MPa to −74.0 – −6.2 MPa, and positive and negative deflections of optimized arch-shaped pylons with fitting axis are reduced by 51.0% and 33.8% respectively.
-
图 2 拱塔斜拉桥布置(单位：cm)
Figure 2. Overview of arch-shaped pylon cable-stayed bridge (unit：cm)
图 6 不同荷载工况下拱塔弯矩
Figure 6. Bending moment of arch-shaped pylon under different load conditions
图 7 主力组合下拱塔弯矩包络图
Figure 7. Bending moment envelope diagram of arch-shaped pylon under the combination of main forces
图 8 主力 + 附加力组合下拱塔弯矩包络图
Figure 8. Bending moment envelope diagram of arch-shaped pylon under the combination of main forces and additional forces
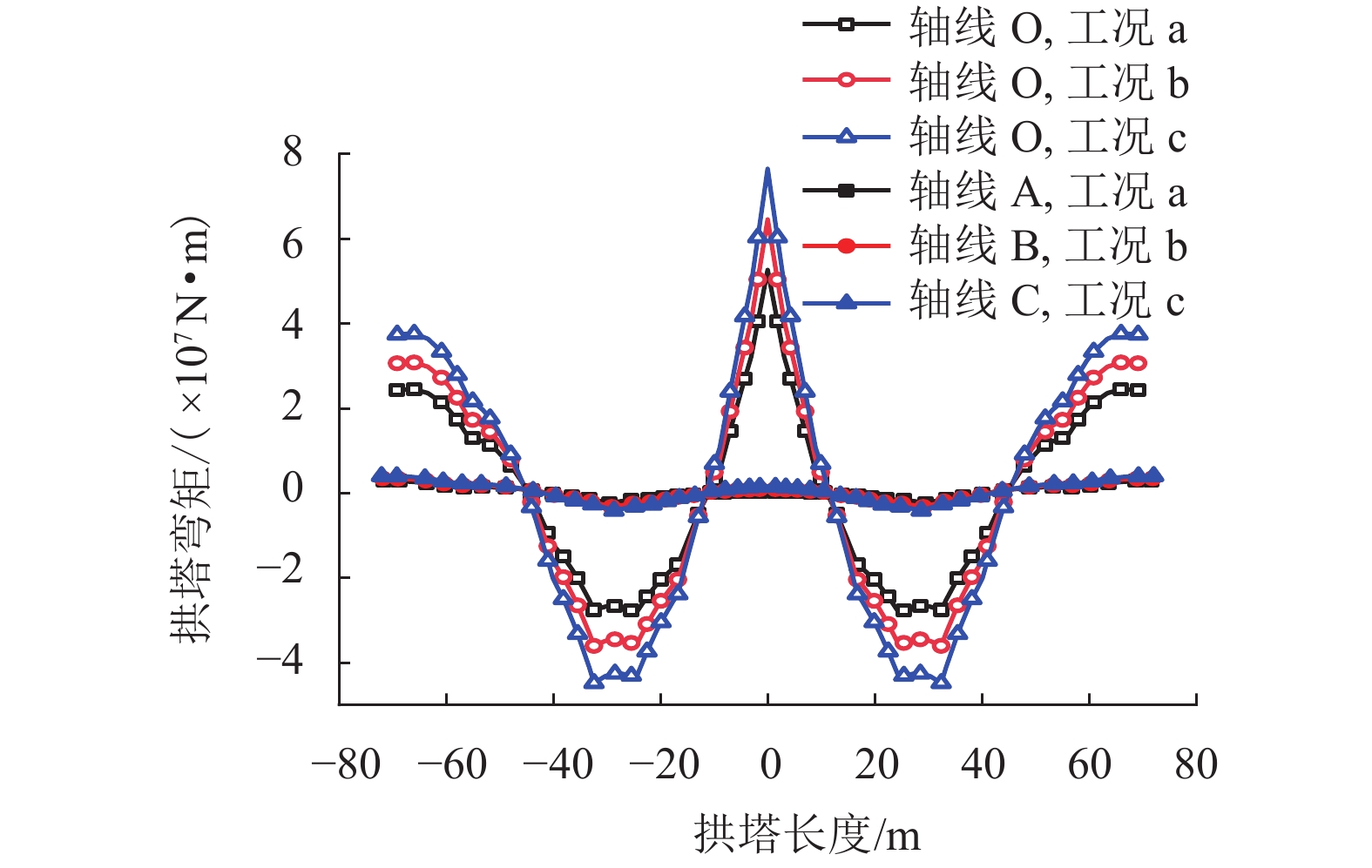
表 1 不同荷载工况下拱塔弯矩最大值及其变化率
Table 1. Maximum bending moment of arch-shaped pylon and its change rate under different load conditions
工况 轴线 正弯矩 负弯矩 最大值/
（kN•m）减小率/% 最大值/
（kN•m）减小率/% a O 52 642 94.4 −28 324 91.5 A 2 945 −2 409 b O 64 552 94.7 −32 608 89.8 B 3 448 −3 325 c O 76 514 94.8 −44 835 90.7 C 3 987 −4 168 
下载: 导出CSV
表 2 荷载组合下拱塔弯矩最大值及其变化率
Table 2. Maximum bending moment of arch-shaped pylon and its change rate under the combination of design loads
荷载组合 轴线 正弯矩 负弯矩 最大值/
（kN•m）减小率/
%最大值/
（kN•m）减小率/
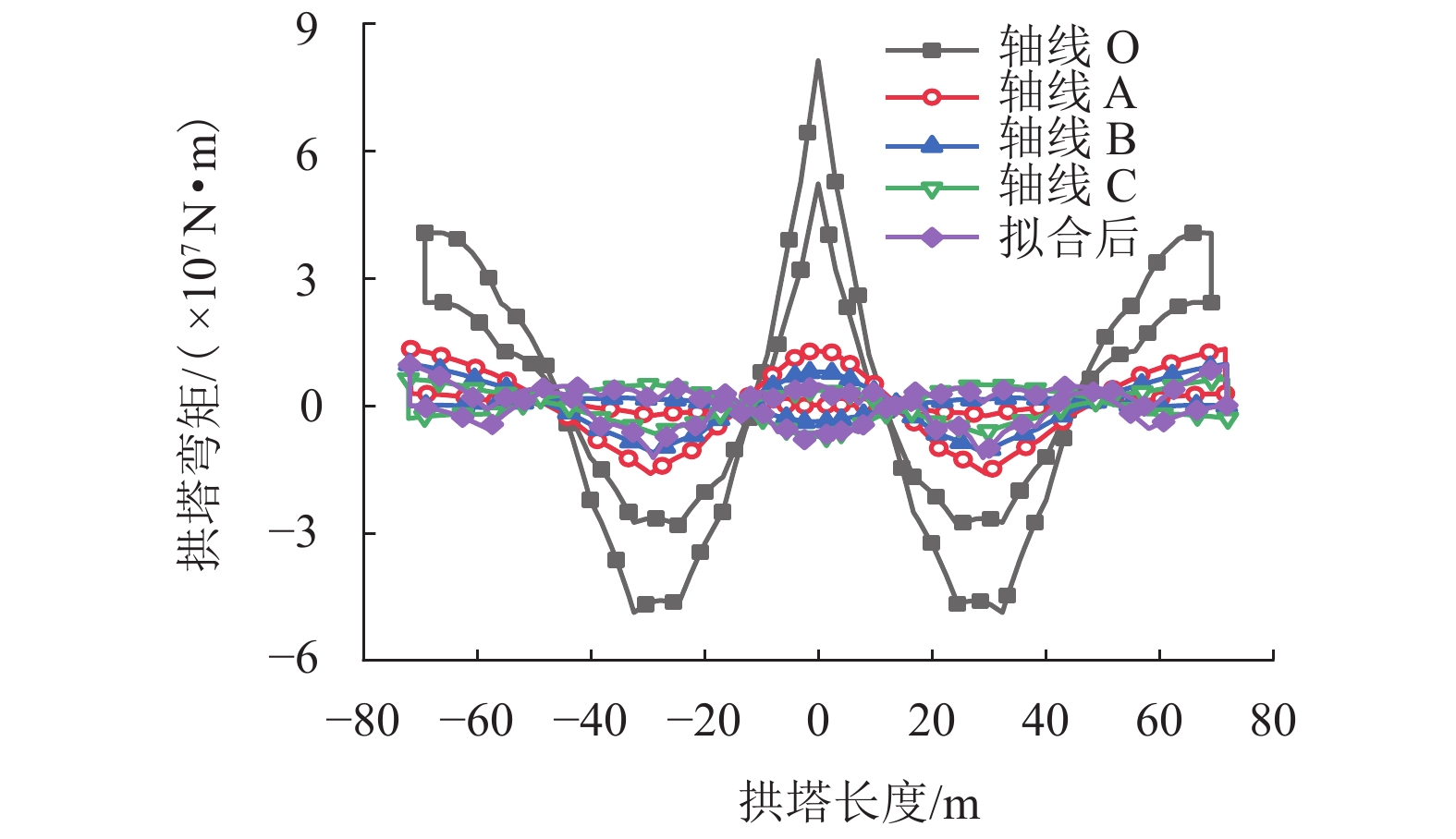
%主力 O 81333 −48709 A 13393 83.5 −15989 67.2 B 9815 87.9 −11028 77.4 C 6309 92.2 −7377 84.9 拟合 9649 88.1 −12257 74.8 主力 + 附加力 O 83191 −50417 A 19080 77.1 −17853 64.6 B 15528 81.3 −12916 74.4 C 12046 85.5 −9003 84.9 拟合 15355 81.5 −14103 72.0
下载: 导出CSV
表 3 荷载组合下拱塔正应力极值及其变化率
Table 3. The maximum normal stress of arch-shaped pylon and its change rate under the combination of design loads
荷载
组合拱塔
轴线正弯矩 负弯矩 最大值/
（kN•m）减小率/
%最大值/
（kN•m）减小率/
%主力 O 169.7 −169.5 A 15.0 91.2 −80.0 52.8 B −3.2 101.9 −65.2 61.4 C −11.2 106.6 −52.0 69.3 拟合 −14.3 108.4 −70.2 58.6 主力 +
附加力O 179.5 −172.6 − A 19.4 89.2 −84.6 51.0 B 5.1 97.2 −69.0 60.0 C 10.6 94.1 −56.6 67.2 拟合 −6.2 103.5 −74.0 57.1
下载: 导出CSV
表 4 位移极值绝对值及其变化量
Table 4. Absolute values of extreme displacements and its change
构件 拱塔轴线 负挠度 正挠度 |γ1|/
mm减小量/
mm减小率/
%|γ2|/
mm减小量/
mm减小率/
%拱塔 O 6.8 10.2 A 5.4 1.4 20.6 5.8 4.4 43.1 B 5.0 1.8 26.5 5.2 5.0 49.0 C 4.6 2.2 32.4 4.8 5.4 52.9 拟合 4.5 2.3 33.8 5.0 5.2 51.0 主梁 O 10.4 77.6 A 12.3 1.9 18.3 71.4 6.2 8.0 B 12.5 2.1 20.2 70.8 6.8 8.8 C 12.6 2.2 21.2 70.4 7.2 9.3 拟合 12.6 2.2 21.2 70.5 7.1 9.1
下载: 导出CSV
-
SUNG Y C, CHANG D W, TEO E H. Optimum post-tensioning cable forces of Mau-Lo Hsi cable-stayed bridge[J]. Engineering Structures, 2006, 28(10): 1407-1417. doi: 10.1016/j.engstruct.2006.01.009 余文洋. 斜拉桥拱形钢桥塔受力分析与设计[D]. 成都: 西南交通大学, 2018. 孔玲,钟文香,李志玲. 京新五环立交的选型和设计[J]. 公路交通科技(应用技术版),2018,14(2): 180-182.KONG Ling, ZHONG Wenxiang, LI Zhiling. Selection and design of Beijing—Xinjiang fifth ring interchange[J]. Journal of Highway and Transportation Research and Development (Applied Technology Edition), 2018, 14(2): 180-182. HU N, DAI G L, YAN B, et al. Recent development of design and construction of medium and long span high-speed railway bridges in China[J]. Engineering Structures, 2014, 74(9): 233-241. 李鑫,梁力,王福春,等. 公路钢拱塔斜拉桥车致振动试验与数值分析[J]. 桥梁建设,2011,41(4): 37-40,56.LI Xin, LIANG Li, WANG Fuchun, el al. Testing and numerical analysis of vehicle-induced vibration of a highway cabled-stayed bridge with steel arch pylons[J]. Bridge Construction, 2011, 41(4): 37-40,56. 曹一山,徐强,李克冰. 大跨度拱形钢塔斜拉桥模型试验研究[J]. 公路交通科技,2016,33(5): 73-77. doi: 10.3969/j.issn.1002-0268.2016.05.012CAO Yishan, XU Qiang, LI Kebin. Experimental study on model of long-span cable-stayed bridge with arch-shaped steel pylon[J]. Journal of Highway and Transportation Research and Development, 2016, 33(5): 73-77. doi: 10.3969/j.issn.1002-0268.2016.05.012 林阳子,黄侨,任远. 拱桥拱轴线的优化与选形[J]. 公路交通科技,2007,24(3): 59-63. doi: 10.3969/j.issn.1002-0268.2007.03.014LIN Yangzi, HUANG Qiao, REN Yuan. Optimization and selection of arch bridge axis[J]. Journal of Highway and Transportation Research and Development, 2007, 24(3): 59-63. doi: 10.3969/j.issn.1002-0268.2007.03.014 刘毓湘,高敬红. 基于4次样条函数拱轴线优化设计的T-V求解法[J]. 公路交通科技,2007,24(6): 80-85. doi: 10.3969/j.issn.1002-0268.2007.06.019LIU Yuxiang, GAO Jinghong. Topkis-Veinott feasible direction method for optimum axis of arch bridge based on quartic spline function[J]. Journal of Highway and Transportation Research and Development, 2007, 24(6): 80-85. doi: 10.3969/j.issn.1002-0268.2007.06.019 TADJBAKHSH I G. Stability and optimum design of arch-type structures[J]. International Journal of Solids & Structures, 1981, 17(6): 565-574. SERRA M. Optimal arch:approximate analytical and numerical solutions[J]. Computers & Structures, 1994, 52(6): 1213-1220. HERNÁNDEZ-DÍAZ A M, BUENO-CRESPO A, PÉREZ-ARACIL J, et al. Multi-objective optimal design of submerged arches using extreme learning machine and evolutionary algorithms[J]. Applied Soft Computing, 2018, 71(10): 826-834. 栗怀广,郑凯锋,文曙东,等. 横向拱塔斜拉桥的拱轴线逐段设计算法研究[J]. 工程力学,2009,26(2): 131-136.LI Huaiguang, ZHEN Kaifeng, WEN Shudong, el al. An incremental design algorithm of arch axis of arch-shaped tower for cable-stayed bridge[J]. Engineering Mechanics, 2009, 26(2): 131-136. 胡常福,郑恒,任伟新,等. 考虑几何非线性的新型索拱桥拱轴线优化[J]. 土木建筑与环境工程,2014,36(4): 9-14.HU Changfu, ZHENG Heng, REN Weixin, el al. Arch axis optimization of new type arch bridge with diagonal web cables based on geometric nonlinear mechanical analysis[J]. Journal of Civil,Architectural & Environmental Engineering, 2014, 36(4): 9-14. 李晓龙. 拱形钢塔斜拉桥施工与运营一体化监测方法研究[D]. 重庆: 重庆交通大学, 2013. HASSAN M M. Optimization of stay cables in cable-stayed bridges using finite element,genetic algorithm,and B-spline combined technique[J]. Engineering Structures, 2013, 49(2): 643-654. 肖汝诚,项海帆. 斜拉桥索力优化的影响矩阵法[J]. 同济大学学报(自然科学版),1998,26(3): 235-240.XIAO Rucheng, XIANG Haifan. Influence matrix method of optimization cable tensions for cable-stayed bridges[J]. Journal of Tongji University (Natural Science), 1998, 26(3): 235-240. 梁鹏,肖汝诚,张雪松. 斜拉桥索力优化实用方法[J]. 同济大学学报(自然科学版),2003,31(11): 1270-1274.LIANG Peng, XIAO Rucheng, ZHANG Xuesong. Practical method of optimization cable tensions for cable-stayed bridges[J]. Journal of Tongji University (Natural Science), 2003, 31(11): 1270-1274. CHAPRA S C, CANALE R P. Numerical methods for engineers[M]. New York: Mcgraw-Hill, 1998: 142-146 -
下载:
点击查看大图
计量
- 文章访问数: 432
- HTML全文浏览量: 234
- PDF下载量: 10
- 被引次数: 0