Overtopping Failure of Moraine Dams under Action of Earthquake-Induced Resonant Water Surges
-
摘要: 为了研究冰碛坝在地震共振涌浪作用下的漫顶溃决机制，设计了振动台造波模型实验. 首先，通过对比实验获取了地震共振涌浪运动规律和最大波高的影响因素，并通过量纲分析建立了共振条件下涌浪最大波高计算公式；其次，依据非均匀沙起动临界水头高度与溃坝输沙临界水量条件，建立涌浪作用下堰塞坝漫顶溃决临界条件与溃决风险评估程式；最后，以帕隆藏布流域川藏铁路交通廊道沿线34个小型冰碛堰塞湖为例说明评估程式的作业流程. 研究结果表明：地震触发小型水体共振时涌浪运动幅度远超同等条件下的非共振涌浪幅度，且地震作用停止后涌浪波幅缓慢衰减，在共振涌浪时程曲线中存在稳态幅值持续运动阶段；当考虑地震共振效应后，帕隆藏布流域危险冰碛湖数量由3增至11，并在地震动水平地震加速度（PGA）较小区域均有分布；研究可为川藏铁路等沿线堰塞湖地震溃坝风险评估提供科学依据.Abstract: Shaking table model experiments were designed to study the overtopping failure mechanism of moraine dams under action of earthquake-induced resonant water surges (ERWSs). Firstly, movements of earthquake-triggered surges under resonant and non-resonant conditions were compared to examine the main influencing factors of maximum height of ERWSs, and a prediction equation for the maximum height was proposed through dimensional analysis. Then, based on the critical water head condition for coarse particle initiation and the critical water volume condition for sediment transportation in dam break, critical conditions of overtopping failure for barrier dams under water surge actions were established and a risk assessment procedure was developed. Finally, taking the 34 small-scale moraine-dammed lakes located in the Parlung Zangbo River basin as examples, the operation of the proposed procedure was demonstrated. Results show that compared with non-resonant surges, ERWSs have greater amplitudes and a much slower process of attenuation with time, and a steady state with continuous large-amplitude wave motion exists in the time history of the resonant surge. When the seismic resonance effect is considered, the number of dangerous moraine-dammed lakes in the Parlung Zangbo River basin increases from 3 to 11, and the distribution extends to the areas with smaller peak ground acceleration (PGA). The results provide a scientific basis for seismic risk assessment of barrier lakes along the Sichuan-Tibet Railway.
-
Key words:
- earthquake /
- surges /
- resonance /
- moraine-dammed lake /
- overtopping failure
-
随着基础设施建设的推进，公路与铁路工程建设中为了保证线路的顺直，越来越多的隧道衬砌结构工程穿行大型滑坡区域，形成滑坡-隧道相互作用、相互影响的工程特征[1]，隧道衬砌结构势必会承受滑坡推力作用，当滑坡作用力足够大时，隧道衬砌结构会产生相应变形或破坏.
目前，国内外对这种滑坡-隧道相互作用的特征及机理投入了较多关注，主要表现在三方面，一是对滑坡-隧道相互作用模型体系进行了总结与归纳，如吴红刚等[2]从滑面与隧道相处位置出发，建立了以平行体系、正交体系和斜交体系为核心的较为完备的受力变形模式；张鲁新等[3]分析了滑坡与隧道变形特征并提出五种地质结构模型；陈小云等[4]对于正交体系下隧道与滑带相交力学模型进行了研究. 二是采用多种手段研究了滑坡作用下隧道衬砌结构受力机理以及滑坡-隧道相互作用机理，如陶志平[5]采用室内模型试验方法，分析了滑坡地段隧道的变形机理，研究了隧道围岩和隧道衬砌压力的变化规律；毛坚强等[6]运用接触面来模拟滑面，应用有限元算法分析了滑坡-隧道间的相互作用机理以及隧道的受力变形规律；陈刚[7]分别讨论了隧道开挖和降雨作用对滑坡体变形的影响；王旭[8]结合具体的工程实例，考虑隧道与滑面相对位置关系变化，计算了边坡的安全系数和隧道衬砌结构变形. 同时，国外一部分学者[9-14]确定了隧道在滑坡应力作用下的变形机理，并采用现代传感、监测新技术对滑坡-隧道模型进行研究. 另一部分学者[15-19]通过二维和三维数值模拟方法探讨隧道开挖诱发深部滑坡问题及隧道-滑坡相互作用机理. 特别地，Chiu等[20]通过隧道衬砌变形情况来反应滑坡作用下隧道所受作用力. 第三方面是滑坡-隧道治理措施上开展了卓有成效的研究，如杜升涛[21]通过选用抗滑桩支挡和排水工程综合治理的方案治理襄渝线赵家塘隧道滑坡；陶志平等[22]采用抗滑桩来治理滑坡地段隧道的变形问题；郑颖人等[23]以重庆某高速公路隧道出口段的滑坡治理工程为背景，采用有限元强度折减法研究了滑动面位置与抗滑桩位置和桩间距的关系. 总体来说，目前治理方式一般应用滑坡治理措施和隧道加固措施的原则，主要采用预应力锚索和抗滑桩等来治理滑坡，围岩注浆和增强隧道衬砌等方式来加固隧道，如赣龙铁路马蹄径隧道[24]和相田二号隧道[25]等. 虽然以上研究得了一定的成果，但所有研究主要依托于某一具体滑坡-隧道相互作用案例开展相关滑坡稳定性、隧道变形机理或治理措施相关的研究，还没有出现专门探讨滑坡滑带角度变化对隧道衬砌结构受力变化及对衬砌结构影响的相关研究.
因此，本文采用室内模型试验、数值模拟的方法，探讨针对不同滑带角度条件滑坡作用对隧道衬砌结构受力的影响，得到滑坡作用下偏压隧道衬砌受力[26]变化规律，这对于弥补滑坡-隧道相互作用研究的不足，更加清楚的掌握滑坡作用下隧道衬砌结构受力的变化有一定的现实意义.
1. 滑坡隧道室内模型试验设计
1.1 滑坡隧道工程实例
通过分析国内多个典型滑坡-隧道特征[1, 4, 26-28]可以得出，滑坡滑动带的倾角基本在0°～50°，破坏点基本位于拱脚处. 因此，以下研究主要以大（同）准（格尔）铁路K20南坪隧道为研究原型，考虑不同滑带角度作用下隧道衬砌结构受力变化特征及变化规律. 大（同）准（格尔）铁路K20南坪隧道洞顶回填区为宽缓平台，平台高程为1 205～1 207 m，宽43～77 m. 其地形、岩性结构剖面如图1. 其滑带与隧道夹角约为10°.
南坪隧道受滑坡影响变形较为严重，裂缝多位于拱壁墙边，以纵向为主最长达28 m. 在16～18避车间变形最大实测最大累计变形达24 mm （2016年1月14日—2016年5月1日），工务段实测最大累计变形达77 mm （2015年3月14日— 4月13日）. 避车洞墙边位移过大，导致水沟挤压变形：K20 + 082～K20 + 058段水沟被挤压扭曲，隧道表面混凝土面层产生脱落现象，位移量达28 cm；K20 + 41～K20 + 58段水沟受挤压，盖板鼓起，位移量达6 cm，在与滑带相交处产生了较大的局部剪切变形.
1.2 模型试验相似比
以南坪滑坡隧道为原型，几何比设为1∶100，将重要的滑坡体参数容重γ、黏聚力c、内摩擦角φ根据相似材料进行配比，隧道衬砌弹性模量E以及泊松比μ按照一定的比例进行配置. 按照相似比理论，各变量对应的相似比为CL=100，Cγ=1，Cμ=Cc=Cφ=1，Cσ=CE= 100，其中L为几何尺寸，σ为应力.
1.3 模型试验设计与制作
根据几何相似比，试验模型长2.5 m，宽0.5 m，高0.9 m，如图2. 滑带厚度为3.0 cm，滑动区为滑动面的角度分别设为0°、10°、20°、30°、40°、50°. 滑带材料采用黏性土加少量石膏，滑体由砾石粉粒分层压实组成，使其参数满足相似比要求. 滑床采用中等风化碎石同少量黏土石灰混合、夯实，以减少实验时不必要的沉降变形. 试验材料参数如表1.
表 1 模型试验材料力学参数Table 1. Mechanical parameters of model materials名称 密度 ρ/
（kg•m−3）E/MPa c/kPa φ/（°） 滑坡体 1 900 18.65 27.79 25.35 滑带 1 800 9.36 15.82 15.63 滑床 2 200 23.72 54.24 54.32 隧道衬砌 2 100 289.61 236.65 61.71 在滑体内部放置一长0.5 m、厚1.0 cm的石膏材料隧道. 模型隧道按照模型尺寸订做模具，模具材料为2.0 cm厚的PVC塑料板，并用螺杆穿起拼装为整体，隧道衬砌内模由两块弧形钢板拼成. 模具组装前，先在模具内铺设间距12.0 mm钢丝网，用螺杆拼接，采用石膏∶水＝2∶1比例进行隧道整体浇筑，形成模型试验用隧道结构.
模型试验按滑带角度0°、10°、20°、30°、40°、50° 分别制作相应模型进行试验，即一种滑带角度模型试验完成后，重新制作模型，进行下一种滑带角度模型试验.
1.4 测点布置
滑坡体表面设置位移计监测加载过程中位移变形情况（如图2）. 为了能够详细掌握不同滑带角度作用下隧道衬砌结构应力变化，内外分别布置20个应变片测点（N1～N20、W1～W20），如图3（a）所示. 在隧道横截面布置10个粘贴应变花的测点（J1～J10）监测隧道衬砌受剪情况（图3（b））. 微型压力盒（1～7）布置在隧道衬砌的外侧，用以监测隧道衬砌受到的滑坡推力或压力变化（图3（c））. 同时，为得到隧道衬砌结构上竖向压应力值，采用应变片的方法采集数据，应变片黏贴位置与图3（c）一致（图中未画出）.
1.5 加载方案
根据滑坡隧道演化规律，采用多级加载. 详细的装载方案见表2. 荷载施加在滑坡隧道模型的后缘. 在第一阶段，施加的荷载为500 N，保持20 min. 第二阶段施加1 000 N的荷载，并保持40 min. 从第三阶段到第六阶段，在20 min的时间间隔内平稳地增加了荷载，然后保持40 min，这一过程一直持续到滑坡模型破坏失效.
表 2 模型试验加载方案Table 2. Loading scheme in model test滑带角度/（°） 荷载/kN 加载时
间/min维持时
间/min0、10、20、30、40、50 0.5 10 20 1.0 10 20 5.0 20 40 10.0 20 40 15.0 20 40 20.0 30 40 25.0 30 40 1.6 试验结束标准
经过多次预试验及参考已有模型试验成果，模型试验结束标准选为坡体从隧道顶部滑出，同时加载测力计数值下降，此时判定为模型破坏、失效. 除坡体位移监测外，其他监测元件数据采用测力计为最大值时的监测值作为最终计算数据.
2. 模型试验结果与分析
2.1 模型试验破坏特征
依次开展了滑带角度为0°、10°、20°、30°、40°、50° 的滑坡隧道模型试验. 试验结束后，坡体产生两条裂缝，滑坡产生较大位移，隧道顶部的坡体（坡脚处）基本滑移出模型槽. 隧道顶部坡体表层位移监测点的位移如图4. 随着加载时间的推移，位移逐渐增长，滑带角度为0° 时，模型破坏时位移达到160 mm，滑带角度为50° 时，模型破坏时位移约10 mm. 可以看出：滑带角度越小，坡体变形越大，滑带角度越大，坡体变形越小. 另外，在模型加载初始阶段，滑带小角度变形增长最快，有突然增大过程，但滑带角度达到30° 以后，坡体位移初始阶段增长较慢. 同时，在滑坡推力作用下，隧道衬砌结构产生一定程度的变形，并且隧道衬砌结构相对于原位置产生了一定的位移，0° 时隧道所产生的位移最大约为10 mm，30° 时产生约4 mm的变形，50° 时几乎未产生位移. 可以得到，随着滑带角度的增大，在相同滑坡推力作用下，隧道的变形逐渐减小.
图 4 不同滑带角度条件下坡体位移Figure 4. Displacements of slope with various angles of sliding zone2.2 隧道衬砌结构受力特征
1） 弯矩与剪应力特征
根据图3中隧道衬砌结构上的应变片等测试元件，按照一定的关系式可以计算不同滑带角度下作用于隧道衬砌结构上的应力与弯矩值，如表3.
表 3 不同滑带角度下隧道弯矩与剪应力值Table 3. Bending and shear stress values of tunnel under different angles of sliding zone滑带角度/（°） 弯矩/（kN•m） 剪力/kN 0 
10 
20 
30 
40 
50 
从表3中可以看出：对于隧道衬砌结构上所受弯矩，滑带角度0° 时弯矩最大值为463 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为201 kN•m，左右两侧弯矩相差2.3倍，两侧受力不均，形成典型偏压隧道. 滑带角度30° 时，弯矩最大值为178 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为65 kN•m，左右两侧弯矩相差2.7倍. 当滑带角度50° 时，弯矩最大值为87 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为27 kN•m，左右两侧弯矩相差3.2倍. 可见，弯矩在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受弯矩越小.
对于隧道衬砌结构上所受剪力，基本与弯矩规律类似. 滑带角度 0° 时剪力最大值为20.3 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为18.5 kN. 滑带角度30° 时，剪力最大值为16.8 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为5.7 kN. 当滑带角度50° 时，剪力最大值为7.3 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为2.9 kN. 可见，剪力在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受剪力越小，被剪切破坏的可能性减小.
2） 土压力特征
由压力盒的监测数据计算得到滑坡推力作用在隧道衬砌结构上的土压力，如表4. 可以看出：作用在隧道衬砌结构上的土压力在靠山侧大于另一侧1～2倍，拱脚处大于拱肩、拱顶处的土压力，沿着隧道衬砌结构截面分布出现出左右不均的偏压现象. 由于滑带的作用，靠山侧拱脚处土压力值最大，在滑带角度为0° 时，土压力为16.4 kPa，30° 时，土压力为9.6 kPa，50° 时，土压力为7.4 kPa，仅为滑带角度为0° 时的0.45倍，可见随着滑带角度逐渐增大，作用在拱脚处的土压力逐渐减小.
表 4 不同滑带角度下隧道土压力值Table 4. Distribution of earth pressure on tunnel under different angles of sliding zone滑带角度/（°） 土压力分布/kPa 0 
10 
20 
30 
40 
50 
3） 偏压应力比
将同样埋深情况下隧道衬砌结构左右侧洞壁上对应点的竖向应力比值定义为偏压应力比[26]. 为了全面掌握不同滑带角度作用下的偏压应力比，布置了如图3（c）所示的7个隧道衬砌结构竖向压应力分析点.
如图3（c），对于其中顶部和底部应力比，底部采用点4、5的平均值. 分别对应拱顶（点1），左右拱肩（点2、7），拱脚（点3、6）以及拱底（点4、5）. 按照拱肩（点2、7）偏压应力比Δ1，以及拱脚（点3、6）偏压应力比Δ2进行计算分析.
Δ1=σ2σ7, (1) Δ2=σ3σ6, (2) 式中：σ2、σ7和σ3、σ6分别为隧道衬砌结构监测点测得左右拱肩（点2、7）和拱脚（点3、6）应力值.
由监测元件数据换算，并根据式（1）、（2）得到表5的数值，可以得出：在拱肩位置，当滑带角度为0° 时偏压应力比为1.17，滑带角度为30° 时，偏压应力比为1.07，50° 时，偏压应力比1.01. 可见，随着滑带角度的增大，偏压应力比逐渐减小，即随着滑带角度的增大，在拱肩位置处隧道衬砌拱结构左右应力差越来越小，越来越趋于平衡拱. 在拱脚位置，当滑带角度0° 时偏压应力比为1.08，滑带角度为30°时，偏压应力比为1.29，50° 时，偏压应力比1.87. 可见，随着滑带角度的增大，偏压应力比逐渐增大，即随着滑带角度的增大，在拱脚位置处隧道衬砌拱结构左右所受应力差越来越大，趋向于偏压隧道.
表 5 模型试验下不同滑带角度隧道衬砌偏压应力比Table 5. Bias stress ratio at different sliding angles in model test滑带角度/（°） Δ1 Δ2 0 1.17 1.08 10 1.09 1.25 20 1.04 1.27 30 1.07 1.29 40 1.02 1.54 50 1.01 1.87 3. 隧道衬砌结构受力数值模拟
3.1 模型建立
根据大准铁路南坪隧道原型结构，采用有限单元法进行不同滑带角度作用下隧道衬砌结构受力分析，数值模拟中所用模型参数如表1. 模拟中设置了桩与土、隧道结构与土之间的接触单元[29-31]，材料参数中桩接触单位极限剪切力0.99 N/m，法向刚度系数0.99 kN；隧道接触单元主应力刚度模量2.45 MPa，剪切刚度模量0.245 MPa，摩擦角36°.
分别采用 0°、10°、20°、30°、40°、50°，6种滑带角度条件进行模拟分析，分析模型如图5（限于篇幅，其他未列出）.
3.2 模拟结果分析
如图6所示为 30° 滑带角度滑坡推力作用下隧道衬砌结构位移变形（其他滑带角度作用下隧道位移云图规律类似，仅位移值不同），当滑带角度为 0° 时最大变形量为121 mm，滑带角度为30° 时最大变形为59.8 mm，滑带角度为 50° 时最大变形为0.2 mm，最大变形位置均发生在靠山侧的拱脚处. 可见，随着滑带角度的增大，隧道衬砌结构变形逐渐减小，这与模型试验得出的位移规律基本一致，仅在变形量数值上略有差别.
图7为数值模拟所得隧道衬砌结构所受弯矩（其他滑带角度作用下隧道弯矩云图规律类似，仅弯矩值不同）. 与模型试验所得规律基本一致，最大弯矩值分布在靠山侧的拱脚处，当滑带角度为 0° 时最大弯矩量为487.90 kN•m，滑带角度为30° 时最大弯矩为187.00 kN•m，滑带角度为50° 时最大弯矩为89.03 kN•m. 同样地，随着滑带角度的增大，隧道衬砌结构所受弯矩逐渐减小. 在滑坡推力作用下，隧道衬砌结构拱左右受力不均，存在偏压现象.
3.3 数值模拟与模型试验对比分析
数值模拟中设置如图3的监测点，得到隧道衬砌结构上7个监测点的应力值，并根据式（1）、（2）计算出偏压应力比，如表6，与模型试验中的监测数值进行比较，数值上接近，反映出的规律一致，在拱肩位置处，随着滑带角度的增长，拱左右两侧所受竖向应力差逐渐减少，趋于平衡拱，在拱脚位置处，由于滑坡推力的作用，随着滑带角度的增大，拱左右两侧的竖向应力值越来越大，更趋于偏压隧道.
表 6 数值模拟下不同滑带角度隧道衬砌偏压应力比Table 6. Bias stress ratios in numerical simulation滑带角度/（°） Δ1 Δ2 0 1.21 0.98 10 1.20 1.22 20 1.14 1.25 30 1.11 1.48 40 1.09 1.83 50 1.06 2.34 4. 结 论
以大准铁路K20南坪隧道为例，采用室内模型试验、数值模拟手段，开展了不同滑带角度的滑坡作用下隧道衬砌结构受力特征相关研究，得到如下结论：
1） 穿越滑坡区的隧道由于滑坡推力的作用，隧道衬砌结构容易产生变形或破坏.
2） 滑坡滑带角度的不同，对隧道衬砌结构的力学作用也不同. 对于隧道衬砌结构上所受弯矩与剪应力，在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受弯矩与剪应力越小. 作用在隧道衬砌结构上的土压力在靠山侧大于另一侧1～2倍，拱脚处大于拱肩、拱顶处的土压力，沿着隧道衬砌结构截面分布出现出左右不均的偏压现象，随着滑带角度逐渐增大，作用在拱脚处的土压力逐渐减小.
3） 计算得到隧道衬砌结构上不同位置处的竖向压应力，并计算出其左右两侧的偏压应力比，得出在拱肩位置，随着滑带角度的增大，隧道衬砌拱结构左右应力差越来越小，越来越趋于平衡拱. 在拱脚位置，随着滑带角度的增大，偏压应力比逐渐增大，隧道衬砌拱结构左右两侧所受应力差越来越大，趋向于偏压隧道.
在实际工程中，对于穿行大型滑坡区域的隧道，在设计过程中可在隧道衬砌结构拱脚处加强设置，同时采用抗滑桩等滑坡支挡措施抵御滑坡推力的作用.
-
图 2 白噪声激励下涌浪波高时程傅立叶幅值谱
Figure 2. Fast Fourier transform (FFT) spectrum of wave height time history due to white noise excitation
图 3 E1地震波及相应的非共振涌浪时程曲线（水深30.0 cm）
Figure 3. E1 earthquake wave and the induced non-resonant water wave (water depth = 30.0 cm)
图 4 E2地震波及相应的共振涌浪时程曲线（水深30 cm）
Figure 4. E2 earthquake wave and the induced resonant water wave (water depth = 30 cm)
图 5 不同水深条件下地震共振涌浪最大波高随PGA变化
Figure 5. Variations of maximum wave elevation with increasing PGA at different water depths
图 7 涌浪作用下堰塞坝溃决风险评估程式
Figure 7. Risk assessment procedure for the overtopping failure of natural dams due to earthquake-induced water waves
-
刘宁, 程尊兰, 崔鹏, 等. 堰塞湖及其风险控制[M]. 北京: 科学出版社, 2013: 352-372. WILFRIED H. On the morphodynamics of iceldebris-transport systems in cold mountain areas[J]. Norsk Geografisk Tidsskrift, 1996, 50(1): 3-9. doi: 10.1080/00291959608552346 CLAUGE J J, EVANS S G. A review of catastrophic drainage of moraine-dammed lakes in British Columbia[J]. Quaternary Science Reviews, 2000, 19(17/18): 1763-1783. doi: 10.1016/S0277-3791(00)00090-1 AWAL R, BAYABIL H K, FARES A. Experimental study on glacial lake outburst floods due to waves overtopping and erosion of moraine dam[J]. Annuals of Disaster Prevention and Research Institute, 2010, 53: 583-594. 石振明,王友权,彭铭,等. 余震作用下堰塞坝体破坏及溃决过程大型振动台试验研究[J]. 工程地质学报,2014,22(1): 71-77. doi: 10.3969/j.issn.1004-9665.2014.01.010SHI Zhengming, WANG Youquan, PENG Ming, et al. Large scale shaking table tests on failure and breach process of landslide dams under aftershocks[J]. Journal of Engineering Geology, 2014, 22(1): 71-77. doi: 10.3969/j.issn.1004-9665.2014.01.010 WESTERGAARD H M. Water pressures on dams during earthquakes[J]. Transactions of the American Society of Civil Engineers, 1933, 98(3): 418-433. CHWANG A T, HOUSNER G W. Hydrodynamic pressures on sloping dams during earthquakes. part 1. momentum method[J]. Journal of Fluid Mechanics, 1978, 87(2): 335-341. doi: 10.1017/S0022112078001639 CHEN B F, YUAN Y S. Hydrodynamic pressures on arch dam during earthquakes[J]. Journal of Hydraulic Engineering, 2010, 137(1): 34-44. SATO Q. Seismic waves in reservoirs generated by earthquake[J]. Civil Engineering Materials, 1967, 9: 480-482. DEMIREL E, AYDIN I. Numerical simulation and formulation of wave run-up on dam face due to ground oscillations using major earthquake acceleration records[J]. Journal of Engineering Mechanics, 2016, 142(6): 06016001.1-06016001.10. DU C, YAO L, HUANG Y, et al. Effects of seismic surge waves and implications for moraine-dammed lake outburst[J]. Frontiers of Earth Science, 2016, 10(3): 570-577. doi: 10.1007/s11707-015-0533-4 周亦良. 地震动水压力及冰碛堰塞坝失稳机理研究[D]. 成都: 西南交通大学, 2017. 姚令侃,邱燕玲,魏永幸. 青藏高原东缘进藏高等级道路面临的挑战[J]. 西南交通大学学报,2012,47(5): 719-734. doi: 10.3969/j.issn.0258-2724.2012.05.001YAO Lingkan, QIU Yanling, WEI Yongxing. Challenges in construction of railway and highway from Sichuan to Tibet through eastern margin of Tibetan Plateau[J]. Journal of Southwest Jiaotong University, 2012, 47(5): 719-734. doi: 10.3969/j.issn.0258-2724.2012.05.001 CHEN X Q, CUI P, LI Y, et al. Changes in glacial lakes and glaciers of post-1986 in the Poiqu River basin,Nyalam,Xizang (Tibet)[J]. Geomorphology, 2007, 88(3/4): 298-311. doi: 10.1016/j.geomorph.2006.11.012 WU G X, MA Q W, TAYLOR R E. Numerical simulation of sloshing waves in a 3D tank based on a finite element method[J]. Applied Ocean Research, 1998, 20(6): 337-355. doi: 10.1016/S0141-1187(98)00030-3 BALMFORTH N J, VON H J, PROVENZALE A, et al. Dam breaking by wave-induced erosional incision[J]. Journal of Geophysical Research Atmospheres, 2008, 113: 341-356. 蒋忠信,崔鹏,蒋良潍. 冰碛湖漫顶型溃决临界水文条件[J]. 铁道工程学报,2004,84(4): 21-26. doi: 10.3969/j.issn.1006-2106.2004.04.006JIANG Zhongxin, CUI Peng, JIANG Liangwei. Critical hydrologic condition for overflow burst of moraine lake[J]. Journal of Railway Engineering Society, 2004, 84(4): 21-26. doi: 10.3969/j.issn.1006-2106.2004.04.006 崔鹏,马东涛,陈宁生,等. 冰湖溃决泥石流的形成、演化与减灾对策[J]. 第四纪研究,2003,23(6): 621-62. doi: 10.3321/j.issn:1001-7410.2003.06.005CUI Peng, MA Dongtao, CHEN Ningsheng, et al. The initiation,motion and mitigation of debris flow caused by glacial lake outburst[J]. Quaternary Sciences, 2003, 23(6): 621-62. doi: 10.3321/j.issn:1001-7410.2003.06.005 吴积善, 田连权, 康志成, 等. 泥石流及其综合治理[M]. 北京: 科学出版社, 1993: 129-130. 董华飞,李俊青. 洪水漫顶条件下涌浪越坝的试验研究[J]. 人民珠江,2015(4): 13-16. doi: 10.3969/j.issn.1001-9235.2015.04.005DONG Huafei, LI Junqing. Experimental study on over-dam surge under the condition of flood overtopping[J]. Pearl River, 2015(4): 13-16. doi: 10.3969/j.issn.1001-9235.2015.04.005 张金牛,吴卫,刘桦,等. 孤立波作用下斜坡堤越浪量的实验研究[J]. 水动力学研究与进展A辑,2014,29(6): 656-662.ZHANG Jinniu, WU Wei, LIU Hua, et al. An experimental study on overtopping of solitary wave against a slope dike[J]. Chinese Journal of Hydrodynamics, 2014, 29(6): 656-662. 王欣, 刘时银, 丁永建. 中国喜马拉雅山冰碛湖溃决灾害评价方法与应用研究[M]. 北京: 科学出版社, 2016: 56-61. 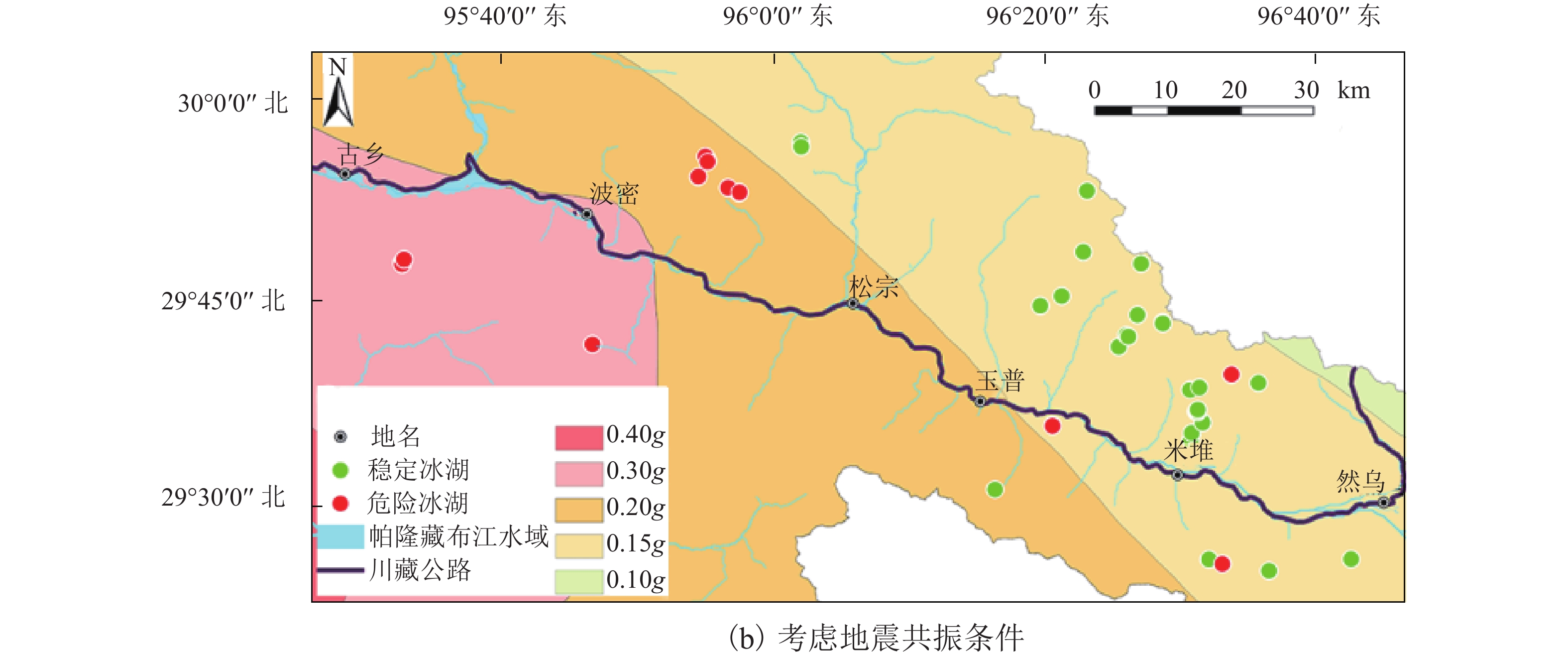中国地震局. 中国地震动参数区划图: GB 18306—2015[S]. 北京: 中国标准出版社, 2016. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 583
- HTML全文浏览量: 285
- PDF下载量: 16
- 被引次数: 0