Effect of Defect on Fatigue Property of EA4T Axle Steel
-
摘要: 为了研究和准确评估不同尺寸的缺陷对EA4T车轴钢疲劳性能的影响,采用钻孔法在光滑试样表面人为引入缺陷,使用旋转弯曲疲劳试验机对光滑试样和不同尺寸缺陷的试样进行疲劳试验,以获得不同试样的疲劳极限;使用扫描电镜(SEM)观察断口形貌,使用Neuber公式(基于缺口敏感性)和修正的El-Haddad模型(基于断裂力学方法)评估带缺陷试样的疲劳极限. 研究结果表明:当试样等效缺陷尺寸小于59.64 μm时,其疲劳极限与光滑试样相同,都为360 MPa;当等效缺陷尺寸大于59.64 μm时,缺陷会降低光滑试样的疲劳极限,并且引入缺陷尺寸越大,疲劳极限越低;基于Neuber公式预测的疲劳强度能得到较为保守的疲劳强度估算值,而修正的El-Haddad模型可以更好地预测和评估不同尺寸的圆孔型三维缺陷对EA4T车轴钢疲劳强度的影响.
-
关键词:
- 缺陷 /
- EA4T车轴钢 /
- 疲劳极限 /
- Neuber公式 /
- El-Haddad模型
Abstract: In order to accurately evaluate the effects of different size defects on the fatigue property of EA4T axle steel, the drilling method was used to artificially introduce defects on the surface of the smooth specimen, and the fatigue test was carried out to obtain the fatigue limits on the smooth specimens and the specimens with different size defects by the rotary bending fatigue machine. The fracture morphology was observed by a scanning electron microscopy (SEM). Finally, the fatigue limits of specimens with defects were assessed using Neuber's formula (based on notch sensitivity) and a modified El-Haddad model (based on fracture mechanics). The result show that when the defect size of the specimen is less than 59.64 μm, the fatigue limit is the same as the smooth specimen, both of which are 360 MPa, however, when the defect size is larger than 59.64 μm, the defect will reduce the fatigue limit of the smooth specimen, and the larger the introduced defect size, the lower the fatigue limit. Fatigue strength prediction based on the Neuber formula is conservative, however, the modified El-Haddad model can better predict and evaluate the effect of different size of 3D hole defects on the fatigue strength of EA4T axle steel.-
Key words:
- defect /
- EA4T axle steel /
- fatigue limit /
- Neuber formula /
- El-Haddad model
-
表 1 EA4T化学成分(质量分数)
Table 1. Chemical compositions of EA4T steel
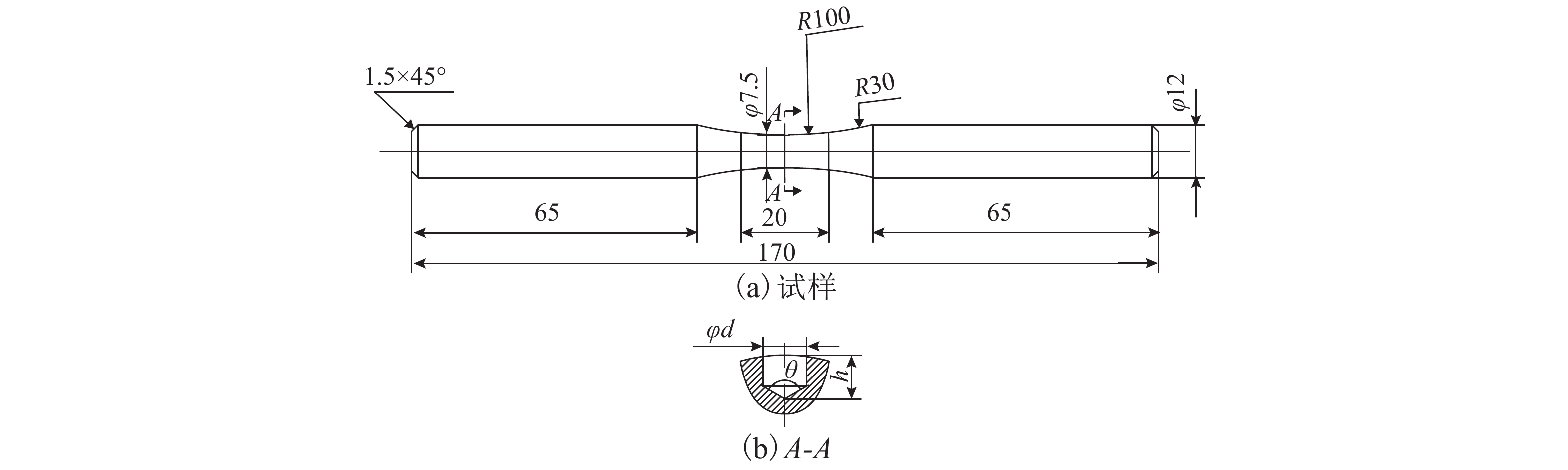
% 元素 C Si Mn P S Cr Cu Ni Mo Fe 质量分数 0.27 0.39 0.72 0.0075 0.0013 1.11 0.01 0.25 0.25 余量 表 2 缺陷尺寸
Table 2. Defect size
μm 试样编号 d h S 1 100 50 59.64 2 100 100 92.50 3 200 200 185.00 4 300 300 277.51 5 500 500 462.51 6 1000 1000 925.02 表 3 不同试样的疲劳极限
Table 3. Fatigue limit of different specimen
试样编号 d/μm h/μm σw/MPa 光滑试样 0 0 360 1 100 50 360 2 100 100 330 3 200 200 290 4 300 300 280 5 500 500 240 6 1000 1000 190 表 4 模拟结果
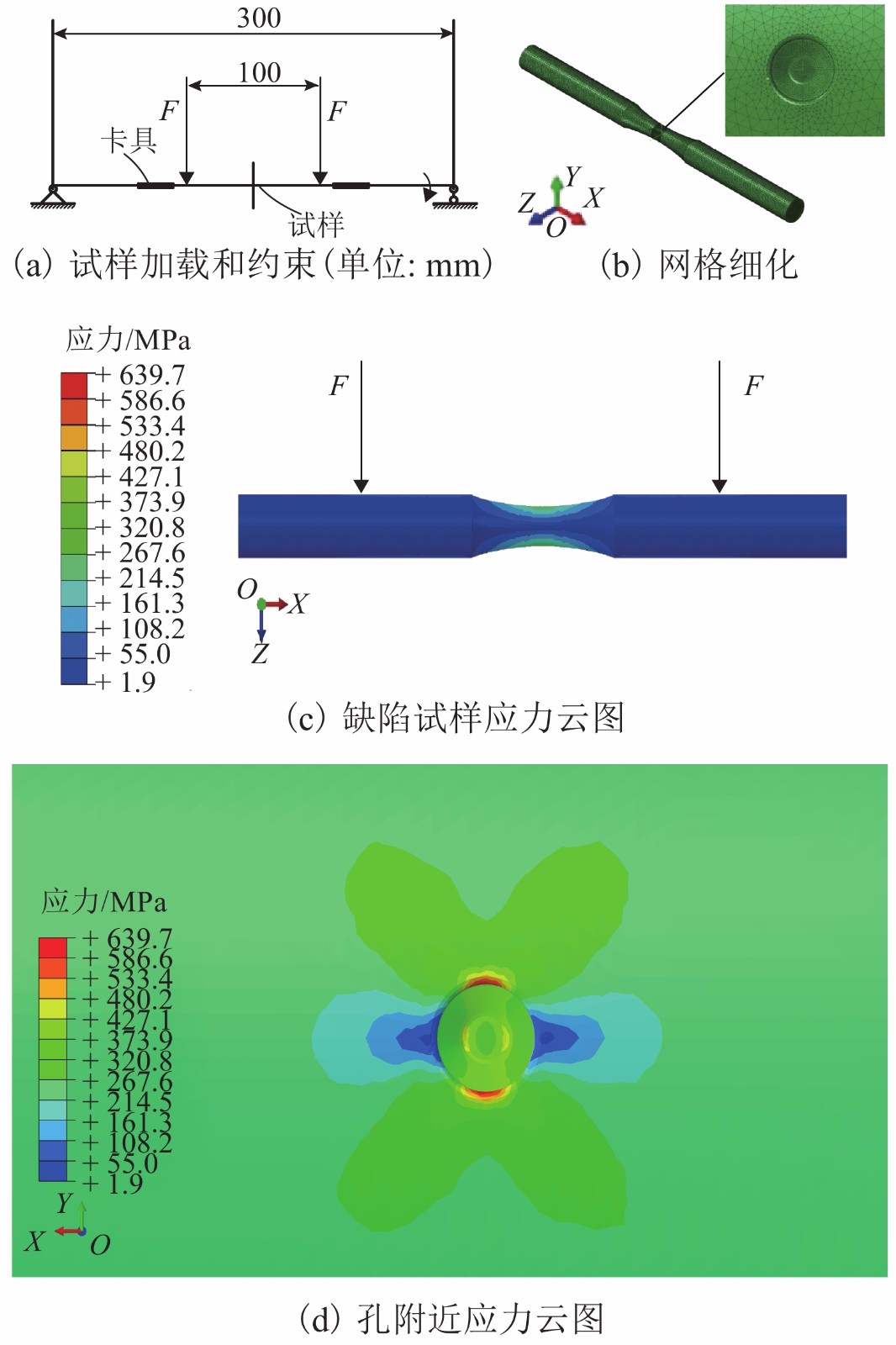
Table 4. Simulated results
试样编号 F/N σnom/MPa σpeak/MPa 1 158.27 390 787.5 2 146.09 360 778.3 3 129.86 320 690.5 4 125.80 310 703.3 5 109.57 270 639.7 6 89.28 220 544.6 表 5 疲劳极限预测结果
Table 5. Result of fatigue limit prediction
试样编号 q Kt Kf σest/MPa σw/MPa ε/% 1 0.44 2.02 1.45 249 360 −31 2 0.44 2.16 1.51 238 325 −27 3 0.53 2.16 1.61 223 290 −23 4 0.57 2.26 1.73 208 280 −26 5 0.64 2.37 1.87 195 240 −20 6 0.71 2.48 2.05 175 190 −8 -
马利军. 断裂力学的含缺陷车轴服役寿命评估方法研究[D]. 北京: 北京交通大学, 2016. 徐忠伟. 高速铁路外物损伤车轴疲劳评估方法[D]. 成都: 西南交通大学, 2018. 吴圣川,徐忠伟,康国政,等. 外物损伤对合金车轴钢疲劳性能的影响[J]. 西南交通大学学报,2018,40(9): 1000-1005.WU Shengchuan, XU Zhongwei, KANG Guozheng, et al. Fatigue strength of railway axle used alloy steel due to foreign object damage[J]. Journal of Southwest Jiaotong University, 2018, 40(9): 1000-1005. 周素霞. 高速列车空心车轴损伤容限理论与方法研究[D]. 北京: 北京交通大学, 2010. 高杰维,戴光泽,赵君文,等. 压痕对车轴钢疲劳极限的影响[J]. 工程科学学报,2016,38(6): 827-833.GAO Jiewei, DAI Guangze, ZHAO Junwen, et al. Indentation effect on the fatigue limit of axle steel[J]. Chinese Journal of Engineering, 2016, 38(6): 827-833. 景启明,曲顺德,季亚奇,等. 国产EA4T车轴钢的缺口疲劳性能[J]. 机械工程材料,2015,39(10): 106-110. doi: 10.11973/jxgccl201510023JING Qiming, QU Shunde, JI Yaqi, et al. Notch fatigue property of domestic EA4T axle steel[J]. Materials for Mechanical Engineering, 2015, 39(10): 106-110. doi: 10.11973/jxgccl201510023 BERETTA S, GHIDINI A, LOMBARDO F. Fracture mechanics and scale effects in the fatigue of railway axles[J]. Engineering Fracture Mechanics, 2005, 72(2): 195-208. doi: 10.1016/j.engfracmech.2003.12.011 MURAKAMI Y. Metal fatigue: effects of small defects and nonmetallic inclusions[M]. Tokyo: Elsevier, 2002: 35-55. PETERSON R E. Stress concentration design factors[M]. New York: [s.n.], 1953: 28. NEUBER H. Theory of notch stresses: principles for exact calculation of strength with reference to structural form and material[M]. Second Edition. Berlin: Springer-Verlag, 1958: 230-238. STEPHENS R I, FATEMI A, STEPHENS R R. Metal fatigue in engineering[M]. Second Edition. New York: [s.n.], 2001: 196-200. EL-HADDAD M, TOPPER T H, SMITH K N. Prediction of non propagating cracks[J]. Engineering Fracture Mechanics, 1979, 11(3): 573-584. doi: 10.1016/0013-7944(79)90081-X KITAGAWA H, TAKAHASHI S. Applicability of fracture mechanics to very small cracks or the cracks in the early stage[C]//Proceedings of The Second International Conference on Mechanical Behavior of Materials. Metals Park: ASM International, 1976: 627-631. ATZORI B, LAZZARIN P, MENEGHETTI G. Fracture mechanics and notch sensitivity[J]. Fatigue & Fracture of Engineering Materials & Structures, 2010, 26(3): 257-267. MURAKAMI Y, ENDO M. Quantitative evaluation of fatigue strength of metals containing various small defects or cracks[J]. Engineering Fracture Mechanics, 1983, 17(1): 1-15. doi: 10.1016/0013-7944(83)90018-8 REGAZZI D, BERETTA S, CARBONI M. An investigation about the influence of deep rolling on fatigue crack growth in railway axles made of a medium strength steel[J]. Engineering Fracture Mechanics, 2014, 131: 587-601. doi: 10.1016/j.engfracmech.2014.09.016 POKORNY P, VOJTEK T, NÁHLÍK L, et al. Crack closure in near-threshold fatigue crack propagation in railway axle steel EA4T[J]. Engineering Fracture Mechanics, 2017, 185: 2-19. doi: 10.1016/j.engfracmech.2017.02.013 WU S C, XU Z W, KANG G Z, et al. Probabilistic fatigue assessment for high-speed railway axles due to foreign object damage[J]. International Journal of Fatigue, 2018, 117: 90-100. doi: 10.1016/j.ijfatigue.2018.08.011 -





 下载:
下载: