Hydrodynamic Pressures Study of Barrier Lake under Coaction of Earthquake and Clastic Flow Landslide
-
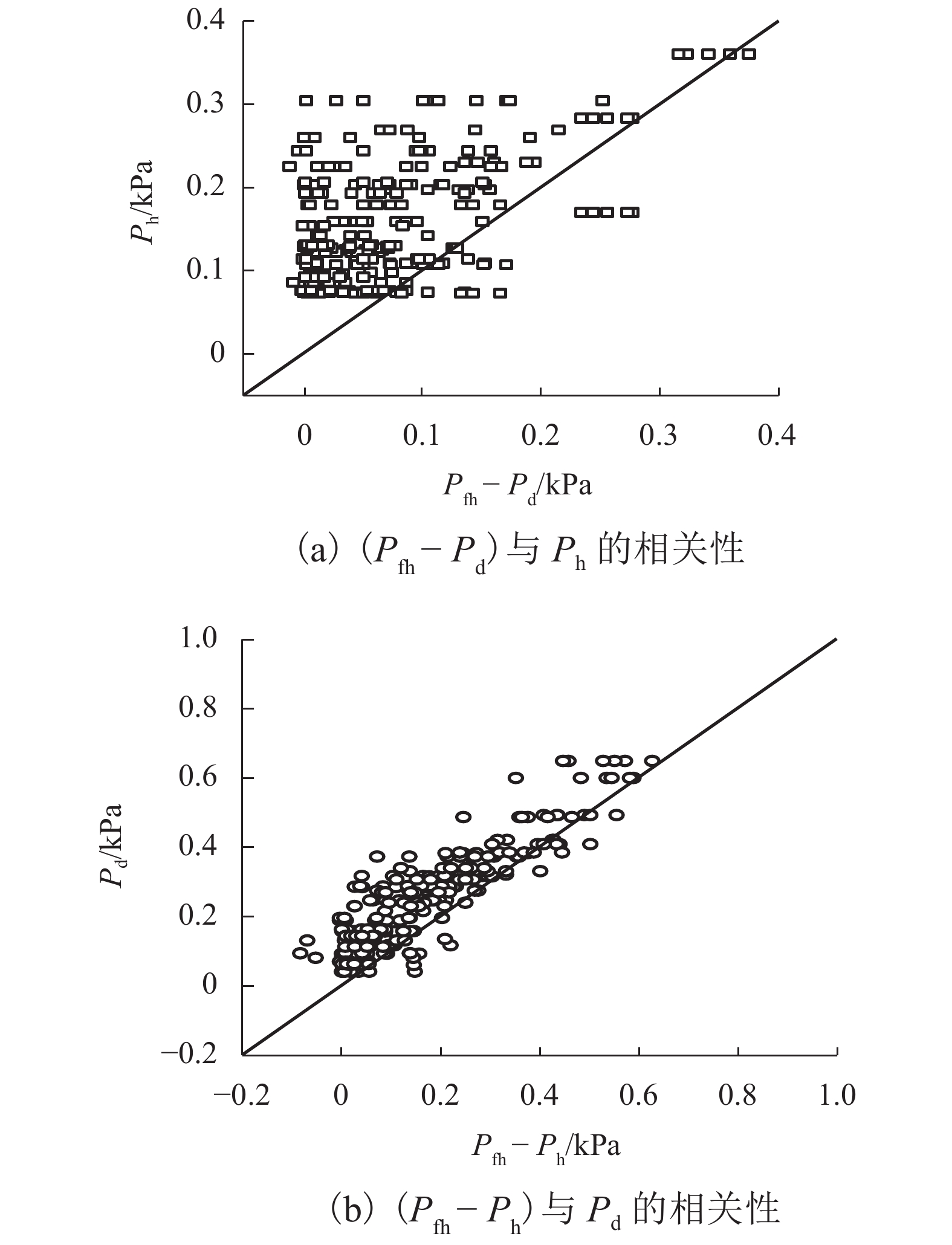
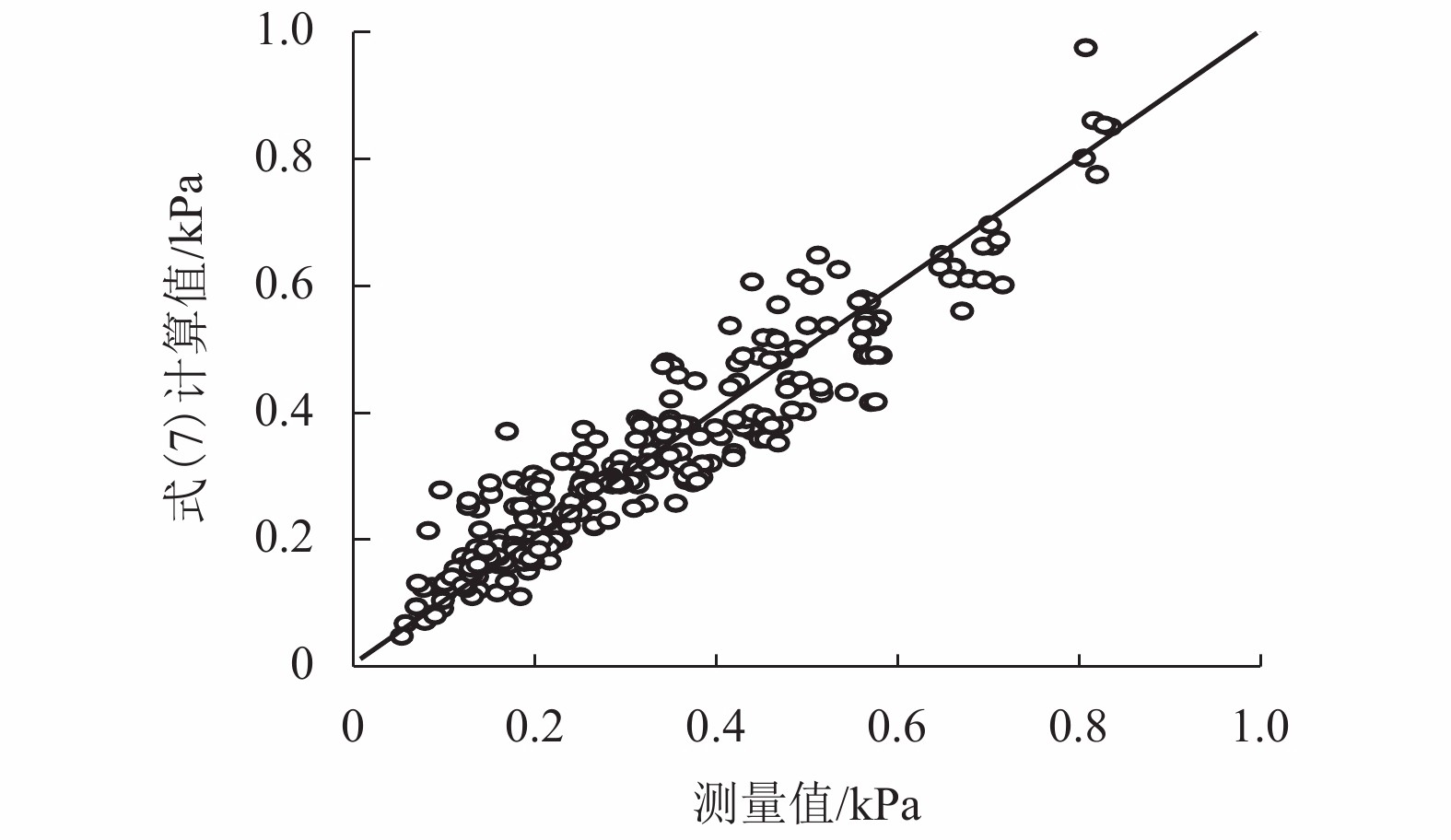
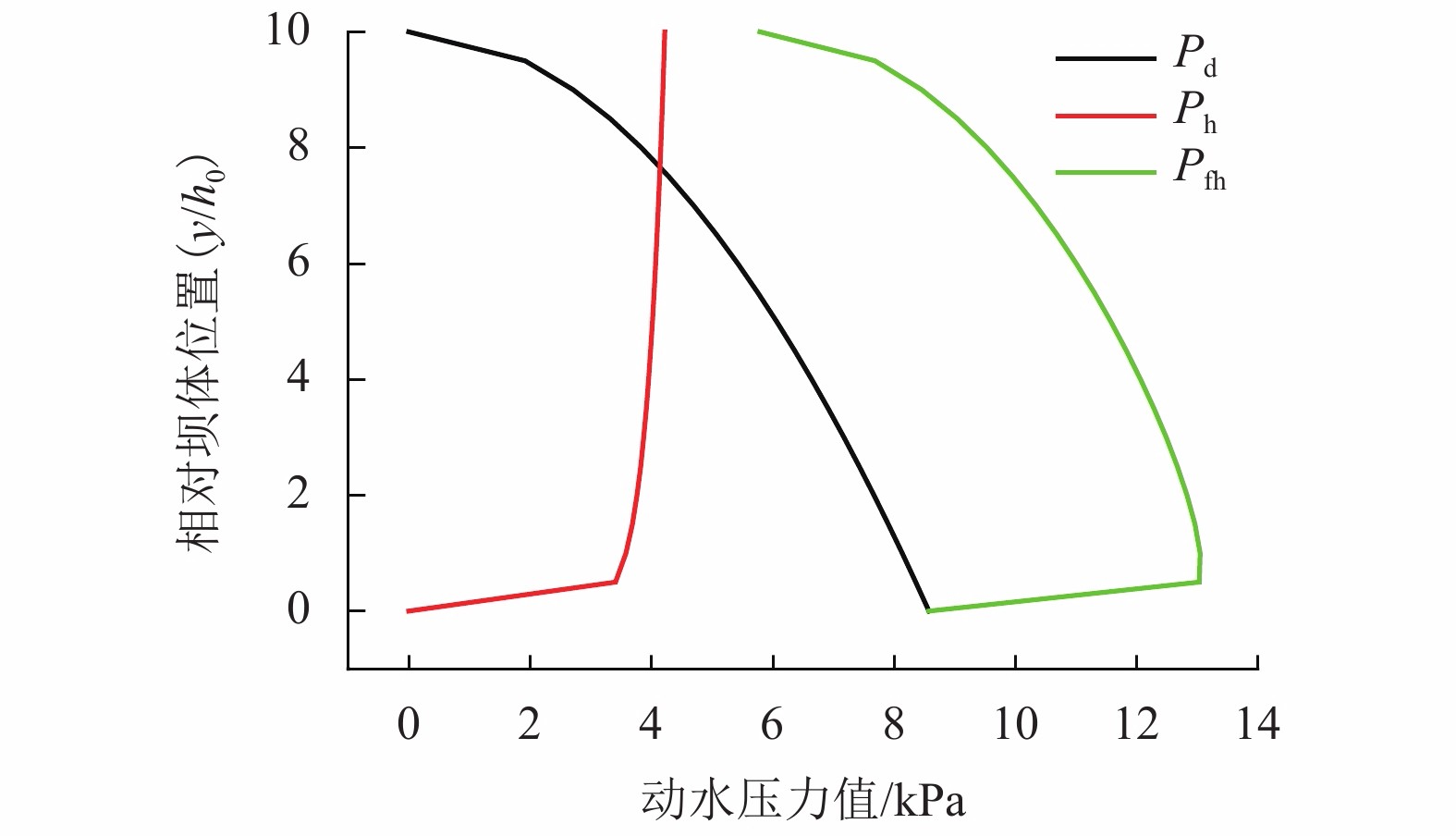
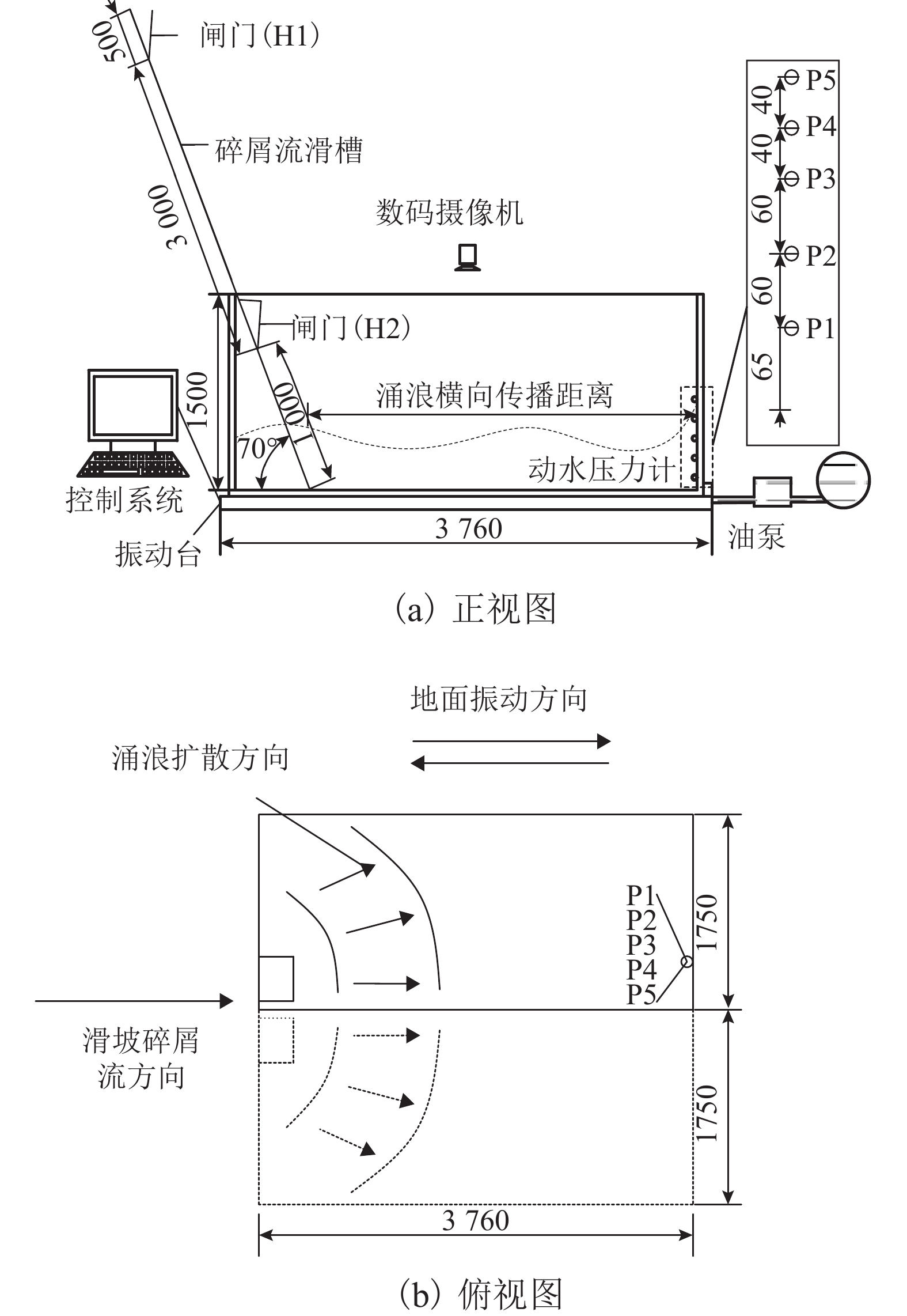
摘要: 为了研究堰塞湖水体在地震以及同震滑坡碎屑流共同作用下产生的涌浪动水压力，设计了振动台造波模型试验，开展了地震作用下堰塞湖涌浪动水压力试验，获取单独地震作用下动水压力数据并同已有地震动水压力计算公式进行比较；开展了滑坡碎屑流作用下的堰塞湖涌浪动水压力试验，获取单独滑坡碎屑流作用下动水压力数据，进而建立了计算滑坡碎屑流作用下的堰塞湖涌浪动水压力的统计公式；开展了地震和滑坡碎屑流综合作用下的堰塞湖涌浪动水压力试验，最终建立了复合动水压力的计算公式. 研究结果表明：地震涌浪动水压力与水深和地震峰值加速度的关系可用Westergaard公式描述；滑坡碎屑流涌浪动水压力与初始水深负相关，与碎屑流入水速度和碎屑流体积正相关；复合动水压力小于单独地震动水压力和单独滑坡碎屑流动水压力二者之和，约为二者和的51%～95%.Abstract: A shaking table model experiment was designed to study the hydrodynamic pressures of the barrier lake under the action of an earthquake and a clastic flow landslide. Firstly, an experiment was carried to study the hydrodynamic pressure of the barrier lake under the action of an earthquake to obtain the hydrodynamic pressure data, which was compared with the existing calculation formula of seismic hydrodynamic pressure. Then, an experiment was carried to study the hydrodynamic pressure caused by the surge of the barrier lake under the action of a clastic flow landslide to obtain the hydrodynamic pressure data and a statistical formula was established. Finally, an experiment was carried to study the combined hydrodynamic pressure under the effect of an earthquake and a co-seismic clastic flow landslide and a formula for calculating the combined hydrodynamic pressure caused by an earthquake and a clastic flow landslide was established. The results show that the relationship between the hydrodynamic pressure caused by an earthquake and water depth and seismic peak acceleration can be described by Westergaard’ formula. The hydrodynamic pressure caused by a clastic flow landslide is negatively related to the initial water depth, positively related to the inflow velocity and volume of landslide. The combined hydrodynamic pressure is less than the sum of the single hydrodynamic pressure under the action of an earthquake and the single hydrodynamic pressure under the action of a clastic flow landslide, which is about 51% − 95% of the sum of two.
-
Key words:
- earthquake /
- clastic flow landslide /
- barrier lake /
- combined hydrodynamic pressures
-
我国目前在青藏地区建成的高原铁路包括青藏、拉日和拉林线等，由于高原铁路面临日温差大、阳光辐射强、阴阳坡间温差大、气压及含氧量低等一般跨区间无缝线路中未遇到的问题，对轨道几何状态稳定性、无缝线路的铺设锁定与稳定运营提出了较高的挑战[1-2]. 而目前国内外尚无海拔4 km以上高原铁路道岔无缝化的工程先例，现有的高原铁路均按照区间无缝、岔区有缝的区间无缝线路设计. 而道岔与钢轨接头两大线路薄弱环节重叠布置，使得岔区轨道病害发展快速，给现场养护维修带来较大压力[3-4].
由于跨区间无缝线路有利于提高乘车舒适性，减少线路养护维修工作量，可延长线路各部的使用寿命，同时某高原铁路提出了运营时速达到200 km的建设要求. 因此，采用跨区间无缝线路的应用是列车在高原铁路高速运营的必要保障条件，也是减缓轨道病害发展的优先选择. 开展铺设锁定轨温差对高原铁路无缝道岔受力特性影响分析，可为高原铁路修建提供理论和工程基础.
为保证无缝线路的安全服役性能，跨区间无缝线路应始终保持高可靠性、稳定性与平顺性，并在列车荷载、温度变化、基础变形及环境影响共同作用下能保证列车安全、平稳和不间断的运行. 针对无缝道岔结构力学特性，国内外众多学者开展了广泛而深入研究[5-9]：刘浩等[10]考虑道床在服役过程中的局部阻力退化现象，探明了无缝线路道床阻力演变对无缝线路力学行为的影响；高亮等[11]构建无缝线路-超大跨径桥梁空间耦合模型，探明了温度作用下桥梁空间变形所致的梁轨相互作用激励，提出了有关“实际锁定轨温”测试与应用的新方法；徐浩等[12]构建了线-桥-墩一体化空间离散有限元模型，揭示了桥梁墩数、简支钢桁梁桥墩纵向水平刚度、线路阻力布置方式和桥梁支座布置方式对无缝线路伸缩力的影响；Ruge等[13]考虑叠加荷载作用下简支梁桥钢轨纵向力分布规律，探明了理想弹塑性卸载条件和荷载线性叠加情况下的钢轨纵向力规律；王平等[14]梳理了不同线下基础道岔无缝化设计方法的研究现状和存在问题；Ren等[15]提出了一种研究钢轨固有频率与无缝线路临界失稳的动态有限元模型，揭示了钢轨临界轮轨力、横向稳定性与无缝线路自振频率的相关性.
从以上研究可知，有关高原铁路无缝化的工程实践近乎空白，无缝线路在恶劣高原气候环境下的受力特性研究机理不清. 另外，在道岔实现无缝化的过程中，由于海拔4 km以上的高原地区日气温变化率极快[16]，道岔升级改造和无缝化的过程中难免存在一定的铺设轨温差，叠加高原地区恶劣的气候环境影响，会对无缝道岔的受力性能和稳定性造成影响，进而威胁行车平稳性和安全性. 因此，揭示铺设轨温差对无缝道岔受力特性和稳定性的影响，探明道岔无缝化后跨区间无缝线路对高原环境的适应性十分必要.
1. 高原地区气候环境监测和调研
1.1 高原地区典型无缝道岔试验段选取
为验证跨区间无缝线路对高原环境的适应性，考虑不同自然环境和线路运营条件的基础上，沿青藏线自北向南分别选择唐古拉北站、望昆站、那曲站和达琼果站作为研究对象，其海拔、纬度和线路条件等如表1中所示.
表 1 典型试验车站Table 1. Typical experiment stations站名 海拔/m 纬度/（°） 线路条件 唐古拉北 4955 34.2 最低温、最高海拔车站 那曲 4500 31.6 西藏段、较高海拔 达琼果 4375 30.5 低纬度、较高海拔，类似
川藏条件望昆 4484 35.7 青海段、高纬度、较高海拔 上述车站分别考虑了不同海拔、不同纬度等因素，可全面验证不同气候环境和线路运营条件下铺设轨温差的影响，论证无缝道岔对高原气候的适应性.
1.2 气温与轨温关系
由于高原铁路海拔较高，其最高气温远低于平原地区，使用最高年轨温约等于年最高气温加20 ℃的预测方法不够精确，因此，揭示高原铁路气温和轨温的数学关系非常重要.
为实时掌握高原铁路无缝道岔的高原气候环境参数，对当地气温和无缝化后道岔的轨温、位移等开展长期监测，通过将各传感器和轨道状态监测系统分别安装于轨道结构和道旁，使用信号线缆将传感器和相关采集仪器设备进行连接，基于无线网络技术进行数据传输，测试钢轨温度和环境温度随时间的变化，掌握道岔所处位置的环境温度与轨温的数学关系，可为后续理论计算提供真实可靠的数据基础. 以纬度最高的望昆站和海拔较高的唐古拉北站为例，其气温、轨温的部分测试结果如图1所示.
从图1可知：钢轨温度和环境温度变化趋势相同；轨温和环境温度的最小值基本一致，但轨温最大值明显高于环境温度. 结合实测气温和轨温数据，基于BP神经网络算法（反向传播神经网络算法）训练各个车站的气温-轨温预测模型，并在该模型的基础上预测实际轨温.
BP 神经网络是基于误差逆向传播算法来进行训练的多层前馈神经网络模型，是最为经典的模型之一[17]. BP神经网络基于最速下降法，利用逆向传播对网络阈值及权值进行调整，进而实现网络误差平方和的最小化. 首先对连接权值进行初始化来计算神经元的输出值$ {{\textit{z}}_{{\mathrm{rs}}}} $：
{fk=f1(n1∑j=1w1kjxj),j=1,2,⋯,n1,k=1,2,⋯,n2,zrs=f2(n2∑k=1w2ikfk),i=1,2,⋯,n3, (1) 式中：$ {f_{{k}}} $为连接权值的初始化函数；$ {f_1} $(·)和$ {f_2} $(·)为sigmoid函数；$ {w_{1kj}} $和$ {w_{2ik}} $为隐含层和输出层的连接权值；$ {x_j} $为输入变量，j、k和i分别为输入神经元、隐含层神经元和输出层神经元个数.
随后基于梯度下降法，结合式（2）对每层连接权值进行修正.
{Δw2ik=−η∂ΔE∂w2ik=η(Zrs−Zs)f2′fk,Δw1kj=−η∂ΔE∂w1kj=η(Zrs−Zs)f2′w2ikf1′xj, (2) ΔE=1n3n3∑i=1(Zrs−Zs)2, (3) 式中：$ \eta $为学习速度，$ {Z_{{\mathrm{rs}}}} $为实际输出变量，$ {Z_{\mathrm{s}}} $为输出变量，$ \Delta E $为拟合误差.
将权值初始值和调整值之和作为新的权值进行反复循环计算，直至误差平方和达到允许范围内即可. 将气温作为输入变量，经过训练生成可考虑高原条件下的BP神经网络预测方法. 为验证BP神经网络预测精度，以望昆站气温和轨温的训练结果为例，结合神经网络中的训练数据、验证数据和测试数据的回归图进行判断，如图2，图中：Y为实际数据值，T为训练模型预测值. 从图2可以发现R值（拟合优度）接近1，说明模型预测结果精度可信.
根据当地车间提供的实测全年气温范围，基于神经算法预测的轨温如表2所示.
表 2 典型车站轨温预测Table 2. Prediction of rail temperature in typical stations站名 年气温/℃ 预测轨温/℃ 验证数据 R 值 唐古拉北 −45.23～24.75 −45.22～35.84 0.9498 那曲 −38.02～27.28 −37.26～42.18 0.9652 达琼果 −10.04～31.06 −6.84～49.68 0.9857 望昆 −26.52～35.58 −24.32～54.63 0.9728 2. 道岔关键传力部件力学特性测试
针对岔区不同结构形式下的关键传力部件力学特性进行了室内参数测试. 测试对象主要包括岔区间隔铁、限位器、岔区扣件以及道床纵向阻力等. 试验仪器包含千斤顶、位移计、拉力传感器、IMC（integrated measurement & control）数据采集仪等. 室内试验在铁科院耐候试验台开展，模拟低温等特殊高原气候环境条件对钢轨及其部件的影响.
2.1 扣件阻力测试
扣件纵向阻力是影响无缝线路及无缝道岔受力与变形的重要因素之一，由于望昆站采用新统型
4249 道岔，其扣件主要包含弹性夹滑床板和预埋铁座Ⅱ型弹条分开式扣件. 唐古拉北站、那曲站和达琼果站采用旧的专线4249 道岔，扣件类型包含岔枕螺栓弹条分开式扣件和弹片式滑床板扣件，如图3所示. 因此，针对岔枕螺栓分开式扣件（轨下胶垫有、无沟槽）、弹片式滑床板扣件（有、无弹片）、弹性夹滑床板扣件（有、无弹性夹）以及预埋铁座Ⅱ型弹条分开式扣件进行了测试，螺栓扭矩分别取60、90、120、150 N·m，如图4.由于高原气候环境温度较低，需同时考虑低温环境对其阻力的影响，其中螺栓扭矩取为150 N•m. 通过测试，道岔扣件低温性能如图5所示.
通过上述4种结构的纵向阻力测试可以发现：随着扣件系统螺栓扭矩的增大，扣件阻力值随之增加；无弹片和弹性夹时纵向阻力极小，且不稳定，易造成结构失稳；轨下垫板沟槽对纵向阻力影响较大；随着温度的降低，扣件阻力减小，−20 ℃比常温扣件阻力降低约4.5%，−40 ℃比常温降低约27%.
2.2 道床阻力测试
道床阻力测试在高原铁路十分必要[18]，本文针对望昆站小曲线段与直线地段的道床阻力进行了测试，如图6所示. 测试地段道床状态良好，无翻浆冒泥现象，道岔采用Ⅲ型混凝土轨枕，轨枕间隔为0.6 m，道床阻力测试时的环境温度为−5 ℃.
从图7可知，道床阻力随轨枕水平位移的变化主要分为2个阶段：第一阶段为道床横向阻力的线性增长阶段，该阶段的特点为道床阻力随位移线性增长；第二阶段为道床阻力的稳定阶段，该阶段的特点为道床横向阻力不随轨枕的位移而增长，即道床此时已发生剪切破坏. 因此，直线地段和曲线地段道床纵向阻力变化趋势基本一致.
图 7 直线和曲线工况下的道床阻力Figure 7. Ballast bed resistance under straight and curve line conditions2.3 道岔其余传力部件阻力测试
间隔铁及限位器是道岔辙跟及辙叉的重要传力机构，其阻力特性直接影响着无缝道岔的受力与变形. 螺母扭矩为800、
1000 N·m时，间隔铁、限位器和接头等道岔传力部件纵向阻力测试结果如表3和表4所示.表 3 限位器和间隔铁阻力测试Table 3. Resistance test of limiting stopper and filler对象 螺母扭矩/（N·m） 最大滑移荷载/kN 限位器 800 345 1000 462 间隔铁 800 364 1000 486 表 4 接头阻力测试Table 4. Resistance test of joints接头 夹板扭矩/（N·m） 最大荷载/kN 胶接冻结接头 800 799 1100 1110 普通接头 800 307 1100 442 由表3、4可知：接头、间隔铁和限位器最大滑移位移对应的最大荷载随扭矩的增加而增加；胶接冻结夹板的最大荷载显著大于普通接头夹板，间隔铁所对应最大滑移荷载大于限位器结构. 一般而言，传力部件阻力越大，伸缩位移越小，温度力自尖轨传递至导轨和基本轨的温度力更大，能更好适应高原复杂气候环境条件.
3. 铺设锁定轨温差影响因素分析
以青藏线路升级改造铺设的12号道岔（图号4249）为例进行计算分析，铺设时道岔与区间线路存在一定的锁定轨温差，道岔前后线路无纵向爬行. 道岔扣件与道床阻力根据2.1和2.2中试验实测值，其余诸如限位器和间隔铁等传力部件采用2.3中试验实测值，并将该阻力视为作用于钢轨中部的集中力.
基于ANSYS软件的无缝道岔有限单元计算方法求解温度荷载下的道岔受力特性. 如图8所示，道岔计算模型全长
37800 mm，前长16592 mm，后长21208 mm[19-20]，模型中的钢轨截面积为77.45 cm2 ；弹性模量为2.1 × 1011 N/m2；线膨胀系数为 11.8 × 10−6/℃；岔枕间距为0.6 m；岔枕截面顶宽、底宽和高度分别为260、300、220 mm；混凝土的弹性模量为34.5 × 109 N/m2，混凝土Ⅲ型枕每公里铺设1667 根. 根据TB2034-88《铁路轨道强度检算法》选取区间线路纵向阻力.采用铝热焊焊接道岔直侧股，当地车间提供的唐古拉北站、望昆站、达琼果站和那曲站设计锁定轨温分别为（10±3）℃、（12±3）℃、（15±3）℃和（11±3）℃ [20]，结合设计锁定轨温和表2中轨温数据获得设计锁定轨温上限Tu和下限Td，通过式（4）获得升温和降温最大幅度.
{ΔTumax=Tmax−Td,ΔTdmax=Tu−Tmin, (4) 式中：$ \Delta {T_{{\mathrm{u}}\max }} $为最大升温幅度，$ \Delta {T_{{\mathrm{d}}\max }} $为最大降温幅度.
根据TB 10015—2012《铁路无缝线路设计规范》第7.26条中规定，无缝道岔应在设计锁定轨温 ±3 ℃范围内锁定，且相邻单元轨节间的锁定轨温差应不大5 ℃. 无缝道岔直侧股、左右股和线路及道岔单元轨节存在铺设轨温差分别为3、5、10 ℃和20 ℃时，铺设轨温差对无缝道岔受力特性和稳定性的影响如图9、10所示.
图 9 铺设锁定轨温差对无缝道岔受力与变形的影响Figure 9. Influence of stress-free temperature difference on force formation of seamless turnout由图9可知：无缝道岔与相邻线路锁定轨温差越大，传递至无缝道岔的温度力也越大，因此，基本轨和曲基本轨附加温度力、基本轨伸缩位移均随锁定轨温差的增大而增大，尖轨跟端位移也略有增大；若无缝道岔锁定轨温低于相邻区间线路的锁定轨温，基本轨附加温度拉力及各钢轨的伸缩位移将会增大；以唐古拉北车站为例，对于直基本轨和曲基本轨附加温度力，铺设锁定轨温差每增长1 ℃，其附加温度力增长约6 kN，而直基本轨和尖轨跟端位移增加不明显.
图 10 铺设锁定轨温差对无缝道岔稳定性的影响Figure 10. Influence of stress-free temperature difference on stability of seamless turnout由图10可知：以温差更为显著的唐古拉北站为例，道岔左右股、直侧股及线路单元轨节存在铺设轨温差时对钢轨横向位移影响较小. 左右股铺设轨温差每存在1 ℃差值，其横向位移最大值增加约0.002 mm；当直侧股铺设轨温差每存在1 ℃差值，其横向位移最大值增加约
0.0041 mm；当线路单元轨节与道岔单元轨节铺设轨温差每存在1 ℃差值时，其横向位移最大值增加0.011 mm. 直侧股和左右股存在铺设轨温差时对道岔稳定性影响较小，而线路单元轨节与道岔单元轨件存在铺设轨温差对道岔稳定性性影响较大. 铺设锁定轨温差达到3～20 ℃时，经过稳定性、位移等研究，其值均满足要求，随着铺设轨温差的增加，道岔最大横向位移的增加速率显著提升. 另外，考虑到道岔涉及多股钢轨锁定，易造成锁定轨温差相差较大，为提高安全冗余，建议高原地区铺设无道岔时的锁定轨温差仍控制在±3 ℃，相邻轨节锁定轨温差不超过5 ℃，高原条件应和现有规范保持一致.4. 结 论
本文对无缝道岔区扣件阻力、道床阻力、间隔铁及限位器阻力等力学特性进行了测试，结合神经网络揭示了高原地区气温和轨温的映射关系，并分析了铺设锁定轨温差对高原铁路无缝道岔受力和变形影响，得到以下结论：
1） 结合高原地区轨温和气温监测数据，基于BP神经网络算法提出了可适应高原气候的轨温预测方法.
2） 首次针对道岔不同类型的传力部件纵向阻力进行了测试，随着传力系统螺栓扭矩的增大，道岔传力部件阻力值逐渐增加，且扣件和道床的阻力随温度的降低而降低.
3） 若无缝道岔与相邻线路或相邻道岔间存在铺设锁定轨温差，在升温或降温的情况下，由相邻线路传递至无缝道岔上的纵向力将增大，导致基本轨附加温度力、限位器和间隔铁受力增大，对尖轨和基本轨伸缩位移影响不大.
4） 当线路所处温差越大，铺设锁定轨温差引起的温度附加力增加速度越快，铺设锁定轨温差对无缝道岔受力与变形影响较大，当铺设锁定轨温差越大时，其附加温度力增加明显. 而左右轨、直侧轨温差和线路轨节和道岔轨节的铺设锁定轨温差对道岔失稳影响较小.
致谢：感谢中国铁道科学研究院集团有限公司科研项目（2020YJ208）对本文试验的资助.
-
图 2 不同初始水深下复合涌浪动水压力的比较
Figure 2. Comparison of composite hydrodynamic pressures at different initial water depths
图 4 使用式（7）计算值和测量值之间的比较
Figure 4. Comparison between measured value and calculated value used by eq. (7)
表 1 123组试验组合
Table 1. Experimental conditions for 123 laboratory tests
组号 编号 地震波地震动加速度峰值（PGA）/（×g） 碎屑质量 s/kg 初始水深/m 入水速度/（m•s−1） A 1～15 0.1，0.2，0.3，0.4，0.5 0.1，0.2，0.3 B 16～33 10，20，30 0.1，0.2，0.3 1.64，3.28 C 34～123 0.1，0.2，0.3，0.4，0.5 10，20，30 0.1，0.2，0.3 1.64，3.28 
下载: 导出CSV
-
殷跃平. 汶川八级地震滑坡高速远程特征分析[J]. 工程地质学报,2009,17(2): 153-166. doi: 10.3969/j.issn.1004-9665.2009.02.002YIN Yueping. Rapid and long run-out features of landslides triggered by the Wenchuan earthquake[J]. Journal of Engineering Geology, 2009, 17(2): 153-166. doi: 10.3969/j.issn.1004-9665.2009.02.002 CUI P, ZHU X. Surge generation in reservoirs by landslides triggered by the wenchuan earthquake[J]. Journal of Earthquake & Tsunami, 2011, 5(5): 461-474. FRITZ H M. Lituya bay case rockslide impact and wave run-up[J]. Science of Tsunami Hazards, 2001, 19(1): 3-19. HOLMEN J O. Fatigue of concrete by constant and variable amplitude loading[J]. Fatigue Concrete Structure, 1982, 75: 71-110. CORNELISSEN H, REINHARDT H. Uniaxial tensile fatigue failure of concrete underconstant-amplitude and programme loading[J]. Magazine Concrete Research, 1984, 36(129): 216-226. SALEH S, MADABHUSHI S P G. Response of concrete dams on rigid and soil foundations under earthquake loading[J]. Journal of Earthquake and Tsunami, 2011, 4(3): 251-268. 刘宁, 程尊兰, 崔鹏, 等. 堰塞湖及其风险控制[M]. 北京: 科学出版社, 2013: 16-21. KONG P, NA C, FINK D, et al. Moraine dam related to late quaternary glaciation in the Yulong mountains,southwest China,and impacts on the Jinsha river[J]. Quaternary Science Reviews, 2009, 28(27): 3224-3235. WESTERGAARD H M. Water pressures on dams during earthquakes[J]. Transactions of the American Society of Civil Engineers, 1933, 98(3): 418-433. CHWANG A T, HOUSNER G W. Hydrodynamic pressures on sloping dams during earthquakes, part 1:momentum method[J]. Journal of Fluid Mechanics, 1978, 87(2): 335-341. CHWANG A T. Hydrodynamic pressures on sloping dams during earthquakes, part 2:exact theory[J]. Journal of Fluid Mechanics, 1978, 87(2): 343-348. PELECANOS L, KONTOE S, ZDRAVKOVIC L. Numerical modelling of hydrodynamic pressures on dams[J]. Computers and Geotechnics, 2013, 53: 68-82. 黄锦林. 库岸滑坡涌浪对坝体影响研究[D]. 天津: 天津大学, 2012. 杨艳. 山区河道型水库滑坡涌浪对架空直立式码头结构作用影响研究[D]. 重庆: 重庆交通大学, 2014. CHEN H Y, CUI P, CHEN X Q, et al. Laboratory experiments of water pressure loads acting on a downstream dam caused by ice avalanches[J]. Landslides, 2015, 12(6): 1131-1138. 游勇,程尊兰. 西藏波密米堆沟泥石流堵河模型试验[J]. 山地学报,2005,23(3): 288-293. doi: 10.3969/j.issn.1008-2786.2005.03.006YOU Yong, CHENG Zunlan. Modeling experiment of debris flow in Midui gully,Tibet[J]. Journal of Mountain Research, 2005, 23(3): 288-293. doi: 10.3969/j.issn.1008-2786.2005.03.006 李德基, 游勇. 西藏波密米堆冰湖溃决浅议[J]. 山地学报, 1992, 10(4): 219-224.LI Deji, YOU Yong. Bursting of the Midui moraine lake in Bomi, Xizang.[J]. Mountain Research, 1992, 10(4): 219-224. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 577
- HTML全文浏览量: 300
- PDF下载量: 14
- 被引次数: 0