Hilbert-Huang Transfer Analysis on Vehicle-Induced Vibration Signal of Continuous Bridges Based on ICEEMDAN
-
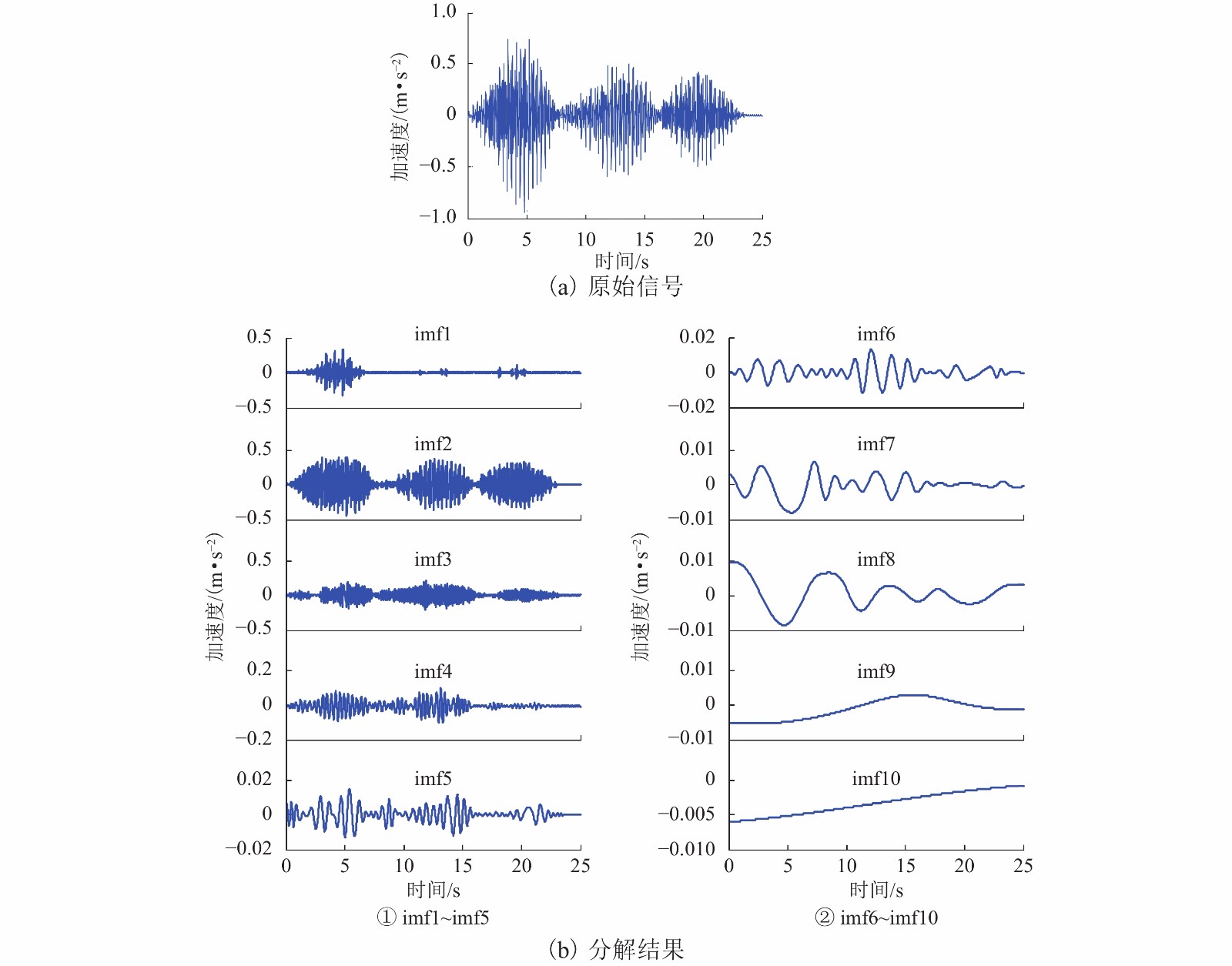
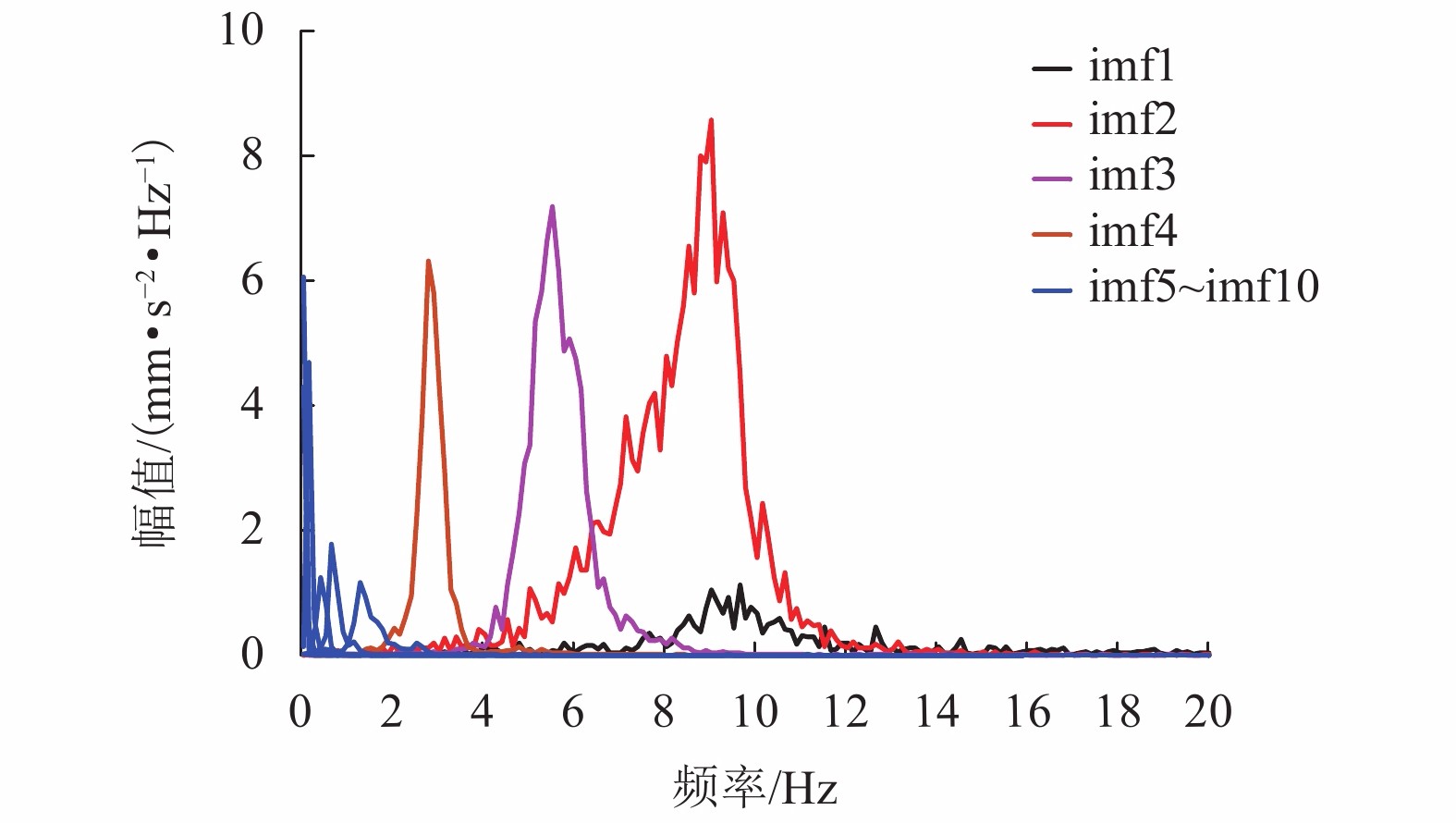
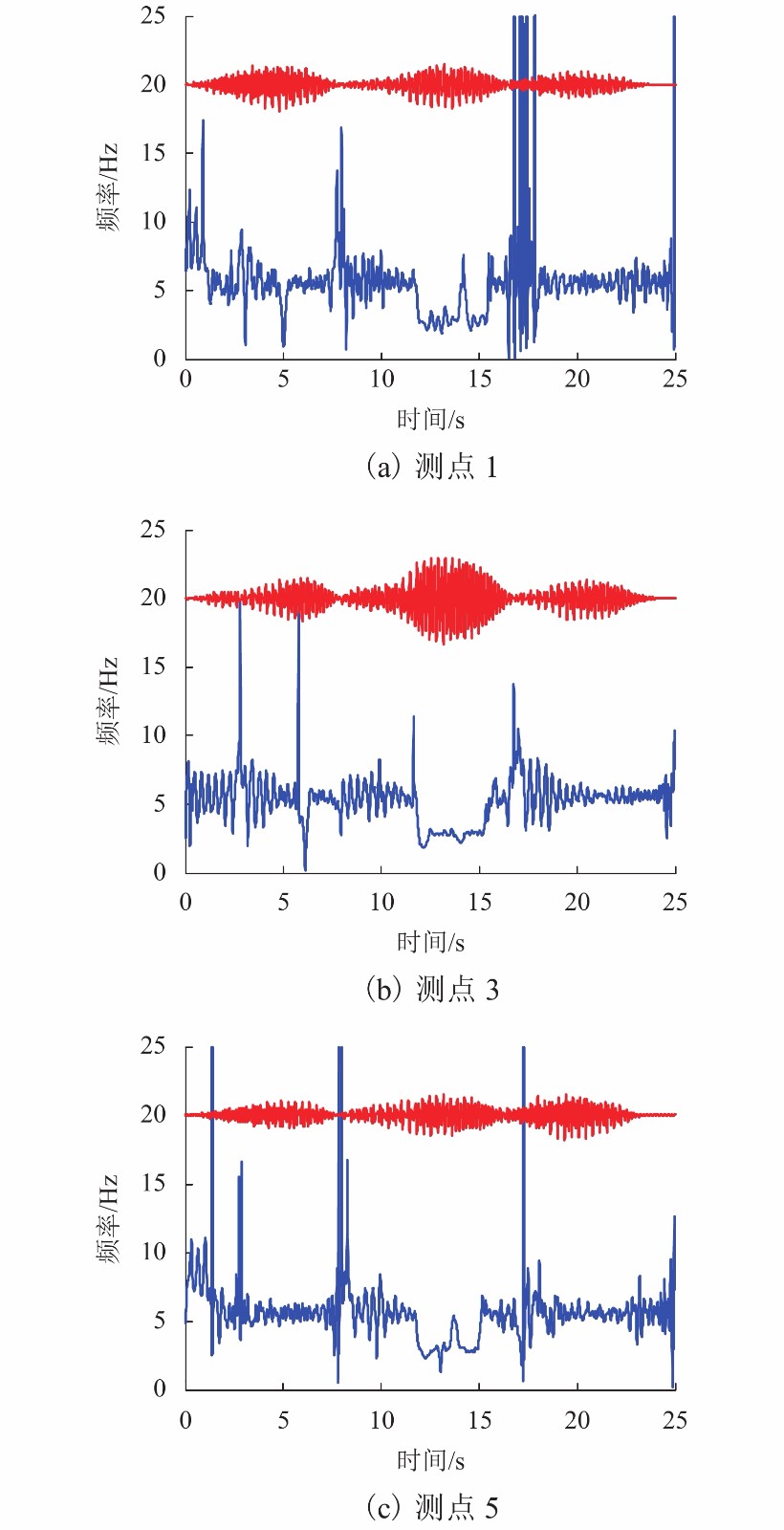
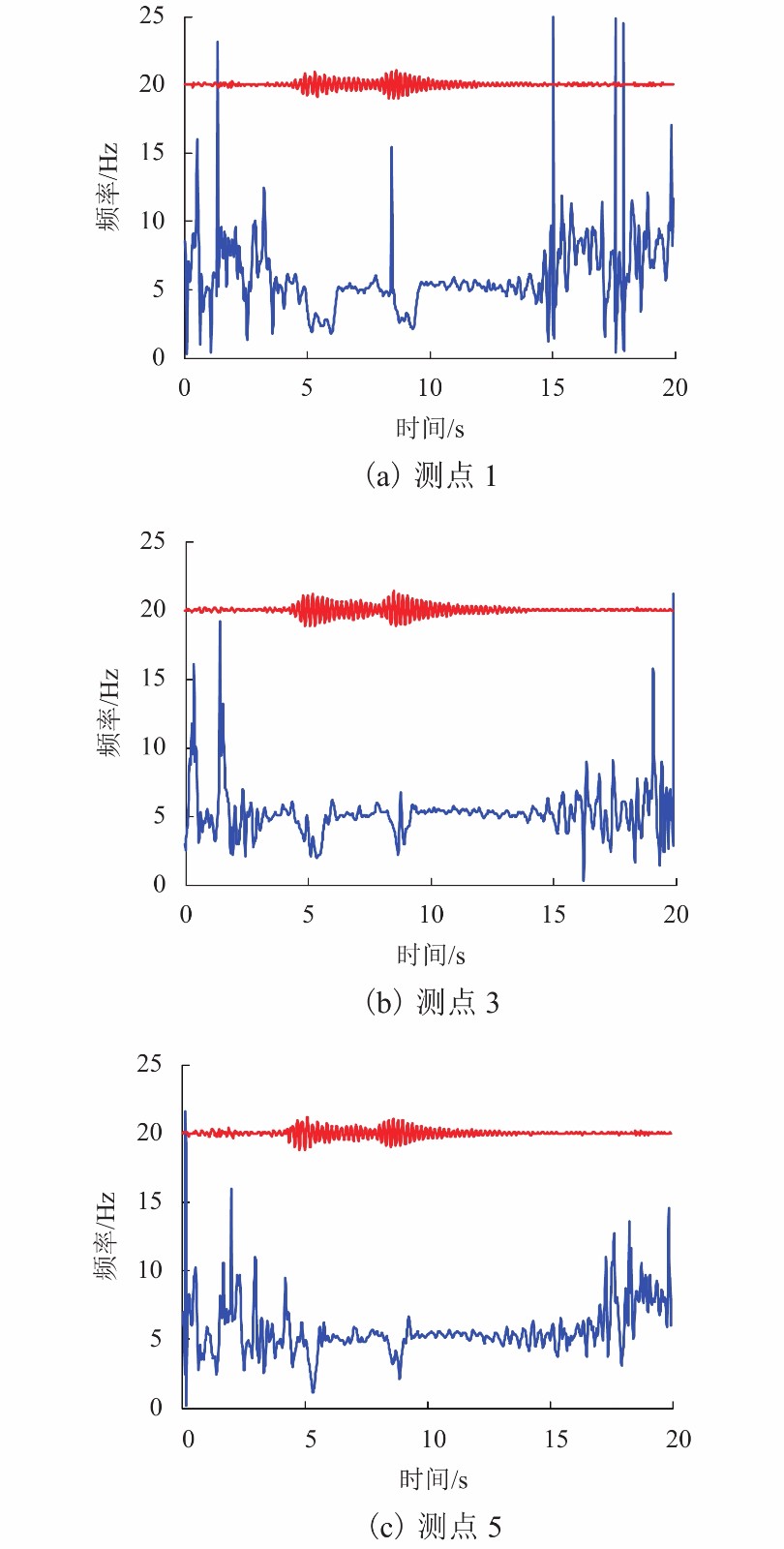
摘要: 改进的带有自适应噪声的完备集合经验模式分解（improved complete ensemble empirical mode decomposition with adaptive noise，ICEEMDAN）是传统经验模式分解（empirical mode decomposition，EMD）方法的发展，在桥梁结构损伤识别领域具有较好的应用前景. 首先，以数值模拟信号为对象，采用ICEEMDAN方法进行桥梁车致动信号的数据分解和Hilbert谱分析，提取损伤引起的频谱特征变化和建立损伤识别方法；然后，利用该方法对实测振动信号的振型分量进行识别；最后，以实测信号的一阶振型分量为对象，对其Hilbert瞬时频率谱的特征进行了分析和讨论. 研究结果表明：模拟信号中的振型振动分量数比实测信号中多，其中模拟信号中不显著的高阶竖弯振动分量在实测信号中没有发现； 一阶振型振动分量的瞬时频率可作为桥梁损伤识别的特征参数，用于进行损伤有无、损伤定位甚至损伤定量的判断； 损伤识别效果受测点位置影响很小； 该方法不依赖有限元模型即可完成桥梁损伤有无的识别和损伤定位，且数据采集简单，具有实际工程中应用可行性.
-
关键词:
- 连续梁桥 /
- 改进的带有自适应噪声的完备集合经验模式分解 /
- 车致振动 /
- Hilbert-Hang变换（HHT） /
- 损伤识别
Abstract: As an improvement of the empirical mode decomposition (EMD), the improved complete ensemble empirical mode decomposition with adaptive noise (ICEEMDAN) has a good application potential in the field of structure damage identification of bridges. In this study, ICEEMDAN and Hilbert transforms were firstly performed on the simulated vehicle-induced vibrations of bridge, and the spectral feature changes caused by the damage were extracted with the established damage identification method. The established method was then applied on the measured vibration data of a real bridge, and the mode components of the vibration signals were identified. The characteristics of Hilbert instantaneous frequency spectrum were finally analyzed and discussed based on the first-order mode components of the measured signal. The results are shown as follows: There are more vibration components in the simulated signal than in the measured signal, and the insignificant mode components in the simulated signal do not appear in the measured signal; The instantaneous frequency of the first-order mode vibration component can be used as the characteristic parameter of bridge damage identification for the determination of the occurrence of damage, the damage location or even the quantification of the damage; The damage recognition capability of the established method is insensitive to the position of the measurement point; The proposed method has a feasibility in engineering practice, which completes the identification of bridge damage and damage location with a simple data acquisition procedure, and without relying on finite element model calculations. -
图 4 跑车试验测点布置及编号（单位：cm）
Figure 4. Measuring points layout and number in running tests (unit：cm)
图 8 无损伤状态各IMF分量的Hilbert边际谱
Figure 8. Hilbert marginal spectrum of IMF components in undamaged state
图 9 有损伤状态各IMF分量的Hilbert边际谱
Figure 9. Hilbert marginal spectrum of IMF components with damage
图 11 模拟信号及其一阶振型振动分量的Hilbert瞬时频率谱
Figure 11. Simulated acceleration signal and Hilbert instantaneous frequency spectrum of first-order mode vibration components
图 12 实测信号及其一阶振型振动分量的Hilbert瞬时频率谱
Figure 12. Measured acceleration signal and Hilbert instantaneous frequency spectrum of first-order mode vibration components
图 13 环境激励下一阶振型分量的Hilbert瞬时频率谱
Figure 13. Hilbert instantaneous frequency spectrum of first-order mode component under environmental excitation
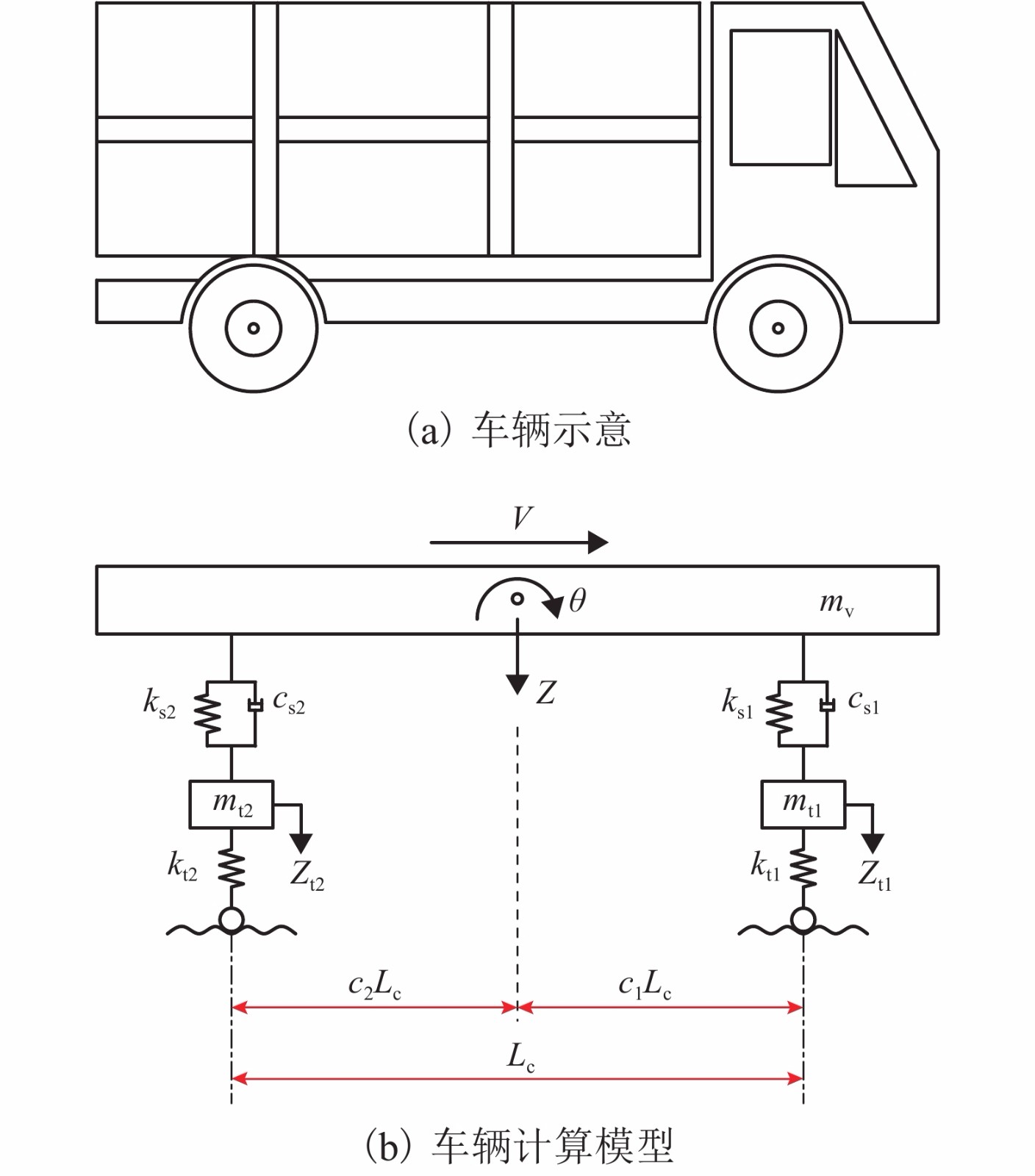
表 1 车辆模型的计算参数
Table 1. Calculation parameters of vehicle model
参数 值 参数 值 mv/kg 17000 Jθ/（kg•m2） 2.4 × 104 mt1/kg 500 mt2/kg 2000 ks1/（N•m−1） 8 × 106 ks2/（N•m−1） 16 × 106 cs1, cs2/（N•s•m−1） 4 × 104 kt2/（N•m−1） 16.0 × 106 kt1/（N•m−1） 4.5 × 106 c1 0.65 Lc/m 4.27 c2 0.35 
下载: 导出CSV
表 2 移动车辆前、后轮到达特征截面时间
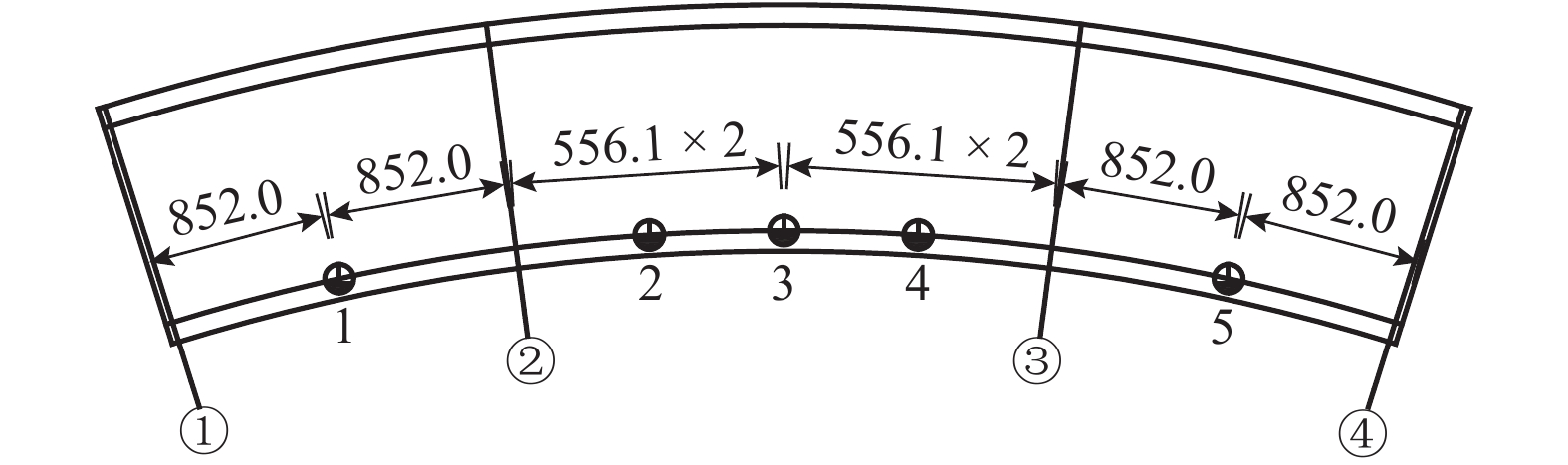
Table 2. Time when front and rear wheels of moving vehicle reach the characteristic sections
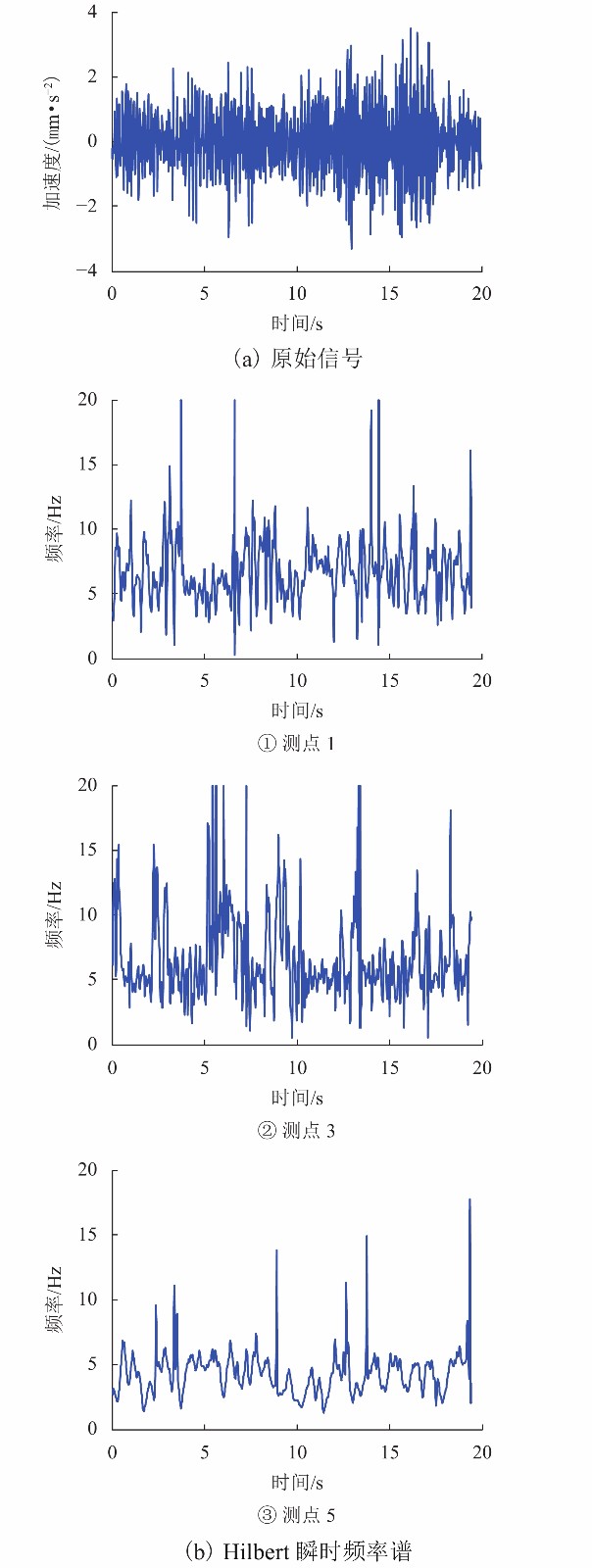
s 截面位置 行车速度/（km•h−1） 10 20 30 测点 1 前轮 3.24 1.62 1.08 后轮 4.78 2.39 1.59 中墩 ② 前轮 6.48 3.24 2.16 后轮 8.02 4.01 2.67 测点 3 前轮 10.71 5.36 3.57 后轮 12.25 6.12 4.08 中墩 ③ 前轮 14.94 7.47 4.98 后轮 16.48 8.24 5.49 测点 5 前轮 18.18 9.09 6.06 后轮 19.72 9.86 6.57
下载: 导出CSV
-
闫宇智,战家旺,张楠,等. 基于小波相关性的简支梁桥损伤评估方法[J]. 振动与冲击,2018,37(12): 67-74.YAN Yuzhi, ZHAN Jiawang, ZHANG Nan, et al. A damage evaluation method for simply-supported bridges based on wavelet transform correlation[J]. Journal of Vibration and Shock, 2018, 37(12): 67-74. 孙增寿,李晓鹏,韩培琰,等. 基于小波包样本熵的连续梁桥损伤识别[J]. 振动、测试与诊断,2018,38(5): 916-1078.SUN Zenshou, LI Xiaopeng, HAN Peiyan, et al. Damage identification for continuous girder bridge based on wavelet packet sample entropy[J]. Journal of Vibration,Measurement & Diagnosis, 2018, 38(5): 916-1078. 余竹,夏禾. 基于移动荷载作用下的结构响应及小波分析的桥梁损伤诊断[J]. 北京交通大学学报,2014,38(3): 55-61. doi: 10.11860/j.issn.1673-0291.2014.03.010YU Zhu, XIA He. Bride damage detection based on moving load induced structural response and wavelet analysis[J]. Journal of Beijing Jiaotong University, 2014, 38(3): 55-61. doi: 10.11860/j.issn.1673-0291.2014.03.010 KHORRAM A, BAKHTIARI-NEJAD F, REZAEIAN M. Comparison studies between two wavelet based crack detection methods of a beam subjected to a moving load[J]. International Journal of Engineering Science, 2012, 51: 204-215. doi: 10.1016/j.ijengsci.2011.10.001 ROVERI N, CARCATERRA A. Damage detection in structures under traveling loads by Hilbert-Huang transform[J]. Mechanical Systems and Signal Processing, 2012, 28: 128-144. doi: 10.1016/j.ymssp.2011.06.018 LIU H B, NGUYEN H H. Damage detection of simply supported beam under effect of moving load by Hilbert-Huang transform[J]. Applied Mechanics and Materials, 2012, 166/167/168/169: 984-993. doi: 10.4028/www.scientific.net/AMM.166-169.984 AIED H, GONZÁLEZ A, CANTERO D. Identification of sudden stiffness changes in the acceleration response of a bridge to moving loads using ensemble empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2016, 66: 314-338. ZHANG W, LI J, HAO H, et al. Damage detection in bridge structures under moving loads with phase trajectory change of multi-type vibration measurements[J]. Mechanical Systems and Signal Processing, 2017, 87: 410-425. doi: 10.1016/j.ymssp.2016.10.035 HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London,Series A:Mathematical,Physical and Engineering Sciences, 1998, 454: 903-995. doi: 10.1098/rspa.1998.0193 WU Z H, HUANG N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2005, 1(1): 1-41. YEH J R, SHIEN J S, HUANG N E. Complementary ensemble empirical mode decomposition:a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156. doi: 10.1142/S1793536910000422 TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Prague: IEEE, 2011: 4144-4147. COLOMINAS M A, SCHLOTTHAUER G, TORRES M E. Improved complete ensemble EMD:a suitable tool for biomedical signal processing[J]. Biomedical Signal Processing and Control, 2014, 14: 19-29. doi: 10.1016/j.bspc.2014.06.009 邢世玲. 公路混凝土曲线连续梁桥在移动车辆荷载作用下的动反应研究[D]. 南京: 东南大学, 2014. 张佳. 移动车辆荷载作用下连续梁桥振动信号的HHT分析与应用[D]. 南京: 南京工业大学, 2018. -
下载:
点击查看大图
计量
- 文章访问数: 699
- HTML全文浏览量: 334
- PDF下载量: 19
- 被引次数: 0