大跨度斜拉桥地震易损性及可恢复性分析

武芳文; 孟园英; 陈月; 纪全有; 杨源源; 吴志达

doi:10.3969/j.issn.0258-2724.20180449

大跨度斜拉桥地震易损性及可恢复性分析

doi: 10.3969/j.issn.0258-2724.20180449

基金项目: 国家自然科学基金（51408040）；陕西省交通厅科技计划项目（17-15K）；安徽高校自然科学研究项目计划（KJ2019A1134）

详细信息

作者简介:
武芳文（1980—），男，副教授，研究方向为桥梁抗震及振动控制，E-mail：wufangwen2004@163.com

中图分类号: V221.3
计量
- 文章访问数: 685
- HTML全文浏览量: 298
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2018-05-31
- 修回日期: 2018-09-25
- 网络出版日期: 2018-10-08
- 刊出日期: 2020-02-01

Analysis of Seismic Fragility and Recoverability of Long-Span Cable-Stayed Bridge

摘要

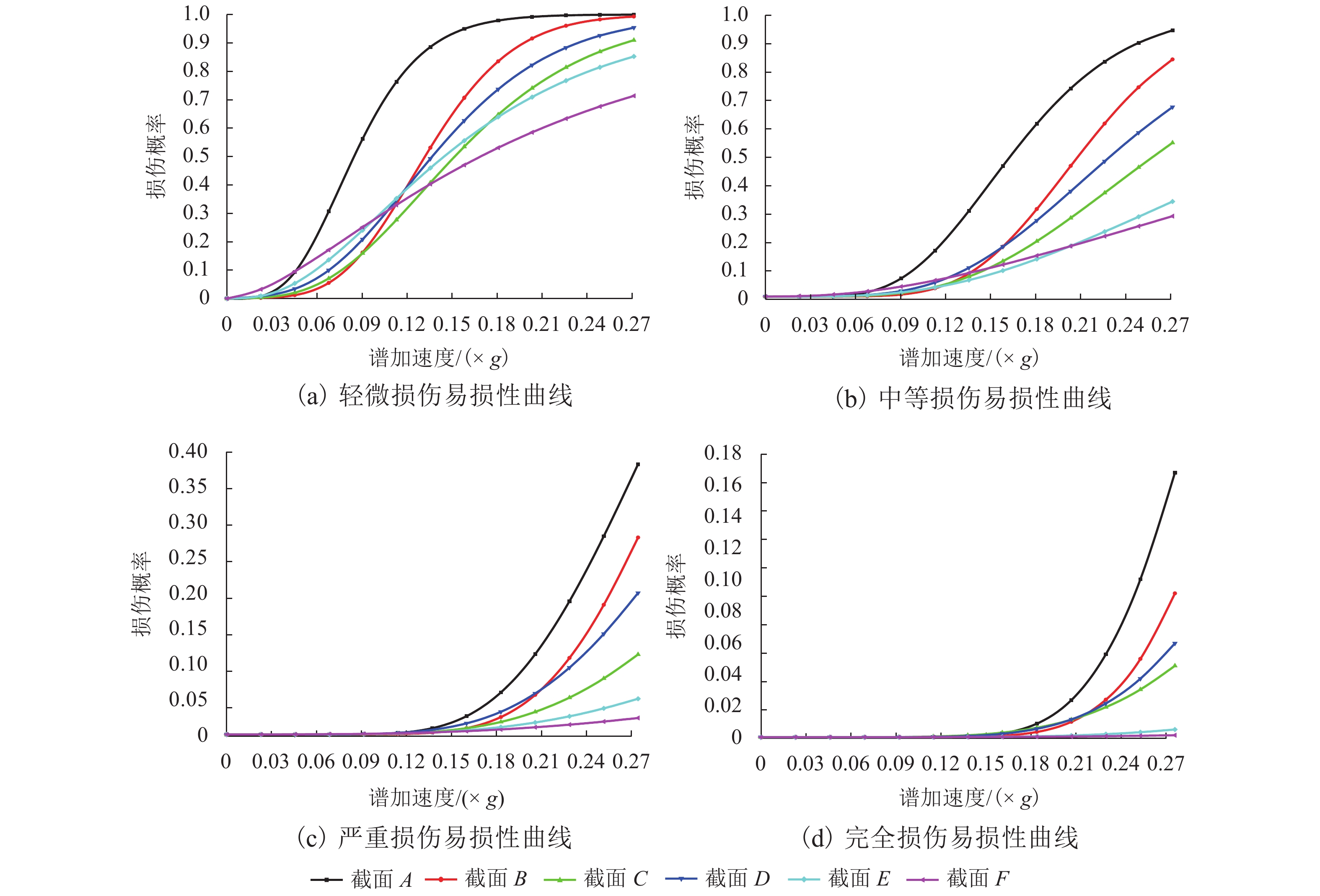
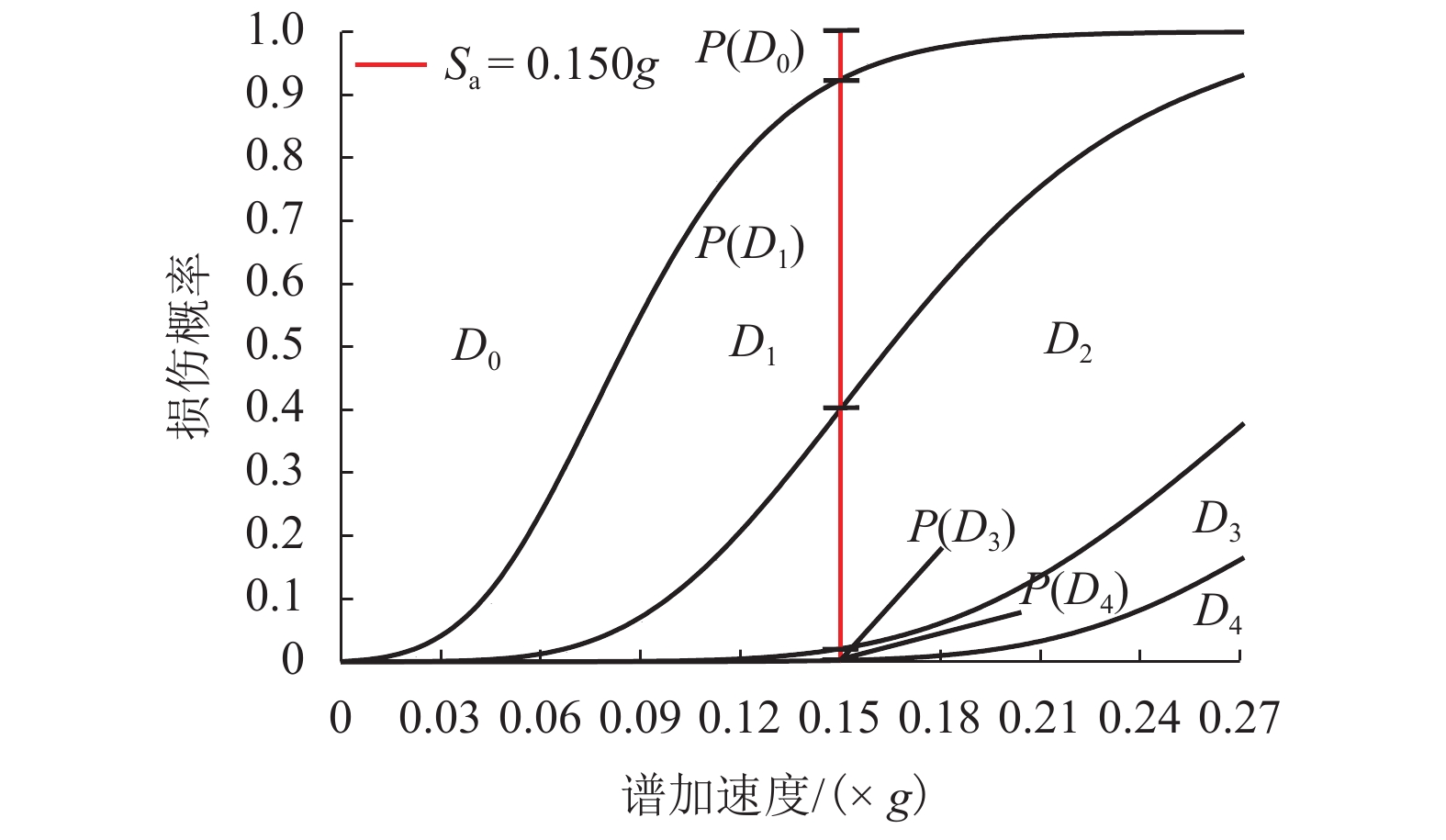
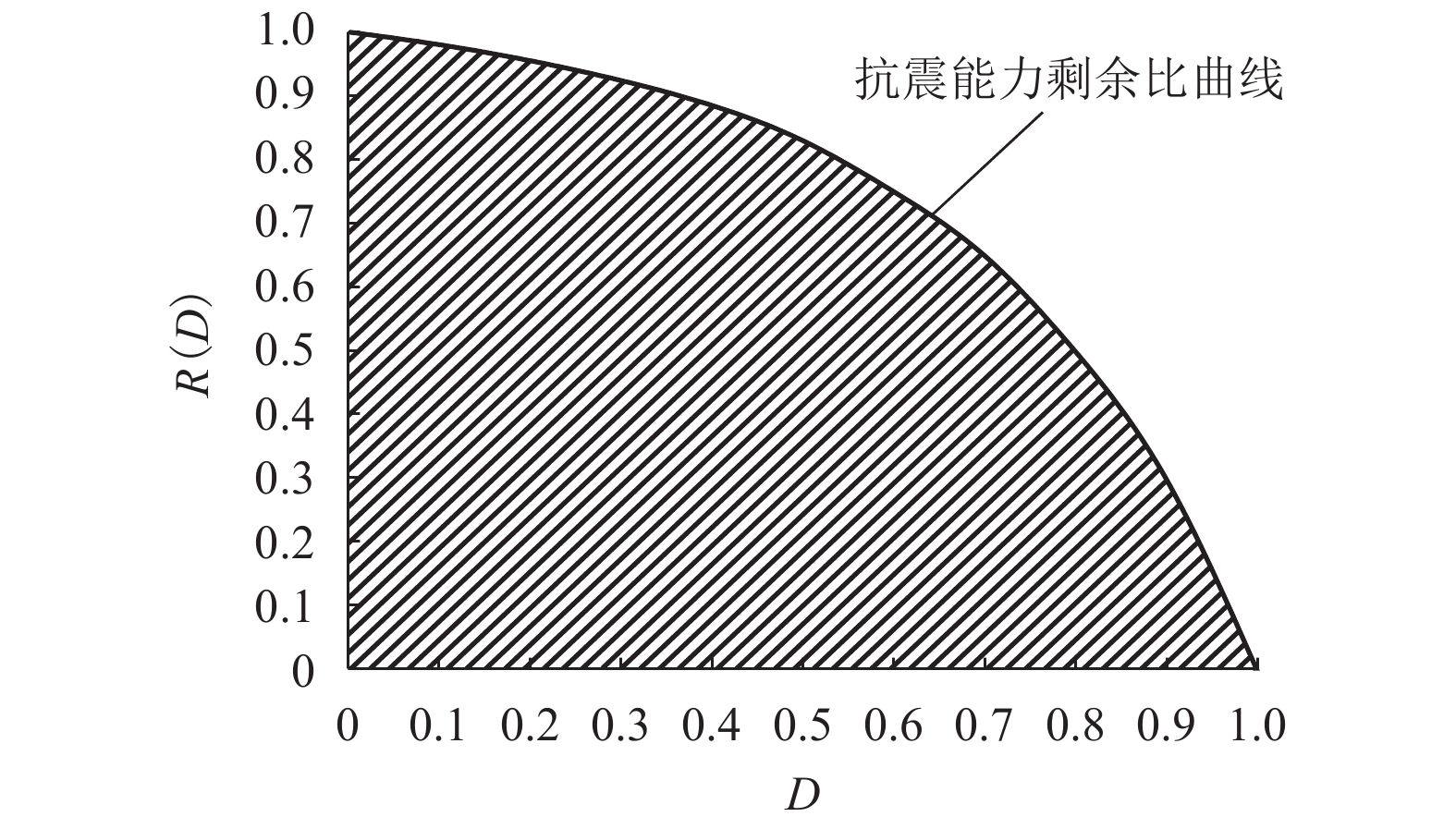
摘要: 为了研究地震作用下斜拉桥主塔的抗震能力，评估其抗震可恢复性，以一座独柱式大跨径混凝土斜拉桥为例，采用SAP2000有限元分析程序建立结构动力计算模型，通过增量动力分析法（IDA）分析结构的横向地震响应；选用X-TRACT软件对主塔划分的各关键截面进行了弯矩-曲率分析和损伤标定，对IDA分析的数据进行处理，拟合得到了主塔各关键截面的地震易损性曲线，确定主塔容易损伤部位及演变规律；基于可恢复性的理念开展结构的抗震可恢复性分析. 研究结果表明：在横向地震作用下，主塔底部截面是所选截面中最容易损坏的部位；在地震动强度0.150g和0.271g作用后，自身的抗震能力由80.6%降到46.7%，随着地震动强度的增大，抗震储备能力不断降低.
- 斜拉桥 /
- 动力分析 /
- 地震响应 /
- 地震易损性分析 /
- 抗震可恢复性
Abstract: To study the seismic capacity of the main tower of cable-stayed bridge under earthquake and evaluate its seismic recoverability, the structural dynamic calculation model was established by the finite element analysis program SPA2000 based on a single-column long-span concrete cable-stayed bridge, the seismic response of the transverse cable-stayed bridge was analyzed by incremental dynamic analysis (IDA). The moment-curvature curves of the tower key sections were studied and the curvature damages were calibrated by analysis software X-TRACT, then the data from IDA analysis were processed, and the seismic vulnerability curve of each key sections of the main tower was obtained, and the vulnerable part of the main tower and its evolution law were determined. Based on the concept of recoverability, the seismic restorability analysis of the structure was carried out. The results show that under the action of transverse seismic, the bottom section of the tower is the vulnerable section. When the action of seismic intensities are 0.150g and 0.271g, its own seismic capacity decrease from 80.6% to 46.7%, with the increase of seismic intensity, the bridge’s seismic reserve capacity decrease.
- cable-stayed bridge /
- dynamic analysis /
- seismic response /
- seismic fragility analysis /
- seismic recoverability

HTML全文

道岔是机车车辆从一股轨道转入或越过另一股轨道的线路设备，是铁路轨道的重要组成部分，也是线路上的薄弱环节^[1]. 轨距和轨底坡是高速道岔重要的设计技术条件，其参数的设置直接影响行车安全和行车品质. 60N钢轨在区间线路上的使用取得了成功，为提升列车过岔的平稳性和轮轨接触力学特性，在高速道岔区同样需要应用60N钢轨. 列车运行过程中，车轮始终处于动态磨损状态，对轮轨接触行为影响较大.

致谢：京沪高速铁路股份有限公司科技研究项目（京沪科研-2020-11）.

针对线路上的轨距和轨底坡参数，国内外学者做了大量的研究. 杜星等^[2]建立了LMD车轮和CHN60钢轨匹配的动力学模型，分析同一轨道在不同轨底坡条件下的动力学行为发现，轨底坡变化对列车直线运行时的平稳性、舒适性影响很大. 钱瑶等^[3]对比分析了不同轨底坡下60N钢轨和高速车轮LMA、XP55、S1002G匹配时的轮轨接触行为，匹配较优的轨底坡是1/20和1/30. 陈嵘等^[4-5]研究了我国地铁线路常用的LM型面与CHN60钢轨在不同轨距和非对称轨底坡下的轮轨接触特性，发现增大轨距和改变轨底坡可改善轮轨匹配关系. Cui等^[6]提出一种优化轮轨廓形的“正向求解法”，车辆动力学行为结果表明，轨底坡1/30、轨距1435 mm是优化后廓形的最优轨道参数. Sánchez等^[7]开发了一个严谨的测量轨距和轨底坡的程序确保测量过程的准确性. 李超等^[8]分析了转辙器区采用动态轨距加宽技术的轮轨接触作用，该技术可减轻尖轨磨耗和滚动接触疲劳. Ye等^[9]通过建立多体动力学模型，分析轨道参数对车轮磨耗的影响，发现轨道参数对车轮磨耗和脱轨安全性有较大影响. 闫正等^[10]分析了高速动车组车轮踏面和高速60N钢轨道岔断面的静态接触特性，发现适当地增大轨距和轨底坡有利于改善轮轨接触状态. 上述研究表明，改变轨距和轨底坡参数对轮轨接触行为影响较大，且现行的1/40轨底坡和1435 mm轨距往往不是最优的轨道参数，而国内的研究主要集中在区间线路或是针对CHN60钢轨道岔，因此，有必要对新型350 km/h 60N钢轨18号高速道岔的合理轨距和轨底坡展开研究.

本文根据实测LMA磨耗车轮型面和60N钢轨高速道岔关键断面，基于迹线法原理和三维非赫兹滚动接触理论，建立道岔区轮轨滚动接触模型，计算不同轨距和轨底坡下的接触几何参数和静力学指标，并与CHN60钢轨高速道岔进行对比.

1. 道岔关键断面和磨耗车轮

1.1 60N钢轨关键断面

利用CAD导出各关键断面离散数据，将尖轨和基本轨分开，并线性插值，得到如图1所示60N钢轨18号高速道岔转辙器区钢轨模型，X为沿钢轨的纵向里程坐标，Y为钢轨横坐标，Z为钢轨竖向坐标，尖轨顶宽35 mm钢轨断面位于轮载过渡段，其接触行为较为复杂，轮轨相互作用剧烈，对研究道岔区的轮轨接触行为具有代表性，因此，本文选取尖轨顶宽35 mm关键断面进行计算. 60N与CHN60钢轨高速道岔在尖轨顶宽35 mm处钢轨廓形见图2.

图 1 60N钢轨高速道岔直尖轨模型

Figure 1. 60N rail model of high-speed turnout straight switch rail

下载: 全尺寸图片幻灯片

图 2 尖轨顶宽35 mm处钢轨廓形

Figure 2. Rail profiles at 35 mm width of top surface of switch rail

下载: 全尺寸图片幻灯片

1.2 LMA磨耗车轮

跟踪记录某线路上运行的CRH2型动车组上LMA车轮型面演变^[11]，从标准LMA磨耗车轮到运营里程15万km，再到25万km，磨耗量增大较为明显，本文取这三种磨耗车轮进行分析. 车轮凹型磨耗对轮对接触具有较大影响^[12]，随着列车运营里程的增加，凹型磨耗车轮的磨耗量大致呈线性增大，如图3所示. 对磨耗车轮廓形通过三次样条函数进行插值、拟合.

图 3 不同运营里程LMA车轮型面

Figure 3. LMA wheel profile with different operating mileages

下载: 全尺寸图片幻灯片

2. 计算原理

2.1 轮轨接触几何计算原理

利用二维迹线法原理，不考虑车轮摇头角，由最小距离法搜索轮轨接触点. 接触点位置的求解有两个等价几何条件：1）轮轨接触点处轮轨垂直距离为0，非接触点轮轨垂直距离大于0；2）轮轨接触点处轮轨的轮廓线具有相同的斜率. 本文采用条件1求解轮轨接触点，再用条件2对结果加以验证.

2.2 UIC 519标准计算等效锥度

EN 15302标准^[13]中，等效锥度的计算采用轮对周期运动的假设，这个方法称之为UIC 519标准^[14]等效锥度. 自由轮对在轨道上的运动用微分方程表示为

$\ddot y + \frac{{v}^{2}}{e{r}_{0}}\text{Δ}r=0,$

(1)

式中： $y$ 为轮对在钢轨上的横向位移； $v$ 为车辆前进速度； $e$ 为接触点跨距； ${r_0}$ 为名义滚动圆半径； $\Delta r$ 为右侧和左侧车轮滚动半径差.

最后应用Klingel公式计算等效锥度 ${\gamma _e}$ ：

${\gamma _e} = 2e{r_0}{\left(\frac{{\text{π }}}{\lambda }\right)^2}$

(2)

式中： $\lambda$ 为轮对在钢轨上做正弦运动的波长，其求解见文献[14].

2.3 轮轨滚动接触力学原理

本文在接触力学部分采用Kalker的三维非赫兹滚动接触理论及其数值程序CONTACT，这是目前为止最为完善的滚动接触理论^[15]. 该理论将轮轨接触问题转化为数学规划问题，利用Bossinesq-Cerruti公式可得轮轨滚动接触离散模型为：

$\left\{ {\begin{array}{l} \underset{{p}_{Jj}}{\mathrm{min}\;C}=\dfrac{1}{2}{p}_{Ii}{A}_{IiJj}{p}_{Jj} +\\\\ \quad [({g}_{0J}-q){p}_{J{\textit{z}}}\; + ({W}_{J\tau }-{u}_{J\tau }){p}_{J\tau }]{A}_{0},\\ {p}_{J{\textit{z}}}\geqslant 0,\;\left|{p}_{J\tau }\right|\leqslant {b}_{J},　　\forall x\in {A}_{{\rm{c}}},\end{array} } \right.$

(3)

式中： $C$ 为接触问题的余能； $I、J$ 为接触斑上离散单元的编号； $i、j、{\textit{z}}$ 为 ${X}、{Y}、{Z}$ 坐标轴的方向； $\tau$ 为切向，对应 ${{XOY}}$ 平面； ${p_{Ii}}$ 为单元 $I$ 沿方向 $i$ 的接触应力； ${p}_{Jj}、{p}_{J{\textit{z}}}、{p}_{J\tau }$ 分别为单元J上沿Y轴、Z轴及方向 $\tau$ 的接触应力； ${A_{IiJj}}$ 为影响函数，表示单元J方向j上单位力引起的单元I方向i上位移； ${g_{0J}}$ 为单元J中心处轮轨变形前接触面间的法向间隙；q为渗透量； ${W_{J\tau }}$ 为单元J中心处从前时刻 $t'$ 到当前时刻t总的刚性滑动量； ${u_{J\tau }}$ 为轮轨滚动接触过程中时刻t时单元J中心处的弹性位移差； ${A_0}$ 为单元J的面积； ${b_J}$ 为是单元J中心处Coulomb极限摩擦力；x为轮轨在X轴上坐标； ${A_{\rm{c}}}$ 为接触斑内坐标集合；

车轮和尖轨的接触为异型接触，容易产生接触疲劳现象. 本文采用基于安定图模型的表面滚动接触疲劳因子预测不同工况下的轮轨表面滚动接触疲劳伤损. 轮轨接触斑中任一点的轮轨表面滚动接触疲劳系数 $f_{\rm{I}}({\text{•}})$ 定义为

$\left\{ \begin{gathered} f_{\rm{I}}(x,y) = {f_{\rm{t}}} - \frac{k}{{{p_{\textit{z}}}(x,y)}}, \\ {f_{\rm{t}}} = \frac{{\sqrt {{{({p_x}(x,y))}^2} + {{({p_y}(x,y))}^2}} }}{{{p_{\textit{z}}}(x,y)}}, \\ \end{gathered} \right.$

(4)

式中： ${f_{\rm{t}}}$ 为牵引系数； $y、{\textit{z}}$ 分别为接触斑在 ${Y}、{Z}$ 轴上坐标值； ${p_x}({\text{•}})$ 、 ${p_y}({\text{•}})$ 、 ${p_{\textit{z}}}({\text{•}})$ 分别为轮轨纵向、横向和法向接触应力； $k$ 为材料自身的剪切屈服强度，取350 MPa.

式（4）是根据赫兹接触理论得到，对于非赫兹接触问题，依据条带法，认为条带中间位置符合赫兹假设条件，从而将式（4）的应用扩展至非赫兹接触的范围，求得接触斑内任一单元的轮轨表面滚动接触疲劳系数，轮轨表面滚动接触疲劳因子定义为接触斑内滚动接触疲劳系数的最大值.

3. 计算结果与分析

3.1 轮轨接触点

轮轨几何接触是解释轮轨接触关系的基础^[4]. 利用迹线法原理计算轮轨接触点，计算参数有：轮背距1353 mm，名义滚动圆半径460 mm，轮背到名义滚动圆处水平距离为70 mm，以Y轴正向为正，轮对横移量取−12 ~ 12 mm，横移量步长取0.5 mm. 以往研究表明，加宽轨距和改变轨底坡往往能够改善轮轨匹配关系^[3-5]，因此，对轨距1433、1435、1437、1439 mm，轨底坡1/10、1/20、1/30、1/40、1/50进行计算分析.

不同轨距和轨底坡参数下的接触点分布如图4和图5所示. 由图4可见：随着轨距的变化，轮轨接触点分布存在明显的差异；随着轨距的增加，轮轨接触点更多地分布在尖轨顶部，不易发生轮缘接触；随着轨距的增大，轮轨接触点由基本轨转移到尖轨所需要的横移量增大，也即轮载过渡延后，有利于减小尖轨受力，但会增大轮载过渡时轮轨接触点的跳跃，横向不平顺增大；在相同轨距下，随着车轮的磨耗，轮轨接触点更多地分布在基本轨，轮载过渡位置延后，横向不平顺增大.

图 4 不同轨距下轮轨接触点分布

Figure 4. Distribution of wheel-rail contact points under different rail gauges

下载: 全尺寸图片幻灯片

图 5 不同轨底坡下轮轨接触点分布

Figure 5. Distribution of wheel-rail contact points under different rail cants

下载: 全尺寸图片幻灯片

由图5可见：不同轨底坡条件下，轮轨接触点的分布存在较大差异. 当轨底坡为1/10、1/20时，发生轮缘接触需要的轮对横移量最大，但和其余轨底坡相差较小；当轨底坡为1/10、1/20时，轮载过渡延后，横向不平顺增大；不同轨底坡下，发生轮载过渡时所需要的横移量最大为1/10，其次为1/20和1/30，最后为1/40和1/50.

3.2 等效锥度

等效锥度作为轮轨接触线性化指标，被广泛用于表征轮轨接触几何特征. 计算等效锥度的方法有简化法、谐波法和UIC 519法，UIC 519法采用轮对周期运动的假设，计算更准确^[16]，本文通过UIC 519标准^[14]计算等效锥度.

在不同轨距下，磨耗车轮和60N关键断面匹配时的等效锥度见图6. 增大轨距有利于减小车轮踏面的等效锥度，从而提升列车过岔的平稳性；当轨距为1439 mm时，等效锥度基本上小于0.05，横移量相同条件下，其等效锥度是轨距1435 mm时的20%左右，极大减小了车轮等效锥度，提升了列车过岔平稳性；轨距变化对运营里程为25万km车轮的等效锥度影响较小.

图 6 不同轨距下等效锥度

Figure 6. Equivalent conicity of different rail gauges

下载: 全尺寸图片幻灯片

图7为不同轨底坡和不同磨耗车轮条件下的等效锥度. 对于标准车轮和运营里程25万km车轮，1/30、1/40、1/50轨底坡条件下的等效锥度相差较小；当轨底坡为1/10、1/20，在横移量小于6 mm时，和轨底坡为1/30、1/40、1/50相比，等效锥度普遍较大，车辆过岔平稳性较差，横移量大于8 mm时，结果相反；在车轮运营里程为15万km时，1/30轨底坡条件下的等效锥度较小，列车过岔平稳性较好.

图 7 不同轨底坡下等效锥度

Figure 7. Equivalent conicity of different rail cants

下载: 全尺寸图片幻灯片

3.3 接触斑面积

相同法向轮轨力作用下，轮轨接触斑面积越大，其接触应力越小. 轮轨接触应力是影响轮轨磨耗和接触疲劳的重要因素. 利用非赫兹接触理论，计算轮轨接触斑面积和滚动接触疲劳因子，分析轨道参数取值对轮轨静力学接触行为的影响. 不同轨道参数工况下的参数取值：轴重14 t，单侧车轮轮心施加一半轴重，剪切模量82 GPa，泊松比0.28，摩擦系数0.3，划分网格单元0.2 mm × 0.2 mm，轮对横移量取0 ~ 12 mm. 选取右轮轨作为分析对象.

不同轨距和不同磨耗车轮条件下的接触斑面积如图8所示. 当横移量小于9 mm时，轨距和接触斑面积参数呈负相关，而当轮对横移量大于9 mm时，轨距和接触斑面积参数大致呈正相关；轮对横移量小于8 mm时，不同轨距条件下的轮轨接触斑面积相差较小，但当轮对横移量大于8 mm时，轨距越大，轮轨接触斑面积普遍越大；在轮对横移量大于8 mm时，轨距加宽有利于增大轮轨接触斑面积，减小轮轨接触应力.

图 8 不同轨距下接触斑面积

Figure 8. Contact spot area under different rail gauges

下载: 全尺寸图片幻灯片

不同轨底坡和不同磨耗车轮条件下的接触斑面积如图9所示. 1/10轨底坡下的轮轨接触斑面积普遍较小，且随车轮磨耗量的增大，其接触斑面积远小于其余轨底坡条件下的，说明1/10轨底坡下的轮轨接触力学性能较差，且会随着车轮磨耗变得更差. 由标准轮轨条件下，轨底坡和接触斑面积大致呈负相关. 随车轮磨耗量增大，1/30 ~ 1/50轨底坡的接触斑面积相差较小.

图 9 不同轨底坡下接触斑面积

Figure 9. Contact spot area under different rail cants

下载: 全尺寸图片幻灯片

3.4 滚动接触疲劳因子

利用式（4）计算轮轨滚动接触疲劳因子，分析轮轨在不同轨道参数下的接触疲劳现象. 不同轨道参数下的表面滚动接触疲劳因子分布如图10、11所示. 由图10可知：在轮对横移量小于7 mm时，不同轨距下的表面滚动接触疲劳因子相差较小，在横移量大于 7 mm时，增大轨距可延缓轮轨表面进入滚动接触疲劳区；车轮运营里程达到15万km，在横移量为3 ~ 7 mm时，易发生轮轨间的两点接触，导致轮轨表面材料易进入疲劳区，从而产生疲劳破坏；增大轨距有利于减少轮轨材料出现接触疲劳现象，延长轮轨服役寿命.

图 10 不同轨距下表面滚动接触疲劳因子

Figure 10. Surface rolling contact fatigue factors under different rail gauges

下载: 全尺寸图片幻灯片

图 11 不同轨底坡下表面接触疲劳因子

Figure 11. Surface contact fatigue factors under different rail cants

下载: 全尺寸图片幻灯片

由图11可知：标准轮轨条件下，轨底坡和滚动接触疲劳因子大致呈正相关；车轮磨耗导致轮轨滚动接触疲劳因子减小，原因是轮轨过渡位置延后，有利于减少尖轨磨耗，在横移量大于8 mm时，1/10和1/20轨底坡能延缓轮轨材料进入滚动接触疲劳区，但在横移量较小时，其滚动接触疲劳因子明显较大；1/10和1/20轨底坡下的轮轨滚动接触疲劳因子普遍较大，易引起轮轨材料进入滚动接触疲劳区，降低轮轨材料的使用寿命，轨底坡为1/30、1/40、1/50时，滚动接触疲劳因子相差较小.

随着车轮磨耗加深，道岔区的轮轨接触行为变得更为复杂. 运营里程15万km车轮和60N钢轨高速道岔在轨距1439 mm条件下发生轮轨两点接触时的接触斑分布如图12所示，接触斑中箭头指向表示切向应力合力的方向，箭头长短代表合力大小，滑动区轮轨表面间发生了相对滑移，黏着区轮轨间存在滑动趋势，但没有相对滑移. 由图12（a）可见，轨距1439 mm，轮对横移量5 ~ 7 mm时，发生了轮载过渡行为，随着横移量的增大，轮载更多由尖轨承载. 由图12（b）可见：在轮对横移量5 ~ 6 mm时，尖轨上存在较大的滑动区，在轮对横移量7 mm时，基本轨上存在较大的滑动区，两点接触导致了较大滑动区的存在，易导致车轮在钢轨上空转，引起道岔钢轨的磨损，从而缩短道岔区钢轨服役寿命. 需要指出的是，法向接触应力较小时同样可能存在较大滑动区，如图12中轮对横移量为5、7 mm时所示.

图 12 轮轨接触斑分布

Figure 12. Wheel-rail contact spot distribution

下载: 全尺寸图片幻灯片

3.5 60N和CHN60钢轨高速道岔轮轨接触几何对比

为对比60N和CHN60钢轨高速道岔的轮轨接触几何行为，在轨距1439 mm和轨底坡1/30、1/40、1/50条件下，计算60N、CHN60钢轨高速道岔35 mm顶宽关键断面与三种磨耗车轮的等效锥度，如图13.

图 13 等效锥度对比

Figure 13. Comparison of equivalent conicities

下载: 全尺寸图片幻灯片

由图13可知：相同轨底坡和轮对横移量条件下，相比于CHN60钢轨，60N钢轨高速道岔区的等效锥度更小，列车过岔平稳性更优；车轮运营里程达到25万km时，当车轮横移量小于5 mm时，60N钢轨高速道岔区等效锥度普遍更小，具有较好的过岔平稳性，车轮横移量大于5 mm时，60N钢轨高速道岔区等效锥度普遍更大，轮对的对中性能更好；随车轮磨耗量增加，等效锥度整体呈增加趋势.

4. 结　论

1）轨距对轮轨接触行为影响较大. 轨距加宽有利于减少轮缘接触，较大程度减小等效锥度，提升列车过岔的平稳性；轨距加宽可减小轮对横移量大于8 mm时的轮轨接触应力和表面滚动接触疲劳因子，减少轮轨材料发生接触疲劳，延长尖轨使用寿命. 轮对横移量小于8 mm时，轨距加宽对运营里程25万km车轮的接触性能影响较小.

2）轨底坡对轮轨接触行为影响较大. 标准轮轨条件下，轨底坡和接触斑面积大致呈负相关，与滚动接触疲劳因子大致呈正相关. 轨底坡为1/10和1/20时，轮载过渡位置延后，横向不平顺增大，车轮横移量小于6 mm时，等效锥度普遍较大；1/10和1/20轨底坡下的接触斑面积普遍较小，轮轨滚动接触疲劳因子普遍较大，较易引起轮轨材料进入滚动接触疲劳区，降低轮轨材料的使用寿命，且1/10轨底坡对车轮磨耗的适应性较差. 轨底坡为1/30、1/40、1/50时，轮轨接触参数相差较小，匹配性能较优.

3）和CHN60钢轨高速道岔相比，60N钢轨的等效锥度普遍更小，列车过岔平稳性更优；车轮运营里程为25万km时，当轮对横移量小于5 mm时，60N钢轨的等效锥度普遍更小，当轮对横移量大于5 mm时，结果相反.

4）车轮磨耗易引起道岔区轮轨间的两点接触，在较小轮轨法向接触应力下，接触斑上也易出现较大滑动区，导致车轮空转，引起钢轨伤损. 随车轮磨耗量增加，轮轨间等效锥度整体呈增加趋势.

致谢：京沪高速铁路股份有限公司科技研究项目（京沪科研-2020-11）的支持.

图 1 结构抗震能力剩余比

Figure 1. Residual ratio of seismic capacity of structure

下载: 全尺寸图片幻灯片

图 2 结构阶段抗震能力剩余比

Figure 2. Residual ratio of stage seismic capacity of structure

下载: 全尺寸图片幻灯片

图 3 结构动力计算模型

Figure 3. Dynamic calculation model of structural

下载: 全尺寸图片幻灯片

图 4 主塔各关键截面（单位：cm）

Figure 4. Key sections of the main tower (unit：cm)

下载: 全尺寸图片幻灯片

图 5 主塔不同截面的地震易损性曲线

Figure 5. Fragility curves of the different sections of main tower

下载: 全尺寸图片幻灯片

图 6 截面A整体抗震能力剩余比曲线

Figure 6. Residual ratio of seismic capacity of section A

下载: 全尺寸图片幻灯片

图 7 截面A阶段抗震能力剩余比曲线

Figure 7. Residual ratio of stage seismic capacity of section A

下载: 全尺寸图片幻灯片

图 8 截面A不同区间易损性曲线

Figure 8. Fragility curves of different Intervals of section A

下载: 全尺寸图片幻灯片

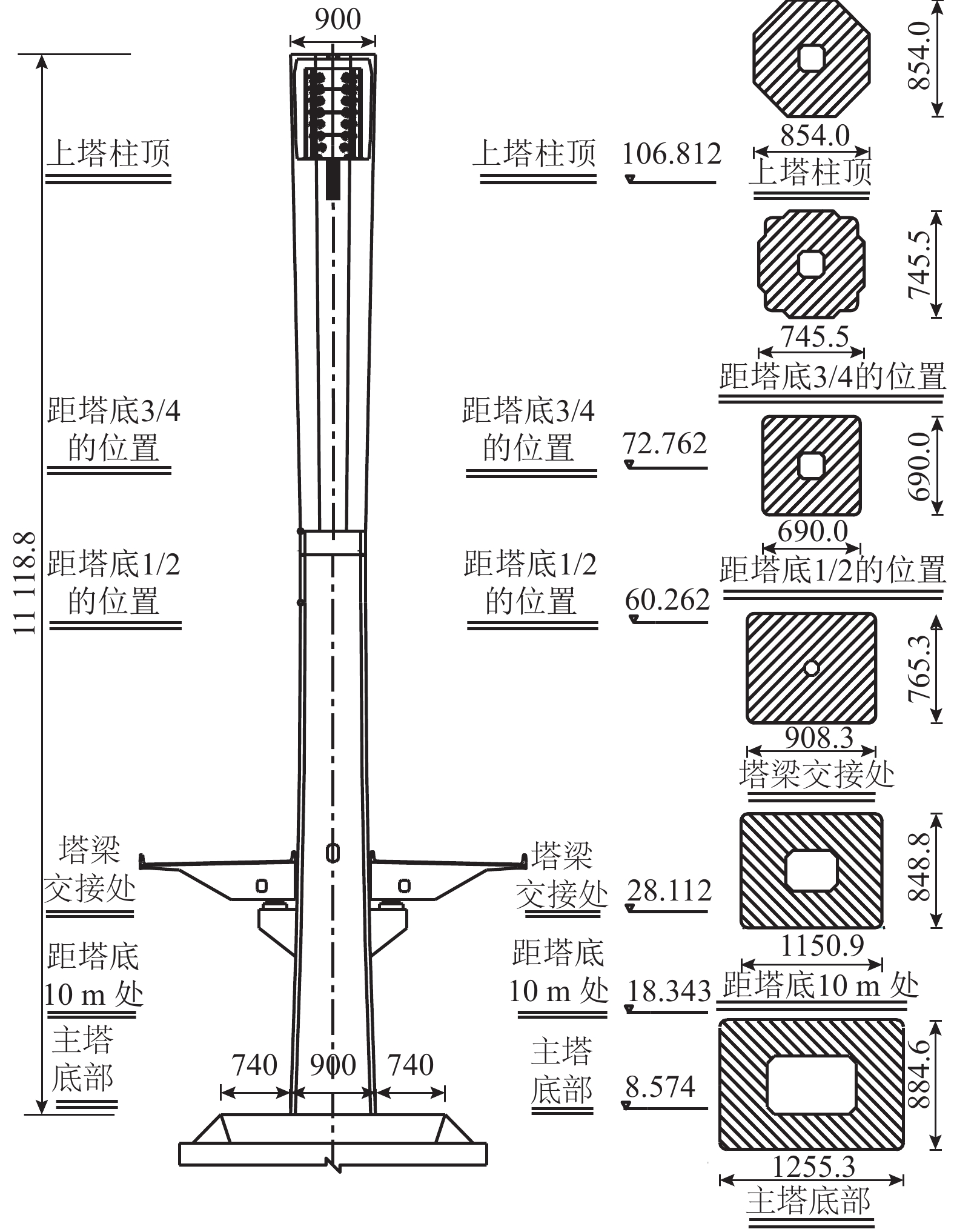
表 1 斜拉桥边界约束条件

Table 1. Boundary constraint condition of cable-stayed bridge

自由度	主塔与主墩联系	主塔与主梁联系	主梁与主墩联系
U1	1	0	0
U2	1	0	1
U3	1	1	1
R1	1	0	0
R2	1	0	0
R3	1	0	0
注：U1、U2、U3 分别对应于图3整体坐标系中的X、Y、　　　 Z 方向的位移自由度；R1、R2、R3 分别对应于图3　　　整体坐标系中的X、Y、Z方向的转角自由度.

下载: 导出CSV

表 2 斜拉桥动力特性

Table 2. Dynamic characteristics of cable-stayed bridge

阶数	自振频率/Hz	自振周期/s	振型特征
第 1 阶	0.342	2.924	主塔对称横向侧弯
第 2 阶	0.353	2.828	主塔反对称横向侧弯
第 3 阶	0.408	2.452	主梁一阶对称竖弯
第 4 阶	0.578	1.730	塔梁对称横向侧弯
第 5 阶	0.594	1.684	主塔纵弯+主梁纵飘

下载: 导出CSV

表 3 IDA分析选用的地震波情况

Table 3. Seismic waves for IDA analysis

编号	地震波名称	时间	地震动加速度峰值/ (× g)	谱加速度/ (× g)
地震波 1	Kobe	1995年	0.345	0.052 0
地震波 2	CHICHI	1999年	0.361	0.059 1
地震波 3	Landers	1992年	0.780	0.002 8
地震波 4	WC	2008年	0.978	0.033 4
地震波 5	Northridge	1994年	0.568	0.100 7
地震波 6	Hollister	1961年	0.195	0.034 5
地震波 7	Friuli	1976年	0.351	0.033 2
地震波 8	Imperial Valley	1979年	0.315	0.101 0
地震波 9	Loma Prieta	1989年	0.367	0.144 5
地震波 10	LS	2013年	1.026	0.009 9
地震波 11	Kocaele	1999年	0.350	0.346 5
地震波 12	Trinidad	1983年	0.194	0.007 7

下载: 导出CSV

表 4 地震波强度等级划分

Table 4. Intensity levels classification of seismic waves

强度等级	谱加速度/ (× g)	强度等级	谱加速度/ (× g)
等级 1	0.023	等级 6	0.136
等级 2	0.045	等级 7	0.181
等级 3	0.068	等级 8	0.203
等级 4	0.090	等级 9	0.226
等级 5	0.113	等级 10	0.249

下载: 导出CSV

表 5 主塔各截面损伤状态的曲率量化

Table 5. Curvature quantification of the damage states of the main tower sections

损伤状况	钢筋混凝土应变
无损伤	最外侧纵筋不出现屈服
轻微损伤	最外侧纵筋屈服应变小于初始应变、非约束混凝土的压应变小于0.004
中等损伤	纵筋应变小于0.55倍的极限拉应变、约束混凝土小于0.75倍极限压应变
严重损伤	纵筋应变小于极限拉应变、约束混凝土不大于极限压应变

下载: 导出CSV

表 6 主塔各关键截面的曲率损伤指标汇总

Table 6. Curvature damage indicators for key sections of the main tower × 10⁻³/m

主塔关键截面	轻微损伤	中等损伤	严重损伤	完全损伤
截面 A	0.587	2.010	7.960	1.060
截面 B	0.544	1.910	7.280	9.300
截面 C	0.508	1.240	5.230	7.790
截面 D	0.524	1.250	5.880	8.290
截面 E	0.507	1.130	5.630	8.200
截面 F	0.525	2.020	5.020	7.680

下载: 导出CSV

表 7 截面A不同损伤区间的抗震可恢复性指标与相应发生概率

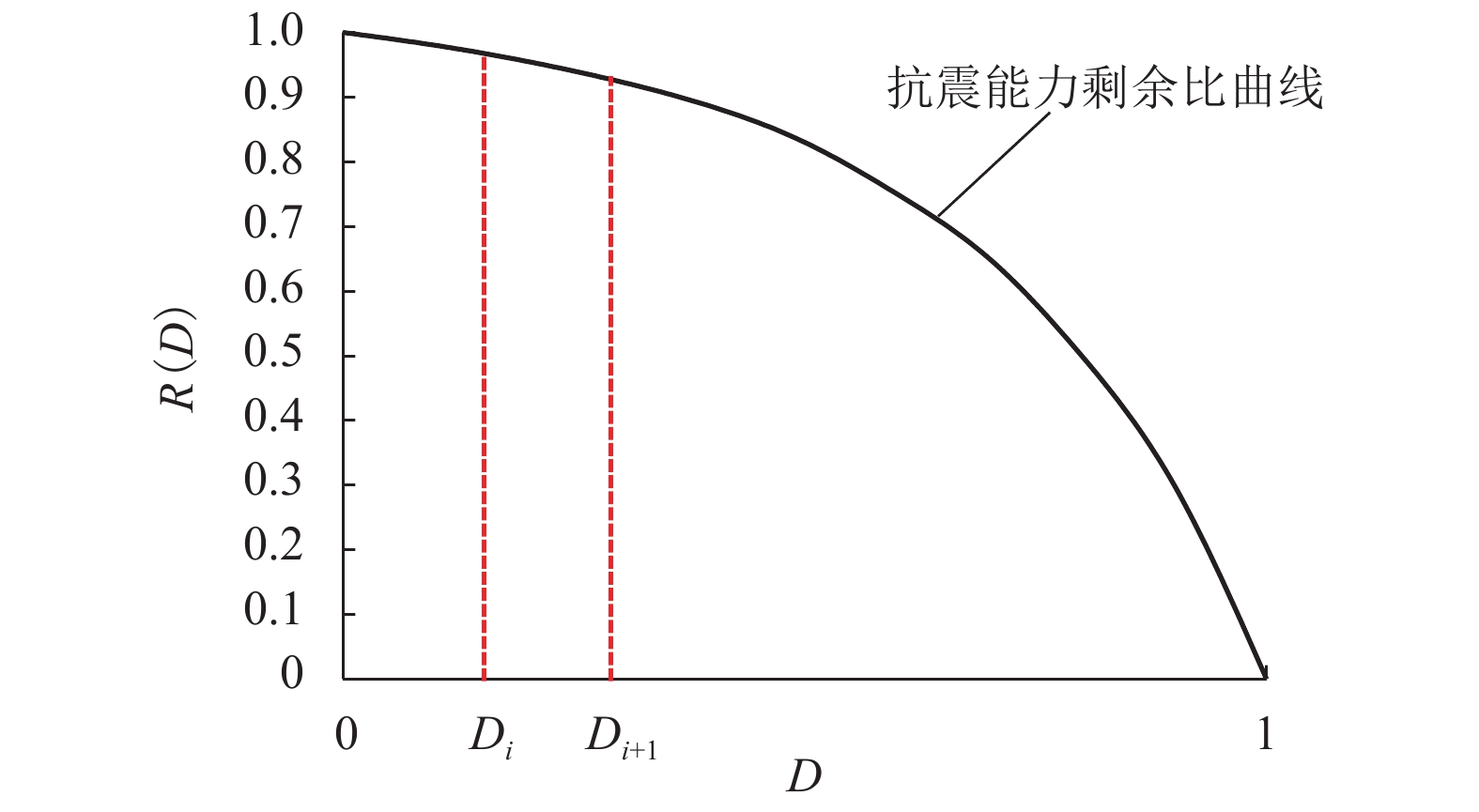
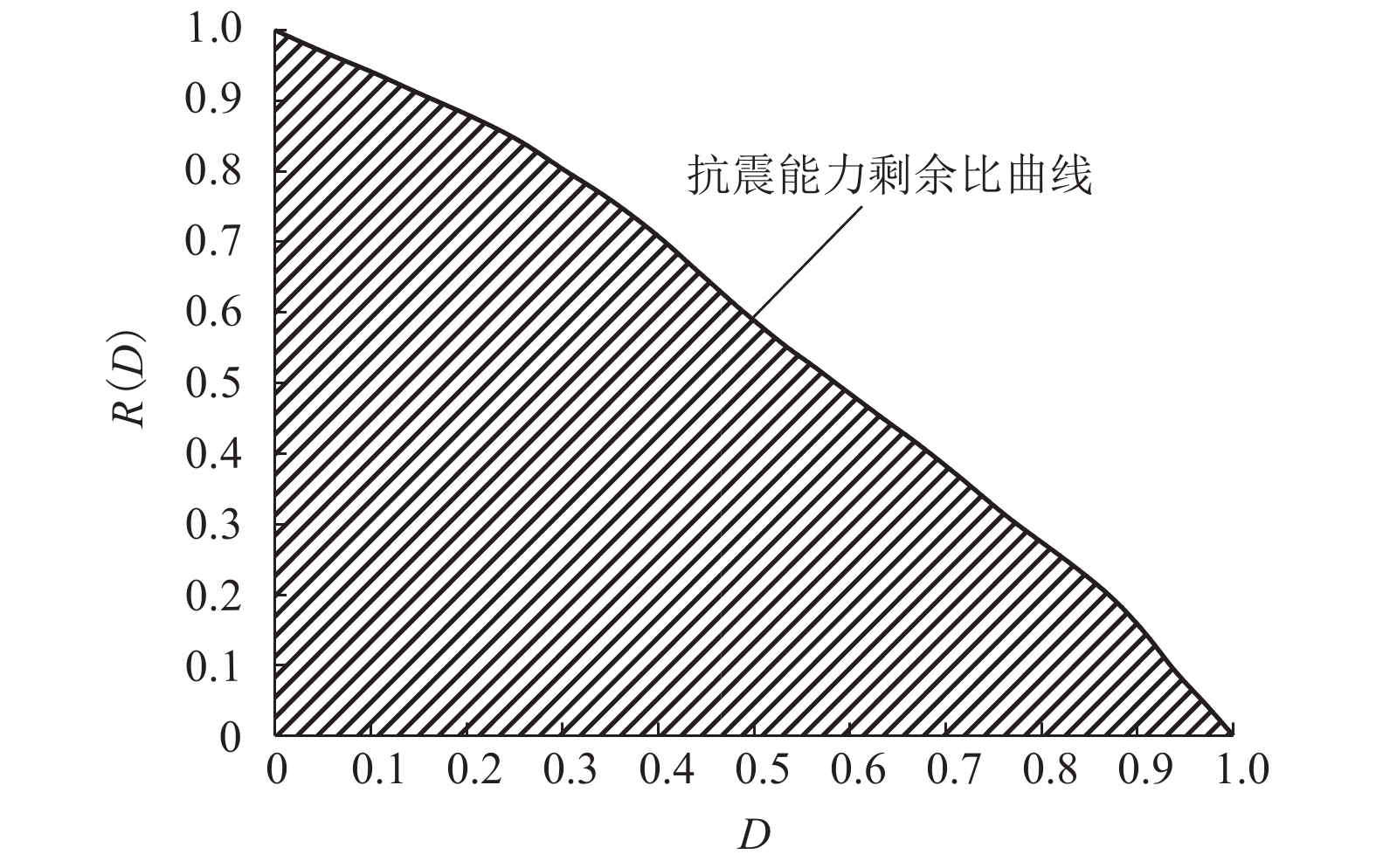
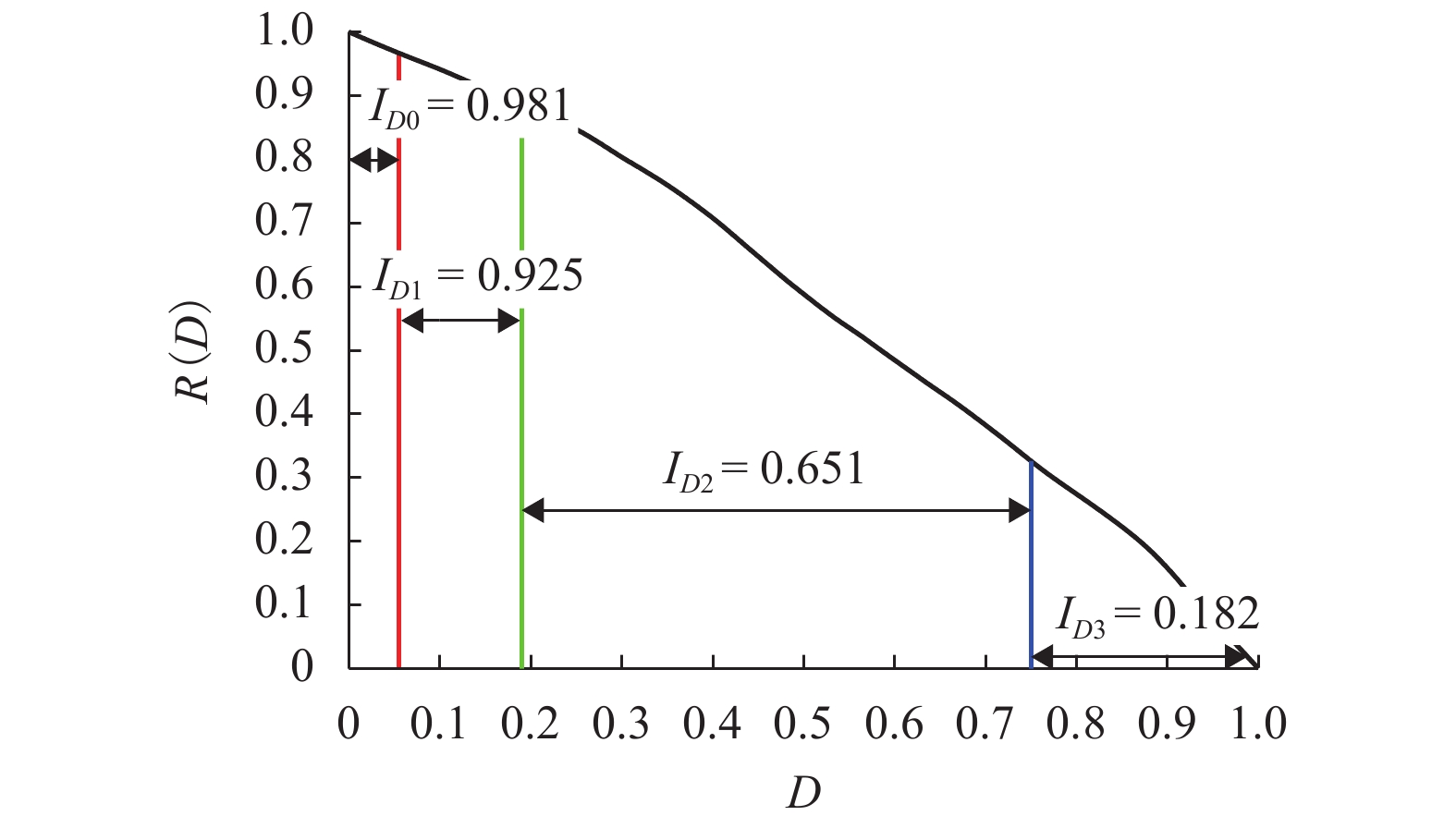
Table 7. Seismic recoverability index and corresponding occurrence probability of different damage intervals of section A

损伤状态	阶段抗震可恢复性指标 ${I_{{\mathop{D}\nolimits}_{i}}}$	发生概率P(D_i)
完好状态	0.981	0.075
轻微损伤	0.925	0.525
中等损伤	0.651	0.372
严重损伤	0.182	0.026
完全损伤	0.000	0.002

下载: 导出CSV

参考文献(17)

庞于涛,袁万城. 考虑材料劣变过程的桥梁地震易损性分析[J]. 同济大学学报(自然科学版),2013,12(3): 348-354.

PANG Yutao, YUAN Wancheng. Stochastic fragility analysis of bridges with a considertaion of material deterioration[J]. Journal of Tongji Univertisty (Natural Science), 2013, 12(3): 348-354.

丰丙龙. 基于性能的大跨径斜拉桥地震易损性及风险分析[D]. 西安: 长安大学, 2017.

KIM S H. Fragility analysis of bridges under ground motion with the spatial variation[D]. California: University of California, 2002.

张菊辉. 基于数值模拟的规则梁桥墩柱的地震易损性分析[D]. 上海: 同济大学, 2006.

谷音, 钟华, 卓卫东. 基于性能的矮塔斜拉桥结构地震易损性分析[J]. 土木工程学报, 2015, 45（增刊1）: 218-222.

GU Yin, ZHONG Hua, ZHOU Weidong. Lower-tower cable-stayed bridge seismic vulnerability analysis[J]. China Civil Engineering Journal, 2015, 45（S1）: 218-222.

焦驰宇. 基于性能的大跨斜拉桥地震易损性分析[D]. 上海: 同济大学, 2008.

BRUNEAU M, CHANG S E, EGUCHI R T, et al. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. Earth-quake Spectra, 2003, 19(4): 733-752. doi: 10.1193/1.1623497

吕西林,陈云,毛苑君. 结构抗震设计的新概念—— 可恢复功能结构[J]. 同济大学学报(自然科学版),2011,39(7): 941-948.

LU Xilin, CHEN Yun, MAO Yuanjun. New concept of structural seismic design:earthquake resilient structures[J]. Journal of TongJi university (Natural Science), 2011, 39(7): 941-948.

何政,安宁,徐菁菁. 考虑损伤的结构抗震可恢复性[J]. 工程力学,2017,34(5): 179-187.

HE Zheng, AN Ning, XU Jingjing. Structural seismic resilience considering damage[J]. Engineering Mechanics, 2017, 34(5): 179-187.

肖明洋. 高墩混凝土连续刚构桥地震易损性分析[D]. 成都: 西南交通大学, 2009.

张少雄. 高墩桥梁地震易损性分析研究[D]. 成都: 西南交通大学, 2014

HWANG H,刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报,2004,37(6): 47-51. doi: 10.3321/j.issn:1000-131X.2004.06.009

HWANG H, LIU Jingbo. Seismic fragility analysis of reinforced concrete bridges[J]. China Civil Engineering Journal, 2004, 37(6): 47-51. doi: 10.3321/j.issn:1000-131X.2004.06.009

DECò A, BOCCHINI P, FRANGOPOL D M. A probabilistic approach for the prediction of seismic resilience of bridges[J]. Earthquake Engineering & Structural Dynamics, 2013, 42(10): 1469-1487.

CHANG S E, SHINOZUKA M. Measuring improvements in the disaster resilience of communities[J]. Earthquake Spectra, 2004, 20(3): 739-755. doi: 10.1193/1.1775796

陈志伟,蒲黔辉,李晰,等. 行波效应对大跨连续刚构桥易损性影响分析[J]. 西南交通大学学报,2017,52(1): 23-29,37. doi: 10.3969/j.issn.0258-2724.2017.01.004

CHEN Zhiwei, PU Qianhui, LI Xi, et al. Fragility analysis of large-span continuous rigid bridge considering wave passage[J]. Journal of Southwest Jiaotong University, 2017, 52(1): 23-29,37. doi: 10.3969/j.issn.0258-2724.2017.01.004

FARAHNAZ S, SUJITH M, REGINALD D. Seismic resilience of concrete bridges with flared columns[J]. Procedia Engineering, 2017, 199: 3065-3070. doi: 10.1016/j.proeng.2017.09.417

陈力波,黄才贵,黄勇冰,等. 公路规则梁桥地震易损性模型及简化计算方法[J]. 西南交通大学学报,2018,53(1): 146-155. doi: 10.3969/j.issn.0258-2724.2018.01.018

CHEN Libo, HUANG Caigui, HUANG Yongbing, et al. Seismic vulnerabilitu models and simplified calculation method for regular highway girder bridges[J]. Journal of Southwest Jiaotong University, 2018, 53(1): 146-155. doi: 10.3969/j.issn.0258-2724.2018.01.018

施引文献

附加材料(0)

访问统计