桥梁结构非线性地震响应极值分布的估算方法

陈志强; 郑史雄; 周强; 陈志伟; 李晰

doi:10.3969/j.issn.0258-2724.20180948

桥梁结构非线性地震响应极值分布的估算方法

doi: 10.3969/j.issn.0258-2724.20180948

陈志强^1,2,,
郑史雄^1,2, ,,
周强^1,2,
陈志伟^1,2,
李晰^1,2

基金项目: 国家自然科学基金（U1434205，51508473）

详细信息

作者简介:
陈志强（1993—），男，博士研究生，研究方向为桥梁抗风抗震， E-mail：zhqchen163@163.com

通讯作者:
郑史雄（1965—），男，教授，研究方向为桥梁抗风抗震，E-mail：zhengsx@home.swjtu.edu.cn

中图分类号: U452.2+8
计量
- 文章访问数: 694
- HTML全文浏览量: 380
- PDF下载量: 21
- 被引次数: 0
出版历程
- 收稿日期: 2018-11-05
- 修回日期: 2019-01-07
- 网络出版日期: 2020-02-21
- 刊出日期: 2020-08-01

Extreme Value Distribution Estimation Method for Nonlinear Seismic Response of Bridge Structures

CHEN Zhiqiang^{1,2
,},
ZHENG Shixiong^{1,2
, ,},
ZHOU Qiang^1,2,
CHEN Zhiwei^1,2,
LI Xi^1,2

摘要

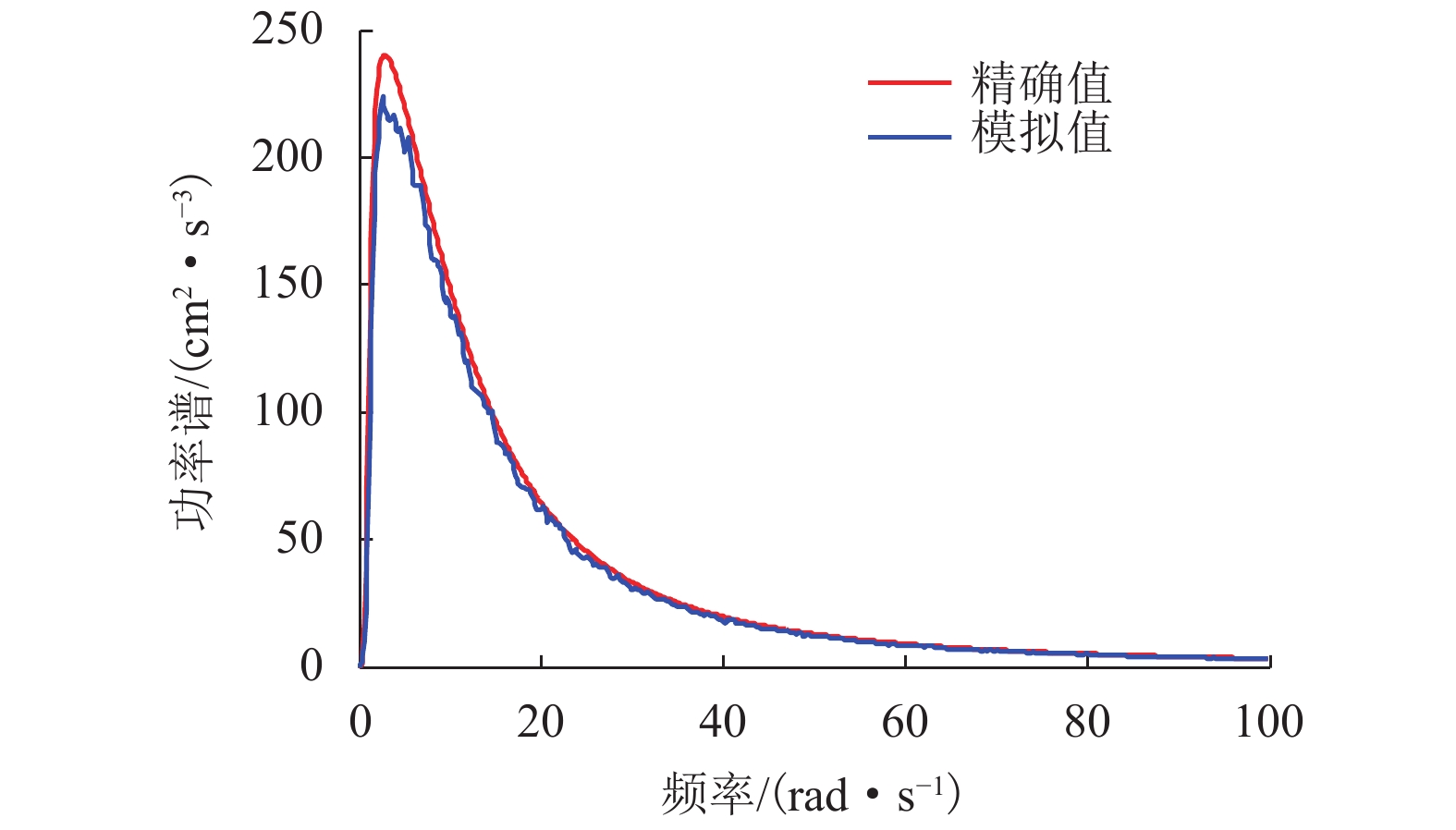
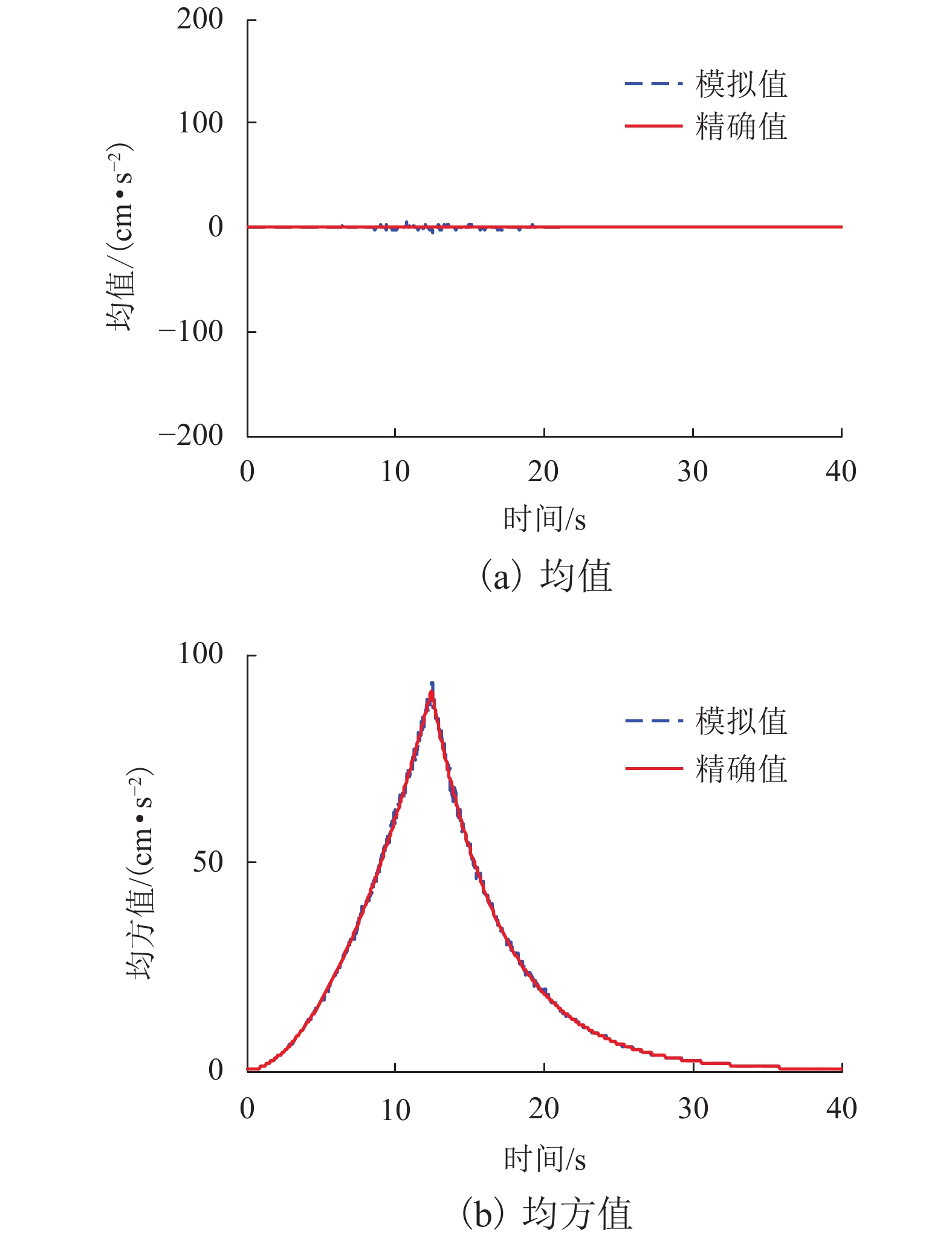
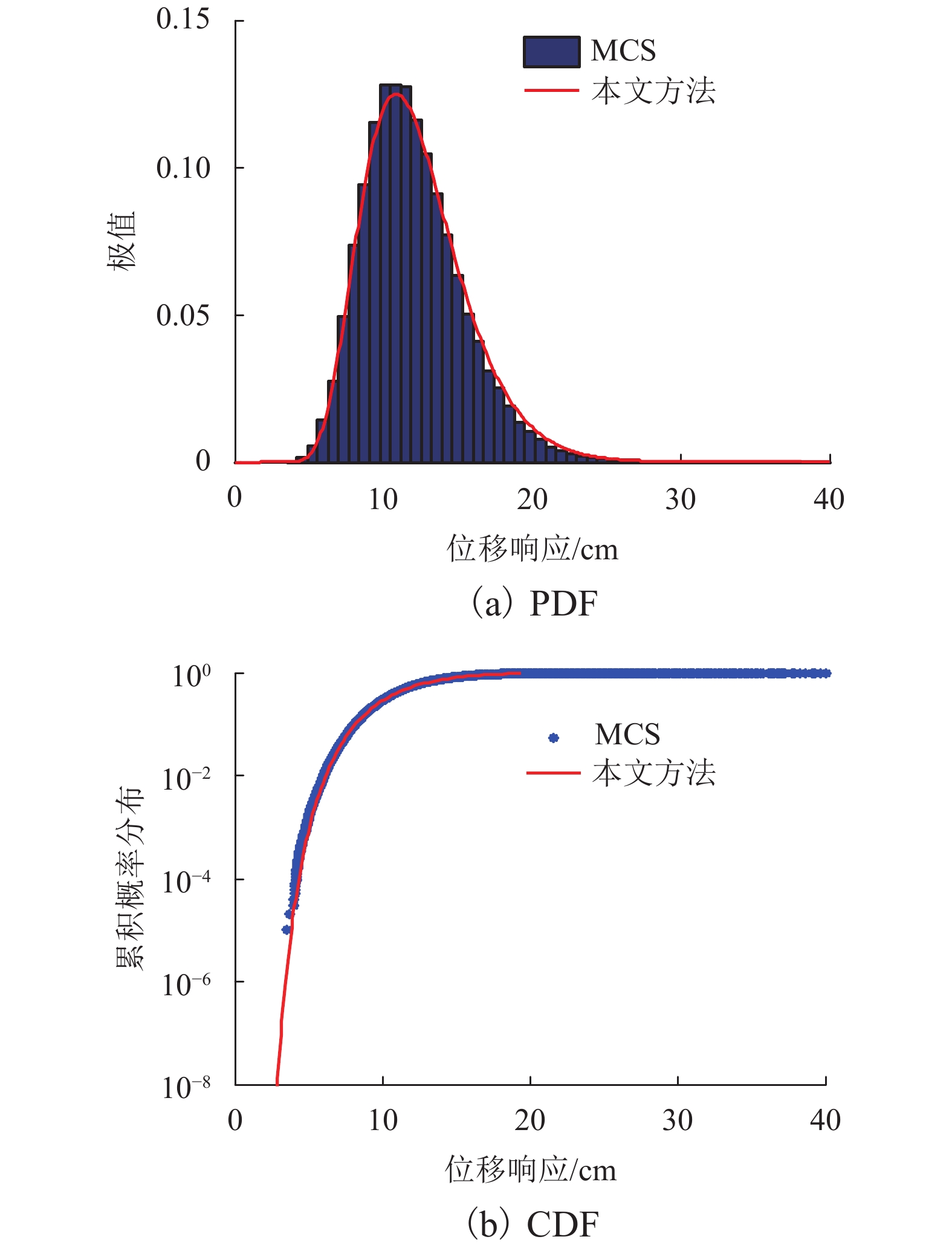
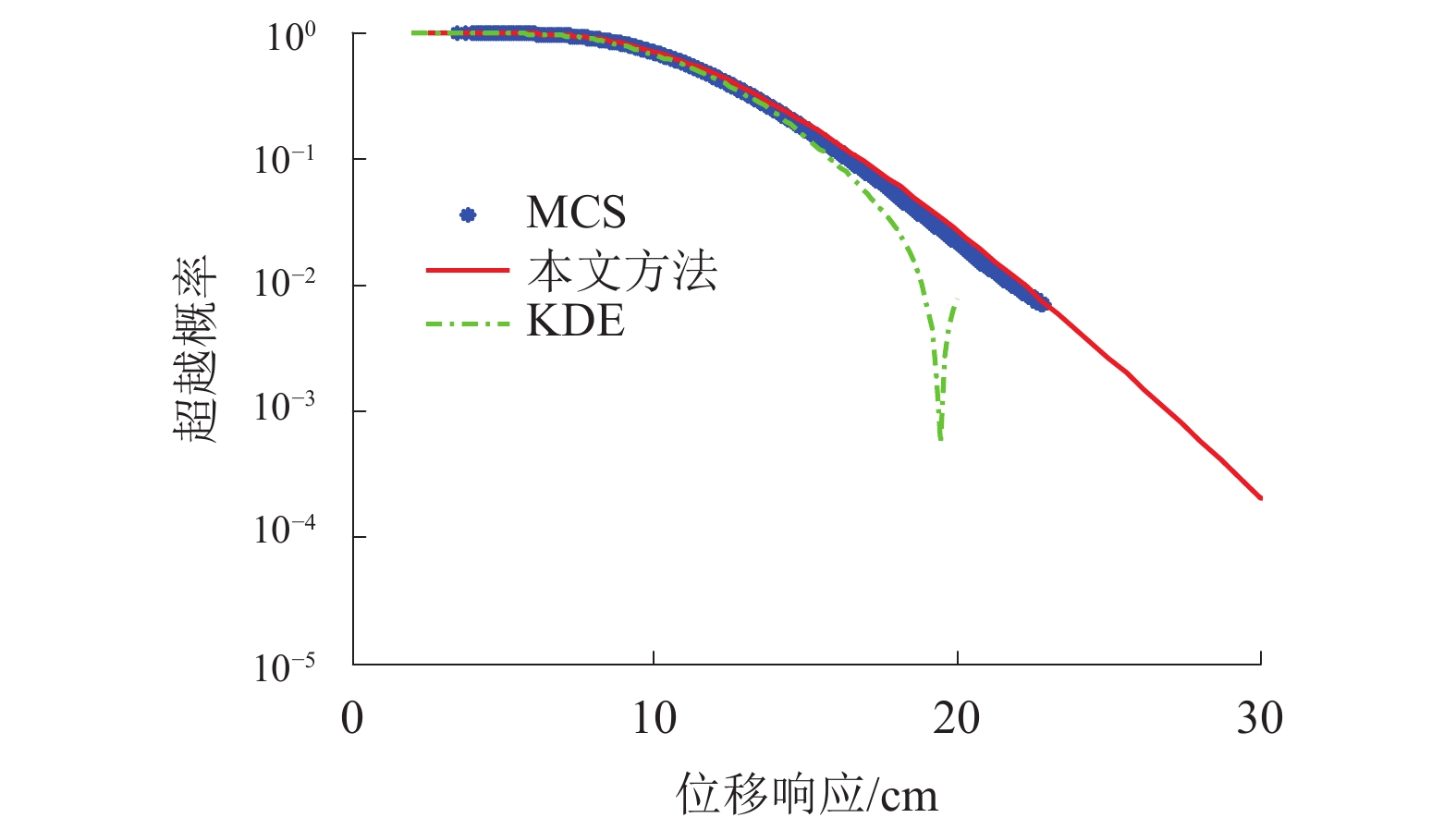
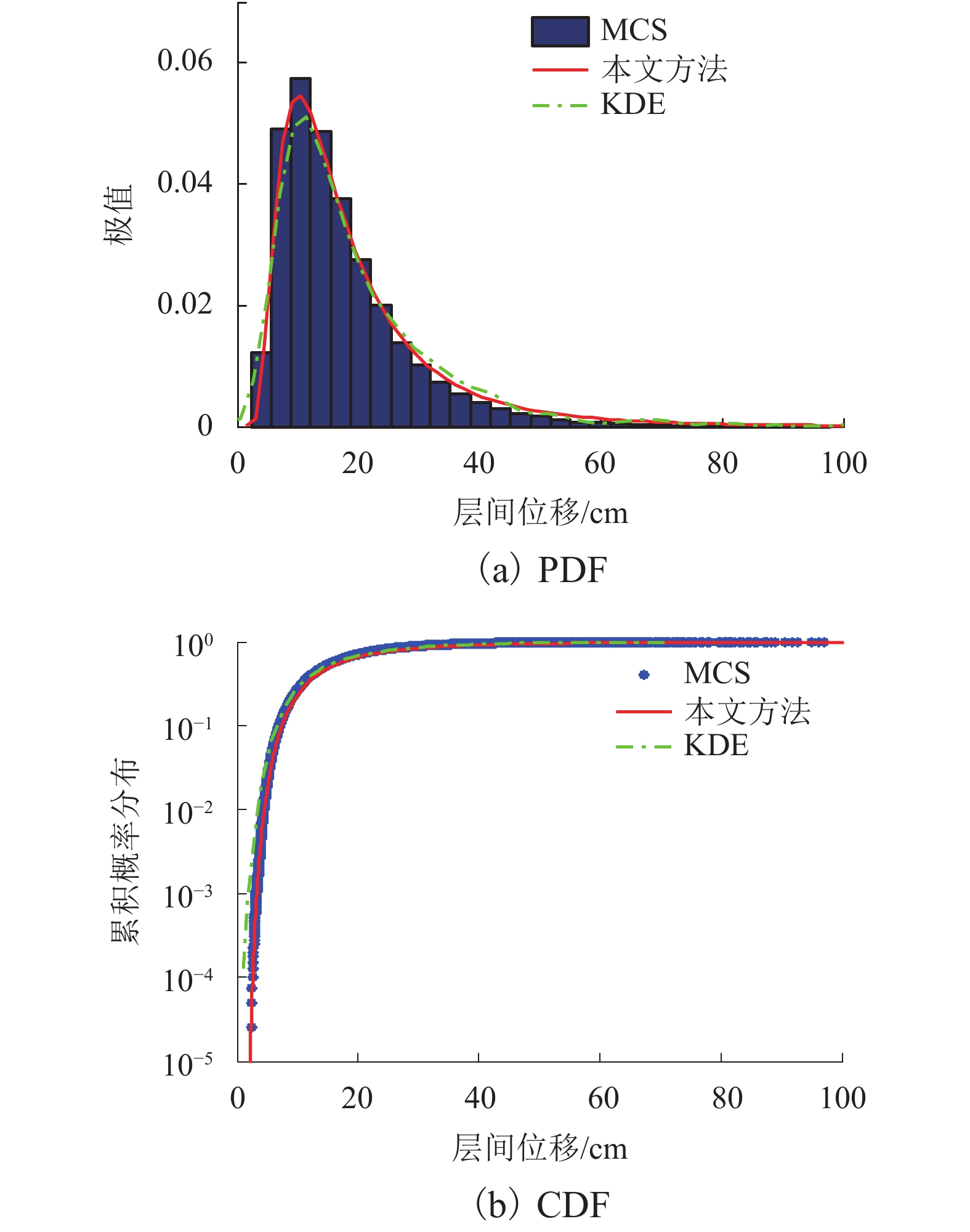
摘要: 为了研究近断层脉冲地震作用下桥梁非线性地震响应极值分布，进行小失效概率下的桥梁动力可靠度精确计算，提出了一种有效的近断层脉冲地震作用下桥梁结构非线性地震响应极值分布分析方法. 首先考虑桥梁结构的非线性和地震动的不确定性，采用拉丁超立方抽样对近断层脉冲地震动随机参数和结构随机参数进行随机抽样，通过模拟的高频地震动均方值和与精确值的相对误差确定出所需要的样本数量；其次以合成的近断层脉冲地震动作为地震激励，通过时程分析对结构非线性动力方程进行求解，从而得到结构非线性地震响应极值样本，再采用改进的分数阶矩最大熵原理获得结构非线性地震响应的极值分布；最后通过非线性单自由度系统和三层非线性剪切框架验证了该方法的有效性. 研究结果表明：该方法不仅能够有效的模拟近断层脉冲地震作用时，桥梁结构与地震动双重不确定性影响下的动力响应极值分布，更能在兼顾效率和计算精度时，精确估计桥梁结构非线性地震响应极值的尾部分布，能够为桥梁结构非线性动力可靠度评估提供一种有效的途径.
- 极值分布 /
- 动力可靠度 /
- 近断层脉冲 /
- 拉丁超立方抽样 /
- 分数阶矩
Abstract: To study the extreme value distribution (EVD) of nonlinear seismic response of bridges subjected to near-fault impulse ground motion and accurately estimates the dynamic reliability of bridges at small failure probability level, an effective method is proposed and validated. Considering the nonlinearity of bridge structures and the uncertainty of ground motions, the random parameters of near-fault impulse ground motion and structure are sampled by Latin hypercube sampling (LHS). The required number of seismic samples is determined by the relative error between the mean square value of simulated high-frequency ground motion and the exact value. Using synthetic near-fault impulse ground motions as seismic excitation, the structural nonlinear dynamic equation is solved by time history analysis, and the structural nonlinear seismic response extreme value samples are obtained. Then, the improved maximum entropy principle with fraction moment is adopted to obtain the EVD of bridges. The accuracy and efficiency of the proposed method are verified by a single degree freedom system and a three-story shear frame structure in comparison with the Monte Carlo simulation. Results indicate that the proposed method can not only effectively simulate the EVD of dynamic response of bridge under the double uncertainties influence of structure and ground motion, but also accurately estimate the tail distribution of the extreme value of nonlinear seismic response of bridge structure, with a balanced between efficiency and calculation accuracy. This method provides an effective way for evaluating the non-linear dynamic reliability of bridge structures.
- extreme value distribution /
- dynamic reliability /
- near-fault impulse /
- Latin hyper-cube sample /
- fractional moments

HTML全文

纤维增强复合材料（FRP）轻质、高强，且热膨胀系数与混凝土相近，可与混凝土变形协调，具有裁剪不易松散变形、易于浸溃、施工便捷等优点^[1-2]. 超高性能混凝土（UHPC）是一种高强、高韧和高耐久性的新型水泥基复合材料，具有优异的力学性能和耐久性^[3-4]. 用FRP侧向约束UHPC，可以充分发挥UHPC和FRP的优点，提高核心UHPC的强度和变形能力^[5].

Lam等^[6]对18个FRP约束UHPC短柱进行了轴压试验研究发现，在FRP约束下UHPC短柱的极限强度和应变显著提高. Guler^[7]对碳纤维增强复合材料（CFRP）、玻璃纤维增强复合材料（GFRP）和芳纶纤维增强复合材料（AFRP）约束UHPC圆柱进行了轴向加载，并对不同纤维增强复合材料对UHPC圆柱极限强度和应变的提升程度做了对比分析. Wang等^[8]对FRP约束UHPC的轴压性能进行研究，并比较FRP对UHPC、高强混凝土和普通混凝土约束性能，结果表明，由于FRP约束的UHPC具有超高强度和独特的微观结构，比FRP约束的NSC和HSC表现出更多的脆性. 邓宗才等^[9-10]对FRP约束UHPC圆柱进行轴心抗压试验，结果表明，约束比和侧向约束刚度是影响试件极限强度和极限应变的关键参数，FRP的约束作用对核心UHPC的强度和延性具有提高效果. 黄美珍^[11]基于细观力学方法对UHPC本构模型受钢纤维掺量的影响进行研究发现，适量的钢纤维能够显著提高UHPC的峰值应变与轴心抗压强度. 田会文等^[12]利用LS-DYNA建立FRP约束UHPC圆柱细观有限元模型，研究FRP厚度、纤维缠绕角度和钢纤维体积掺量对其轴压性能的影响，结果表明，FRP显著提高核心UHPC的极限强度和延性.

目前，国内外对FRP约束UHPC圆形短柱轴心受压力学性能的研究大多都是基于FRP层数、混凝土强度等变量的研究，对钢纤维影响短柱轴压性能的研究相对较少. 同时，现有研究多集中于单一变量对短柱轴压性能的影响，对多个变量耦合作用的研究较少，且缺少多个变量下短柱轴压性能的对比分析. 此外，现有研究中对FRP约束UHPC本构模型的理论分析也有待深入.

为此，本文以FRP层数、FRP种类和钢纤维体积掺量为变量，研究FRP约束UHPC圆形短柱的轴压性能及变量的影响规律；并在考虑钢纤维体积掺量的影响下，提出FRP约束UHPC圆形短柱抗压强度和极限应变的计算模型，并进一步给出FRP约束UHPC的本构模型.

1. 试验方案

1.1 试件设计

试验共设计制作21组FRP约束UHPC圆形短柱和3组UHPC圆形短柱，所有试件的高度均为200 mm，直径均为100 mm. 试件编号见表1，表中：首字母“P”代表无约束试件，“G”表示GFRP约束UHPC圆形短柱，“C”表示CFRP约束UHPC圆形短柱，N为试件的峰值荷载；ɛ_y为试件的轴向极限应变.

表 1 试件编号及试验结果

Table 1. Specimen numbering and experimental results

试件编号	钢纤维掺量/%	FRP 层数/层	N/kN	ɛ_y	试件编号	钢纤维掺量/%	FRP 层数/层	N/kN	ɛ_y
P1	1		805.0	0.0024	G32	3	2	1392.2	0.0088
P2	2		874.2	0.0029	G33	3	3	1511.9	0.0120
P3	3		917.3	0.0029	G34	3	4	1657.5	0.0148
G11	1	1	1197.1	0.0044	C11	1	1	1312.9	0.0056
G12	1	2	1318.1	0.0063	C12	1	2	1546.4	0.0087
G13	1	3	1409.6	0.0082	C13	1	3	1787.3	0.0138
G14	1	4	1532.8	0.0106	C21	2	1	1336.0	0.0073
G21	2	1	1239.3	0.0061	C22	2	2	1675.7	0.0125
G22	2	2	1351.6	0.0080	C23	2	3	1931.9	0.0176
G23	2	3	1469.5	0.0109	C31	3	1	1375.4	0.0084
G24	2	4	1620.4	0.0136	C32	3	2	1696.8	0.0145
G31	3	1	1283.1	0.0075	C33	3	3	2065.1	0.0210

下载: 导出CSV

| 显示表格

1.2 材料性能

UHPC的配合比见表2. 根据T/CECS864−2021《超高性能混凝土试验方法标准》^[13]对UHPC进行抗压强度试验，试件制作时浇筑3组边长为100 mm、钢纤维体积掺量分别为1%、2%和3%的UHPC立方体，立方体的尺寸符合GB/T 50081—2016《普通混凝土拌合物性能试验方法标准》^[14]的有关规定. 测得3组立方体的平均抗压强度分别为129.2、144.5、153.3 MPa. FRP力学性能指标见表3.

表 2 UHPC的配合比

Table 2. Mix proportion of UHPC kg/m³

名称	水胶比	水泥	硅灰	石英砂	粉煤灰
配合比	0.15	1.00	0.32	1.46	0.30

下载: 导出CSV

| 显示表格

表 3 FRP的性能指标

Table 3. Performance index of FRP

型号	抗拉强度/MPa	弹性模量/GPa	伸长率/%
GFRP	2381	114	2.7
CFRP	3961	240	1.8

下载: 导出CSV

| 显示表格

1.3 加载方案及测点布置

试验采用的加载设备为200 t压力试验机，如图1. 加载前，应先进行预压，以保证试件轴心受压，并对位移传感器和应变片进行检查和校正；正式加载时，加载速率控制为1.5 kN/s；当荷载达到试件计算强度的90%时，加载速率控制为0.5 kN/s；直到试件破坏后，卸载.

图 1 试验加载装置

Figure 1. Test loading device

下载: 全尺寸图片幻灯片

试件应变测点的布置如图2所示，在试件的中部布置4个轴向应变片测量其轴向应变，并将4个环向应变片垂直于轴向应变片布置，用以测量试件的环向应变. 此外，轴向位移通过固定装置两侧的位移传感器获得，荷载由数据采集系统自动采集.

图 2 应变片的分布

Figure 2. Distribution of strain gauges

下载: 全尺寸图片幻灯片

2. 试验结果及分析

2.1 试件破坏特征

2.1.1 GFRP约束UHPC的破坏特征

GFRP约束UHPC圆形短柱的破坏形态如图3（a）～（d）所示. 在加载初期，试件变形微小，导致GFRP未对其产生约束作用；随着荷载的增加，GFRP发出噼啪裂开的声音；当荷载接近极限强度的90%时，UHPC圆形短柱中部的GFRP逐渐断裂；当试件加载至极限强度时，爆裂声响加剧，试件中部的GFRP断裂频率加快，直至整节断裂，试件破坏.

图 3 试件破坏形态

Figure 3. Failure modes of specimens

下载: 全尺寸图片幻灯片

2.1.2 CFRP约束UHPC的破坏特征

CFRP约束UHPC圆形短柱的破坏形态如图3（e）～（h）所示. 在加载初期，试件无明显变形，CFRP未对其产生约束作用；随着荷载的逐步增加，偶尔听到CFRP破裂的声音，且UHPC圆形短柱中部开始膨胀，CFRP对其约束力也逐渐增强；直至荷载达到试件极限强度的90%时，试样发生显著变形，CFRP从拐角处逐渐断裂，开始与UHPC圆形短柱剥离；当试件加载至极限强度时，CFRP发出爆响，随即被拉断，试件强度急剧下降，此时，UHPC圆形短柱表面产生纵向裂缝，且裂缝贯通至整个试件，轴向应变和环向应变迅速增大，试件破坏.

由图3可知，随着FRP层数增加，其断裂面积逐渐减小. 钢纤维沿裂缝面被拔出，但由于钢纤维在UHPC内部多向分布，发挥了桥接作用，有效阻止了混凝土内部裂缝的扩大和延伸，因此，试件内部的UHPC并没有完全破碎. 钢纤维能够在一定程度上改善FRP约束UHPC圆形短柱的脆性破坏.

2.2 荷载-应变曲线

图4为FRP约束UHPC圆形短柱的荷载-应变曲线（应变大于0为轴向应变，小于0为环向应变）. 从图中可以看出，荷载-轴向应变曲线可分为3个阶段：在加载初期，各试件荷载-应变曲线的变化趋势基本相同，此时试件变形较小，FRP对UHPC圆形短柱产生的约束作用不明显，约束试件的荷载-轴向应变曲线与未约束试件的相似，均呈线性增长；随着荷载的进一步增大，UHPC圆形短柱中部开始膨胀，FRP产生的约束应力随之增加，试件的强度不断提高，此阶段的约束应力不断变化，试件的曲线呈非线性发展；在加载后期，FRP对UHPC圆形短柱的约束应力达到极限，试件的荷载-轴向应变曲线基本呈水平发展趋势，该阶段为试件的强化阶段，对比发现，FRP提高了UHPC圆形短柱的强度和变形能力.

图 4 FRP约束UHPC的荷载-应变曲线

Figure 4. Load-strain curves of FRP-confined UHPC

下载: 全尺寸图片幻灯片

FRP约束UHPC圆形短柱的荷载-环向应变曲线同样可分为3个阶段：在初期加载阶段，其与荷载-轴向应变曲线相似，FRP基本没有对试件产生明显的约束作用，曲线呈线性增长趋势，同时，各约束试件在此阶段的荷载-环向应变曲线基本重合，未受到FRP层数的影响；随着荷载的增加，约束试件的中部开始膨胀，环向应变的增长速率加快，同时，UHPC圆形短柱承受较大荷载，FRP的约束力不断增加，此阶段约束试件的荷载-环向应变曲线呈非线性增长；随着荷载的持续增加，FRP的约束应力达到极限，环向应变迅速增大，直至试件破坏.

2.3 荷载-应变曲线影响因素分析

2.3.1 约束比

定义FRP对UHPC圆形短柱的约束应力与无约束UHPC圆形短柱抗压强度的比值为约束比^[10]. 不同约束比下试件的承载及变形性能如表1和图4所示. 可以看出：试件C12、C22和C32的极限强度相较于C11、C21和C31分别提高了17.8%、25.4%和23.4%，极限应变分别提高了55.4%、71.2%和72.6%；试件G12、G22和G32的极限强度相较于G11、G21和G31分别提高了10.1%、9.1%和8.5%，极限应变分别提高了43.2%、31.1%和17.3%. 由此可得，随着FRP层数的增加，试件的轴向极限强度和极限应变均得到提高，但极限应变的提高幅度更加明显.

钢纤维体积掺量为1%时，被1层、2层和3层CFRP缠绕包裹的UHPC圆形短柱的极限强度比同条件下的GFRP缠绕包裹的分别提高了9.7%、7.8%和7.2%；钢纤维体积掺量为2%时，上述条件下试件的极限强度分别提高了17.3%、24%和21.9%，极限应变分别提高了38.1%、56.3%和64.8%. 可以看出，CFRP对UHPC圆形短柱极限强度和极限应变的改善程度要明显优于GFRP. 此外，FRP层数和种类的改变实质上反映的是约束应力的改变，由此可见，约束比是影响试件荷载-应变曲线的关键因素.

2.3.2 钢纤维体积掺量

不同钢纤维掺量下试件的极限强度及变形性能如表1和图4所示. 由不同钢纤维体积掺量下FRP约束UHPC圆形短柱的荷载-轴向应变曲线可知：随着钢纤维体积掺量的增加，荷载-轴向应变曲线在加载前期并没有受到影响；但在加载后期，试件的极限强度及极限应变均有一定幅度的提高. 而根据试件的荷载-环向应变曲线发现：钢纤维体积掺量为2%和3%时，试件在相同荷载下的环向应变明显比钢纤维体积掺量为1%的试件小，说明钢纤维的体积掺量越大，核心混凝土的极限强度和延性越大. 由此可知，随着加载荷载的增加，钢纤维在UHPC圆形短柱中产生了防止其自身横向膨胀的纤维约束力，在加载后期明显抑制了UHPC圆形短柱的横向变形；且钢纤维体积掺量越大，产生的约束作用越强.

3. FRP约束UHPC的本构模型

3.1 受力机理

在加载初期，FRP材料并未产生明显的约束作用. 随着荷载的持续增加，UHPC圆形短柱在受压状态下内部逐渐出现微裂纹，试件的变形逐渐增大并产生侧向膨胀，环向应变迅速增长，此时外包FRP开始参与工作，对核心混凝土提供有效约束，使核心混凝土处于三向受力状态，并限制其裂缝的产生和发展. 随着荷载继续增加，混凝土进入裂缝扩展阶段，其内部裂缝及侧向变形快速增大，FRP产生的约束应力不断提高，直至其达到极限抗拉强度，发生断裂，此时FRP约束UHPC圆形短柱的轴压荷载达到峰值. FRP约束UHPC圆形短柱受力状态如所示，图中： ${{f}}_{{\rm{ccc}}}、{{f}}_{{\rm{coc}}}$ （ ${{\varepsilon }_{{\rm{ccc}}}}、{{\varepsilon }_{{\rm{coc}}}}$ ）分别为约束试件、非约束试件的峰值应力（极限应变）， ${\sigma _{\rm{r}}}$ 为径向应力， $\sigma$ 为短柱的轴向应力， $\varepsilon$ 为短柱的环向应变.

图 5 FRP约束UHPC圆形短柱受力示意

Figure 5. Force of FRP-confined UHPC circular stub column

下载: 全尺寸图片幻灯片

3.2 抗压强度和极限应变计算公式

根据已有研究^[15-16]可知，FRP是高性能单向材料，抗拉不抗压，因此在理论分析时仅考虑FRP的环向抗拉强度. 当FRP达到其极限抗拉强度时，将不会再对混凝土产生约束作用^[17]，FRP约束UHPC圆形短柱时，其侧向受力均匀连续，如图6所示. 图中：f_f为FRP的极限抗拉强度，θ 为约束力方向与x轴之间夹角的大小.

图 6 约束力计算模型

Figure 6. Calculation model of constraining force

下载: 全尺寸图片幻灯片

根据平衡原理积分可得侧向约束力为

$\int_0^{\text{π}} d/2{{f_{\rm{l}}}\sin \;\theta } {\text{d}}\theta = 2{f_{\rm{f}}}t，$

(1)

式中：f_l为FRP对UHPC的约束力，如式（2）；d为UHPC 圆形短柱的直径；t为FRP的总厚度.

${f_{\rm{l}}} = 2{f_{\rm{f}}}t/d.$

(2)

考虑到钢纤维对UHPC圆形短柱轴压性能的影响，引入纤维约束力，如式（3）.

${f_{{\rm{lf}}}} = {\alpha _1}{V_{\rm{f}}}\frac{{{l_{\rm{f}}}}}{{{d_{\rm{f}}}}}{\tau _{{\text{bond}}}},$

(3)

式中： ${\alpha _1}$ 为纤维影响系数，取值参考文献[18]；V_f为钢纤维掺量；l_f为钢纤维的长度；d_f为钢纤维的直径；τ_bond为基体黏结强度.

通过改变试件的约束比及钢纤维体积掺量，研究其对试件峰值参数的影响，各试件的峰值荷载及其对应的轴向极限应变如表1所示. 以试件约束比（f_L/f_co，其中：f_L为FRP约束力f_l与钢纤维约束力f_lf之和，f_co为非约束柱的极限强度）为控制因素，通过对试验数据进行回归分析，得到FRP约束UHPC峰值应力及峰值应变拟合曲线，如图7所示.

图 7 拟合曲线

Figure 7. Fitting curves

下载: 全尺寸图片幻灯片

图7中：y=（f_ccc/f_coc）−1，x=f_L/f_coc，代入方程最终得FRP约束UHPC的极限抗压强度计算公式，如式（4）；y₁=（ɛ_ccc/ɛ_coc）−1，代入方程得到极限应变的计算公式，如式（5）.

${f_{{\text{ccc}}}}/{f_{{\text{coc}}}} = 1 + 2.{\text{45}}{\left( {{f_{\rm{L}}}/{f_{{\text{coc}}}}} \right)^{0.92}},$

(4)

${\varepsilon _{{\text{ccc}}}}/{\varepsilon _{{\text{coc}}}} = 1 + 21.75{\left( {{f_{\rm{L}}}/{f_{{\text{coc}}}}} \right)^{1.62}}.$

(5)

3.3 计算值与试验值对比分析

为更好地验证所提出模型的合理性，收集文献[10,19-20]中的试验数据进行验证. 表4为文献中FRP约束UHPC柱极限强度及峰值应变的计算值与试验值的对比，其中，f_cc和ɛ_cc分别为极限强度和极限应变的试验值.

表 4 试件极限强度和极限应变计算值与试验值对比

Table 4. Comparison between calculated and test results of ultimate strength and ultimate strain of specimens

参考文献	试件编号	V_f/%	f_cc/MPa	ɛ_cc	f_ccc/MPa	ɛ_ccc	f_ccc/f_cc	ɛ_ccc/ɛ_cc
文献[10]		2	130.7	0.0078	175.2	0.0082	1.340	1.047
		2	180.8	0.0116	217.2	0.0155	1.201	1.332
		2	148.8	0.0073	185.3	0.0097	1.245	1.325
		2	162.3	0.0094	211.1	0.0102	1.301	1.085
		2	156.5	0.0065	172.7	0.0078	1.103	1.202
		2	191.4	0.0104	211.8	0.0144	1.107	1.382
文献[19]		2	226.6	0.0086	264.8	0.0075	1.168	0.874
		2	273.5	0.0106	281.8	0.0090	1.030	0.853
		2	298.9	0.0115	298.2	0.0107	0.998	0.934
		2	254.1	0.0068	267.4	0.0077	1.052	1.138
		2	372.2	0.0105	319.7	0.0133	0.859	1.263
文献[20]	UHPC-1C	1	168.0	0.0068	178.1	0.0057	1.060	0.836
	UHPC-2C	1	180.8	0.0073	194.2	0.0071	1.074	0.970
	UHPC-3G	1	171.5	0.0076	195.0	0.0072	1.137	0.942
	UHPC-5G	1	182.0	0.0073	214.5	0.0094	1.178	1.291

下载: 导出CSV

| 显示表格

通过上述计算方法所得极限强度计算值与试验值比值的平均值与标准差分别为1.124和0.123，极限应变计算值与试验值比值的平均值与标准差分别为1.098和0.191，这表明计算方法得到的极限应力、极限应变的计算值与试验值较为吻合，考虑钢纤维体积掺量影响后所得的计算公式能够较好地预测FRP约束UHPC的峰值应力和应变.

3.4 本构模型

通过对已有模型分析，选用Mander^[21]本构方程作为FRP约束UHPC圆形短柱的主动约束模型，将f_cc和ɛ_cc代入Mander^[21]本构方程，以此得到FRP约束UHPC的本构模型，如式（6）所示.

$\sigma = {f_{{\text{cc}}}}x_{{\rm{c}}}r/(r - 1 + {x_{\rm{c}}^r})\text{，}$

(6)

式中：x_c = ɛ_c/ɛ_cc，ɛ_c为约束柱的轴向应变；r =E_c/（E_c−E_sec），E_sec为约束柱达到极限强度时的割线模量，E_sec =f_cc/ɛ_cc，E_c为UHPC的弹性模量.

从21个约束试件中选取6个试件，分别采用Lam模型^[22]、Zohrevand模型^[19]、邓宗才模型^[10]和本文建立的模型，计算得到相应的应力-应变全过程曲线，与试验结果进行对比，如图8所示.

图 8 应力-应变曲线对比

Figure 8. Comparison of stress-strain curves

下载: 全尺寸图片幻灯片

图8中：曲线的前期阶段，所有模型与试验结果无较大差异，后期阶段则差异化明显. 综合对比下，本文建立的模型与试验结果吻合程度较好.

4. 结　论

1）随着FRP层数的增加，UHPC圆形短柱的极限抗压强度和极限应变均提高，但极限应变的提高幅度更加明显. 试件C12、C22和C32的极限强度相较于试件C11、C21和C31分别提高了17.8%、25.4%和23.4%，极限应变分别提高了55.4%、71.2%和72.6%；试件G12、G22和G32的极限强度相较于试件G11、G21和G31分别提高了10.1%、9.1%和8.5%，极限应变分别提高了43.2%、31.1%和17.3%.

2）钢纤维可在一定程度上改善FRP约束UHPC圆形短柱的脆性特征；适量的钢纤维还可提高试件的极限抗压强度与极限应变. 试件C31的极限强度和极限应变比试件C21（C11）的分别提高了2.9%和15.1%（4.7%和50.0%）.

3）相同层数及钢纤维体积掺量下，CFRP对UHPC圆形短柱极限抗压强度和极限应变的提升幅度比GFRP更高. 试件C11、C12和C13的极限应变分别比试件G11、G12和G13的提高了27.3%、19.7%和12.0%.

4）分析了FRP约束UHPC圆形短柱的受力机理，在考虑钢纤维体对UHPC约束的影响下，提出了FRP约束UHPC圆形短柱抗压强度和极限应变的计算模型，并进一步给出了FRP约束UHPC的本构模型，计算结果与试验结果吻合较好.

图 1 高频分量功率谱与目标值的比较

Figure 1. Comparison of simulated PSD with the target

下载: 全尺寸图片幻灯片

图 2 高频分量均值和均方值与目标值的比较

Figure 2. Comparisons of simulated mean and standard deviation of high-frequency component with the exact one

下载: 全尺寸图片幻灯片

图 3 SDOF系统地震响应极值分布和累积概率分布

Figure 3. PDF and CDF of the SDOF system subjected to near-fault impulse ground motions

下载: 全尺寸图片幻灯片

图 4 SDOF系统地震响应超越概率

Figure 4. POE of the SDOF system seismic response

下载: 全尺寸图片幻灯片

图 5 3层框架结构示意

Figure 5. Schematic diagram of three-storey frame structure

下载: 全尺寸图片幻灯片

图 6 框架结构非线性地震响应极值分布

Figure 6. EVD of nonlinear seismic response of frame structures

下载: 全尺寸图片幻灯片

表 1 单自由度系统地震响应估计值与MCS的比较

Table 1. Comparison of estimated SDOF system seismic response with MCS

方法	μ	$\sigma '$	E(X ^(0.25))	E(X ^(1.20))
LHS	12.17	3.454	1.854 3	20.250 0
MCS（10⁵ 次）	12.05	3.424	1.849 7	20.000 0
相对误差/%	1.04	0.88	0.25	1.26

下载: 导出CSV

表 2 单自由度系统地震响应极值最大熵分布参数

Table 2. MaxEnt distribution parameters of SDOF system

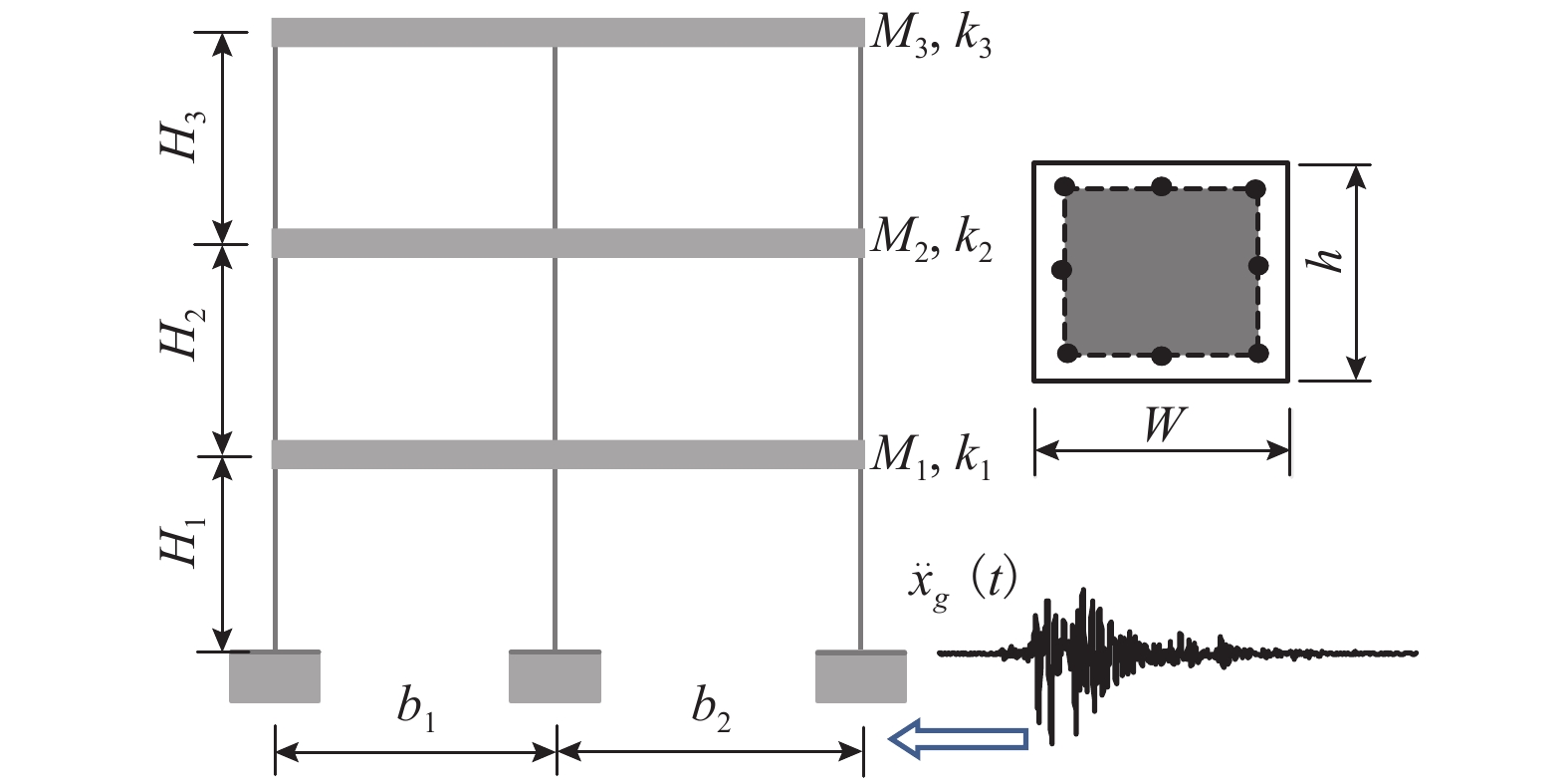
分布	r	λ_r	α_r	$M_X^{ {(\alpha _r)} }$	I（λ，α）
1	0	14.537 0
2	1	1.672 1	0.863 9	8.622 1	2.603 4
3	2	−13.279 3	0.303 9	2.119 4
4	3	86.647 8	−1.617 5	0.020 7

下载: 导出CSV

表 3 框架结构的集中质量和层间刚度

Table 3. Lumped mass and lateral inter-story stiffness of the frame

变量	均值	变异系数	分布类型
M₁	2.71 × 10⁵ kg		正态
M₂	2.71 × 10⁵ kg	0.10
M₃	2.71 × 10⁵ kg
k₁	2.42 × 10⁷ N/m
k₂	2.42 × 10⁷ N/m	0.15
k₃	2.42 × 10⁷ N/m

下载: 导出CSV

参考文献(22)

CHANG Z, SUN X, ZHAI C, et al. An improved energy-based approach for selecting pulse-like ground motions[J]. Earthquake Engineering & Structural Dynamics, 2016, 45(14): 2405-2411.

SOMERVILLE P G, SMITH N F, GRAVES R W, et al. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J]. Seismological Research Letters, 1997, 68(1): 199-222. doi: 10.1785/gssrl.68.1.199

郑史雄,陈志强,陈志伟,等. 近场多脉冲地震作用下高墩桥梁地震响应分析[J]. 西南交通大学学报,2019,54(5): 897-907.

ZHENG Shixiong, CHEN Zhiqiang, CHEN Zhiwei, et al. Seismic response analysis of high-pier bridge under near-fault multiple pulse record excitation[J]. Journal of Southwest Jiaotong University, 2019, 54(5): 897-907.

武芳文,孟园英,陈月,等. 大跨度斜拉桥地震易损性及可恢复性分析[J]. 西南交通大学学报,2020,55(1): 126-133.

WU Fangwen, MENG Yuanying, CHEN Yue, et al. Analysis of seismic fragility and recoverability of long-span cable-stayed bridge[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 126-133.

GRIGORIU M, SAMORODNITSKY G. Reliability of dynamic systems in random environment by extreme value theory[J]. Probabilistic engineering mechanics, 2014, 38: 54-69. doi: 10.1016/j.probengmech.2014.08.005

CHEN J B, LI J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters[J]. Structural Safety, 2007, 29(2): 77-93. doi: 10.1016/j.strusafe.2006.02.002

GOLLER B, PRADLWARTER H J, SCHUËLLER G I. Reliability assessment in structural dynamics[J]. Journal of Sound & Vibration, 2013, 332(10): 2488-2499.

MELCHERS R E. Importance sampling in structural system[J]. Structural Safety, 1989, 6(1): 3-10. doi: 10.1016/0167-4730(89)90003-9

AU S K, BECK J L. Subset simulation and its application to seismic risk based on dynamic analysis[J]. Journal of Engineering Mechanics, 2003, 129(8): 901-917. doi: 10.1061/(ASCE)0733-9399(2003)129:8(901)

XU J, DING Z, WANG J. Extreme value distribution and small failure probabilities estimation of structures subjected to non-stationary stochastic seismic excitations[J]. Structural Safety, 2018, 70: 93-103. doi: 10.1016/j.strusafe.2017.10.007

LOW Y M. A new distribution for fitting four moments and its applications to reliability analysis[J]. Structural Safety, 2013, 42(3): 12-25.

MICHAEL S. Large sample properties of simulations using latin hypercube sampling[J]. Technometrics, 1987, 29(2): 143-151. doi: 10.1080/00401706.1987.10488205

LI S, ZHANG F, WANG J, et al. Effects of near-fault motions and artificial pulse-type ground motions on super-span cable-stayed bridge systems[J]. Journal of Bridge Engineering, 2016, 22(3): 1-17.

YANG D, ZHOU J. A stochastic model and synthesis for near-fault impulsive ground motions[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(2): 243-264.

ZHANG X, PANDEY M D. Structural reliability analysis based on the concepts of entropy,fractional moment and dimensional reduction method[J]. Structural Safety, 2013, 43: 28-40. doi: 10.1016/j.strusafe.2013.03.001

XIONG F, GREENE S, CHEN W, et al. A new sparse grid based method for uncertainty propagation[J]. Structural & Multidisciplinary Optimization, 2010, 41(3): 335-349.

SOBCZYK K, TRCEBICKI J. Approximate probability distributions for stochastic systems:maximum entropy method[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 168(1/2/3/4): 91-111.

JAYNES E T. Information theory and statistical mechanics[J]. Physical Review, 1957, 106(4): 620. doi: 10.1103/PhysRev.106.620

CHEN B, HU J, ZHU Y. Computing maximum entropy densities:a hybrid approach[J]. Signal Processing:An International Journal(SPIJ), 2010, 4(2): 114.

MIRANDA E, RUIZ-GARCÍA J. Evaluation of approximate methods to estimate maximum inelastic displacement demands[J]. Earthquake Engineering & Structural Dynamics, 2010, 31(3): 539-560.

IWAN W D. Estimating inelastic response spectra from elastic spectra[J]. Earthquake Engineering & Structural Dynamics, 2010, 8(4): 375-388.

欧进萍, 王光远. 结构随机振动[M]. 北京: 高等教育出版社, 1998: 295-303.

施引文献

附加材料(0)

访问统计

点击查看大图

图(6) / 表(3)

计量

文章访问数: 694
HTML全文浏览量: 380
PDF下载量: 21
被引次数: 0

1. 试验方案
1.1 试件设计
1.2 材料性能
1.3 加载方案及测点布置
2. 试验结果及分析
2.1 试件破坏特征
2.2 荷载-应变曲线
2.3 荷载-应变曲线影响因素分析
3. FRP约束UHPC的本构模型
3.1 受力机理
3.2 抗压强度和极限应变计算公式
3.3 计算值与试验值对比分析
3.4 本构模型
4. 结　论

1. 试验方案
1.1 试件设计
1.2 材料性能
1.3 加载方案及测点布置
2. 试验结果及分析
2.1 试件破坏特征
2.2 荷载-应变曲线
2.3 荷载-应变曲线影响因素分析
3. FRP约束UHPC的本构模型
3.1 受力机理
3.2 抗压强度和极限应变计算公式
3.3 计算值与试验值对比分析
3.4 本构模型
4. 结　论

参考文献(22)

施引文献

附加材料(0)

访问统计

桥梁结构非线性地震响应极值分布的估算方法

doi: 10.3969/j.issn.0258-2724.20180948

作者简介: 陈志强（1993—），男，博士研究生，研究方向为桥梁抗风抗震， E-mail：zhqchen163@163.com

通讯作者: 郑史雄（1965—），男，教授，研究方向为桥梁抗风抗震，E-mail：zhengsx@home.swjtu.edu.cn

计量

出版历程