离散单元法（DEM）由Cundall等提出^[1]，目前广泛应用于节理边坡^[2]、隧道工程^[3-4]、山体滑坡^[5]、泥石流^[6]、浅基础承载力^[7]等方面的数值计算. 与有限元法和有限差分法不同，离散元法可以模拟开裂、分离等非连续现象，从微观尺度了解土体的力学机理，建立土体微观结构与宏观力学现象之间的联系. 颗粒流软件PFC （particle flow code）是基于离散单元法开发的商业软件^[8]，国内外的学者通过标定PFC模型的细观参数，使之与土体宏观力学参数相对应，进而应用于大量工程问题的模拟计算与分析^[9-14]. 使用DEM模拟土体时，试样的孔隙比和均匀性会对计算结果产生影响. 例如，DEM模拟边坡降雨入渗时，孔隙比将影响土体的渗透系数和土颗粒之间的基质吸力^[15-19]. 在研究土体抗剪强度时，土体的孔隙比对DEM中双轴试验的模拟结果产生影响^[8]. 此外，Ng等^[20]指出侧向土压力系数K₀与孔隙比具有非线性的函数关系，且K₀与孔隙比的变化对钻孔竖井的侧向摩阻力产生影响. 因此，研究不同制样方法对岩土工程问题模拟计算结果的影响具有重要意义.

浅基础承载力是岩土工程中的重要问题^[17-19]，目前已有许多学者使用DEM研究浅基础承载力问题：Wang等^[21]利用PFC^2D模拟加筋土体基础承载力试验，将未加筋与加筋土承载力进行对比，分析得出两层加筋土能够显著提高边坡承载力，且在微观上分析了土与土工格栅之间力的传递行为；Fu等^[22]模拟了浅板载荷试验，研究了基础的承载力、破坏模式和尺寸效应，讨论了基础的粗糙程度对承载力的影响及土体破坏面的变化；Xu等^[23]从微观探究浅基础加压过程中土体稳定力链的变化过程，发现了从加载板传递的荷载力链随着加压呈梯形逐渐增大，且稳定力链结构也会逐渐增加直到趋于稳定；Cha等^[24]通过逐渐减小颗粒的大小来研究矿物溶解对浅基础承载力的影响，分析得出在基础底部的矿物溶解对承载力影响最大；蒋明镜等^[25]模拟4种宽度的载荷试验，研究地基的尺寸效应，发现土体强度包线的非线性并不是导致尺寸效应的原因.

由于DEM中不同的制样方法将导致试样孔隙比和均匀性的不同，进而对承载力的计算结果产生影响，而以往的研究尚未系统分析DEM中不同制样方法的影响，因此本文在2D条件下使用DEM中常用的4种方法：粒径放大法^[23]、Distribute法^[8]、GM法 （grid method）^[22-27]和欠层压实法^[28]制备目标孔隙比e=0.2的无黏性砂土，通过分析试样孔隙比、K₀值和均匀性等因素，研究不同方法对浅基础承载力模拟计算结果的影响. 为便于描述，本文将粒径放大法、Distribute法、GM法和欠层压实法生成的试样分别命名为L-S、D-S、G-S、Q-S. 本研究中，试样在10g的重力作用下模拟离心试验以提高计算效率，利用测量圆得到土体的孔隙比、水平应力、竖向应力和K₀值^[23]，并进行浅基础承载力试验来探究不同制样方法对浅基础承载力的影响. 条形浅基础承载力通常被假设为平面应变问题^[29]. 理论上，在平面应变问题中，垂直于分析平面的应力不为0，但DEM 2D中对垂直于模型平面方向上的应力和应变均不予以考虑^[8]. 虽然同样的制样方法在2D条件下得到的试样e和K₀会比3D条件更小，同时偏应力状态和配位数也和3D条件存在一定差异，但是这些指标整体趋势相同^[23]. 此外，由于计算条形浅基础极限承载力时需要考虑尺寸效应（基础与模型边界之间设置足够的宽度）和粒径效应（土样粒径与基础宽度的比例不能过大）^[30-33]，因此，考虑到模型的计算效率，与多数使用DEM计算浅基承载力的研究^[22-24]一样，本文在2D条件下对浅基础承载力问题进行建模计算.

1.   模型建立与细观参数选取

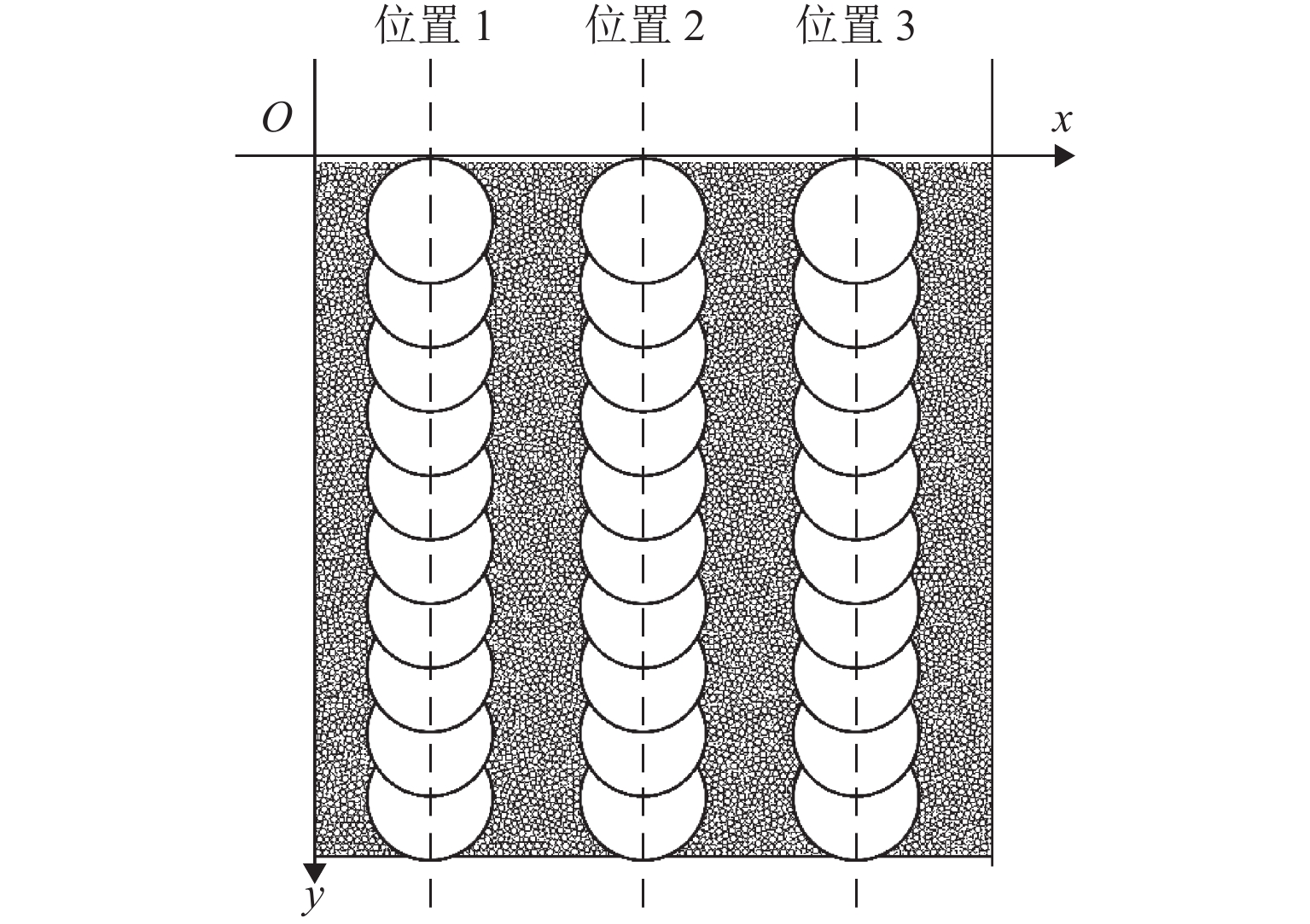
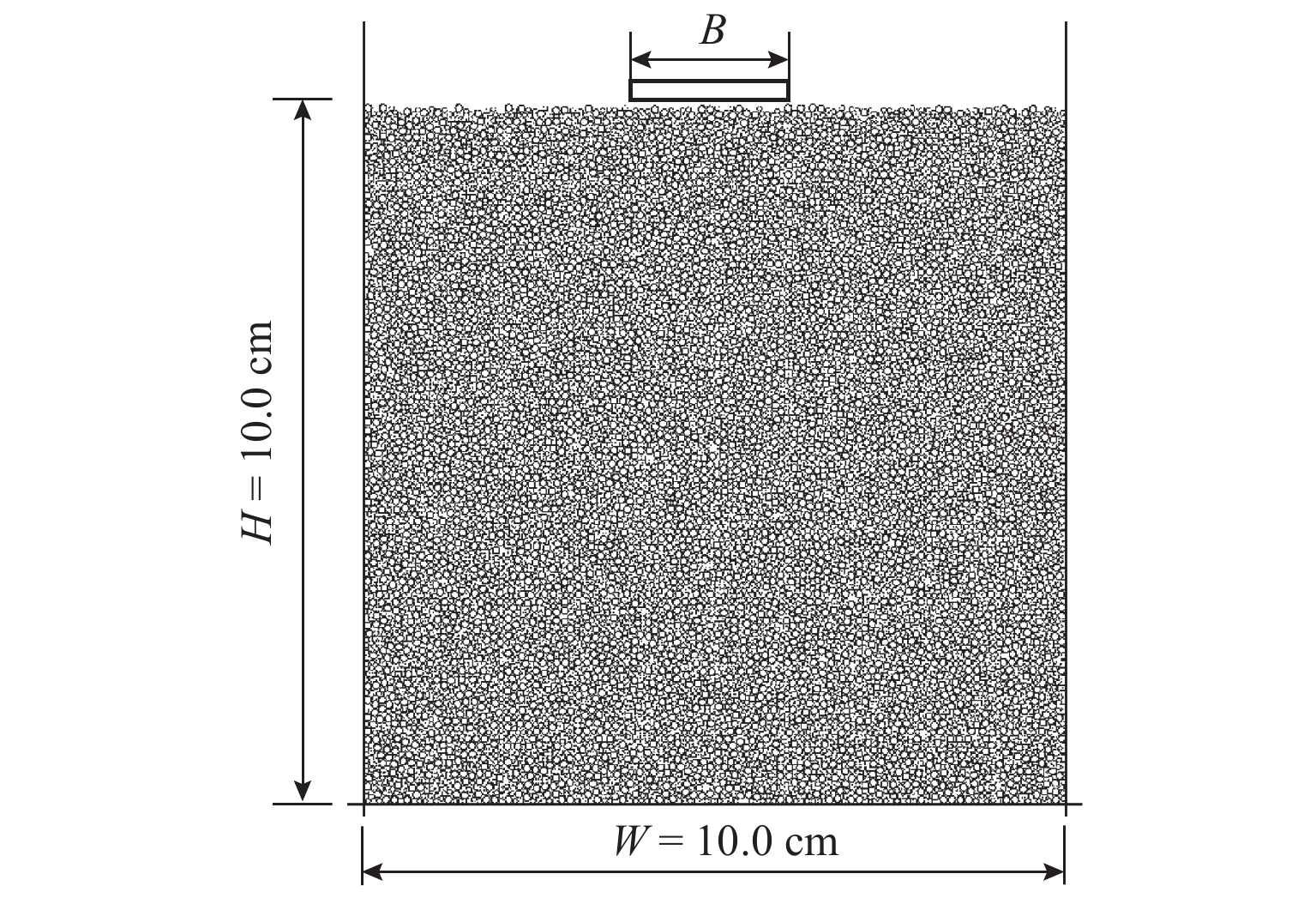
如图1所示，本文在矩形盒中生成高度H=0.1 m、宽度W=0.1 m的试样，并且在x=0.02，0.05，0.08 m处分别设置3列半径相同的测量圆来获得土体不同位置的孔隙比和应力分布. 细观参数如表1所示，已有研究^[23]表明，DEM生成密样时须设置较小的摩擦系数使试样更加致密，因此，本文将初始摩擦系数设置为μ₁=8.7 × 10⁻⁴. 砂土颗粒自重平衡后的摩擦系数μ₂一般为0～1，且较大的摩擦系数可以模拟更大的宏观内摩擦角^{[5,22-23,34-35]}，本文根据已有研究设置μ₂=0.839^[23]. 墙体与颗粒间摩擦系数μ₃设置为0.

图  1  DEM模型

Figure  1.  Model of DEM

下载: 全尺寸图片 幻灯片

表  1  模型细观参数

Table  1.  Microscopic parameters of the model

参数	值
粒径/mm	0.8～1.2
颗粒密度/（kg•m−3）	2650
初始孔隙比	0.2
颗粒法向刚度 kn/ （N•m−1）	5 × 107
颗粒切向刚度 ks/ （N•m−1）	2.5 × 107
墙体法向刚 knw/ （N·m−1）	1 × 109
墙体切向刚 ksw/ （N•m−1）	1 × 109
初始摩擦系数 μ1	8.7 × 10−4
最终摩擦系数 μ2	0.839
墙体与颗粒摩擦系数 μ3	0

下载: 导出CSV 

| 显示表格

本文使用到的4种制样方法和步骤简要介绍为

1） 粒径放大法：颗粒半径先缩小一定比例随机分布在指定区域，颗粒间没有接触和重叠，最后颗粒尺寸放大数次到原始尺寸，弹开平衡后得到初始试样. 其中放大次数过少会导致初始应力过大，过多会使计算效率降低，因此本文将放大次数设置为5次^[8].

2） Distribute法：颗粒可按照一定级配及孔隙率随机分布在指定区域，颗粒间允许重叠. 虽然Distribute法在制样时可能会导致初始条件下试样存在较大的法向接触力，但该方法可以迅速生成大量级配的颗粒，在生成颗粒簇clump中具有优势，且平衡时间较快^[8,36-37]. 也有研究通过伺服的方式释放颗粒间的内应力^[23,38]，但整个过程耗时长，且边界墙的位置会发生变化从而改变原有模型设定的边界条件，同时试样的均匀性也会受到影响. 因此本文采用未伺服的Distribute法用于对比研究.

3） GM法：在指定区域分成n × n个方块，每个方块由4个互相垂直的墙面组成，生成方块的顺序由左至右，由下至上. 从左下角的第一个方块生成一定孔隙率的颗粒，弹开平衡后在第二个方块生成颗粒，以此类推，最后将所有方块的墙面删除，重力平衡后得到试样. 其中方块的数量和大小可能会对制样结果造成影响，根据已有的研究^[27]，本文将方块设置为10 × 10=100个方块. 由于GM法分多次生成颗粒并进行平衡，在这个连续的过程中释放了内应力，克服了Distribute法生成颗粒造成的内应力过大的问题，但制样时间会较长，实现步骤较复杂.

4） 欠层压实法：先将试样分成m层，按照分层欠压理论选择合适欠压比，在指定区域随机生成无重叠的圆形颗粒，固定侧墙和底墙，以恒定速率向下移动顶墙，达到第一层孔隙比后，在第一层上部指定区域生成第二层颗粒，重复第一层制样过程，直至m层成样结束. 该方法中分层数量和欠压比可能会对制样结果产生影响，根据已有经验^[28]，本文将层数分为10层，第一层的初始欠压比U_n0设置为11.6. 欠层压实法制样过程耗时比粒径放大法和Distribute法久，但略快于GM法.

2.   不同制样方法所得土体的孔隙比和均匀性对比

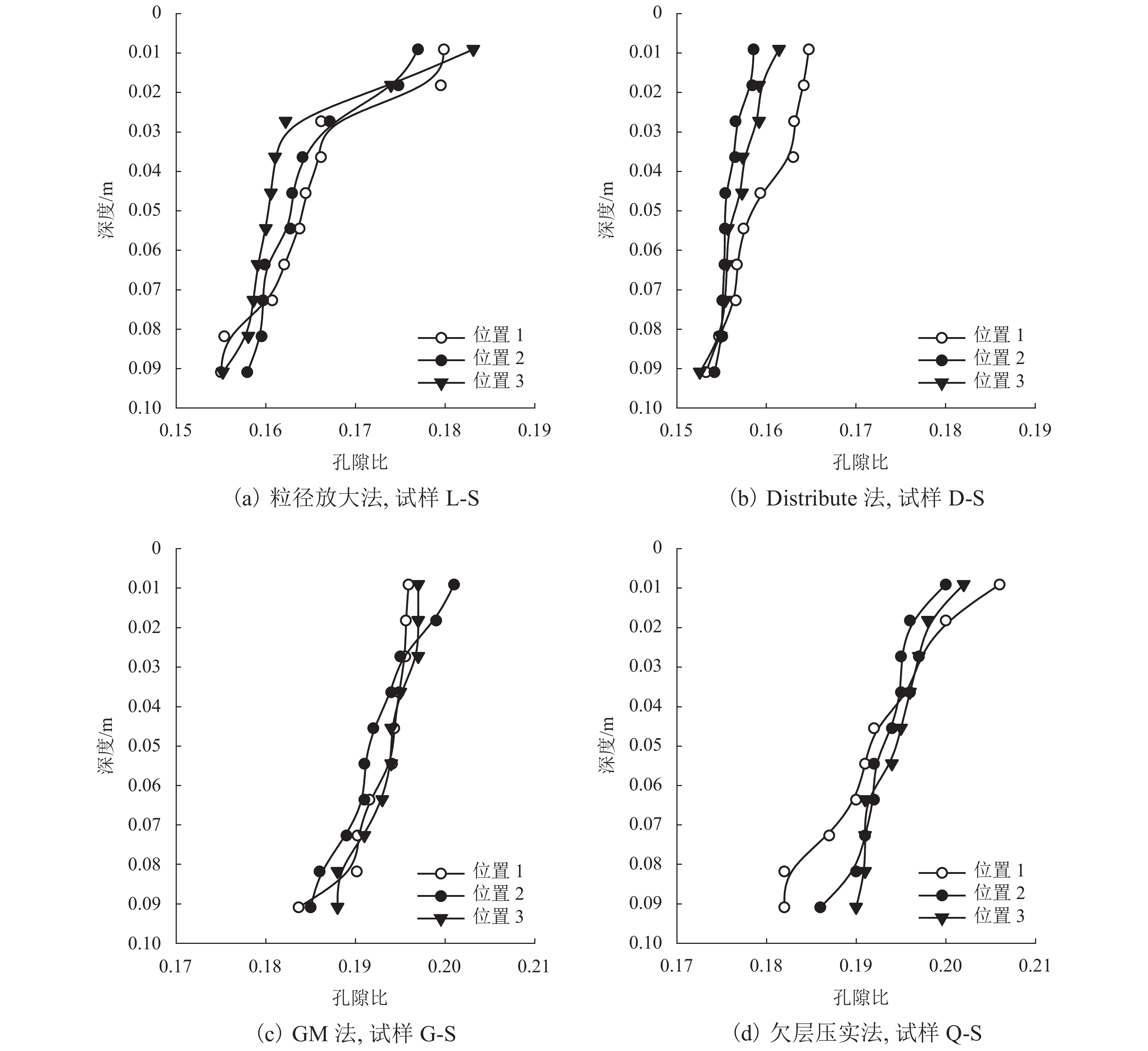
2.1   竖直方向孔隙比分布

如图2所示，4种方法所制备的土体均呈孔隙比随深度的增大而减小的趋势，其中L-S、D-S、G-S、Q-S的平均孔隙比分别为0.164、0.157、0.194、0.193. 由图2可以看出：GM法和欠层压实法更接近目标孔隙比值（0.2），差异为3.5%；粒径放大法和Distribute法得到的试样平均孔隙比更小；L-S在较浅深度时孔隙比的变化趋势较其他3种方法更大，反映出试样L-S在竖直方向的均匀性劣于另外3种试样，原因可能在于使用粒径放大法制样时，在浅层放大后的颗粒重叠比深层的颗粒大，导致平衡时颗粒初始应力较大，使得浅层土体的孔隙比变化较大.

图  2  位置1～3土体孔隙比随深度变化

Figure  2.  Variation of soil void ratio with depth in location 1−3

下载: 全尺寸图片 幻灯片

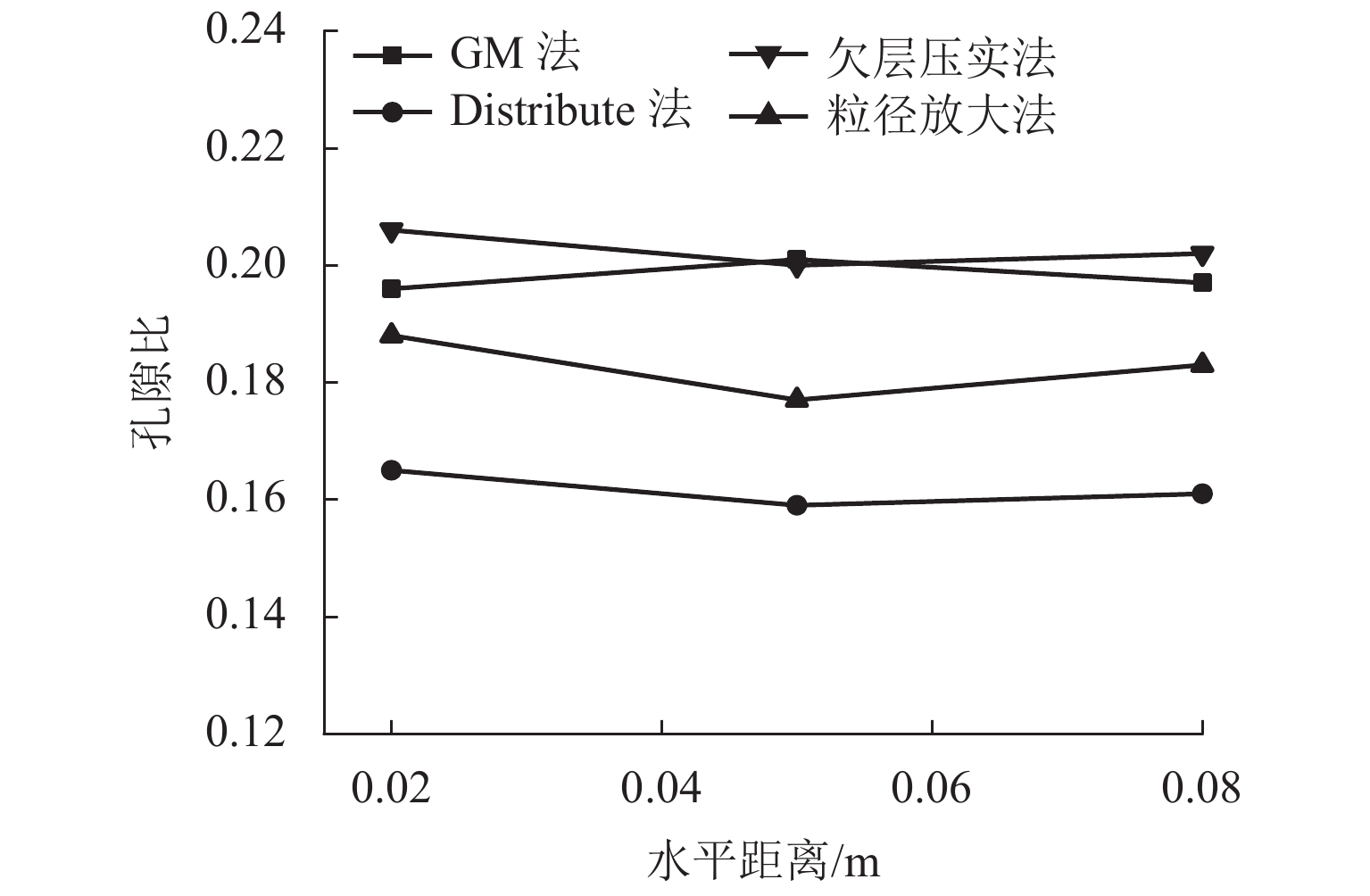
2.2   水平方向孔隙比分布

如图3所示，在深度为0.01 m时，获得4种试样在水平方向孔隙比的分布情况. 通过计算得出试样L-S孔隙比与目标孔隙比相差11.5%，且在不同水平距离孔隙比波动较大，均匀性较差；试样D-S孔隙比在0.16附近，与目标孔隙比相差20.0%，水平方向孔隙比波动较小，在水平方向均匀性较好；试样G-S孔隙比比目标孔隙比偏小，最大误差为2.0%，在水平距离x=0.05 m时误差最小，为0.5%；试样Q-S孔隙比比目标孔隙比偏大，最大误差为3.0%，在x=0.05 m时误差最小，为0.1%. 4个试样的平均孔隙比从大到小依次为Q-S > G-S > L-S > D-S.

图  3  深度0.01 m时水平方向孔隙比

Figure  3.  Horizontal porosity ratios at 0.01 m depth

下载: 全尺寸图片 幻灯片

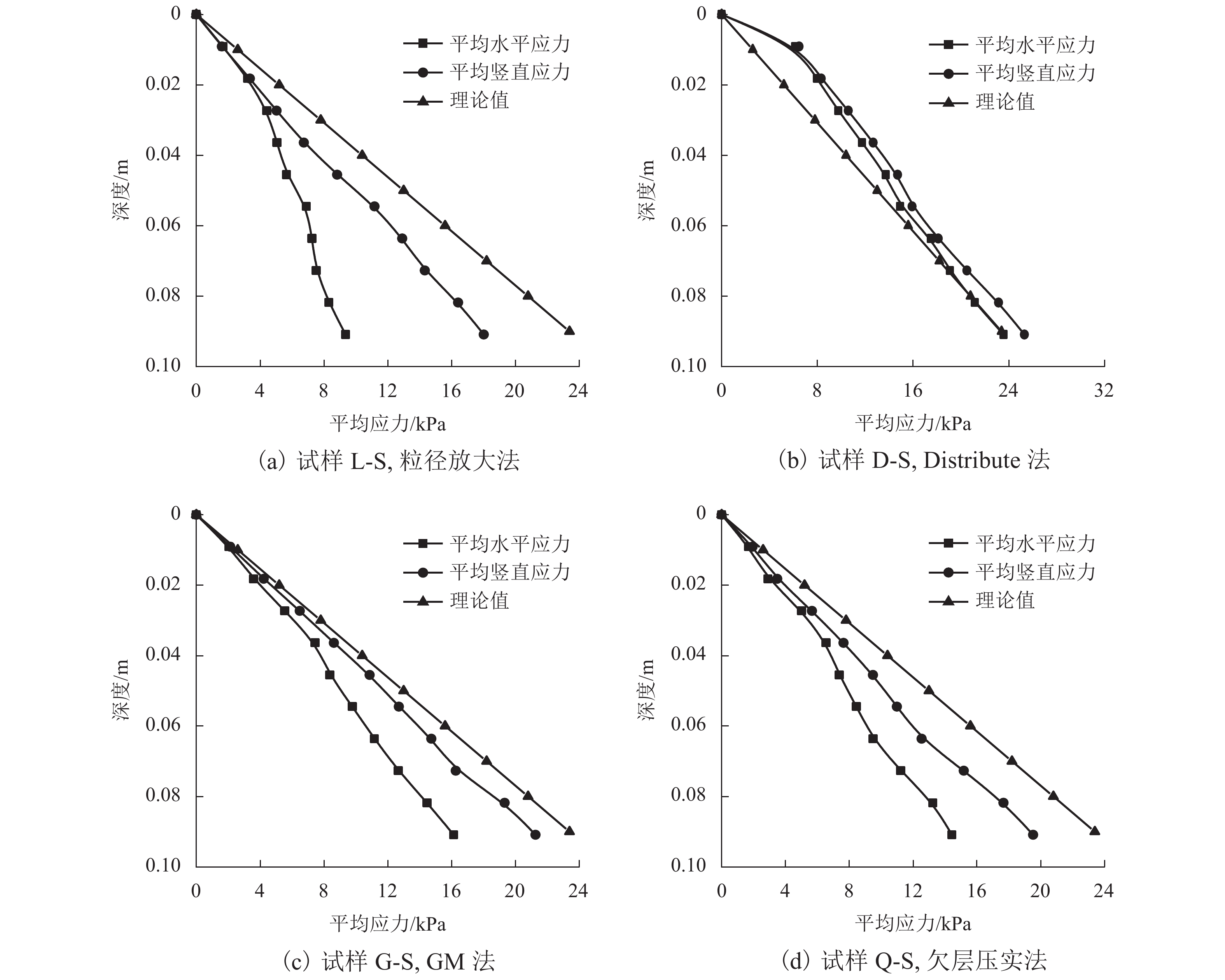
2.3   平均应力分布

利用测量圆从试样L-S、D-S、G-S、Q-S中分别得到不同深度的水平和竖向应力并求其平均值. 如图4所示，地应力平衡后，4个试样的水平和竖向应力符合随深度的增加而增大的趋势且大致呈线性分布. 其中试样L-S、G-S、Q-S的竖向应力略小于理论值，而D-S的水平和竖向应力均大于理论值. 出现两种相反结果的原因在于Distribute法相比于其他3种制样方法在最初制样过程中会产生较大的内应力，致使颗粒间横向和竖向应力均大于理论值. 对比已有的研究可以看出，以上制样方法得到试样的K₀值在合理范围内，但较小的K₀值更符合真实的砂土材料^[26-27].

图  4  位置1～3土体平均水平应力与竖向应力分布

Figure  4.  Distribution of average horizontal and vertical stresses of soil in location 1−3

下载: 全尺寸图片 幻灯片

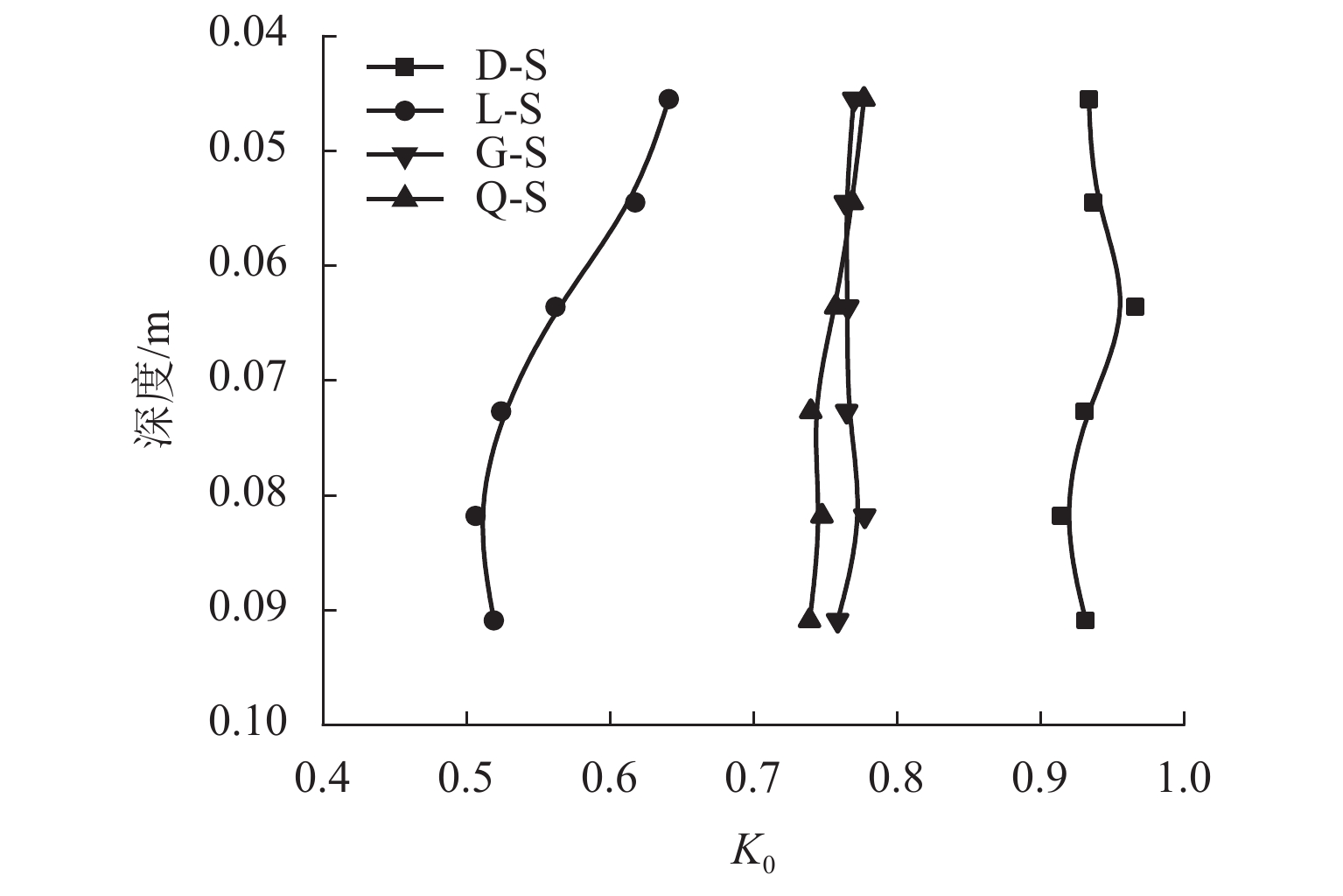
图5描述了试样在不同深度K₀的分布情况^[26]，其中K₀大致随着深度的增大而减小，K₀平均值从小到大排序依次为：L-S < Q-S < G-S < D-S. 本文利用方差来描述不同制样下K₀在不同深度的离散程度，方差从小到大排列依次为：G-S（0.006） < Q-S（0.014） < D-S（0.015） < L-S（0.051）. 方差不同的原因在于制样方法的不同导致K₀的不稳定，其中，L-S的K₀在较深的深度变化较大，可能是制样过程中颗粒在竖直方向的重叠量比水平方向的重叠量更大，使得深处的K₀值变小的趋势比其他3种制样方法制备的试样大. 综合对K₀的分布和砂土材料的真实情况，试样的均匀性由好到劣依次为：G-S、Q-S、L-S、D-S.

图  5  不同深度下试样K₀分布

Figure  5.  Distribution of K₀ at different depths

下载: 全尺寸图片 幻灯片

3.   不同制样方法所得土体的浅基础承载力计算结果分析

为得出有关不同制样方法对浅基础承载力计算结果影响的一般性规律，基于理想砂土模型^[22]，采用DEM中不会产生变形的墙体单元模拟浅基础，考虑到计算效率，许多研究将模型尺寸限制在一定范围^[22-24]，故本文中浅基础宽度B设置为2 cm，高度为0.2 cm，如图6所示. 其中B/d=20（d为平均粒径），H/B=5，B/W=5，因此可以忽略试验中颗粒的尺寸效应和粒径效应 ^[33-36]. 根据已有的有关基础宽度对地基承载力的影响研究^[22]，本文得到的计算结果可以为计算不同宽度浅基础承载力提供参考. 在计算过程中，将基础沉降深度S与B的比值即S/B=0.1作为极限承载力，设置基础的加载速度为2 mm/s.

图  6  浅基础离散元模型

Figure  6.  DEM model of shallow foundation

下载: 全尺寸图片 幻灯片

表2统计了不同制样方法所得试样对应的e、均匀性和承载力. 根据前文分析所得的试样e和K₀随深度变化的分布情况，试样均匀性的良好程度如表2所示，从上到下依次排列，即G-S > Q-S > D-S > L-S. 同时可以看出，平均孔隙比较小的试样承载力较大，即极限承载力的关系为D-S > L-S > Q-S > G-S. 在平均孔隙比相近的情况下，K₀和均匀性的不同可能是导致承载力变化的原因. 如表2所示，试样G-S与Q-S 对应的e非常接近（相差约0.5%），但承载力相差约4.0%，这一差异可能是由K₀ （G-S比Q-S 小2.7%），尤其是均匀性的差异导致. 相对而言，试样G-S与D-S对应的K₀值比较接近时（相差10.5%），D-S的e比G-小23.6%，但承载力大了51.6%. 综上可以分析得出：试样e比较接近时，K₀越大，承载力越大；K₀有一定差异时，e越小会使得承载力更大，即e对试样承载力影响占主导地位.

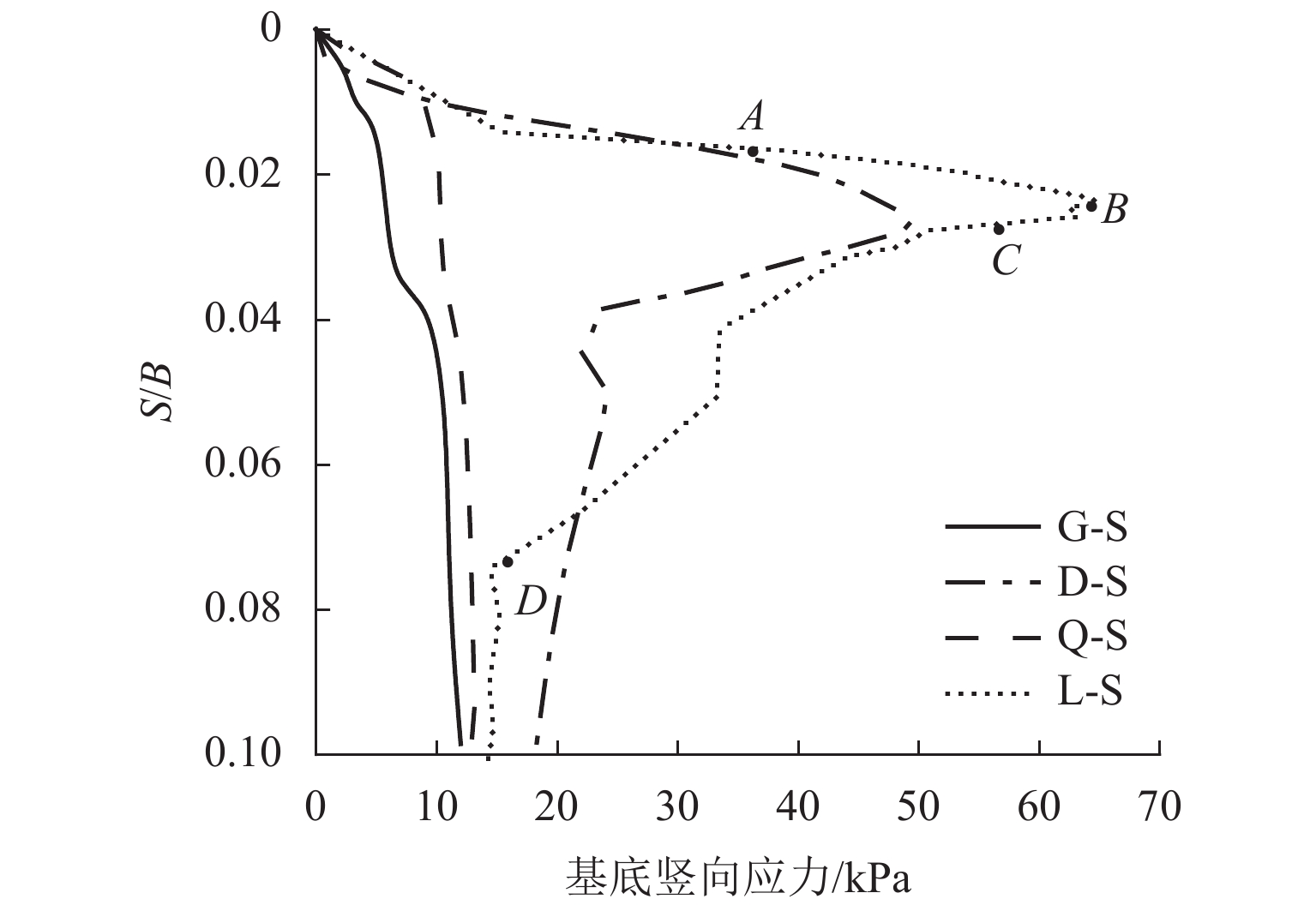
表  2  试样的极限承载力

Table  2.  Ultimate bearing capacity of samples

制样方法	试样	e	均匀性	极限承载力/kPa
GM 法	G-S	0.194	1	12.00
欠层压实法	Q-S	0.193	2	12.50
Distribute 法	D-S	0.157	3	18.19
粒径放大法	L-S	0.164	4	14.30

下载: 导出CSV 

| 显示表格

不同制样方法对浅基础承载力模拟的影响还体现在荷载-位移曲线中的破坏过程. 由图7可知，本文所分析试样对应的加载过程可以分为两种：第一种为e较大的试样（即G-S和Q-S）呈现出的破坏过程，由于试样的e较大，浅基础在加载过程中试样逐渐压实，其荷载随着位移的增加逐渐增大，直至S/B = 0.1时承载力并未出现明显的极值点；第二种为e较小的试样（即D-S和L-S）呈现的破坏过程. 以L-S为例，其破坏过程分为4个阶段，首先是从初始位置至点A为土体压缩阶段，承载力近似呈直线上升；AC为剪切阶段，其中AC间出现承载力的峰值点B；CD段为土体软化阶段，期间承载力急剧下降；D点过后是残余阶段，土体的残余强度逐渐趋于稳定. 这种破坏过程也曾在前人使用DEM进行浅基础承载力模拟计算的研究中被观察到^[39]. 试样D-S 与L-S的K₀值相差44.0%，孔隙比相差4.5%，浅基础的破坏过程没有发生改变；而试样D-S与Q-S的K₀值相差11.7%，孔隙比相差23.0%，此时试样Q-S浅基础的破坏过程与D-S 截然不同. 由此推断出孔隙比对加载过程的变化起到关键作用.

图  7  荷载-位移曲线

Figure  7.  Load-displacement curves

下载: 全尺寸图片 幻灯片

从微观层面分析试样的受力也可以解释图7中不同试样的位移-荷载曲线变化过程. 图8显示了不同制样方法在浅基础加载过程中颗粒间接触力链的分布情况. 对比图7、8可知：1） D-S和L-S在加载过程中力链呈现出弱−强−弱的过程：接触力链首先在基础底部逐渐增加、变密（如图8（a）①、②），随后在基础底部形成多条强力链，此时浅基础承载力达到峰值（图8（a）③），之后强力链转变为弱力链，且力链数量开始逐渐减少、变疏，对应软化阶段和残余阶段（图8（a）③、④）. 这一加载过程的力链变化，对应了D-S和L-S承载力的变化过程（图7）. 2） G-S与Q-S力链的演变过程也与其承载力的破坏过程（图7）相对应：首先基础底部接触力链迅速增加、变密（图8（c）①、②），与D-S和L-S力链变化过程不同，试样G-S与Q-S基础底部没有生成明显的强力链，且力链的数量在缓慢增加，没有出现减少的趋势（图8（c）③、④），对应图7中试样Q-S承载力缓慢增大的过程（无明显极值点）.

图  8  加载过程中力链分布

Figure  8.  Distribution of force chain during loading

下载: 全尺寸图片 幻灯片

4.   结　论

本文使用DEM系统地对比了Distribute法、粒径放大法、GM法和欠层压实法，为后续有关研究提供便捷合理的制样参考，避免繁琐的调试过程，并对不同制样方法生成试样的孔隙比、K₀值和均匀性进行分析，探究了不同制样方法对浅基础承载力模拟计算的影响，得到以下结论：

1） DEM中4种制样方法对制备一定孔隙比和均匀性的试样具有影响，经过一次制样后，GM法和欠层压实法制备的试样的孔隙比能更好地接近目标孔隙比，差异为3.5%；Distribute法和粒径放大法会使试样的最终孔隙比小于目标孔隙比，差异分别为20.0%和11.5%. 因此，在考虑浅基础承载力问题时，所选制样方法优先考虑GM法和欠层压实法.

2） 不同试样中，e的不同对承载力的影响最为明显，即e越小承载力越高. 4个试样的侧向土压力系数K₀值均小于1，其中不同试样K₀最大相差约44.0%. 一般情况下，DEM制备试样的平均竖向应力会略小于理论值. e非常相近的试样在浅基础承载力试验中，K₀值越大，承载力越大.

3） 由于不同制样方法得到的4种试样的e不同，在DEM浅基础承载力模拟计算中，地基的破坏过程会因孔隙比的变化呈现出两种不同模式，其中e较小的试样在破坏过程中承载力具有明显的峰值，力链呈现弱−强−弱的过程；e较大的试样在破坏过程中没有明显的极值点，且力链从开始迅速增加、变密，随后缓慢增长，直至破坏.