Modeling and Characteristic Analysis of an Electromagnetic Isolation System with High Static Stiffness and Low Dynamic Stiffness
-
摘要:
为改善传统线性隔振系统尺寸参数确定后就无法取得更低起始隔振频率的缺陷,基于电磁线圈嵌套永磁体结构,提出一种具有高静-低动刚度特性的电磁式可变刚度隔振系统. 采用分子电流法建立隔振系统磁力的数学模型;充分考虑隔振系统力学模型中二次与三次非线性刚度项的影响,建立单自由度被动隔振系统强非线性动力学模型;采用增量谐波平衡法(IHB)求解动力学模型,分析激励、电流等对隔振系统位移传递率的影响规律;构建实验测试系统,验证所提出新型隔振系统的有效性. 实验结果和理论计算表明:通入电流比未通入电流时隔振系统的起始隔振频率降低了19.25%,拓宽了隔振频带,实现了其对不同振源的适应性.
Abstract:Traditional linear vibration isolation system fails to achieve a lower initial vibration isolation frequency after setting the dimensional parameters. To address this issue, this article presented an electromagnetic vibration isolation system with variable stiffness based on the structure of a permanent magnet nested in an electromagnetic coil. To be specific, the system was characterized by high static stiffness and low dynamic stiffness. The mathematical model of the magnetic force of the system was created using the molecular current method. In addition, the strongly nonlinear dynamic model of the single-degree-of-freedom passive vibration isolation system was established by fully considering the quadratic and cubic nonlinear stiffness terms in the mechanical model of the vibration isolation system. The article used the incremental harmonic balance (IHB) method to solve the dynamic model and analyze the influence of excitation, current, and other factors on the displacement transmissibility of the system. An experimental test system was then created to validate the effectiveness of the proposed vibration isolation system. The experimental results and theoretical calculation demonstrate that the initial vibration isolation frequency of the system is reduced by 19.25% after introducing the current. This expands the frequency range of vibration isolation and improves system adaptability to different vibration sources.
-
高承载能力和低固有频率之间的矛盾是低频隔振技术发展的瓶颈[1-3]. 具有高静-低动刚度特性的非线性隔振系统可以很好地解决上述问题. Carrella等[4-5]将一个垂直弹簧与2个倾斜弹簧并联,当承载质量偏离平衡位置时,倾斜弹簧产生的负刚度与垂直弹簧的正刚度抵消,构建了具有高静-低动刚度特性的隔振系统;周加喜等[6]采用滚轮-凸轮结构设计了一种非线性隔振系统,当凸轮离开平衡位置,带有滚轮的水平弹簧与凸轮组成的机构在竖直方向产生负刚度,从而抵消竖直弹簧的正刚度. 上述方式往往存在布局、结构相对较大,一旦结构尺寸固定,起始隔振频率也就固定,无法对不同振源做出适应性调整的问题[7-10]. 除此之外,目前还有采用欧拉梁或气动弹簧产生负刚度来构建非线性隔振系统[7-8].
近年来,随着永磁材料性能的提升,采用永磁材料间的非线性力学特性构建具有高静-低动刚度特性的隔振系统,受到越来越多的重视. 李爽等[11]利用双环永磁体结构提出一种具有高静-低动刚度特性的隔振器,双环永磁体提供负刚度,与机械弹簧产生的正刚度抵消. Zhou等[12-13]使用2块电磁铁与一块永磁铁设计了一种磁力弹簧机构,通过调节电磁铁的电流大小与方向实现了磁力弹簧负刚度可调节.
借鉴上述方式的优点,本文提出一种利用永磁体结合空心电磁线圈,构建具有高静-低动刚度特性的非线性隔振系统,采用永磁体直接构建正负刚度,且提供轴向的承载力,通过改变电磁线圈中的电流大小、方向来改变结构中的电磁磁通,从而调节系统轴向刚度,以达到改变起始隔振频率的目的,且该系统结构更紧凑. 采用增量谐波平衡法求解该系统的位移传递率,考虑了传统方法分析二次非线性项较困难的问题[14],并分析了线圈电流变化对系统位移传递率的影响.
1. 隔振系统结构与工作原理
1.1 结 构
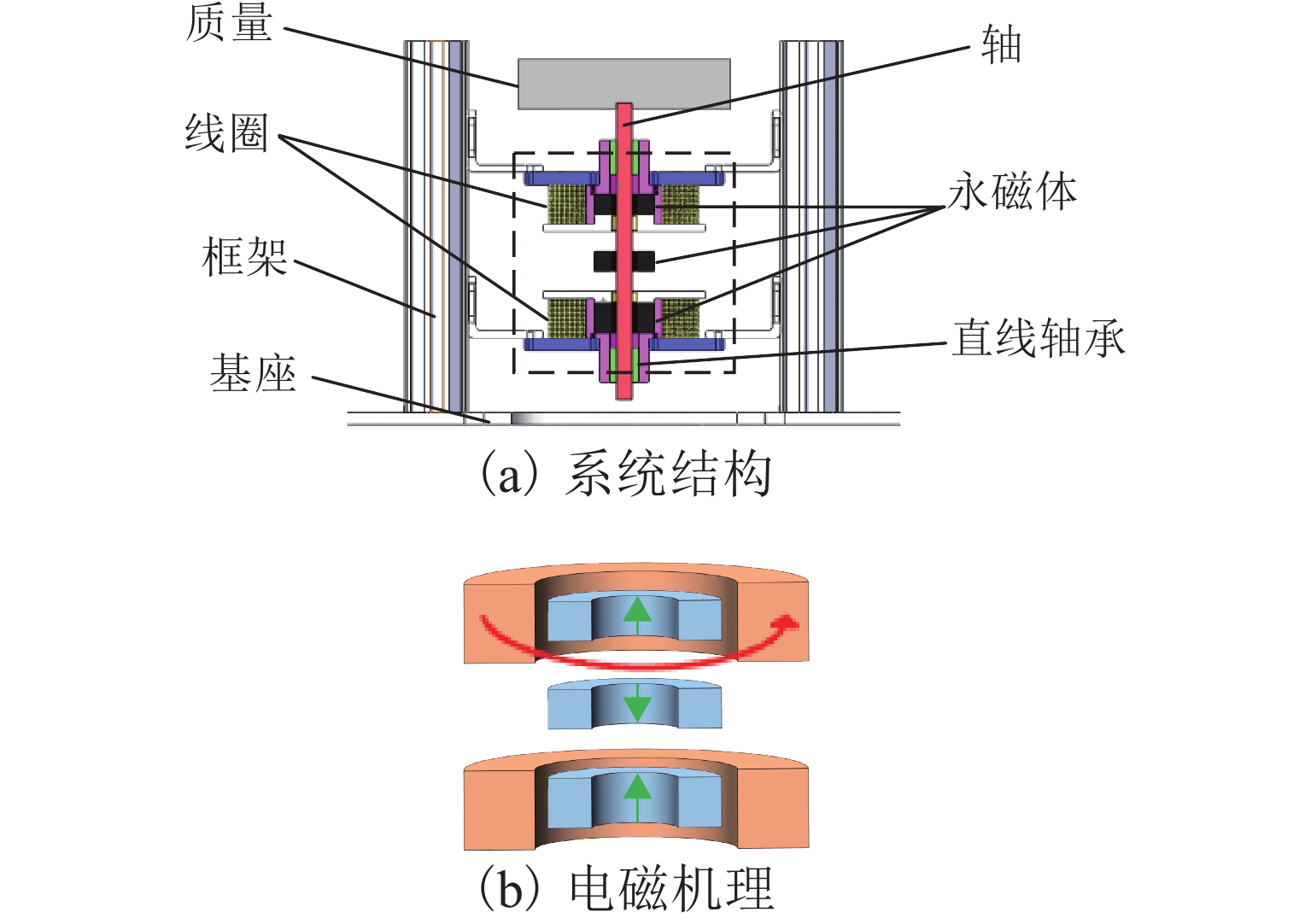
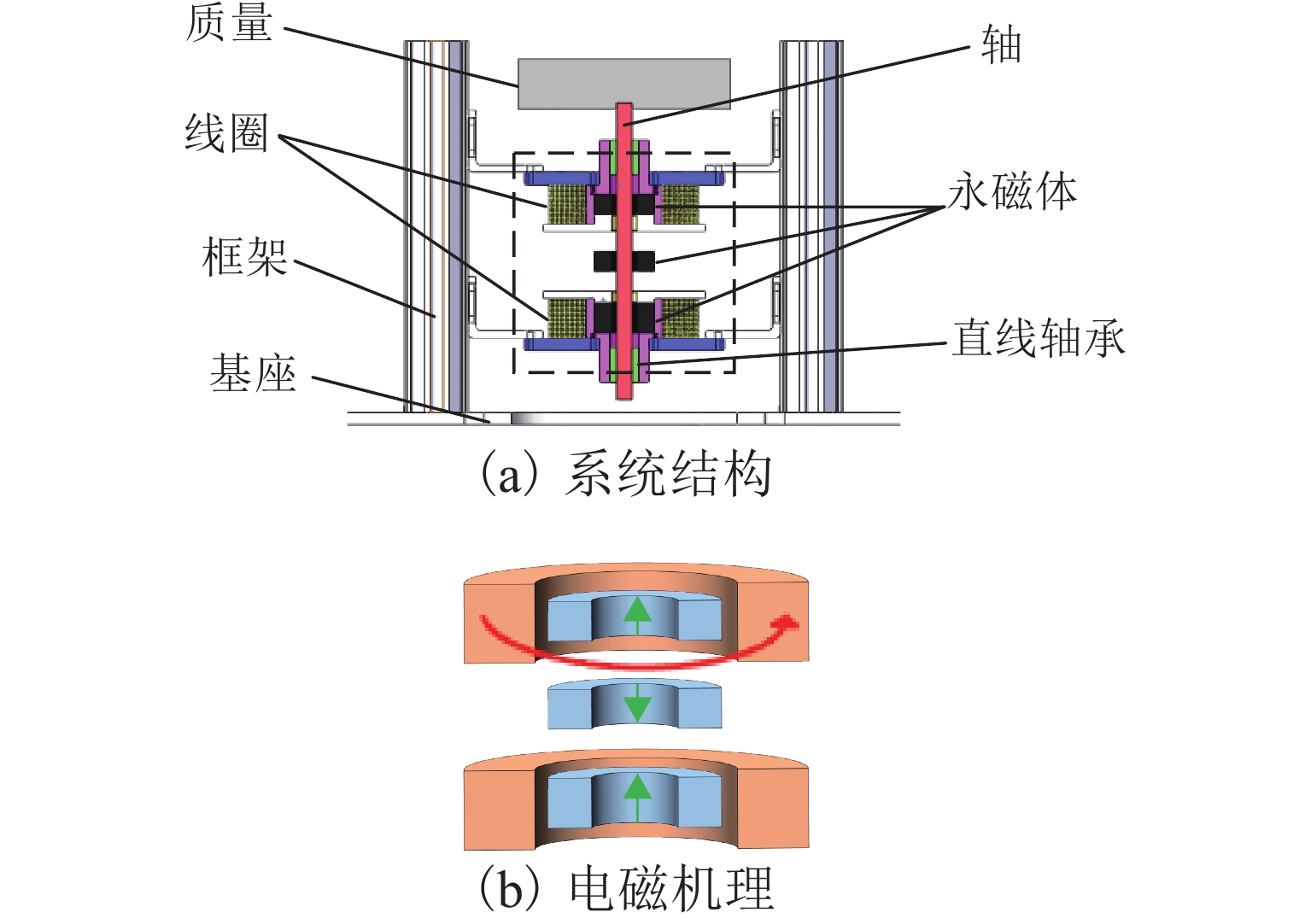
提出了一种具有高静-低动刚度特性的非线性隔振系统,由3个环形永磁体和2个空心线圈构成,如图1(a). 3个永磁体同轴排列,两端电磁线圈分别与对应永磁体同中心同轴布置,且两端永磁体和线圈通过连接件刚性连接在框架的特定位置,框架刚性连接在基座上. 中间永磁体固定在轴上,随轴进行轴向的往复移动,中间永磁体通过轴与质量块连接. 所有永磁体都是轴向磁化的,相邻的永磁体磁化方向相反. 2个线圈中的电流极性始终相同,永磁体的磁化方向和线圈中的电流极性如图1(b)所示,图中绿色箭头为永磁体磁化方向,红色箭头为电流极性.
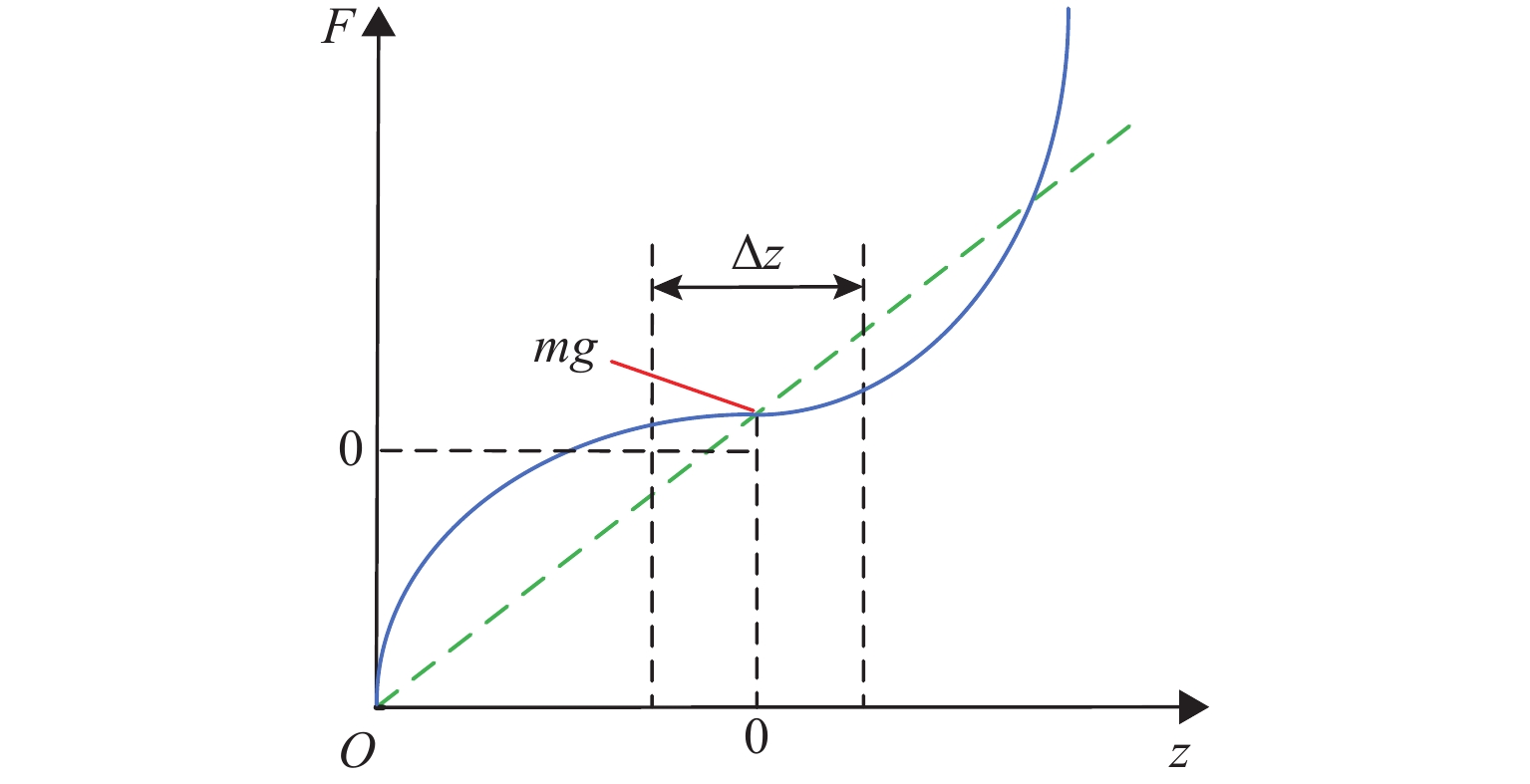
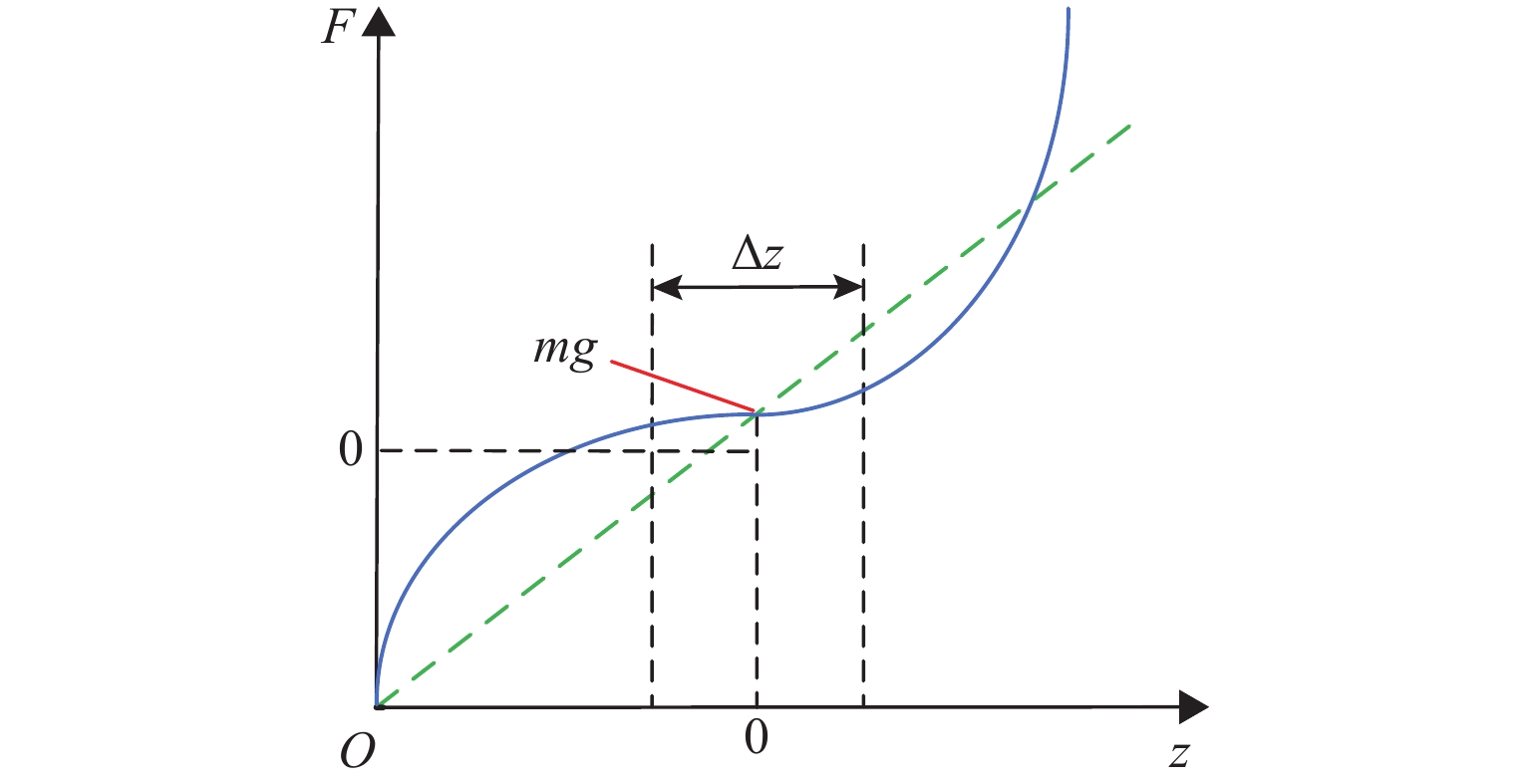
永磁体嵌套在电磁线圈中,减小了整体结构的尺寸. 如图1(b)所示,底部磁环厚度大于上部和中部磁环,会在平衡位置产生一个向上的磁力差. 如图2所示,当隔振器承载与差值相等的隔振质量m时,中间磁环刚好回归平衡位置. 图中:F为轴向力,Δz为在平衡位置处的微小位移,z为轴向位移.
1.2 工作原理
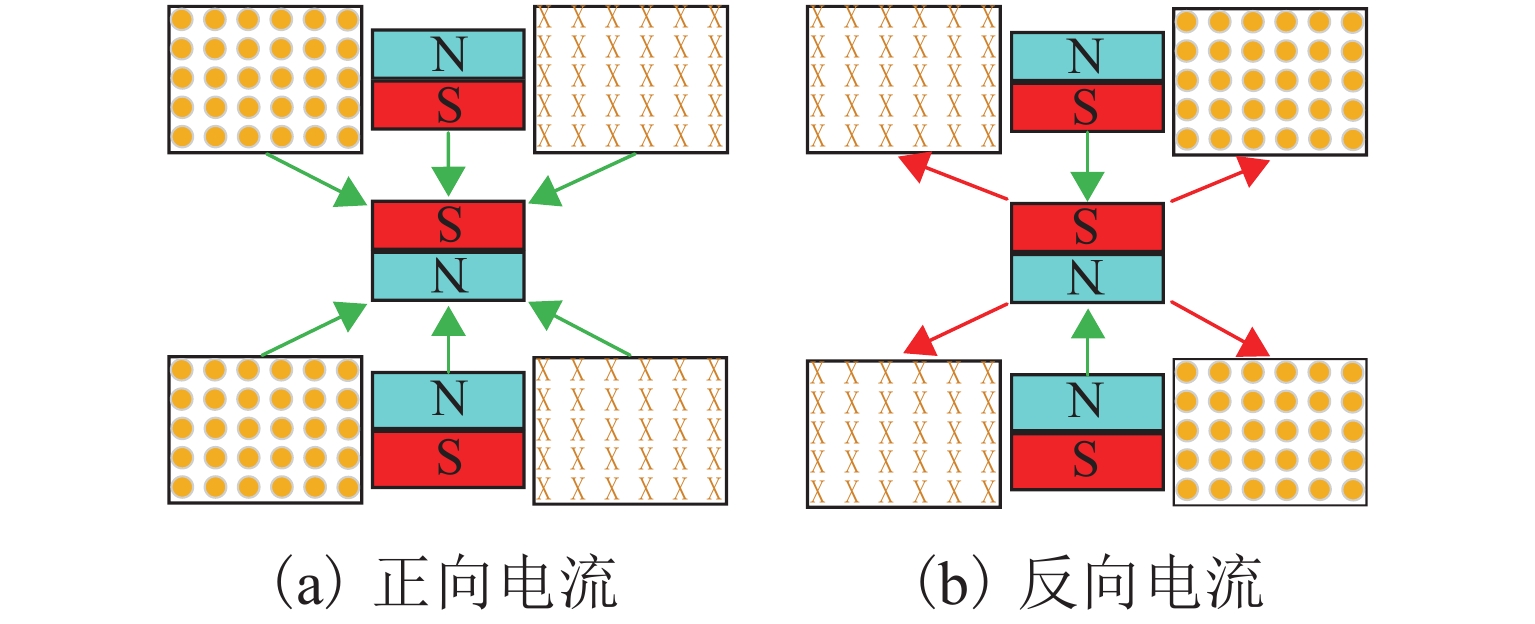
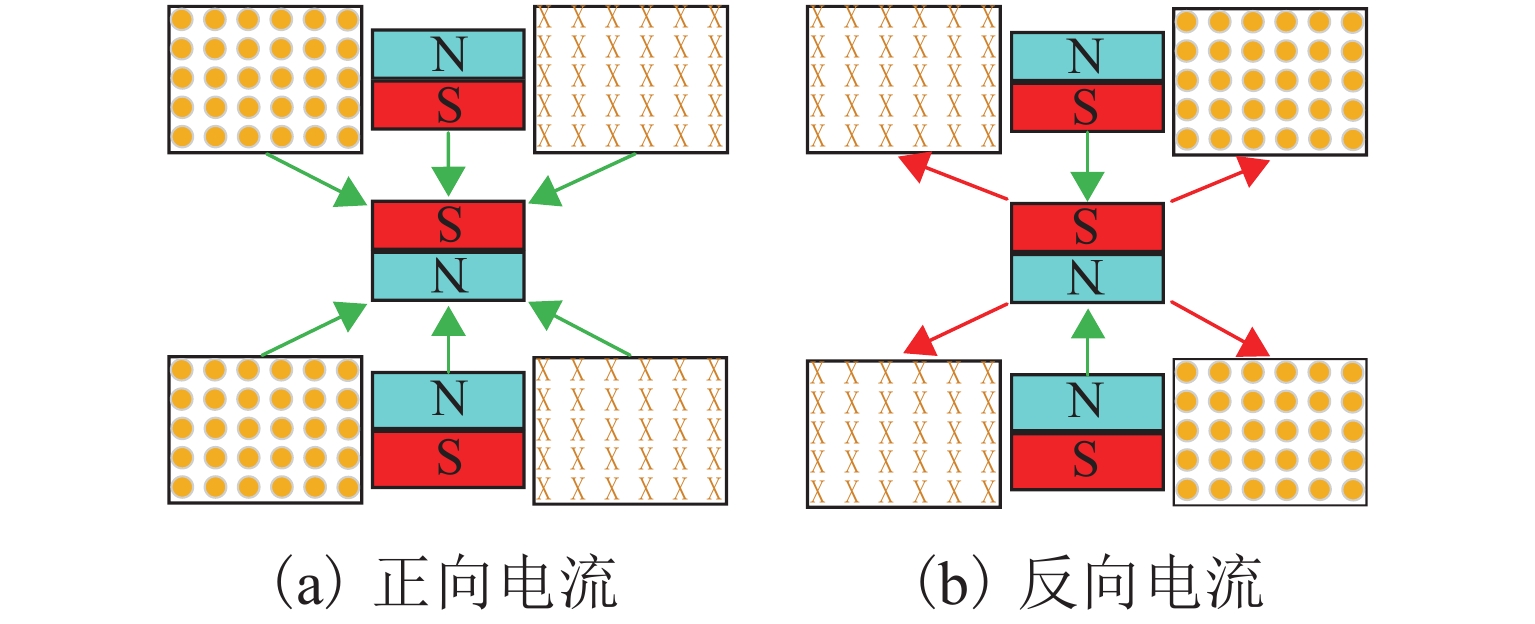
永磁环间磁力差与隔振质量的重力保持平衡,使中间磁环保持在平衡位置. 未加载电流时,依靠永磁环间非线性斥力实现被动隔振,此时系统刚度为永磁体间磁力刚度. 当线圈加载额定的正向激励电流时,线圈与磁环耦合将产生排斥的电磁力,与两端磁环产生的斥力叠加,施加在中间磁环上的合力和系统的等效刚度都将增加,如图3(a),图中绿色箭头为斥力,红色箭头为吸引力. 当线圈加载额定的反向激励电流时,线圈与磁环耦合将产生吸引的电磁力,与两端磁环产生的斥力抵消,施加在中间磁环上的合力和系统的等效刚度都将减小,如图3(b).
2. 结构参数设计
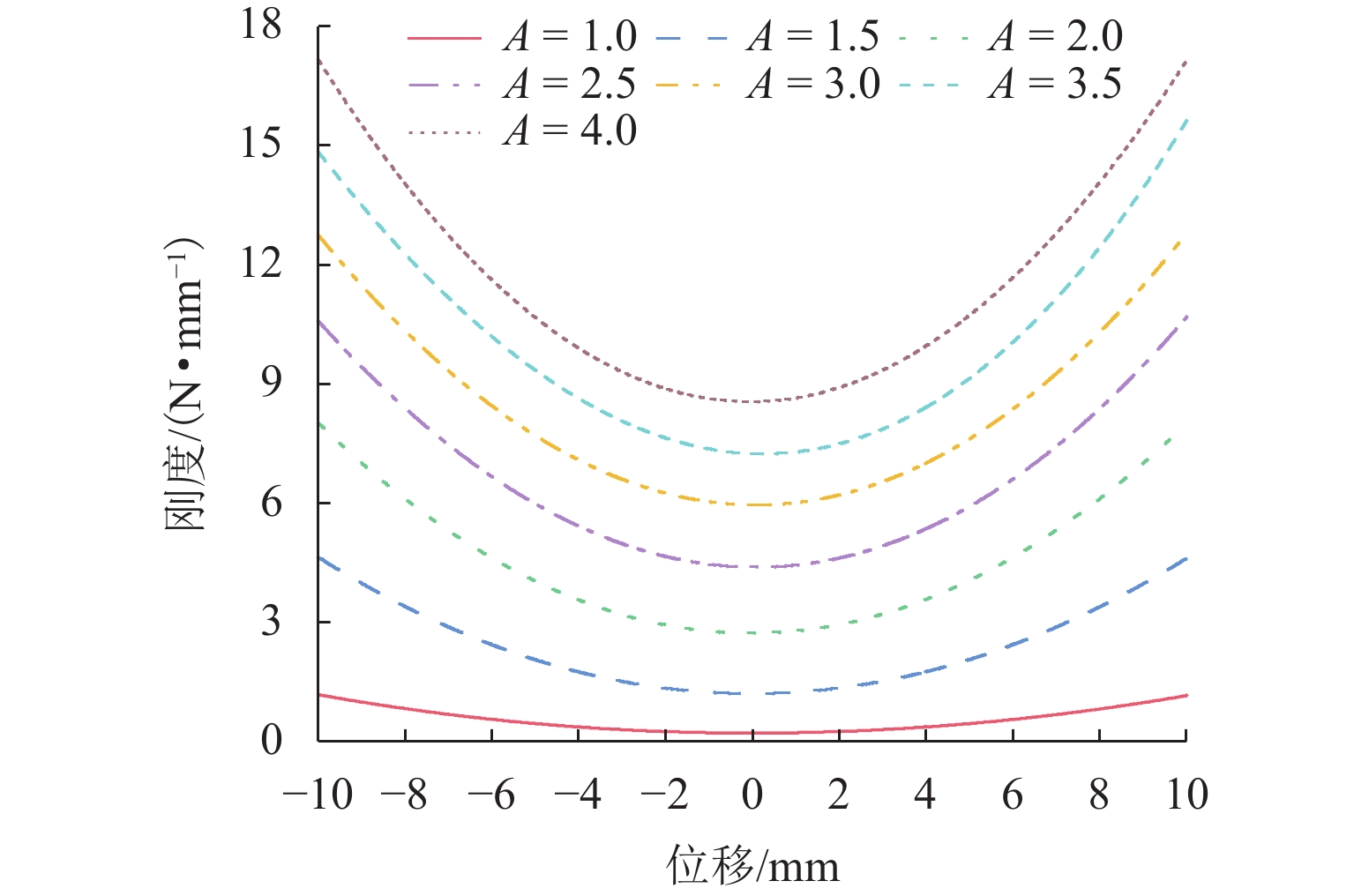
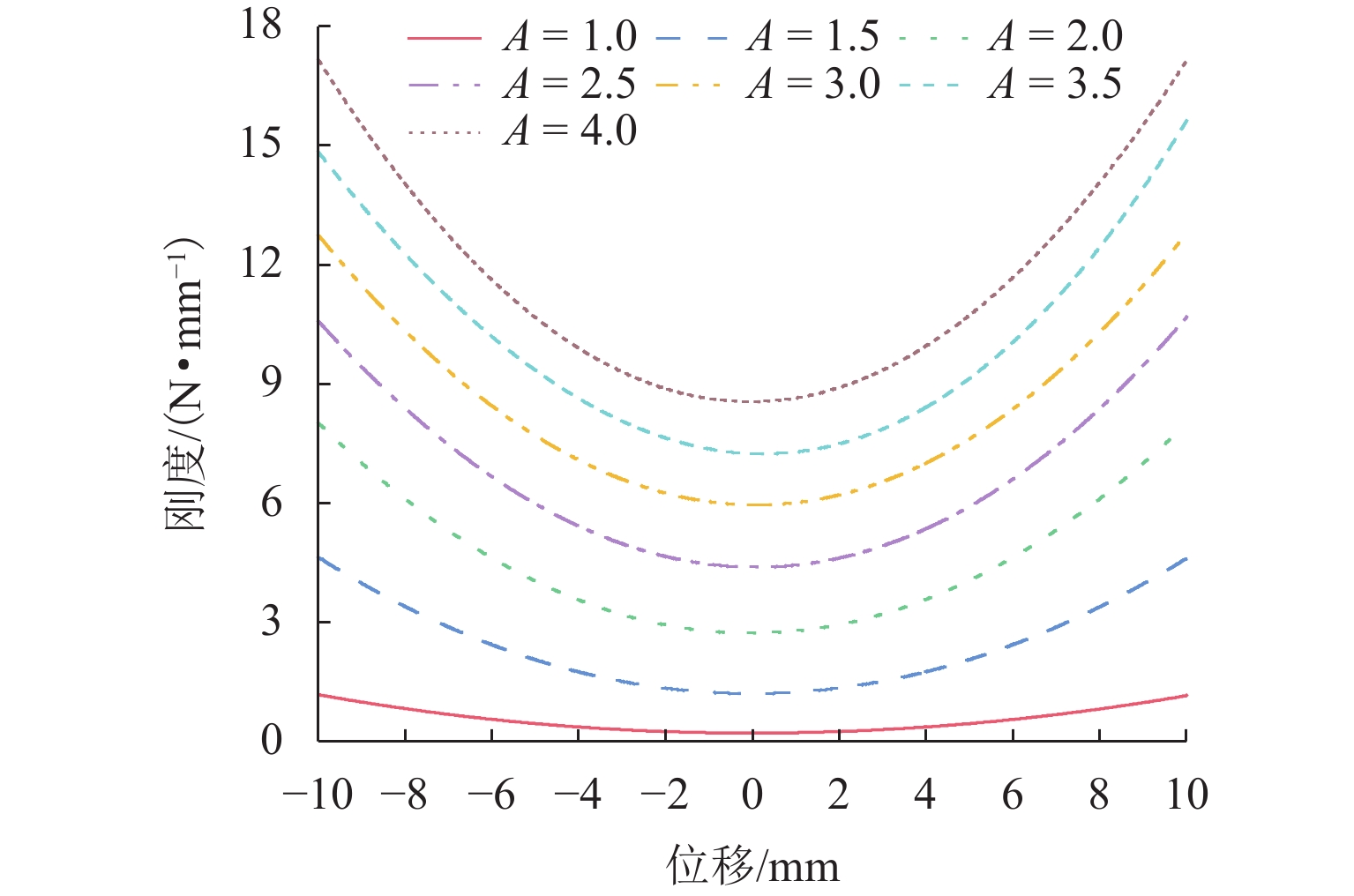
该隔振系统涉及的结构参数主要包括磁环的内(外)半径Rm(rm)和轴向厚度Lm,线圈的内(外)半径Rc(rc ,匝数决定)和轴向厚度Lc. 考虑到磁环需要连接轴,中间需要设计圆孔,永磁铁嵌套在线圈中,所以磁环内径rm,线圈内径rc值固定,不再多做讨论. 所以最终优化设计参数为Rm、Lm、Rc、Lc. 以Lm为基准定义优化变量, 磁环径厚比A=Rm/Lm,变化范围为[1.0,4.0]时,系统刚度变化曲线如图4.
系统刚度随着动磁环位移增加呈非线性规律增加,位移较小时,系统刚度较小;随着A的增大,系统的等效刚度整体增大,刚度变化平稳区域减小,非线性变化规律逐渐增强.
由工作原理可知,当通入负电流时可降低系统的等效刚度,所以,在线圈与磁环的厚度比变化和线圈径厚比变化的仿真时给定电流−8 A,观察系统刚度降低的变化.
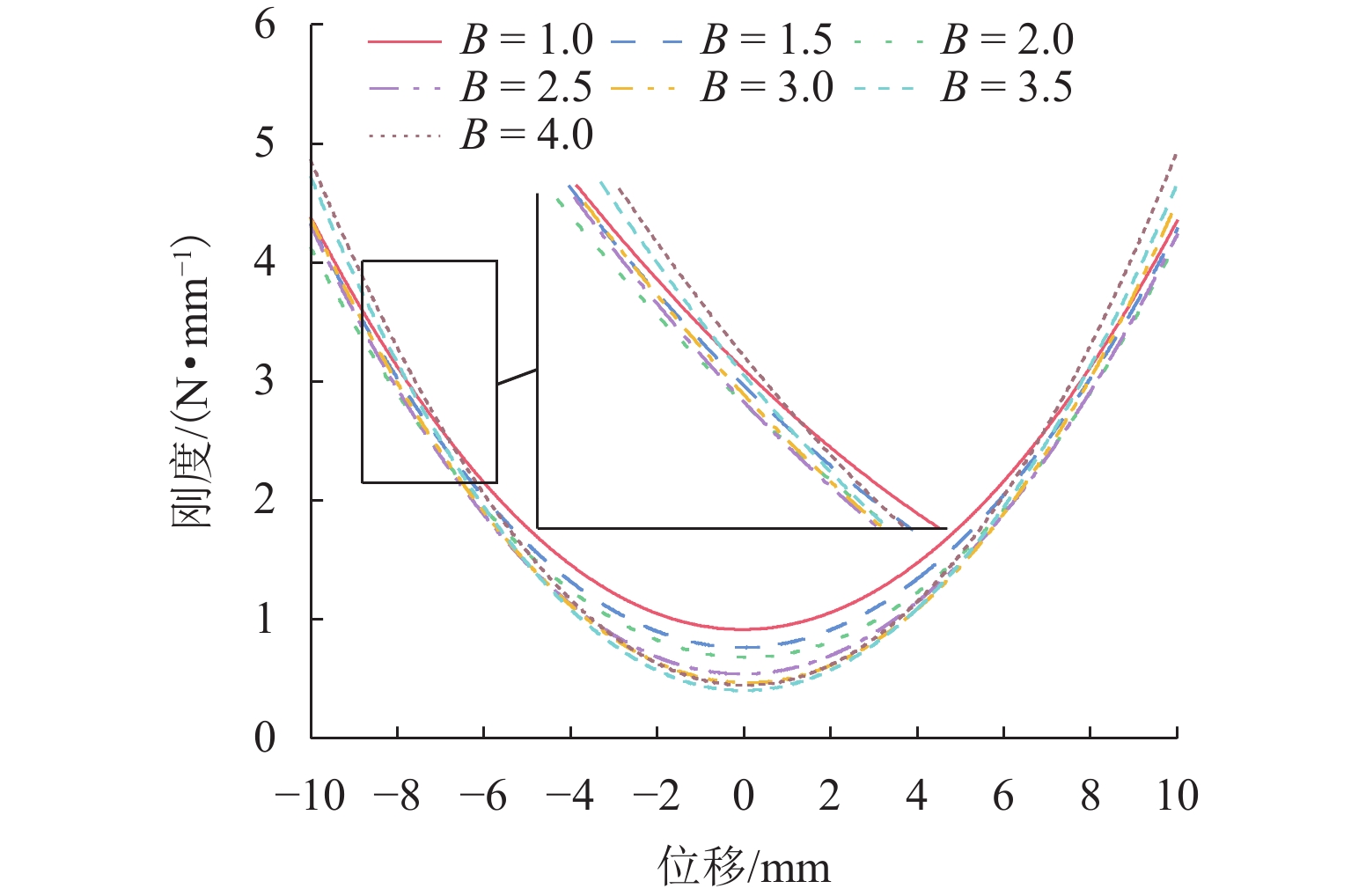
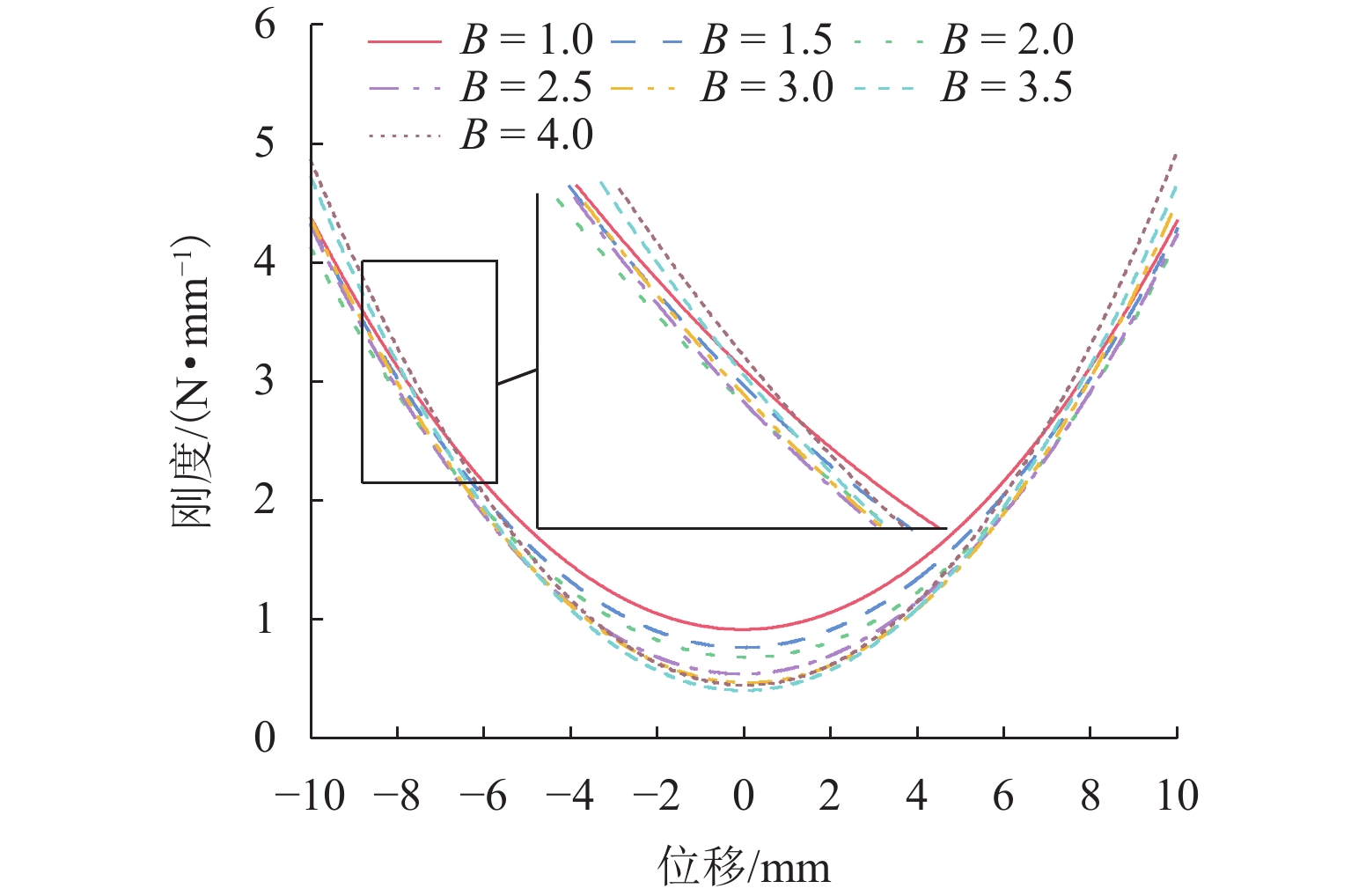
线圈与磁环的厚度比B=Lc/Lm,变化范围为[1.0,4.0]. 线圈匝数不变,电流一定时,系统刚度的变化如图5所示. 起初系统起始刚度随着B增大而减小,但当B增加到一定值时,系统的起始刚度会增加. 然而,系统的刚度变化平稳区域却始终减小,非线性变化趋势增强, 且随着位移增加,B=3.5和B=4.0的最大刚度会超过B=1.0.
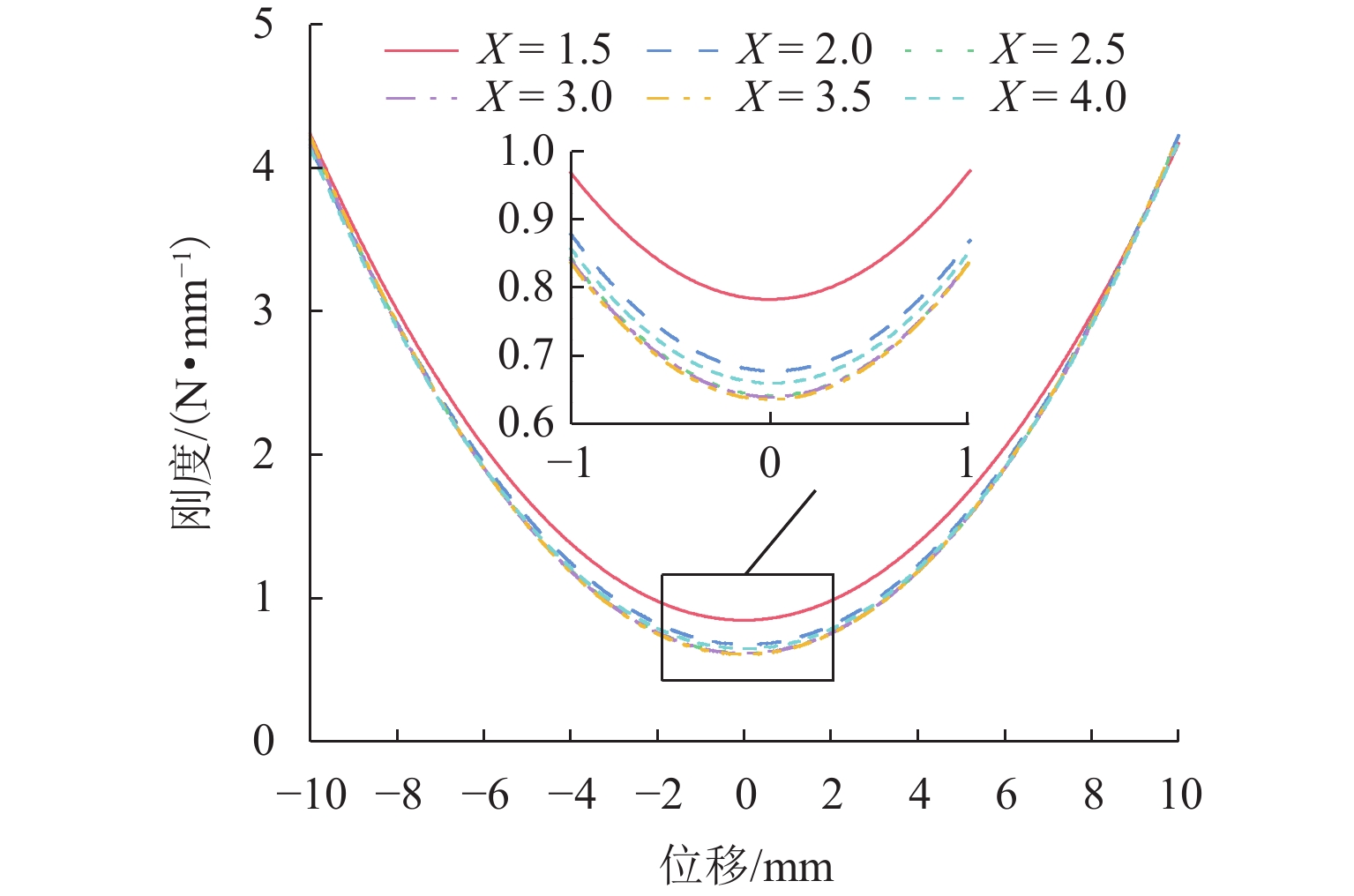
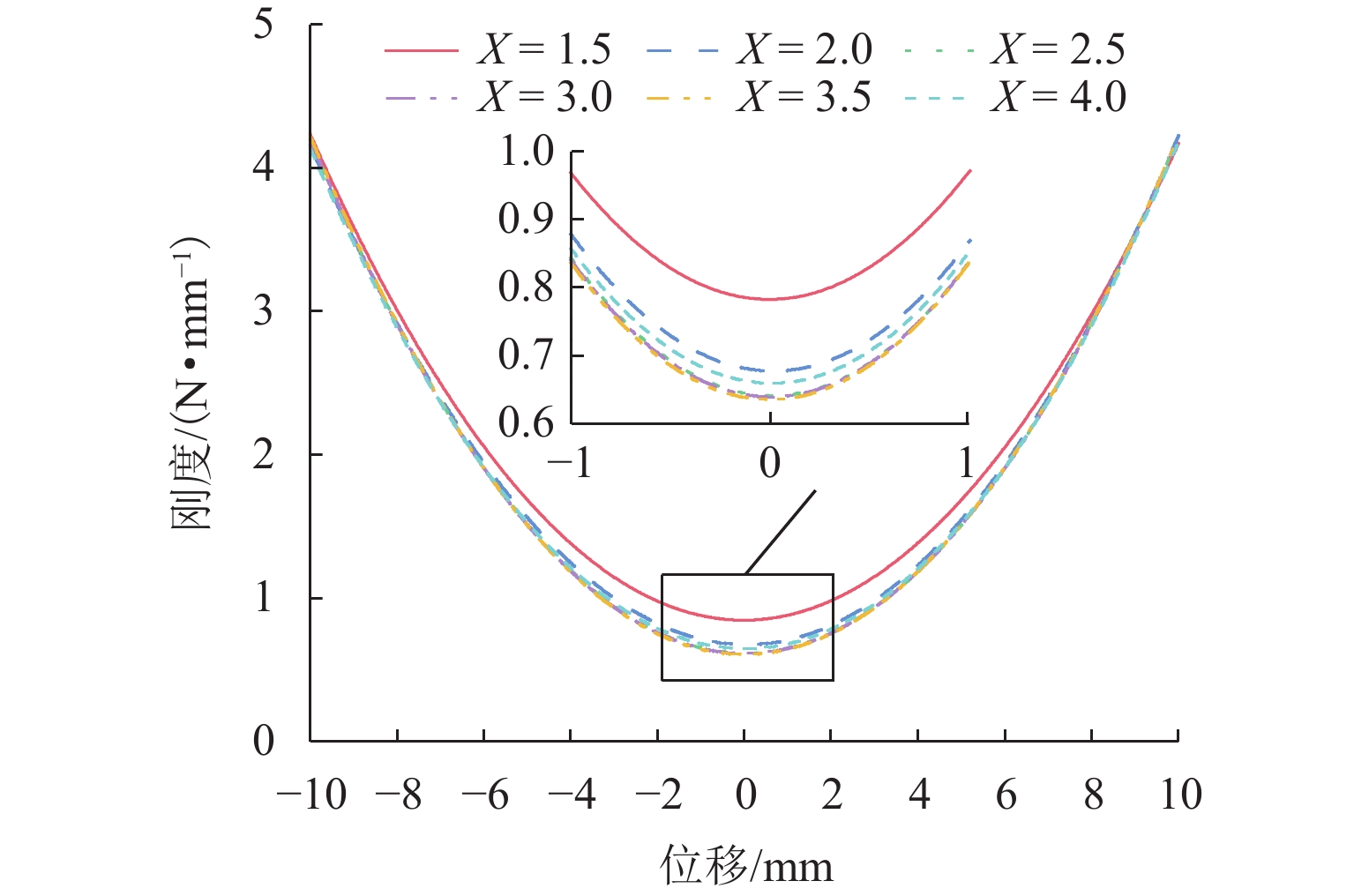
影响系统刚度变化的另一指标就是线圈的匝数,将匝数与线圈的半径关联,定义优化变量X=Rc/Lc,取值范围为[1.5,4.0],以线圈厚度Lc为基准,则X增加,线圈的匝数增加. 如图6所示,随着X增大,系统刚度降低,刚度变化平稳区域减小,随着X继续增大,X对系统刚度的影响逐渐减小,当X增加到一定值时,其对系统刚度影响作用趋于饱和.
通过仿真计算并结合工程实际情况,选取表1中的参数作为非线性隔振系统的结构尺寸.
表 1 结构参数Table 1. Structural parametersmm 参数 数值 磁环内径 5 磁环外径 12 磁环厚度 8(上、中),12(下) 线圈内径 15 线圈外径 30 线圈厚度 16 工作气隙 Z 15 线径 s 1 3. 力学模型
3.1 磁环间轴向磁力
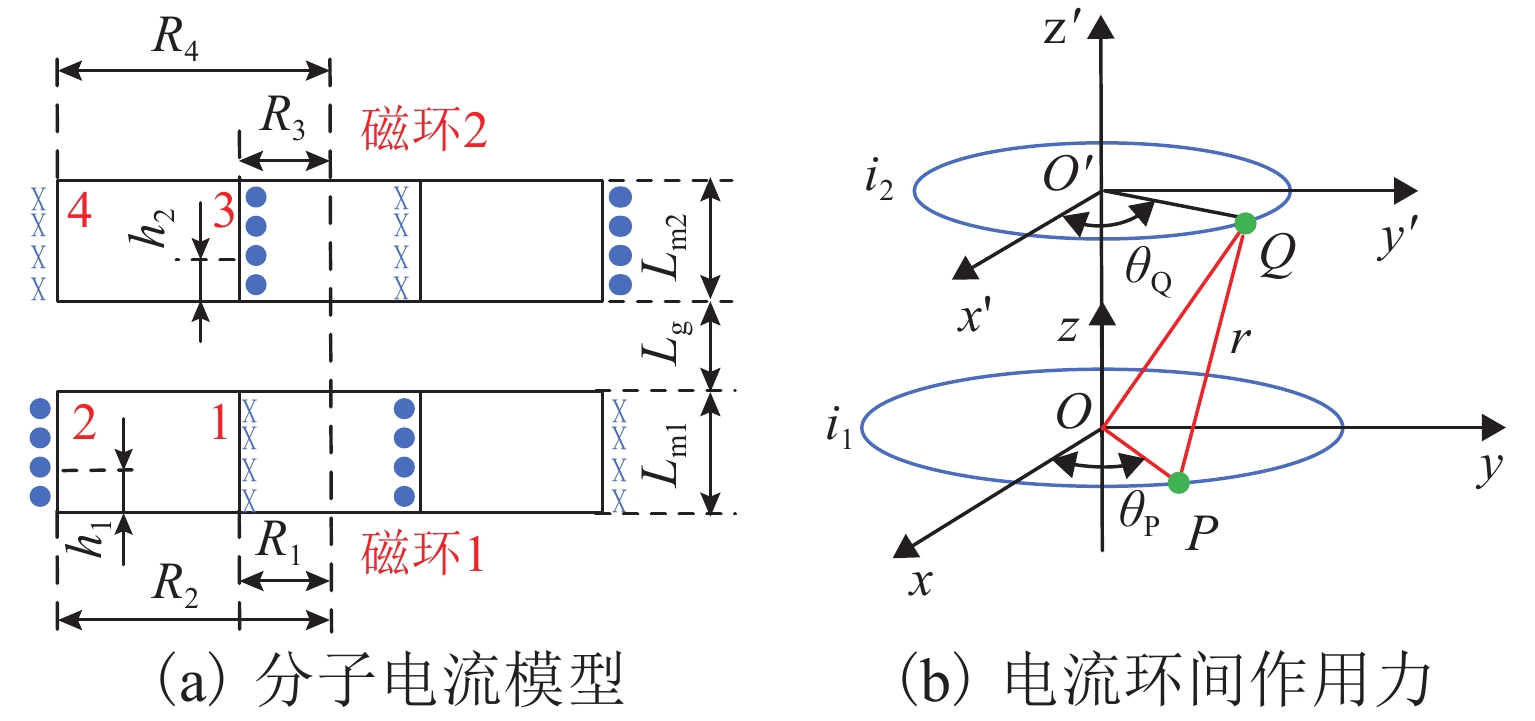
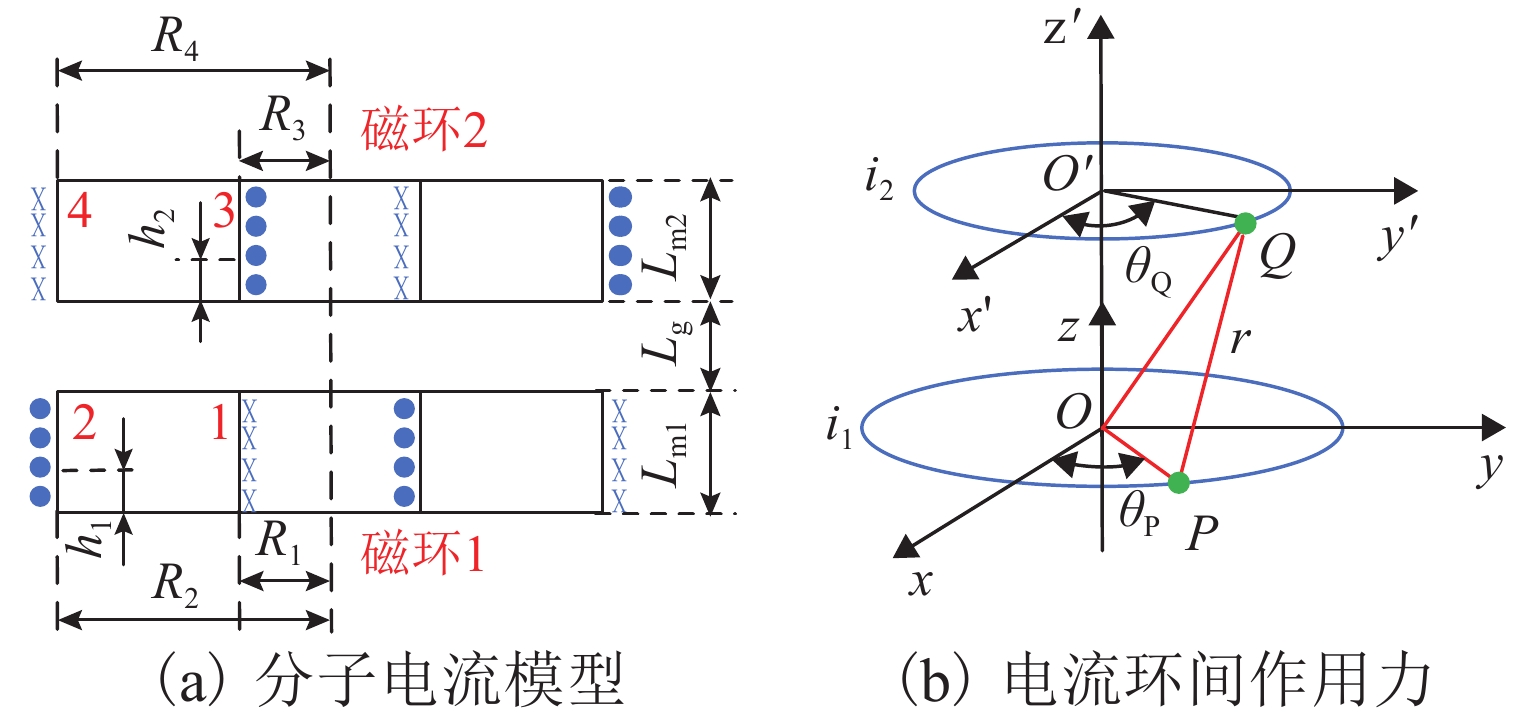
根据分子电流法,假设永磁环由2组电流大小相等、方向相反的等效表面电流构成[15-16]. 图7(a)为一对永磁环的分子电流模型,图中:“1”和“2”分别为永磁环1的内外表面,“3”和“4”分别为永磁环2的内外表面;Lg为两磁环间的气隙;Lm1、Lm2分别为磁环1、2的厚度. R1、R2、R3、R4分别为面1、2、3、4的半径,h1、h2分别为面“2”“3”上分子电流环的轴向位置.
以磁环1的“2”面和磁环2的“3”面为例,计算其作用力F23. 图7(b)为“2”面上任意环电流对“3”面上任意环电流之间的作用力示意. 图中:P、Q为在“2”面和“3”面电流环上任意取的电流微元,θP、θQ分别为P、Q点在O-xy坐标平面上相对于x的夹角,i1、i2分别为“2”面、“3”面的等效电流强度,r为点P到点Q的标量距离.
根据毕奥-萨瓦尔-拉普拉斯定律可以得到载流环上点P在点Q处产生的磁感应强度为
dB=μ0i14πr3•[dl1×r]•dh1, (1) 式中:dl1、dh1为“2”面上假想电流微元的长度和厚度,μ0为真空磁导率,r为Q点相对于P点的矢量位置.
由几何关系可以推出
r=(−R2cosθP+R3cosθQ)i+(−R2sinθP+R3sinθQ)j+(Lm1−h1+Lg+h2)k, (2) dl1=−R2sinθPdθPi+R2cosθPdθPj+0k, (3) r=[(−R2cosθP+R3cosθQ)2+(−R2sinθP+R3sinθQ)2+(Lm1−h1+Lg+h2)2]1/2, (4) 式中:i、j、k分别为x轴、y轴、z轴的正向单位矢量.
对dB积分,可以得到磁环1环面“2”上的分子电流在点Q处的磁感应强度为
B=μ0i1R24π∫2π0∫Lm10(Lm1+Lg−h1+h2)cosθPr3i+(Lm1+Lg−h1+h2)sinθPr3j+R2−R3(sinθPsinθQ+cosθPcosθQ)r3kdθPdh1. (5) 由电磁场理论可知,点Q处电流微元所受到的作用力为
dF23=[dl2×B]i2dh2, (6) 式中:dl2=−R3sinθQdθQi+R3cosθQdθQj+0k,dl2、dh2分别为“3”面上假想电流微元的长度和厚度.
对dF23进行积分,得到“2”面和“3”面之间的磁力为
F23=μ0i1i2R2R34π∫2π0∫2π0∫Lm10∫Lm20cosβ(R2−R3cos(θP−θQ))r3i+sinβ(R2−R3cos(θP−θQ))r3j+(Lm1+Lg−h1+h2)cos(θP−θQ)r3kdθPdθQdh1dh2. (7) 该隔振系统只有轴向磁力起作用,所以式(7)中只需要保留k项,“2”面和“3”面之间的轴向磁力为
Fm23=μ0i1i2R2R34π∫2π0∫2π0∫Lm10∫Lm20(Lm1+Lg−h1+h2)cos(θP−θQ)r3dθPdθQdh1dh2. (8) 同理可分别推导出“1”“3”面、“1”“4”面和“2”“4”面之间的轴向磁力Fm13、Fm14、Fm24,可得两磁环间轴向磁力为
Fm1=Fm13+Fm14+Fm23+Fm24. (9) 同理可求另一侧永磁环间的轴向磁力Fm2,系统中永磁环产生的总轴向磁力为
Fm=Fm1+Fm2. (10) 3.2 线圈与磁环间的轴向磁力
将线圈等效为多层同向表面电流叠加,永磁环依然等效为2组电流大小相等但方向相反的等效表面电流.
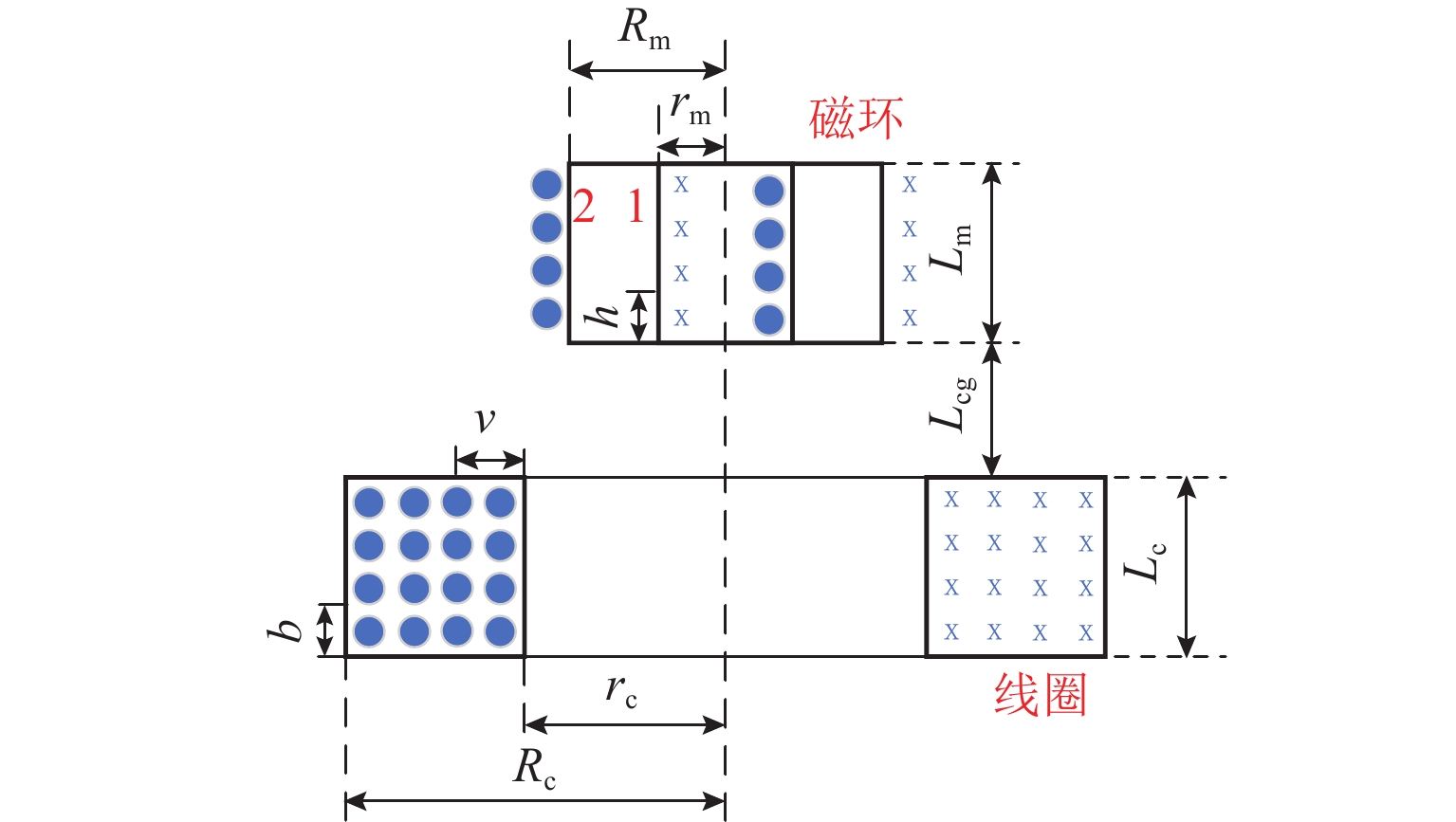
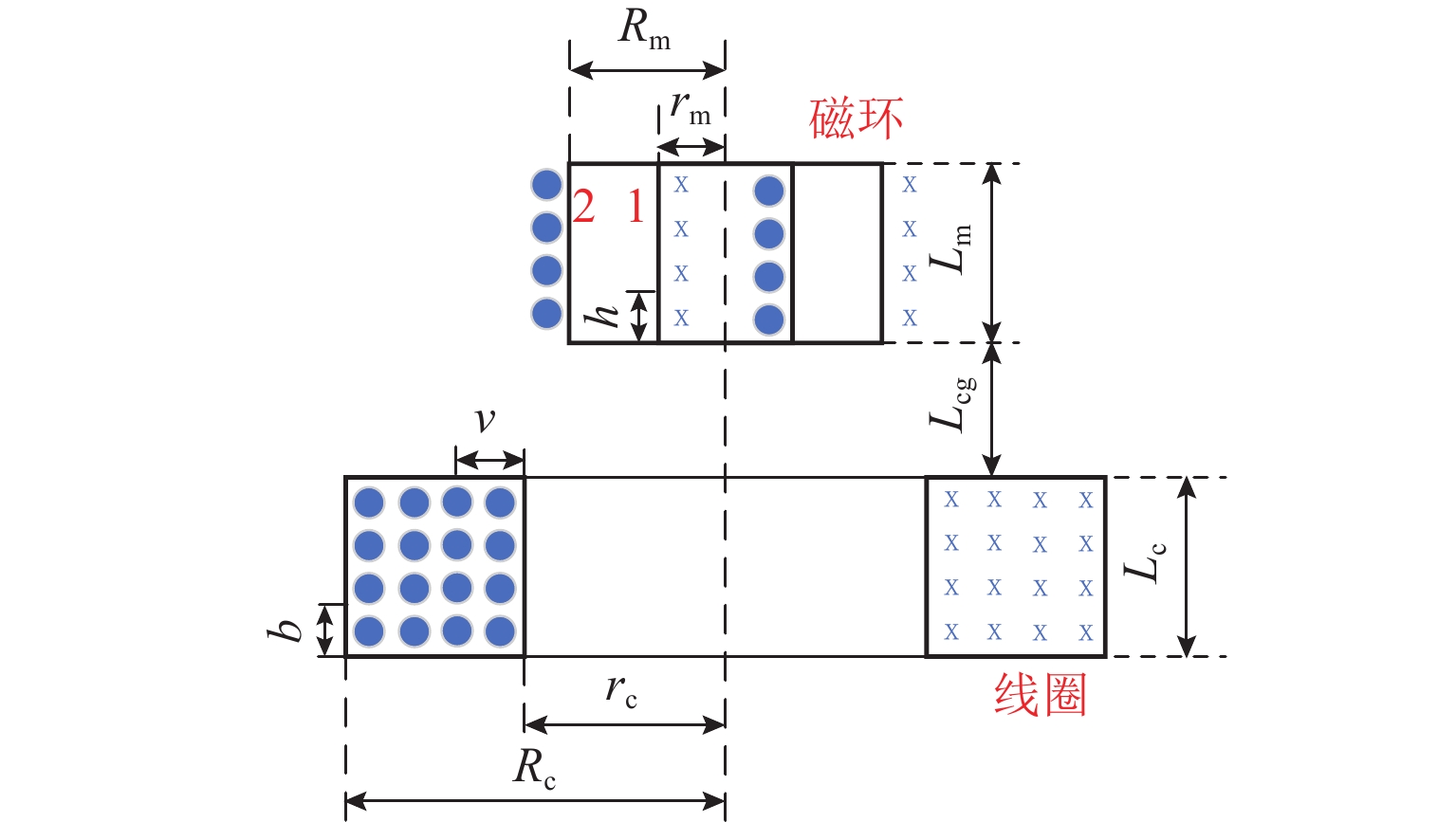
如图8所示,为线圈-磁环分子电流模型示意,图中:“1”和“2”分别为磁环的内、外表面,h为磁环面“1”上分子电流环轴向位置,b、v分别为线圈上分子电流环的轴向与径向位置,Lcg为磁环与线圈间的气隙.
通过模型可知,线圈等效电流i3为
i3=NcILc(Rc−rc), (11) 式中:Nc为线圈匝数,I为实际通入电流.
同永磁环分子电流模型推导步骤相同,线圈与永磁环“1”面之间的轴向磁力为
Fc1=μ0i3i2rm4π∫2π0∫2π0∫Lc0∫Lm0∫Rcrcv(Lc+Lcg−b+h)cos(θP−θQ)rcm3dθPdθQdbdhdv, (12) rcm=[(−vcosθP+R2cosθQ)2+(−vsinθP+R2sinθQ)2+(Lc−b+Lcg+h)2]1/2, (13) 式中:rcm为线圈上分子电流环与磁环上分子电流环的标量距离;db、dv分别为线圈上假想电流微元的厚度和径向厚度,dh为永磁体“1”面上假想电流微元的长度.
同理可求得线圈与面“2”之间的轴向磁力Fc2,因此,系统中单个线圈与永磁环间的轴向磁力为
Fc12=Fc1+Fc2. (14) 同理可得另一线圈对永磁环的轴向磁力Fc21,线圈对磁环的总轴向磁力为
Fc=Fc12+Fc21. (15) 通过3.1、3.2节的推导,系统的总轴向磁力为
Fz=Fm+Fc. (16) 3.3 简化表达式
为得到显式表达式用于刚度建模和动力学方程求解,需要对式(16)进行近似处理. 式(16)在零刚度点z0附近是连续的,可以对式(16)在z0进行关于轴向位移z的三阶泰勒展开,如式(17).
Fz=k0+k1(z−z0)+k2(z−z0)2+k3(z−z0)3+o(z), (17) 式中:k0=Fz|z=z0,k1=kz|z=z0,k2=12∂kz∂z|z=z0,k3=16∂2kz∂z2|z=z0,kz为轴向位移,o(z)是z大于3阶的高阶小项,在这里进行省略.
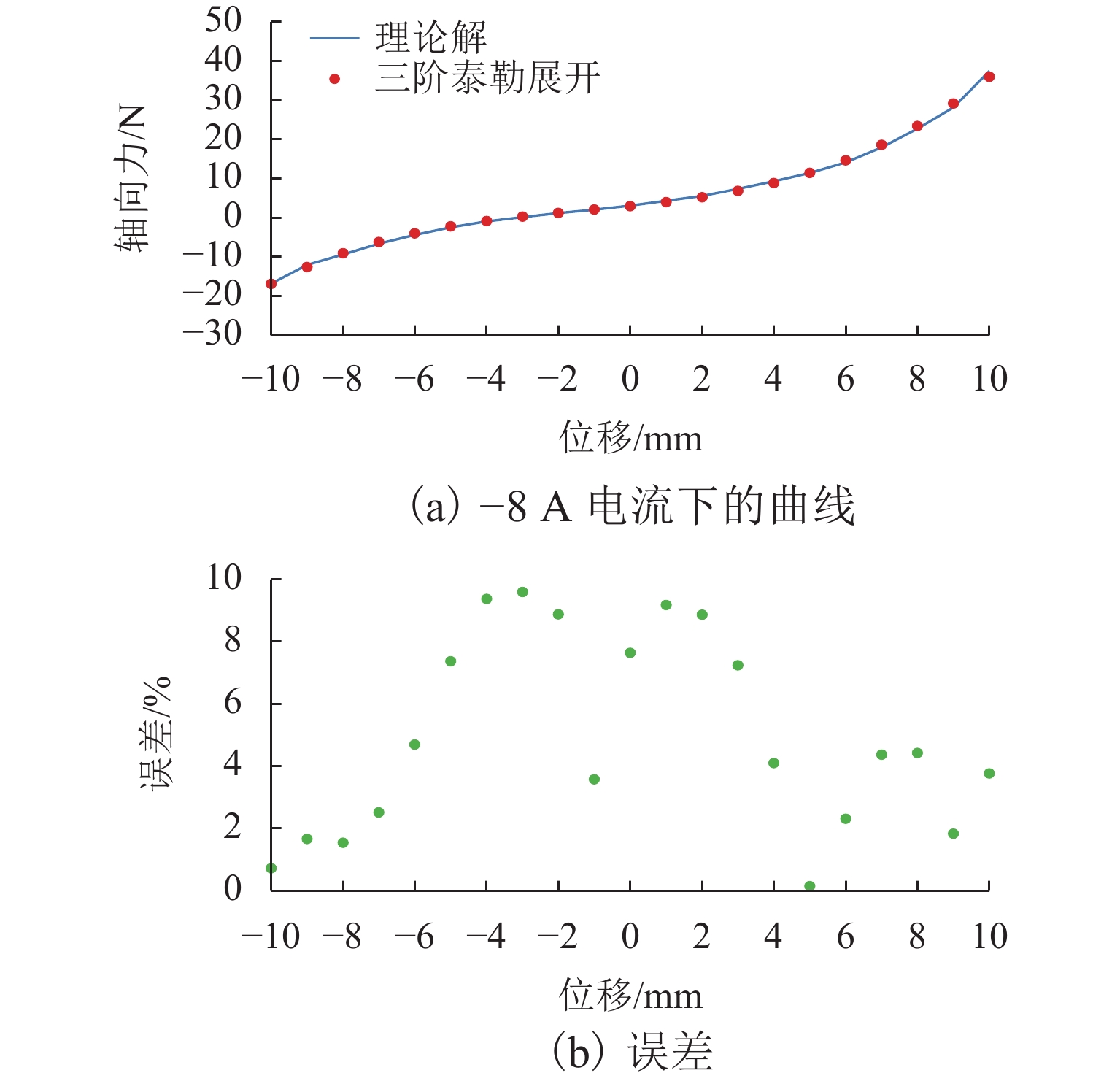
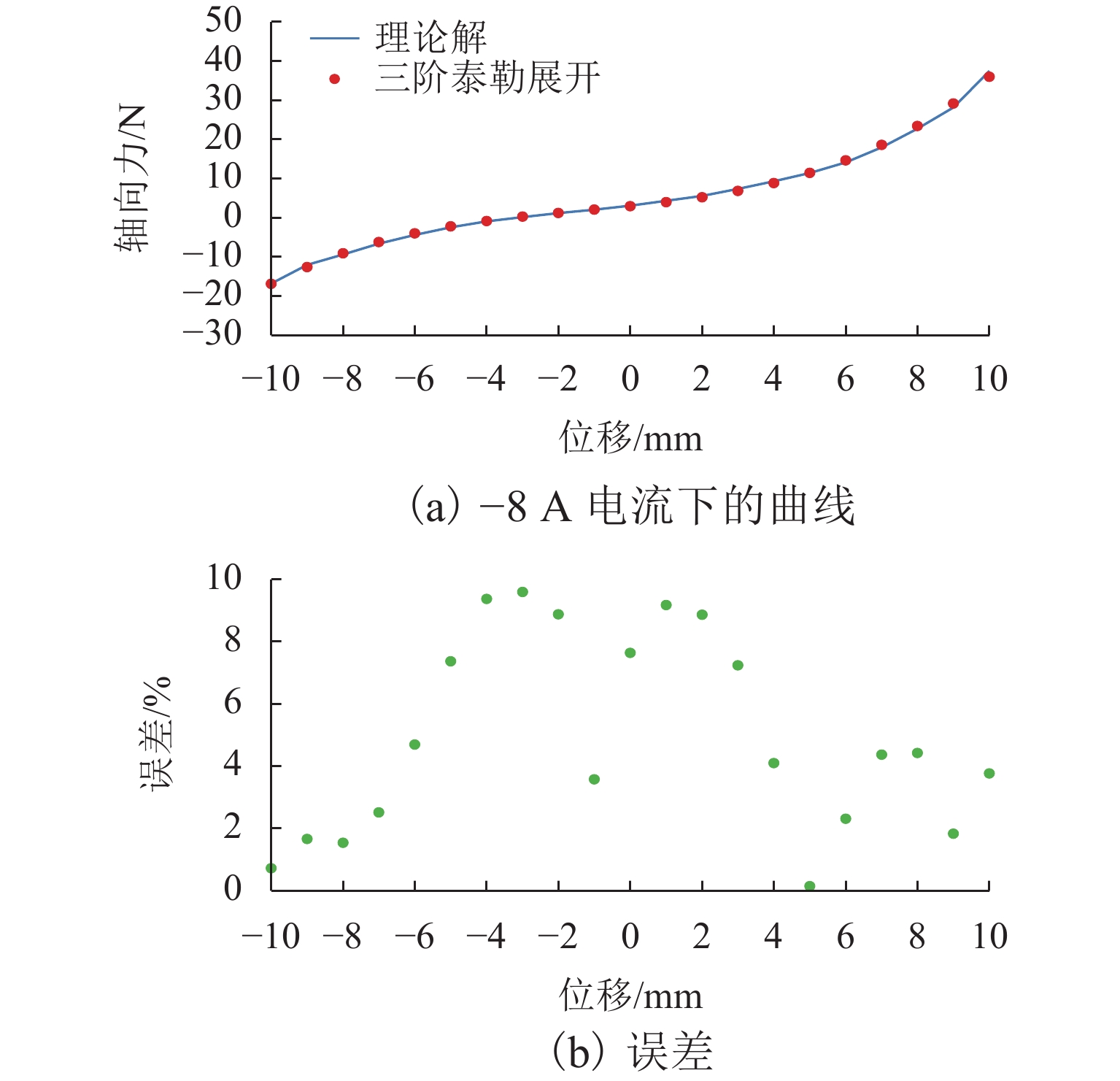
将理论解与−8 A电流时的三阶泰勒展开曲线求得的解进行比较,如图9所示,计算结果与三阶泰勒展开结果吻合较好,误差小于10%,可以基本满足隔振系统工程实际需求.
4. 动力学分析
4.1 动力学方程
假设隔振系统承受额定隔振质量m时,支撑平台的静平衡位置为零刚度点z0. 此时,隔振器可以看作为单自由度系统,在平衡位置的静力学方程为
k0+k1(z−z0)+k2(z−z0)2+k3(z−z0)3−mg=0. (18) 为便于表达和计算,设置零刚度点z0为坐标原点0,式(18)可以简化为
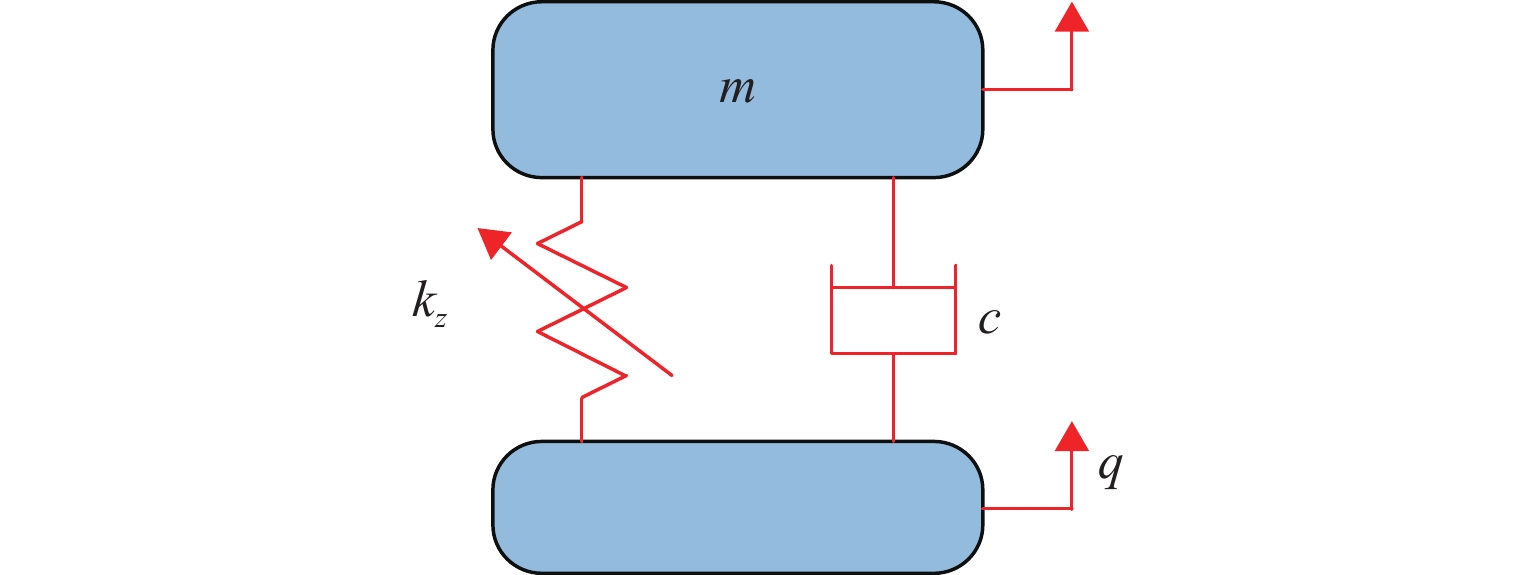
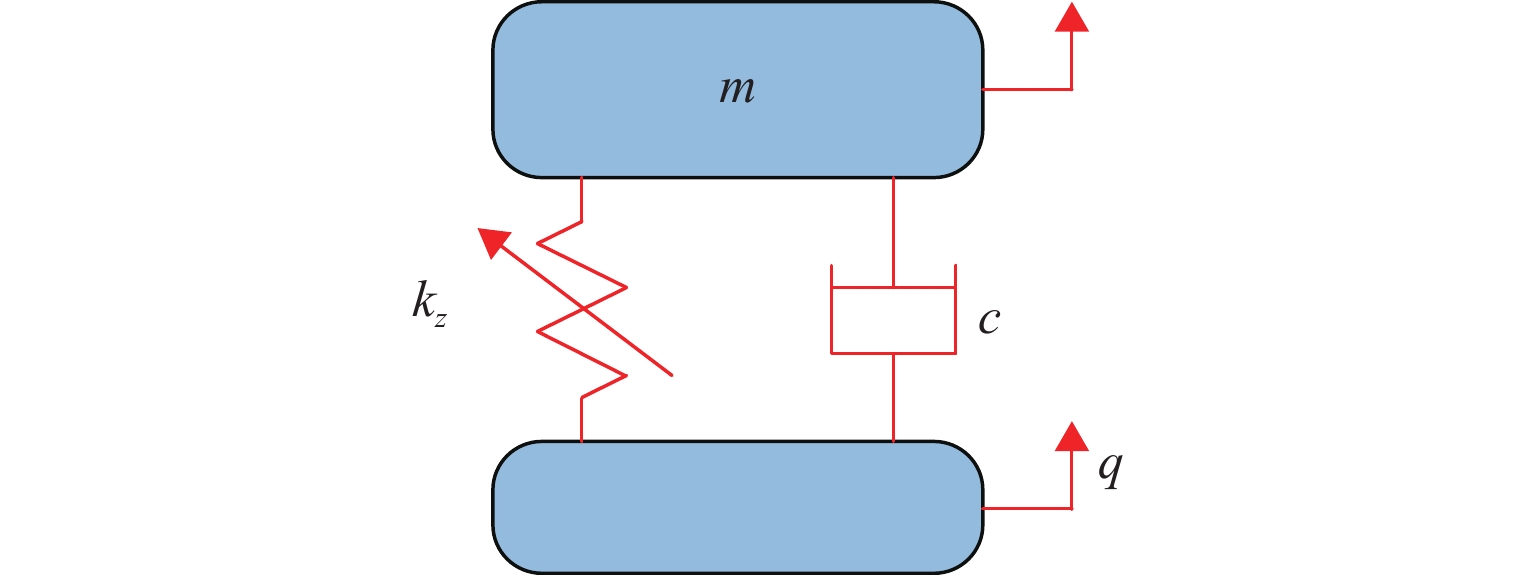
k0+k1z+k2z2+k3z3−mg=0. (19) 当底座受到激励时,隔振系统的动力学简化模型,如图10所示,q为激励幅值,c为系统阻尼. 对其进行动力学分析,在激励频率ω的外部位移激励zq=qcos ωt作用下,隔振系统在基座处的动力学方程为
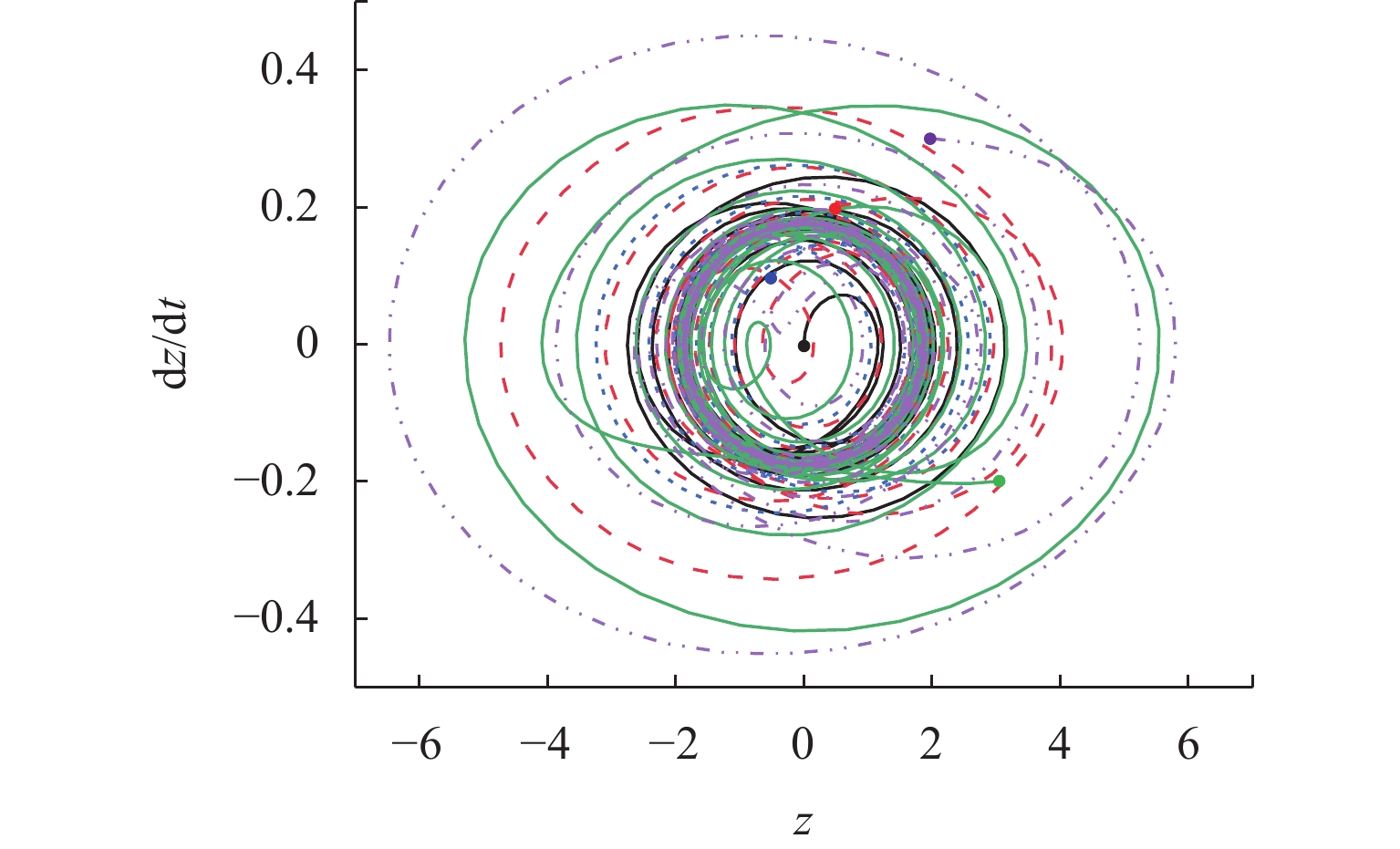
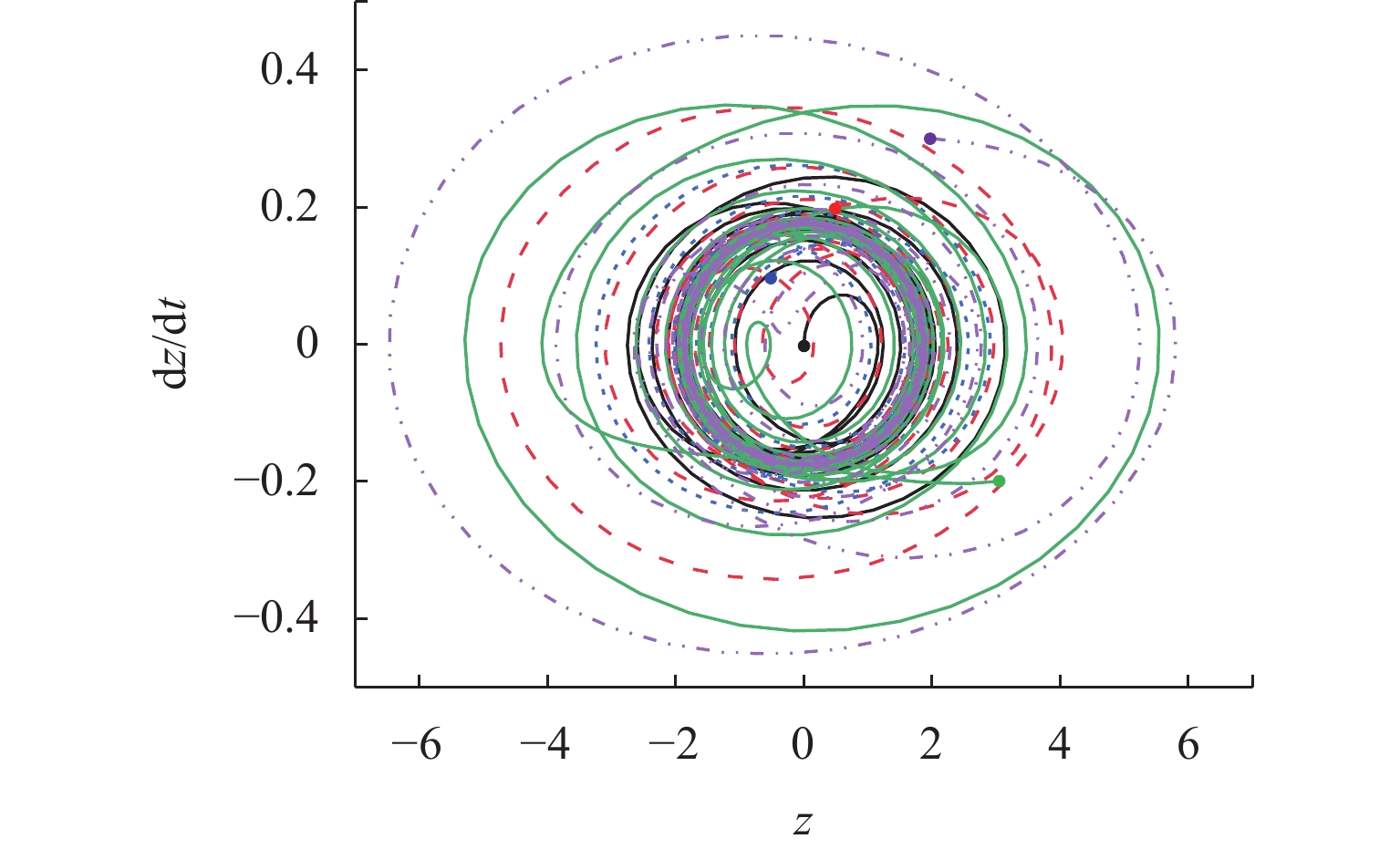
m¨z+c˙z+k0+k1z+k2z2+k3z3−mg=−m¨zq. (20) 由式(21)可知,系统为高阶非线性时变系统,通过四阶龙格库塔方法求得系统相平面图,如图11所示,随着时间t的不断增加,所有轨线最后都收敛于中间的一个极限环处,则该系统是稳定的.
在动力学求解中,以往的做法通常是省略k2项,只保留一次项和三次项系数,但本系统轴向力两侧不对称,二次项系数不能省略. 为更好地进行对比,引入一个线性弹簧刚度ks,所以线性弹簧的固有频率为ωn=√ks/m,将其引入到无量纲方程中. 因此,运动方程可以无量纲化为
ˆz″ (21) 式中:求导是对无量纲时间τ进行的,\hat {\textit{z}}为无量纲相对位移幅值,\xi 为无量纲阻尼比,\;\beta 为无量纲频率比, \eta 、\alpha 、\gamma 为无量纲刚度系数.
\begin{split} \hat {\textit{z}} = \frac{{\textit{z}}}{q},\zeta = \frac{c}{{2m{\omega _{\mathrm{n}}}}},\beta = \frac{\omega }{{{\omega _{\mathrm{n}}}}}, \eta = \frac{{{k_1}}}{{{k_{\mathrm{s}}}}},\alpha = \frac{{{k_2}q}}{{{k_{\mathrm{s}}}}}, \gamma = \frac{{{k_3}{q^2}}}{{{k_{\mathrm{s}}}}}, \end{split} \tau = {\omega _{\mathrm{n}}}t .
通常谐波平衡法(HB)只考虑基波项进行求解,无法考虑二次非线性项,如果想要正确反映各刚度系数的影响,就需要取更多的谐波项,求解比较困难. 所以本文采用增量谐波平衡法(IHB)求解,考虑了二次和三次非线性项的影响[17-18].
设 {\hat{{\textit{z}}}}_{0}、{\beta }_{0} 是式(21)的解,则其临近点可表示为 \hat{{\textit{z}}}={\hat{{\textit{z}}}}_{0} + \Delta \hat{{\textit{z}}},\beta ={\beta }_{0} + \Delta \beta ,其中, \Delta \hat{{\textit{z}}}、\Delta \beta 为增量. 令\beta \tau = \phi ,将 \hat{{\textit{z}}}、\beta 代入式(21),并略去高阶小量后得到增量方程为
\begin{split} & \beta _0^2\Delta \hat {\textit{z}}'' + 2\xi {\beta _0}\Delta \hat {\textit{z}}' + \left( {\eta + 2\alpha {{\hat {\textit{z}}}_0} + 3\gamma \hat {\textit{z}}_0^2} \right)\Delta \hat {\textit{z}} = \\ &\quad R - \left( {2{\beta _0}{{\hat {\textit{z}}''}_0} + 2\xi {{\hat {\textit{z}}'}_0} - 2{\beta _0}\cos \;\phi } \right)\Delta \beta , \end{split} (22) 式中:R = \beta _0^2\cos \;\phi - \left( {\beta _0^2{{\hat {\textit{z}}''}_0} + 2\xi {\beta _0}{{\hat {\textit{z}}'}_0} + \eta {{\hat {\textit{z}}}_0} + \alpha \hat {\textit{z}}_0^2 + \gamma \hat {\textit{z}}_0^3} \right) .
设式(22)的解为
{\hat {\textit{z}}} = \sum\limits_{n = 0}^N {\left( {{a_n}\cos \;n\phi + {b_n}\sin \; n\phi } \right)} \text{,} (23) \Delta \hat {\textit{z}} = \sum\limits_{n = 0}^N {\left( {\Delta {a_n}\cos \;n\phi + \Delta {b_n}\sin \;n\phi } \right)} . (24) 将式(23)、(24)代入式(22)中,求得以 \Delta {a}_{n}、 \Delta {b}_{n} 的代数方程组,取项数N=5,求得a1,…,an、b1,…,bn的值.
4.2 位移传递率
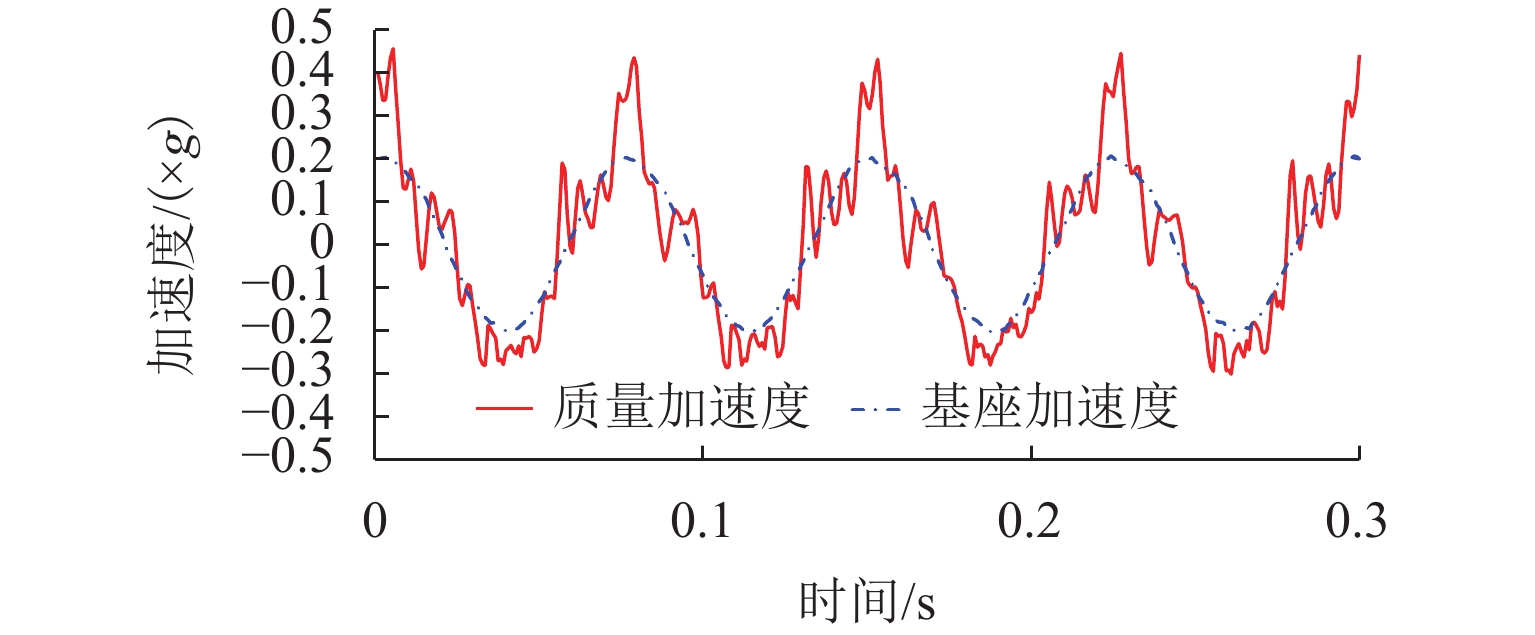
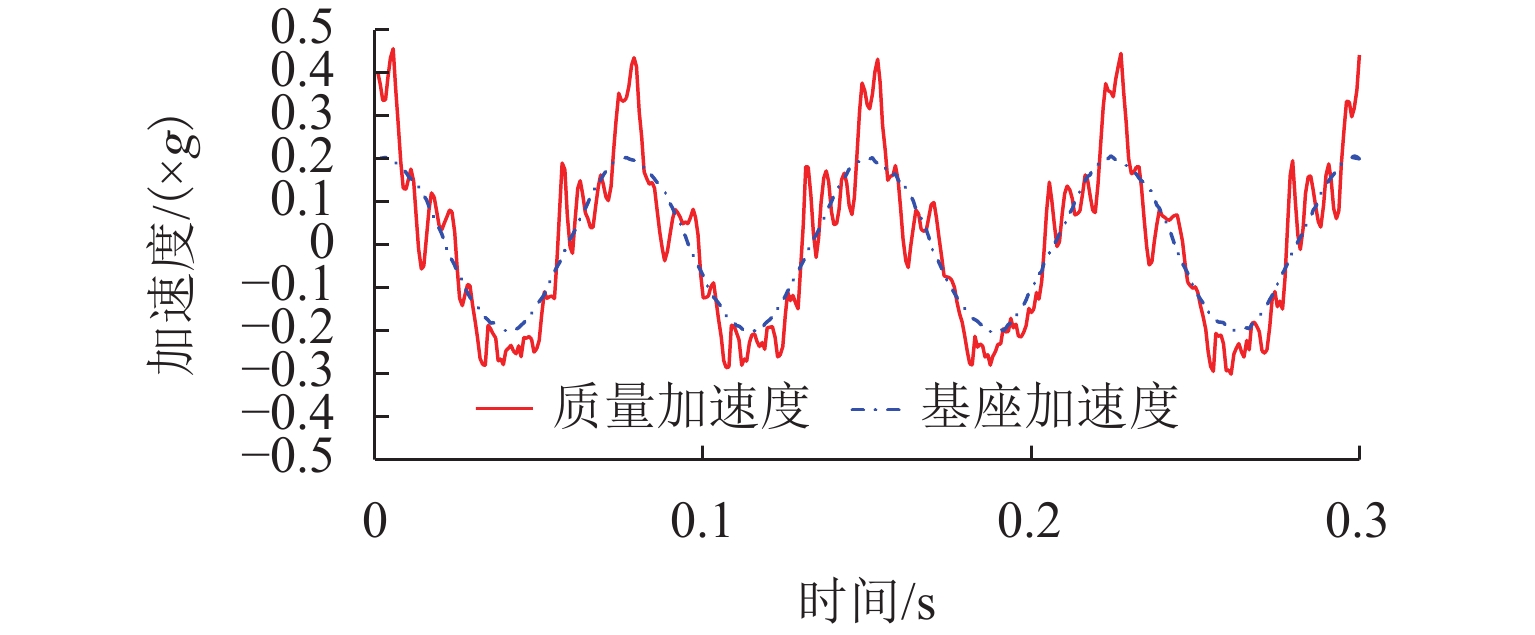
一般计算位移传递率 T的方法是忽略高次谐波项的影响,只取基波项,由质量位移幅值与基座位移幅值之比计算,存在一定误差. 在实际测量质量加速度时,波形含有高次谐波项,系统在13.5 Hz下采集的加速度图像如图12所示,所以,使用隔振质量位移响应对外部激励的均方根比来定义位移传递率.
通过4.1节求解,幅值\hat{{\textit{z}}} 可表示为
\hat{{\textit{z}}}={\displaystyle \sum _{n=0}^{5}({a}_{n}\mathrm{cos}\;n\phi + {b}_{n}\mathrm{sin}\;n\phi })={A}_{n}\mathrm{cos}(\beta \tau + {\theta }_{n}) \text{,} (25) 式中: {A}_{{n}}=\sqrt{{a}_{{n}}{}^{2} + {b}_{{n}}{}^{2}} , {\theta }_{n}=\mathrm{arctan} \left(-\dfrac{{b}_{n}}{{a}_{n}}\right) .
基座无量纲位移为\hat{{\textit{z}}}_q =cos βτ,所以质量的无量纲位移\hat{{\textit{z}}}_m 为\hat{{\textit{z}}} 和\hat{{\textit{z}}}_q 的和,如式(26).
{\hat{{\textit{z}}}}_{m}={\hat{{\textit{z}}}}_{q} + \hat{{\textit{z}}}=\mathrm{cos}\;\beta \tau + {A}_{n}\mathrm{cos}(\beta \tau + {\theta }_{n}). (26) 故位移传递率T表示为
T = \frac{{{\mathrm{RMS}}({{\hat {\textit{z}}}_m}(t))}}{{{\mathrm{RMS}}({{\hat {\textit{z}}}_q}(t))}}. (27) 4.3 系统隔振效率分析
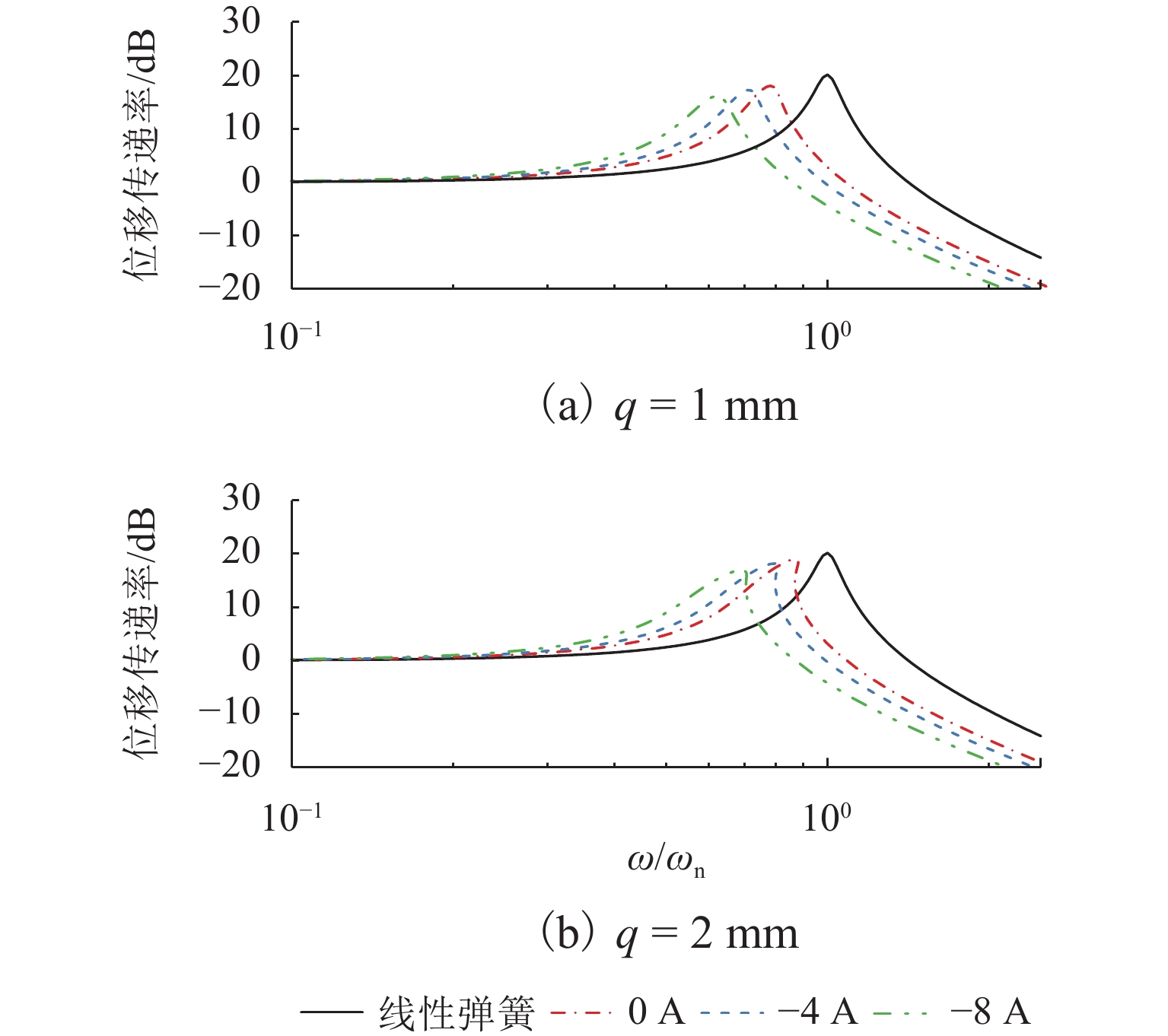
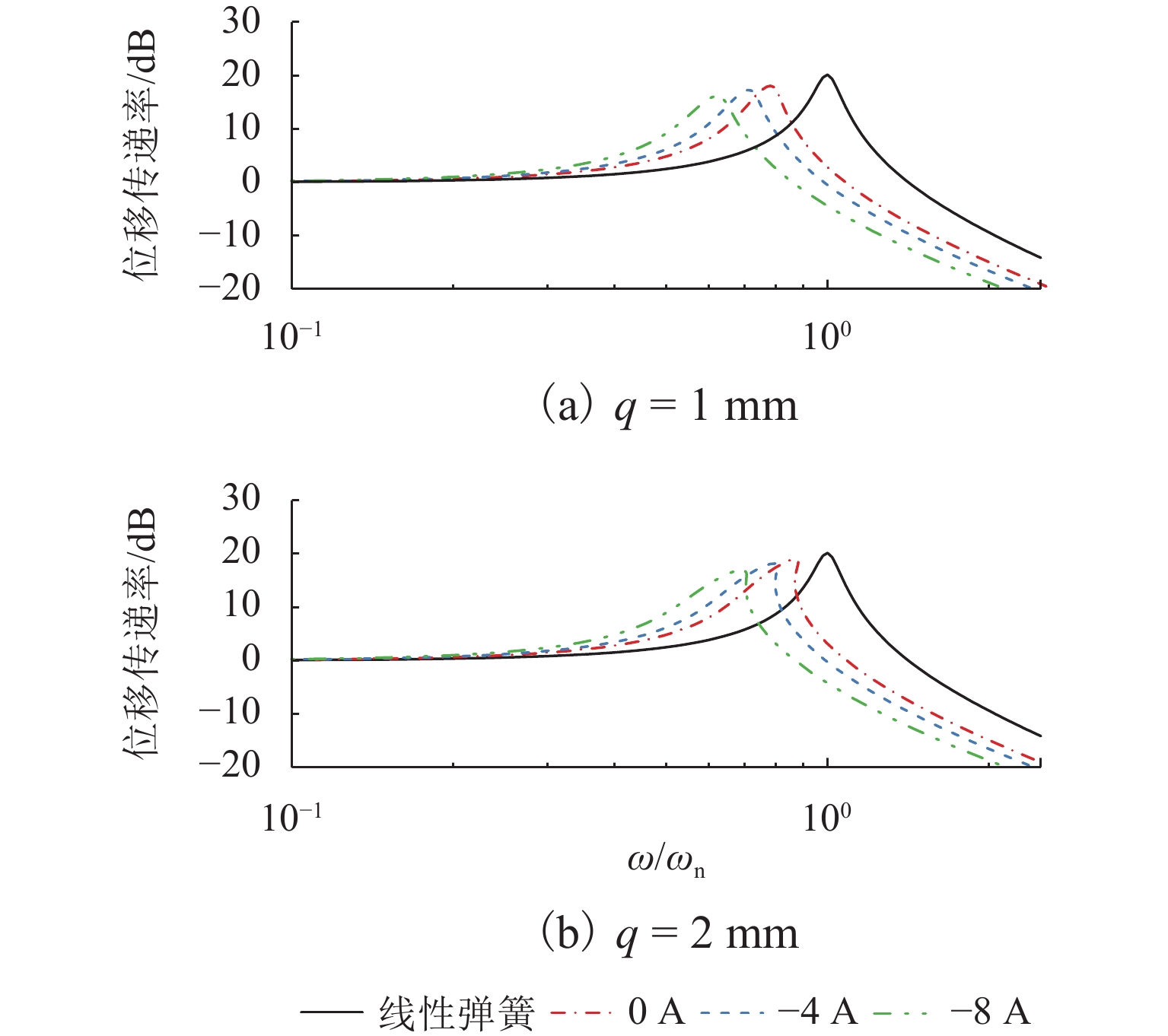
由于存在二次项与三次项等非线性项,该隔振系统表现出较为明显的非线性. 为了进一步分析该系统的隔振特性,通过数值仿真对比了不同电流下激励幅值q=1 mm与q=2 mm时系统的传递率曲线,如图13.
在数值仿真过程中隔振质量m=0.4 kg,磁环在闭合线圈中运动将会产生涡流阻尼. 但在本文中,动磁环的运动在线圈的外部,产生涡流阻力与主动控制的电磁力不在一个数量级,建模计算时将其忽略不计. 系统阻尼主要为直线轴承摩擦阻尼与空气阻尼构成,采用自由振动法,将系统阻尼估算为常数c.
由图13中可以看出:当q=1 mm时系统固有频率与最大传递率均随着负电流的增大而减小,整个系统表现出较强的线性特征;当q=2 mm时,系统固有频率与最大传递率同样随着电流的增大而减小,传递率曲线向右弯曲,表现出典型的渐硬弹簧特性.
5. 实验验证
搭建隔振系统实验测量系统,如图14所示. 隔振系统刚性垂直连接在VT6300-40型振动平台上,振动台的外部激励信号由VCS振动控制器和SA3K型功率放大器控制. 在振动平台和承载质量块上分别布置型号为1A213E和1A113E的加速度传感器.
加载不同电流信号,测量所设计的非线性隔振系统的位移传递率. 隔振质量为0.4 kg,加载正弦激励信号,基座位移幅值为1 mm,进行线性扫频实验. 忽略其他部分的影响,系统阻尼近似为常数.
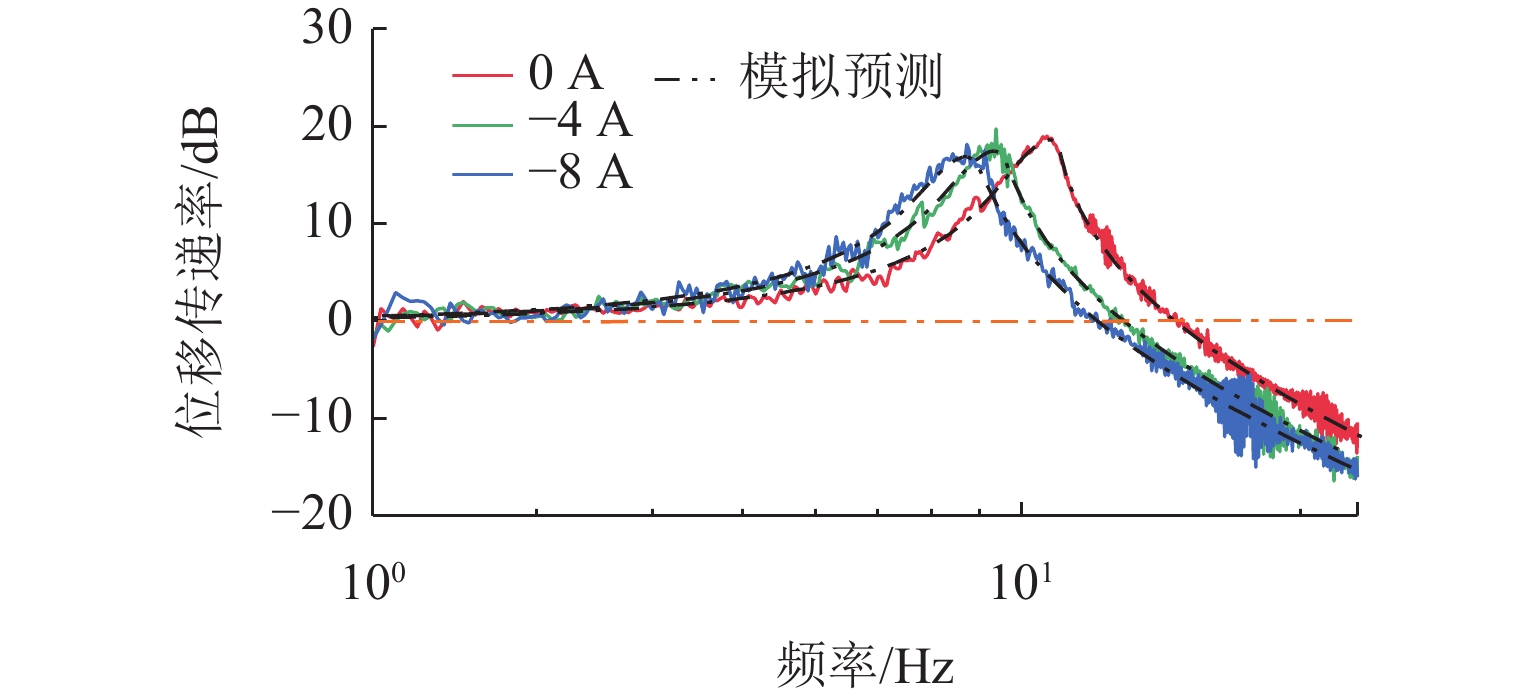
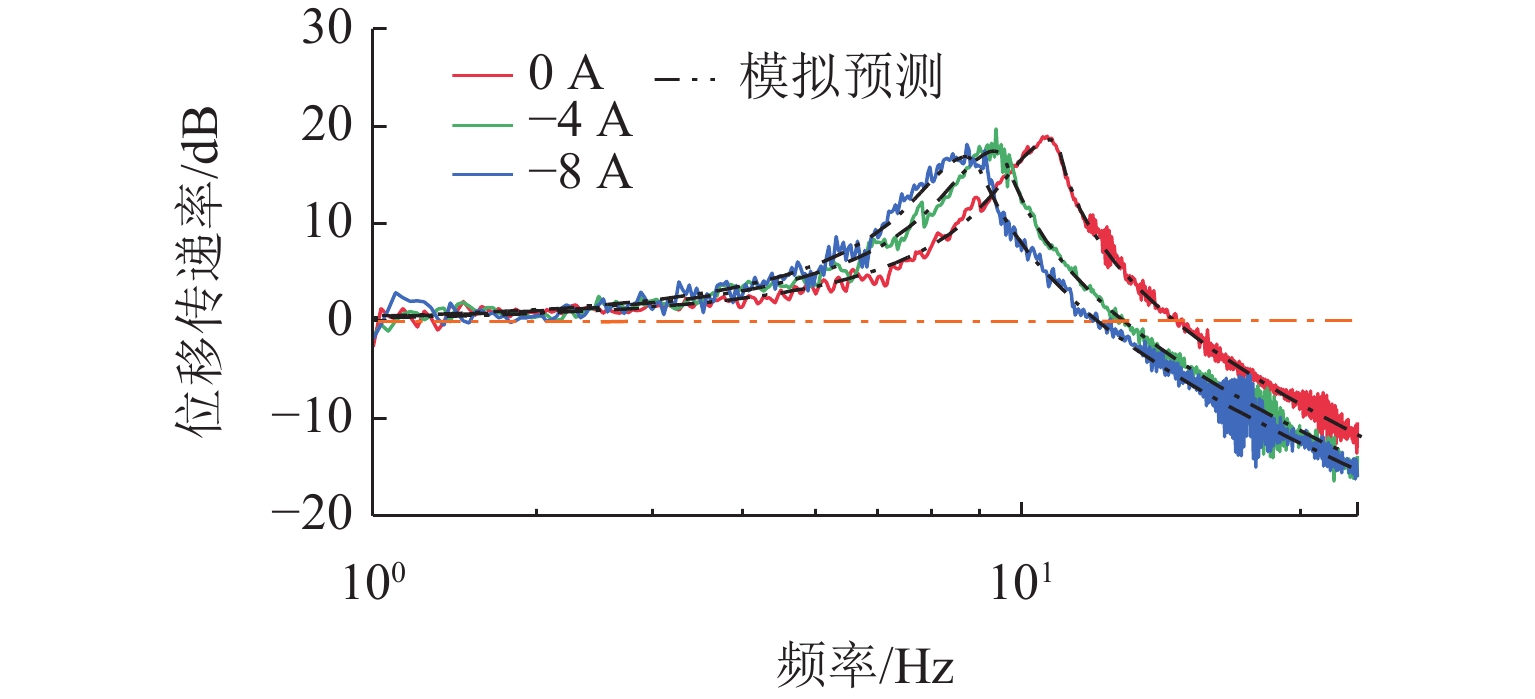
隔振器位移传递率实验测量结果如图15所示. 当电磁线圈通入负电流时,可以降低起始隔振频率,改善隔振性能,且随着负电流的增大,隔振性能改善越明显;当通入−8 A电流时,系统固有频率从10.62 Hz降低到8.64 Hz,起始隔振频率从14.86 Hz降低到12.00 Hz,传递率峰值从18.57 dB降到16.81 dB. 在此区间内可以通过改变电流值实现对不同振源的适应,实验测量结果与计算分析结果基本吻合.
6. 结 论
本文基于电磁线圈嵌套永磁体的结构,提出一种高静-低动刚度的新型可变刚度隔振系统. 通过数值仿真和实验分析了激励、电流等因素对系统位移传递率的影响规律.
由仿真得到了系统参数对其刚度特性的影响规律,确定了结构的尺寸参数. 运用分子电流法构建了系统的力学模型及动力学模型. 采用增量谐波平衡法求解位移传递率,考虑了传统方法分析二次非线性项影响较困难的问题.
搭建了实验测试系统,由结果可知,当通入−8 A电流时,系统固有频率相对于未通入电流降低18.64%,起始隔振频率降低19.25%,且位移传递率的峰值降低了1.76 dB,使隔振系统的隔振效果进一步提升.
-
表 1 结构参数
Table 1. Structural parameters
mm 参数 数值 磁环内径 5 磁环外径 12 磁环厚度 8(上、中),12(下) 线圈内径 15 线圈外径 30 线圈厚度 16 工作气隙 Z 15 线径 s 1 -
[1] 翟明达,张博,李晓龙,等. 基于模糊PID控制的准零刚度磁悬浮隔振平台的设计与实现[J]. 西南交通大学学报,2023,58(4): 886-895.ZHAI Mingda, ZHANG Bo, LI Xiaolong, et al. Design and implementation of magnetic suspension vibration isolation platform with quasi-zero stiffness based on fuzzy PID control[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 886-895. [2] 韩俊淑,孙景工,孟令帅. 一种曲面-弹簧-滚子机构的非线性隔振器特性分析[J]. 振动与冲击,2019,38(3): 170-178.HAN Junshu, SUN Jinggong, MENG Lingshuai. Design and characteristics analysis of a nonlinear vibration isolator using a curved surface-spring-roller mechanism as negative stiffness element[J]. Journal of Vibration and Shock, 2019, 38(3): 170-178. [3] SUN Y, ZHAO J L, WANG M, et al. High-static–low-dynamic stiffness isolator with tunable electromagnetic mechanism[J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(1): 316-326. doi: 10.1109/TMECH.2019.2954910 [4] CARRELLA A, BRENNAN M J, KOVACIC I, et al. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J]. Journal of Sound and Vibration, 2009, 322(4/5): 707-717. [5] CARRELLA A, BRENNAN M J, WATERS T P, et al. Force and displacement transmissibility of a nonlinear isolator with high-static—low-dynamic-stiffness[J]. International Journal of Mechanical Sciences, 2012, 55(1): 22-29. doi: 10.1016/j.ijmecsci.2011.11.012 [6] 周加喜,王心龙,徐道临,等. 含凸轮-滚轮机构的准零刚度系统隔振特性实验研究[J]. 振动工程学报,2015,28(3): 449-455.ZHOU Jiaxi, WANG Xinlong, XU Daolin, et al. Experimental study on vibration isolation characteristics of the quasi-zero stiffness isolator with cam-roller mechanism[J]. Journal of Vibration Engineering, 2015, 28(3): 449-455. [7] 刘兴天,张志谊,华宏星. 新型低频隔振器的特性研究[J]. 振动与冲击,2012,31(5): 161-164.LIU Xingtian, ZHANG Zhiyi, HUA Hongxing. Characteristics of a novel low-frequency isolator[J]. Journal of Vibration and Shock, 2012, 31(5): 161-164. [8] 陆文昌,杨帆,汪少华,等. 气动可调阻尼同轴一体式减振支柱阻尼特性研究[J]. 振动与冲击,2015,34(20): 115-119,128.LU Wenchang, YANG Fan, WANG Shaohua, et al. Damping characteristics of a coaxial integrated strut with adjustable pneumatic damping[J]. Journal of Vibration and Shock, 2015, 34(20): 115-119,128. [9] ZHANG F, SHAO S B, TIAN Z, et al. Active-passive hybrid vibration isolation with magnetic negative stiffness isolator based on Maxwell normal stress[J]. Mechanical Systems and Signal Processing, 2019, 123: 244-263. doi: 10.1016/j.ymssp.2019.01.022 [10] 高双,朱翔,谌宗琦,等. 基于欧拉梁的准零刚度隔振系统动力特性分析[J]. 中国机械工程,2016,27(21): 2869-2876.GAO Shuang, ZHU Xiang, CHEN Zongqi, et al. Analyses on dynamics characteristics of a quasi-zero-stiffness vibration isolation system based on Euler beam[J]. China Mechanical Engineering, 2016, 27(21): 2869-2876. [11] 李爽,楼京俊,杨庆超,等. 双环永磁体型高静低动刚度隔振器设计、建模与试验研究[J]. 振动工程学报,2019,32(4): 675-684.LI Shuang, LOU Jingjun, YANG Qingchao, et al. Design and experiment of a vibration isolator using double-ring permanent magnets springs with negative stiffness[J]. Journal of Vibration Engineering, 2019, 32(4): 675-684. [12] ZHOU N, LIU K. A tunable high-static–low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273. doi: 10.1016/j.jsv.2009.11.001 [13] ZHOU N B, LIU K F. Characterization of an electromagnetic vibration isolator[J]. Journal of Electromagnetic Analysis and Applications, 2011, 3(12): 519-528. [14] 陈树辉. 强非线性振动系统的定量分析方法[M]. 北京:科学出版社,2007:167-180. [15] 王洪昌,蒋书运,梁玉飞. 基于分子电流法轴向永磁轴承轴向刚度的分析[J]. 机械工程学报,2009,45(5): 102-107. doi: 10.3901/JME.2009.05.102WANG Hongchang, JIANG Shuyun, LIANG Yufei. Analysis of axial stiffness of permanent magnet bearings by using the equivalent surface currents method[J]. Journal of Mechanical Engineering, 2009, 45(5): 102-107. doi: 10.3901/JME.2009.05.102 [16] 张海波,邱玉江,蒋书运. 永磁轴承承载能力分子电流模型的积分定义求解方法[J]. 机械工程学报,2016,52(7): 54-59. doi: 10.3901/JME.2016.07.054ZHANG Haibo, QIU Yujiang, JIANG Shuyun. Analysis of the equivalent surface current model for the permanent magnet bearing by using the integral definition[J]. Journal of Mechanical Engineering, 2016, 52(7): 54-59. doi: 10.3901/JME.2016.07.054 [17] LAU S L, ZHANG W S. Nonlinear vibrations of piecewise-linear systems by incremental harmonic balance method[J]. Journal of Applied Mechanics, 1992, 59(1): 153-160. doi: 10.1115/1.2899421 [18] ZHOU J X, ZHANG L. Incremental harmonic balance method for predicting amplitudes of a multi-d. o. f. non-linear wheel shimmy system with combined Coulomb and quadratic damping[J]. Journal of Sound and Vibration, 2005, 279(1/2): 403-416. 期刊类型引用(1)
1. 张明,李洪涛,崔浩东,孙凤,孙兴伟,周冉. 一种半主动式高静-低动刚度电磁隔振器研究. 振动工程学报. 2025(04): 777-784 .  百度学术
百度学术其他类型引用(0)
-






 下载:
下载:














 下载:
下载:

 百度学术
百度学术