高速列车转向架区域气动噪声源的特征识别

王毅刚; 朱朗贤; 王玉鹏; 张昊; 焦燕

doi:10.3969/j.issn.0258-2724.20210636

高速列车转向架区域气动噪声源的特征识别

doi: 10.3969/j.issn.0258-2724.20210636

王毅刚^{1, 2,},
朱朗贤^{1, 2},
王玉鹏^{1, 2},
张昊^{1, 2},
焦燕^{1, 2}

1.
同济大学上海地面交通工具风洞中心，上海 201804
2.
同济大学上海市地面交通工具空气动力与热环境模拟重点实验室，上海 201804

基金项目: 高速铁路基础研究联合基金（U1834201）

详细信息

作者简介:
王毅刚（1964—），男，教授，研究方向为气动噪声、噪声与振动控制，E-mail：yigang.wang@sawtc.com

中图分类号: U270.16
计量
- 文章访问数: 589
- HTML全文浏览量: 273
- PDF下载量: 85
- 被引次数: 6
出版历程
- 收稿日期: 2021-08-18
- 修回日期: 2022-02-17
- 网络出版日期: 2022-11-19
- 刊出日期: 2022-03-17

Characteristic Identification of Aerodynamic Noise Sources in High-Speed Train Bogie Area

WANG Yigang^{1, 2
,},
ZHU Langxian^{1, 2},
WANG Yupeng^{1, 2},
ZHANG Hao^{1, 2},
JIAO Yan^{1, 2}

1.
Shanghai Automotive Wind Tunnel Center, Tongji University, Shanghai 201804, China
2.
Shanghai Key Laboratory of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, Shanghai 201804, China

摘要

摘要:
为了创建高速列车气动噪声源识别方法，以气动声学基本波动方程为基础，将高速列车气动声源等效为无数微球形声源组成，利用声辐射和流场物理量之间的关系，并结合高速列车气动数值仿真技术，建立了高速列车偶极子声源和四极子声源的识别方法，从全新的角度对某高速列车头车气动噪声源进行识别；基于涡声方程声源项特征，进一步揭示了偶极子声源和流场流动的关系. 研究结果明确了高速列车主要偶极子和四极子声源的强弱和分布特征，表明了气流的直接撞击和分离现象是产生声源的主要原因，头车及转向架区域气动噪声源以偶极子声源为主；偶极子声源强度较大位置出现在边沿较为尖锐的地方，在绝大多数情况下流体经过时涡量急剧增加，成为其形成强声源的主要原因.
- 高速列车 /
- 偶极子声源 /
- 四极子声源 /
- 数值仿真 /
- 涡声方程 /
- 风洞实验
Abstract:
In order to create an identification method of aerodynamic noise source of high-speed trains, based on the wave equation of aeroacoustics, the high-speed train aerodynamic sound source was equivalent to countless micro-spherical sound sources. Using the relationship between sound radiation and physical quantities of the flow field, combined with the high-speed train aerodynamic numerical simulation technology, identification methods of dipole sound source and quadrupole sound source of high-speed train were established. The aerodynamic noise sources of a high-speed train head coach were identified from a new perspective by the methods. Based on the characteristics of the sound source term of the vortex sound equation, the relationship between the dipole sound source and the flow field was revealed. The research results clarify the strength and distribution characteristics of the main dipole and quadrupole sound sources of high-speed train, and indicate that the direct impact and separation of the airflow are the main reasons for the sound sources. The aerodynamic noise sources in the head coach and bogie area are mainly dipole sound sources. The strong dipole sound sources appear at the sharp edges of the parts. In most cases, the vorticity increases sharply when the fluid passes by those sharp edges, which becomes the main reason for the formation of a strong sound source.
- high-speed train /
- dipole sound source /
- quadrupole sound source /
- numerical simulation /
- vortex sound equation /
- wind tunnel test

HTML全文

高速列车的主要气动噪声源（如受电弓、转向架、车厢连接处的风挡、头车和尾车的鼻尖和曲线段等）分布广、噪声强度大，对车内外均产生强的噪声干扰，对其的认识和控制一直以来都是研究的难题. 本研究将聚焦与空气相互作用相对剧烈的头车，并重点关注产生气动噪声较大的转向架区域，分析其气动噪声源特征及其产生的内在诱因，为认识和控制气动噪声提供依据.

高速列车气动噪声现象可以抽象为高速运动的固体壁面和空气相互作用在近壁湍流区产生气动声源并辐射声能的物理过程. 对这一物理现象规律的揭示可以追溯到Lighthill^[1-2]最早提出的声比拟思想，其著名的声比拟方程能反映声源和其声传播特征. Curle^[3]将Lighthill理论进一步推广到了可以考虑静止的固体边界，Ffowcs和Hawkings^[4-5]又进一步考虑了运动的固体边界，推导出著名的FW-H方程. Powell^[6]通过引入涡量概念提出了涡声理论，揭示了涡与声的关系. 这些研究中，方程的声源项将声源区分为单极子、偶极子和四极子的基本声源特征，能反映声源和流动物理量之间的关系，揭示了声产生的本质，其传播项反映了声辐射和传播特征. 尽管这些方程看似反映了气动声源及其声传播的规律，但对于像高速列车这样高速行驶的物体，方程难以求解，只能定性描述，难以具体和定量描述，实质上难以揭示复杂流动产生声及其传播规律. 随着数值仿真技术的发展，FW-H方程也仅用于远场噪声计算，近声场及流场内的声源及其辐射和传播仍缺少准确的研究方法. 对于流场内声场的研究，后续也有如Bogey等^[7]通过分解流场中的物理量并代入Euler方程，得到线性化的欧拉方程求解声源. Ewert等^[8]在此基础上推导出的声波扰动方程（APE）可以对近声场问题进行求解，但其近似度偏高. 近年来，本团队基于经典的声学方程（FW-H方程、涡声方程）源项特征，结合流体数值仿真技术，直接从源项入手，不涉及噪声的辐射和传播，描述声源特性. 如以圆柱绕流和汽车整车为研究对象，结合涡声方程、非齐次声波波动方程对声源进行了分析^[9-10]，能够清晰给出声源大小和分布，但结果发现不该发声的部位有声源分布（假声源）. 总之，对气动声源的认识和描述在方法上的探究将是持久的具有挑战性的难题.

气动噪声是高速列车最主要的噪声源^[11-12]之一，当列车速度达到一定值时，其噪声的主要噪声源来自转向架、轮轨接触位置、受电弓和车间风挡，而头车迎风的第一个转向架噪声远大于其他转向架^[13-14]，因而，头车转向架区域气动噪声成为研究的重要内容. 风洞试验和线路实测成为识别气动噪声现象的重要手段. 如日本Nagakura^[15]采用声学镜分别在声学风洞和实车路试中发现头车转向架区域和排障器区域噪声最大. He等^[16]通过传声器阵列对实车进行声源识别测量表明头车转向架为主要噪声源，其中心频率630 Hz的噪声能量大于受电弓和车厢连接处. Lauterbach等^[17]、Atsushi^[18]分别于德国、日本等风洞中开展了转向架区域气动噪声特性研究. 国内近些年来利用低速风洞也开展了大量的转向架区域气动噪声特性和控制研究^[14]，仿真计算成为高速列车气动噪声研究的重要手段. 在研究气动噪声现象的同时，结合流体仿真结果分析产生气动噪声的原因，也有对气动噪声控制的探索. 如上所述，仿真计算主要基于FW-H方程计算远场辐射噪声. 如张亚东等^[19]考虑了高速列车转向架的细微结构，不考虑车体对声辐射的屏蔽作用，仅对单独转向架模型进行了声源仿真分析. 黄莎等^[20]利用1∶8模型预测了转向架区域增加裙板时列车远场气动噪声，指出适当增加裙板面积，降噪量增大. 朱剑月等^[21]基于可穿透声源积分面的FW-H方程研究了简化转向架区域气动噪声，并结合流场分析指出转向架区域（轮对、车轴等钝体、舱壁）具有复杂的涡系结构，是该区域气动噪声的主要产生机理. Han等^[22]利用边界元方法研究了简化转向架模型表面的气动噪声源分布特性，结果表明，简化转向架末端的第二根轮轴以及轮组表面是主要的气动噪声源. 基于APE方法模拟时间和空间域中由流动诱导引起的噪声也得到了一定的应用. 高阳等^[23]基于大涡模拟和声扰动方程，对1∶8缩比列车模型近场噪声进行了预测，探索了转向架区域的声场特性. 总之，对高速列车转向架区域的气动噪声研究，无论测试手段还是仿真手段，主要关注气动噪声现象和特性，探询气动噪声问题并试图控制. 即便是声源识别技术也难以给出声源局部分布特征，仿真计算也仅能较为准确计算远场噪声. 可见，在目前技术条件下难以清晰和准确获得转向架区域气动噪声的产生机制.

在上述研究现状基础上，首先基于球形声源声辐射理论和高速列车非定常流场物理量特性，建立声场、气动声源和流场之间的关系，确定声源辐射声压和流场物理量的关系，探索气动声源识别方法；在此基础上聚焦头车区域，重点关注转向架区域，对气动声源的特性进行识别，进一步结合涡声理论，探索主要气动噪声源产生的诱因.

1. 声源识别方法建立

假设高速列车高速行驶时，其车体和空气相互作用产生的流场流动为理想不可压缩流体流动，则其近壁面湍流区域呈现偶极子气动声源特征，空间湍流区域呈现四极子气动声源特征^[24]. 进一步假设湍流区域气动噪声源由无数个微小的球形声源组成，则每个球形声源向空间传播的声波动球坐标方程为

$\begin{split} & \frac{{{\partial ^2}p}}{{c_0^2\partial {t^2}}} - \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}\frac{{\partial p}}{{\partial r}}} \right) - \frac{1}{{{r^2}\sin \;\varphi }}\left( {\sin \;\varphi \frac{{\partial p}}{{\partial \varphi }}} \right) - \\ & \quad \frac{1}{{{r^2}{{\left( {\sin \;\varphi } \right)}^2}}}\frac{{{\partial ^2}p}}{{\partial {\alpha ^2}}} = 0\text{，} \end{split}$

(1)

式中： $p$ 、 ${c_0}$ 分别为声压和声速； $r$ 、 $t$ 分别为声波传播的距离和时间； $\varphi$ 、 $\alpha$ 分别为球源的方位角和极角.

1.1 偶极子声源识别方法

考虑偶极子球形声源为力源，沿一个方向的振动，其表面声压分布不随极角 $\alpha$ 变化，由式（1）求解其辐射声压为

$p(r,\varphi ,t) = {\text{i}}\frac{{{\rho _0}{c_0}k{a^3}{v_{\rm{a}}}(1 + {\text{i}}kr)\cos \;\varphi }}{{{r^2}[ {2 - {{(ka)}^2} +2 {\text{i}}ka} ]}}{{\rm{e}}^{{\text{i}}\left[ {{\omega _0}t - k(r - a)} \right]}}\text{，}$

(2)

式中： ${\rho _0}$ 为空气密度； $k$ 、 ${\omega _0}$ 分别为波数和角频率； $a$ 、 ${v_{\rm{a}}}$ 分别为球源半径和空间粒子的脉动速度.

假设流场中每个微元对应一个偶极子球形声源，该声源的单位体积脉动力f决定了声源的强度. 图1为偶极子声源脉动力和其边界上的脉动速度示意. 图中： ${v_{\rm{r}}}$ 、 ${v_{\text{φ}} }$ 分别为球边界面上径向和周向脉动速度； $s$ 为球源表面积. 根据声源边界面上速度连续和作用力与反作用力相等、方向相反原则，可得

图 1 偶极子声源脉动和声辐射示意

Figure 1. Schematic diagram of dipole sound source pulsation and sound radiation

下载: 全尺寸图片幻灯片

$\boldsymbol{f}{{\rm{e}}}^{{\rm{i}}{\omega }_{0}t}={\int } _{s}p(a,\varphi ,t){\rm{cos}}\;\varphi {\rm{d}}{s} \text{，}$

(3)

${v_{\rm{a}}} = {v_{\rm{r}}} .$

(4)

经过推导可以得到，沿任意方向脉动力所致的单个偶极子声源所辐射的声压为

$\begin{split} & p(r,\varphi ,t) = \frac{{3\boldsymbol{f}\sqrt {1 + {{(kr)}^2}} \cos \;\varphi }}{{4{\text{π}} {r^2}\sqrt {1 + {{(ka)}^2}} }}\times \\ & \quad {{\rm{e}}^{{\rm{i}}\left[ {{\omega _0}t - k(r - a) + \arctan (kr)- \arctan (ka)} \right]}}. \end{split}$

(5)

将式（5）变换成笛卡尔坐标下的方程，并考虑声源的位置不在坐标原点，而位于 ${\boldsymbol{y}} = ({{{y}}_1},{{{y}}_2},{{{y}}_3})$ 的一般情况，对于单色生源，则 ${\boldsymbol{x}} = \left( {{{{x}}_1},{{{x}}_2},{{{x}}_3}} \right)$ 处的声压为

$p(\boldsymbol{x},t)=-\boldsymbol{f}{\nabla }\frac{{{\rm{e}}}^{{\rm{i}}({\omega }_{0}t-k\left|\boldsymbol{x}-\boldsymbol{y})\right|}}{4{\text{π}} \left|\boldsymbol{x}-\boldsymbol{y}\right|} \text{，}$

(6)

式中： ${\nabla }$ 为哈密尔顿算子.

对于非单色声源，式（6）可改写为

$p(\boldsymbol{x},t)=-\frac{1}{4{\text{π}} }\frac{\partial }{\partial {x}_{i}}\left[\frac{{\boldsymbol{f}}({\boldsymbol{y}},t-\left|\boldsymbol{x}-\boldsymbol{y}\right|/{c}_{0})}{\left|\boldsymbol{x}-\boldsymbol{y}\right|}\right]_{\boldsymbol{y}} .$

(7)

利用链式微分法则，对式（7）进一步求导展开可以得到单个偶极子声源向远场辐射声压为

$p({\boldsymbol{x}},t) = \frac{{{{{x}}_i} - {{{y}}_i}}}{{4{\text{π}} {r^2}}}\left[\frac{1}{{{c_0}}}\frac{{\partial {\boldsymbol{f}}({\boldsymbol{y}},t - r/{c_0})}}{{\partial t}} + \frac{{{\boldsymbol{f}}({\boldsymbol{y}},t - r/{c_0})}}{r}\right] \text{，}$

(8)

式中： ${\boldsymbol{f}}({\boldsymbol{y}},t)$ 为时间t时作用于位置 ${\boldsymbol{y}}$ 处流体上的力矢量，根据数学知识可知，矢量函数 ${\boldsymbol{f}}$ 可由式（9）获得； ${{{y}}}_{i}、{{{x}}}_{i}$ 分别为距第i个声源的坐标及观测点的坐标.

$\boldsymbol{f}={\nabla p}_{0} + \nabla \times \boldsymbol{u},$

(9)

式中： ${p_0}$ 为流场中的压力； ${\boldsymbol{u}}$ 为速度^[24].

从式（7）可以看出，对 ${\boldsymbol{f}}$ 求散度，即对式（9）求散度， $\nabla \cdot \nabla \times {\boldsymbol{u}}{\text{ = }}0$ ，即 $\nabla \times {\boldsymbol{u}}$ 也不可能产生声，因此，可令 ${\boldsymbol{f}} = \nabla {p_0}$ . 则式（8）单个偶极子源产生的声压表达式可改写为

$p(\boldsymbol{x},t)=\frac{{{{x}}}_{i}-{{{y}}}_{i}}{4{\text{π}} {r}^{2}}\left[\frac{1}{{c}_{0}}\frac{\partial \nabla {p}_{0}}{\partial t} + \frac{\nabla {p}_{0}}{r}\right] .$

(10)

式（10）中 $\dfrac{\nabla {p}_{0}}{r}$ 随距离的增加衰减较快，对远场声辐射而言可以忽略，主要辐射的声压为第一项. 因此，源的辐射能力可由式（11）表示.

$p({\boldsymbol{x}},t) = \frac{{{{{x}}_i} - {{{y}}_i}}}{{4{\text{π}} {r^2}}}\frac{1}{{{c_0}}}\frac{{\partial \nabla {p_0}}}{{\partial t}}.$

(11)

1.2 四极子声源识别方法

四极子源可以等效成两个距离很近、相位相反、强度相等的偶极子声源的叠加. 采用两个大小相等，方向相反的力点源 ${\boldsymbol{f}}$ 和 ${\boldsymbol{ - f}}$ 组成四极子声源，如图2所示. 其中，单个力点源所致声场为式（6）所示，则两个力点源所致的四极子单色声源声场为

图 2 由一对力点源构成的四极子声源

Figure 2. Quadrupole sound source composed of pair of force point sources

下载: 全尺寸图片幻灯片

$\begin{split} &p_2({\boldsymbol{x}},t)=-\boldsymbol{f}({{\boldsymbol{y}}}_{{\rm{d}}1}){\text{•}}{\nabla }\frac{{{\rm{e}}}^{{\rm{i}}({\omega }_{0}t-k\left|{{{\boldsymbol{x}}}}-{{{{\boldsymbol{y}}}}}_{{\rm{d}}1}|\right)}}{4{\text{π}} \left|{\boldsymbol{x}}-{{{{\boldsymbol{y}}}}}_{{\rm{d}}1}\right|} +\\ &\quad \boldsymbol{f}({{\boldsymbol{y}}}_{{\rm{d}}2}){\text{•}}{\nabla }\frac{{{\rm{e}}}^{{\rm{i}}({\omega }_{0}t-k\left|{\boldsymbol{x}}-{{\boldsymbol{y}}}_{{\rm{d}}2}|\right)}}{4{\text{π}} \left|{\boldsymbol{x}}-{{{{\boldsymbol{y}}}}}_{{\rm{d}}2}\right|} , \end{split}$

(12)

式中：y_d1为源1的坐标；y_d2为源2的坐标.

令 ${{\boldsymbol{\delta}} _y}$ 为两个力点源的距离，两个力源的位置分别为 ${{{{\boldsymbol{y}}}}_{{\rm{d}}1}} = {\boldsymbol{y}} - {{\rm{\delta}} _y}/2$ 和 ${{{{\boldsymbol{y}}}}_{{{\rm{d}}2}}} = {\boldsymbol{y}}{\text{ + }}{{\rm{\delta }}_y}/2$ ，采用两个力点源组合得到的四极子声源的声场解为^[24]

$p_2({\boldsymbol{x}},t)=\frac{1}{4{\text{π}} }{\nabla } \boldsymbol{f}(\boldsymbol{y})\left[{\delta }_{{y}}{\nabla }\frac{{{\rm{e}}}^{{\rm{i}}({\omega }_{0}t-k\left|{\boldsymbol{x}}-{\boldsymbol{y}}\right|)}}{\left|{\boldsymbol{x}}-{\boldsymbol{y}}\right|}\right] .$

(13)

$\underset{{\delta }_{{\boldsymbol{y}}}\to 0}{{\rm{lim}}}\boldsymbol{f}\left({\boldsymbol{y}}\right)({\delta }_{y}{)}_{j}={T}_{ij}(\boldsymbol{y})$ 为湍流应力. 式（13）可变为

$p_2(\boldsymbol{x},t)=\frac{1}{4{\text{π}} }{T}_{ij}\left(\boldsymbol{y}\right)\frac{{\partial }^{2}}{\partial {x}_{i}\partial {x}_{j}}\frac{{{\rm{e}}}^{{\rm{i}}({\omega }_{0}t-k\left|\boldsymbol{x}-\boldsymbol{y}\right|)}}{\left|\boldsymbol{x}-\boldsymbol{y}\right|}.$

(14)

将式（14）变为非单色四极子声源的声压解为

$p_2({\boldsymbol{x}},t) = \frac{1}{{4{\text{π}} }}\frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}\frac{{{T_{ij}}({\boldsymbol{y}},t - \left| {{\boldsymbol{x}} - {\boldsymbol{y}}} \right|/{c_0})}}{{\left| {{\boldsymbol{x}} - {\boldsymbol{y}}} \right|}}.$

(15)

利用复合函数链式求导法则，可以将 ${T_{ij}}({\boldsymbol{y}},t - {{\left| {{\boldsymbol{x}} - {\boldsymbol{y}}} \right|} \mathord{\left/ {\vphantom {{\left| {{\boldsymbol{x}} - {\boldsymbol{y}}} \right|} {{c_0}}}} \right. } {{c_0}}})$ 对接收点的位置导数转换成对时间t的时间导数形式，从而使得声源函数可以解释为一个反映湍流应力 ${T_{ij}}({\boldsymbol{y}}) = {\rho _0}{{\boldsymbol{u}}_i}{{\boldsymbol{u}}_j}$ 随时间变化的量，从而使之具有实际物理意义^[24]，其中： ${{\boldsymbol{u}}_i}$ 和 ${{\boldsymbol{u}}_j}$ 是速度分量，则式（15）可变为单个四极子声源向远场辐射声压的公式，如式（16）.

$\begin{split} &p_2(\boldsymbol{x},t)=\frac{({{{x}}}_{i}-{{{y}}}_{i})({{{x}}}_{j}-{{{y}}}_{j})}{4{\text{π}} {r}^{3}}\left[\frac{{\rho }_{0}}{{{c}^{2}_{0}}}\frac{{\partial }^{2}}{\partial {t}^{2}}{{\boldsymbol{u}}^{2}_{{{\rm{r}}}}} + \right.\\ &\quad \left. 3\frac{{\rho }_{0}}{{c}_{0}r}\frac{\partial }{\partial t}{{\boldsymbol{u}}^{2}_{{{\rm{r}}}}} + 3\frac{{\rho }_{0}}{{r}^{2}}{{\boldsymbol{u}}^{2}_{{{\rm{r}}}}}\right], \end{split}$

(16)

式中： ${{\boldsymbol{u}}_{{{\rm{r}}}}}$ 为脉动速度，因为是同一漩涡，脉动速度分量 ${{\boldsymbol{u}}_{{{{\rm{r}}i}}}}$ 、 ${{\boldsymbol{u}}_{{{{\rm{r}}j}}}}$ 相关，所以可令 ${{\boldsymbol{u}}_{{{{\rm{r}}i}}}} = {{\boldsymbol{u}}_{{{{\rm{r}}j}}}} = {{\boldsymbol{u}}_{{{\rm{r}}}}}$ ^[24].

同样，式（16）中方程右端中括号内的第二项和第三项分别随着距离的一次方和二次方衰减较快，对远场声辐射而言，主要辐射的声压为第一项. 因此，源的辐射能力可由式（17）表示

$p_2(\boldsymbol{x},t)=\frac{({{{x}}}_{i}-{{{y}}}_{i})({{{x}}}_{j}-{{{y}}}_{j})}{4{\text{π}} {r}^{3}}\frac{{\rho }_{0}}{{{c}_{0}}^{2}}\frac{{\partial }^{2}}{\partial {t}^{2}}{{\boldsymbol{u}}^{2}_{{{\rm{r}}}}} .$

(17)

式（11）和式（17）分别给出单个偶极子和单个四极子气动声源的辐射声压表达式. 令式中距观察点的距离 $r$ 趋向于声源半径，两式分别反应了偶极子声源和四极子声源辐射声压的能力. 进一步将流场中任一微元作为声源，应用式（11）和式（17）对声压值进行求解，就能得到流场中反应声源的大小和分布特征，由此建立识别声源的方法. 该方法用于高速列车的气动噪声源识别，从新的视角揭示其气动噪声源特性和分布.

2. 列车模型风洞实验及仿真计算

用于计算湍流场中偶极子声源和四极子声源特征的式（11）、（17），其右端项各项物理量要通过流体数值仿真手段获取. 为了保证高速列车数值仿真计算的准确性，研究采用了风洞实验结果和仿真计算结果对比的方式，验证并保证计算方法的可靠性.

2.1 高速列车1∶8三车编组风洞声学实验

实验在同济大学上海地面交通工具风洞中心的低速气动-声学风洞中进行. 该风洞具有良好的气动和声学环境，满足本研究的实验需求. 考虑到气动噪声数值仿真计算量和风洞试验段大小的限制，研究对象选取了某高速列车1∶8的三车编组模型，包括头车、中间车和尾车（和头车相同），不含受电弓、空调进出风口等结构. 实验中用特别设计的板结构模拟地面，并安装有列车轨道. 列车通过车轮和轨道相连固定在地板上. 图3为1∶8高速列车模型在风洞试验段的位置和安装情况. 列车模型产生的气动噪声大小通过布置在射流流场外的自由场传声器进行测量，测点布置（高度0.8 m）如图3和图4所示. 实验选用的喷口风速为250 km/h.

图 3 风洞试验段高速列车模型安装及测点

Figure 3. Installation of high-speed train model and measuring points in wind tunnel test section

下载: 全尺寸图片幻灯片

图 4 流场外传声器测点分布（单位： m）

Figure 4. Distribution of measuring points of microphones outside the flow field （unit: m）

下载: 全尺寸图片幻灯片

2.2 数值计算

为了给后续声源计算提供有效可靠的流场数值仿真计算数据，研究主要计算高速列车模型向远场的噪声辐射. 该计算必须对流场进行非定常计算，继而基于FW-H方法计算远场声压，其计算的准确性能够反映数值计算方法和过程的准确性. 所以，对远场声压仿真计算的验证可保证后续声源计算所需数据的可靠性.

数值仿真采用了和风洞实验完全相同的高速列车1∶8的三车编组模型，含地面和轨道. 模型长9.5 m，宽0.42 m，高0.50 mm. 计算域尺寸长29.0 m，宽5.50 m，高4.95 m，头车鼻尖距离入口边界6.5 m，尾车鼻尖距离出口边界13 m. 整车面网格数约为350万，体网格数约为1.7亿. 远场噪声测点布置与风洞实验相同.

流场入口边界条件设置为速度入口，来流速度250 km/h，出口边界条件为压力出口，静压为一个大气压. 列车和地面为无滑移网格壁面，计算域的顶面和侧面设置为对称性边界条件.

计算采用商业软件STAR-CCM + ，计算过程中先用K-Omega模型进行定常流场的求解，将定常结果作为非定常计算的初始条件，使得非定常计算能够快速收敛. 非定常计算的湍流模型采用LES （ large eddy simulation）大涡模拟，亚格子尺度模型选用WALE Subgrid Scale模型. 首先进行大时间步长的非定常仿真计算，让流场快速稳定，时间步长为5 × 10⁻⁴s，共1000时间步. 然后进行小时间步长的非定常仿真计算，时间步长为5 × 10⁻⁵s，在2000时间步后，流场稳定，开始声场计算，用FW-H方程计算远场噪声测点的噪声数据，共采集2000个时间步的数据.

为了保证计算的准确性，本文对网格无关性进行了计算分析，计算结果如表1所示. 在网格量为4500万时，计算结果已具有一定可接受的精度；在 7000万时，精度进一步提高，再结合频谱结果，说明已能满足精度要求，此时网格具备了独立性.

表 1 网格独立性测试结果

Table 1. Grid independence test results

网格量/万	图 4 中测点 3/ 总声压级	与风洞实验总声压级差值
3800	79.8	2.3
4000	80.2	2.7
4500	78.6	1.1
7000	78.4	0.9

下载: 导出CSV

| 显示表格

为了确保整个声源识别区域的网格大小一致，将该区域的网格加密成相同的大小，使得网格增加到1.7亿，会使计算结果更好.

2.3 仿真与实验结果对比

图5给出了图4中测点2和测点3处风洞实验和数值仿真计算获得的1/3倍频程声压级频谱（风洞实验数据的频率分辨率为12 Hz，数值计算的频率分辨率为10 Hz）. 从两个频谱可以看出：仿真计算结果和风洞实验测量结果一致性较好，最大偏差仅约3 dB（A），计算结果具有一定的可靠性，其非定常流动的计算结果可以用于本研究关于声源识别和分析中.

图 5 风洞实验和仿真计算的声压级对比

Figure 5. Comparison of sound pressure level between wind tunnel experiment and simulation

下载: 全尺寸图片幻灯片

3. 头车及转向架区域气动噪声源特征

式（11）和式（17）给出了单个偶极子声源和四极子声源的计算方法，上述的非定常仿真计算给出了两式中各气动量的计算结果，两者结合就可以得出列车流场区域以辐射声压能力描述的声源强度和特征.

3.1 偶极子声源分布特性

偶极子声源为近壁面上流体和壁面的相互作用产生. 图6为靠近头车表面空间面上（近似看成车体表面上）偶极子声源的分布特征，RMS为均方根值. 从图中可知：列车车身表面除了曲线部位和鼻尖型线有量值较小、沿型线分布的偶极子声源外，大面积平顺表面几乎不存在偶极子声源. 尽管这些区域由于边界层的存在会呈现壁面和流体的相互作用，有产生偶极子声源的可能，但相比列车下部声源，其量值小，可以忽略.

图 6 近头车表面的偶极子声源分布

Figure 6. Dipole sound source distribution near the surface of the head coach

下载: 全尺寸图片幻灯片

从图6中可知：偶极子声源主要出现在排障器前沿、前后车轮下方边沿（图6（a）、（b））、轮轴两端迎风棱边、流体与转向架撞击的棱边位置（尤其位于两侧被气流冲击的杆件位置）、转向架舱后沿，两侧裙板下边沿（图6（b）、（c）、（d））及车轮与轮轨相接触位置（图6（a）、（e）），同时由于排障器导致的气流分离，在其前缘下方的地面上也有偶极子声源产生（图6（e））.

进一步分析可看出：偶极子声源出现在流体直接冲击的物体表面附近，其气流的直接撞击和分离现象明显，在其撞击和分离位置，壁面和流体的作用明显，是产生偶极子声源的主要原因. 前5个较大声源从强到弱的顺序为前车轮下方前沿、排障器前沿、暴露在流场中的转向架杆件、裙板边沿和后车轮下方前沿.

3.2 四极子声源分布特性

四极子声源位于空间湍流场区域，为了清晰呈现头车和转向架区域的特征，在3个方向上选取了不同截面来呈现四极子声源的大小和分布，如图7所示.

图 7 头车上的不同截面位置

Figure 7. Different cross-section positions on the head coach

下载: 全尺寸图片幻灯片

图8为图7中不同截面上四极子声源的分布特征. 由图8可知：最大四极子声源出现在排障器前沿分离的湍流区贴近壁面，其次是排障器尾沿后的剪切层区域、前轮后下方的尾迹区及转向架杆件的尾迹区；在转向架和地面间、舱尾段区的空间湍流场中，都存在四极子声源，但量级较小. 和偶极子产生声源的原因类似，流体与固体壁面作用产生分离形成湍流尾迹和剪切层流动是四极子声源产生的主要原因.

图 8 四极子声源的分布

Figure 8. Distribution of the quadrupole sound source

下载: 全尺寸图片幻灯片

偶极子声源和四极子声源相比较表明：1）偶极子声源声压强度最大量值约4.3 × 10⁹，四极子声源声压强度最大量值约9.9 × 10⁷，两者相差约一个数量级，前者较大强度的声源分布区域比后者大，说明了头车及转向架区域气动噪声源以偶极子声源为主，这和以往研究结论一致；2）偶极子声源和四极子声源的分布区域几乎相同（除了剪切层区域），虽两者形成的机制不同，但其都会在流体分离区出现，可能在同一位置出现，即某些区域声源可能是两者的叠加.

4. 转向架区域气动声源与流动关系

4.1 涡声方程

Powell^[6]通过引入涡量的概念提出涡声理论，揭示了涡和声场之间的关系，如式（18）.

$\begin{split} & \frac{{{\partial ^2}{\rho _0}}}{{\partial {t^2}}} - c_0^2{\nabla ^2}{\rho _0} = {\kern 1pt} \nabla \left[ {{\rho _0}\left( {{\text{ω}} \times {\boldsymbol{u}}} \right) - {\boldsymbol{u}}\frac{{\partial {\rho _0}}}{{\partial t}}} \right.- \\ &\quad \left. {{\kern 1pt} \frac{{{{\boldsymbol{u}}^2}}}{2}\nabla {p_0} + \nabla \left( {{p_0} - {\rho _0}{c_0}^2 + {\rho _0}\frac{{{{\boldsymbol{u}}^2}}}{2}} \right)} \right], \end{split}$

(18)

式中： ${\text{ω}}$ 为流动涡矢量.

上述研究表明，头车及转向架区域气动噪声源以偶极子声源为主，放此处不考虑四极子声源，仅聚焦偶极子声源. 在低马赫数等熵条件下，忽略高阶小量，式（18）可简化为

${\nabla ^{\text{2}}}p - \frac{1}{{{c_0}^2}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} = - {\rho _0}{\rm{div}}({\text{ω}} \times {\boldsymbol{u}}).$

(19)

式（19）左端为传播项，右端为偶极子声源项，反映了偶极子声源强度和流动物理量涡量、流速及其夹角之间的关系. 若声源强度降低，除了 ${\text{ω}}$ 和 ${\boldsymbol{u}}$ 变小外，两者之间的夹角越小越好.

4.2 偶极子声源与流场物理量的关系

前述将声源识别方法和仿真计算结合给出了转向架区域偶极子声源的强弱和分布特征，此处将根据式（19）并利用流场数值计算结果，对前6个较大声源和流场涡量、速度及其夹角的关系进行分析，探究声源产生的原因.

1）前车轮

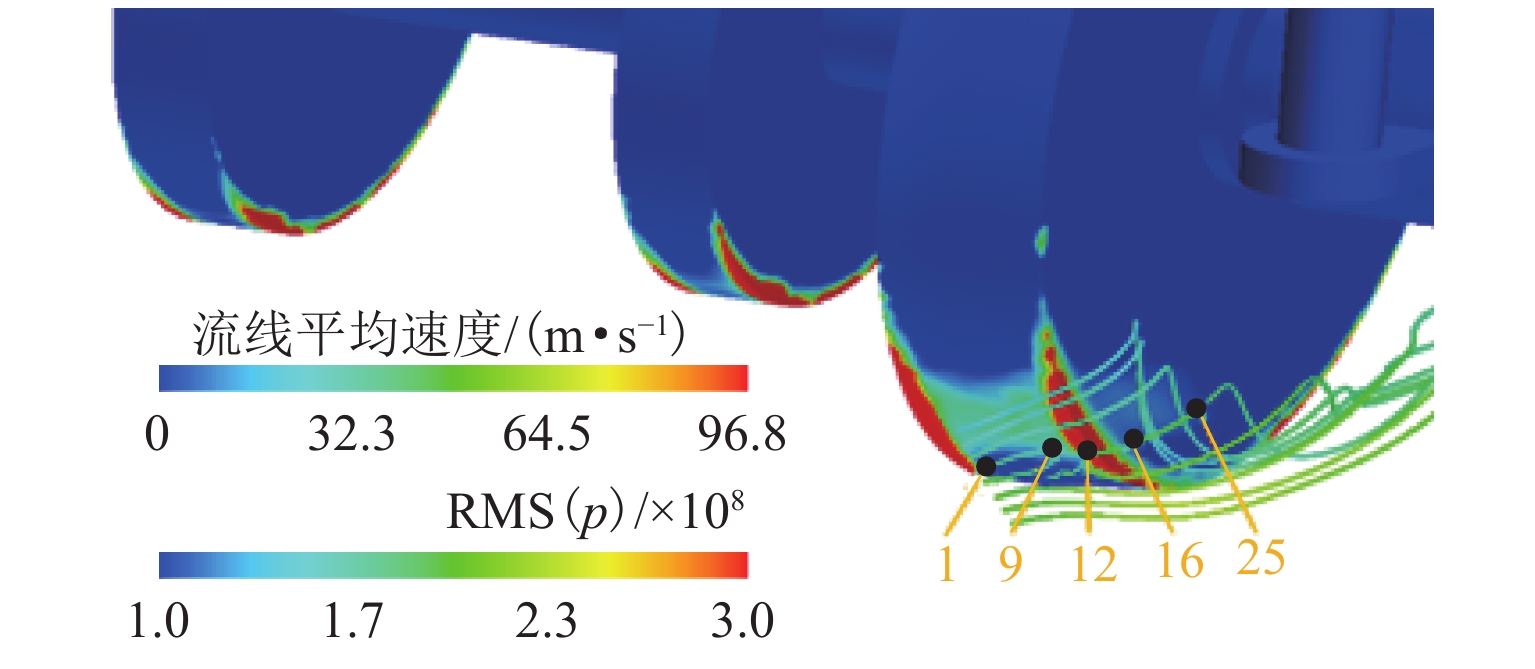
图9为前车轮上偶极子声源分布以及经过车轮最大声源位置的一族流线. 选取其中一根流线（标有圆点），对该流线上各点的 ${\rm{div}}({\text{ω}} \times {\boldsymbol{u}})$ 、 ${\text{ω}}$ 、 ${\boldsymbol{u}}$ 及后两者夹角 $\theta$ 的正弦 $(\sin \;\theta)$ 进行计算，结果如图10所示. 为了将物理量放在同一张图上进行比较，每一种物理量各点的取值为每一点的值除以所选流线上所有点的平均值（后续图12、14、16、18、20相同）. 从图10中可以看出：流体流经车轮边沿附近时（点12），声源强度量 ${\rm{div}}({\text{ω}} \times {\boldsymbol{u}})$ 急剧增加，经过棱边后又急剧减小，流体的涡量随之也增加（略有延迟）（点13），流速略有提升，涡量和速度的夹角接近90°；对于声源强度而言， ${\text{ω}}$ 的变化对声源强度起决定作用， $\theta$ 接近90° 也是该处声源强度大的重要原因.

图 9 前车轮声源区域及部分流线

Figure 9. Sound source area of front wheel and part of the streamline

下载: 全尺寸图片幻灯片

图 10 前车轮声源区域物理量沿流线变化的对比

Figure 10. Comparison of physical quantities’ changes along a streamline around the front wheel

下载: 全尺寸图片幻灯片

图 12 排障器声源区域物理量沿流线变化的对比

Figure 12. Comparison of physical quantities’ changes along a streamline around the cowcatcher

下载: 全尺寸图片幻灯片

图 14 转向架突出杆件声源区域物理量沿流线变化的对比

Figure 14. Comparison of physical quantities’ changes along a streamline around the bogie protruding rod

下载: 全尺寸图片幻灯片

图 16 裙板声源区域物理量沿流线变化的对比

Figure 16. Comparison of physical quantities’ changes along a streamline around the apron

下载: 全尺寸图片幻灯片

图 18 后车轮声源区域物理量沿流线变化的对比

Figure 18. Comparison of physical quantities’ changes along a streamline around the rear wheel

下载: 全尺寸图片幻灯片

图 20 转向架舱后沿声源区域物理量沿流线变化的对比

Figure 20. Comparison of physical quantities’ changes along a streamline around the rear edge of bogie cavity

下载: 全尺寸图片幻灯片

2）排障器

图11为排障器前缘附近偶极子声源分布以及经过该位置的一族流线，选取其中标有圆点的一根流线进行计算分析. 图12为声源项各物理量的计算结果. 从图中可以看出：靠近排障器前沿时声源强度急剧增加，出现两个峰值，分别位于流线经过排障器转角前（点9）和转角后（点12）；在此过程中，涡量随之急剧增加（略有延迟），过了棱边后又急剧降低；流体在遇到前沿棱边前开始加速，到棱边位置达到最大，后又快速下降；声源强度的第一个峰值和流体加速及涡量增加有关，而后一个峰值由于涡量增加较大，成其形成的主要原因；同样涡量和速度的夹角接近90° 也是此处声源强度大的重要原因.

图 11 排障器声源区域及部分流线

Figure 11. Sound source area of cowcatcher and part of the streamline

下载: 全尺寸图片幻灯片

3）突出的杆件

图13为转向架突出杆件附近偶极子声源分布以及经过该位置的一族流线，选取其中标有圆点的一根流线进行计算分析. 图14为声源项各物理量的计算结果. 由图14可知：所选流线表明流体碰撞到杆件时减速，沿壁面流动时加速，涡量也急剧增加，两者到边沿时达到最大（点10），而声源强度略超前达到最大，说明涡量和流速对声源都有贡献，而前者更为明显；同样涡量和速度的夹角接近90° 也是此处声源强度大的重要原因.

图 13 转向架突出杆件声源区域及部分流线

Figure 13. Sound source area of bogie protruding rod and part of the streamline

下载: 全尺寸图片幻灯片

4）裙板

图15为裙板边沿附近偶极子声源分布以及经过该位置的一族流线，选取其中标有圆点的一根流线进行计算分析. 图16为声源项各物理量的计算结果. 从图中可以看出：流体流经裙板边沿时，涡量急剧增加（点11～12），而速度增加不明显，因而，涡量变化成为产生声源的主要原因；同时，涡量和速度的夹角经过棱边时有一定的减小，随后又增加到接近90°，造成声源强度出现两个峰值.

图 15 裙板声源区域及部分流线

Figure 15. Sound source area of apron and part of the streamline

下载: 全尺寸图片幻灯片

5）后轮

图17为后轮边沿附近偶极子声源分布以及经过该位置的一族流线，选取其中标有圆点的一根流线进行计算分析. 图18为声源项各物理量的计算结果. 从图中可以看出：流体沿着车轮正面流动时，涡量增加缓慢，当达到边沿时急剧增加（点16），后又急剧减小，成为该部分产生声源的主导因素，尽管流速也有增加，涡量和速度夹角有所变化，但其影响较小.

图 17 后车轮声源区域及部分流线

Figure 17. Sound source area of rear wheel and part of the streamline

下载: 全尺寸图片幻灯片

6）转向架舱后沿

图19为转向架舱后沿附近偶极子声源分布以及经过该位置的一族流线，选取其中标有圆点的一根流线进行计算分析. 图20为声源项各物理量的计算结果. 从图中可以看出：在气流达到棱边（点13）之前，流体加速，涡量增加，两者共同的作用使该区域（点10～16）声源强度增加.

图 19 转向架舱后沿声源区域及部分流线

Figure 19. Sound source area of the rear edge of bogie cavity and part of the streamline

下载: 全尺寸图片幻灯片

上述分析可以看出：出现在列车部件表面附件的偶极子声源，其强度较大位置出现在边沿形状较为尖锐的地方，而流体经过时通常涡量急剧增加，流动也有一定的加速，且两者夹角均在90° 附近，导致该出产生强度较大的声源，而涡量在绝大多数情况下增加剧烈，成为该部分形成强声源的主要原因.

5. 结　论

基于气动声学基本波动方程，利用球形声源声辐射和流场物理量之间的关系，建立了描述气动声源强度的方法，并结合高速列车气动数值仿真技术，建立了高速列车近表面偶极子声源和湍流场中四极子声源的识别方法，从全新的角度对某高速列车头车及其转向架区域的气动噪声源进行识别. 同时，基于涡声方程声源项特征，对主要声源部件，揭示了其产生偶极子声源和流场流动的关系. 研究表明：

1）较强偶极子声源从强到弱的顺序为前车轮下方前沿、排障器前沿、暴露在流场中的转向架杆件、裙板边沿和后车轮下方前沿. 该声源出现在流体直接冲击的物体表面附近，气流的直接撞击和分离现象是产生偶极子声源的主要原因.

2）较强四极子声源从强到弱的顺序为排障器前沿分离的湍流区、排障器尾沿后的剪切层区域、前轮后下方的尾迹区及转向架杆件的尾迹区；和偶极子产生声源的原因类似，流体与固壁作用产生分离形成湍流尾迹和剪切层流动是四极子声源产生的主要原因.

3）偶极子声源声压强度远大于四极子声源，说明了头车及转向架区域气动噪声源以偶极子声源为主；两声源的分布区域几乎相同，都在流体分离区（除了剪切层区域），偶极子声源为近壁面，四极子声源为湍流场中.

4）偶极子声源强度较大位置出现在边沿较为尖锐的位置，在绝大多数情况下流体经过时涡量急剧增加，成为该部分形成强声源的主要原因.

致谢：本文研究工作得到了上海市地面交通工具空气动力与热环境模拟重点实验室（18DZ2273300）项目支持，作者由衷表示感谢.

图 1 偶极子声源脉动和声辐射示意

Figure 1. Schematic diagram of dipole sound source pulsation and sound radiation

下载: 全尺寸图片幻灯片

图 2 由一对力点源构成的四极子声源

Figure 2. Quadrupole sound source composed of pair of force point sources

下载: 全尺寸图片幻灯片

图 3 风洞试验段高速列车模型安装及测点

Figure 3. Installation of high-speed train model and measuring points in wind tunnel test section

下载: 全尺寸图片幻灯片

图 4 流场外传声器测点分布（单位： m）

Figure 4. Distribution of measuring points of microphones outside the flow field （unit: m）

下载: 全尺寸图片幻灯片

图 5 风洞实验和仿真计算的声压级对比

Figure 5. Comparison of sound pressure level between wind tunnel experiment and simulation

下载: 全尺寸图片幻灯片

图 6 近头车表面的偶极子声源分布

Figure 6. Dipole sound source distribution near the surface of the head coach

下载: 全尺寸图片幻灯片

图 7 头车上的不同截面位置

Figure 7. Different cross-section positions on the head coach

下载: 全尺寸图片幻灯片

图 8 四极子声源的分布

Figure 8. Distribution of the quadrupole sound source

下载: 全尺寸图片幻灯片

图 9 前车轮声源区域及部分流线

Figure 9. Sound source area of front wheel and part of the streamline

下载: 全尺寸图片幻灯片

图 10 前车轮声源区域物理量沿流线变化的对比

Figure 10. Comparison of physical quantities’ changes along a streamline around the front wheel

下载: 全尺寸图片幻灯片

图 12 排障器声源区域物理量沿流线变化的对比

Figure 12. Comparison of physical quantities’ changes along a streamline around the cowcatcher

下载: 全尺寸图片幻灯片

图 14 转向架突出杆件声源区域物理量沿流线变化的对比

Figure 14. Comparison of physical quantities’ changes along a streamline around the bogie protruding rod

下载: 全尺寸图片幻灯片

图 16 裙板声源区域物理量沿流线变化的对比

Figure 16. Comparison of physical quantities’ changes along a streamline around the apron

下载: 全尺寸图片幻灯片

图 18 后车轮声源区域物理量沿流线变化的对比

Figure 18. Comparison of physical quantities’ changes along a streamline around the rear wheel

下载: 全尺寸图片幻灯片

图 20 转向架舱后沿声源区域物理量沿流线变化的对比

Figure 20. Comparison of physical quantities’ changes along a streamline around the rear edge of bogie cavity

下载: 全尺寸图片幻灯片

图 11 排障器声源区域及部分流线

Figure 11. Sound source area of cowcatcher and part of the streamline

下载: 全尺寸图片幻灯片

图 13 转向架突出杆件声源区域及部分流线

Figure 13. Sound source area of bogie protruding rod and part of the streamline

下载: 全尺寸图片幻灯片

图 15 裙板声源区域及部分流线

Figure 15. Sound source area of apron and part of the streamline

下载: 全尺寸图片幻灯片

图 17 后车轮声源区域及部分流线

Figure 17. Sound source area of rear wheel and part of the streamline

下载: 全尺寸图片幻灯片

图 19 转向架舱后沿声源区域及部分流线

Figure 19. Sound source area of the rear edge of bogie cavity and part of the streamline

下载: 全尺寸图片幻灯片

表 1 网格独立性测试结果

Table 1. Grid independence test results

网格量/万图 4 中测点 3/
总声压级与风洞实验
总声压级差值

3800 79.8 2.3
4000 80.2 2.7
4500 78.6 1.1
7000 78.4 0.9

下载: 导出CSV

参考文献(24)

[1]	LIGHTHILL M J. On sound generated aerodynamically Ⅰ: general theory[J]. Proceedings of the Royal Society of London Series A, Mathematical and Physical Sciences, 1952, 211(1107): 564-587.
[2]	LIGHTHILL M J. On sound generated aerodynamically Ⅱ: turbulence as a source of sound[J]. Proceedings of the Royal Society of London Series A, Mathematical and Physical Sciences, 1954, 222(1148): 1-32.
[3]	CURLE N. The influence of solid boundaries upon aerodynamic sound[J]. Proceedings of the Royal Society of London Series A, Mathematical and Physical Sciences, 1955, 231(1187): 505-514.
[4]	FFOWCS W J E, HAWKINGS D L. Boundary-layer pressure and the corcos model: a development to incorporate low-wavenumber constraints[J]. Journal of Fluid Mechanics, 1965, 22: 505-519.
[5]	FFOWCS W J E, HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion[J]. Philosophical Transactions of the Royal Society of London Series A (1934-1990), 1969, 264(1151): 321-342.
[6]	POWELL A. Theory of vortex sound[J]. The Journal of the Acoustical Society of America, 1964, 36(1): 177-195. doi: 10.1121/1.1918931
[7]	BOGEY C, BAILLY C, JUVÉ D. Computation of flow noise using source terms in linearized Euler’s equations[J]. AIAA Journal, 2002, 40(2): 235-243. doi: 10.2514/2.1665
[8]	EWERT R, SCHRÖDER W. Acoustic perturbation equations based on flow decomposition via source filtering[J]. Journal of Computational Physics, 2003, 188(2): 365-398. doi: 10.1016/S0021-9991(03)00168-2
[9]	王毅刚,黄晓胜,危巍,等. 涡声理论在汽车A柱气动噪声优化中的应用[J]. 噪声与振动控制,2017,37(2): 107-112. doi: 10.3969/j.issn.1006-1355.2017.02.022 WANG Yigang, HUANG Xiaosheng, WEI Wei, et al. Aerodynamic noise optimization of vehicle’s A-pillar based on vortex sound theory[J]. Noise and Vibration Control, 2017, 37(2): 107-112. doi: 10.3969/j.issn.1006-1355.2017.02.022
[10]	杨志刚,刘洋,王毅刚. 有限长圆柱绕流气动噪声源特性分析[J]. 声学技术,2019,38(1): 5-14. YANG Zhigang, LIU Yang, WANG Yigang. Study of aeroacoustic noise source induced by a cylindrical flow of finite length[J]. Technical Acoustics, 2019, 38(1): 5-14.
[11]	MELLET C, LÉTOURNEAUX F, POISSON F, et al. High speed train noise emission: latest investigation of the aerodynamic/rolling noise contribution[J]. Journal of Sound and Vibration, 2006, 293(3/4/5): 535-546.
[12]	张卫华. 高速列车顶层设计指标研究[J]. 铁道学报,2012,34(9): 15-19. doi: 10.3969/j.issn.1001-8360.2012.09.003 ZHANG Weihua. Study on top-level design specifications of high-speed trains[J]. Journal of the China Railway Society, 2012, 34(9): 15-19. doi: 10.3969/j.issn.1001-8360.2012.09.003
[13]	张曙光. 350 km·h⁻¹高速列车噪声机理、声源识别及控制[J]. 中国铁道科学,2009,30(1): 86-90. ZHANG Shuguang. Noise mechanism, sound source localization and noise control of 350 km·h⁻¹ high-speed train[J]. China Railway Science, 2009, 30(1): 86-90.
[14]	高阳,王毅刚,王金田,等. 声学风洞中的高速列车模型气动噪声试验研究[J]. 声学技术,2013,32(6): 506-510. GAO Yang, WANG Yigang, WANG Jintian, et al. Testing study of aerodynamic noise for high speed train model in aero-acoustic wind tunnel[J]. Technical Acoustics, 2013, 32(6): 506-510.
[15]	NAGAKURA K. Localization of aerodynamic noise sources of Shinkansen trains[J]. Journal of Sound and Vibration, 2006, 293(3/4/5): 547-556.
[16]	HE B, JIN X S. Investigation into external noise of a high-speed train at different speeds[J]. Journal of Zhejiang University Science A, 2014, 15: 1019-1033. doi: 10.1631/jzus.A1400307
[17]	LAUTERBACH A, EHRENFRIED K, LOOSE S, et al. Microphone array wind tunnel measurements of Reynolds number effects in high-speed train aeroacoustics[J]. International Journal of Aeroacoustics, 2012, 11(3/4): 411-446.
[18]	ATSUSHI Y N I. Evaluation methods for aerodynamic noise from a high-speed train bogie in a wind tunnel test[C]//INTER-NOISE and NOISE-CON Congress and Conference Proceedings, 2011(6): 1543-1553.
[19]	张亚东,张继业,张亮,等. 高速列车动车转向架气动噪声数值分析[J]. 西南交通大学学报,2016,51(5): 870-877. doi: 10.3969/j.issn.0258-2724.2016.05.008 ZHANG Yadong, ZHANG Jiye, ZHANG Liang, et al. Numerical analysis of aerodynamic noise of motor car bogie for high-speed trains[J]. Journal of Southwest Jiaotong University, 2016, 51(5): 870-877. doi: 10.3969/j.issn.0258-2724.2016.05.008
[20]	黄莎,杨明智,李志伟,等. 高速列车转向架部位气动噪声数值模拟及降噪研究[J]. 中南大学学报(自然科学版),2011,42(12): 3899-3904. HUANG Sha, YANG Mingzhi, LI Zhiwei, et al. Aerodynamic noise numerical simulation and noise reduction of high-speed train bogie section[J]. Journal of Central South University (Science and Technology), 2011, 42(12): 3899-3904.
[21]	朱剑月,王毅刚,杨志刚,等. 高速列车转向架区域裙板对流场与气动噪声的影响[J]. 同济大学学报(自然科学版),2017,45(10): 1512-1521. doi: 10.11908/j.issn.0253-374x.2017.10.014 ZHU Jianyue, WANG Yigang, YANG Zhigang, et al. Effect of bogie fairing on flow and aerodynamic noise behaviour around bogie of high-speed train[J]. Journal of Tongji University (Natural Science), 2017, 45(10): 1512-1521. doi: 10.11908/j.issn.0253-374x.2017.10.014
[22]	HAN J, LAN J. Research on the radiation characteristics of aerodynamic noises of a simplified bogie of the high-speed train[J]. Journal of Vibroengineering, 2017, 19(3): 2280-2293. doi: 10.21595/jve.2017.18229
[23]	高阳,李启良,陈羽,等. 高速列车头型近场与远场噪声预测[J]. 同济大学学报(自然科学版),2019,47(1): 124-129. doi: 10.11908/j.issn.0253-374x.2019.01.018 GAO Yang, LI Qiliang, CHEN Yu, et al. Prediction of near field and far field noise for high-speed train head shape[J]. Journal of Tongji University (Natural Science), 2019, 47(1): 124-129. doi: 10.11908/j.issn.0253-374x.2019.01.018
[24]	张强. 气动声学基础[M]. 北京: 国防工业出版社, 2012.

施引文献

期刊类型引用(3)

1.	李向东，聂连飞，朱宝龙，林其，于时恩. 脉冲风洞天平基础动力特征的简化计算方法. 西南交通大学学报. 2024(02): 413-422 . 本站查看
2.	张洪军，王钟辉，徐育敏，高阳，王毅刚，朱朗贤. 高速列车转向架区域远场气动噪声计算方法探究. 机车电传动. 2024(03): 53-60 . 百度学术
3.	朱宝龙，李凯，林其，于时恩. 层状地基对脉冲风洞天平基础振动特征影响分析. 地震工程与工程振动. 2024(06): 125-137 . 百度学术