Microscopic Model Analysis of Shield Tunnel Backfill Grouting Based on Displacement Effect
-
摘要:
当盾构隧道位于水位线以下时,为了分析壁后注浆浆液驱动地下水体过程,基于毛细管组渗透理论,将浆液的渗流路径概化为毛细管,考虑牛顿流体浆液驱动地下水(牛顿流体)进行扩散,推导了半球形及柱形模型浆液渗流扩散半径计算式,并讨论了注浆压力、浆液水灰比、地层渗透系数的影响. 研究结果表明:浆液扩散半径主要与注浆压力、渗透率、注浆时间、孔隙率、浆液和地下水黏度等因素有关,浆液水灰比对于浆液扩散半径影响最为显著,浆液的黏度由0.004 7 Pa•s降至0.001 9 Pa•s时,浆液扩散半径在注浆时间为1 h时降低幅度为46.7%,相同注浆条件下可增大水灰比来增大浆液扩散半径;浆液扩散半径随渗透系数的增大而增大,地层的渗透系数大小一定程度上反映了浆液扩散的难易程度;在计算出浆液扩散半径(浆液加固范围)的基础上提出了注浆压力下限值计算方法,用以指导盾构隧道壁后注浆工程施工.
Abstract:When a shield tunnel under construction is below the water level, the shield backfill grouting slurry will drive the groundwater. In order to analyze this driving process, the seepage path of slurry in the soil is generalized to a capillary by capillary group penetration theory, the grout diffusion radius of hemispherical and cylindrical models are deduced considering the diffusion by Newtonian fluid slurry-driven water (Newtonian fluid), and the effects of grouting pressure, water-cement ratio, and formation permeability coefficient are discussed. Results show that the grout diffusion radius is mainly related to the grouting pressure, permeability, grouting time, porosity, and grout and groundwater viscosity. Especially, the grout water-cement ratio has the most significant effect on the grout diffusion radius. When the viscosity of the grout decreases from 0.004 7 to 0.001 9 Pa•s, the spreading radius of grout decreases by 46.7% at 1 h after grouting, indicating that the spreading radius of grout can be increased by adopting a higher water-cement ratio under the same grouting condition. Besides, the grout diffusion radius increases with an increase in the permeability coefficient, and the formation permeability coefficient reflects the difficulty of grout diffusion to a certain extent. Based on the calculation of grout diffusion radius (grout reinforcement range), a calculation method for the lower limit of the grouting pressure is proposed to guide the construction of backfill grouting of shield tunnel.
-
Key words:
- shield tunnel /
- backfill grouting /
- penetration grouting /
- displacement effect
-
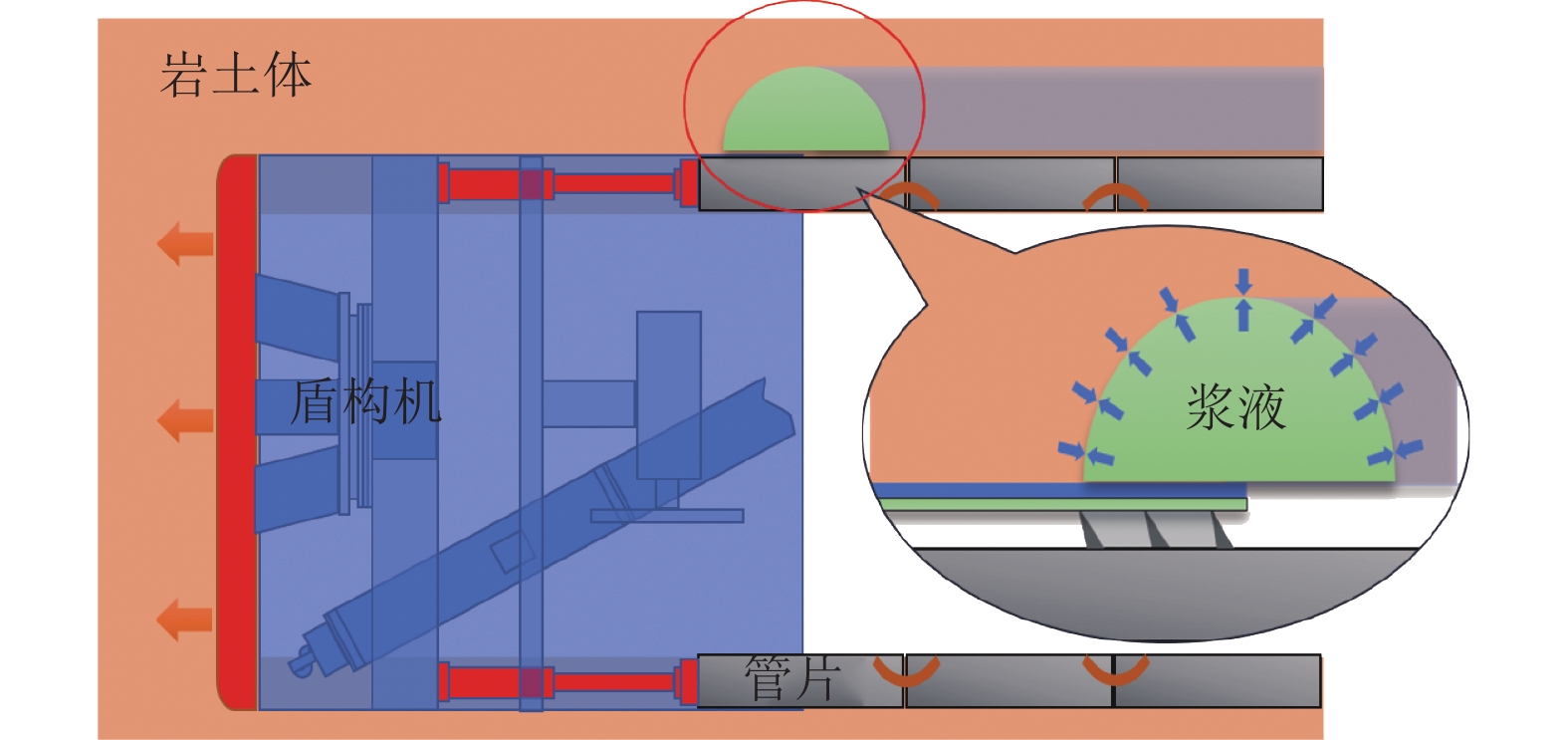
1818年Brunel首次提出盾构的思想距今已有两百多年,盾构隧道工法经过多年的发展,已出现了泥水盾构工法、土压盾构工法等. 对盾构隧道而言,采用的隧道衬砌大多为预制管片,在开挖时,盾构机半径一般大于管片半径,致使管片与周围土体存在空隙[1],如不进行处理将造成上部地表沉降开裂. 在实际施工中,这一部分土体损失一般采用浆液填充,同时,壁后注浆形成的注浆层还具有防止管片上浮、优化管片受力等作用[2].
在已有的研究中,通常将壁后注浆过程分为充填注浆、渗透注浆、压密注浆和劈裂注浆[3]:在充填注浆中,李志明等[4]根据流体力学原理,推导了牛顿及宾汉姆流体浆液在黏土地层条件下的压力分布;白云等[5]以牛顿流体浆液为研究对象,运用流体力学与极限平衡法基本原理,推导出盾尾空隙横断面内浆液压力的分布模型;对于渗透注浆,张莎莎等[6]基于达西定律、力学平衡原理和广义虎克定律推导分析浆液压力消散规律;叶飞等[7-8]基于Darcy定律并结合注浆施工条件,将地下水压力作为边界条件对盾构隧道壁后注浆进行了理论分析. 在以往研究中,往往忽略了渗透注浆过程中地下水的影响,仅将地下水的影响作为边界条件进行分析.
在壁后注浆施工中,注浆压力是重要的施工参数,其大小应谨慎选取[9-10]. 注浆压力的设定不宜过小或过大,过小将引起地表变形过大,过大则会造成土体劈裂[11]. 许多学者也针对其取值做了卓有成效的研究:文献[12]建议注浆压力一般在0.1~0.3 MPa;文献[13]基于深圳地铁大东区间隧道,提出注浆压力应控制在0.3~0.5 MPa,以保证管片与围岩之间充填密实;文献[14]认为注浆压力一般大于注浆口处静水压或土压0.1~0.2 MPa. 从上面可以看出,在施工中注浆压力的确定主要是依靠经验选取,缺乏理论依据.
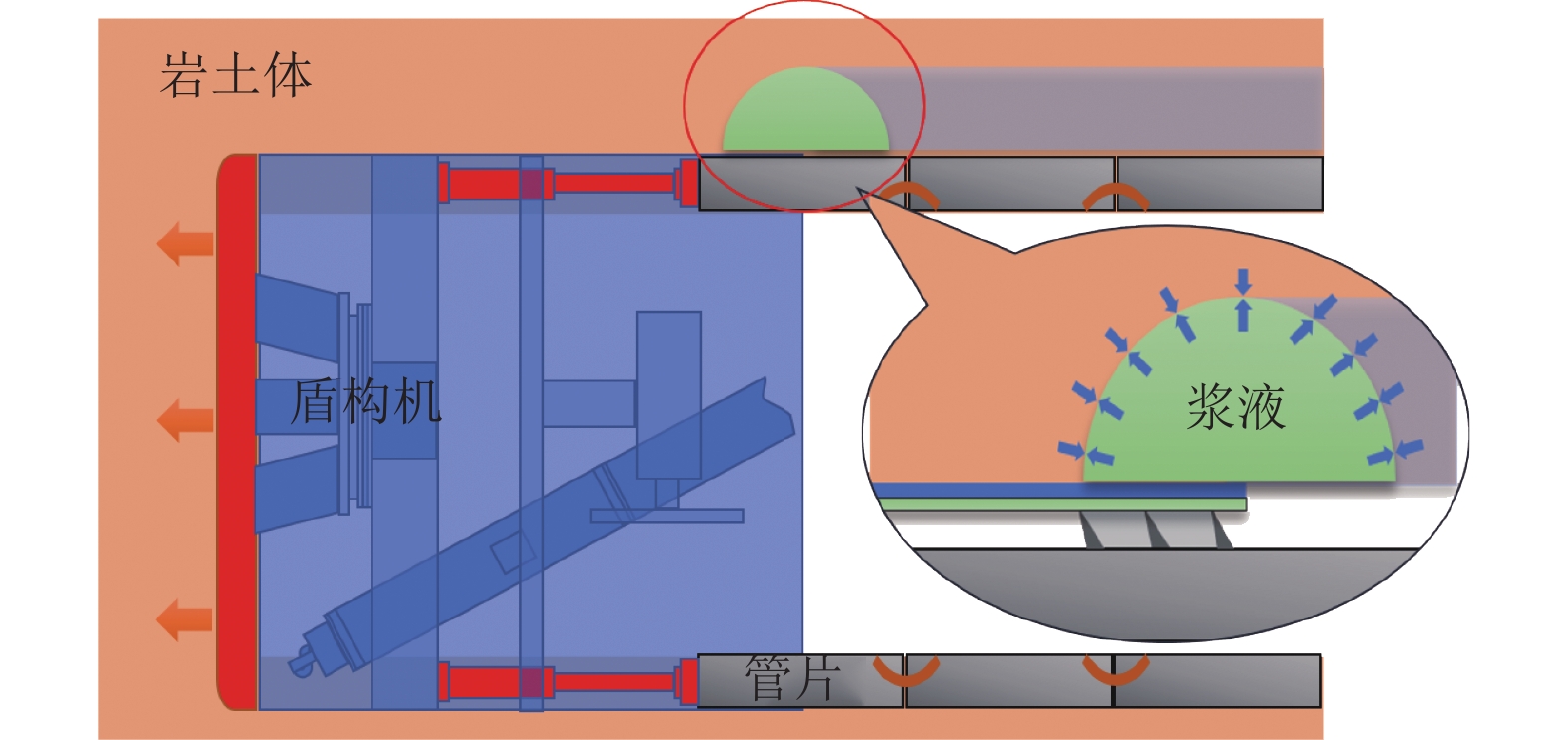
在盾构隧道注浆过程中,随着浆液的注入,浆液将占据原土体中地下水的位置,此即为驱替效应. 地下水在流型上可以划分为牛顿流体,根据注浆浆液流型的不同,驱替注浆可以看作牛顿流体驱替牛顿流体、宾汉姆流体驱替牛顿流体、幂律流体驱替牛顿流体[15]等3种形式,本文主要基于毛细管模型讨论浆液为牛顿流体的情形,即牛顿流体驱替牛顿流体,建立了相应的毛细管驱替模型,并根据模型计算出的浆液扩散半径提出了注浆压力下限值的计算方法.
1. 浆液扩散方程推导
1.1 基本假设
为了简化计算,做出了如下假设:
1) 周围岩土体均质,渗透系数不发生突变;
2) 浆液扩散半径远远大于注浆孔半径,因此计算浆液扩散半径时忽略注浆孔半径;
3) 浆液在毛细管中驱替流动时,浆液与水体不发生混溶,浆液前端存在锋面;
4) 浆液的渗流半径与管片半径相比较而言比较小,因此忽略管片曲率的影响.
1.2 毛细管流动推导
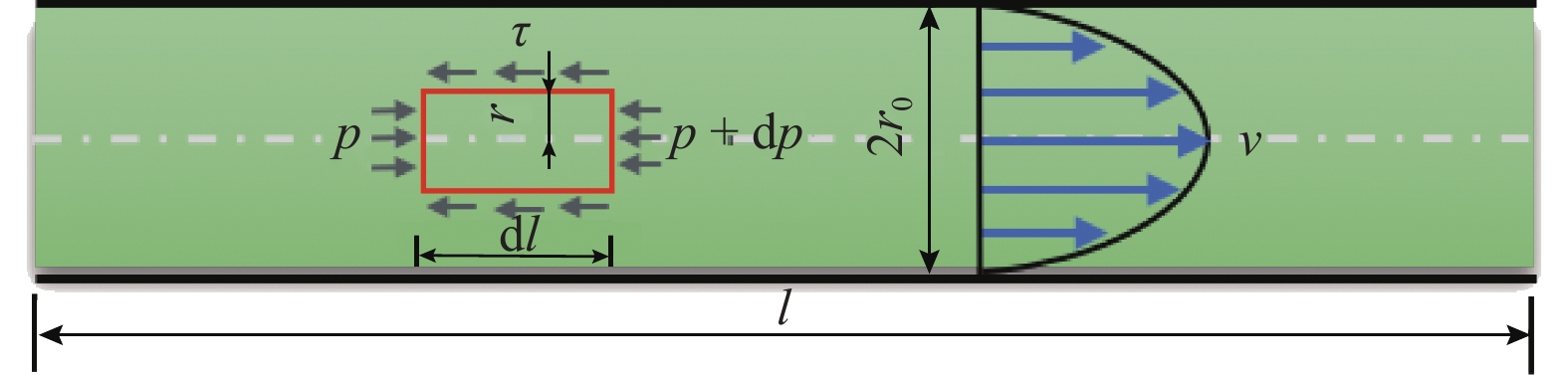
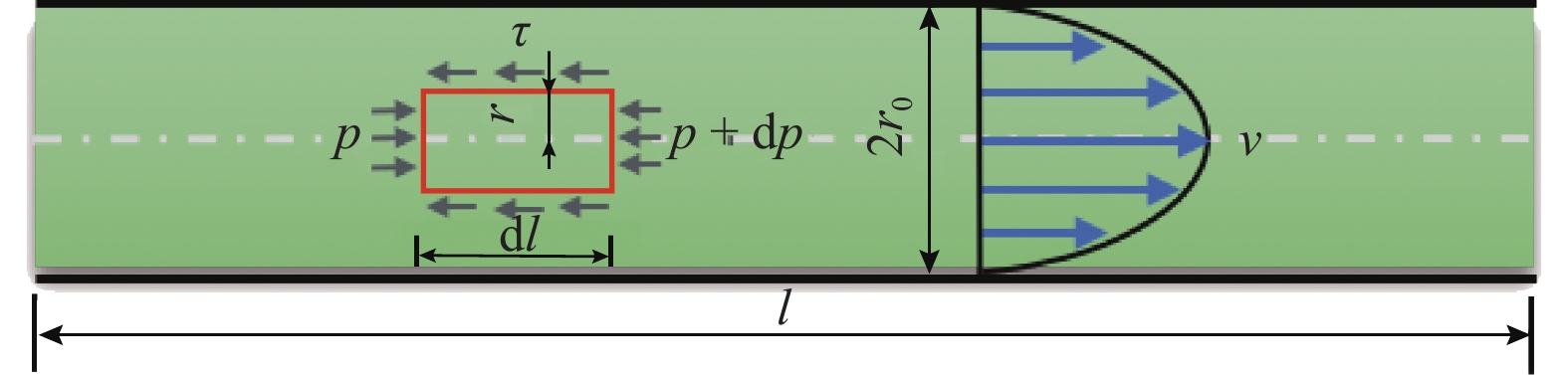
假设浆液在毛细管中流动(毛细管组理论),即被注土体的空隙理想化为毛细管组,土体颗粒看作实体结构,其在概化模型中毛细管如图 1所示. 图中:l为定义的毛细管长度,dl为一个微段;
τ 为剪切应力;r0 为毛细管半径;v 为浆液流速;p 为驱动压力,dp为微压力;r 为微元体dl 的半径.牛顿流体浆液本构方程(流变方程)为
τ=−μgγ, (1) 式中:
μg 为浆液黏度;γ 为应变速率.对于毛细管中的浆液取微元体
dl 为研究对象,力学平衡方程为2τπrdl+(p+dp)πr2=pπr2. (2) 式(2)简化可得
τ=−r2dpdl. (3) 当
r=r0 时,毛细管壁的剪切应力为τp=−r02dpdl. (4) 联立式(1)及式(3),考虑
γ=−dv/dvdrdr 得dv=−r2μgdpdldr. (5) 当
r=r0 时,v=0 ,则对式(5)积分可得v=14μgdpdl(r20−r2). (6) 将毛细管中浆液速度积分得毛细管中浆液流量为
q=∫r002πrvdr=πr408μgdpdl. (7) 求解毛细管中浆液平均流速为
ˉv=qπr20=r208μgdpdl. (8) 联立式(4)和式(8)得毛细管壁的剪切应力为
τp=−ˉv4μgr0. (9) 1.3 模型推导
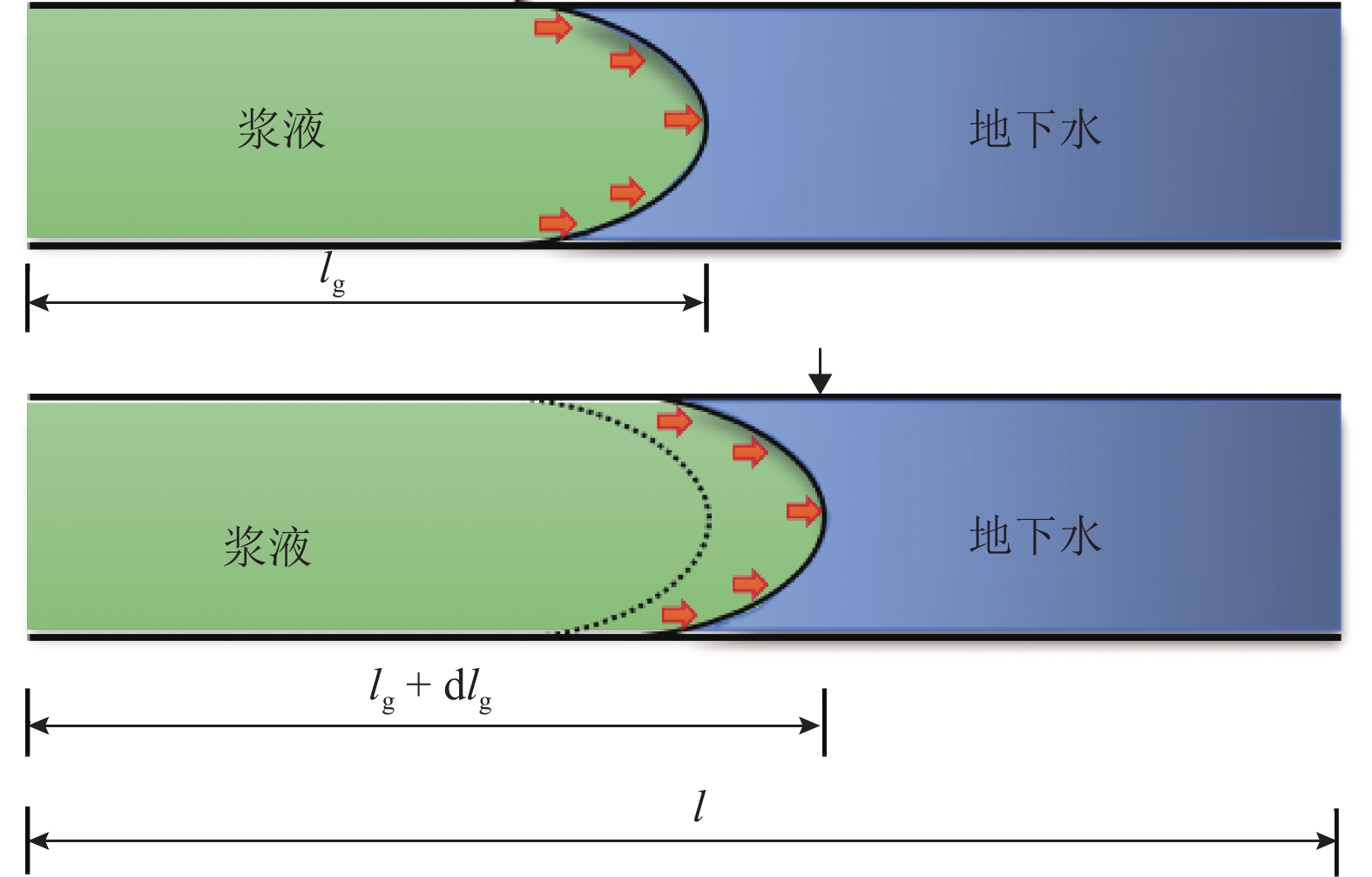
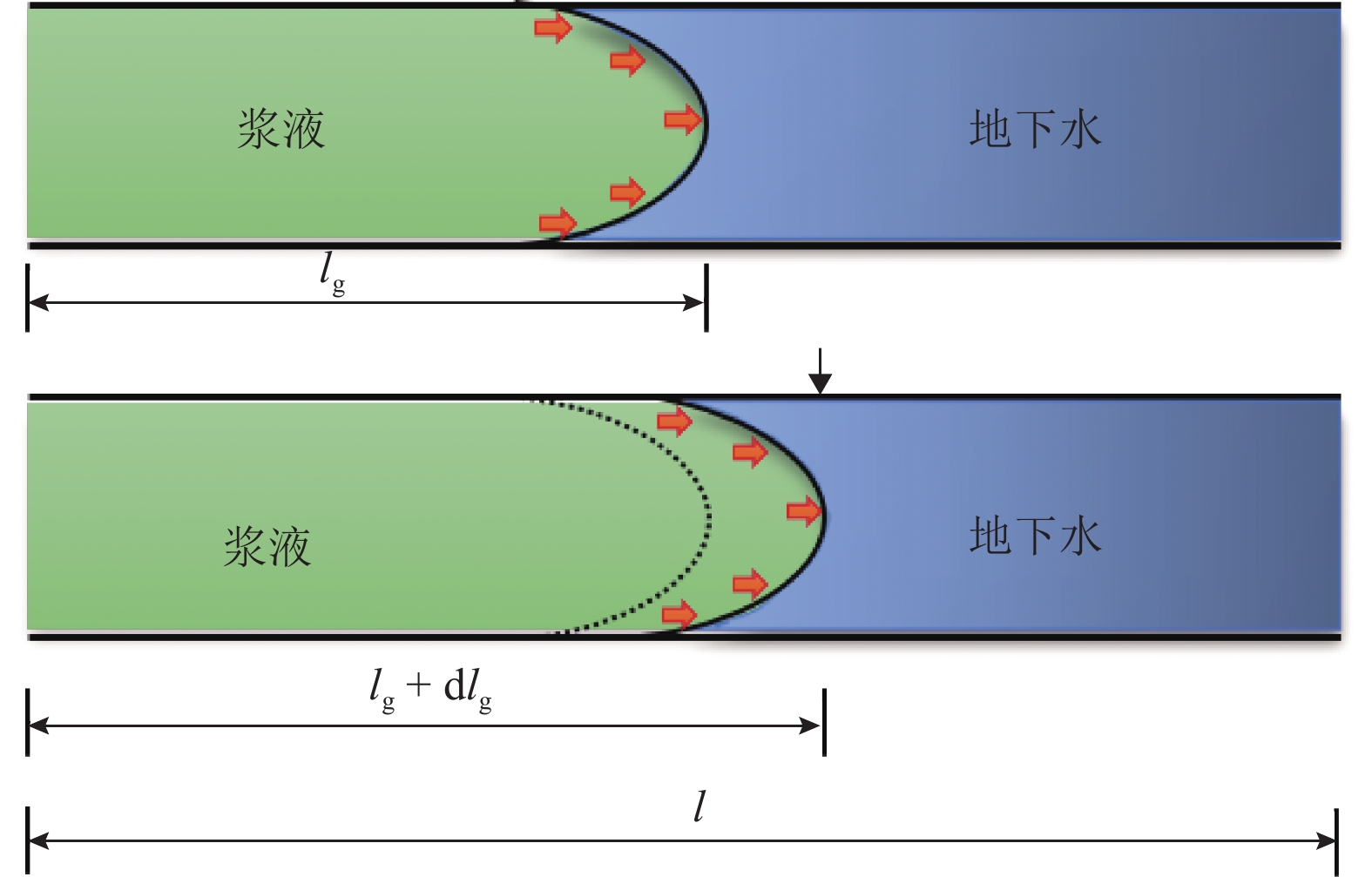
毛细管中浆液流动驱替地下水流动示意如图2. 图中:lg为毛细管内浆液驱替长度.
根据牛顿第二定律,对毛细管中浆液进行受力分析,即
ma=F+f, (10) 式中:
m 为研究流体的质量,m=[ρg(lg+dlg)+ρw×(l−lg−dlg)]πr2 ,ρg 为浆液密度,ρw 为地下水密度;F 为毛细管内所受的压力差,F=πr2(P0−Pw) ,P0 为注浆压力,Pw 为lw (浆液扩散半径)处的地下水压力;a为加速度;f 为浆液与地下水与毛细管壁产生的摩擦阻力,f=2πrτrg(lg + dlg)+2πrτrw(l−lg−dlg) ,τrg 为浆液毛细管壁剪切应力,τrw 为地下水毛细管壁剪切应力.式(10)可写为
[ρg(lg+dlg)+ρw(l−lg−dlg)]πr2d2lgdt2=πr2(P0−Pw)+2πr[τrg(lg+dlg)+τrw(l−lg−dlg)]. (11) 当浆液为牛顿流体时,模型简化为牛顿流体驱替牛顿流体,结合式(9)可得
[ρg(lg+dlg)+ρw(l−lg−dlg)]πr2d2lgdt2=πr2(P0−Pw)−8ˉvπ[μg(lg+dlg)+μw(l−lg−dlg)], (12) 式中:
μw 为地下水黏度.假设毛细管内流体为层流,
a=d2lg/d2lgdt2dt2≈0 ,则式(12)可化简为8ˉvπ[μg(lg+dlg)+μw(l−lg−dlg)]=πr2(P0−Pw). (13) 忽略
dl 的高阶无穷小,根据Dupuit-Forchheimer准则(V = ϕˉv )将毛细管内浆液速度转化为地层中浆液的渗透速度,如式(14).V=r2ϕ(P0−Pw)8[(μg−μw)l+μwl], (14) 式中:
V 地层中浆液的渗透速度;ϕ 为地层孔隙率.对半球形模型浆液流量和浆液量关系如式(15).
{q=2πl2gV=v0πd2,Q=qt=23ϕπl3g=v0πld2t, (15) 式中:
v0 为注浆管浆液流速;d 注浆管半径;t为注浆时间.化简后为
{V=v0d22l2g,v0=2ϕl3g3d2t. (16) 联立式(15)、(16)可得
V=ϕlg3t, (17) 代入式(14)可得
lg=3tr2(P0−Pw)8[(μg−μw)lg+μwl]. (18) 在毛细管模型中
r=√8K/8Kϕϕ ,其中,K 为渗透率,则式(18)可写为lg=3tK(P0−Pw)ϕ[(μg−μw)lg+μwl]. (19) 对于柱形模型,边界条件有
V=ϕlg2t, (20) 代入式(14)可得
lg=2tK(P0−Pw)ϕ[(μg−μw)lg+μwl]. (21) 2. 参数分析
在上面计算中可以看出:浆液扩散半径主要与注浆压力、渗透率、注浆时间、孔隙率、浆液和地下水黏度等因素有关. 本节主要分别对注浆压力、浆液水灰比、地层渗透系数影响因素进行分析.
从1.3节可以看出:半球形模型与柱形模型可统一用
lg=AtK(P0−Pw)ϕ[(μg−μw)lg+μwl] 表示,其中,A 为系数,半球形模型取3,柱形模型取2. 两模型表达形式一致,规律相同,因此在参数分析中仅选取半球形模型为代表进行分析.在计算中选取在l=5 m处地下水压力Pw=0.06 MPa,土体孔隙率
ϕ =0.3,μw=0.00101 Pa•s.K 与渗透系数k 的关系为K=kμw/kμwγγ ,其中,γ 为流体重度.2.1 浆液水灰比的影响
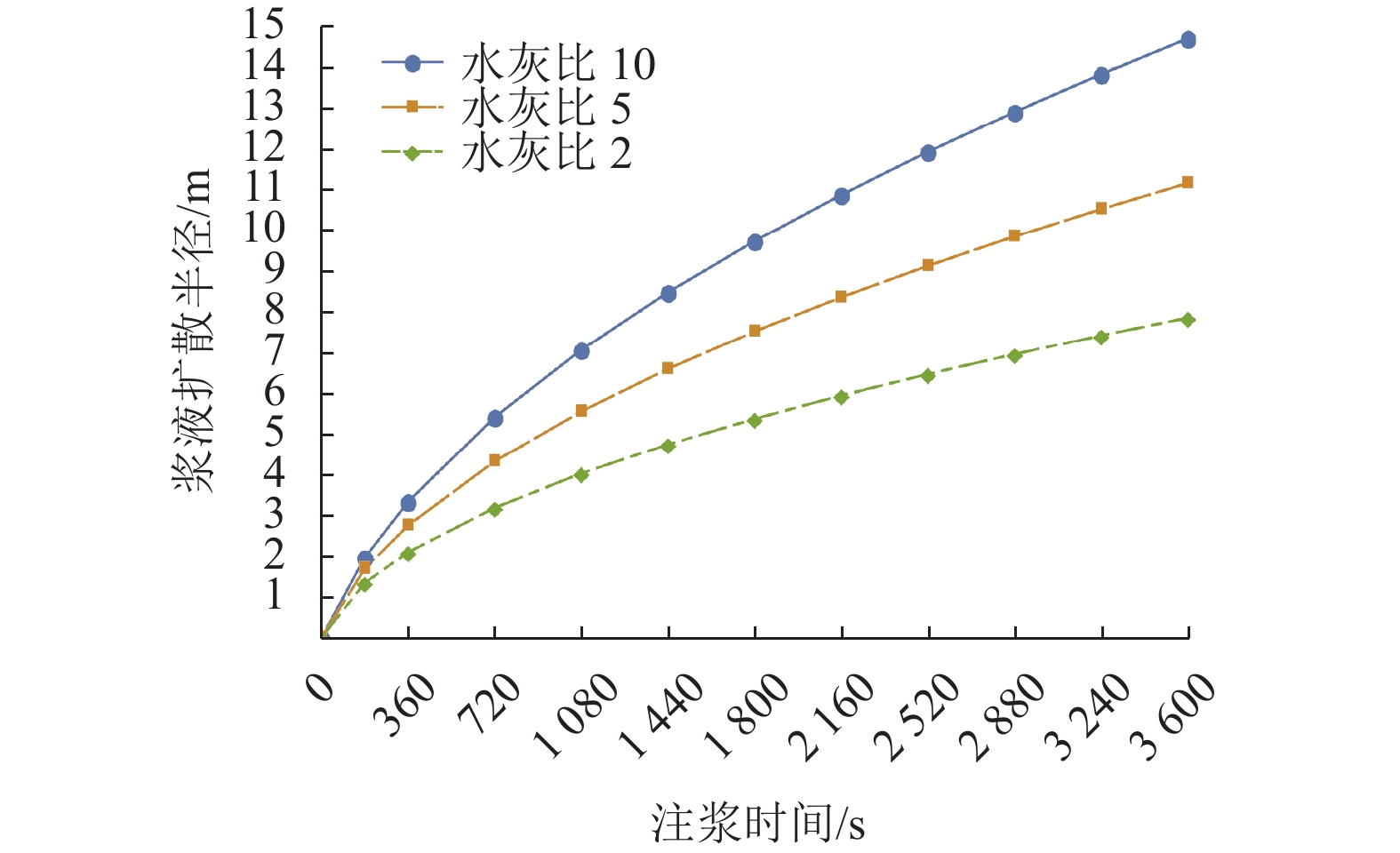
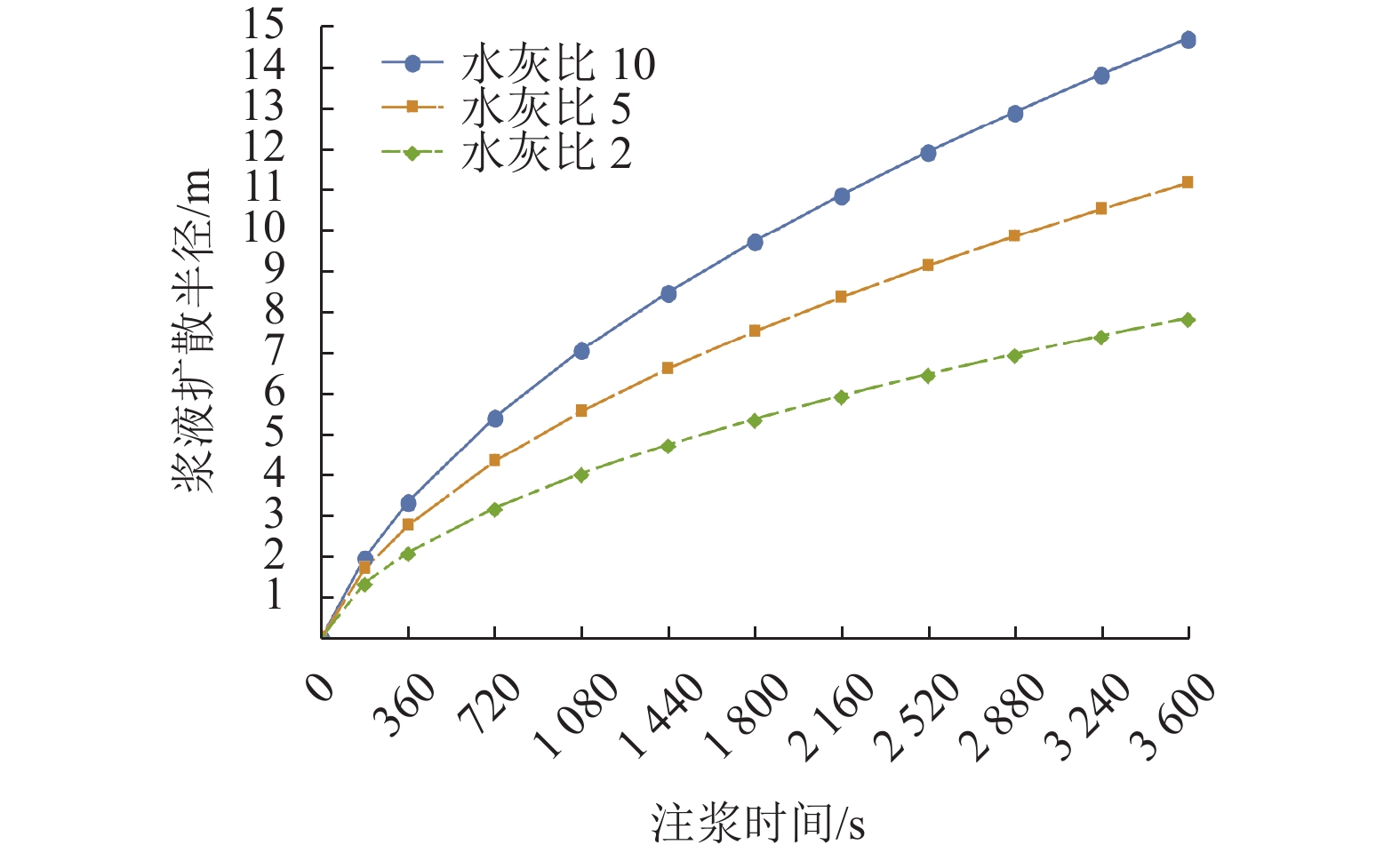
本文采用文献[16]得出的结果对水灰比的影响进行分析,浆液水灰比的不同主要体现在浆液黏度的不同(如表1). 在上述条件不变的情况下,选取注浆压力为0.3 MPa,基于半球形模型对不同的水灰比(2、5、10)影响进行分析.
分别选取不同水灰比下浆液扩散半径变化规律如图3所示. 由图可知:浆液水灰比越大(浆液黏度越小),浆液扩散半径越大;浆液的黏度分别为0.00470、0.00270、0.00190 Pa•s时,浆液扩散半径在注浆时间为1 h时分别达到了14.719、11.167、7.852 m,降低的幅度为46.7%;浆液黏度对浆液扩散半径影响显著,相同条件下可增大水灰比来增大浆液扩散半径,但水灰比的增大将会造成结石体强度降低,因此浆液水灰比的选取应平衡这两个因素.
2.2 注浆压力的影响
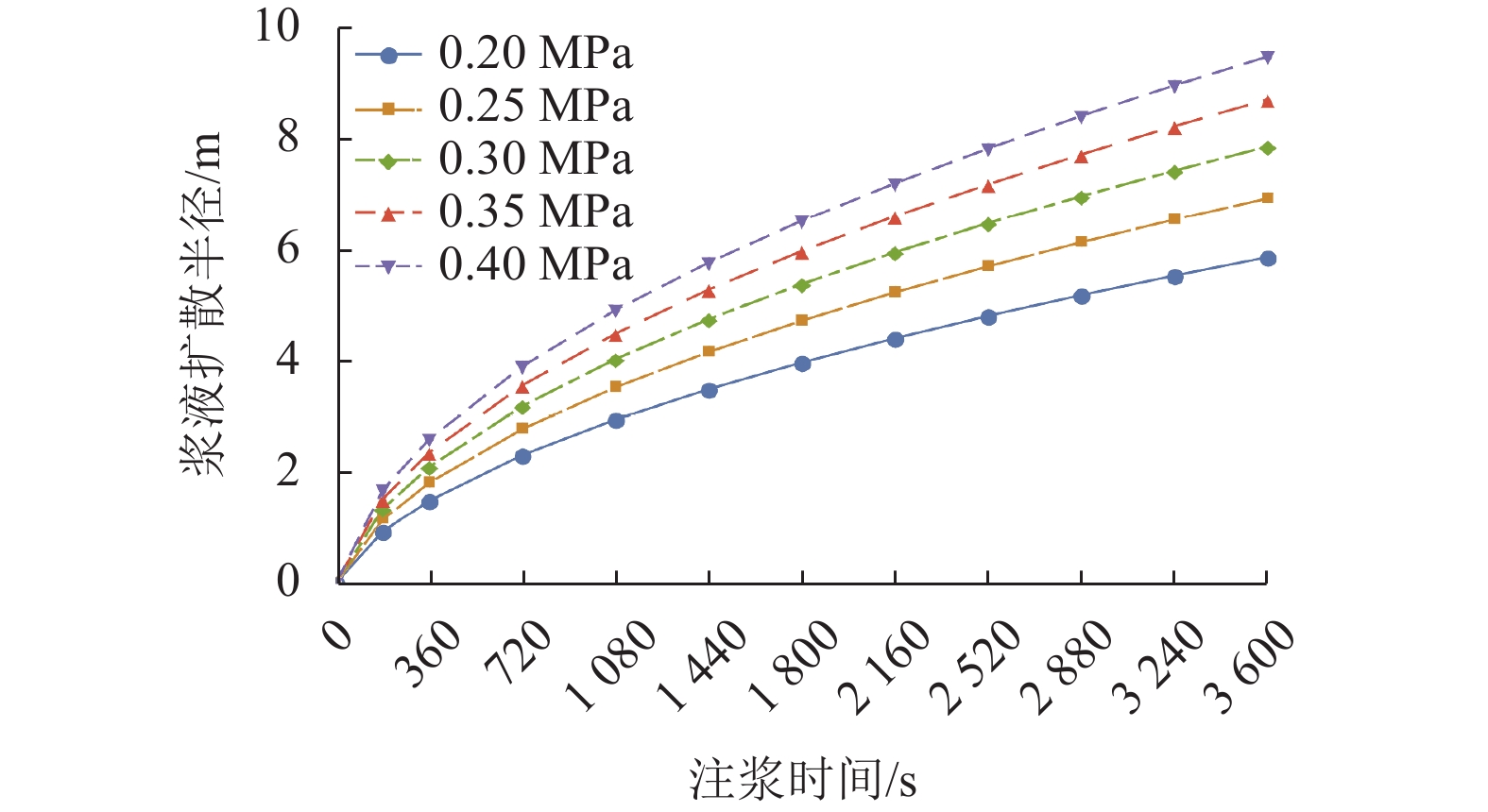
在浆液水灰比为2时,浆液黏度为0.00470 Pa•s(见表1),地层渗透系数为0.03 cm/s的条件下,分别选取不同的注浆压力对半球形模型浆液扩散半径进行分析,计算结果如图4所示.
如图4所示:随着注浆压力的增加,浆液扩散半径也随之增大;图中曲线斜率代表了浆液的扩散速度,曲线的斜率呈逐渐减小的趋势,即浆液扩散速度逐渐减小;注浆压力由0.20 MPa增加到0.40 MPa时,注浆时间1 h的浆液扩散半径由5.850 m增加到了9.463 m,增加的幅度达到了61.8%,注浆压力对浆液扩散半径影响显著. 在实际施工过程中,为加大浆液扩散范围可以考虑提高注浆压力的方式.
2.3 地层渗透系数的影响
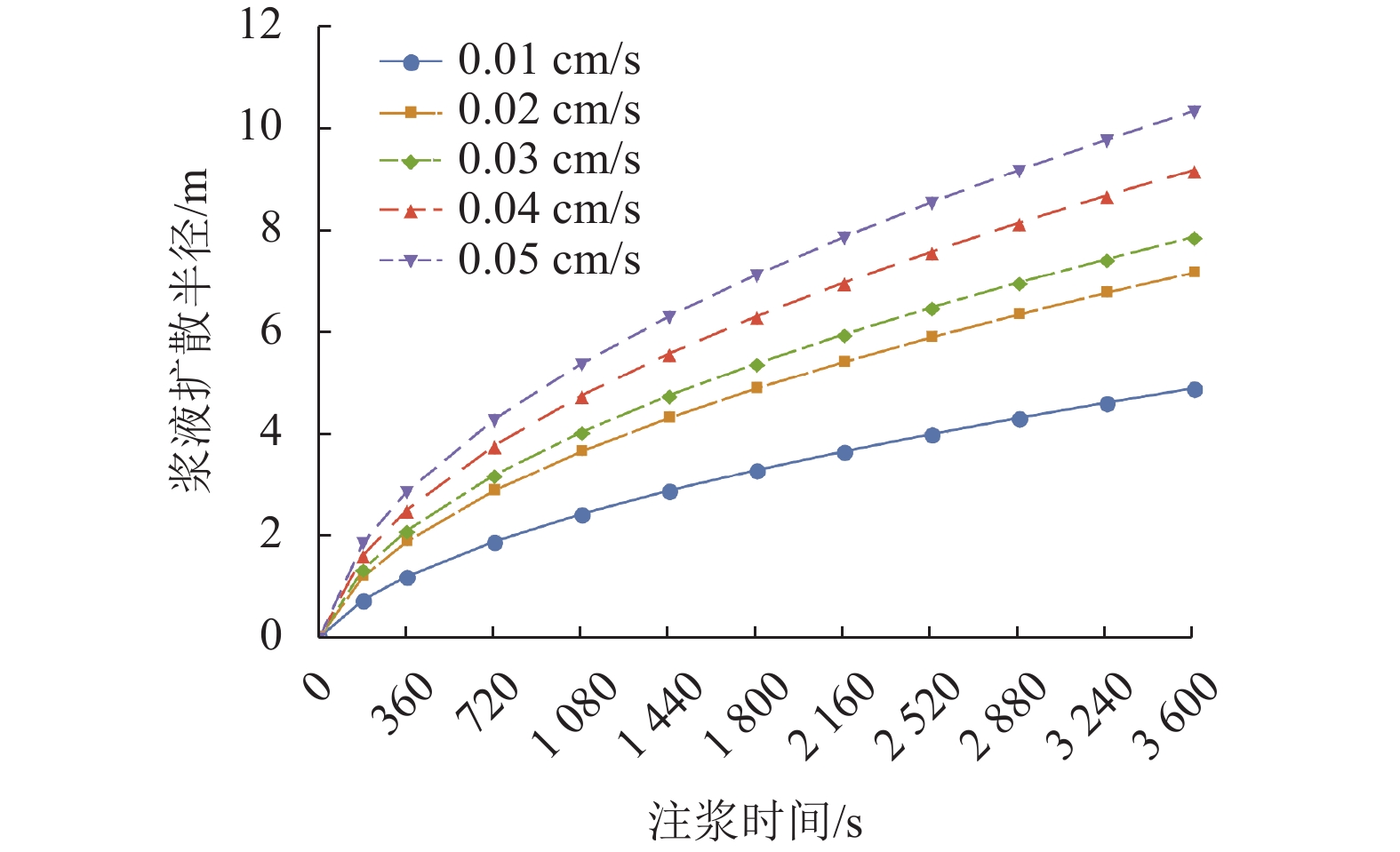
在上述计算参数的基础上,选取注浆压力为0.30 MPa,水灰比为2,基于半球形模型对不同渗透系数的影响进行分析.
不同渗透系数下浆液扩散半径变化规律如图5所示. 由图可知:随着渗透系数的增大,浆液扩散半径随之增大. 地层的渗透系数大小一定程度上反映了浆液扩散的难易程度;在5种渗透系数条件下,浆液在注浆时间为1 h时浆液扩散半径为4.877、7.150、7.852、9.164、10.321 m,随着注浆时间的增加,各渗透系数对应的浆液扩散半径差值也随之增大. 在不同的地层条件下,应根据不同的渗透系数选取不同的注浆压力、浆液水灰比等注浆施工参数.
3. 模型对比
常用的模型还有Darcy渗流模型,牛顿流体浆液在Darcy定律条件下满足
v=−Kμgdpdl. (22) 根据边界条件和盾构隧道注浆条件可推导得到半球形模型浆液毛细管长度满足
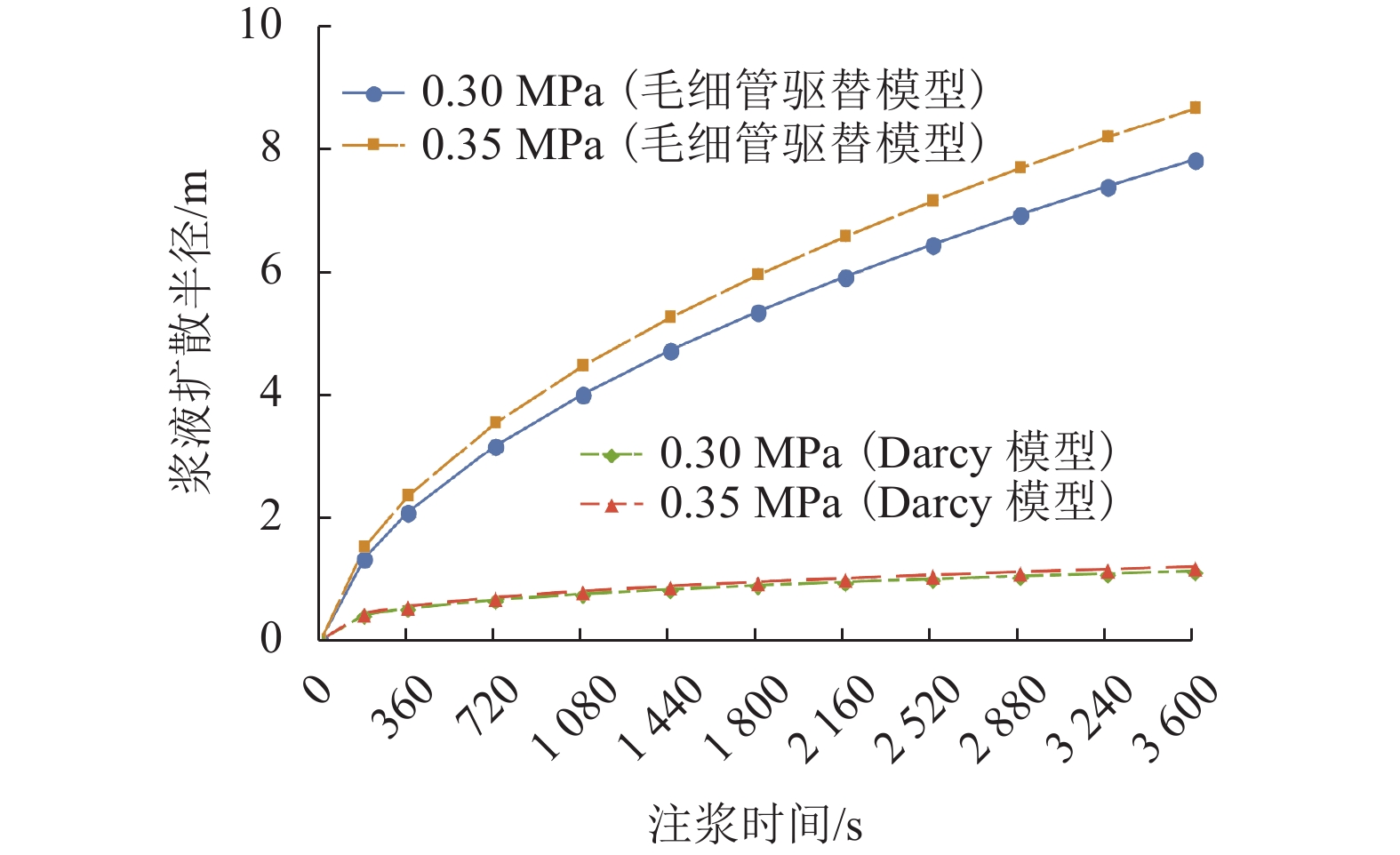
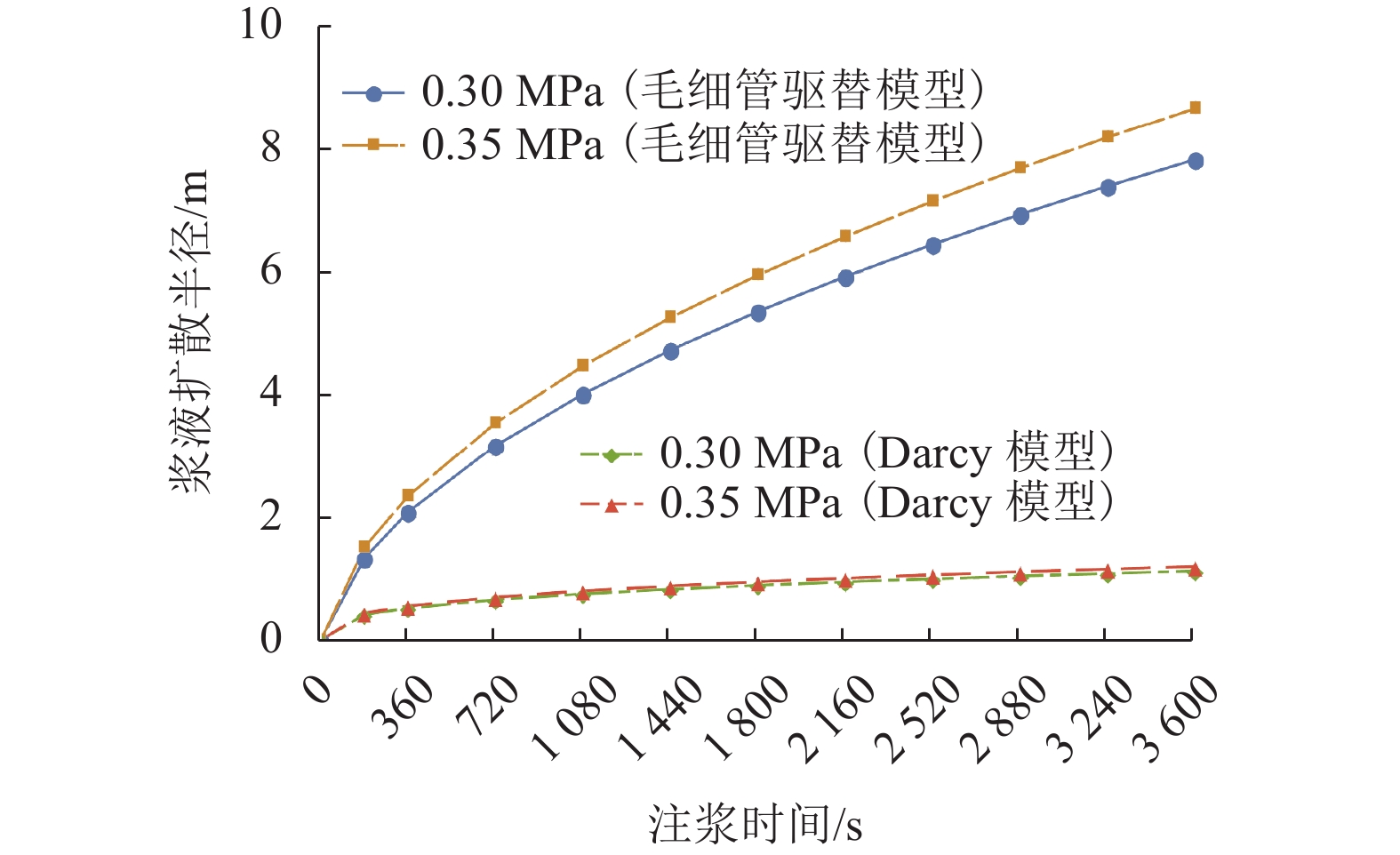
l=3√3K(P0−Pw)l0lwμgϕ(lw−l0)t. (23) 当浆液水灰比取2,注浆压力分别取0.30 MPa和0.35 MPa时,两模型的计算结果如图6.
从图6可知:Darcy模型在注浆前期阶段(360 s)就出现了浆液扩散半径的平稳发展阶段,毛细管驱替模型则未表现出明显变缓的趋势,但总体上浆液扩散半径增长也逐渐变慢. 由于两模型浆液扩散半径增长趋势的差异,在注浆时间达到1 h时,毛细管模型的浆液扩散半径达到了Darcy模型的6倍之多. 造成上述差异的原因在于毛细管驱替模型推导过程存在隐性条件注浆口处浆液流量不变,而在Darcy模型的推导中则不存在这样的限制. 在盾构隧道施工中,一般注浆口处流量是恒定的,因此本文提出的此种模型更符合壁后注浆过程.
4. 注浆压力下限值的确定
从半球形或柱形模型浆液扩散半径计算式可以看出:注浆压力选取与浆液扩散半径、浆液水灰比(浆液黏度)、地下水压力、地下水黏度、渗透率(渗透系数)、孔隙率有关. 本小节通过对浆液加固范围的考虑,分盾尾注浆和管片注浆两种情况,提出了盾构隧道施工过程中注浆压力下限值的计算.
4.1 盾尾同步注浆
对于盾尾注浆(如图7所示),注浆管均匀分布,在此假设为
n 个,因此要满足注浆加固范围填满管片外部土体,毛细管长度应满足l⩾πRn, (24) 式中:
R 为管片外半径.第3节推导出的浆液扩散半径方程是
P0 和t 的函数,对浆液扩散半径方程进行变形即可求解出在一定时间内满足注浆加固范围的注浆压力为p01⩾p0(πRn,t), (25) 式中:
p0 为在一定时间内满足注浆加固范围的注浆压力.4.2 管片注浆
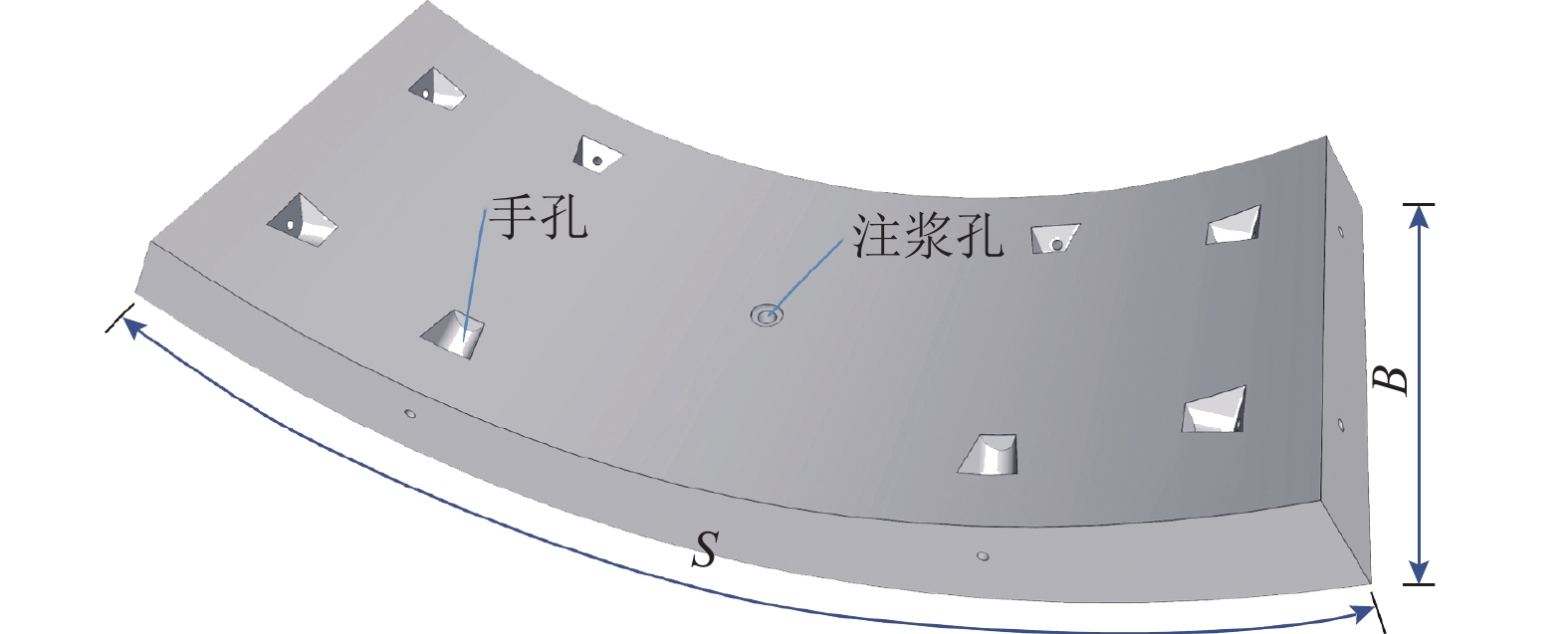
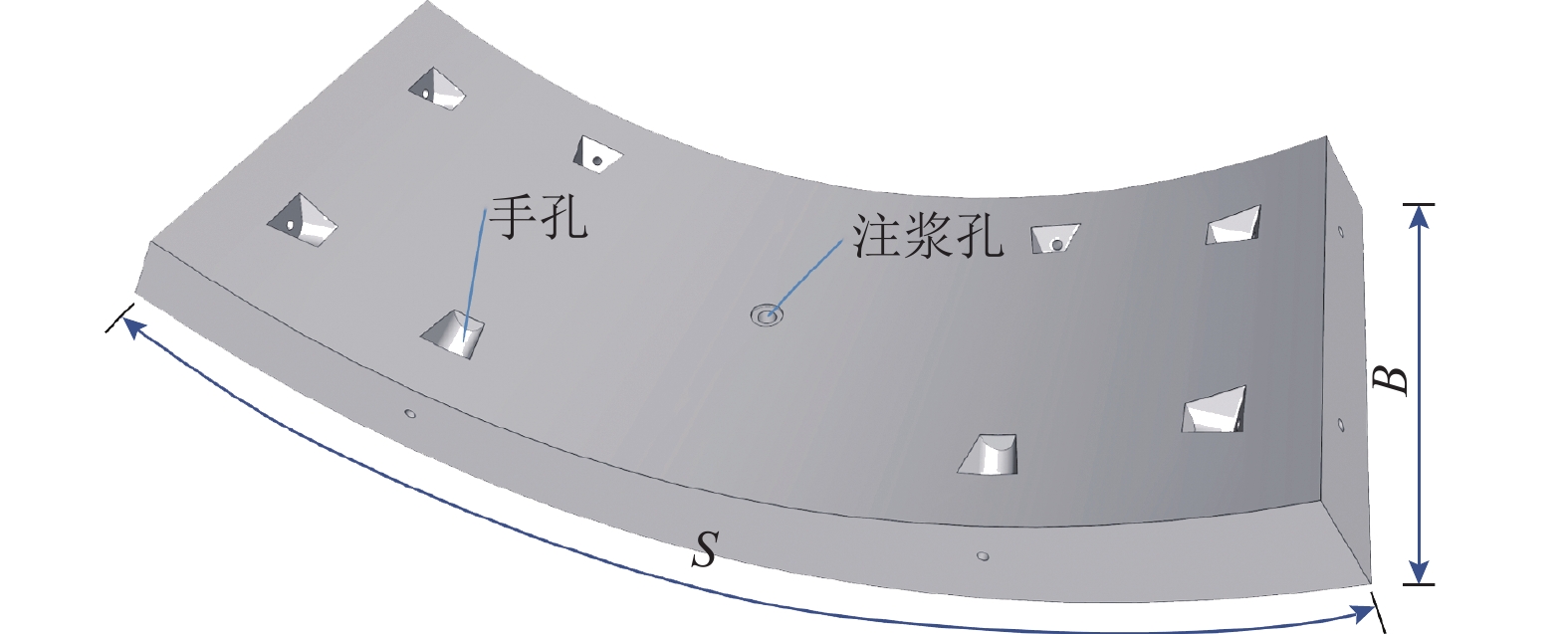
管片注浆的注浆孔在管片中心处(见图8,图中:
S 为管片外弧长;B为环宽. ),注浆孔两侧浆液扩散半径相同,因此要满足注浆范围填满管片外部土体,l (浆液扩散半径)应满足l⩾S2. (26) 对浆液扩散半径方程进行变形可求解出在一定时间内满足注浆加固范围的注浆压力,如式(27).
p01⩾p0(S2,t). (27) 4.3 实例计算
在盾尾注浆中取
n = 4 ,即有4个注浆孔,R =3 m,S = 3.526 m ,πR/πRnn = 2.356 m ,S/S22 = 1.763 m ,浆液水灰比取2,μg=0.0047Pa•s . 注浆压力下限值如表2所示.从表2可看出:土体渗透系数越大,满足浆液加固范围时的注浆压力下限值越小;注浆时间越短对应的注浆压力下限值越大;盾尾注浆所需加固范围大于管片注浆,在满足注浆加固范围的前提条件下,盾尾注浆压力下限值大于管片注浆;注浆压力下限值的计算与地层渗透系数、注浆时间等多种因素有关,明显不能基于某一单一条件确定,例如注浆口处静水压力,因此本文建议在实际应用中应根据具体工程多种条件进行确定.
表 2 注浆压力Table 2. Values of grouting pressure渗透系数/(cm•s−1) t/min P0/MPa 盾尾注浆 管片注浆 0.02 30 0.147 0.115 0.02 60 0.104 0.089 0.03 30 0.118 0.097 0.03 60 0.089 0.078 0.04 30 0.104 0.087 0.04 60 0.082 0.074 5. 结 论
本文建立了毛细管驱替渗透模型,并推导出了浆液扩散半径计算式. 在此基础上,通过考虑浆液加固范围得出了施工过程中注浆压力下限值的计算方法. 主要得出了以下结论:
1) 浆液扩散半径主要与注浆压力、渗透率、注浆时间、孔隙率、浆液和地下水黏度等因素有关.
2) 在注浆压力、水灰比、渗透系数3种影响因素中,浆液扩散半径与浆液压力、渗透系数正相关,与水灰比呈负相关关系. 且水灰比因素对于浆液扩散半径的影响最为显著,其次为渗透系数及注浆压力. 在壁后注浆施工中,可优先选择增大水灰比来增大浆液扩散半径,但水灰比的增大将会造成结石体强度降低,因此,浆液水灰比的选取应平衡这两个因素.
3) 地层渗透系数大小一定程度上反映了浆液扩散的难易程度. 随着注浆时间的增加,各渗透系数对应的浆液扩散半径差值也随之增大,在施工中应根据不同的地层渗透系数选取不同的注浆压力、浆液水灰比等注浆施工参数.
4) 注浆压力下限值的计算与地层渗透系数、注浆时间等多种因素有关,在实际工程应用中应综合具体工程的多种因素进行确定.
-
水灰比 流变方程 浆液黏度/(Pa•s) 2 τ = 0.0372 + 0.0047γ 0.00470 5 τ = 0.0880 + 0.0027γ 0.00270 10 τ = 0.0454 + 0.0019γ 0.00190 表 2 注浆压力
Table 2. Values of grouting pressure
渗透系数/(cm•s−1) t/min P0/MPa 盾尾注浆 管片注浆 0.02 30 0.147 0.115 0.02 60 0.104 0.089 0.03 30 0.118 0.097 0.03 60 0.089 0.078 0.04 30 0.104 0.087 0.04 60 0.082 0.074 -
[1] 张凤祥, 朱合华, 傅德明. 盾构隧道[M]. 北京: 人民交通出版社, 2004. [2] GUGLIELMETTI V, GRASSO P, MAHTAB A, etal. Mechanized tunnelling in urban areas[M]. London: CRC Press, 2008 [3] 《岩土注浆理论与工程实例》协作组. 岩土注浆理论与工程实例[M]. 北京: 科学出版社, 2001. [4] 李志明,廖少明,戴志仁. 盾构同步注浆填充机理及压力分布研究[J]. 岩土工程学报,2010,32(11): 1752-1757.LI Zhiming, LIAO Shaoming, DAI Zhiren. Theoretical study on synchronous grouting filling patterns and pressure distribution of EPB shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1752-1757. [5] 白云,戴志仁,张莎莎,等. 盾构隧道同步注浆浆液压力扩散模式研究[J]. 中国铁道科学,2011,32(4): 38-45.BAI Yun, DAI Zhiren, ZHANG Shasha, etal. Study on the grout pressure dissipation model in simultaneous backfill grouting during shield tunneling[J]. China Railway Science, 2011, 32(4): 38-45. [6] 张莎莎,戴志仁,白云. 盾构隧道同步注浆浆液压力消散规律研究[J]. 中国铁道科学,2012,33(3): 40-48. doi: 10.3969/j.issn.1001-4632.2012.03.07ZHANG Shasha, DAI Zhiren, BAI Yun. Research on the dissipation law of grout pressure during the simultaneous grouting of shield tunnel[J]. China Railway Science, 2012, 33(3): 40-48. doi: 10.3969/j.issn.1001-4632.2012.03.07 [7] 叶飞,朱合华,何川. 盾构隧道壁后注浆扩散模式及对管片的压力分析[J]. 岩土力学,2009,30(5): 1307-1312. doi: 10.3969/j.issn.1000-7598.2009.05.020YE Fei, ZHU Hehua, HE Chuan. Back-filled grouts diffusion model and its pressure to segments of shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(5): 1307-1312. doi: 10.3969/j.issn.1000-7598.2009.05.020 [8] 叶飞,陈治,贾涛,等. 盾构隧道管片注浆幂律流型浆液渗透扩散模型[J]. 岩土工程学报,2016,38(5): 890-897. doi: 10.11779/CJGE201605014YE Fei, CHEN Zhi, JIA Tao, etal. Penetration diffusion model of exponential fluid for backfill grouting through segments of shield tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 890-897. doi: 10.11779/CJGE201605014 [9] 袁小会,韩月旺,钟小春. 盾构隧道壁后注浆压力分布模型[J]. 西南交通大学学报,2011,46(1): 18-23. doi: 10.3969/j.issn.0258-2724.2011.01.003YUAN Xiaohui, HAN Yuewang, ZHONG Xiaochun. Pressure distribution model of simultaneous backfill grouting of shield tunnel[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 18-23. doi: 10.3969/j.issn.0258-2724.2011.01.003 [10] 王明年,黄海斌,汤渊,等. 盾构施工对盾尾浆液压力波动变化的影响[J]. 西南交通大学学报,2019,54(3): 461-467,586. doi: 10.3969/j.issn.0258-2724.20170199WANG Mingnian, HUANG Haibin, TANG Yuan, et al. Influence of shield construction on pressure fluctuation of segment grout[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 461-467,586. doi: 10.3969/j.issn.0258-2724.20170199 [11] 宋天田,周顺华,徐润泽. 盾构隧道盾尾同步注浆机理与注浆参数的确定[J]. 地下空间与工程学报,2008,4(1): 130-133.SONG Tiantian, ZHOU Shunhua, XU Runze. Mechanism and determination of parameters of synchronous grouting in shield tunneling[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(1): 130-133. [12] 张凤祥, 傅德明, 杨国祥, 等. 盾构隧道施工手册[M]. 北京: 人民交通出版社, 2005. [13] 陈湘生, 李兴高. 复杂环境下盾构下穿运营隧道综合技术[M]. 北京: 中国铁道出版社, 2011. [14] 王江涛, 陈建军, 吴庆红, 等. 南水北调中线穿黄工程泥水盾构施工技术[M]. 郑州: 黄河水利出版社, 2010. [15] YE F, QIN N, HAN X, etal. Displacement infiltration diffusion model of power-law grout as backfill grouting of a shield tunnel[J]. European Journal of Environmental and Civil Engineering, 2020, 24(1): 1-14. doi: 10.1080/19648189.2017.1363664 [16] 阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报,2005,27(1): 69-73. doi: 10.3321/j.issn:1000-4548.2005.01.011RUAN Wenjun. Research on diffusion of grouting and basic properties of grouts[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 69-73. doi: 10.3321/j.issn:1000-4548.2005.01.011 期刊类型引用(1)
1. 秦鹏飞,钟宏伟,刘坚,苏丹娜,孙卓宇. 考虑浆土应力耦合作用的劈裂注浆机理分析. 西南交通大学学报. 2023(03): 584-591 .  本站查看
本站查看其他类型引用(7)
-





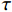
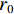
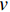
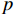

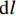

 下载:
下载:

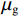
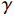
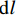
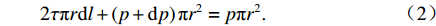



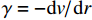


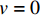
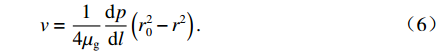
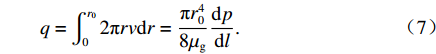




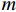
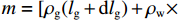
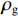
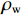
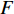

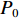
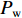
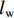
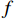
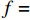

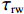
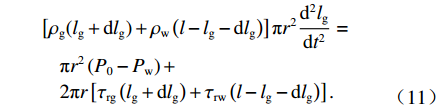
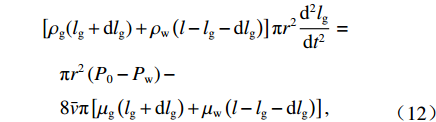
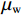
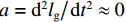
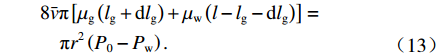
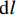
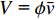

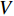
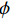
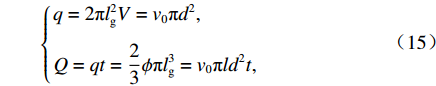
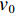
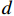



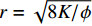
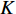
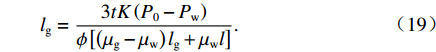

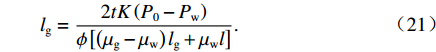
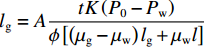


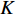
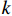
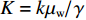






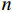

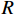

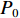


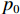
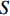






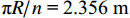
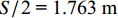
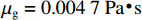
 下载:
下载: