考虑浆土应力耦合作用的劈裂注浆机理分析

秦鹏飞; 钟宏伟; 刘坚; 苏丹娜; 孙卓宇

doi:10.3969/j.issn.0258-2724.20220433

考虑浆土应力耦合作用的劈裂注浆机理分析

doi: 10.3969/j.issn.0258-2724.20220433

秦鹏飞^{1, 2, 3,},
钟宏伟³,
刘坚²,
苏丹娜³,
孙卓宇³

1.
兰州大学西部灾害与环境力学教育部重点实验室，甘肃兰州 730000
2.
河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京 370000
3.
郑州铁路职业技术学院铁道工程学院，河南郑州 451000

基金项目: 国家自然科学基金青年基金（62003313）；中央高校基本科研业务费专项资金资助（lzujbky-2021-kb03）；河海大学岩土力学与堤坝工程教育部重点实验室开放基金（2022LP002）

详细信息

作者简介:
秦鹏飞（1985—），男，副教授，研究方向为岩土与地下工程，E-mail：929163723@qq.com

中图分类号: TU43.1
计量
- 文章访问数: 535
- HTML全文浏览量: 124
- PDF下载量: 81
- 被引次数: 15
出版历程
- 收稿日期: 2022-05-20
- 修回日期: 2022-09-02
- 网络出版日期: 2023-04-10
- 刊出日期: 2023-01-05

Analysis of Split Grouting Mechanism Considering Coupling Effect of Slurry and Soil Stress

1.
Key Laboratory of Mechanics on Disaster and Environment in Western China, The Ministry of Education, Lanzhou University, Lanzhou 730000, China
2.
Key Laboratory of Geotechnical Mechanics and Dam Engineering of the Ministry of Education, Hohai University, Nanjing 370000, China
3.
School of Railway Engineering, Zhengzhou University of Railway Vocational Technology, Zhengzhou 451000, China

摘要

摘要:
浆土应力耦合作用对劈裂注浆浆液扩散规律具有显著影响，砂土劈裂注浆设计应充分考虑这种影响作用. 将劈裂注浆视作平面无限域的圆形扩张过程，基于牛顿型本构方程分析了浆液流场变化特征，并将劈裂通道下侧砂层视作半无限空间弹性体，采用弹性力学推导了均布荷载下劈裂通道宽度、浆液压力的分布方程. 通过设置不同的浆液黏度、砂土弹性模量参数，深刻揭示了耦合效应下砂土劈裂注浆基本机理. 结合郑州地铁某在建工程进行了对比验证. 研究结果表明：浆液压力在孔口及远端处急速衰减，而在中间区段呈稳定变化趋势，劈裂通道宽度基本由浆液压力决定，其分布趋势与浆液压力分布趋势相同；浆液黏度、砂土弹性模量是影响劈裂扩散半径的重要因素，黏度和模量均与扩散半径正相关，黏度与劈裂宽度正相关，模量则与劈裂宽度负相关；本文理论计算值与现场开挖实际值偏差12%～15%，基本符合预期要求.
- 浆-土耦合效应 /
- 劈裂注浆 /
- 起劈压力 /
- 扩散机理 /
- 工程应用
Abstract:
The coupling effect of slurry and soil stress has a significant influence on the slurry diffusion law of split grouting, which should be fully considered in the design phase of split grouting. The split grouting is regarded as a circular expansion process in an infinite plane domain. Based on the Newtonian constitutive equation, variation characteristics of the slurry flow field are analyzed. The sand layer under the splitting channel is regarded as a semi-infinite elastic body. The distribution equations of the splitting channel width and the slurry pressure under the uniform load are derived by elastic mechanics. By setting different slurry viscosity and sand elastic modulus parameters, the basic mechanism of split grouting in sandy soil under coupling effect is revealed. The results show that the slurry pressure decreases rapidly at the orifice and the far end, but changes slowly in the middle section. The width of the splitting channel is basically determined by the slurry pressure, and has a distribution trend the same as that of the slurry pressure. The viscosity of slurry and the elastic modulus of sand are important factors affecting the splitting diffusion radius , and both are positively related to the diffusion radius. The slurry viscosity is positively related to the splitting width, while the modulus is negatively related to the splitting width. Finally, a comparison was made through a project under construction, and it was found that the deviation between the theoretical calculation value and the actual excavation value was 12%−15%, which basically met the expected requirements.
- slurry-soil coupling effect /
- split grouting /
- splitting pressure /
- diffusion mechanism /
- engineering application

HTML全文

劈裂注浆形成的浆脉可起到“加筋”和骨架支撑作用，显著提升砂层的整体力学性能，目前是富水砂层加固治理的重要方法^[1-4]. 劈裂注浆过程中，浆液在注浆压力作用下劈开级配砂土，产生劈裂缝并在砂层中对称流动、扩张^[5-7]. 张连震等^[8]指出劈裂注浆过程伴随着土体的非线性压密变形，土体变形对浆脉扩展具有重要影响；张庆松等^[9]指出劈裂注浆改变了砂层的天然应力状态，垂直劈裂扩展方向的压应力受注浆作用影响显著增加；秦鹏飞^[10]指出钻孔周围存在拉压应力场，拉应力作用导致土体结构产生破坏并出现劈裂缝；申时钊等^[11]研究发现，均质同性的土层劈裂注浆形成的浆脉少而窄，软弱不均的夹层土形成的浆脉则宽而广；刘海明等^[12]分析了Hersehel-Bulkley流体的劈裂扩散规律，发现注浆压力、孔隙尺寸及浆液流变参数对扩散半径影响显著.

上述研究大多是基于弹塑性力学的基本原理，假定劈裂一次扩展成型. 实际上劈裂注浆机理非常复杂，其间伴随砂土应力场与浆液流场的动态耦合，浆土应力耦合作用对浆液扩散具有显著影响. 本文基于牛顿型本构方程分析了浆液流场基本特征，并将劈裂注浆视作平面无限域的圆形扩张，采用弹性力学推导均布荷载下劈裂通道宽度、浆液压力分布方程；接下来通过设置不同的浆液黏度、砂土弹性模量等参数，对浆-土耦合效应下劈裂注浆基本规律进行探讨；最后结合郑州某区间隧道进行验证.

1. 劈裂注浆理论

1.1 基本假定

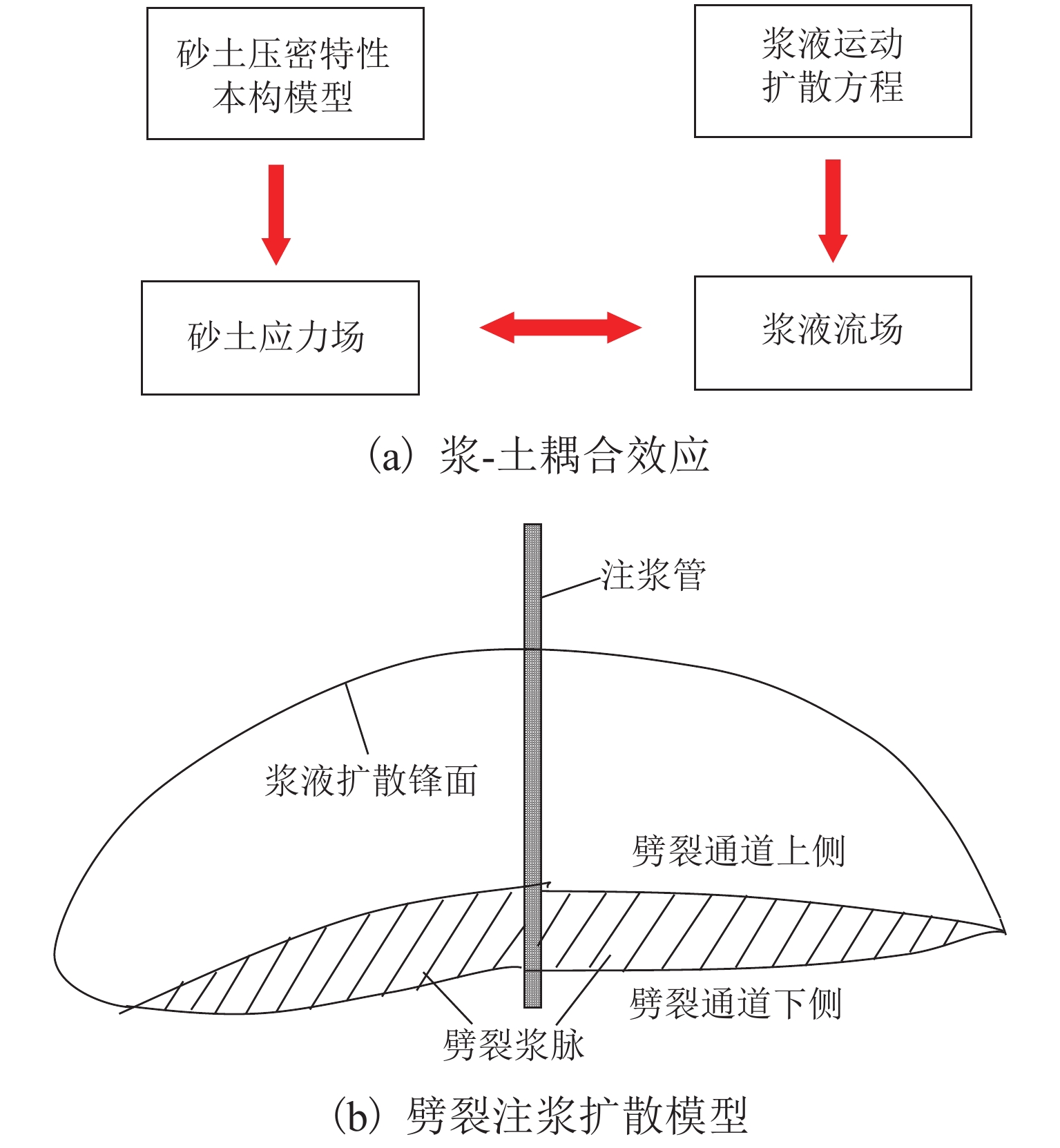
伴随着起劈位置移动、劈裂通道扩展，浆液扩散半径不断增加，劈裂通道宽度则向浆液锋面处逐渐衰减^[13-14]. 为准确分析砂土劈裂注浆基本规律，特作以下假设：1）浆液流型不因黏度、水灰比发生改变，在扩散路径上始终为均质、不可压缩的牛顿流体，砂土为各向同性的弹性介质；2）劈裂通道上下侧壁浆液流动速度为0，严格满足无滑移边界条件；3）劈裂流动的浆液质量保持守恒，不考虑渗透扩散到砂层通道以外的质量损失；4）砂层应力场分布均匀，忽略浆液自身重力对浆脉形成的影响，浆液在砂土内呈水平圆形扩张流动；5）劈裂通道侧壁与水平面平行，浆液压力垂直作用于劈裂通道上下侧壁（图1）.

图 1 砂土劈裂注浆机理分析

Figure 1. Mechanism analysis of split grouting in sandy soil

下载: 全尺寸图片幻灯片

1.2 浆液劈裂扩展机制

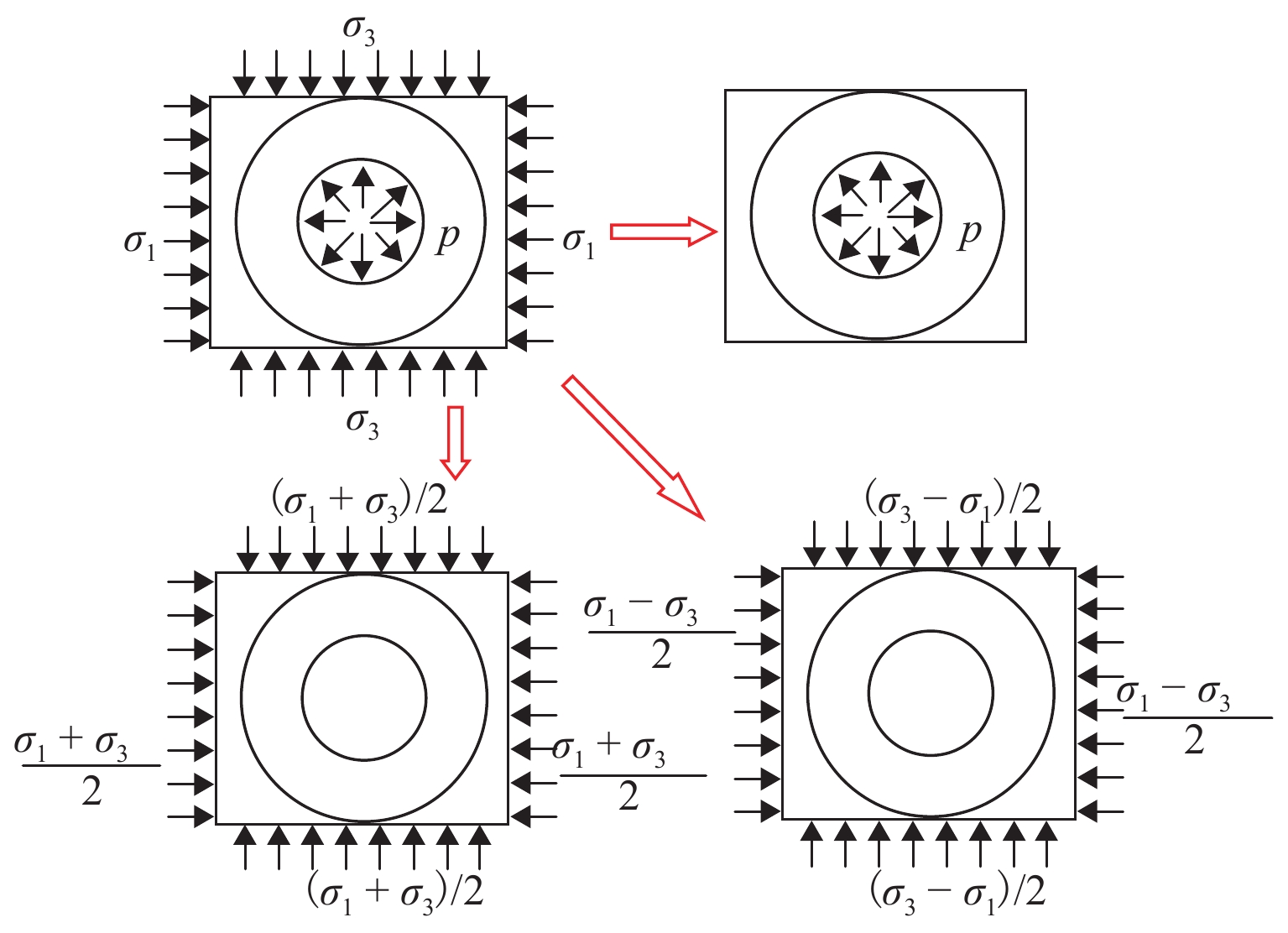
劈裂注浆力学机理及推导分析过程见图2. 图中：p为注浆压力；σ₁、σ₃分别为砂土层最大、最小主应力.

图 2 劈裂注浆力学机理分析

Figure 2. Mechanical mechanism analysis of split grouting

下载: 全尺寸图片幻灯片

根据弹性力学分析方法^[15-17]，钻孔附近应力可分解为3种相互对称的作用力，由此得环向拉应力为

$\begin{split} &{\sigma _\alpha }= \frac{{({a^2} + 3a_0^2)({\sigma _1} - {\sigma _3})}}{{2{a^2}}}\cos \,2\alpha - \\ &\quad\frac{{{\sigma _1} + {\sigma _3}}}{2} + \frac{{a_0^2}}{{{a^2}}}p, \end{split}$

(1)

式中：α为劈裂注浆分析作用点的方位角；a为该分析作用点距离注浆孔的距离；a₀为钻孔半径.

钻孔周围应力场在注浆压力作用下不断发生变化，当钻孔周围拉应力大于砂土抗拉强度σ_t时，砂土结构破坏并产生劈裂缝，此时对应的注浆压力即为起劈压力，即

${p_{\rm{s}}}= {\sigma _{\rm{t}}} - {\sigma _1} + 3{\sigma _3} .$

(2)

砂土被起劈后，在注浆压力作用下劈裂缝沿小主应力面向四周扩展. 根据断裂力学理论，劈裂缝扩展压力为

${p_{\rm{e}}} = \left( {1 - \frac{{M(d/{a_0})}}{{N(d/{a_0})}}} \right){\sigma _1} + \frac{{M(d/{a_0})}}{{N(d/{a_0})}}{\sigma _3} + \frac{{{F_1}}}{{N(d/{a_0}){\text{π}} d}},$

(3)

式中：M(d/a₀)，N(d/a₀)为劈裂扩展计算函数，d为劈裂扩展距离；F₁为劈裂扩展临界强度因子.

分析发现，当d≥10a₀时，M(d/a₀)≈N(d/a₀)≈1，式（3）可化简为

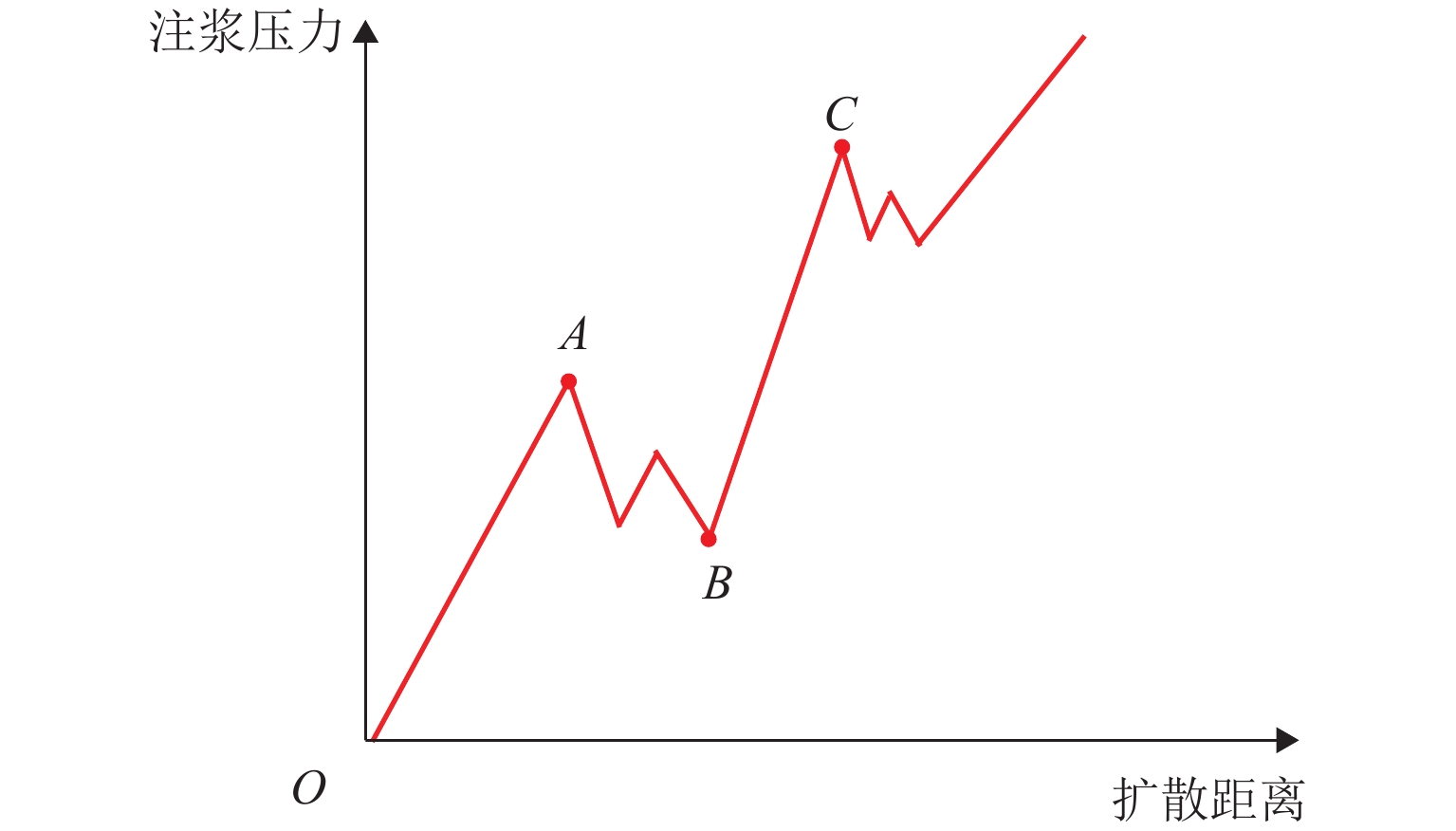
${p_{\rm{e}}} = {\sigma _3} + \frac{{{F_1}}}{{{\text{π}} d}}.$

(4)

工程实测发现，局部松散砂土层中，浆液劈裂扩散半径可达20～30 m，为便于分析，可将式（4）的第2项忽略不计，即认为劈裂通道扩展压力与最小主应力相等. 与起劈注浆压力相比，劈裂通道扩展压力在数值上有所降低，因而，浆液压力在扩散通道上呈现起伏跌宕的状况（图3）. 图3中：点A为初次劈裂压力；点B为初次劈裂后回缩压力；点C为二次劈裂压力.

图 3 注浆压力沿程分布

Figure 3. Grouting pressure distribution

下载: 全尺寸图片幻灯片

1.3 浆液劈裂扩展基本规律

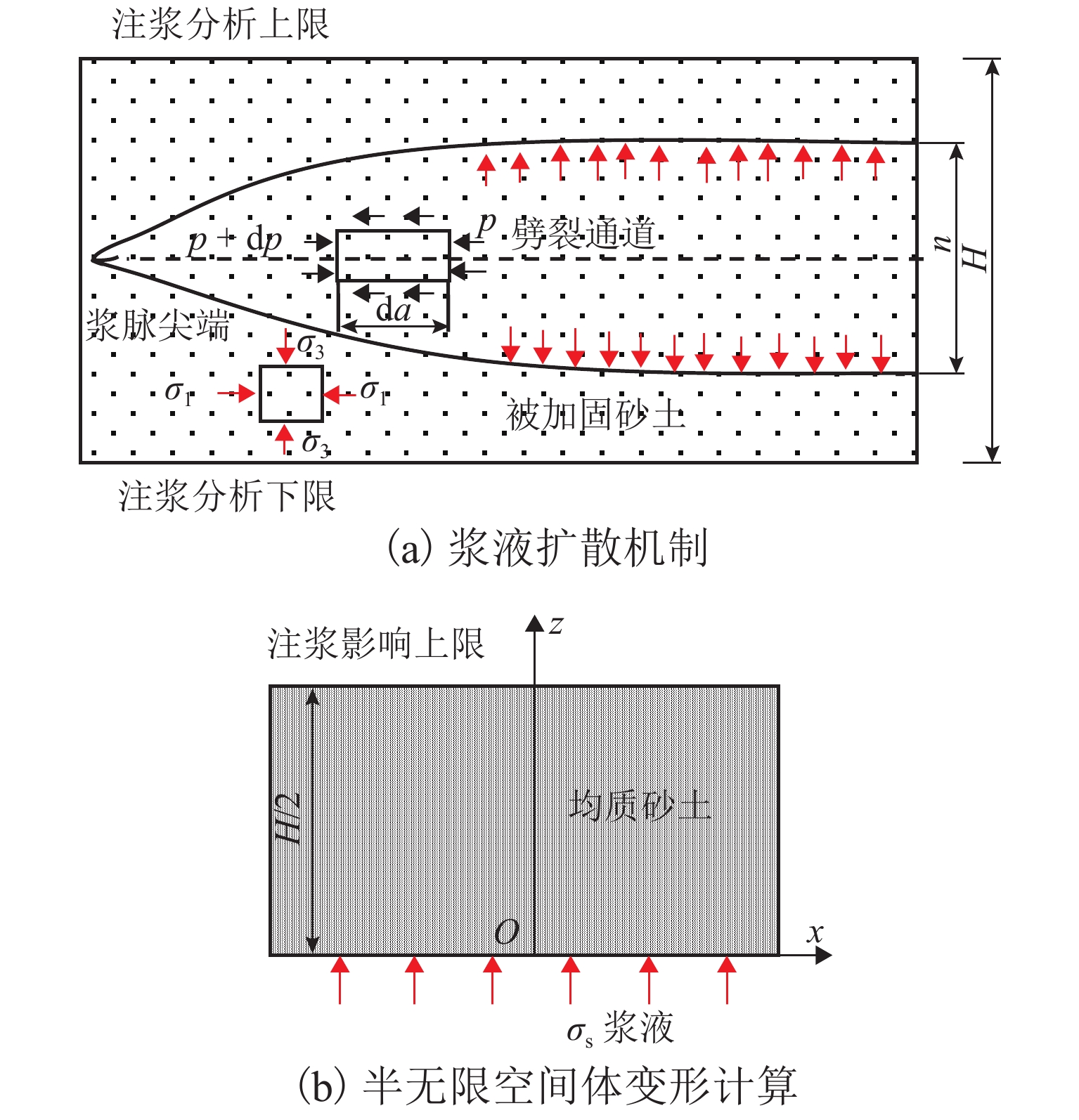
图4为考虑浆土界面应力耦合作用的劈裂注浆机理分析示意，取通过注浆孔的竖直剖面进行砂土劈裂注浆基本规律分析，图中：n为劈裂通道宽度；H为劈裂注浆有效影响深度；σ_s为附加应力：da为浆液分析区段长度；dp为两侧压力差. 在劈裂通道中心线上取一浆液微元体，通过对微元体的受力分析可建立起牛顿型浆液的运动扩散方程.

图 4 劈裂注浆浆-土耦合作用分析

Figure 4. Slurry-soil coupling effect analysis of split grouting

下载: 全尺寸图片幻灯片

微元体水平向受力平衡方程^[18-19]为

$h{\rm{d}}p + \tau {\rm{d}}a = 0 ,$

(5)

式中：τ为浆液表面剪切应力；h为中线上半部分微元体高度.

由式（5）可推导出浆液表面剪切应力为

$\tau = - h{\rm{d}}p/{\rm{d}}a.$

(6)

牛顿流体的剪应力与剪切速率呈线性关系，其本构方程为

$\tau=\mu_{{\rm{B}}} \gamma=-\mu_{{\rm{B}}} \mathrm{d} v / \mathrm{d} h \text{，}$

(7)

式中：μ_B为塑性黏度；v为浆液流速； $\gamma$ 为剪切速率.

由无滑移边界条件可知h=±n/2，v=0，结合推导式（6）、（7）可得浆液在砂土层内的平均流速为

$\bar{v}=-\frac{n^{2}}{12 \mu_{{\rm{B}}}}\frac{\mathrm{d}p}{\mathrm{d} a} .$

(8)

由于不考虑浆液损失，根据质量守恒可得浆液在扩散通道上的压力梯度为

$\frac{{\rm{d}} p}{{\rm{d}} a}=-\frac{6 \eta \mu_{{\rm{B}}}}{n^{3} {\text{π}} a},$

(9)

式中：η为注浆速率.

1.4 劈裂通道宽度计算

起劈发生后浆液在劈裂通道上持续流动，对通道上下侧砂层产生垂直压力，砂土受压后分别向上、下移动，为劈裂注浆拓展了空间. 砂土的位移量取决于砂层弹性模量和浆液压力. 劈裂通道宽度在扩散方向上由近及远逐渐变小，导致浆液压力作用方向与铅垂线存在一个微小夹角，考虑到浆液辐射扩散范围足够大，因而可忽略该夹角的存在^[20-23]. 砂土变形、劈裂通道宽度计算模型可被简化为半无限空间弹性体呈受均布压力作用的物理模型^[24-25].

以浆-土接触界面为xOy平面、通过注浆孔的铅锤面为xOz平面，建立空间直角坐标系. 分析可知，由于浆液呈平面辐射圆对称扩散，砂土x、y方向均不产生位移. 砂土z方向的位移s_z可由弹性理论推导求出，即

${s_{{\textit{z}}}} = f(E,p,{\sigma _{\textit{z}}}),$

(10)

式中：E为砂土弹性模量；σ_z为竖向应力.

砂土在注浆压力作用下产生竖向位移，促使砂土变形的应力σ_s=p－σ₃. 由于砂土均质各向同性，其变形符合广义胡克定律：

$\left\{ \begin{aligned} &{\varepsilon _x} = \frac{1}{E}[{\sigma _x} - \mu ({\sigma _y} + {\sigma _{\textit{z}}})],\\ &{\varepsilon _y} = \frac{1}{E}[{\sigma _y} - \mu ({\sigma _x} + {\sigma _{\textit{z}}})],\\ &{\varepsilon _{\textit{z}}} = \frac{1}{E}[{\sigma _{\textit{z}}} - \mu ({\sigma _x} + {\sigma _y})], \end{aligned} \right.$

(11)

式中：σ_x、σ_y、σ_z分别为x、y、z方向的应力；ε_x、ε_y、ε_z分别为x、y、z方向的应变，ε_x=ε_y=0；μ为砂土泊松比.

由上述分析可推导出砂层竖直方向的应变为

${\varepsilon _{\textit{z}}} = \frac{{{\rm{d}}{s_{{\textit{z}}}}}}{{{\rm{d}}{\textit{z}}}} = \frac{{(1 + \mu )(1 - 2\mu ){\sigma _{\textit{z}}}}}{{(1 - \mu )E}}.$

(12)

砂土承受垂直劈裂通道方向的压应力，而向两侧侧移. 将几何方程 $\varepsilon_{\textit{z}}$ = ds_z/dz代入砂层应变量分析式（式（12）），可得砂土竖向位移为

${s_{{\textit{z}}}} = \frac{{(2{\mu ^2} + \mu - 1){\textit{z}}{\sigma _{\rm{s}}}}}{{(1 - \mu )E}} + D,$

(13)

式中：σ_s为附加应力；D为待定常数.

砂土劈裂注浆只在有限范围内发生，劈裂注浆有效影响深度为H. 显然z=h/2，s_z=0，将此边界条件代入式（13），有

${s_{{\textit{z}}}} = \frac{{(H - 2{\textit{z}})(1 - \mu - 2{\mu ^2}){\sigma _{\rm{s}}}}}{{2(1 - \mu )E}}.$

(14)

砂土最大竖向位移s_max存在于浆-土界面上，令z=0，则有

${s_{\max }} = \frac{{(1 - \mu - 2{\mu ^2}){\sigma _{\rm{s}}}H}}{{2(1 - \mu )E}}.$

(15)

由对称性可得劈裂通道宽度n=2s_max. 将σ_s=p−σ₃代入式（15），可得劈裂通道宽度控制方程为

$n = (1 - \mu - 2{\mu ^2})\frac{{(p - {\sigma _3})H}}{{(1 - \mu )E}} = I(p - {\sigma _3}),$

(16)

式中： $I = H(1 - \mu - 2{\mu ^2})/(E - E\mu )$ ，为与浆土耦合效应相关的力学性能常数.

1.5 浆液空间分布特征分析

将式（16）与劈裂扩展通道上的压力梯度相联合，可得到劈裂宽度在砂层内变化的微分方程：

${\text{π}} {n^3}{{\rm{d}}n} = {\rm{ － }}\frac{{6{\mu _{\rm{B}}}\eta I}}{a}{\rm{d}}a.$

(17)

对式（17）两侧积分，可求得

$n = \sqrt[\uproot{10}{{4 }}]{{C - \frac{{24{\mu _{\rm{B}}}\eta I}}{{\text{π}} }\ln \, a}}\;,$

(18)

式中：C为常数.

劈裂通道宽度在扩散路径上不断衰减，直至为0. 由边界条件a=a_max，n=0可求得

$C = \frac{{24{\mu _{\rm{B}}}\eta I}}{{\text{π}} }\ln {a_{\max }},$

(19)

式中：a_max为劈裂扩展极限半径.

将常数C代入式（18），整理可得

$n = \sqrt[\uproot{10}{{4 }}]{{\frac{{24{\mu _{\rm{B}}}\eta I}}{\text{π}}\ln {\frac{{{a_{\max }}}}{a}} }}.$

(20)

联立式（16）、（20），经恒等变形可得浆液压力的衰减分布方程：

$p = \sqrt[\uproot{10}{{4 }}]{{\frac{{24{\mu _{\rm{B}}}\eta }}{{{\text{π}} {I^3}}}\ln {\frac{{{a_{\max }}}}{a}} }} + {\sigma _3} .$

(21)

令a=a₀，并对式（21）两端取两次平方，可求出劈裂扩展极限半径^[26-28]为

${a_{\max }} = {a_0}\exp \left( {\frac{{{\text{π}} {I^3}{{({p_{\rm{c}}} - {\sigma _3})}^4}}}{{24{\mu _{\rm{B}}}\eta }}} \right),$

(22)

式中：p_c为注浆孔起始压力.

2. 劈裂扩散规律分析

郑州地铁7号线地质状况复杂，多处开挖区段，所揭露地层为密实卵石、砂土层. 本节以郑州地铁7号线项目建设为工程背景，对砂土劈裂注浆机理进行分析探讨. 分析计算所选取砂土物理力学性能参数见表1. 现场灌注采用矿渣硅酸盐水泥，μ_B=11 MPa·s，η=57 L/min，注浆管半径r₀=0.04 m. 理论推导表明，劈裂扩展压力p_e在量值上与砂土层σ₃相当，因此，孔口初始压力与扩散远端压力之差Δp = p_c−σ₃，决定着浆液劈裂扩散半径. 将砂土力学参数、浆液性能参数代入式（20）、（23）、（25），对浆液压力、扩散半径及浆脉宽度等进行了系统分析.

表 1 郑州地铁区间隧道砂土力学参数

Table 1. Mechanical parameters of sandy soil in Zhengzhou Metro Tunnel

参数	天然密度/（g·cm⁻³）	干密度/（g·cm⁻³）	弹性模量/MPa	泊松比	含水率/%	含泥量/%	注浆影响范围/m
取值	2.01	1.68	5.94	0.38	23.3	11.8	10

下载: 导出CSV

| 显示表格

2.1 不同压力下浆液扩散半径分析

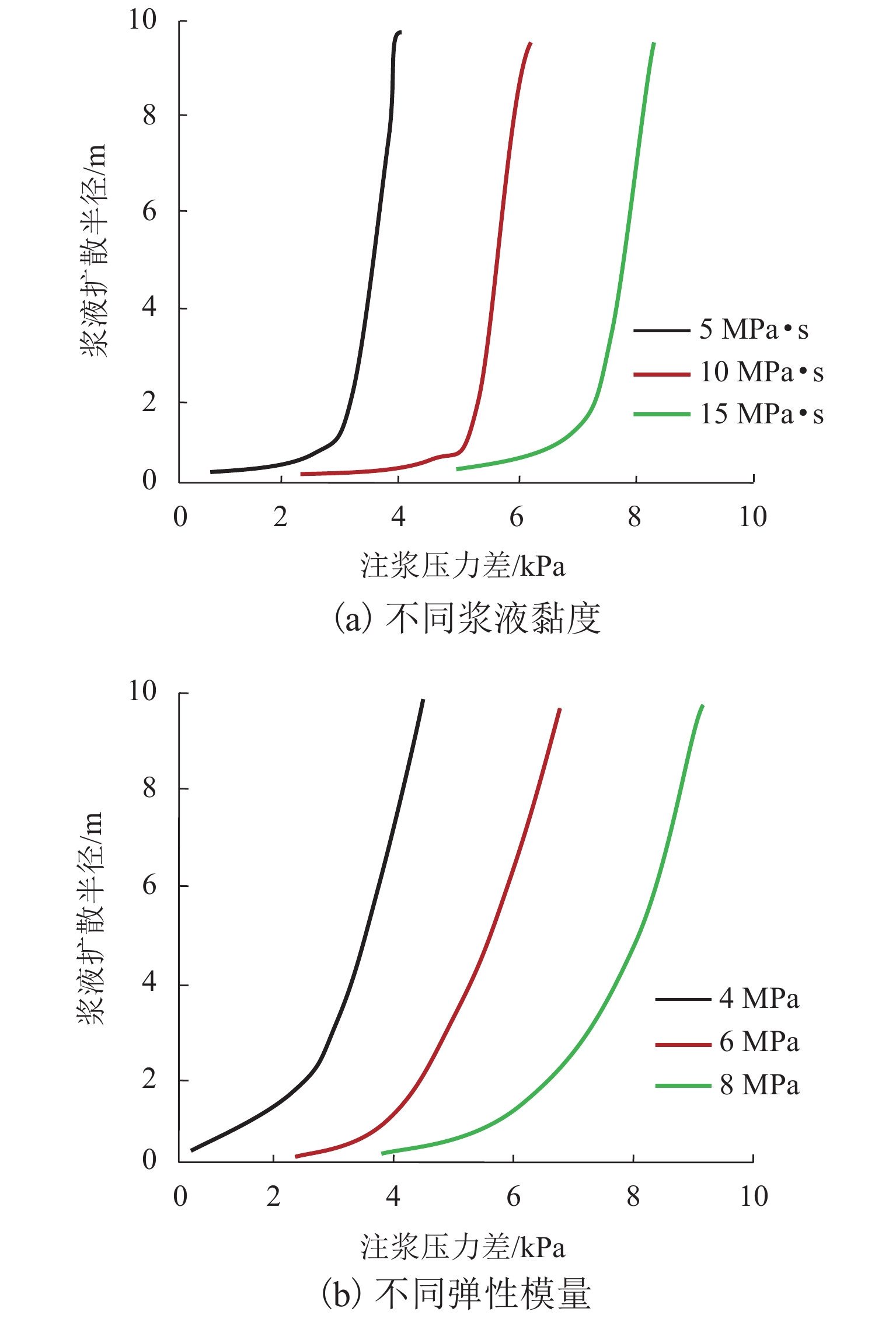
图5为注浆压力差0～10 kPa下浆液扩散半径变化情形. 由图可知：1）注浆压力是决定浆液扩散范围的重要因素，低压时浆液扩散范围仅有2 m，压力增加到某一临界值时，砂层结构产生劈裂破坏，浆液扩散半径陡然增加至10 m. 2）浆液自身流变性能与地质参数对劈裂注浆效果有一定影响，浆液流动性能越强、砂土密实度越小，浆液劈裂扩散半径越大；反之则越小. 3）实际工程由于受地质历史、人类活动，及砂土自然结构性、复杂性的影响，劈裂扩散半径一般远低于本文理论计算值. 实际编制注浆设计计算预案时，可在详尽的地质勘察资料基础上对理论计算结果进行修正.

图 5 浆液扩散半径与注浆压力差关系

Figure 5. Relationship between slurry diffusion radius and grouting pressure

下载: 全尺寸图片幻灯片

2.2 注浆压力衰减规律

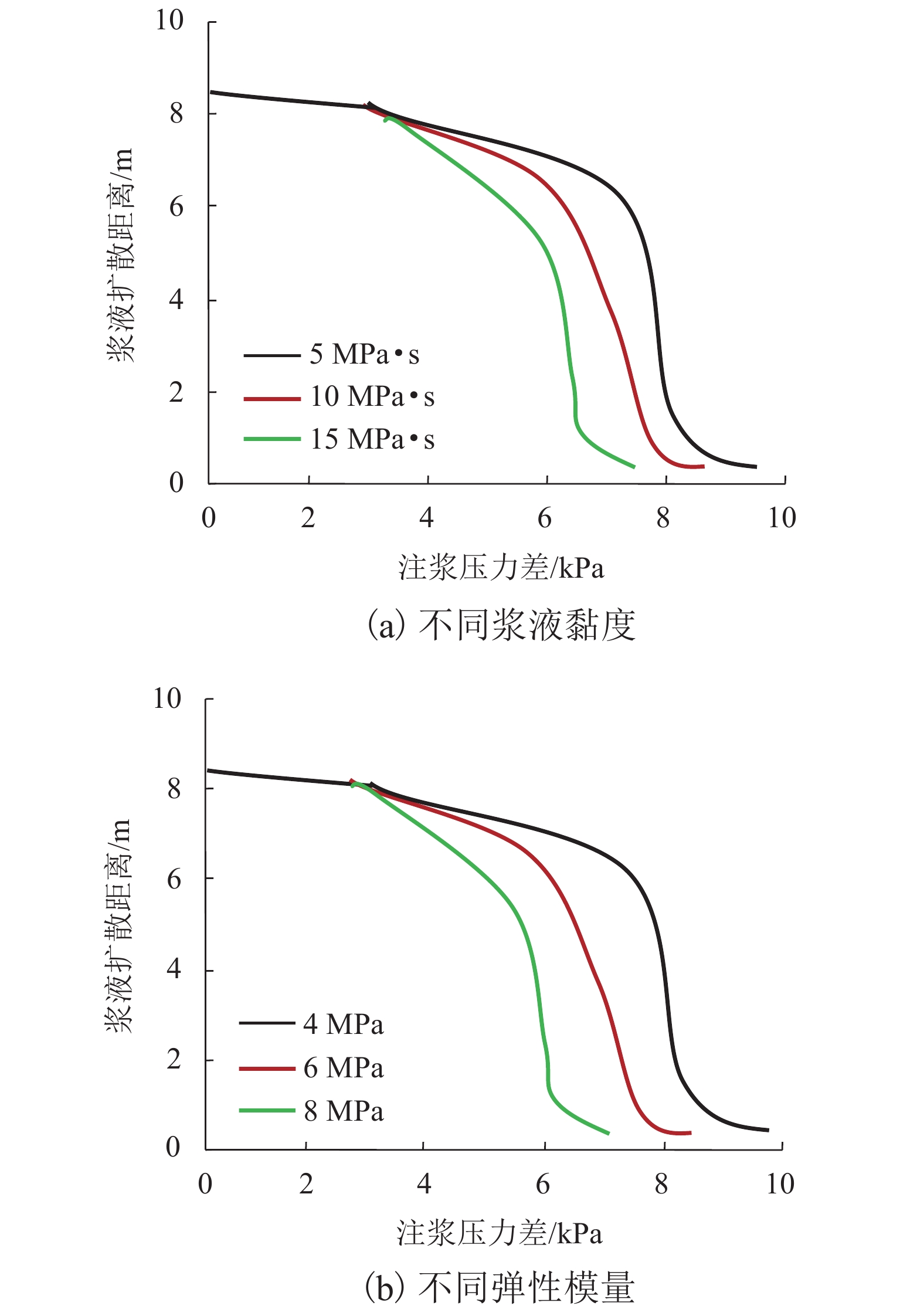
图6为0～10 kPa注浆压力差下砂土内部浆液扩散距离分布情况. 由图可知，浆液压力在扩散通道上由近及远逐渐衰减，至浆液锋面处降低为0，浆液压力在孔口及远端处衰减迅速，而在中间区段则呈稳定变化趋势. 分析原因是钻孔附近浆液压力梯度高，压力衰减趋势明显；扩散远端处浆液受到较大的砂层侧壁阻力，注浆压力也极易损失. 从浆液压力的衰减分布可以看出，其与浆液黏度、砂土弹性模量基本呈正相关.

图 6 注浆压力沿程衰减规律

Figure 6. Relationship between slurry diffusion radius and grouting pressure

下载: 全尺寸图片幻灯片

2.3 劈裂通道宽度衰减规律

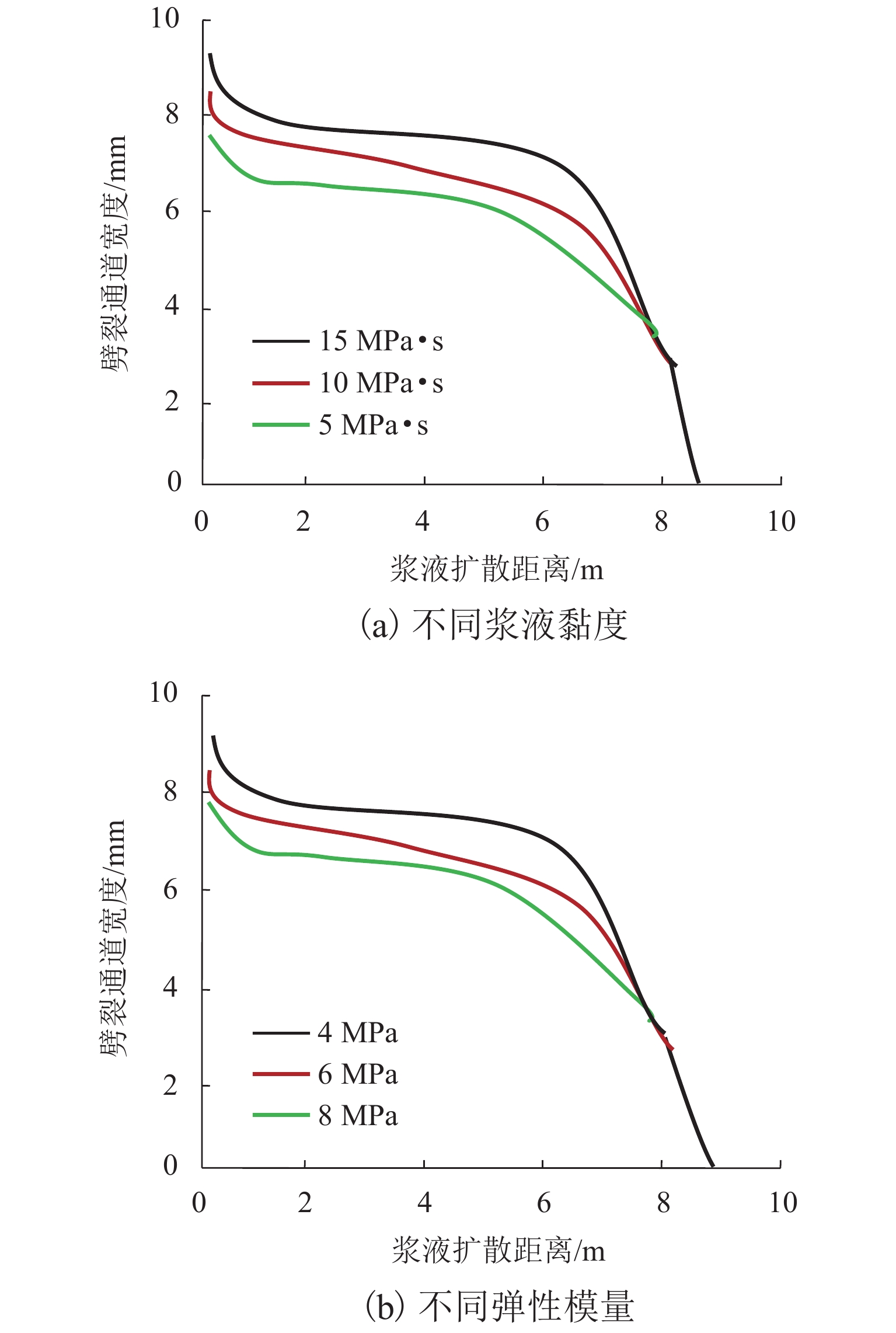
图7为0～10 kPa注浆压力差下劈裂通道宽度分布曲线. 由图可知：1）劈裂通道宽度在孔口附近最大，约为10 mm，沿扩散路径浆脉宽度逐渐缩减，至扩散远端浆脉完全消失. 孔口及扩散远端浆脉宽度衰减较快，而中间区段浆脉衰减较为平稳. 劈裂通道宽度的变化趋势与浆液压力变化趋势完全相同，这是由于劈裂宽度由浆液压力决定并呈严格正比例关系，扩散通道上的浆液压力与劈裂宽度保持同步改变. 2）浆液自身物理力学性能及地质参数对劈裂宽度影响较大，劈裂宽度与浆液黏度呈正相关，而与砂土弹性模量呈负相关. 浆液黏度越大所消耗的能量越多，劈裂宽度相应增加；砂土弹性模量越小密实性越差，劈裂通道宽度也相应增加.

图 7 劈裂宽度沿程衰减规律

Figure 7. Relationship between slurry diffusion radius and splitting gap

下载: 全尺寸图片幻灯片

3. 工程应用研究

郑州地铁7号线陈砦—白庙站为含黏土砂砾层，盾构掘进施工中连续多次发生溃砂、塌方地质灾害，现场采用水灰比0.8∶1的水泥浆进行全断面注浆加固治理. μ_B=12.6 MPa·s，注浆压力2.2～2.4 MPa，速率55～65 L/min. 注浆结束28 d后开挖检测，发现被加固体中存在多种形式的劈裂浆脉. 主浆脉长度76～82 cm，宽度12～15 cm，分支浆脉长度16～20 cm，宽度3～6 cm.

隧道埋深18 m，结合勘察设计单位提供的工程地质资料，计算得到注浆断面处地层最大主应力σ₁ = 1.2 MPa. 参考郑州区域施工经验，侧压力系数k取为0.52，则地层最小主应力σ₃ = 0.62 MPa. 将注浆压力参数、地层和浆液参数代入式（22）、（25），得浆脉最大长度为82～85 cm，宽度为14～18 cm. 与现场开挖检测所揭露浆脉宽度相比，理论计算值偏大12%～15%，计算误差处于工程设计允许范围内（图8）.

图 8 隧道开挖揭露浆脉

Figure 8. Slurry veins exposed during tunnel excavation

下载: 全尺寸图片幻灯片

浆脉宽度理论计算值与实际开挖检测值并不完全一致，分析原因是：1）不良地质区域经过多序次复合注浆后，其力学强度、非线性应力-应变性能显著提升，浆液劈裂扩展的难度随之增加，而理论计算未能合理考虑这一复杂转变过程；2）由于施工条件的复杂性和岩土介质的自然结构性，劈裂注浆过程中会产生包含主干浆脉、次生浆脉在内的多条浆脉，而理论计算假定浆液平面辐射动态扩散，与实际工况存在差异.

4. 结　论

本文将劈裂注浆视作平面无限域的圆形扩张，采用弹性力学方法分析了不同浆液黏度、砂土模量状态下，浆液压力、扩散半径及劈裂通道宽度的变化规律，并结合郑州地铁区间隧道进行了实测验证. 所得结论如下：

1）浆液压力在孔口及扩散锋面处急速衰减，而在中间区段呈稳定变化趋势，劈裂通道宽度分布规律与浆液压力保持一致.

2）浆液扩散半径随注浆压力增加呈指数函数形式增加，受浆液性质及砂土力学参数等因素影响明显；劈裂通道宽度与砂土弹性模量负相关，而与浆液黏度正相关.

3）工程实测对比发现，本文计算值与现场开挖值偏差12%～15%，基本符合预期要求. 这表明考虑浆土耦合效应的劈裂注浆计算方法. 在砂土工程项目建设中具有高度的适用性，有利于丰富和完善劈裂注浆理论.

图 1 砂土劈裂注浆机理分析

Figure 1. Mechanism analysis of split grouting in sandy soil

下载: 全尺寸图片幻灯片

图 2 劈裂注浆力学机理分析

Figure 2. Mechanical mechanism analysis of split grouting

下载: 全尺寸图片幻灯片

图 3 注浆压力沿程分布

Figure 3. Grouting pressure distribution

下载: 全尺寸图片幻灯片

图 4 劈裂注浆浆-土耦合作用分析

Figure 4. Slurry-soil coupling effect analysis of split grouting

下载: 全尺寸图片幻灯片

图 5 浆液扩散半径与注浆压力差关系

Figure 5. Relationship between slurry diffusion radius and grouting pressure

下载: 全尺寸图片幻灯片

图 6 注浆压力沿程衰减规律

Figure 6. Relationship between slurry diffusion radius and grouting pressure

下载: 全尺寸图片幻灯片

图 7 劈裂宽度沿程衰减规律

Figure 7. Relationship between slurry diffusion radius and splitting gap

下载: 全尺寸图片幻灯片

图 8 隧道开挖揭露浆脉

Figure 8. Slurry veins exposed during tunnel excavation

下载: 全尺寸图片幻灯片

表 1 郑州地铁区间隧道砂土力学参数

Table 1. Mechanical parameters of sandy soil in Zhengzhou Metro Tunnel

参数天然密度/（g·cm⁻³）干密度/（g·cm⁻³）弹性模量/MPa 泊松比含水率/% 含泥量/% 注浆影响范围/m

取值 2.01 1.68 5.94 0.38 23.3 11.8 10

下载: 导出CSV

参考文献(28)

[1]	DONGSOON P, JEHEON O. Permeation grouting for remediation of dam cores[J]. Engineering Geology, 2018, 233: 63-75. doi: 10.1016/j.enggeo.2017.12.011
[2]	张庆松,王洪波,刘人太,等. 考虑浆液扩散路径的多孔介质渗透注浆机理研究[J]. 岩土工程学报,2018,40(5): 918-924. doi: 10.11779/CJGE201805017 ZHANG Qingsong, WANG Hongbo, LIU Rentai, et al. Infiltration grouting mechanism of porous media considering diffusion paths of grout[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 918-924. doi: 10.11779/CJGE201805017
[3]	RASOULI R, HAYASHI K, ZEN K. Controlled permeation grouting method for mitigation of liquefaction[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(11): 1-11.
[4]	刘人太,郑卓,李术才,等. 地下工程裂隙型涌水超前注浆治理方法[J]. 西南交通大学学报,2019,54(1): 48-54. LIU Rentai, ZHENG Zhuo, LI Shucai, et al. Pre-excavation grouting to prevent water inflow of jointed rock in underground construction[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 48-54.
[5]	李召峰,李术才,刘人太,等. 富水破碎岩体注浆加固实验与机制研究[J]. 岩石力学与工程学报,2017,36(1): 198-207. doi: 10.13722/j.cnki.jrme.2016.0119 LI Zhaofeng, LI Shucai, LIU Rentai, et al. Grouting reinforcement experiment for water-rich broken rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(1): 198-207. doi: 10.13722/j.cnki.jrme.2016.0119
[6]	张庆松,张连震,张霄,等. 基于浆液黏度时空变化的水平裂隙岩体注浆扩散机制[J]. 岩石力学与工程学报,2015,34(6): 1198-1210. doi: 10.13722/j.cnki.jrme.2014.0958 ZHANG Qingsong, ZHANG Lianzhen, ZHANG Xiao, et al. Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1198-1210. doi: 10.13722/j.cnki.jrme.2014.0958
[7]	叶飞,秦楠,梁兴,等. 基于驱替效应的盾构壁后注浆微观模型分析[J]. 西南交通大学学报,2022,57(2): 339-345. doi: 10.3969/j.issn.0258-2724.20200344 YE Fei, QIN Nan, LIANG Xing, et al. Microscopic model analysis of shield tunnel backfill grouting based on displacement effect[J]. Journal of Southwest Jiaotong University, 2022, 57(2): 339-345. doi: 10.3969/j.issn.0258-2724.20200344
[8]	张连震,李志鹏,张庆松,等. 基于土体非线性压密效应的劈裂注浆机制分析[J]. 岩石力学与工程学报,2016,35(7): 1483-1493. doi: 10.13722/j.cnki.jrme.2015.0565 ZHANG Lianzhen, LI Zhipeng, ZHANG Qingsong, et al. Split grouting mechanism based on nonlinear characteristics of compression process of soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1483-1493. doi: 10.13722/j.cnki.jrme.2015.0565
[9]	张庆松,张连震,刘人太,等. 基于“浆-土”界面应力耦合效应的劈裂注浆理论研究[J]. 岩土工程学报,2016,38(2): 323-330. ZHANG Qingsong, ZHANG Lianzhen, LIU Rentai, et al. Split grouting theory based on slurry-soil coupling effects[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(2): 323-330.
[10]	秦鹏飞. 不良地质体注浆细观力学模拟研究[J]. 煤炭学报,2020,45(7): 2646-2654. doi: 10.13225/j.cnki.jccs.2019.0634 QIN Pengfei. Study on meso-mechanical simulation of grouting in bad geo-body[J]. Journal of China Coal Society, 2020, 45(7): 2646-2654. doi: 10.13225/j.cnki.jccs.2019.0634
[11]	申时钊,涂小兵,雷进生,等. 不同渗透系数的非均质黏土劈裂注浆数值模拟[J]. 水利水运工程学报,2022(5): 102-112. SHEN Shizhao, TU Xiaobing, LEI Jinsheng, et al. Numerical simulation of split grouting of heterogeneous clay with different permeability coefficient[J]. Hydro-Science and Engineering, 2022(5): 102-112.
[12]	刘海明,卢昊正,南敢,等. 基于黏度时变性的Herschel-Bulkley流体劈裂注浆扩散特性研究[J]. 自然灾害学报,2022,31(3): 213-221. LIU Haiming, LU Haozheng, NAN Gan, et al. Research on diffusion characteristics of Herschel-Bulkley fluid fracture grouting based on time variation of viscosity[J]. Journal of Natural Disasters, 2022, 31(3): 213-221.
[13]	周茗如,张建斌,卢国文,等. 扩孔理论在非饱和黄土劈裂注浆中的应用[J]. 建筑结构学报,2018,39(增1): 368-378. doi: 10.14006/j.jzjgxb.2018.S1.048 ZHOU Mingru, ZHANG Jianbin, LU Guowen, et al. Application of expansion hole theory in fracture grouting of unsaturated loess[J]. Journal of Building Structures, 2018, 39(S1): 368-378. doi: 10.14006/j.jzjgxb.2018.S1.048
[14]	蔡德国,叶飞,曹凯,等. 砂性地层盾构隧道壁后注浆浆液扩散室内试验[J]. 中国公路学报,2018,31(10): 274-283. CAI Deguo, YE Fei, CAO Kai, et al. Test of grout diffusion of shield tunnel backfill grouting in sandy strata[J]. China Journal of Highway and Transport, 2018, 31(10): 274-283.
[15]	WANG S Y, CHAN D H, LAM K C, et al. A new laboratory apparatus for studying dynamic compaction grouting into granular soils[J]. Soils and Foundations, 2013, 53(3): 462-468. doi: 10.1016/j.sandf.2013.04.007
[16]	付艳斌,陈湘生,吕桂阳,等. 基于小孔扩张弹塑性理论的注浆起始劈裂压力研究[J]. 中国公路学报,2020,33(12): 154-163. doi: 10.3969/j.issn.1001-7372.2020.12.012 FU Yanbin, CHEN Xiangsheng, LYU Guiyang, et al. Study on initial fracture pressure of grouting based on the elastic-plastic theory of cavity expansion[J]. China Journal of Highway and Transport, 2020, 33(12): 154-163. doi: 10.3969/j.issn.1001-7372.2020.12.012
[17]	徐芝纶. 弹性力学（上册）[M]. 4版. 北京: 高等教育出版社, 2006.
[18]	姚茂宏,谢长岭,程少振,等. 双孔劈裂条件下地应力及孔间应力的耦合分析[J]. 北京交通大学学报,2021,45(3): 61-68. doi: 10.11860/j.issn.1673-0291.20200140 YAO Maohong, XIE Changling, CHENG Shaozhen, et al. Coupling analysis of in-situ stress and inter hole stress under double-hole splitting[J]. Journal of Beijing Jiaotong University, 2021, 45(3): 61-68. doi: 10.11860/j.issn.1673-0291.20200140
[19]	PANTAZOPOULOS I A, MARKOU I N, CHRISTODOULOU D N, et al. Development of microfine cement grouts by pulverizing ordinary cements[J]. Cement and Concrete Composites, 2012, 34(5): 593-603. doi: 10.1016/j.cemconcomp.2012.01.009
[20]	KANG S P, KWON S J. Effects of red mud and Alkali-activated slag cement on efflorescence in cement mortar[J]. Construction and Building Materials, 2017, 133: 459-467.
[21]	PEPPER R A, COUPERTHWAITE S J, MILLAR G J. Comprehensive examination of acid leaching behaviour of mineral phases from red mud: recovery of Fe, Al, Ti, and Si[J]. Minerals Engineering, 2016, 99: 8-18. doi: 10.1016/j.mineng.2016.09.012
[22]	张淼,邹金锋,陈嘉祺,等. 非对称荷载作用下土体劈裂注浆压力分析[J]. 岩土力学,2013,34(8): 2255-2263. ZHANG Miao, ZOU Jinfeng, CHEN Jiaqi, et al. Analysis of soil fracturing grouting pressure under asymmetric loads[J]. Rock and Soil Mechanics, 2013, 34(8): 2255-2263.
[23]	邹金锋,童无欺,罗恒,等. 基于Hoek-Brown强度准则的裂隙岩体劈裂注浆力学机理[J]. 中南大学学报(自然科学版),2013,44(7): 2889-2896. ZOU Jinfeng, TONG Wuqi, LUO Heng, et al. Mechanism of fracture grouting for fractured rock based on Hoek-Brown failure criterion[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2889-2896.
[24]	黄明利,管晓明,吕奇峰. 基于弹性力学的诱导劈裂注浆机制分析[J]. 岩土力学,2013,34(7): 2059-2064. HUANG Mingli, GUAN Xiaoming, LÜ Qifeng. Mechanism analysis of induced fracture grouting based on elasticity[J]. Rock and Soil Mechanics, 2013, 34(7): 2059-2064.
[25]	张连震,张庆松,刘人太,等. 基于浆液-岩体耦合效应的微裂隙岩体注浆理论研究[J]. 岩土工程学报,2018,40(11): 2003-2011. ZHANG Lianzhen, ZHANG Qingsong, LIU Rentai, et al. Grouting mechanism in fractured rock considering slurry-rock stress coupling effects[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2003-2011.
[26]	邹金锋,李亮,杨小礼. 劈裂注浆扩散半径及压力衰减分析[J]. 水利学报,2006,37(3): 314-319. doi: 10.3321/j.issn:0559-9350.2006.03.010 ZOU Jinfeng, LI Liang, YANG Xiaoli. Penetration radius and pressure attenuation law in fracturing grouting[J]. Journal of Hydraulic Engineering, 2006, 37(3): 314-319. doi: 10.3321/j.issn:0559-9350.2006.03.010
[27]	张忠苗,邹健. 桩底劈裂注浆扩散半径和注浆压力研究[J]. 岩土工程学报,2008,30(2): 181-184. ZHANG Zhongmiao, ZOU Jian. Penetration radius and grouting pressure in fracture grouting[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 181-184.
[28]	ZHOU H, LIU H L, ZHA Y H, et al. Influence of stress anisotropy on the cylindrical cavity expansion in undrained elastic-perfectly plastic soil[J]. Science China Technological Sciences, 2018, 61(3): 370-380. doi: 10.1007/s11431-017-9127-7

施引文献

期刊类型引用(8)

1.	马宇佳，孙超，赵一恺，陈宇轩，何佳乐. 中砂介质注浆加固效果研究. 浙江建筑. 2025(01): 80-83 . 百度学术
2.	秦鹏飞，陈涛，周想云. 砂质隧道复合注浆加固技术与其应用研究. 中国农村水利水电. 2025(03): 136-141+147 . 百度学术
3.	秦鹏飞，张颖，王柳舒. 非均质砂土劈裂注浆加固机理分析. 力学与实践. 2024(03): 609-616 . 百度学术
4.	秦鹏飞，晋芳，毕琼媛，王莉. 考虑流固耦合效应的砂土注浆加固机理分析. 黄河科技学院学报. 2024(08): 59-66 . 百度学术
5.	于金艳. 大断面暗挖车站隧道开挖的地表深孔注浆技术. 辽宁省交通高等专科学校学报. 2024(04): 1-6 . 百度学术
6.	秦鹏飞，王文菁. 基于渗滤效应的砂土注浆扩散机理分析. 中国水利水电科学研究院学报(中英文). 2024(06): 623-631 . 百度学术
7.	陈锋，杨杰，张冲，余祯，刘先峰. 注浆渗透扩散的多物理场耦合数值分析. 西南交通大学学报. 2024(06): 1469-1478 . 本站查看
8.	秦鹏飞. 非线性压密效应下砂土劈裂注浆机理研究. 工业建筑. 2023(12): 198-203+61 . 百度学术