大跨度连续梁拱桥多点多维地震响应分析

李小珍; 杨得海; 雷康宁; 肖林; 戴胜勇

doi:10.3969/j.issn.0258-2724.20190400

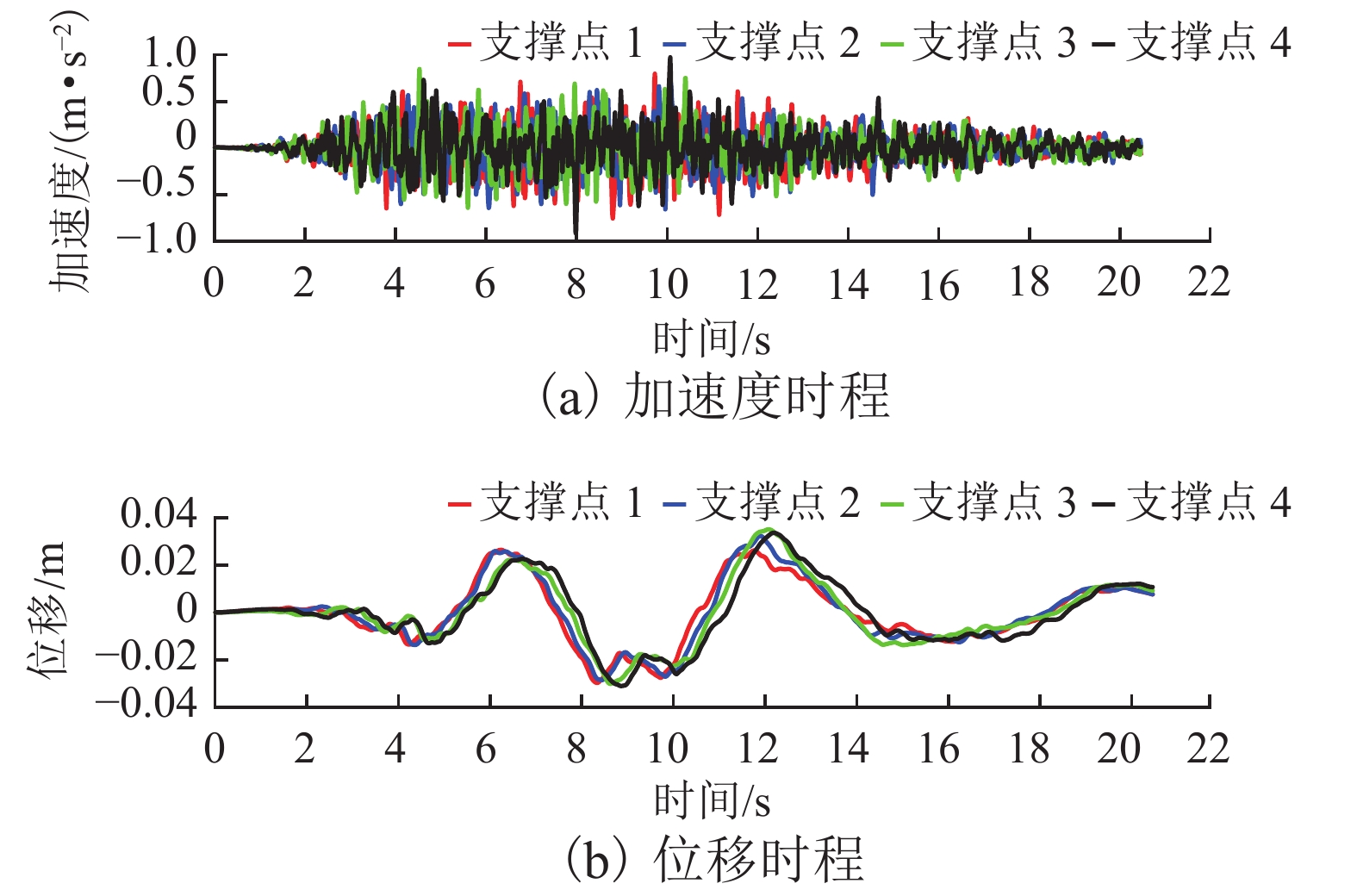
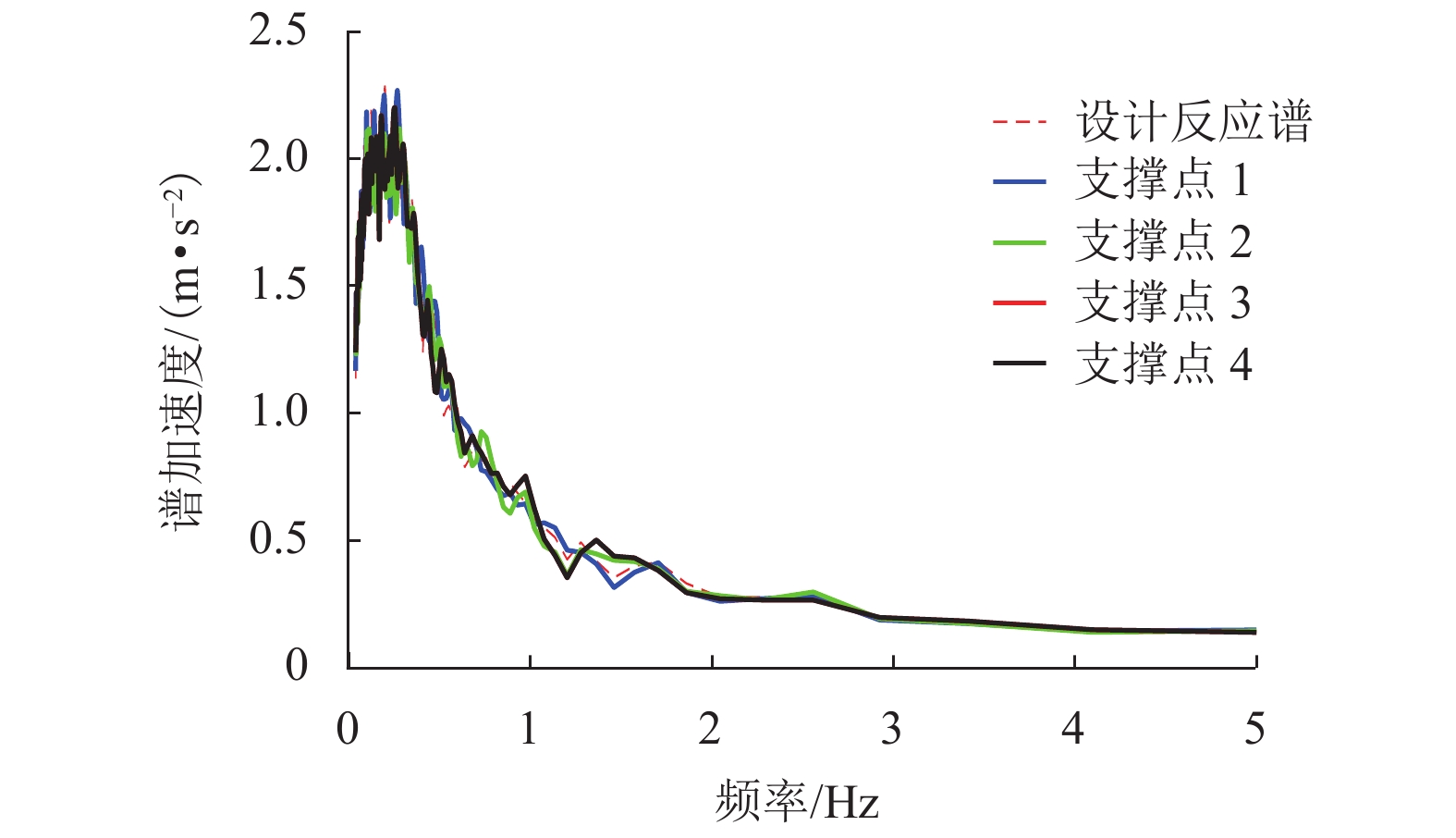
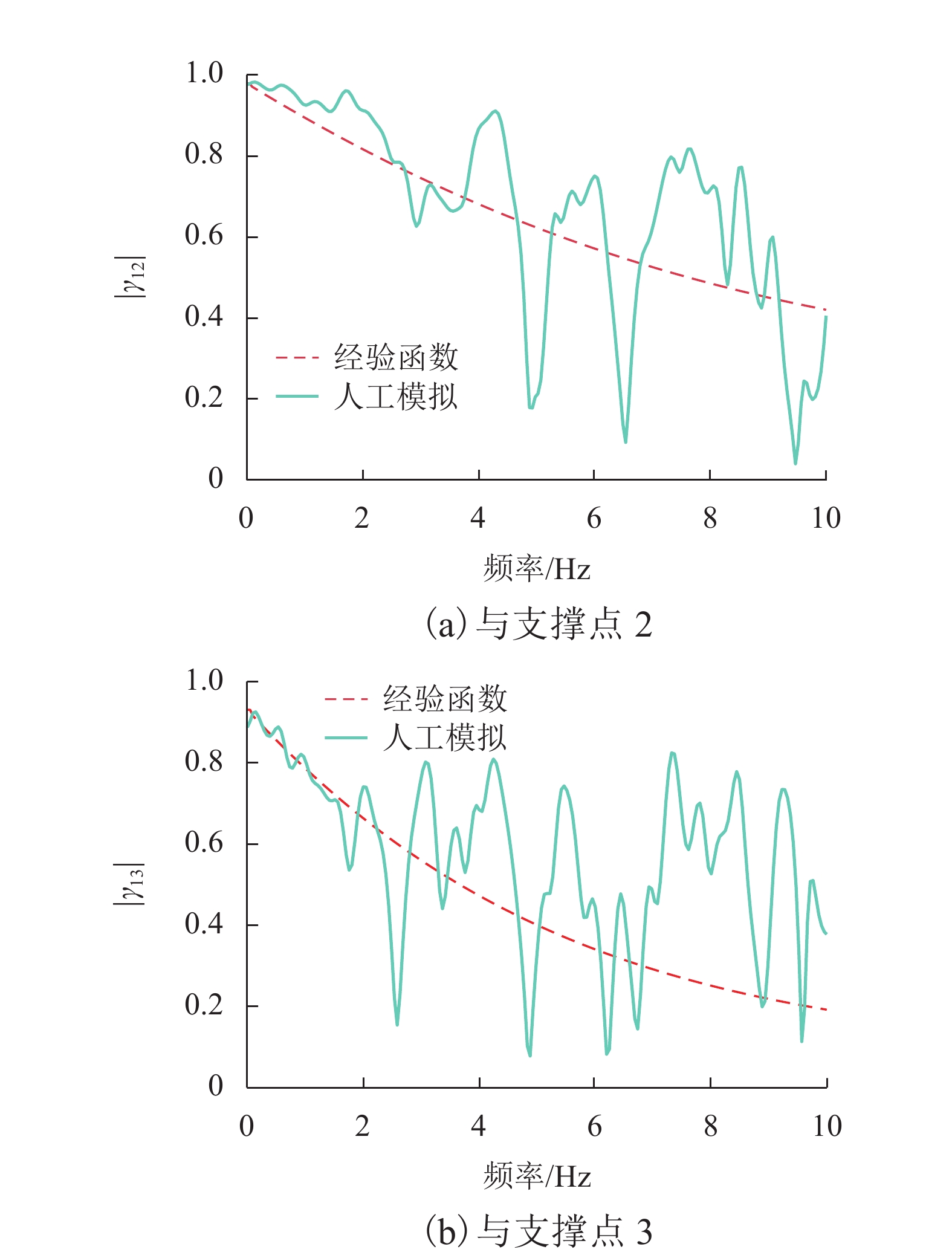
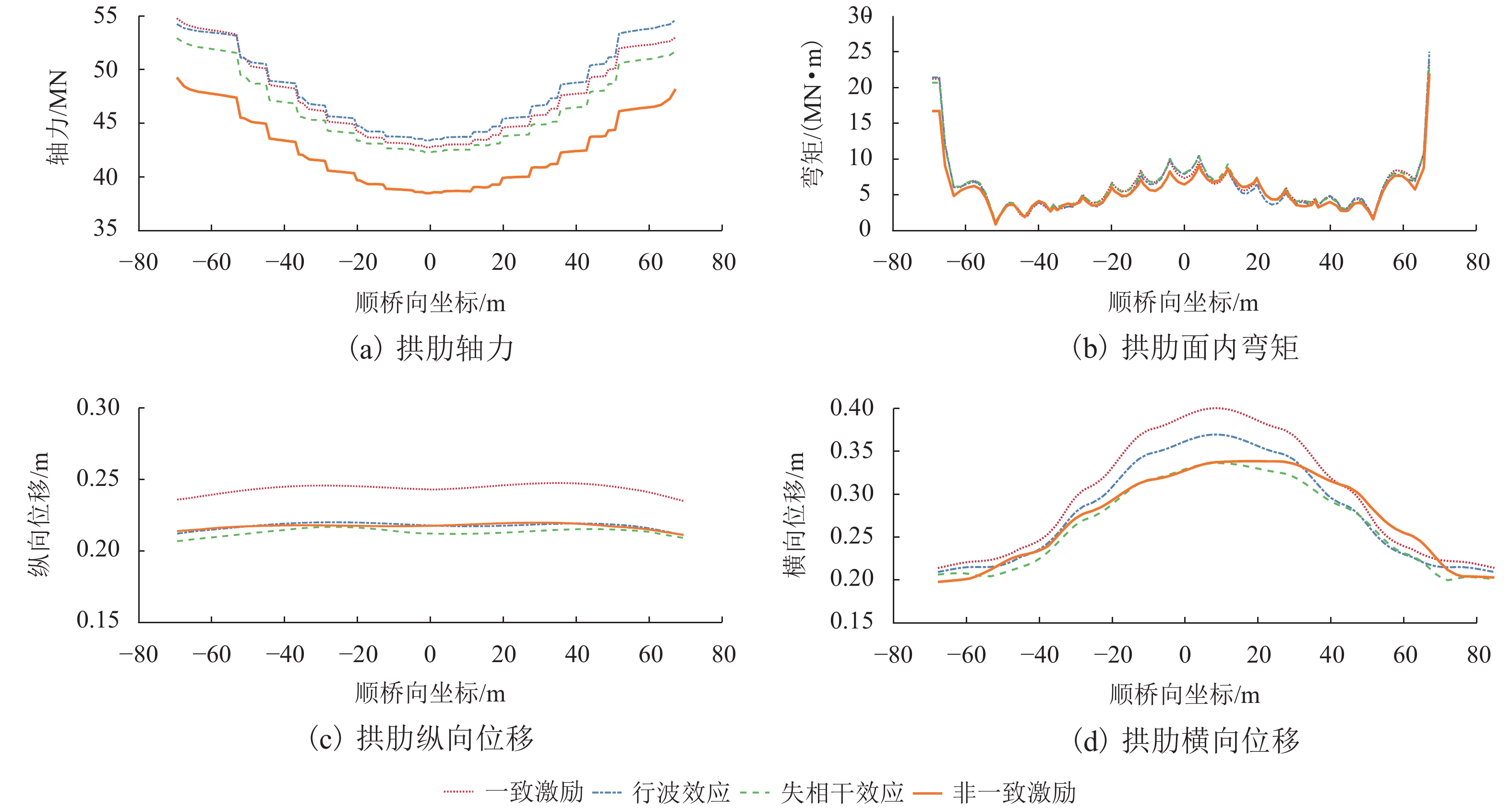
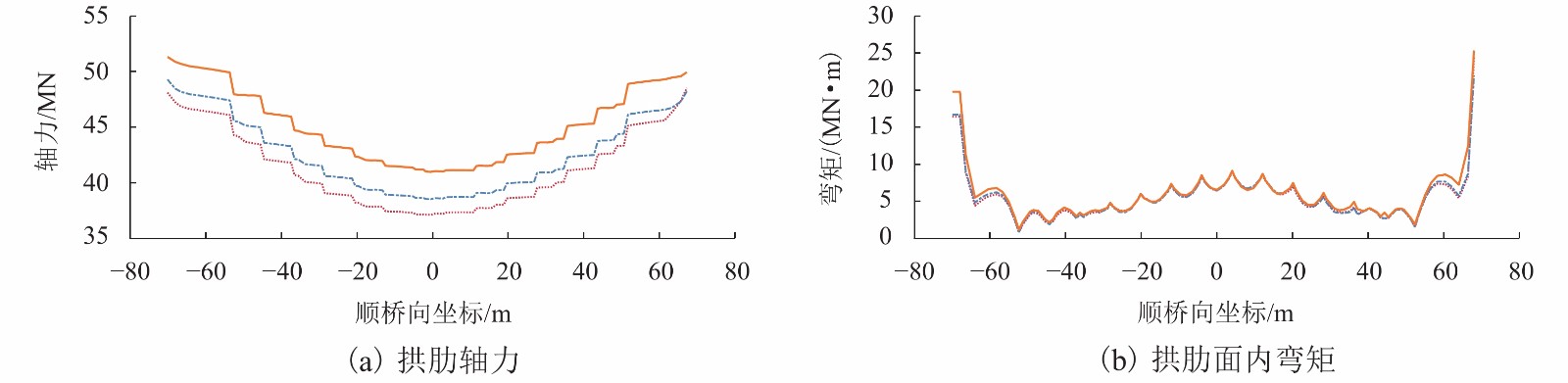
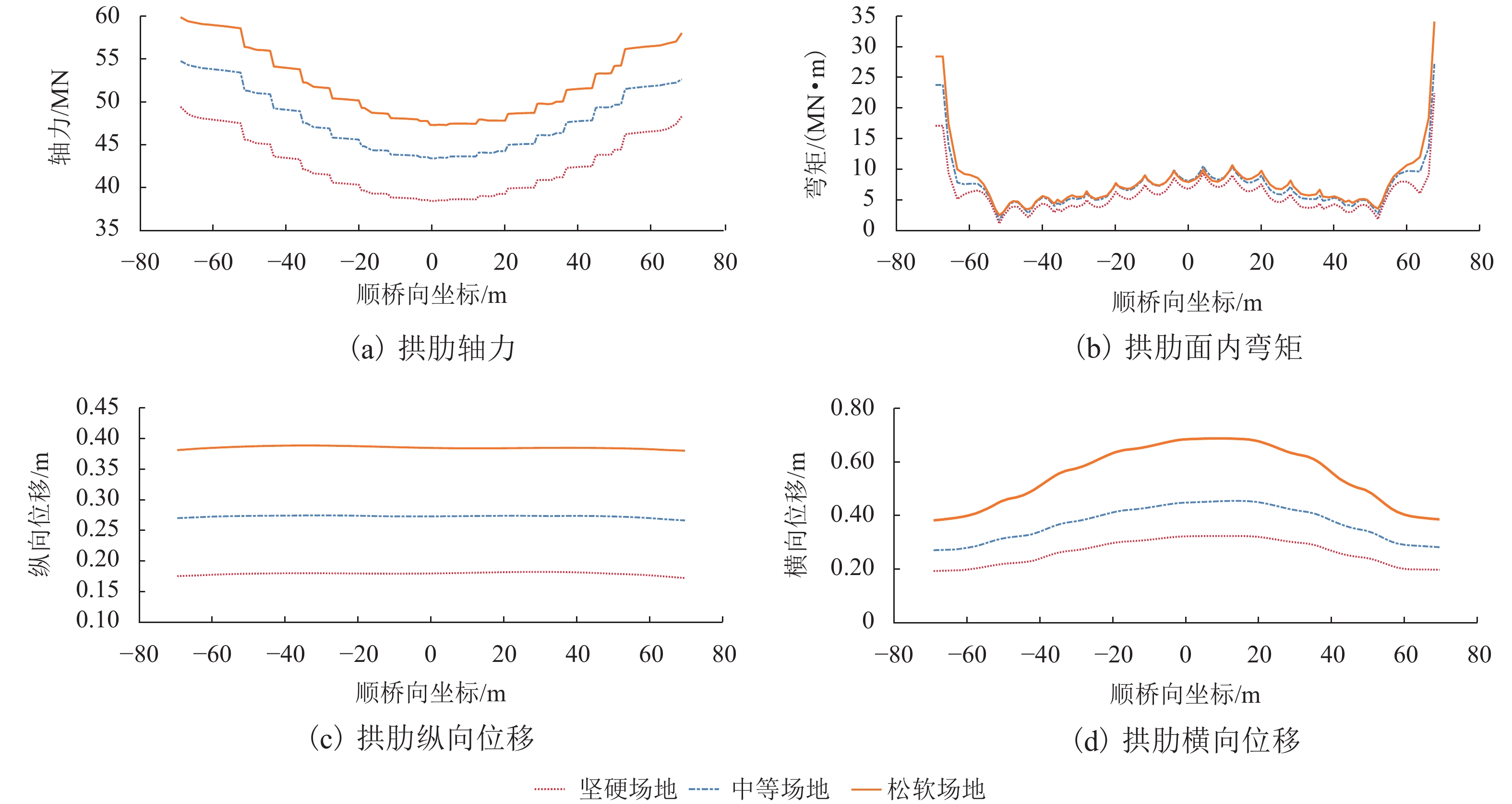
摘要: 为研究多点多维地震动作用下大跨度连续梁拱桥的动力响应，以我国南方某主跨为139 m的钢管混凝土连续梁拱桥为研究对象，基于有限元软件OpenSEES建立桥梁的三维有限元分析模型，人工合成空间非一致地震动，探究地震动的失相干程度、场地条件及行波波速对桥梁动力响应的影响. 研究结果表明：地震波的空间变异性效应会对连续梁拱桥的地震响应产生明显影响，仅考虑一致地震动激励会高估桥梁结构的地震响应；场地效应对桥梁地震响应的影响规律最为突出，随着支撑点处的场地越来越松软，桥梁各个部位的内力及位移响应均大幅增加；地震动的失相干效应越明显，桥梁拱肋的内力越大，位移越小；行波效应对桥梁结构的地震反应没有较为明确的影响规律，但不可忽略其作用，仅考虑行波效应会严重低估下部结构的地震响应；在大跨度桥梁结构的地震响应分析中，应着重考虑地震动的空间变异性效应，并且准确衡量各因素的作用.

关键词:

Abstract: In order to investigate the dynamic responses of a long-span continuous beam-arch bridge subjected to multi-support and multi-dimensional ground motions, a finite element model for a concrete-filled steel tubular arch bridge with a span of 139 m in South China was built using OpenSEES software. The spatially varying ground motions were artificially simulated to investigate the effects of the coherency loss, local site conditions, and wave-passage. The results show that the spatially varying ground motions have significant influence on the dynamic responses of bridge, and considering uniform excitations only might overestimate the responses. The influence of the local site effect on the seismic responses of the bridge is the most prominent. With softer site conditions at the support points, the inner forces and displacements responses of each part of the bridge are greatly increased. Weakly correlated ground motions can lead to larger arch inner forces and smaller arch peak displacements. Although the wave-passage effect has no obvious tendency, its influence is not negligible. Only considering the wave-passage effect may seriously underestimate the seismic responses of the bridge substructure. Therefore, the spatially varying ground motions should be considered in the seismic responses analysis of long-span bridges, and the effect of each factor should be accurately measured.

Key words:

continuous beam-arch bridge /
multi-support and multi-dimensional ground motions /
dynamic response /
seismic design

场地条件对地震动的影响是工程抗震设计中重要课题^[1]. 我国抗震规范设计谱中，场地条件的影响主要通过峰值加速度（peak ground-motion acceleration，PGA）调整系数来调整Ⅱ类场地PGA值，同时调整场地特征周期，得到其他类别场地的设计谱^[2-3]. 场地类别调整系数方法在国外规范中亦常见^[4]. PGA是地震动强度的直观表征参数，是工程结构抗震设计中地震作用大小的直接度量，在我国抗震设计规范中占有重要地位，同时也是地震预警和烈度速报技术中的关键指标^[5]. PGA的获取可以通过强震台站的记录，而对于没有台站以及地震活动性小的地区，则可采用地震动预测方程（ground-motion prediction equation，GMPE）进行预测^[6-7]，或者通过震后震害调查得到的烈度转化^[8]. 采用GMPE对PGA估计本质上是给出具有共同场地特征的某一“类”场地PGA值^[9-10]. 场地土层特别是近地表土层特征对地震动场的影响很大，所以，在针对具体场地PGA估计时，需要根据场地条件特征进行校正. 对于场地校正方法，近期国内外学者通过GMPE预测与实测记录的残差分析提出了“场地特征项”校正GMPE预测值，将场地条件考虑到地震动预测中^[9]]. 然而，场地特征项的确定主要依据丰富的强震数据，确定方法较复杂，实际应用尚不成熟. 因此，面向工程需求的场地条件校正PGA估计是需要解决的问题，校正方法需要简单可靠，可操作性好.

场地PGA放大系数（f_PGA）能够反映场地土层对地震动峰值的影响，已有国内外学者研究放大系数与场地特征参数之间的关联性. Shingaki等^[11]通过土层与基岩的剪切波阻抗比以及近地表30 m土层平均剪切波速（V_s30）和近地表10 m 厚土层平均剪切波速（V_s10）估算场地PGA放大系数，发现V_s10与PGA的相关性较好，而V_s30与PGV （peak ground-motion velocity）的相关性比PGA的相关性要强. Tavakoli等^[12]通过人工神经网络的方法比较不同的土层特性对PGA放大系数的影响，发现剪切波速和土层厚度能更有效地估计PGA放大系数. Hassancebi等^[13]提出了以剪切波速与标贯锤击数之间的经验关系估算场地放大函数的经验方法，但比数值模拟以及地脉动实测方法获取的放大系数偏小. Regnier等^[14]采用KiK-net数据研究场地特征参数与场地放大效应的相关性，指出采用V_s30、场地卓越周期以及剪切波速沿深度梯度的组合能更合理地评估场地放大效应. 可以看出，以上的研究方法主要是确定性方法，尝试构建场地特征参数指标与f_PGA之间的相关性. 然而实测数据显示，场地PGA的放大系数具有随机不确定性，这种不确定性是不可预测的还是与场地条件存在一定的关联性的，是需要确定的问题. 所以，需要深入研究f_PGA与场地条件之间的关联性，并构建关联性的评估方法，且方法应考虑概率意义^[15].

国内外抗震设计规范中，常用场地土层特征参数，如覆盖土层厚度、剪切波速、场地基本周期等进行场地类别的划分，以区分不同场地土层特征的地震反应. 这些参数是场地土层地震反应主要影响参数，在工程上容易获取，技术成熟. 所以，建立f_PGA与这些特征参数之间的关联性，是实现场地条件校正f_PGA的一种途径. 达到这一目的，最直接的方法就是采用实测数据. 日本的KiK-net不仅提供高质量的地表和井下强震记录，而且给出台站场地土层信息，为地震工程研究提供了良好平台. 本文研究基于此数据库，选取数据记录丰富的32个台站，整理其记录的地震加速度数据，包括台站场地土层信息以及地表和井下加速度时程记录. 分析实测PGA放大系数f_PGA及其概率分布特征，构建数学概率模型及其概率密度函数，建立f_PGA与场地特征参数之间的关联性，提出场地条件校正的地表PGA概率预测方法.

1. 地震数据

以日本KiK-net强震数据为基础，选取地震数据丰富的台站，台站名称及场地参数信息如表1.

表1中，V_se为场地土层等效剪切波速值，其计算方法参考《建筑物抗震设计规范（GB 50011—2010）》^[16]；D为地表至剪切波速大于500 m/s的土层顶面距离，即为覆盖土层厚度；T为场地的基本周期，其计算方法有多种，李瑞山等^[17]提出了分层场地基本周期的计算方法，采用子层周期加权累加的方式计算成层场地的基本周期，Wang等^[18]采用8种方法计算KiK-net的473个场地的基本周期，并做了对比评价，指出不同方法得到的周期结果差别不明显.

本文采用金井清^[19]方法计算场地基本周期T，

$T=\sum_{i=1}^{n} \frac{4 D_{i}}{V_{{\rm{s}},i}},$

(1)

式中：n为场地土层数；D_i为分层场地第i层土的厚度；V_s,i为第i分层土的剪切波速.

该方法简单实用，与Wang等^[18]计算结果对比显示，当T < 1.0 s时，二者结果基本一致；当T > 1.0 s时，二者存在差别. 对于周期大于1.0 s的场地主要集中于深厚土层场地，该类场地地震反应较复杂，需要进行专门研究. 本文选取的台站场地的覆盖土层厚度小于50 m，T < 1.0 s，代表常见的一般工程场地.

表 1 所选Kik-net台站场地特征参数

Table 1. Site characteristic parameters from KiK-net

台站	V_s30/(m•s⁻¹)	V_se/( m•s⁻¹)	D/m	T/s	台站	V_s30/(m•s⁻¹)	V_se/( m•s⁻¹)	D/m	T/s
AOMH17	378.4	196.6	8	0.163	IWTH26	371.1	228.2	10	0.175
FKSH09	584.6	244.2	10	0.164	IWTH27	670.3	150.0	4	0.107
FKSH12	448.5	357.1	22	0.244	KMMH02	576.7	218.4	6	0.110
FKSH19	338.1	255.0	20	0.314	KMMH16	279.7	229.2	41	0.533
IBRH11	242.5	197.1	30	0.495	KSRH03	249.8	213.2	34	0.523
IBRH13	335.4	288.0	24	0.318	KSRH10	212.9	185.9	36	0.644
IBRH14	829.1	180.0	2	0.044	MYGH04	849.8	220.0	4	0.073
IBRH16	626.1	205.9	5	0.097	MYGH05	305.3	120.0	2	0.067
IBRH18	558.6	432.0	15	0.139	MYGH06	593.1	200.0	2	0.040
IWTH04	455.9	314.3	15	0.191	MYGH09	358.2	315.8	38	0.400
IWTH05	429.2	276.9	9	0.130	MYGH10	347.5	329.6	34	0.386
IWTH18	891.6	180.0	2	0.044	MYGH11	859.2	210.0	3	0.057
IWTH20	288.8	283.4	46	0.629	TCGH07	419.5	343.8	22	0.253
IWTH21	521.1	326.5	12	0.168	TCGH12	343.7	305.1	50	0.523
IWTH23	922.9	370.0	4	0.043	TCGH14	849.0	275.0	4	0.058
IWTH24	486.4	360.0	10	0.111	TKCH08	353.2	312.0	36	0.390

下载: 导出CSV

| 显示表格

图1为选取台站场地特征参数的统计分布柱状图. 由图1可以看出：V_se均小于500 m/s，其中150～350 m/s占多数；V_s30主要分布在1 000 m/s以内；D和T 分别小于50 m和1.0 s. 本文同时考虑V_se和V_s30，原因是前者是我国抗震设计规范中常用参数，而后者是国外规范中常用参数. 另外，本文没有考虑直接采用场地类别指标，原因在于场地的类别“数少”，场地特征区分度不明显. 而且我国规范中Ⅱ类场地范围太“宽”，离散性较大. 按照《建筑抗震设计规范（GB 50011—2010）》^[16]，选取的32个台站场地中有26场地为Ⅱ类场地，占比超过80%.

图 1 选取台站场地特征参数的统计

Figure 1. Statistic histograms of site characteristic parameters

下载: 全尺寸图片幻灯片

2. 放大系数模型

2.1 数学模型

定义PGA放大系数f_PGA为

$f_{{\rm{PGA}}}=\frac{A_{{\rm{PGA}}}}{A_{{\rm{PGAR}}}},$

(2)

式中：A_PGA为地表加速度峰值；A_PGAR为井下记录的加速度峰值.

地表和井下加速度记录中均包含两个水平向，即南北向（NS）和东西向（EW）. 本文将两水平向独立考虑，以丰富数据量. 已有研究结果表明^[20]，给定井下地震动强度输入情况下，PGA放大系数f_PGA基本服从对数正态分布，可以采用对数概率分布函数来模拟，其概率密度函数如式(3).

$f(x, \lambda, \zeta)=\frac{1}{x \zeta \sqrt{2 {\text{π}}}} {\rm{e}}^{ - \textstyle\frac{{\left( {\sqrt {\ln x - \lambda } } \right){^2}}}{{2{\zeta ^2}}}},$

(3)

式中：x为给定A_PGAR下地表f_PGA值；λ为f_PGA的对数均值；ζ为f_PGA的对数标准差.

确定式（3）的关键是计算λ和ζ. 根据统计学方法，对数正态概率分布的均值和方差可分别由式(4)和式(5)计算得出.

$\lambda=\ln \;\mu-\frac{1}{2} \ln \left(1 + \frac{\sigma^{2}}{\mu^{2}}\right),$

(4)

$\zeta^{2}=\ln \left(1 + \frac{\sigma^{2}}{\mu^{2}}\right),$

(5)

式中：μ和σ分别为f_PGA数据样本的均值和标准差，通过实测数据统计分析得到.

图2举例显示了IWTH20台站场地实测数据f_PGA与A_PGAR的分布. 为建立μ、σ与A_PGAR的经验关系，采用“分组”的方法，即在A_PGAR的一个小区间内（如1 cm/s²）统计f_PGA的均值μ和均方差σ. 图2中的黑点为小区间内f_PGA的均值μ，小细线标记一倍标准差范围. 数据分析以及研究^[20-21]显示，μ、σ与A_PGAR可以简化成对数线性关系，即

$\ln \;\mu = {b_1} + {a_1}\ln \;{\rm{ }}{A_{{\rm{PGAR}}}},$

(6)

$\ln \;\sigma = {b_2} + {a_2}\ln \;{A_{{\rm{PGAR}}}},$

(7)

式中：a₁、b₁和a₂、b₂为待定拟合系数（简称拟合系数）.

图 2 IWTH20台站实测f_PGA随A_PGAR的分布

Figure 2. Distribution of f_PGA from IWTH20 with respect to A_PGAR

下载: 全尺寸图片幻灯片

表2给出了对台站记录数据回归拟合得到的拟合系数值.

表 2 选取台站拟合系数

Table 2. Regressive parameters for selected station sites

台站	a₁	b₁	a₂	b₂	台站	a₁	b₁	a₂	b₂
AOMH17	−0.098	1.724	−0.266	0.741	IWTH26	−0.136	2.085	−0.294	1.163
FKSH09	−0.119	1.994	−0.215	0.945	IWTH27	−0.081	2.134	−0.189	1.005
FKSH12	−0.183	2.654	−0.331	1.855	KMMH02	−0.081	1.617	−0.054	0.473
FKSH19	−0.114	2.266	−0.111	0.740	KMMH16	−0.092	1.924	−0.127	0.854
IBRH11	−0.117	2.332	−0.112	0.966	KSRH03	−0.155	1.754	−0.177	0.567
IBRH13	−0.098	2.311	−0.138	1.118	KSRH10	−0.139	2.036	−0.179	0.816
IBRH14	−0.112	2.128	−0.346	1.427	MYGH04	−0.111	2.023	−0.158	0.943
IBRH16	−0.145	2.421	−0.209	1.386	MYGH05	−0.055	1.149	−0.204	−0.094
IBRH18	−0.103	2.211	−0.154	1.253	MYGH06	−0.022	0.592	−0.068	−0.846
IWTH04	−0.113	1.980	−0.201	0.724	MYGH09	−0.052	1.149	−0.181	−0.046
IWTH05	−0.134	2.212	−0.211	1.026	MYGH10	−0.044	1.614	−0.102	0.157
IWTH18	−0.115	2.168	−0.301	1.314	MYGH11	−0.100	2.002	−0.162	0.859
IWTH20	−0.030	0.831	−0.152	−0.453	TCGH07	−0.145	2.200	−0.257	0.951
IWTH21	−0.120	2.133	−0.114	0.860	TCGH12	−0.081	1.402	−0.132	0.089
IWTH23	−0.090	1.884	−0.201	0.815	TCGH14	−0.251	2.596	−0.636	1.947
IWTH24	−0.027	0.954	−0.075	−0.365	TKCH08	−0.077	1.927	−0.165	0.941

下载: 导出CSV

| 显示表格

从表2可以看出：不同场地的拟合系数值存在差异，这种差异性可能源于场地沉积土层结构特征的差异性. 若可以建立拟合系数a₁、b₁和a₂、b₂与场地特征参数之间的关系式，则证明了f_PGA与场地特征相关. 图3为单个场地特征参数与拟合系数的关系. 由图3可以看出：拟合系数随着单个特征参数的变化其离散性较大，变化趋势规律性不明显. 说明单个场地特征参数与f_PGA相关性较小. 单一参数指标不足以定量描述复杂场地的地震反应，而应该考虑多指标因素的综合效应. 从土层地震反应计算以及数值模拟角度来看，场地剪切波速、覆盖层厚度以及基本周期是场地地震反应计算主要输入参数指标，其应能够合理体现场地地震反应的大小. 所以，本文尝试建立f_PGA与多个场地特征参数之间的数学关系式，以期建立一种f_PGA的简化估计方法.

图 3 拟合系数与场地特征参数的分布

Figure 3. Scattering of regressive coefficients with respect to site characteristic parameters

下载: 全尺寸图片幻灯片

2.2 参数确定

选取工程常用场地特性指标参数，即剪切波速、场地土层厚度以及场地基本周期（频率）作为描述场地条件的定量参数指标. 在前期文献研究中^[20]，场地基本周期的影响未予以考虑. 如前文所述，我国抗震设计规范中常用场地等效剪切波速V_se，而国外规范中常用V_s30，所以采用两套参数指标，即V_s30、D和T，以及V_se、D和T建立多指标参数与f_PGA的关系，首要解决的是指标参数组合方式问题，在组合中，设C₁ ～ C₆为待定系数. 从简单方便角度，建议多指标参数进行线性组合，即定义中间变量：

$Z=C_{1} V_{\mathrm{s} 30} + C_{2} D + C_{3} T.$

(8)

以Z作为表征场地地震反应特性的变量，然后建立拟合系数与Z之间的关系. 假设拟合系数与Z呈线性关系，可以写成式（9）.

$\left\{ \begin{array}{l} {a_j} = {{{C}}_{\rm{4}}} + {{{C}}_5}Z,\\ {b_j} = {{{C}}_{{4}}} + {{{C}}_5}Z, \end{array} \right.$

(9)

式中：j = 1,2.

除了线性关系，亦尝试拟合系数与Z成二次函数关系，即

$\left\{ \begin{array}{l} {a_j} = {{{C}}_{\rm{4}}} + {{{C}}_5}Z + {{{C}}_6}{Z^2},\\ {b_j} = {{{C}}_{\rm{4}}} + {{{C}}_5}Z + {{{C}}_6}{Z^2}.\\ \end{array} \right.$

(10)

根据式（8）～（10）对表1和表2中的数据进行回归拟合，得到待定系数C₁ ～ C₆见表3. 图4和图5分别示显了拟合系数a₁、b₁和a₂、b₂与Z(V_s30, D, T)成线性和二次函数关系的拟合曲线，以及与实测数据的对比. 由图4、5可以看出：线性和二次函数关系均能够描述拟合系数随着Z的变化趋势，且二次函数结果与实测数据的拟合度更好.

表 3 V_s30、D和T参数组合Z情况下待定系数值

Table 3. Regressive coefficients corresponding to Z in combination of V_s30, D and T

函数类型	待定系数	拟合系数
函数类型	待定系数	a₁	b₁	a₂	b₂
线性函数	C₁	0.001	−0.002	−0.008	−0.003
	C₂	−0.044	0.045	0.051	0.044
	C₃	3.905	−3.946	−3.946	−3.935
	C₄	−0.061	1.456	−0.096	0.049
	C₅	−0.060	−0.479	0.025	−0.483
二次函数	C₁	0.001	−0.003	−0.002	−0.003
	C₂	0.031	−0.062	−0.003	−0.046
	C₃	0.409	−3.445	−0.788	−3.235
	C₄	0.038	−0.589	−0.550	−2.427
	C₅	−0.265	−1.603	−0.707	−2.311
	C₆	0.109	−0.228	−0.325	−0.381

下载: 导出CSV

| 显示表格

图 4 拟合系数和Z(V_s30, D, T)线性拟合曲线与实测数据对比

Figure 4. Regressive coefficients linearly predicted by Z(V_s30, D, T) compared with real data

下载: 全尺寸图片幻灯片

同样的计算流程，将式（8）中的V_s30换成V_se，得到的待定系数见表4. 图6和图7分别显示a₁、b₁和a₂、b₂随着Z(V_se, D, T)的线性和二次函数拟合曲线. 由图6、7可以看出：拟合结果与V_s30、D和T组合得到的结果基本一致.

通过残差分析，评价不同参数组合以及函数形式得到结果对数据的拟合优度. 表5给出了不同方法中各拟合系数的残差平方和.

由表5中数值可以看出：不同方法的结果差别不明显；二次函数拟合的结果稍优于线性拟合的结果；采用V_s30、D和T组合比V_se、D和T得到的结果稍好，但差别不明显. 也就是说，采用两套参数均能合理地预测f_PGA.

图 5 拟合系数和Z(V_s30, D, T)二次函数拟合曲线与实测数据对比

Figure 5. Regressive coefficients quadratically predicted by Z(V_s30, D, T) compared with real data

下载: 全尺寸图片幻灯片

表 4 V_se、D和T参数组合Z情况下待定系数值

Table 4. Regressive coefficients corresponding to Z in combination of V_se, D and T

函数类型	待定系数	拟合系数
函数类型	待定系数	a₁	b₁	a₂	b₂
线性函数	C₁	−0.002	−0.003	−0.001	−0.004
	C₂	0.057	0.060	−0.017	0.071
	C₃	−3.932	−3.884	−3.922	−3.899
	C₄	−0.059	1.377	−0.243	0.393
	C₅	0.081	−0.764	−0.032	−0.587
二次函数	C₁	0.004	0.006	−0.001	0.006
	C₂	0.007	0.043	0.028	0.021
	C₃	1.020	2.734	−3.786	2.767
	C₄	0.094	0.651	−0.305	−0.614
	C₅	−0.347	0.990	−0.306	1.424
	C₆	0.134	−0.172	−0.143	−0.306

下载: 导出CSV

| 显示表格

下载: 全尺寸图片幻灯片

图 6 拟合系数和Z(V_se, D, T)线性拟合曲线与实测数据对比

Figure 6. Regressive coefficients linearly predicted by Z(V_se, D, T) compared with real data

下载: 全尺寸图片幻灯片

图 7 拟合系数和Z(V_se, D, T)二次函数拟合曲线与实测数据对比

Figure 7. Regressive coefficients quadratically predicted by Z(V_se, D, T) comparing with data

下载: 全尺寸图片幻灯片

表 5 不同方法中拟合系数的残差平方和

Table 5. Sum of squared residuals of regressive coefficients in different methods

中间变量	函数类型	拟合系数残差平方和
中间变量	函数类型	a₁	b₁	a₂	b₂
Z(V_s30, D, T)	线性函数	0.060	7.042	0.312	10.459
Z(V_s30, D, T)	二次函数	0.054	4.364	0.296	7.734
Z(V_se, D, T)	线性函数	0.060	6.857	0.334	10.937
Z(V_se, D, T)	二次函数	0.051	5.672	0.328	9.708

下载: 导出CSV

| 显示表格

3. 地表PGA概率预测

根据前文建立的场地放大函数f_PGA的数学概率模型及其参数确定方法，可以得到不同概率水平下地表PGA的估计. 这里的概率水平（P）是指给定场地地震动强度输入情况下，地表观测PGA值超过预测值的可能性或者概率. 为验证方法的可行性，图8和图9分别显示了采用两组场地特征参数组合、6个代表性场地的PGA预测结果与实测记录数据的对比. 中间变量Z分别采用了式（8）和式（11）两组. 拟合系数与中间变量的关系采用二次函数形式. 图中的实测记录忽略了A_PGAR＜10 cm/s²的数据，因其工程意义不大.

由图8和图9可以看出：两组场地特征参数组合的情况下，预测结果的差别不明显，且预测结果能够较合理地符合实测值，特别是输入地震动较强（如A_PGAR＞50 cm/s²）的情况，但也会出现一定的偏差. 如图8和图9中的IBRH13场地，两组场地特征参数组合预测的结果均低于实测值；图9中的AOMH17场地V_se、D和T参数组合预测结果稍高于实测值. 这些偏差主要源自采用简单数学模型拟合数据时产生的离散性，但从工程应用角度而言，本文提出的方法具有可行性.

下载: 全尺寸图片幻灯片

图 8 多概率水平下地表PGA预测值与实测数据对比（中间变量Z = C₁V_s30 + C₂D + C₃T）

Figure 8. Prediction of surface PGA under different probability levels compared to observed data (Z = C₁V_s30 + C₂D + C₃T)

下载: 全尺寸图片幻灯片

图 9 多概率水平下地表PGA预测值与实测数据对比（中间变量Z = C₁V_se + C₂D + C₃T）

Figure 9. Prediction of surface PGA under different probability levels compared to observed data (Z = C₁V_se + C₂D + C₃T)

下载: 全尺寸图片幻灯片

4. 结　论

直观表征场地地震动的强度的PGA在工程抗震设计中被广泛应用，且简单方便. 以场地校正PGA方法为研究目标，主要工作及结论归纳如下：

1）给定地震动强度输入情况下，f_PGA具有不确定性，可以采用对数正态分布函数进行模拟，其概率密度函数参数可通过A_PGAR对数线性拟合，拟合系数与场地单一特征参数相关性小，说明单一场地特征参数不足以确定f_PGA，而应该考虑多指标参数的综合影响.

2）通过实测数据的分析，建立了f_PGA与场地条件特征参数（V_se、V_s30、D和T等）之间的数学关系，提出了f_PGA的概率预测模型，并给出了模型参数的经验确定方法.

3）采用f_PGA概率模型，得到不同概率水平下地表PGA的预测，通过与实测数据对比，预测值和实测数据吻合较好，验证了方法的可行性.

本文建立的地表PGA概率预测简化方法，可为PGA预测的场地校正技术提供一种可操作的途径，且考虑多概率水平. 由于数据量的限制，特别是大震数据的欠缺，建立的方法尚需进一步的验证.

图 1 连续梁拱桥立面（单位：cm）

Figure 1. Elevation of the continuous beam-arch bridge (unit: cm)

下载: 全尺寸图片幻灯片

图 2 桥梁有限元模型

Figure 2. Finite element model

下载: 全尺寸图片幻灯片

图 3 各支撑点处非一致地震动加速度与位移时程曲线(工况4)

Figure 3. Generated spatially varying ground motions on different sites (case 4)

下载: 全尺寸图片幻灯片

图 4 人工生成地震波反应谱与设计反应谱对比（坚硬场地）

Figure 4. Comparison of the simulated acceleration and the code response spectrum (firm)

下载: 全尺寸图片幻灯片

图 5 人工生成地震波失相干损失与经验函数对比

Figure 5. Comparison of the coherency loss between simulated ground motions and the empirical function

下载: 全尺寸图片幻灯片

图 6 多点多维地震动下桥梁拱肋峰值响应包络图

Figure 6. Peak seismic responses envelope of arch rib under multi-point and multi-dimensional ground motions

下载: 全尺寸图片幻灯片

图 7 不同失相干程度时拱肋峰值响应包络图

Figure 7. Peak seismic responses envelope of arch rib with different coherency loss

下载: 全尺寸图片幻灯片

图 8 不同场地类型时拱肋峰值响应包络图

Figure 8. Peak seismic responses envelope of arch rib with different soil conditions

下载: 全尺寸图片幻灯片

图 9 不同行波波速时拱肋峰值响应包络图

Figure 9. Peak seismic responses envelope of bridge with different apparent wave velocities

下载: 全尺寸图片幻灯片

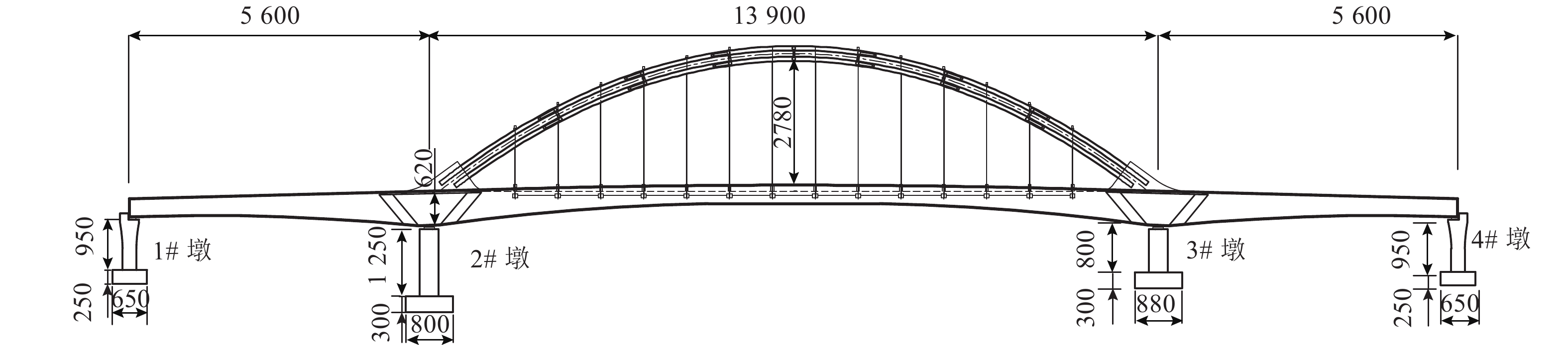
表 1 桥梁自振特性

Table 1. Vibration characteristics of bridge

模态阶数	自振周期/s	频率/Hz	振型描述
1	2.00	0.50	拱肋横向振动
2	0.95	1.05	桥梁纵向振动
3	0.92	1.09	拱肋横向反对称振动
4	0.89	1.12	主梁横向对称振动
5	0.58	1.72	桥梁横向振动

下载: 导出CSV

表 2 空间变异性地震动工况

Table 2. Spatial ground motion cases

工况	场地类型	行波波速/（m•s⁻¹）	相干损失程度
1	FFFF	无穷	无
2	FFFF	500	无
3	FFFF	无穷	中等
4	FFFF	500	中等
5	FMMF	500	中等
6	FSSF	500	中等
7	FFFF	250	中等
8	FFFF	1000	中等
9	FFFF	500	低
10	FFFF	500	高

下载: 导出CSV

表 3 多点多维地震动下桥墩峰值响应

Table 3. Peak seismic responses of pier under multi-point and multi-dimensional ground motions

计算工况	2# 桥墩			3# 桥墩
计算工况	剪力/MN	弯矩/（MN•m）	位移/m	剪力/MN	弯矩/（MN•m）	位移/m
一致激励	380.641	285.262	0.182	402.244	429.243	0.184
仅行波效应	130.215	124.308	0.168	124.670	377.329	0.164
仅失相干	323.037	202.167	0.173	394.313	418.430	0.168
非一致激励	302.871	173.473	0.171	310.209	357.471	0.175

下载: 导出CSV

表 4 不同失相干程度时桥墩峰值响应

Table 4. Peak seismic responses of pier with different coherency loss

相干程度	2# 桥墩			3# 桥墩
相干程度	剪力/MN	弯矩/（MN•m）	位移/m	剪力/MN	弯矩/（MN•m）	位移/m
高相干	470.964	298.238	0.170	449.581	377.796	0.177
中等相干	302.871	173.473	0.171	310.209	357.471	0.175
低相干	226.365	153.311	0.174	528.717	366.331	0.168

下载: 导出CSV

表 5 不同场地类型时桥墩峰值响应

Table 5. Peak seismic responses of pier with different soil conditions

场地类型	2# 桥墩			3# 桥墩
场地类型	剪力/MN	弯矩/（MN•m）	位移/m	剪力/MN	弯矩/（MN•m）	位移/m
坚硬	302.871	173.473	0.171	310.209	357.471	0.175
中等	383.243	241.076	0.254	368.985	411.714	0.260
松软	415.674	237.745	0.349	511.267	437.504	0.360

下载: 导出CSV

表 6 不同行波波速时桥墩峰值响应

Table 6. Peak seismic responses of pier with different apparent wave velocities

行波波速/（m•s⁻¹）	2# 桥墩			3# 桥墩
行波波速/（m•s⁻¹）	剪力/MN	弯矩/（MN•m）	位移/m	剪力/MN	弯矩/（MN•m）	位移/m
1000	339.609	268.676	0.172	308.533	420.712	0.174
500	302.871	173.473	0.171	310.209	357.471	0.175
250	270.429	178.490	0.172	252.022	390.461	0.174

下载: 导出CSV

夏修身. 铁路连续梁拱组合桥基于摩擦摆支座的减隔震研究[J]. 西北地震学报,2012,34(4): 350-354.

XIA Xiushen. Seismic isolation of combined system of continuous girder-arch railway bridge using friction pendulum bearing[J]. Northwestern Seismological Journal, 2012, 34(4): 350-354.

ZANARDO G, HAO H, MODENA C. Seismic response of multi-span simply supported bridges to a spatially varying earthquake ground motion[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(6): 1325-1345.

李晰,何澜,李倩,等. 脉冲型地震动对CFST拱桥抗震性能的影响分析[J]. 西南交通大学学报,2019,54(4): 731-740. doi: 10.3969/j.issn.0258-2724.2014.05.001

LI Xi, HE Lan, LI Qian, et al. Effect of pule-like ground motion on seismic performance of concrete-filled steel tubular arch bridge[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 731-740. doi: 10.3969/j.issn.0258-2724.2014.05.001

王立宪,刘屺阳,狄生奎,等. 非一致激励下钢管混凝土拱桥平稳随机地震响应分析[J]. 兰州理工大学学报,2016,42(2): 124-129. doi: 10.3969/j.issn.1673-5196.2016.02.025

WANG Lixian, LIU Qiyang, DI Shengkui, et al. Analysis of stationary random seismic response of arch bridge with concrete-filled steel tubes under non-uniform excitation[J]. Journal of Lanzhou University of Technology, 2016, 42(2): 124-129. doi: 10.3969/j.issn.1673-5196.2016.02.025

LI B, CHOUW N. Experimental investigation of inelastic bridge response under spatially varying excitations with pounding[J]. Engineering Structures, 2014, 79: 106-116. doi: 10.1016/j.engstruct.2014.08.012

BI K, HAO H, REN W X. Seismic response of a concrete filled steel tubular arch bridge to spatially varying ground motions including local site effect[J]. Advances in Structural Engineering, 2013, 16(10): 1799-1817. doi: 10.1260/1369-4332.16.10.1799

马凯,钟剑,袁万城,等. 非一致地震激励下飘浮体系斜拉桥易损性分析[J]. 同济大学学报 (自然科学版),2017,45(12): 1744-1754.

MA Kai, ZHONG Jian, YUAN Wancheng, et al. Fragility analysis of floating cable-stayed bridge under non-uniform seismic excitation[J]. Journal of Tongji University (Natural Science), 2017, 45(12): 1744-1754.

HAN L H, YAO G H, ZHAO X L. Tests and calculations for hollow structural steel (HSS) stub columns filled with self-consolidating concrete (SCC)[J]. Journal of Constructional Steel Research, 2005, 61(9): 1241-1269. doi: 10.1016/j.jcsr.2005.01.004

SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain ratio Rates[D]. Lulea: Lulea University of Technology, 1989.

MENEGOTTO M. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C]//Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads. Lisbon: IABSE, 1973: 15-22.

JOYNER W B, BOORE D M. Measurement,characterization,and prediction of strong ground motion[J]. Geotechnical Special Publication, 1988, 6(6): 43-102.

贾宏宇,蓝先林,陈航,等. 基于相位差谱的非平稳地震波合成及应用[J]. 西南交通大学学报,2019,54(3): 453-460.

JIA Hongyu, LAN Xianlin, CHEN Hang, et al. Synthesis of non-stationary seismic waves based on phase difference spectrum and its application[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 453-460.

BI K, HAO H. Modelling and simulation of spatially varying earthquake ground motions at sites with varying conditions[J]. Probabilistic Engineering Mechanics, 2012, 29: 92-104. doi: 10.1016/j.probengmech.2011.09.002

HAO H, OLIVEIRA C S, PENZIEN J. Multiple-station ground motion processing and simulation based on SMART-1 array data[J]. Nuclear Engineering and Design, 1989, 111(3): 293-310. doi: 10.1016/0029-5493(89)90241-0

ZHAO L, HAO H, BI K, et al. Numerical study of the seismic responses of precast segmental column bridge under spatially varying ground motions[J]. Journal of Bridge Engineering, 2018, 23(12): 04018096.1-04018096.18.

期刊类型引用(8)

1.	魏星，甘肃. 多跨径连续梁拱组合体系桥梁的抗震分析. 工程建设与设计. 2024(07): 106-108 . 百度学术
2.	邵长江，崔皓蒙，漆启明，韦旺，庄卫林，黄辉，袁得铮. 近远场地震下RC大跨轻柔拱桥减隔震支座方案优化. 西南交通大学学报. 2024(03): 615-626 . 本站查看
3.	冯佳. 深切峡谷上承式钢管混凝土拱桥地震响应分析. 公路交通技术. 2024(03): 62-67 . 百度学术
4.	周乐祥，杨青顺，卫骏，陈飞. 多点激励高烈度区框架结构地震响应分析. 青海大学学报. 2023(01): 57-64 . 百度学术
5.	康厚军，邓力铭，丛云跃. 多跨下承式拱桥面内全局动力学理论与自由振动研究. 动力学与控制学报. 2023(04): 59-66 . 百度学术
6.	高忠虎，吴忠铁，狄生奎，吴云，王晓琴. 考虑行波效应下钢管混凝土系杆拱桥隔震研究. 中外公路. 2023(05): 84-90 . 百度学术
7.	黄永东，罗天，肖华杰. 副拱对连续刚架拱桥的纵向地震响应影响研究. 西部交通科技. 2021(01): 151-154 . 百度学术
8.	廖令军，唐瑞. 基于地震空间变异性效应的大跨度桥梁抗震体系研究. 工程技术研究. 2021(07): 33-34+37 . 百度学术

其他类型引用(11)