Field Measurements Study on High-Altitude Wind Characteristics of Bridge Site in Deep Gorge
-
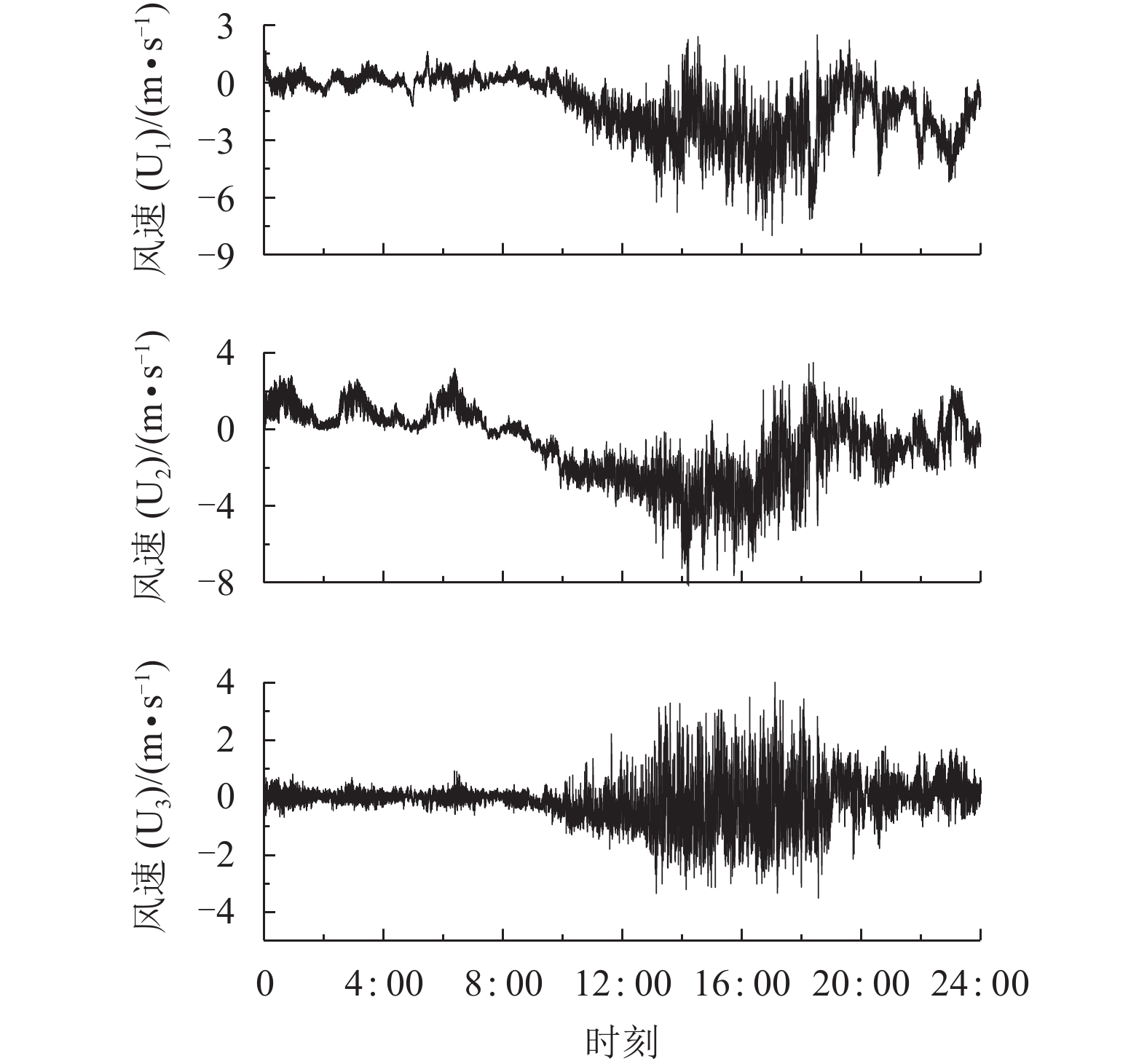
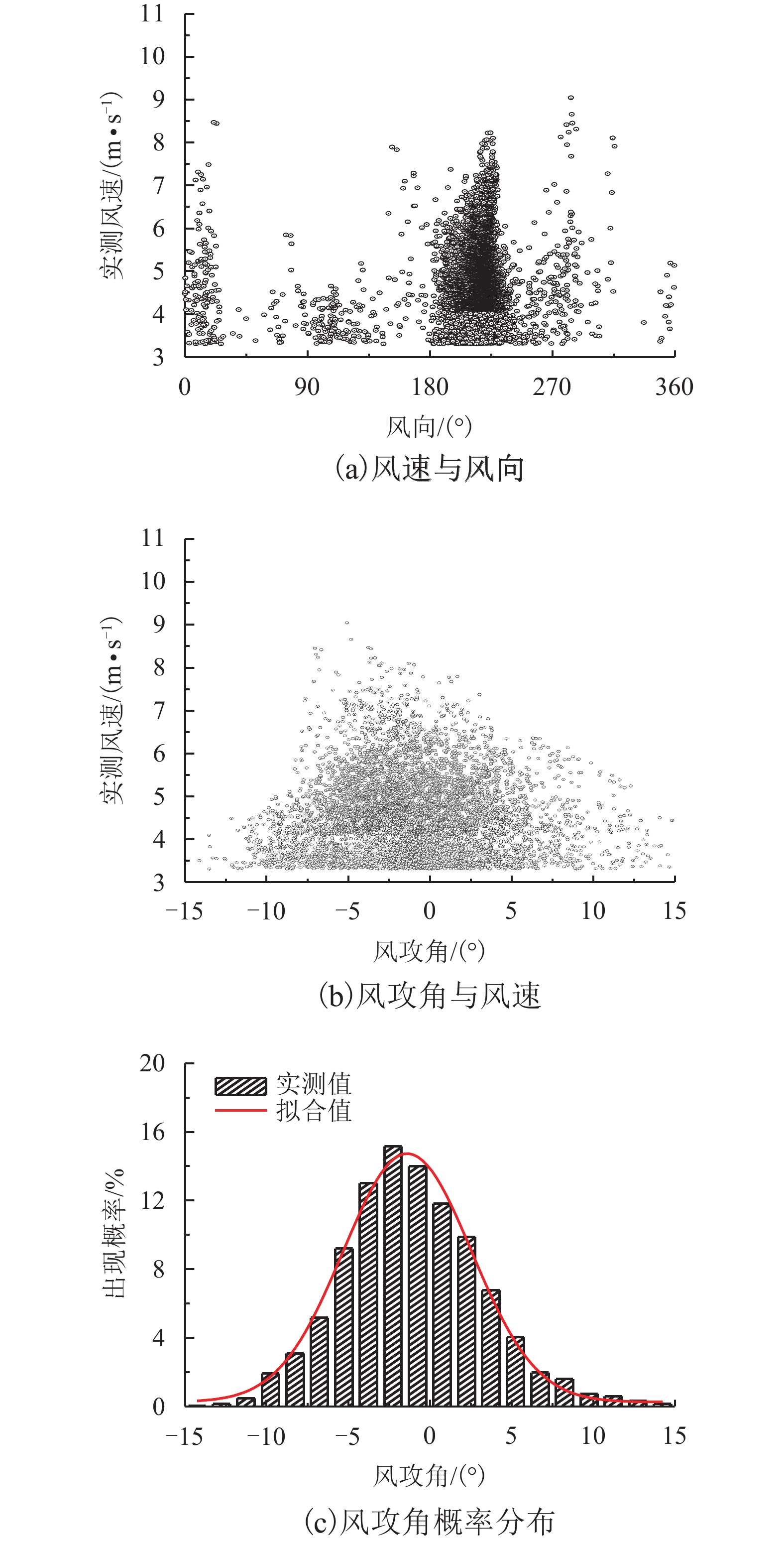
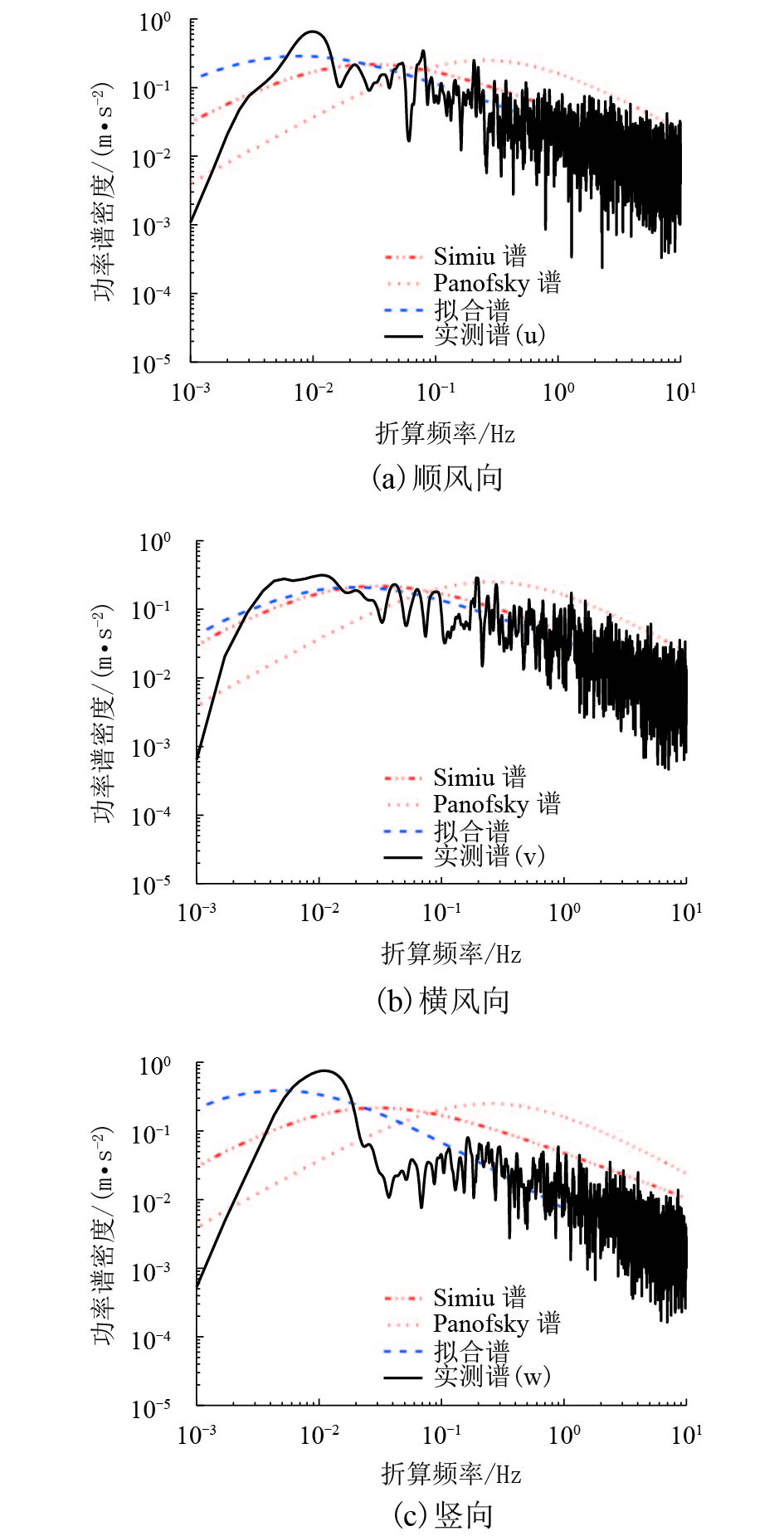
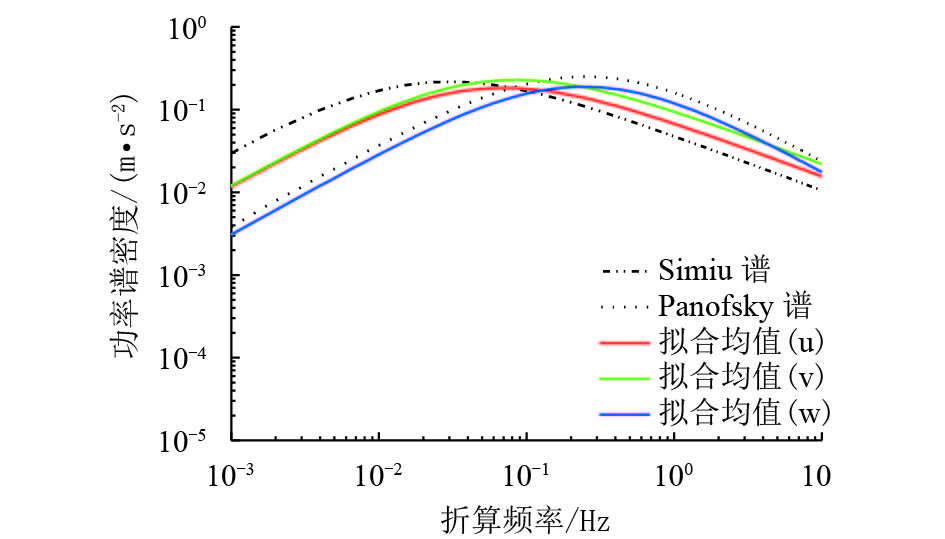
摘要: 架设在深切峡谷中的大跨度桥梁,由于桥址区地形地貌复杂,桥面离开谷底较高,桥址区的风特性一般无法通过抗风规范直接确定. 为确定深切峡谷桥址区高空的风特性,利用大桥施工过程中的猫道,在大桥跨中位置处布置了一套三维超声风速仪,对桥址区高空中的风特性进行了现场实测,获得了7 899条有效的脉动风速时程,以此为基础对桥址区高空的风特性(平均风速、风向、风攻角、紊流度、紊流积分尺度、功率谱)进行了分析. 研究结果表明:深切峡谷桥址区高空风特性受地形的影响已经明显减弱,其风攻角均值趋于0,同时高空的紊流积分尺度更加接近平原地区,紊流积分尺度均值比规范推荐值要大.Abstract: Long-span bridges built in deep gorges are usually inaccessible and it is difficult to obtain wind characteristics of these bridge sites from the wind-resistant design code owing to the complex terrain and the great gap between the deck and the valley bottom. To confirm the high-altitude wind characteristics of a bridge site in a deep gorge, field measurements of such properties were conducted using 3D sonic anemometers located in the mid-span and arranged on the catwalk during the construction process. A total of 7 899 valid fluctuating wind speed time series were obtained. On the basis of this data, the high-altitude wind characteristics of the bridge site were studied, including the average wind speed velocity, wind direction, wind attack angle, turbulence intensity, turbulence integral, and power spectrum densities. The results show that the impact of the landscape on the high-altitude wind characteristics of the bridge site in the deep gorge weakened substantially, while the wind attack angle tends to 0. Simultaneously, the turbulence integral at high altitude is more characteristic of that in plain regions, where the mean value is greater than that recommended by the wind-resistant design code.
-
磁悬浮技术因其无接触、低噪声及摩擦小等优点在磁悬浮列车、磁悬浮轴承等工程领域具有广泛应用[1-2]. 磁悬浮球系统是一个典型的非线性、开环不稳定系统[3],常作为研究悬浮控制方法的实验平台. 近年来,对磁悬浮装置的控制研究已取得了很多成果,如将非线性模型进行线性化处理后对磁悬浮系统采用线性控制方法,应用反馈线性化或前馈线性化技术设计非线性控制器[4-5]. 自适应控制、滑模变结构控制、神经网络控制、模糊控制等非线性控制方法也被广泛应用于磁悬浮控制系统.
文献[6]设计了一种基于磁通观测器的磁悬浮列车系统自适应滑模控制,提升了系统的鲁棒性;文献[7]提出了一种自适应鲁棒输出反馈控制器,跟踪误差通过自适应律得以降低;文献[8]基于径向基函数(RBF)网络逼近原理,设计了一种磁悬浮系统的滑模自适应状态反馈控制器,能有效抑制外界干扰. 在实际工业过程中,滑模控制因其具有响应快速、鲁棒性强以及不确定扰动不敏感等优点而被广泛应用[9].
文献[10]针对飞行机器人设计了一种鲁棒自适应控制策略,有效减弱机械臂扰动和转动惯量变化的影响;文献[11]提出了一种带有观测器的复合自适应神经网络控制,提高了系统的抗干扰能力;文献[12]提出一种自适应非奇异快速终端滑模控制方法,提升了永磁直线同步电机伺服系统的鲁棒性能,可有效削弱抖振现象.
文献[13]表明终端滑模控制器可以提供更快的收敛速度和更高的精度控制;文献[14]提出一种基于改进指数趋近率的滑模观测器,可有效削弱感应电机矢量控制系统的抖振,实现对系统状态的自适应控制;文献[15]在连续快速终端滑模控制基础上提出了一种新的自适应终端滑模趋近律,可以在有限时间内收敛,并能提高跟踪精度;文献[16]提出的离散时间分数阶终端滑模,在直线电机跟踪控制中具有更高的跟踪精度;文献[17]提出一种新型的滑模观测器并将其应用于永磁同步电机无传感器矢量控制系统,提高了系统的稳定性.
与常规线性滑模(linear sliding mode control, LSMC)相比,非奇异终端滑模(non-singular terminal sliding mode control, NTSMC)是一种能够提升系统响应速度和抗干扰能力的滑模控制方法,常规的终端滑模控制虽然提升了系统响应速度,但其动态性能较差. 针对常规线性滑模控制响应速度较慢、抗干扰能力不强以及终端滑模动态性能差的问题,本文提出了一种基于自适应非奇异终端滑模(ANTSMC)的控制器,并将其应用于电磁悬浮控制系统,用自适应控制对滑模控制器的趋近律增益进行自校正调节,并通过李雅普诺夫稳定理论证明了所设计控制器的稳定性. 然后通过仿真和实验验证所设计的控制器具有良好的动态性能和稳态特性.
1. 电磁悬浮球系统
1.1 电磁悬浮球系统组成
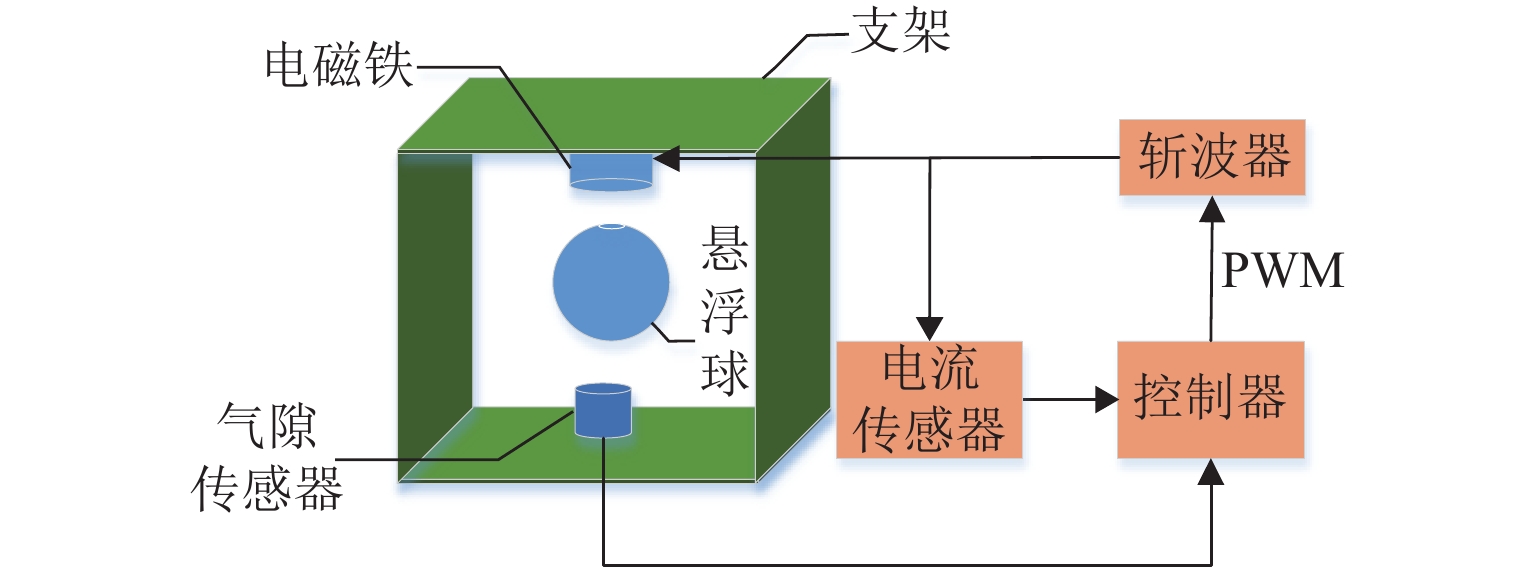
电磁悬浮球系统结构如图1所示. 该系统由悬浮球、电磁铁、斩波器、气隙传感器、电流传感器、A/D转换模块和数字信号处理器(DSP)等部分组成. 间隙传感器和电流传感器分别采集悬浮气隙信号和电磁铁的电流信号,并通过A/D转换模块传输至DSP控制器,DSP控制器将悬浮气隙值与给定值比较得到电流控制量,然后将电磁铁电流与电流控制量比较后输出脉冲宽度调制(PWM)至斩波器,进而调节电磁铁电流,使悬浮球在给定气隙处稳定悬浮.
1.2 电磁悬浮球系统数学模型
电磁悬浮系统的悬浮气隙给定值一般设在8 mm左右,远小于悬浮球的直径,因此可以忽略漏磁通,认为磁通全部通过小球. 为了简化推导过程,通常作以下假定[3]:
1) 忽略悬浮球和电磁铁中的磁阻,即认为电磁铁与悬浮球组成磁路的磁阻全部集中在悬浮气隙处;
2) 忽略铁芯的磁化强度μr,使μr ≈ 1;
3) 忽略剩磁、磁滞及磁饱和现象.
基于以上假定,得到电磁悬浮球系统数学模型[18]为
{m¨x=mg−F(i,x)+f,F(i,x)=μ0N2i2A4x2,mg−F(i0,x0)=0, (1) 式中:m为悬浮球的质量;x为悬浮球悬浮气隙;i为电磁铁电流;F(i,x)为悬浮球所受电磁吸力大小;f为外界施加干扰力;μ0=4π×10−7 H/m为真空磁导率;A为铁芯面积;N为电磁铁线圈匝数;i0、x0分别为平衡点处的电磁铁电流和悬浮气隙.
将系统进行线性化处理,对F(i,x)在平衡点处进行泰勒展开并舍去高次项,可得
F(i,x)=F(i0,x0)+∂F∂i|i=i0x=x0(i−i0)+∂F∂x|i=i0x=x0(x−x0). (2) 忽略干扰力f,将式(2)代入(1),得
m¨x=k1x+k2i, (3) 式中:
k1=μ0N2i0A2x30,k2=−μ0N2i02A2x20 ,分别为气隙刚度系数和电流刚度系数.取x和悬浮球运动速度
˙x 为状态变量,即X=[x ˙x]T ,i为系统输入,x为系统输出,则系统状态方程为{˙X=[01k1/m0]X+[0k2/m]i,Y =[1 0]X. (4) 由式(3)可得系统开环特征方程为
ma2−k1=0, (5) 式中:a为开环极点.
解得
a=±√k1/m ,可知系统有一个极点位于复平面中虚轴的右侧,说明系统是开环不稳定系统,因此必须引入状态反馈构成闭环控制使系统达到稳定状态.2. 自适应非奇异终端滑模控制器
令
x=x1 ,˙x=x2 ,k1/m=a0 ,k2/m=b0 ,则电磁悬浮系统的状态空间方程可写为{˙x1=x2,˙x2=a0x1+b0i,Y=x1. (6) 本节在研究了非奇异终端滑模悬浮控制器基础上设计了一种自适应非奇异终端滑模悬浮控制器,并验证所设计控制器闭环稳定性.
2.1 非奇异终端滑模控制器
令
e1=xr−x1 ,e2=˙xr−x2 ,其中,xr为悬浮气隙的参考值,则终端滑模函数定义[9]为s=e1 + (1/1ββ)ep/q2, (7) 式中:β>0,
1<p/q<2 ,且p和q都为正奇数.对式(7)求导得
˙s=e2 + 1βpqep/q−12, (8) 滑模趋近率采用等速趋近率,如式(9).
˙s=−ξsgns, (9) 式中:ξ为趋近律的系数.
联立式(6)、(8)和式(9)可得基于终端滑模的电磁铁控制电流为
ic=−b−10(−βqpe2−p/q2−ξβpqe1−p/q2sgns−¨xr+a0x1). (10) 为避免
βpqe21−p/q 导致控制电流奇异的问题,参照文献[9]将控制电流改为ic=−b0−1(−βqpe2−p/q2−ξsgns−¨xr+a0x1). (11) 由式(11)可知:控制电流不存在负数次幂,所以避免了奇异问题,下面给出稳定性证明.
证:选取李雅普诺夫函数:
V1=s2/2 可知V1>0,V1对时间求导可得
˙V1=s˙s=s(e2+1βpqep/q−12(¨xr−a0x1−b0i))=s(e2+1βpqep/q−12(−βq/pe2−p/q2−ξsgns))=−1βpqep/q−12ξ|s|. (12) 已知
β ,ε ,ξ >0,因此可得˙V1=−1βpqep/q−12ξ|s|<0, (13) 即该系统是稳定的.
2.2 自适应非奇异终端滑模控制器设计
在实际控制中,通常选择较大的
ξ 以确保系统稳定性. 为了进一步降低ξ 的调节复杂度,在改善系统动态响应的同时保证系统稳态性能和抗干扰能力,设计了以下自适应律:˙ˆξ={φγ−θ(|s|+ηe−|s|)θ,ˆξ>0,φγ−1(|s|+ηe−|s|),ˆξ=0, (14) 式中:
θ=sgn(‖s‖∞−ε) ;ˆξ 为ξ 的观测值;φ、γ和η均为调节自适应律的增益且都为正值,φ和γ影响自适应律调节速度,φ越大γ越小,调节速度越快,但会增大稳态时气隙波动,ε影响滑模函数s的最终界[19].基于自适应非奇异终端滑模的电磁铁控制电流可表示为
ic=−b−10(−βqpe2−p/q2−ˆξsgns−¨xr+a0x1). (15) 由式(14)可以看出:在参数
ξ 的自适应调节过程中,|s| 和ηe−|s| 两个增益项根据 |s| 的大小交替占主导地位,当 |s| 趋于0时,ηe−|s| 较大,可以保证较快的调节速度,同时ηe−|s| 有上限η可以保证不会出现过度调节,下面给出稳定性证明.证:选取李雅普诺夫函数:
V2=12s2+12γφ˜ξ2, (16) 式中:
˜ξ=ˆξ−ξ∗ ,ξ∗ 为ˆξ 的上界,即˜ξ <0.对式(16)求关于时间t的导数,并将式(7)和式(8)代入式(16)得
˙V2=s˙s+γφ˜ξ˙ˆξ=−1βpqep/q−12ξ|s|+γφ˜ξ˙ˆξ. (17) 考虑 |s|>ε和 |s|<ε这两种情况,当 |s|>ε时,将式(14)代入(16)得
˙V2=−1βpqep/q−12ξ|s|+˜ξ(|s|+ηe−|s|)<0. (18) 这说明当 |s|>ε时,
V2 是不断减小的,且在有限时间内s能达到 |s|<ε区域.当滑模函数s进入 |s|<ε的区域时,由于不能保证
˙V2 是非正的,s可能会不断地在该区域进出. 当s离开该区域时 |s|>ε,根据式(18)可知˙V2 的极性变为负,则将使s进入滑模面使系统趋于稳定.3. 仿真结果与分析
为验证所设计悬浮控制器的有效性,在基于Matlab/Simulink环境中搭建电磁悬浮球系统仿真模型,分别使用LSMC、NTSMC和ANTSMC 3种不同的控制器对悬浮性能进行仿真验证,并对控制器参数进行优化,表1是电磁悬浮球系统的参数值.
将表1中的参数值代入式(4),电磁悬浮球系统的状态方程可表示为
{˙X=[0124830]X+[0−7.36]i,Y =[10]X. (19) 表 1 电磁悬浮球系统参数Table 1. Parameters of the electromagnetic levitation ball system参 数 数 值 参 数 数 值 m/kg 0.318 x0/m 0.008 N/匝 530 i0/A 2.7 A/m2 π × 10−4 悬浮球的初始悬浮气隙值设为15 mm,然后分别验证LSMC、NTSMC和ANTSMC的信号跟踪性能、抗干扰能力以及加减载性能,并将仿真结果进行对比. 各悬浮控制器优化后的仿真参数如表2所示.
表 2 悬浮控制器仿真参数Table 2. Simulation parameters of levitation controllers控制器 β ξ φ γ ε η LSMC 50 40 NTSMC 20 40 ANTSMC 10 1000 0.5 0.03 1 3.1 信号跟踪性能
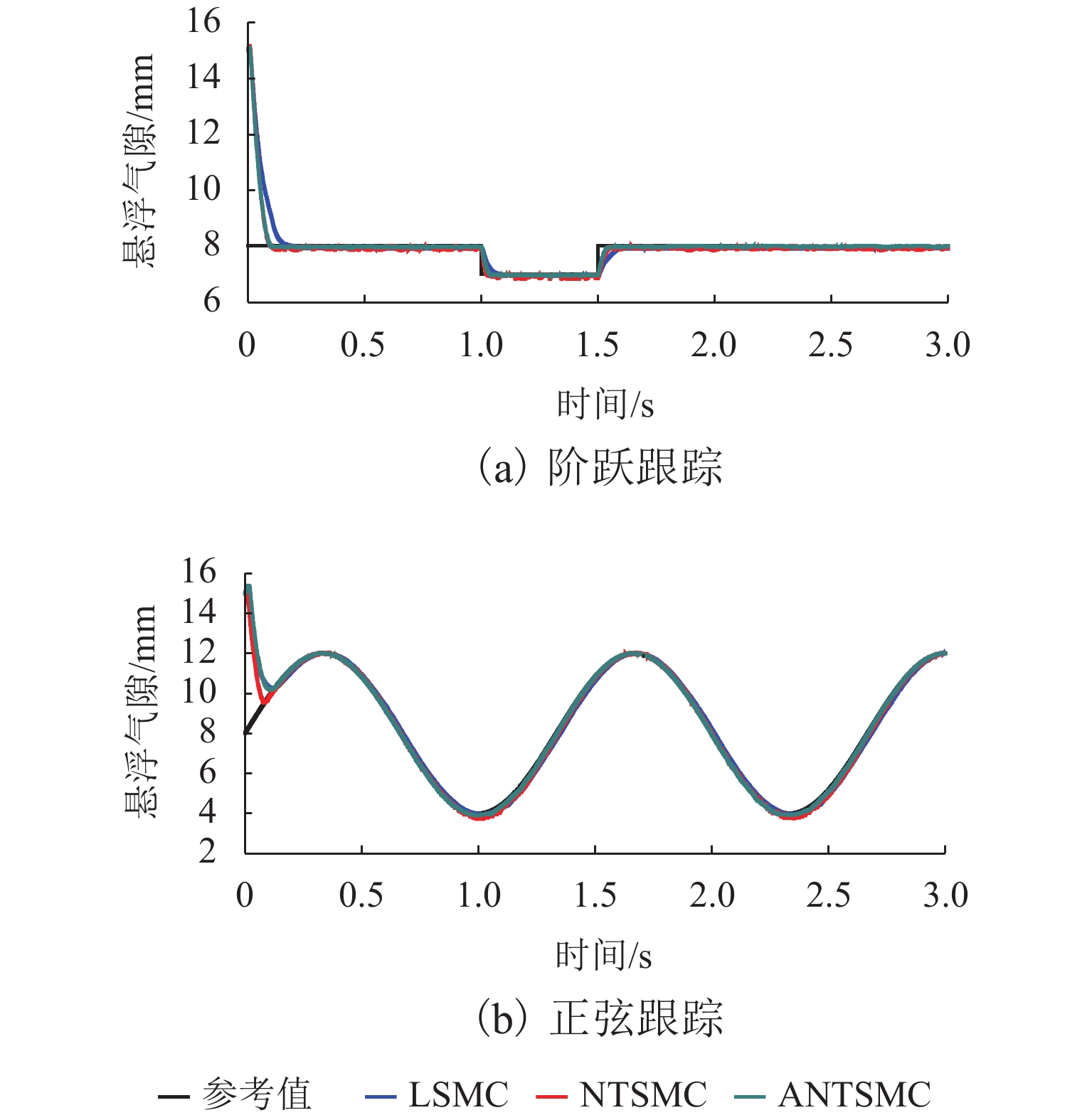
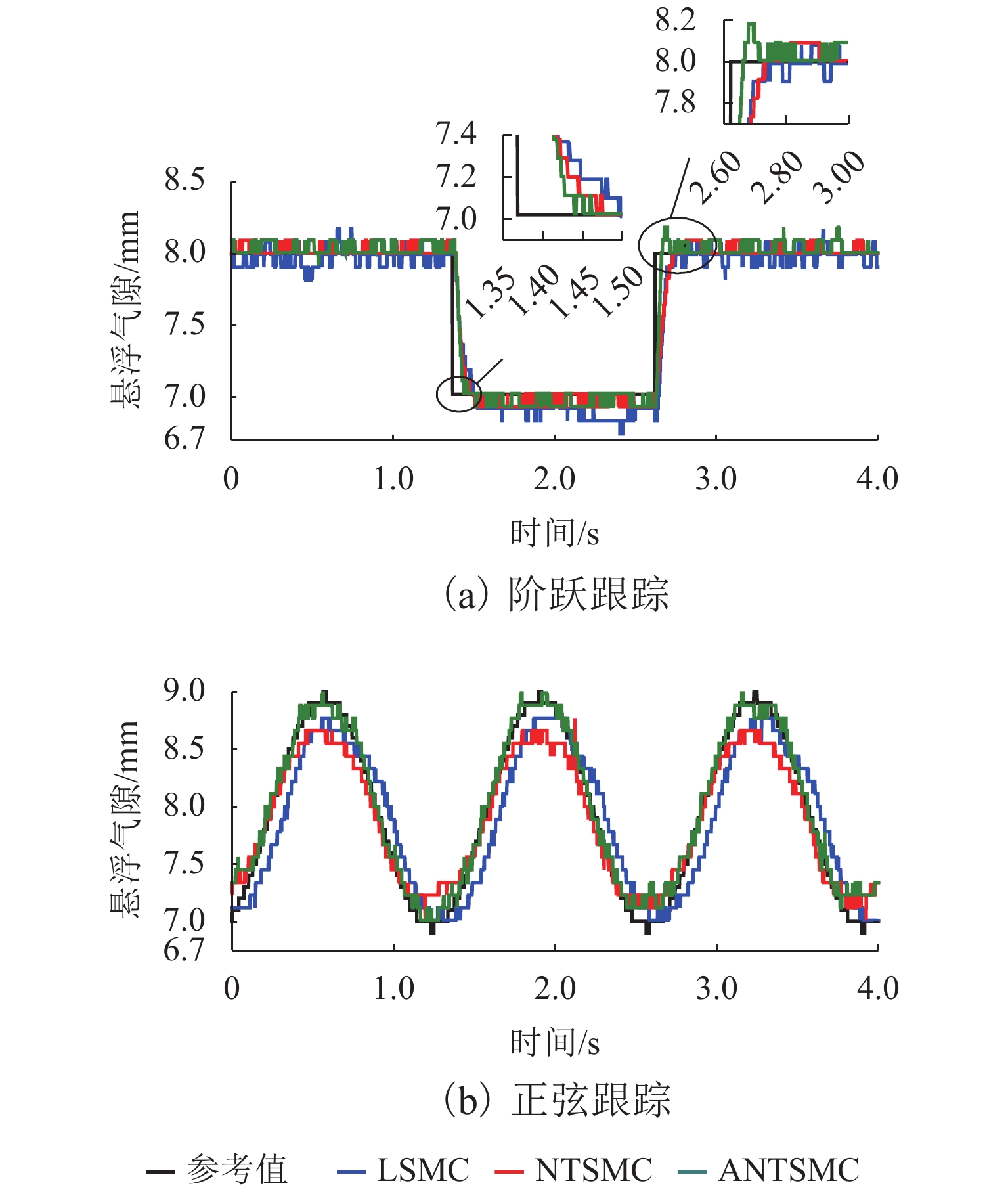
悬浮气隙的参考值分别设定为阶跃信号和正弦信号时,LSMC、NTSMC和ANTSMC 3种控制器的跟踪性能曲线如图2所示. 在图2(a)中设定给定悬浮气隙的初始值为8.0 mm,在1.0 s时,悬浮气隙给定值变为7.0 mm,在1.5 s时,悬浮气隙给定值变回8.0 mm;在图2(b)中,设置悬浮气隙给定值为幅值4.0 mm、频率0.75 Hz、偏置8 mm的正弦信号.
从图2可知:3种控制方法都能较好地跟踪悬浮气隙的参考值,但是与LSMC相比,NTSMC和ANTSMC具有更快的响应速度;ANTSMC的稳态误差最小,而LSMC和NTSMC的稳态误差都较大;使用NTSMC的悬浮系统稳定后响应曲线有较明显的波动,图2(a)中稳定悬浮后NTSMC方法的气隙波动范围为0.165 mm,而ANTSMC方法的气隙波动范围为0.071 mm,说明ANTSMC对这种波动抑制效果较好.
3.2 抗干扰性能
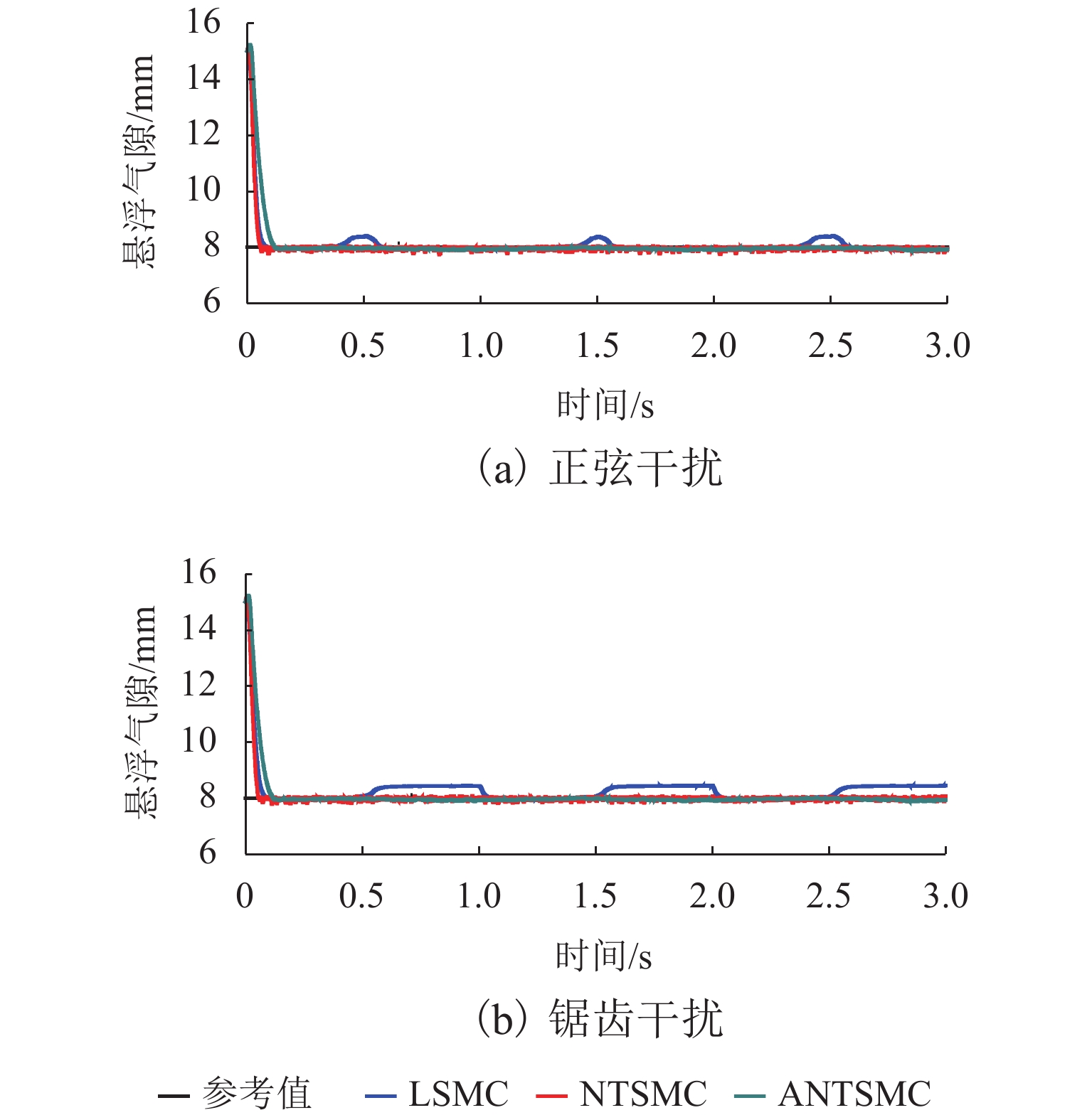
为了验证所设计悬浮控制器的抗干扰性能,在控制器中分别加入正弦波和锯齿波干扰力,图3(a)和图3(b)分别为加入幅值为1、频率为2 Hz的正弦干扰力之后和幅值为2、频率为1 Hz的锯齿波干扰力之后,分别使用3种控制方法的悬浮气隙响应曲线.
从图3的可知:在给定气隙不变的情况下,LSMC的悬浮气隙受干扰力影响较大,由于受电流环跟随性能的影响,气隙曲线并不完全跟随干扰信号呈正弦波或者锯齿波; NTSMC和ANTSMC受干扰影响并不明显,说明NTSMC和ANTSMC控制方法具有更好的抗干扰性能,而ANTSMC相比于NTSMC在稳态时抖动更小.
3.3 加、减载性能
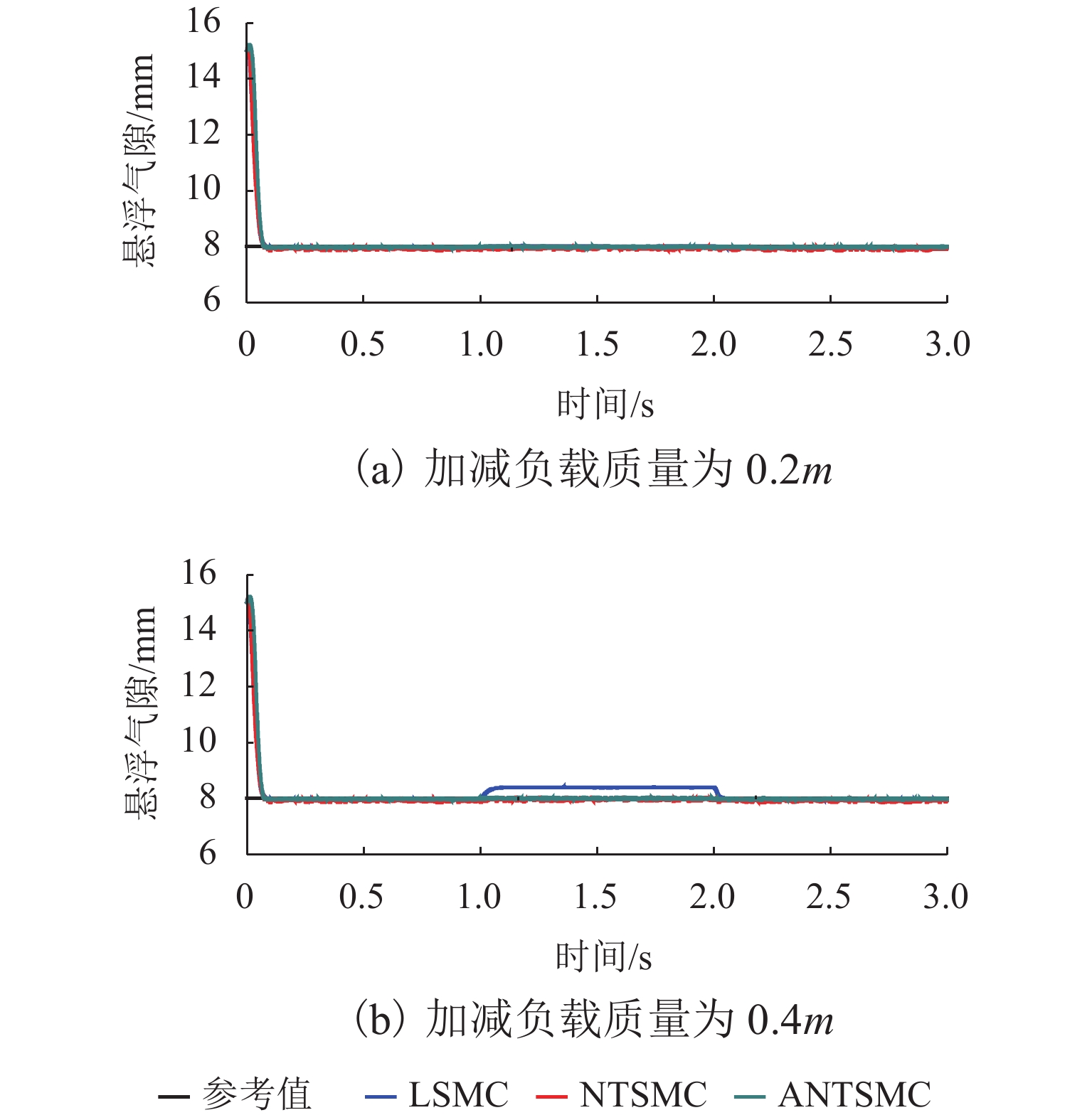
为进一步验证所设计控制器的抗干扰性能,本小节模拟悬浮系统的加减载过程,在第1 s时分别加入质量为0.2m和0.4m的负载,然后在第2 s时去除负载. 3种控制器的悬浮气隙响应曲线如图4所示.
由图4(a) 可知:在1 s时加入了0.2m的负载时,由于悬浮系统质量突然增大,LSMC控制器的悬浮气隙也随之有较小的变化,而NTSMC和ANTSMC控制器的悬浮气隙并无明显变化,但是NTSMC控制器的悬浮气隙抖动现象较严重. 由图4(b)可知:负载增加至0.4m后,LSMC控制器的悬浮气隙输出受负载变化影响很大,由8.0 mm增加至8.4 mm,而NTSMC和ANTSMC两种控制器的输出仍无较大变化,但是NTSMC控制器的悬浮气隙抖动现象较严重.
因此,从仿真波形可知:相较于LSMC,所设计的NTSMC和ANTSMC控制器具有更快的响应速度和更强的抗干扰性能,且ANTSMC比NTSMC的悬浮气隙抖动小,具有更好的静态特性.
4. 实验结果与分析
为进一步验证所设计悬浮控制器的性能,分别进行动态跟踪、抗干扰能力和加减载实验,搭建了电磁悬浮球系统硬件实验平台如图5所示. 该实验平台使用气隙传感器和霍尔电流传感器分别采集悬浮气隙信号和电磁铁电流信号,并通过14位高分辨率ADC芯片转换为数字量传输至DSP控制器,经悬浮控制器输出不同占空比PWM,以实现电磁铁的电流调节. 各悬浮控制器优化后的实验参数如表3. 由于仿真建模时对系统进行了一定简化,因此,仿真模型和实际对象有一定差异,实验时在仿真参数基础上针对实际系统对参数进行优化,导致仿真和实验时的控制器参数不完全一致.
表 3 悬浮控制器实验参数Table 3. Parameters of levitation controllers控制器 β ξ φ γ ε η LSMC 40 1 NTSMC 20 1 ANTSMC 20 100 0.5 0.03 1 4.1 信号跟踪性能
设置初始时刻的悬浮气隙给定值为8.0 mm,在悬浮球稳定悬浮后先加入幅值为 −1 mm的阶跃信号,1 s后加入幅值为1 mm的阶跃信号,3种悬浮控制器的响应曲线如图6(a)所示;设置给定悬浮气隙为幅值1 mm、频率0.75 Hz、偏置8 mm的正弦信号,LSMC、NTSMC、ANTSMC 3种控制器的悬浮气隙响应曲线如图6(b)所示.
从图6(a)可以看出:在给定气隙由8.0 mm变为7.0 mm时,ANTSMC的响应速度最快,能在更短的时间内收敛至给定悬浮气隙处,而LSMC和NTSMC的响应速度较慢,且LSMC的稳态误差较大;在给定气隙由7.0 mm变为8.0 mm时,ANTSMC的响应速度也明显比LSMC和NTSMC快. 从图6(b)中可以看出:在跟踪相同的正弦信号时,LSMC的输出气隙稳态误差较大且响应速度较慢,NTSMC的跟踪速度比LSMC更快,但也有较大的跟踪误差;而与前两者相比,ANTSMC的输出悬浮气隙稳态误差最小,响应速度最快,其跟踪效果比LSMC和NTSMC更好.
4.2 抗干扰能力
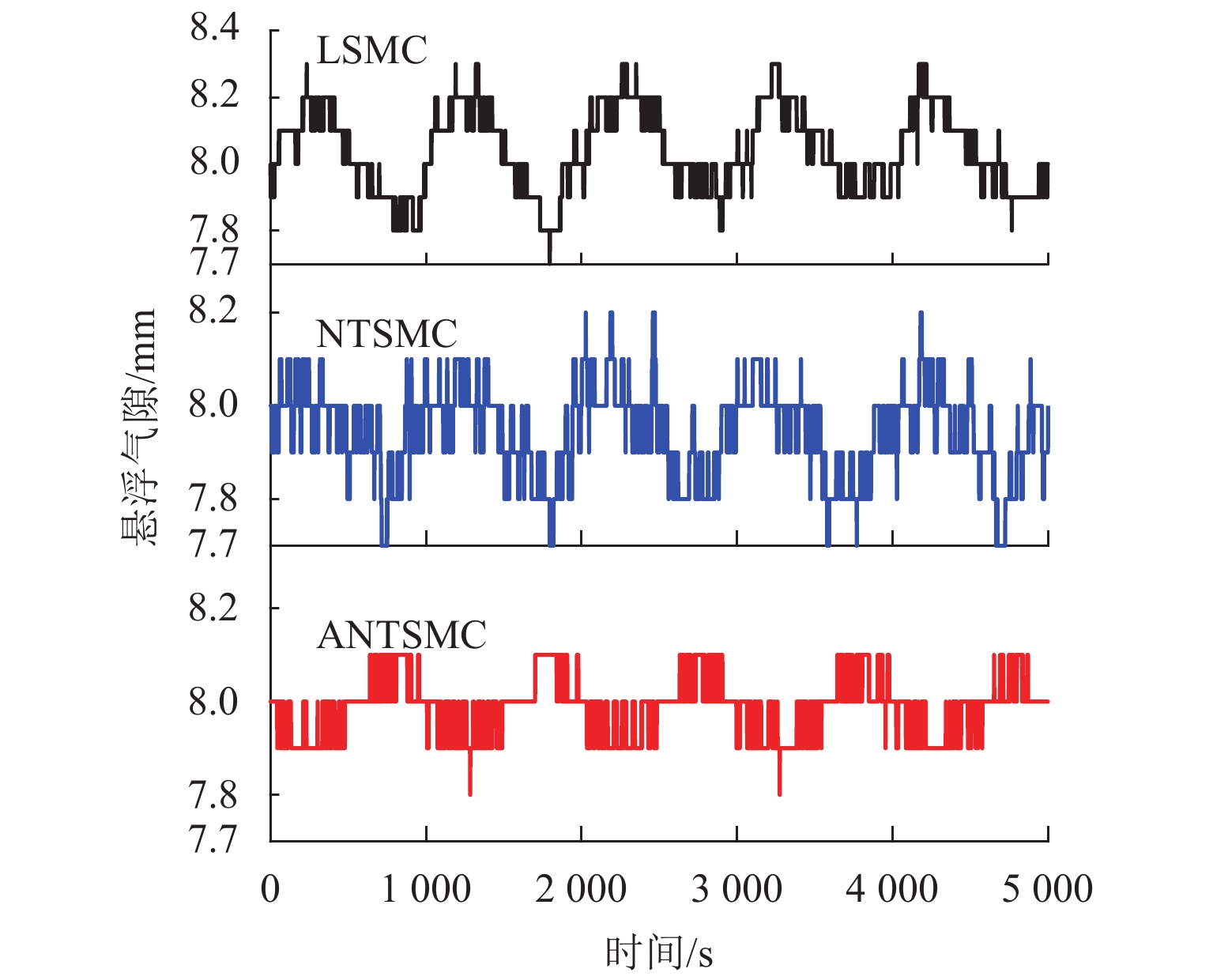
设给定悬浮气隙为8.0 mm,在控制器中模拟加入幅值为1 N,频率为1 Hz的正弦干扰力,则3种控制器的输出悬浮气隙实验曲线如图7所示. 加入幅值为2 N,频率为1 Hz的锯齿干扰力,3种控制器的悬浮气隙实验曲线如图8所示.
由图7和图8可知:在加入同样的正弦干扰力或锯齿干扰力时,LSMC、NTSMC、ANTSMC的悬浮气隙波动峰峰值分别为0.4、0.3、0.2 mm,LSMC的悬浮气隙峰峰值最大,且气隙曲线近似为正弦曲线,而ANTSMC的悬浮气隙峰峰值最小,其悬浮气隙曲线在(8.0 ± 0.1) mm范围内变化,这说明3种控制器中,ANTSMC的抗干扰性能最好,LSMC的抗干扰性能较弱,而NTSMC的抗干扰性比LSMC好,但不如ANTSMC. 由于控制器的仿真参数和实验参数有差异,且悬浮控制性能还受电流环跟随效果、开关器件工作效率等因素的影响,实验波形与仿真波形也会有一定的差异.
4.3 加、减载性能
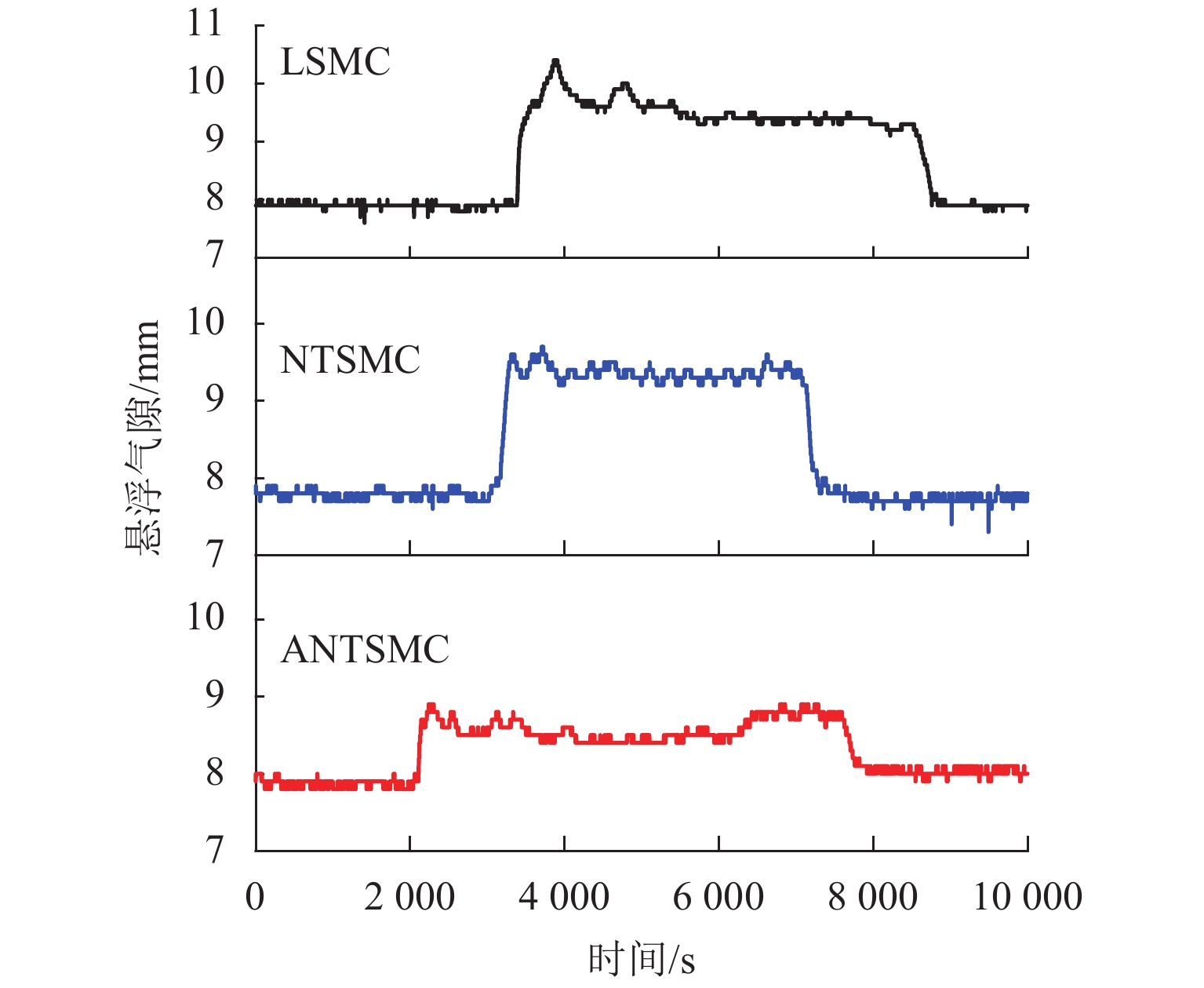
设给定悬浮气隙为8.0 mm,使用质量为0.1 kg的砝码作为负载进行加减载实验,在悬浮球稳定悬浮后进行加载实验,然后在悬浮系统稳定后分别验证3种控制器的抗干扰性能,得到的悬浮气隙响应曲线如图9所示.
本文重点研究控制器的抗干扰性能,控制器中没有引入积分环节,因此在加减载实验中悬浮气隙存在一定的稳态误差. 由图9可以看出:当加入质量为0.1 kg的负载时,LSMC和NTSMC的悬浮气隙在加载后变化较大,分别从8.0 mm增大到9.5 mm和9.4 mm,且LSMC有一定的超调,响应曲线最大值达10.4 mm;ANTSMC的悬浮气隙相对来说变化较小,从8.0 mm变化到8.6 mm左右. 在悬浮系统稳定后减去负载,这时3种控制器都能使系统恢复至平衡位置. 根据3种控制器的加减载实验结果可以看出:ANTSMC比LSMC和NTSMC具有更好的抗干扰性能.
5. 结 论
本文提出了一种基于自适应终端滑模的电磁悬浮系统悬浮控制方法. 首先建立了电磁悬浮系统的数学模型,并分析了系统的稳定性;然后在非奇异终端滑模悬浮控制器的基础上提出一种自适应非奇异终端滑模悬浮控制器,对趋近增益进行在线自适应校正,并根据李雅普诺夫稳定性理论证明了所提出悬浮控制器的稳定性;最后通过仿真和实验对所提出控制器的信号跟踪性能、抗干扰能力、加减载性能等进行验证. 仿真与实验结果表明:与传统滑模悬浮控制器和非奇异终端滑模悬浮控制器相比,所设计的非奇异终端滑模悬浮控制器在保证静态性能和动态响应速度的同时具有更好的抗干扰能力.
-
傅抱璞. 山谷风[J]. 气象科学,1980,1(2): 1-14.FU Baopu. Mountain and valley breezes[J]. Scientia Meteorological Sinica, 1980, 1(2): 1-14. 余锦华,傅抱璞. 山谷地形对盛行气流影响的数值模拟[J]. 气象学报,1995,53(1): 50-61.YU Jinhua, FU Baopu. Numerical simulation of the airflow over and in valley terrain[J]. ACTA Meteorological Sinica, 1995, 53(1): 50-61. 徐大海. 大气边界层内风的若干特性及其应用[J]. 空气动力学学报,1984,2(3): 75-87.XU Dahai. Wind characteristics in the planetary boundary layer and applications[J]. Academy of Meteorological Science, 1984, 2(3): 75-87. 宋丽莉,吴战平,秦鹏,等. 复杂山地近地层强风特性分析[J]. 气象学报,2009,67(3): 452-460. doi: 10.3321/j.issn:0577-6619.2009.03.012SONG Lili, WU Zhanping, QIN Peng, et al. An analysis of the characteristics of strong winds in the surface layer over a complex terrain[J]. Acta Meteorologica Sinica, 2009, 67(3): 452-460. doi: 10.3321/j.issn:0577-6619.2009.03.012 朱乐东,任鹏杰,陈伟,等. 坝陵河大桥桥位深切峡谷风剖面实测研究[J]. 实验流体力学,2011,25(4): 15-21. doi: 10.3969/j.issn.1672-9897.2011.04.003ZHU Ledong, REN Pengjie, CHEN Wei, et al. Investigation on wind profiles in the deep gorge at the Balinghe bridge site via field measurement[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 15-21. doi: 10.3969/j.issn.1672-9897.2011.04.003 沈炼,韩艳,蔡春声,等. 山区峡谷桥址处风场实测与数值模拟研究[J]. 湖南大学学报,2016,43(4): 16-24.SHEN Lian, HAN Yan, CAI Chunsheng, et al. Experiment and numerical simulation for wind field of a long-span suspension bridge located in mountaious canyon[J]. Journal of Hunan University, 2016, 43(4): 16-24. 刘明,廖海黎,李明水,等. 西堠门大桥桥址处风场特性研究[J]. 铁道建筑,2010(5): 18-21. doi: 10.3969/j.issn.1003-1995.2010.05.006LIU Ming, LIAO Haili, LI Mingshui, et al. Wind characteristics of Xihoumen bridge based on monitored data[J]. Railway Engineering, 2010(5): 18-21. doi: 10.3969/j.issn.1003-1995.2010.05.006 张明金,李永乐,余显全,等. 桥塔上风传感器安装位置对测量结果的影响[J]. 西南交通大学学报,2015,50(4): 617-622. doi: 10.3969/j.issn.0258-2724.2015.04.007ZHANG Mingjin, LI Yongle, YU Xianquan, et al. Installation position of wind sensor on the bridge tower in deep gorge Site[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 617-622. doi: 10.3969/j.issn.0258-2724.2015.04.007 张明金,李永乐,唐浩俊,等. 高海拔高温差深切峡谷桥址区风特性现场实测[J]. 中国公路学报,2015,28(3): 60-65. doi: 10.3969/j.issn.1001-7372.2015.03.008ZHANG Mingjin, LI Yongle, TANG Haojun, et al. Field measurement of wind characteristics a bridge site in deep gorge with high altitude and high temperature difference[J]. China Journal of Highway and Transport, 2015, 28(3): 60-65. doi: 10.3969/j.issn.1001-7372.2015.03.008 HU P, LI Y L, HUANG G Q, et al. The appropriate shape of the boundary transition section for a mountain-gorge terrain model in a wind tunnel test[J]. Wind and Structures, 2015, 20(1): 15-35. doi: 10.12989/was.2015.20.1.015 黄国庆,彭留留,廖海黎,等. 普立特大桥桥位处山区风特性实测研究[J]. 西南交通大学学报,2016,51(2): 349-356. doi: 10.3969/j.issn.0258-2724.2016.02.014HUANG Guoqing, PENG Liuliu, LIAO Haili, et al. Field measurement study on wind characteristics at Puli great bridge site in mountainous area[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 349-356. doi: 10.3969/j.issn.0258-2724.2016.02.014 SU Y, HUANG G, XU Y. Derivation of time-varyingmean for nonstationary downburst winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 141: 39-48. doi: 10.1016/j.jweia.2015.02.008 何旭辉,史康,邹云峰,等. 南广铁路西江大桥桥位处良态风特性实测研究[J]. 世界桥梁,2016,44(4): 44-49.HE Xuhui, SHI Kang, ZOU Yunfeng, et al. Study of characteristics of Well-Behaved winds measured an bridge site of Xijiang river bridge on Nanning-Guangzhou high-speed railway[J]. World Bridges, 2016, 44(4): 44-49. 谭波,赵志军. 林芝机场地面大风特征分析及其对飞行的影响[J]. 资源开发与市场,2010,26(12): 1071-1073. doi: 10.3969/j.issn.1005-8141.2010.12.005TAN Bo, ZHAO Zhijun. Effects of wind on flight in Linzhi airport[J]. Resource Development & Market, 2010, 26(12): 1071-1073. doi: 10.3969/j.issn.1005-8141.2010.12.005 李永乐,张明金,徐昕宇,等. 高海拔高温差深切峡谷桥址区日常大风成因[J]. 西南交通大学学报,2014,49(6): 935-941. doi: 10.3969/j.issn.0258-2724.2014.06.001LI Yongle, ZHANG Mingjin, XU Xinyu, et al. Cause analysis of daily strong wind on bridge site in deep gorge with high altitude and high temperature difference[J]. Journal of Southwest Jiaotong University, 2014, 49(6): 935-941. doi: 10.3969/j.issn.0258-2724.2014.06.001 期刊类型引用(8)
1. 付涛,景兴淇,李正雄,任涛. 离散型制造车间AGV小车自主避障路径选择研究. 机械设计与制造. 2024(04): 238-243 .  百度学术
百度学术2. 谢济铭,夏玉兰,秦雅琴,赵荣达,刘兵,段国忠,陈金宏. 基于双向长短期记忆网络的城市快速路合流区车速预测. 西南交通大学学报. 2024(05): 1235-1244 .  本站查看
本站查看3. 吴少峰,陈智威,张高峰,陈钦,徐进. 基于实车数据的高速公路行驶轨迹偏移和车道侧向余宽. 中国公路学报. 2023(05): 197-209 .  百度学术
百度学术4. 徐进,王延鹏,陈海源,张晓波,潘存书. 山区公路回头曲线小客车纵向行驶特性及运行速度模型. 吉林大学学报(工学版). 2023(12): 3432-3445 .  百度学术
百度学术5. 徐进,杨雪敏,张雪榆,张杰,孔繁星,矫成武. 基于自然驾驶数据的高密度立交出入口车辆轨迹特征研究. 交通信息与安全. 2023(06): 20-31+81 .  百度学术
百度学术6. 戴振华,廖祺硕,潘存书,尚彦宇,徐进. 城市干路交叉口右转车辆轨迹流线与曲率特性分析. 交通信息与安全. 2022(04): 157-166 .  百度学术
百度学术7. 陈莹,王晓辉,张晓波,陈海源,徐进,杜志刚. 山区公路回头曲线的车道偏移行为与自由行驶轨迹模型. 交通运输工程学报. 2022(04): 382-395 .  百度学术
百度学术8. 陈钦,陈海源,王晓辉,张晓波,徐进. 山区公路回头曲线车辆横向加速度特性研究. 科学技术与工程. 2022(34): 15372-15381 .  百度学术
百度学术其他类型引用(6)
-






 下载:
下载:
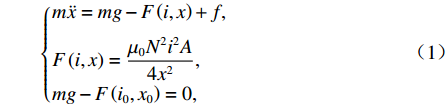
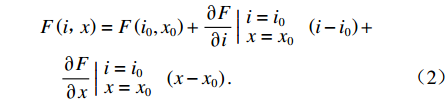

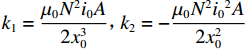


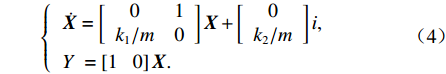

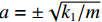
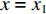
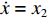
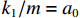
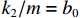

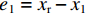
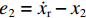




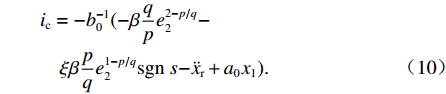

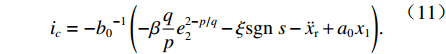
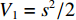

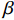
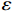

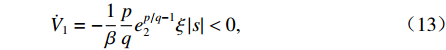
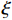

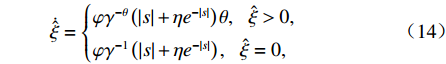
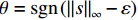
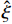
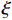
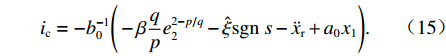
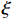
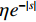
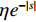
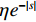


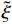

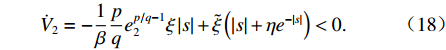
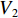

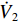










 下载:
下载:



 百度学术
百度学术