城市快速路合流区作为主线道路与匝道交汇的特殊路段，相较于干线路段，其车辆加减速、频繁变换车道等复杂行为，易导致交通紊乱及事故^[1]. 其中，速度控制不当是影响交通事故数量和严重度的主要致因^[2]. 如何深入挖掘交织区速度运行规律，构建更为精准的车速预测模型，进而正确合理地推断未来的交通状况，对于减缓交通拥堵、降低交通事故率有着重要的现实意义和应用前景.

近年来，基于数据驱动^[3]的研究方法在交通参数预测方面逐渐成为热点. 数据驱动的车速预测方法主要是基于参数模型和机器学习. 参数模型预测方法主要有多元线性回归^[4]、自回归移动平均法 （ARIMA）^[5-6]、卡尔曼滤波法^[7]等，其主要依赖于历史数据，难以反映交通参数的非线性变化特征. 随着计算机处理能力的提升，机器学习由于其深层次的数据表达能力成为交通流预测的重要手段. Yao等^[8]建立了一种由时空参数组成的支持向量机回归模型（SVR）进行短时交通速度预测；陈孟等^[9]将基于改进后的时间图卷积网络模型（TK-GCN）应用于短时交通流预测；Zhao等^[10]结合路网在时域和空域的相互作用，提出基于长短期记忆（LSTM）网络的流量预测模型. 上述研究均基于单一模型或方法开展，面对复杂环境下的交通参数预测问题，其适用性仍面临一定的挑战.

通过模型的合理组合或集成，可以克服单一模型的缺陷，成为交通参数预测中应用更广泛、更具潜力的方法^[11-13]，如李桃迎等^[14]考虑高速公路交通流的周期性和趋势性特点，利用卷积神经网络（CNN）和长短期记忆网络、门控循环单元（GRU）构建一种集成深度学习模型（HDL）；陈华伟等^[15]通过组合图卷积神经网络（GCN）和长短期记忆网络建立GCN-LSTM神经网络，能更完整地提取路段速度的时空特征；Li等^[16]提出由CNN和双向长短期记忆（Bi-LSTM）组成的Conv-Bi-LSTM模型进行拥堵预测.

集成模型通常需要大量的参数调节实验来提升模型的结构性能，当已知样本和计算单元受到限制的情况下，机器学习面对已知样本变化序列随机、影响序列因素繁多或高维特征带来的“维数灾难”，其对复杂问题的泛化能力及计算能力同样难以满足要求，无法学习更有用的特征，导致预测困难. 此外，车路协同条件下高精度、高频率的交通信息采集要求对交通参数的有效预测造成一定限制. 近年来，以无人机为代表的空中交通信息采集方式给交通研究带来巨大的机遇，使其从鸟瞰的视角观测和研究交通参数规律变化，等同于车路协同信息采集分析模块，对于全方位解析多车道交织区不同的交通运行状态具有重要作用；另一方面，空中交通信息采集方式也面临巨大的挑战，目前相关的无人机鸟瞰视角下的交通信息预测研究还处于萌芽起步阶段.

综上所述，为深入分析多车道交织区车速运行特性，构建更为精准的车速预测模型，在已有研究的基础上，采用无人机视频提取城市道路典型交织区全样本高精度车辆轨迹数据，针对合流区高峰时段速度变化序列随机、影响因素繁多而不易预测的问题，借助Bi-LSTM，挖掘历史速度数据背后的周期性、趋势性以及时空特征，解决时序数据的长期依赖性问题；考虑Bi-LSTM的超参数设置对预测精度、调参时间等影响，采用贝叶斯优化（BO）对Bi-LSTM模型进行超参数寻优，消除机器学习中调参不当对预测结果的影响；由此构建一种贝叶斯超参数优化的双向长短期记忆网络（BHO-Bi-LSTM）车速预测集成模型，可为单一模型准确率较低、集成模型调参模型时间过长的问题提供一定解决思路.

1.   方法简介

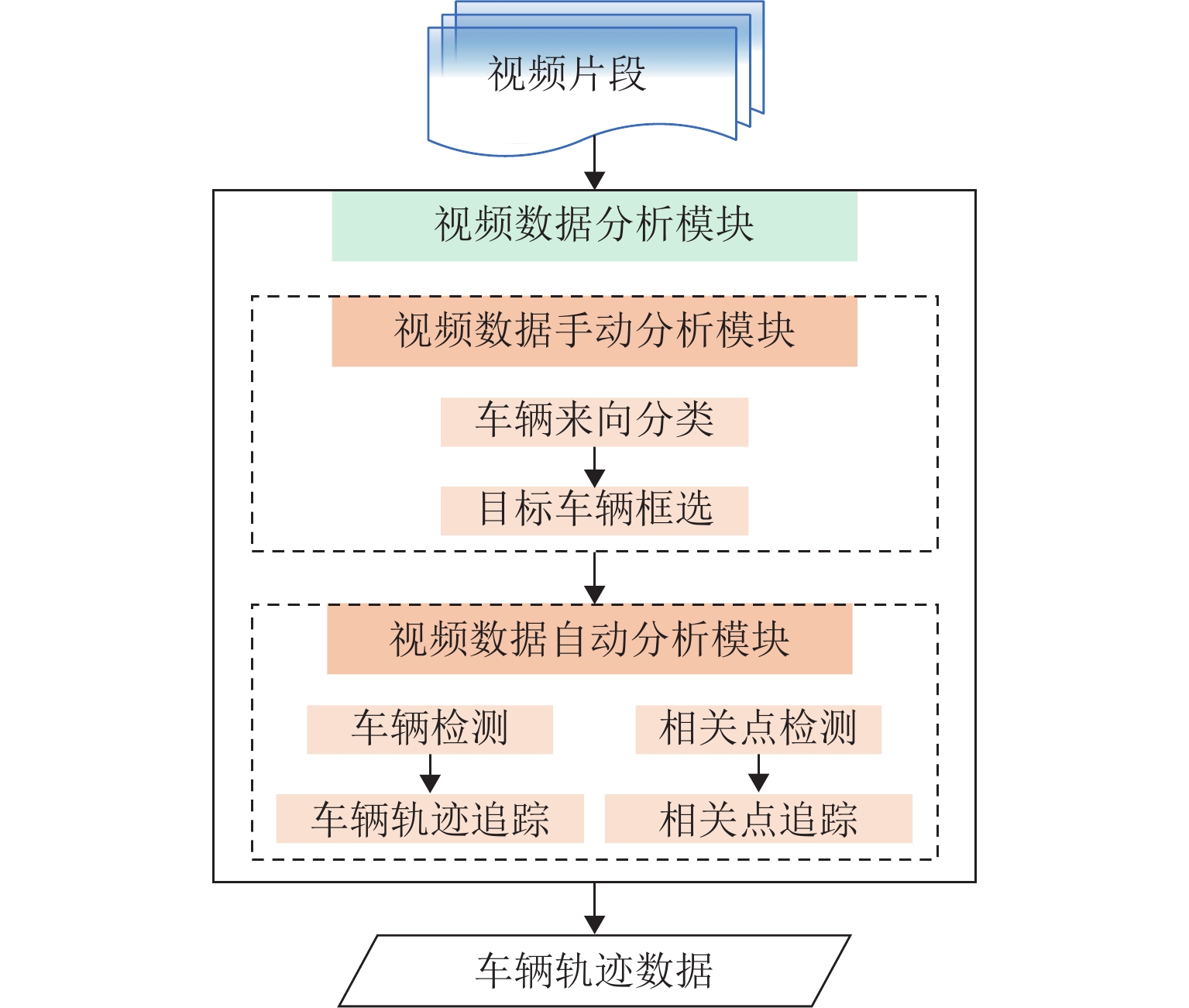
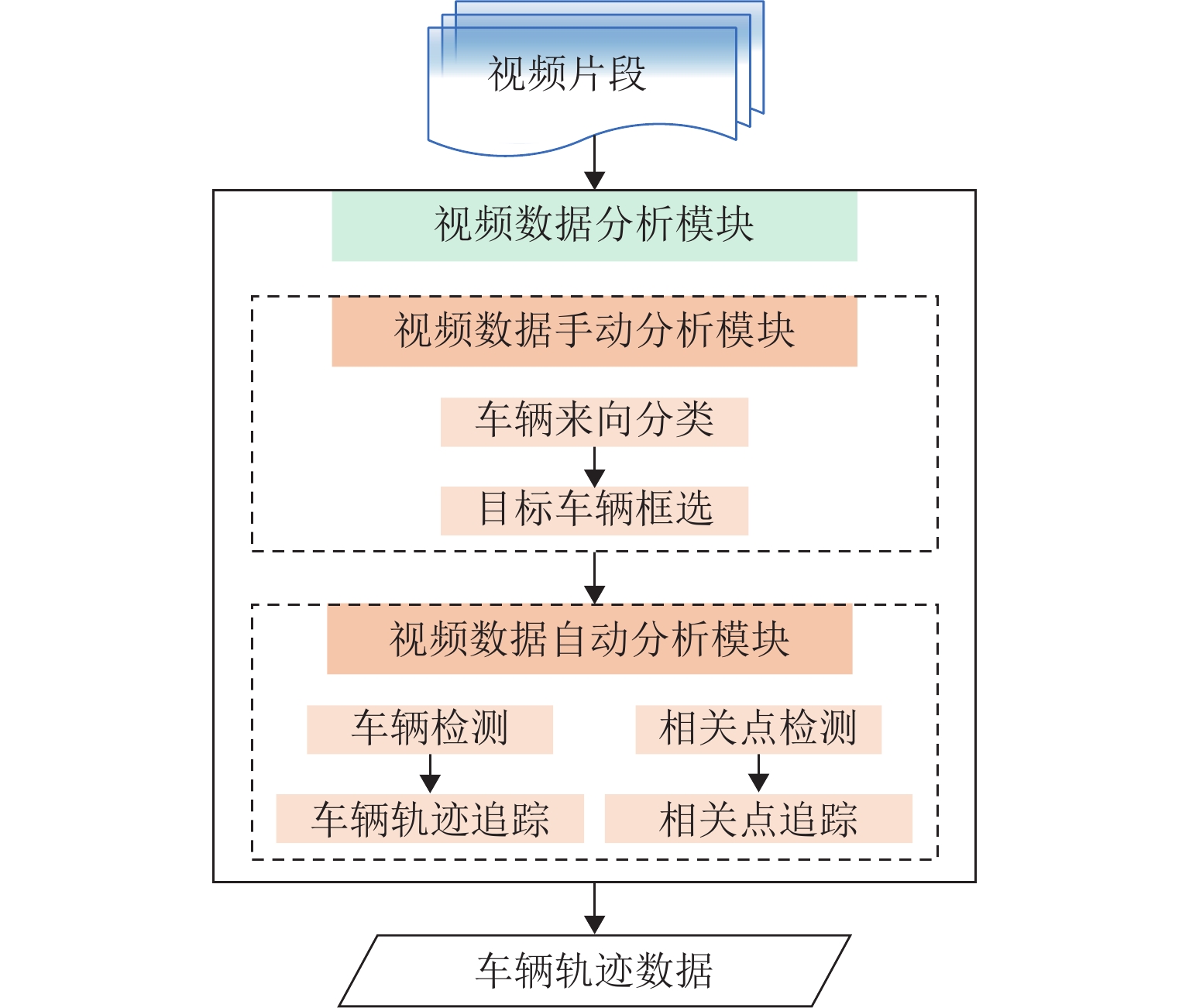
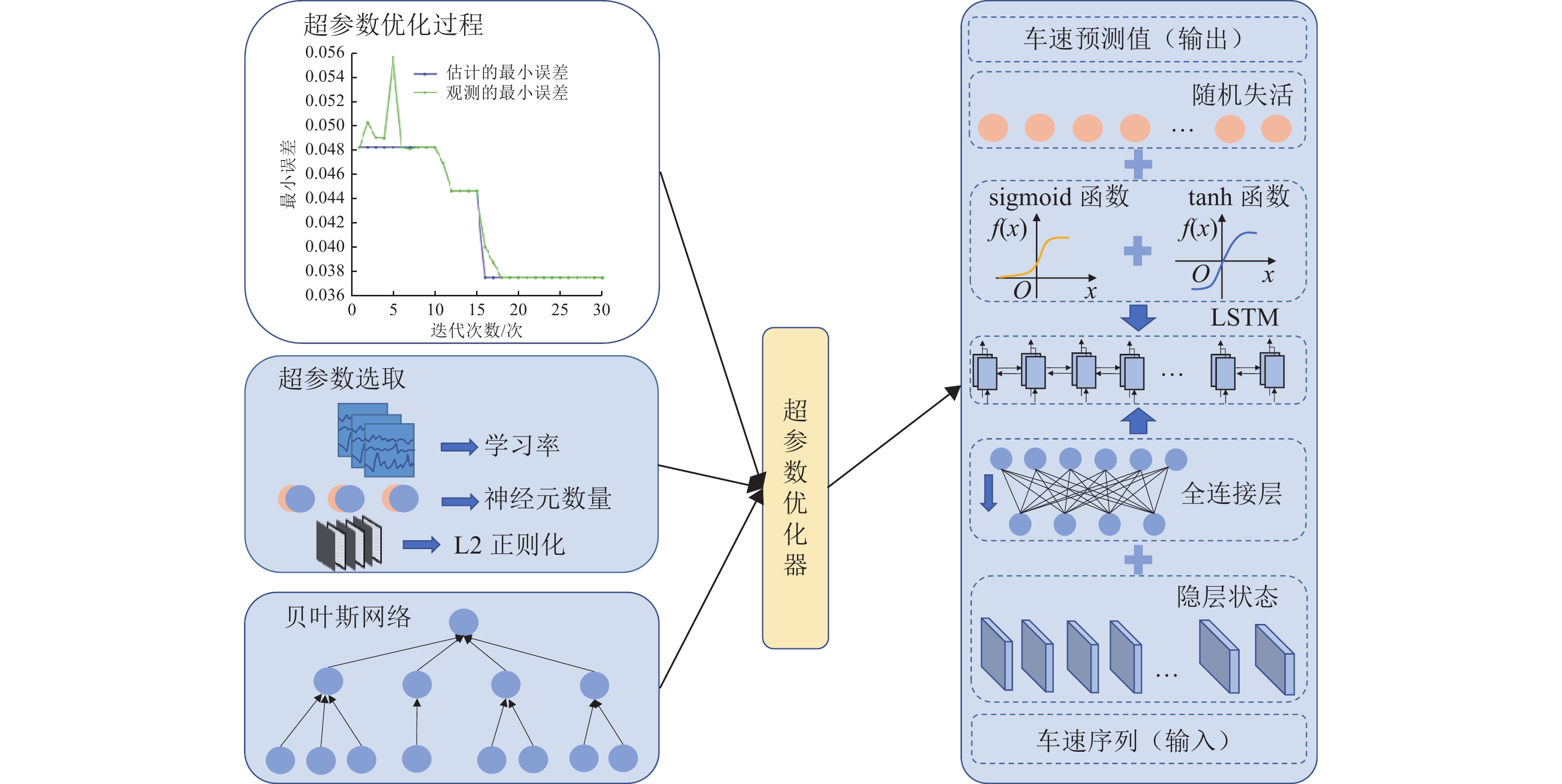
本文主要利用多尺度KCF （kernel correlation filter）车辆跟踪优化算法提取交织区车辆微观轨迹参数，构建BHO-Bi-LSTM，进行高峰时段合流区车辆运行速度预测. 模型框架如图1所示，图中：P为合流区内某一辆车的原始速度序列，v_t为时刻t的速度值，X为P滑动平均和标准化处理后的速度序列，x_t为对v_t进行滑动平均和标准化处理后的结果，h_r,n和h_b,n分别为Bi-LSTM网络中第r层正向LSTM隐含层和第b层反向LSTM隐含层第n个神经元的输出，x_n、y_n分别为Bi-LSTM输出层中第n个神经元的输入和输出. 模型主要包含4个步骤：

图  1  模型框架

Figure  1.  Model framework

下载: 全尺寸图片 幻灯片

步骤1　视频数据采集：选取典型城市快速路多车道交织区，采集高峰、平峰时段高空视频. 利用多尺度KCF车辆跟踪优化算法，以时间尺度每0.1 s划分为一个时间段，对检测图像进行归一化处理，手动框选检测目标，依据方向梯度直方图（histogram of oriented gradient，HOG）特征、连续时间序列的目标中心位置偏移量信息进行车辆轨迹追踪，并对错检漏检目标进行手动校正.

步骤2　全样本车辆轨迹数据集构建：基于车辆轨迹多维数据，获取微观交通运行关键信息. 提取所有行经交织区车辆速度、加速度信息，分析交织区、合流区交通运行特性差异，针对合流区高峰时段车速呈紊乱、随机、离散等复杂特性，采用时空维度排序、标准化处理等手段，构建面向车速预测的轨迹数据集.

步骤3　预测模型构建：速度预测需考虑帧间时空相关信息，选取序列数据建模方面具有独特优势的LSTM模型，针对合流区速度复杂特征，构建面向速度时空参量调整的Bi-LSTM模型，并基于贝叶斯超参数优化模型优化结构性能参数.

步骤4　预测模型的训练与测试：为提升训练稳定性，选取持续t s的原始速度序列$\boldsymbol{P}$做标准化处理，预测未来k s的速度，并进行评估及反馈优化，实现合流区车速预测.

2.   数据采集及提取

2.1   高空视频采集

选取重庆市内环快速路某多车道交织区为研究对象，如图2所示，该交织区承担东西流向主要过境流量，呈现出车辆速度离散、行为随机、冲突集聚的独特交通特性. 为精细捕捉该交织区车辆速度复杂特性，在天气良好的工作日，利用无人机悬停于交织区上方120 m采集车辆运行高清视频. 在实验过程中，为避免数据采集影响交通运行，要求实验人员在人行道或周边高地，使用无人机装置录制高清视频数据.

图  2  高空视频拍摄场景

Figure  2.  High-altitude video shooting scene

下载: 全尺寸图片 幻灯片

2.2   交通信息提取

为有效获取工作日高峰时段的合流区车辆运行微观信息，课题组基于OPEN CV自主开发多尺度KCF车辆跟踪优化算法，从航拍视角对运动车辆进行自动识别和跟踪，并对数据进行坐标变换、数据验证和误差消除等处理分析，提取流程如图3所示，得到帧ID、时间ID、车辆ID、车辆质心坐标等车辆动态属性. 基于此，构建交通流信息与车辆行为信息基础数据库.

图  3  数据提取过程

Figure  3.  Data extraction process

下载: 全尺寸图片 幻灯片

通过车辆自动跟踪及人工标定，得到行经交织区车辆样本1507个，共计30余万条完整微观轨迹数据，包括速度、加速度、跟车间距、密度等. 经验证，轨迹信息自动跟踪算法位置误差仅为3.32%，误差均值为 −0.39 km/h （−0.11 m/s）. 25%分位数误差值约为 −2.3 km/h （−0.64 m/s），75%分位误差值约为1.4 km/h （−0.39 m/s），时间分辨率为0.1 s，空间分辨率为0.1 m/像素，数据颗粒度小，检测结果精度较高.

从视频图像来看，交织区整体像素坐标位于300～1800像素，为便于区分研究区域，划分300～900 像素为合流区，如图4所示. 在此基础上，以80%历史车速（每一辆车行经合流区域过程的瞬时速度）数据作为输入，预测未来20%时域范围的车速.

图  4  微观轨迹信息提取结果

Figure  4.  Results of microscopic trajectory information extraction

下载: 全尺寸图片 幻灯片

2.3   车速特性分析

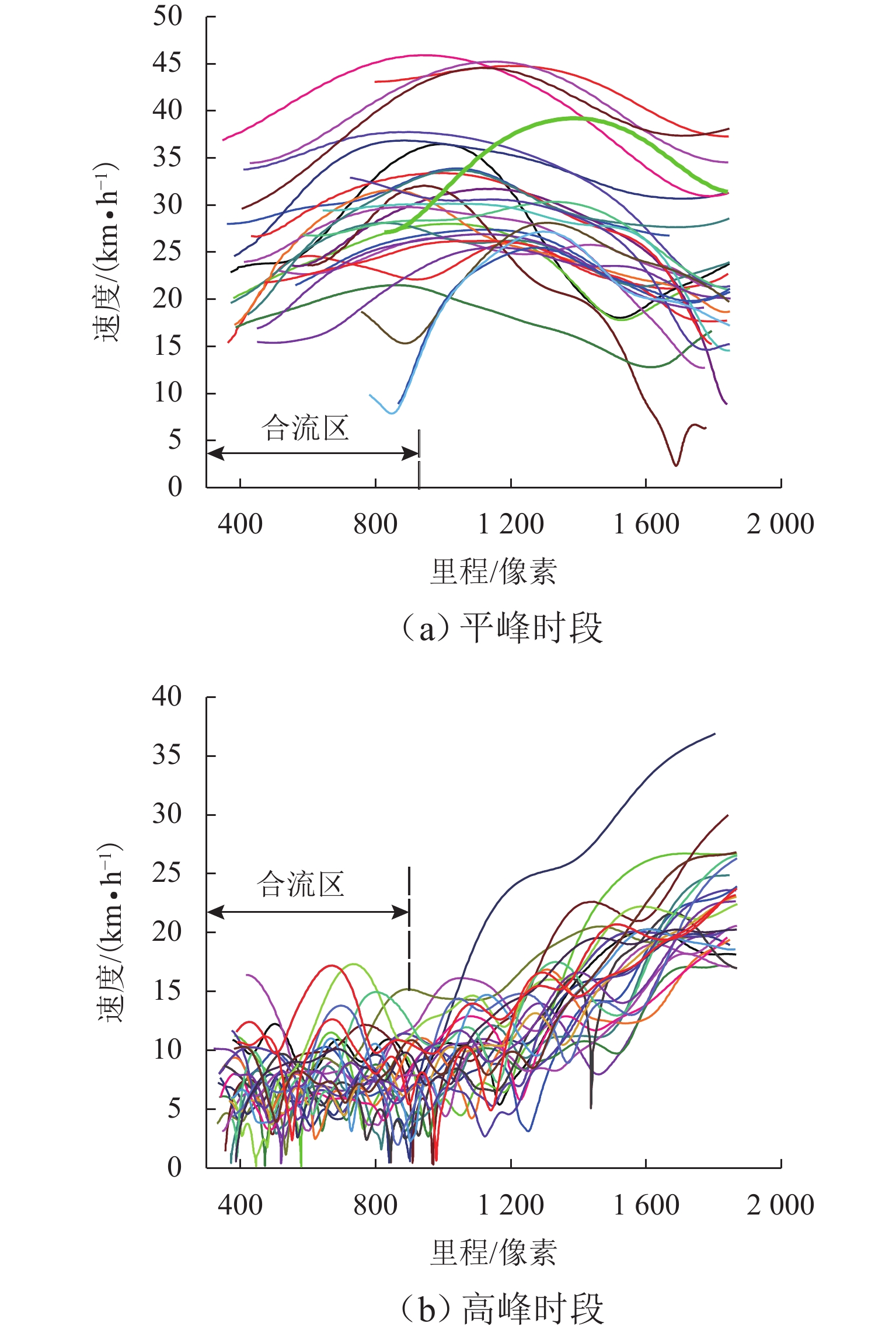
为分析交织区不同位置的车速空间分布差异，随机抽取若干条平（高）峰时段车速数据，如图5所示. 可看出，平（高）峰时段位置-速度分布存在显著差异，具体体现为

图  5  平（高）峰时段交织区车速-位置分布曲线

Figure  5.  Vehicle speed-position distribution curves in weaving area during flat (high) peak hours

下载: 全尺寸图片 幻灯片

1） 平峰时段，车速分布呈二次抛物线状，整体分布趋势稳定一致，随着车辆驶入交织区，速度呈先增加再平缓后降低的趋势，在1000 像素附近才达到速度峰值，说明车辆在合、分流区易受到汇入汇出车辆影响，导致车速明显下降；

2） 高峰时段，车辆驶入合流区时速度紊乱，而行经交织区、驶离分流区时，速度逐渐稳定提升，说明高峰期汇入需求较大，匝道（低速车流）汇入主线（高速车流）时换道困难，导致车速分布离散.

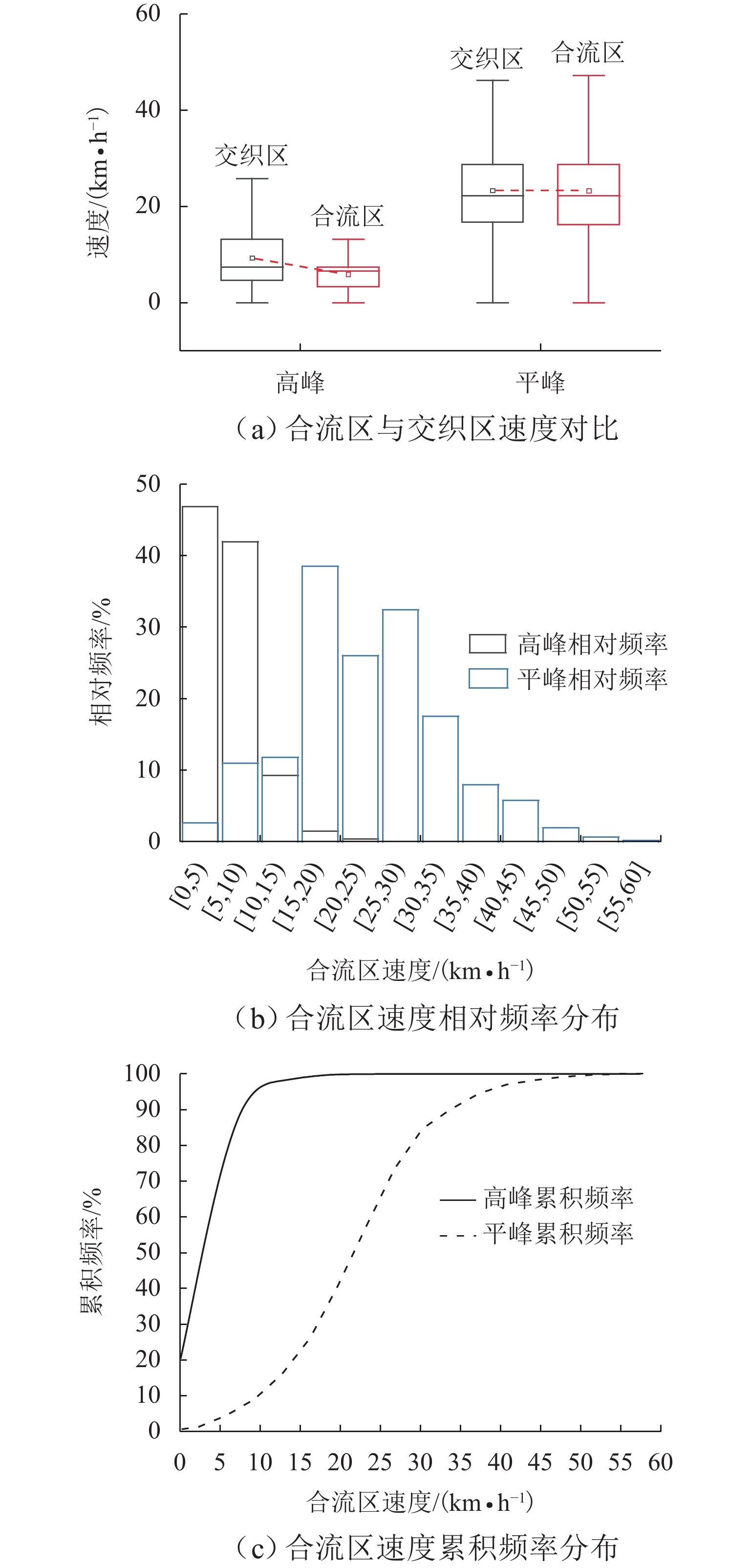
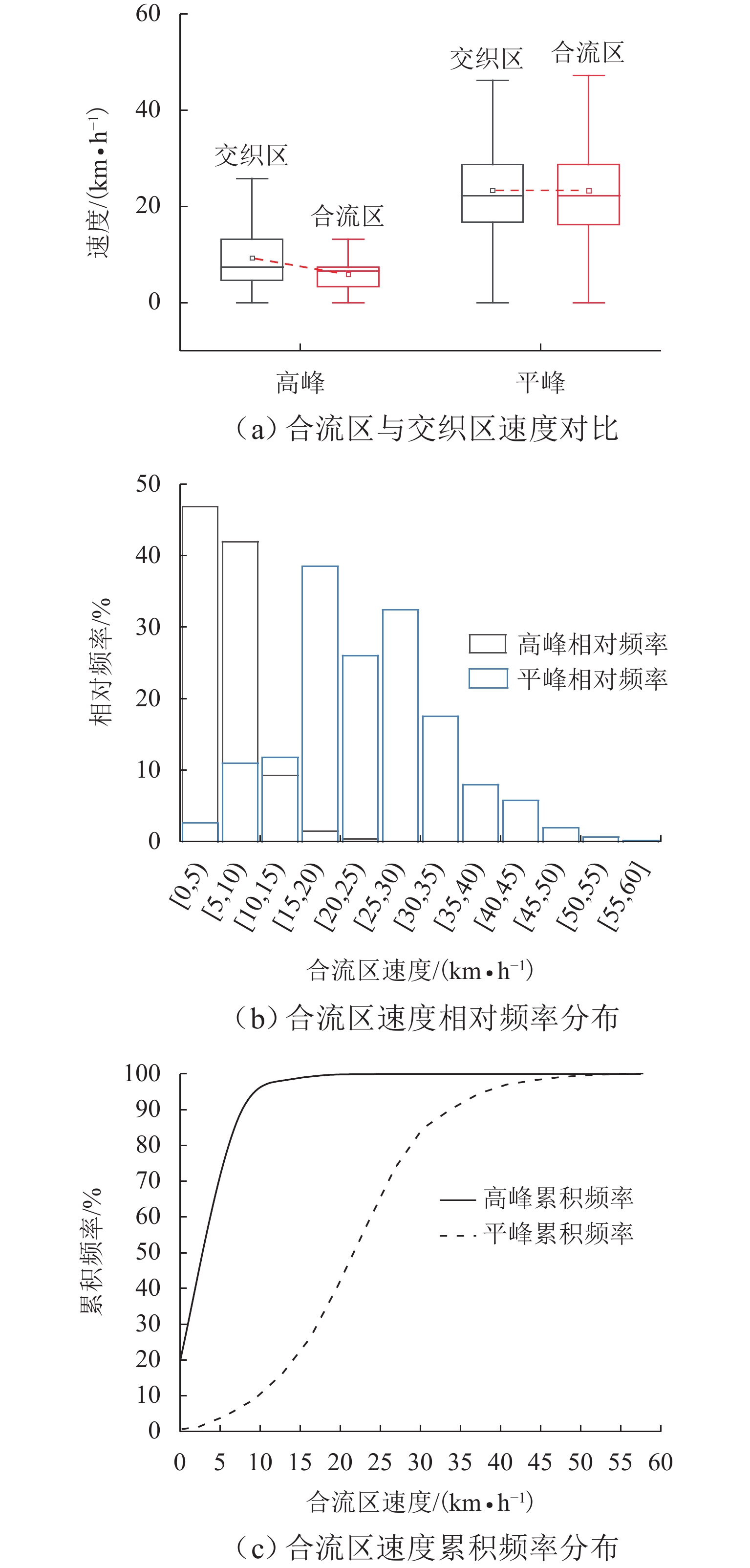
结合图6可以更直观地看出：1） 如图6（a）所示，高峰时段合流区的速度明显低于交织区，而平峰状态合流区与交织区速度整体一致，无明显差异；2） 如图6（b）、（c）所示，合流区平峰的速度频率分布较对称，其85%分位车速约30.00 km/h，高峰85%分位车速约为9.91 km/h，远低于限速值60.00 km/h，车速分布存在一定异常现象.

图  6  平（高）峰时段实例合流区车速分布

Figure  6.  Distribution of traffic speeds in merging area during peak hours

下载: 全尺寸图片 幻灯片

由前述分析可知，实例合流区高峰时段，由于存在路径转换需求的车辆汇入时产生大量换道行为，导致运行速度急剧下降，极易出现拥堵状况，瓶颈效果显著，拥堵自合流区蔓延至紧邻上游路段，具有车速离散、分布紊乱、瓶颈现象等独特的特性，依靠数据统计分布难以刻画其运行规律，导致车速变化难以准确掌握. 面向车路协同系统的速度控制调节，需保证此类非典型场景复杂车速运行状态的精准预测，基于此本文展开车速预测研究.

3.   基于BHO-Bi-LSTM的速度预测模型

由于路段车速受多个历史时刻速度的累计影响，在提取时间特征时，应将其纳入考虑范围. LSTM^[10-16]因其能避免RNN存在的梯度消失问题，可显著提高时间序列特征的提取效率，用于提取车速的时间特征.

借助LSTM，可从窗口目标路段实际速度序列中提取预测时刻目标路段实际速度的时间特征，并映射至预测时刻目标路段的实际速度，从时间序列尺度上实现对运行速度的预测. LSTM计算过程为

式中：${\boldsymbol{f}}_{t}$为时刻t的遗忘门，${\boldsymbol{i}}_{t}$为输入门，${\boldsymbol{c}}_{t}$为记忆细胞，${\boldsymbol{o}}_{t}$为输出门，$\sigma$(·)为sigmoid激活函数，$\odot$为2个向量的哈达玛积，${\boldsymbol{x}}_{t}$为时间序列步输入，${\boldsymbol{c}}_{t}$为时刻t的记忆细胞状态，${\boldsymbol{h}}_{t}$为时刻t的隐层状态，$\mathrm{tanh}$(·)为激活函数，${\boldsymbol{w}}_{f}$、$\boldsymbol{w}_i$、$\boldsymbol{w}_o$、$\boldsymbol{w}_c$为训练所得相应特征的权值，${\boldsymbol{b}}_{f}$、$\boldsymbol{b}_i$、$\boldsymbol{b}_o$、$\boldsymbol{b}_c$为训练所得相应特征的偏移量.

LSTM虽能有效捕捉前向历史速度数据的变化特征，但是车速的有效预测不仅依赖于过去的信息，还要考虑车辆空间位置及其时序性，Bi-LSTM 能够从前、后2个方向整合并处理数据，可解决LSTM在信息处理上只按照单向先后顺序的问题，能有效捕捉交通参数时序信息，更全面地挖掘速度的变化特性.

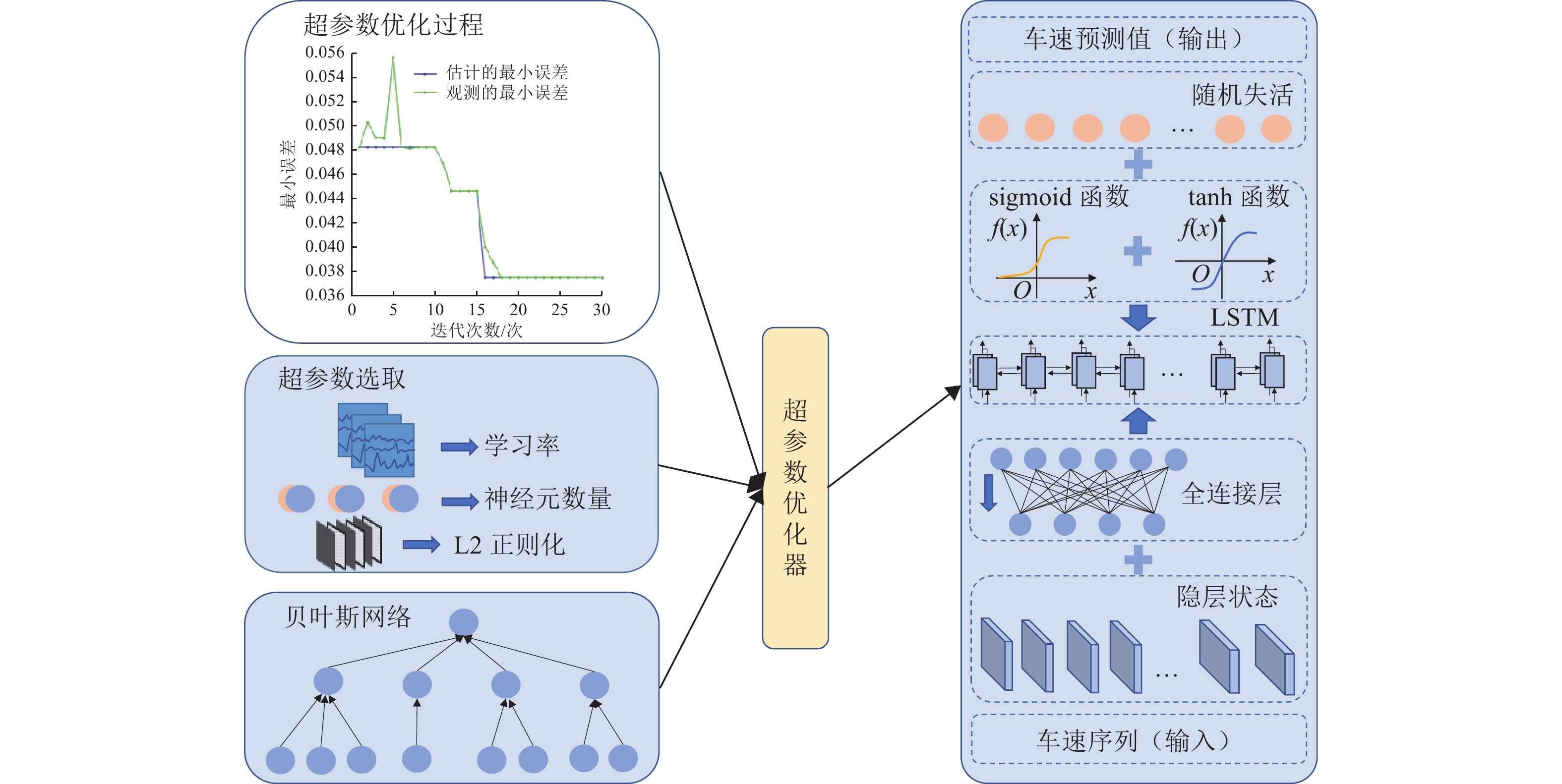
执行车速预测实际任务时，Bi-LSTM需确定隐含层、学习率等参数，以保证算法最优性能. 影响模型性能主要参数为

1） 隐含层单元数（hidden layer units）. 隐含层单元数过少可能导致模型无法学习到足够的有效信息，过多则可能会导致训练时间太长，甚至出现过拟合，使模型的泛化能力下降.

2） 学习率（learning rate）. 较高的学习率会加速模型的收敛并得到次优解，较低的学习率会导致模型在规定的时间内收敛速度缓慢，甚至不收敛.

3） 隐含层（hidden layers）. 隐含层节点过少，模型不能得到充分的学习，节点过多则容易陷入局部最优及收敛缓慢.

4） L2正则化因子（L2 regularization）. 利用L2正则化因子优化Bi-LSTM模型的权值参数，从而避免过拟合.

考虑到Bi-LSTM的训练时间较长，人工设置下训练上述参数对预测性能的影响较大，为保证模型预测性能，本文构建优化算法对参数进行自动寻优. 目前，常用的超参数调优的方法有网格搜索、随机搜索与贝叶斯优化. 网格搜索主要是通过给出较大的搜索范围以及较小的步长进行全局搜索，极为消耗计算资源；随机搜索^[17]则容易导致局部最优；BO^[18-20]通过跟踪过去的评估结果，形成概率代理模型，将超参数映射到目标函数的评估结果，具有迭代次数少，运行速度快的特点，能够有效地搜索可能的超参数空间. 因此，本文采用贝叶斯优化对Bi-LSTM模型进行超参数（隐含层单元数、学习率、隐含层、L2正则化因子）调优，构建基于贝叶斯超参数优化的Bi-LSTM速度预测模型（BHO-Bi-LSTM），如图7所示.

图  7  贝叶斯超参数优化过程

Figure  7.  Bayesian hyperparameter optimization process

下载: 全尺寸图片 幻灯片

4.   模型验证

4.1   模型训练

为体现本文BHO-Bi-LSTM模型的性能优势，人工设置Bi-LSTM模型结构性能使其达到最优. 按隐层数量 × 遍历轮数 × 批大小的形式，设计24组交叉实验进行测试. 模型包含4种隐含层结构，第1种只有1层隐含层，隐含层单元数为100个，表示为$h_{100}$；第2种有2层隐含层，每层隐含层单元数均为100个，表示为$h_{100}\times h_{100}$；其余2种的前2层隐藏层单元数均为100个，第3（4）层隐含层单元数均为75个，分别表示为$h_{100}\times h_{100}\times h_{75}$和$h_{100}\times h_{100}\times h_{75}\times h_{75}$.

训练过程设置基础学习率$\beta$为0.005，随机失活（dropout）值为0.5，采用Adam迭代优化算法，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率，其公式如下：

式中：$\lambda$和$\gamma$分别为一阶矩估计和二阶矩估计的指 数衰减率，通常$\lambda$取0.9，$\gamma$取0.99； ${\boldsymbol{g}}_j$为第j次迭代梯度；${\boldsymbol{m}}_j$为${\boldsymbol{g}}_j$的一阶矩估计，即${\boldsymbol{g}}_j$的指数移动平均值；${\boldsymbol{n}}_j$为${\boldsymbol{g}}_j$的二阶矩估计，即${\boldsymbol{g}}_j^2$的指数移动平均值；$\hat{{\boldsymbol{m}}}_{j}$为${\boldsymbol{m}}_{j}$的偏差纠正；$\hat{{\boldsymbol{n}}}_{j}$为${\boldsymbol{n}}_{j}$的偏差纠正；${\boldsymbol{\theta}}_{j}$为第${{j}}$次迭代的参数向量；$\;\beta$为学习率；$\varepsilon$为残差项，默认取10⁻⁸.

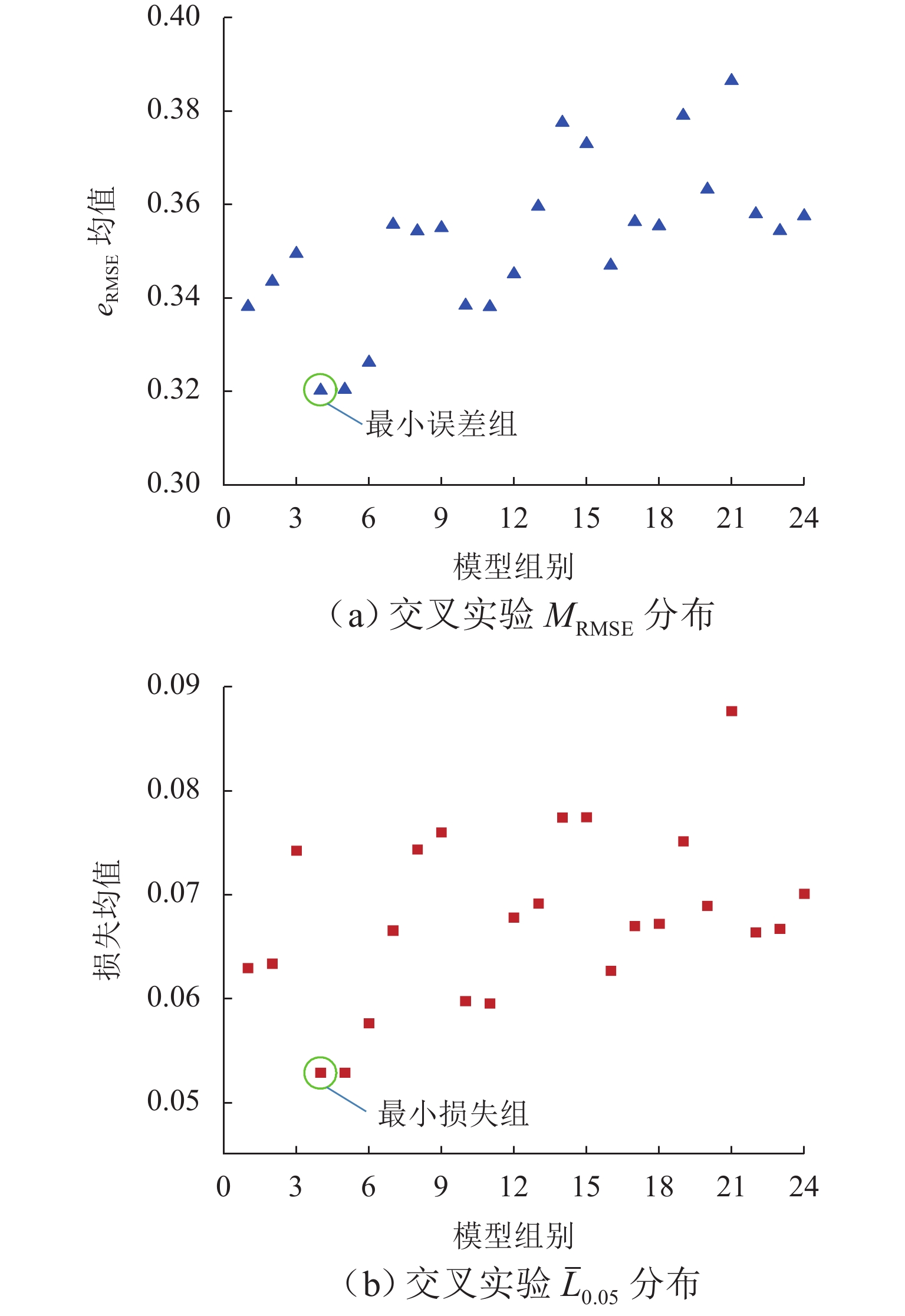
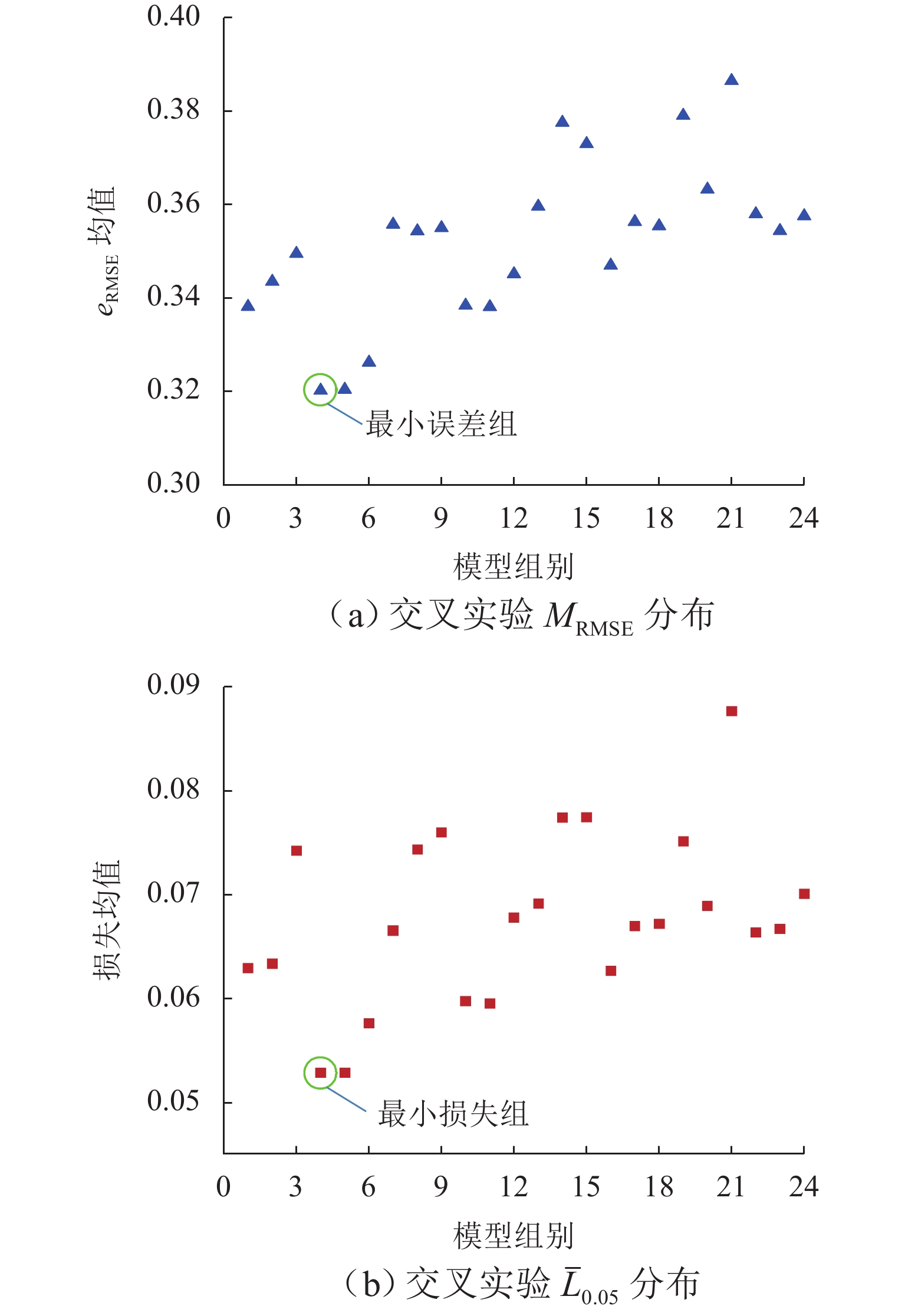
完成24组训练测试后，得到模型的损失均值$\bar L_{0.05}$和均方根误差e_RMSE均值$M_{\text {RMSE }}$分布情况如图8所示.

图  8  交叉实验训练结果

Figure  8.  Cross-experiment training results

下载: 全尺寸图片 幻灯片

由图8可知：

1） 随着隐含层数的增加，$\bar L_{0.05}$、$M_{\text {RMSE }}$曲线随之上升，第4组实验的$\bar L_{0.05}$和$M_{\text {RMSE }}$处于较低水平，即第4组模型的结构性能最优；

2） 在同一隐含层数量的情况下，随着遍历轮数的增加，$\bar L_{0.05}$、$M_{\text {RMSE }}$呈现出下降趋势，以1～6组为例：1～3组（$h_{100} \times 100 \times 32$、$h_{100} \times 100 \times 64$、$h_{100} \times 100 \times 128$）遍历轮数为100轮，4～6组（$h_{100} \times 200 \times 32$、$h_{100} \times 200 \times 64$、$h_{100} \times 200 \times 128$）遍历轮数为200轮，随着遍历轮数的增加，$\bar L_{0.05}$和$M_{\text {RMSE }}$值显著下降；

3） 同一隐含层和同一遍历轮数的情况下，以1～3组为例，随着批大小的增加，$\bar L_{0.05}$、$M_{\text {RMSE }}$也多出现上升趋势.

采用第4组（隐含层单元数为$h_{100}$，批大小为32，遍历轮数为200轮）作为最优Bi-LSTM模型. 为保证模型控制条件唯一，将Bi-LSTM的最优结构参数值代入BHO-Bi-LSTM模型中，使两模型具有相同的初始结构参数.

4.2   模型对比

本文提出基于贝叶斯超参数优化的Bi-LSTM速度预测模型（模型Ⅲ，采用贝叶斯超参数优化算法自动寻优），构建了2个对比模型.

1） 多元线性回归车速预测模型^[21-22]（模型Ⅰ）. 车速$v(t) = {\beta _0} + {\beta _1}{v_0}(t) + {\beta _2}a(t)$，其中：${v_0}(t)$为初速度；$a(t)$为加（减）速度；${\beta _0} = 1.481；$${\beta _1}$、${\beta _2}$为模型参数，${\beta _1} = 0.817，$${\beta _2} = - 0.159$；拟合优度${R^2} = 0.798$；置信度为95%.

2） Bi-LSTM车速预测模型^{[16, 23]}（模型Ⅱ）. 超参数取值：隐含层为$h_{100}$，批大小为32，遍历轮数为200轮.

对车速数据进行标准化、时间窗口滑动处理后，统计实测及3个模型的预测车速数据结果，采用7个指标评估模型性能.

1） 拟合优度R² （式（11））. 用于描述预测速度与真实速度之间的拟合程度，R²取值在[0,1]，R²越接近于1.

式中：$y_{i}$为原始的速度数据（$i=1,2, \cdots, n$），$\hat{y}_{i}$为$y_{i}$的预测值，$\bar y$为$y_{i}$的平均值，S_SR为回归平方和，S_ST为总离差平方和，S_SE为残差平方和，${N}$为样本总量.

2） 误差均值$\;\mu$（式（12））. 用于反映实际预测误差的大小，其值越接近于0越好.

3） 误差的标准差$e_{{\mathrm{stD}}}$式（13）. 用于评价误差的整体水平以及误差的离散程度，标准差越大，表明误差数据越离散.

4） 均方误差$\mathit{e}\mathrm{_{\mathrm{MSE}}}$（式（14））. $\mathit{e}_{\mathrm{MSE}}$越小，预测速度值精度越高.

5） 均方根误差$e_{\mathrm{RMSE}}$（式（15））. $e_{\mathrm{RMSE\mathrm{ }}}$越小，预测速度值精度越高.

6） 归一化均方根误差$e_{\mathrm{NRMSE}}$（式（16））. $e_{\mathrm{NRMSE}}$越小，预测速度值精度越高.

7） 秩相关系数r_s. 用于判断预测速度分布与实际速度分布之间的关联程度，r_s越大速度预测精度越高.

式中：$d_{i}$为两两样本变量的等级差，即变量$x_{i}$与$y_{i}$的差值.

详细结果如表1所示.

表  1  模型总体评价指标对比

Table  1.  Comparison of overall model evaluation indicators

模型	R2	$\mu$	estD	eMSE	eRMSE	eNRMSE	rs
多元线性回归[22] （模型Ⅰ）	0.7980	0.001 7	1.659 5	2.754 2	1.659 6	0.269 0	0.844 0
Bi-LSTM[23] （模型Ⅱ）	0.8882	−0.005 3	0.471 1	0.221 8	0.470 9	0.080 6	0.945 3
BHO-Bi-LSTM （模型Ⅲ）	0.9105	0.056 1	0.455 6	0.210 6	0.458 9	0.078 5	0.948 7
模型Ⅲ对比模型Ⅰ （提升或下降比例）	+0.1125 （↑14.10%）	+ 0.054 4 （↓3 200%）	−1.203 9 （↑72.55%）	−2.543 6 （↑92.35%）	−1.200 7 （↑72.35%）	−0.190 5 （↑70.82%）	+0.1047 （↑12.35%）
模型Ⅲ对比模型Ⅱ （提升或下降比例）	0.2230 （↑3.80%）	+ 0.061 4 （↓1158.49%）	−0.015 5 （↑3.29%）	−0.011 2 （↑5.05%）	−0.012 0 （↑2.548%）	−0.002 1 （↑2.605%）	+0.0034 （↑0.40%）
注：黑体加粗表示最优指标

下载: 导出CSV 

| 显示表格

综合以上指标，可以看出：

1） 整体来看，模型Ⅲ预测效果明显优于模型Ⅰ、Ⅱ，具体体现为，除$\;\mu$外，R²、$\sigma$、$e\mathrm{_{MSE}}$、$e_{\mathrm{RMSE}}$、$e_{\mathrm{NRMSE}}$、$r_{{\mathrm{s}}}$均表现最优，多元线性回归模型$\;\mu$表现出众的原因可能是在$\;\mu$求和过程中，正负误差值相互对称抵消，使其$\;\mu$接近于0.

2） 相比于模型Ⅰ，模型Ⅱ、Ⅲ的综合性能差距明显较小，这说明相对于经典多元线性回归预测模型，LSTM深度学习模型结构在车速预测方面具有明显优势，表现出更好的预测精度.

4.3   模型优选

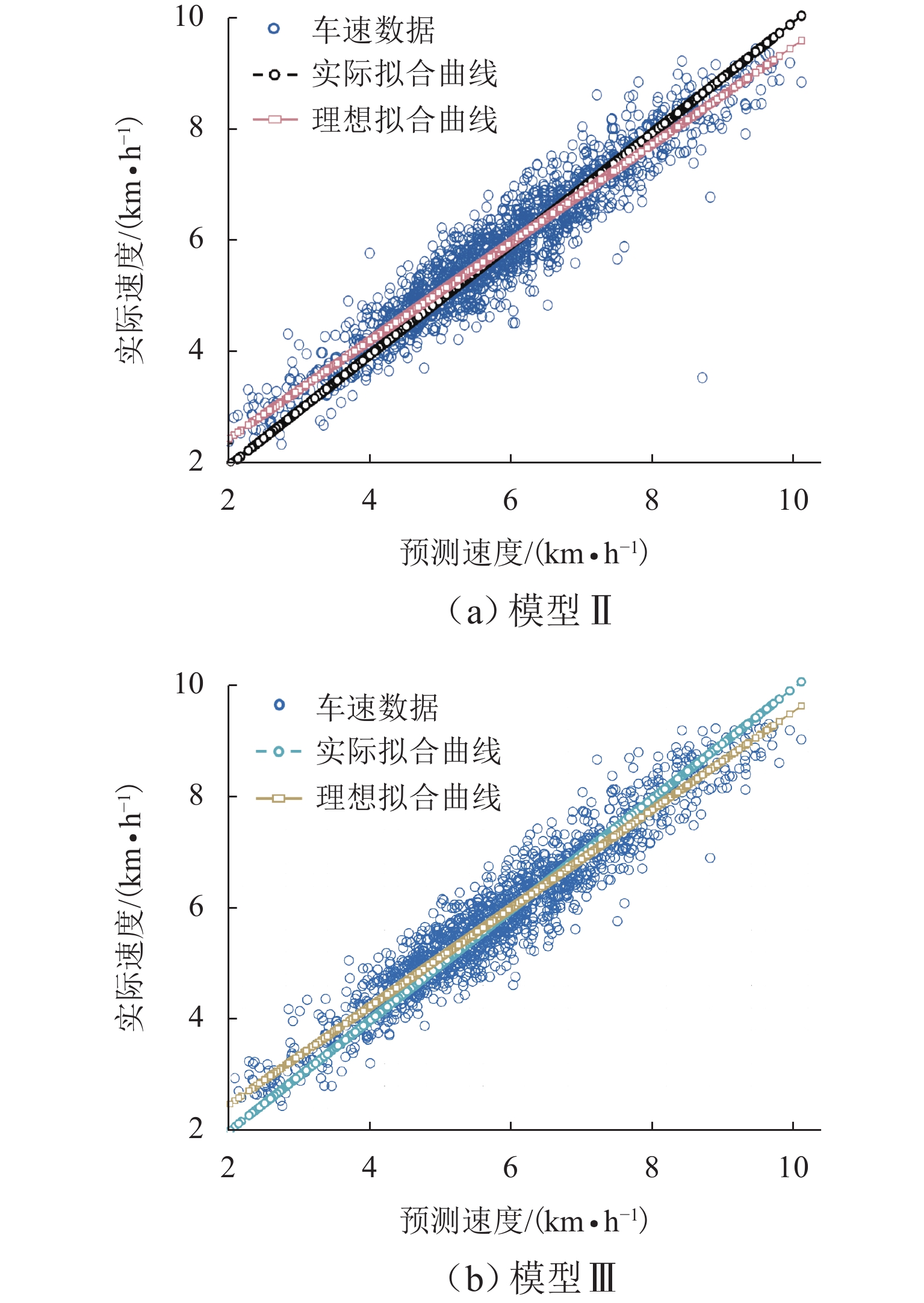
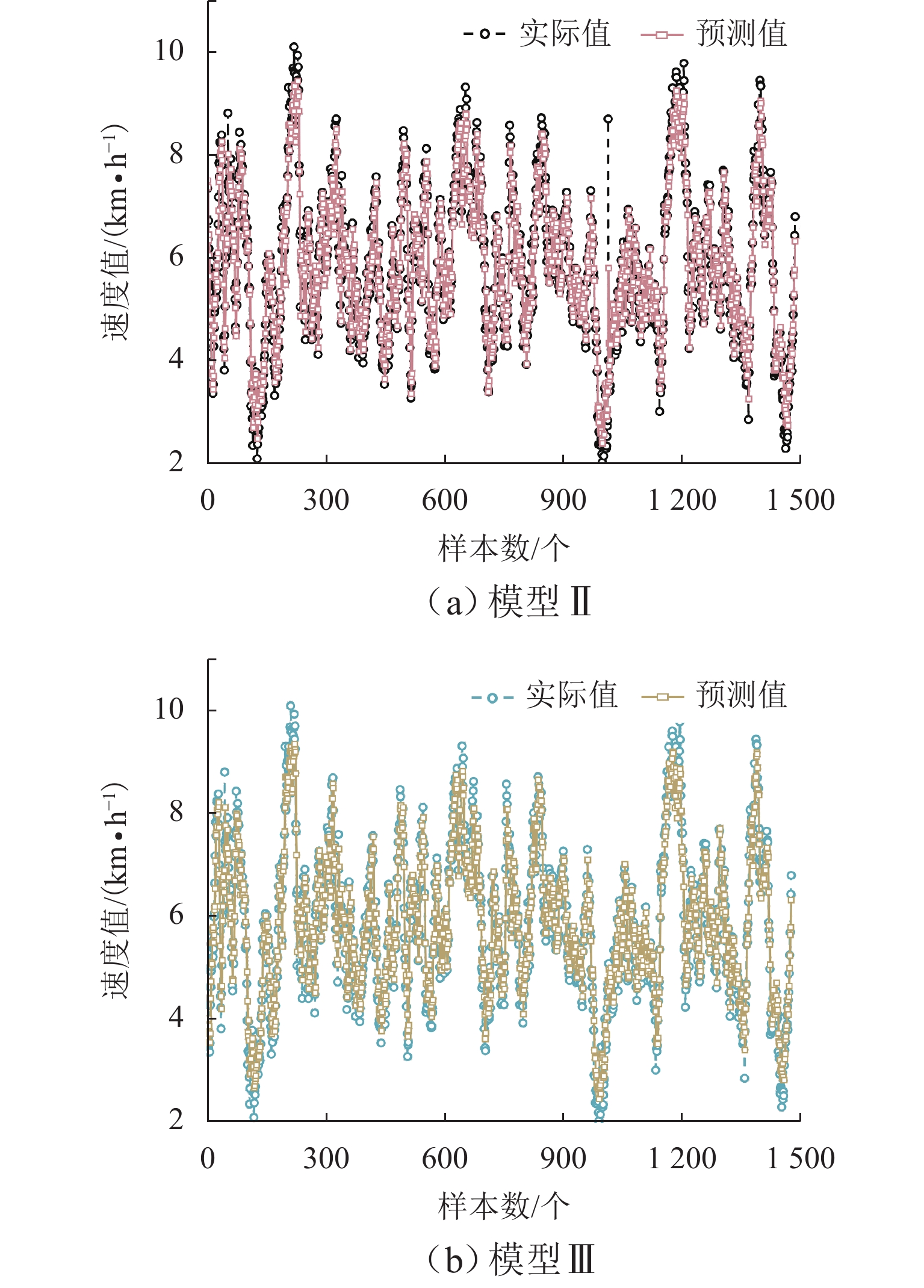
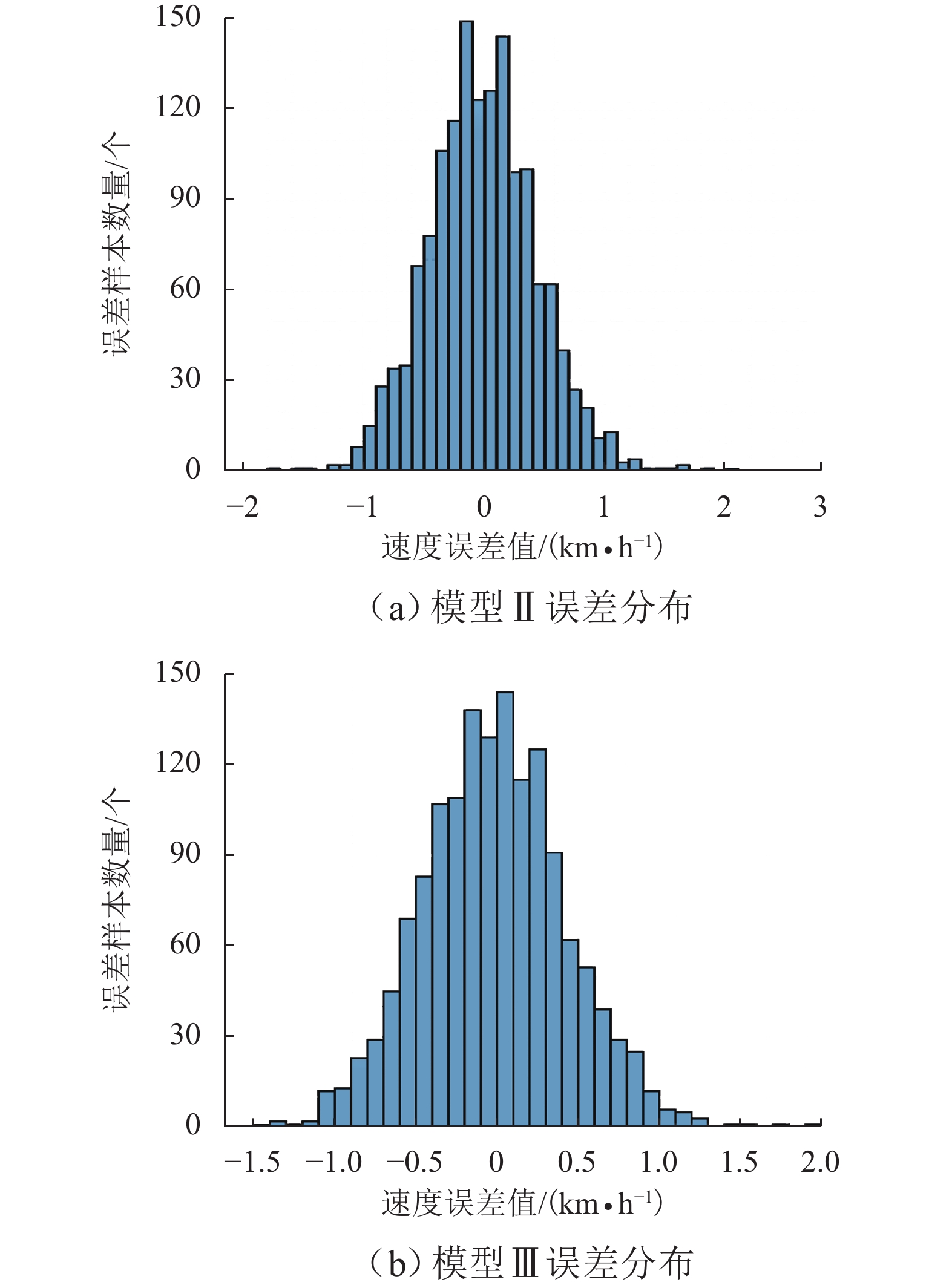
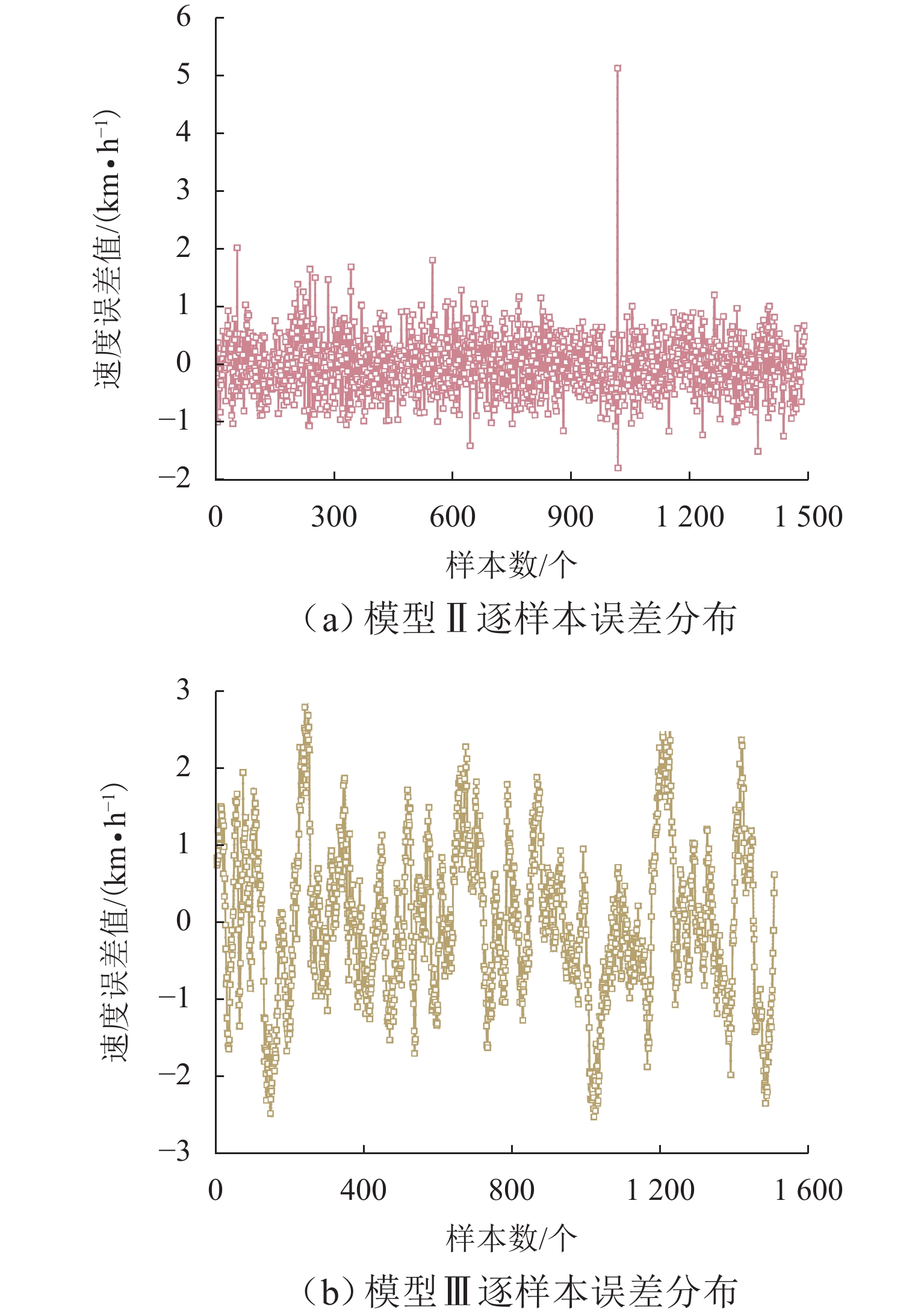
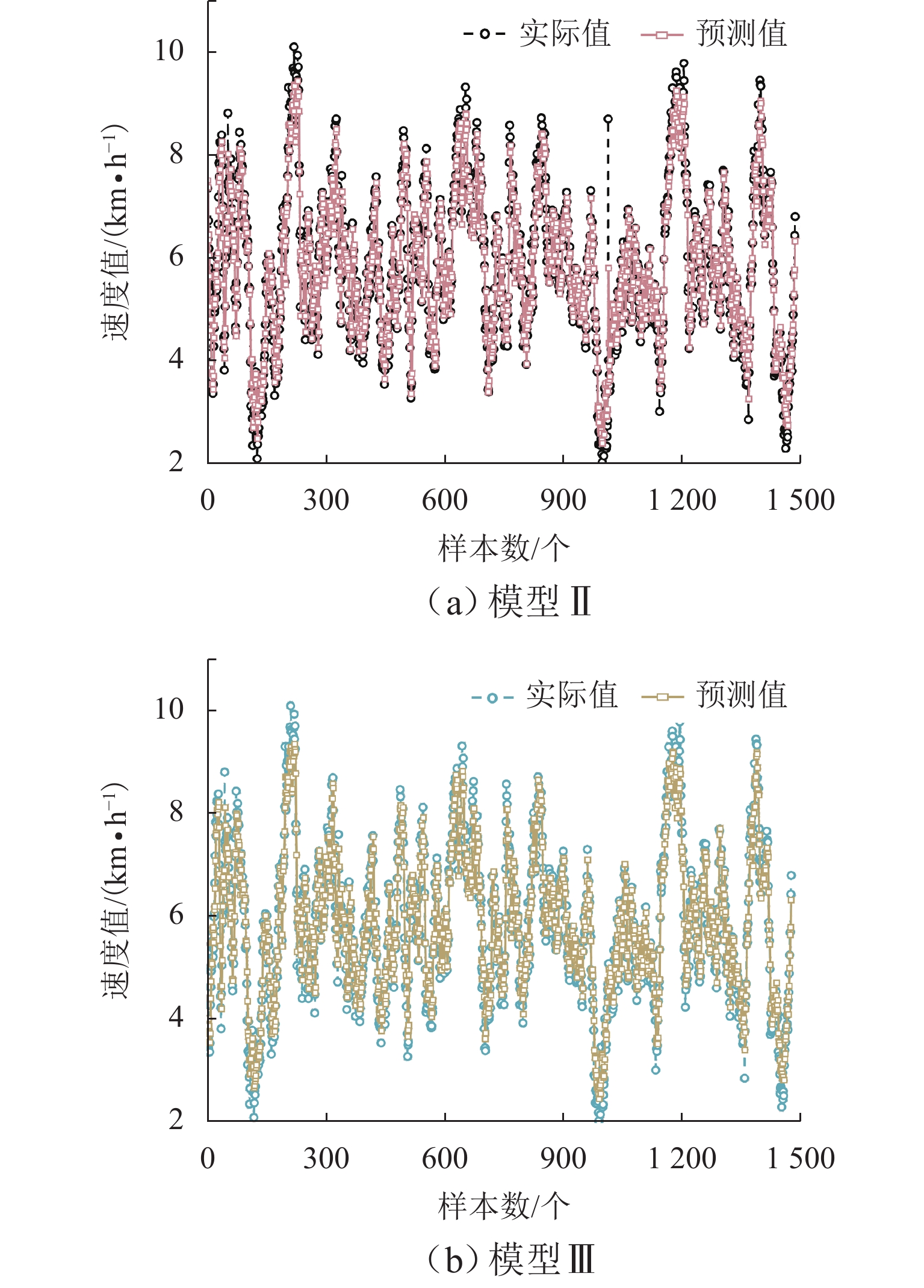
由上述分析可知，基于LSTM深度学习模型结构的模型Ⅱ、Ⅲ在车速预测方面差距较小，为进一步直观讨论模型Ⅱ、Ⅲ性能，绘制拟合对比图、整体误差与逐误差分布、秩相关对比图，如图9～12所示.

图  9  拟合对比

Figure  9.  Fitting comparison

下载: 全尺寸图片 幻灯片

图  10  误差直方图

Figure  10.  Error bar graph

下载: 全尺寸图片 幻灯片

图  11  逐样本误差点线图

Figure  11.  Sample-wise errors

下载: 全尺寸图片 幻灯片

图  12  秩相关对比

Figure  12.  Rank correlation comparison

下载: 全尺寸图片 幻灯片

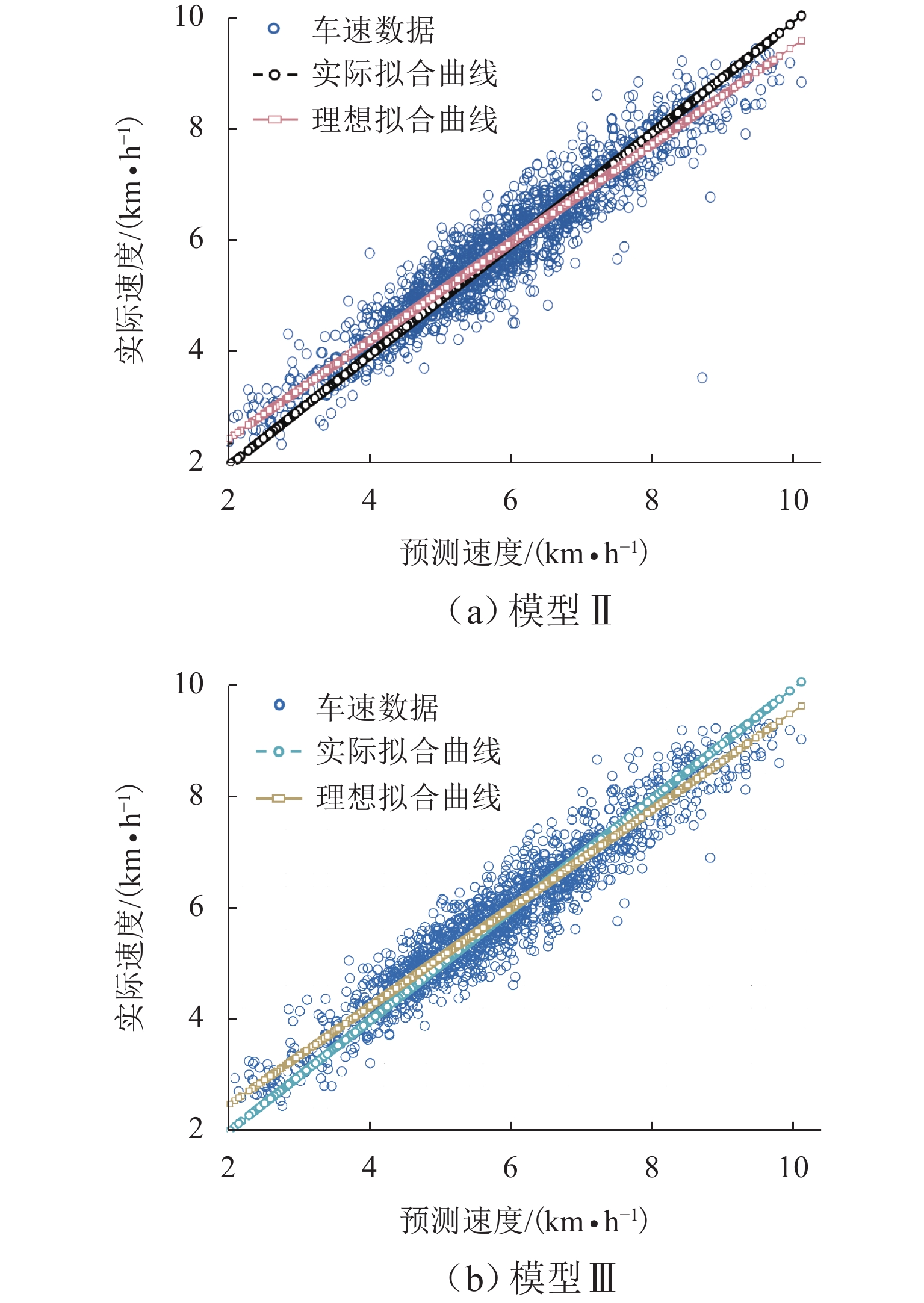
1） R². 如图9、表1所示，模型Ⅱ、Ⅲ的R²分别为0.8882和0.9105，其预测交汇点（蓝色圆圈）分布更为集中、更接近于理想曲线，拟合效果更好. 显然模型Ⅲ的R²更高，速度预测值更加接近实际值.

2） 误差频率分布. 如表1、图10所示，模型Ⅱ、Ⅲ预测模型产生的误差值都较为集中，$e\mathrm{_{stD}}$分别为0.4711和0.4556，模型Ⅲ的误差分布更为紧凑稳定，说明贝叶斯超参数优化过后速度预测结果与实际速度间的偏差更小且集中.

3） 逐样本误差分布. 如表1所示：模型Ⅱ的e_MSE、e_RMSE、e_NRMSE分别为0.2218、0.4709、0.0806；模型Ⅲ分别为0.2106、0.4589、0.0785，模型Ⅲ较模型Ⅱ的e_MSE、e_RMSE、e_NRMSE分别提升5.050%、2.548%、2.605%，且图11中模型Ⅲ误差分布明显更为集中，说明模型Ⅲ性能更为稳定，表现出更好的鲁棒性.

4） 秩相关性. 如表1，模型Ⅱ、Ⅲ的r_s分别为0.9453、0.9487，模型Ⅲ提升0.34%，图12分别展示了模型Ⅱ、Ⅲ秩相关分布情况，2个模型表现基本相当，模型Ⅲ相关性更高.

5.   结束语

1） 本文构建的BHO-Bi-LSTM速度预测模型（模型Ⅲ），与多元线性回归（模型Ⅰ）、Bi-LSTM速度预测模型（模型Ⅱ）作对比，基于R²、μ、σ、e_MSE等7项评价指标，模型Ⅰ速度预测误差显著高于模型Ⅱ、模型Ⅲ，说明采用经典线性回归方法开展合流区高峰时段车速预测并不能很好地体现其适用性，有必要考虑采用LSTM深度学习模型结构开展车速预测实际任务.

2） 得益于贝叶斯超参数方法自动寻优的优势，BHO-Bi-LSTM速度预测模型误差最低、相关性最高，说明基于超参数优化的速度预测模型，可有效适应与预测合流区高峰期复杂的速度特征，表现出更好的鲁棒性与泛化性，可为城市快速路的合流区管控提供理论依据.

3） 由于本文的预测模型是基于合流区高峰状态下的数据建立的，对于分流区高峰状态下的速度预测，后续可采用与本文相似方法进行运行速度预测模型计算. 此外，本文主要针对实例交织区的运行速度进行了分析及预测研究，下一步还应开展其他构型交织区运行速度分析和预测的研究工作.

致谢：中佛罗里达大学LI Xiaobing教授和重庆交通大学彭博教授在文章撰写中提供的宝贵意见.