c

蒋启龙; 姚卫丰; 张晔

doi:10.3969/j.issn.0258-2724.20250067

c

doi: 10.3969/j.issn.0258-2724.20250067

蒋启龙^1,,
姚卫丰^2, ,,
张晔¹

1.
西南交通大学电气工程学院，四川成都 611756
2.
深圳职业技术大学机电工程学院，广东深圳 518055

基金项目: 国家自然科学基金项目（52277166）

详细信息

作者简介:
蒋启龙（1969—），男，教授，博士，研究方向为电力电子技术及其应用、磁悬浮列车技术、电力传动及控制，E-mail：double_long@126.com

通讯作者:
姚卫丰（1971—），女，副教授，研究方向为工业自动化、建筑智能化，E-mail：yao1971@szpu.edu.cn

中图分类号: TH133.3；TP13
计量
- 文章访问数: 26
- HTML全文浏览量: 2
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2025-02-24
- 修回日期: 2025-06-03
- 网络出版日期: 2025-06-18

Fault Diagnosis of Suspended Electromagnet Based on Current Change Rate Increment

1.
School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China
2.
School of Mechanical and Electrical Engineering, Shenzhen Polytechnic University, Shenzhen 518055, China

摘要

摘要:
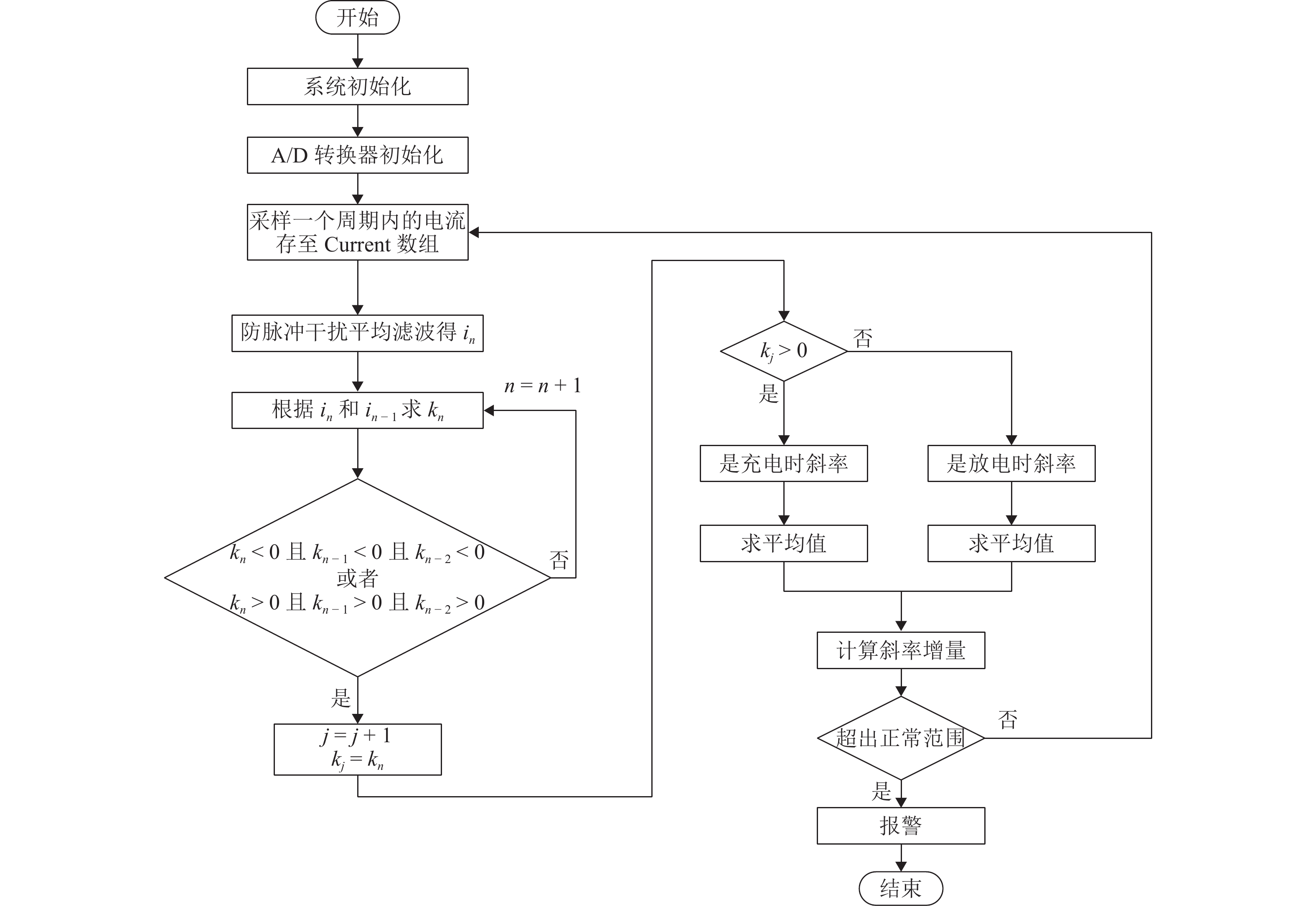
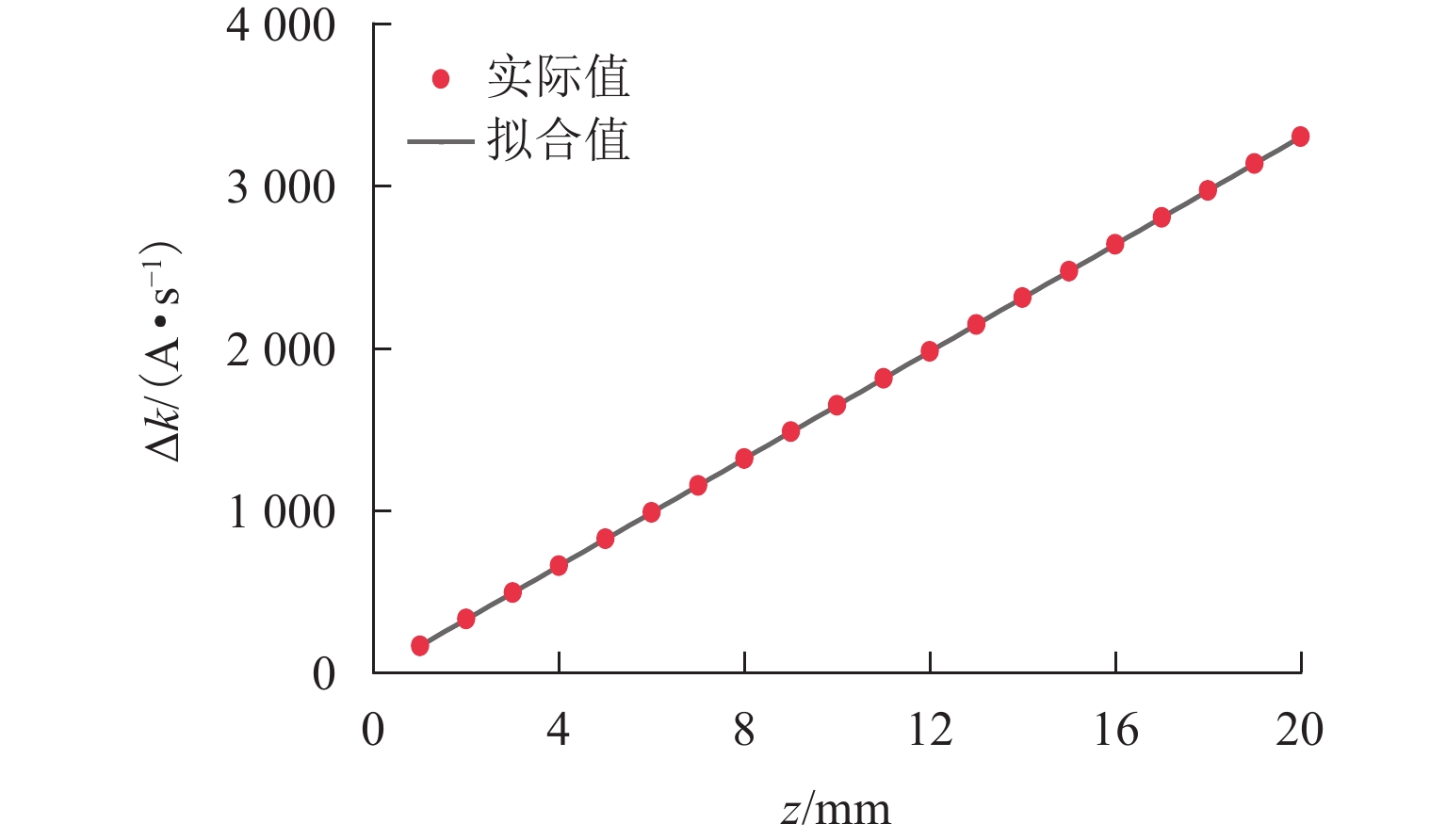
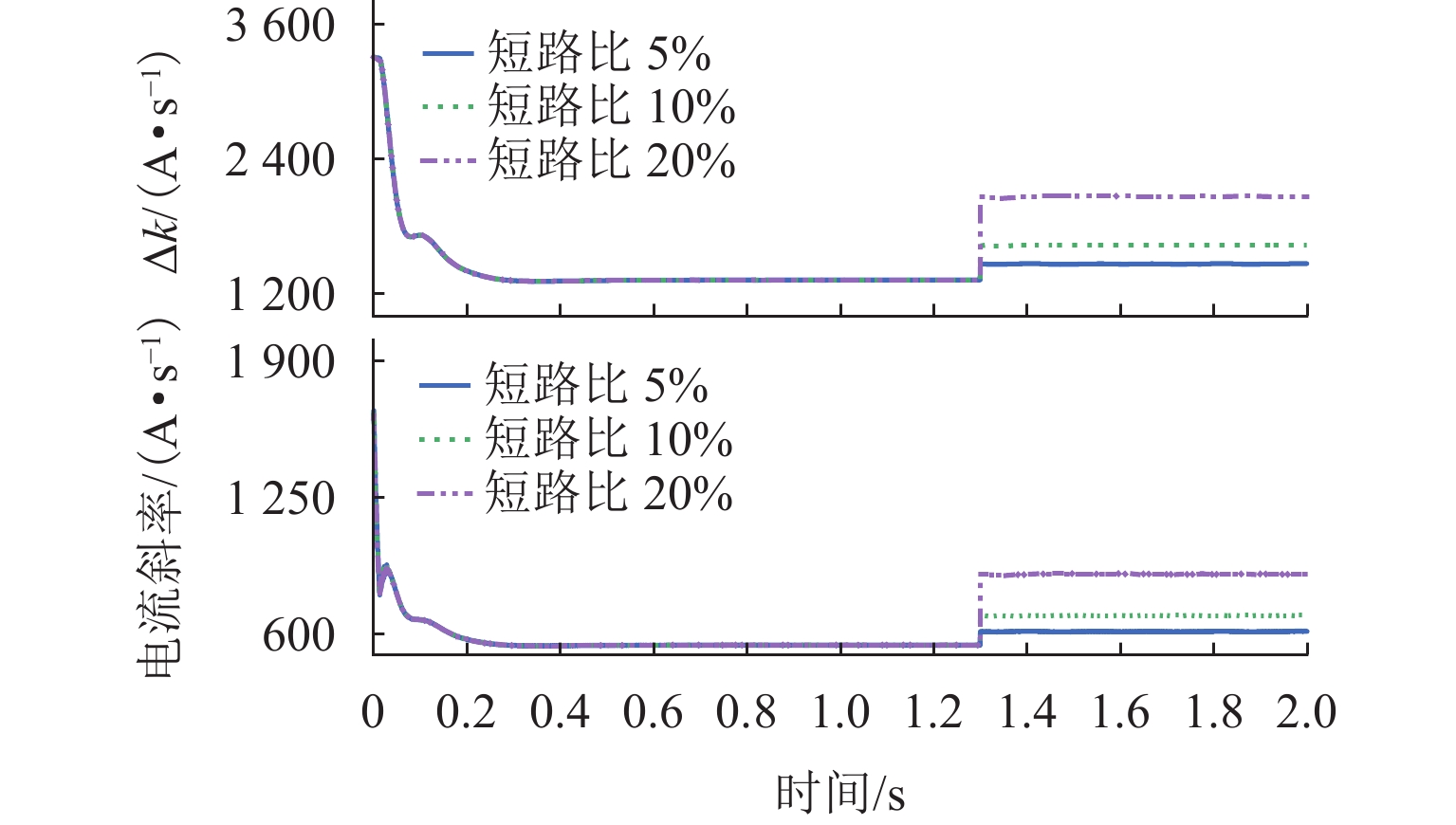
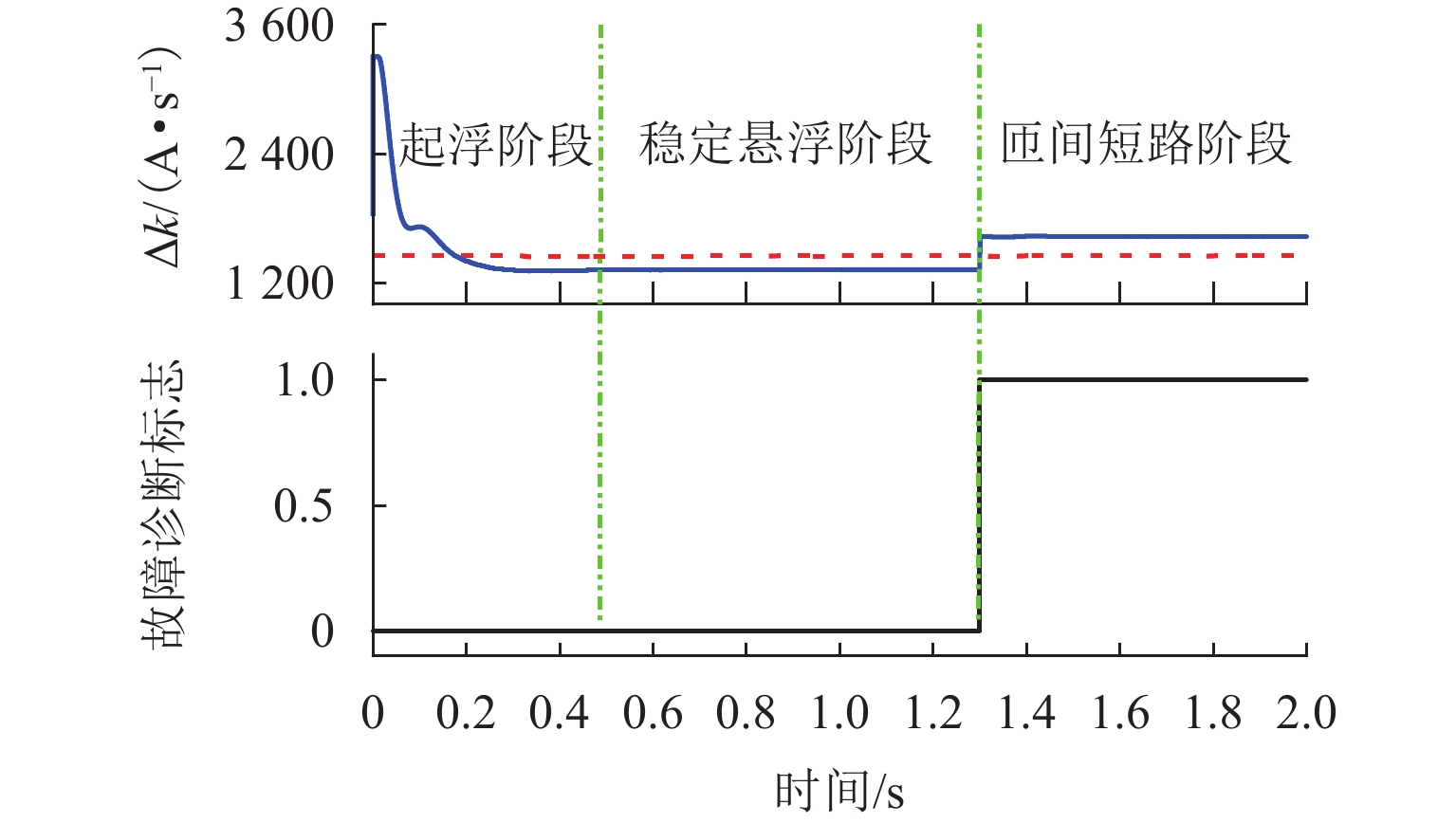
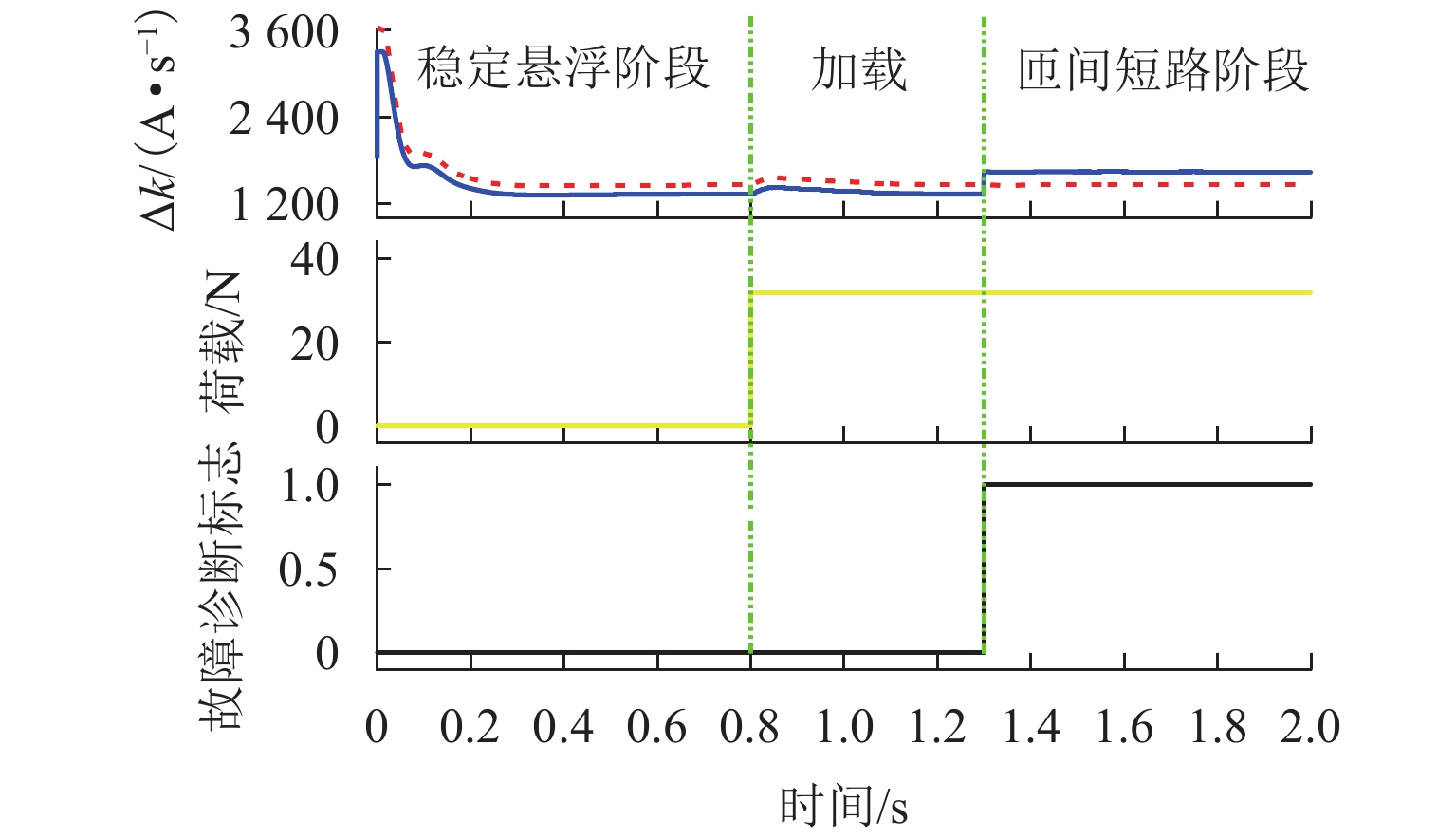
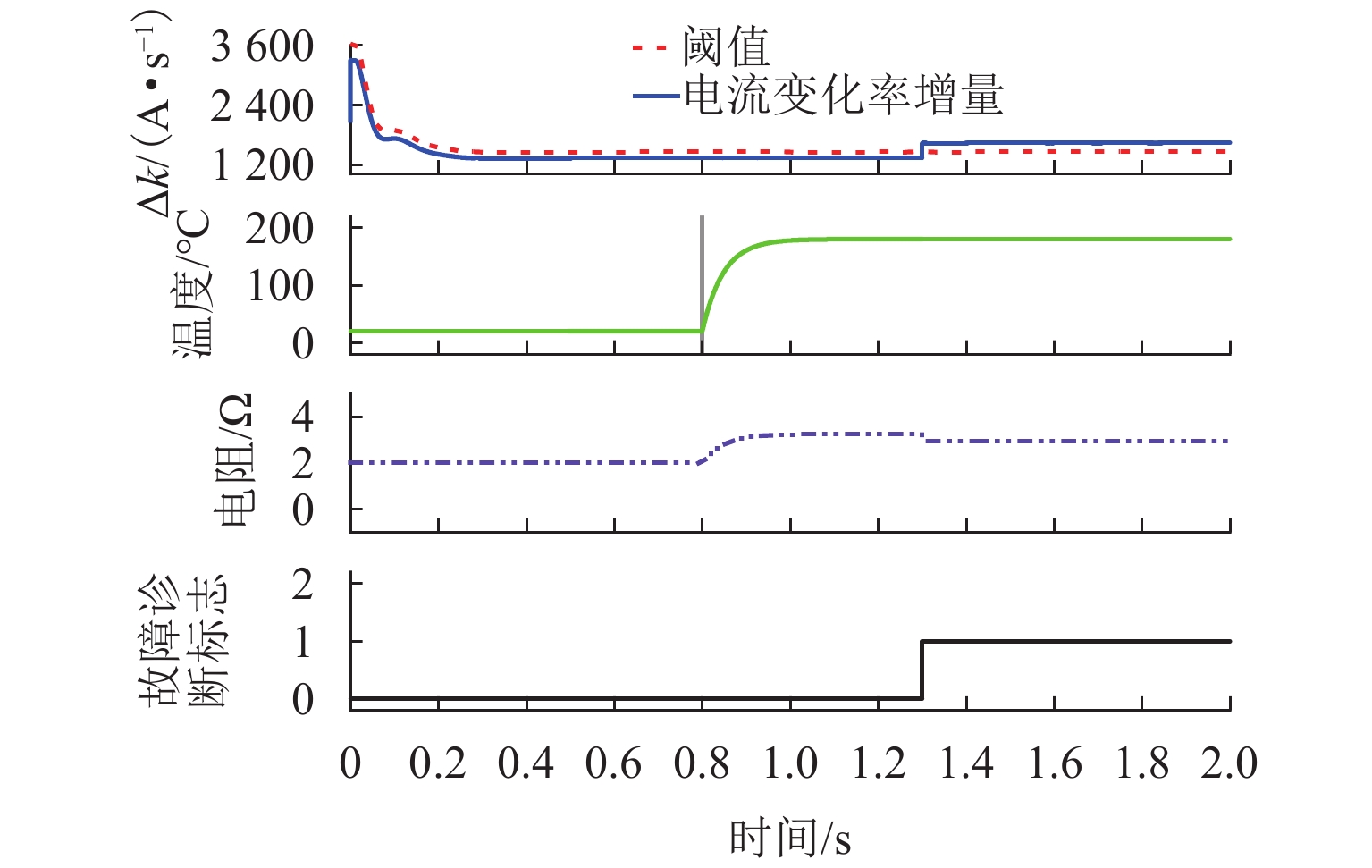
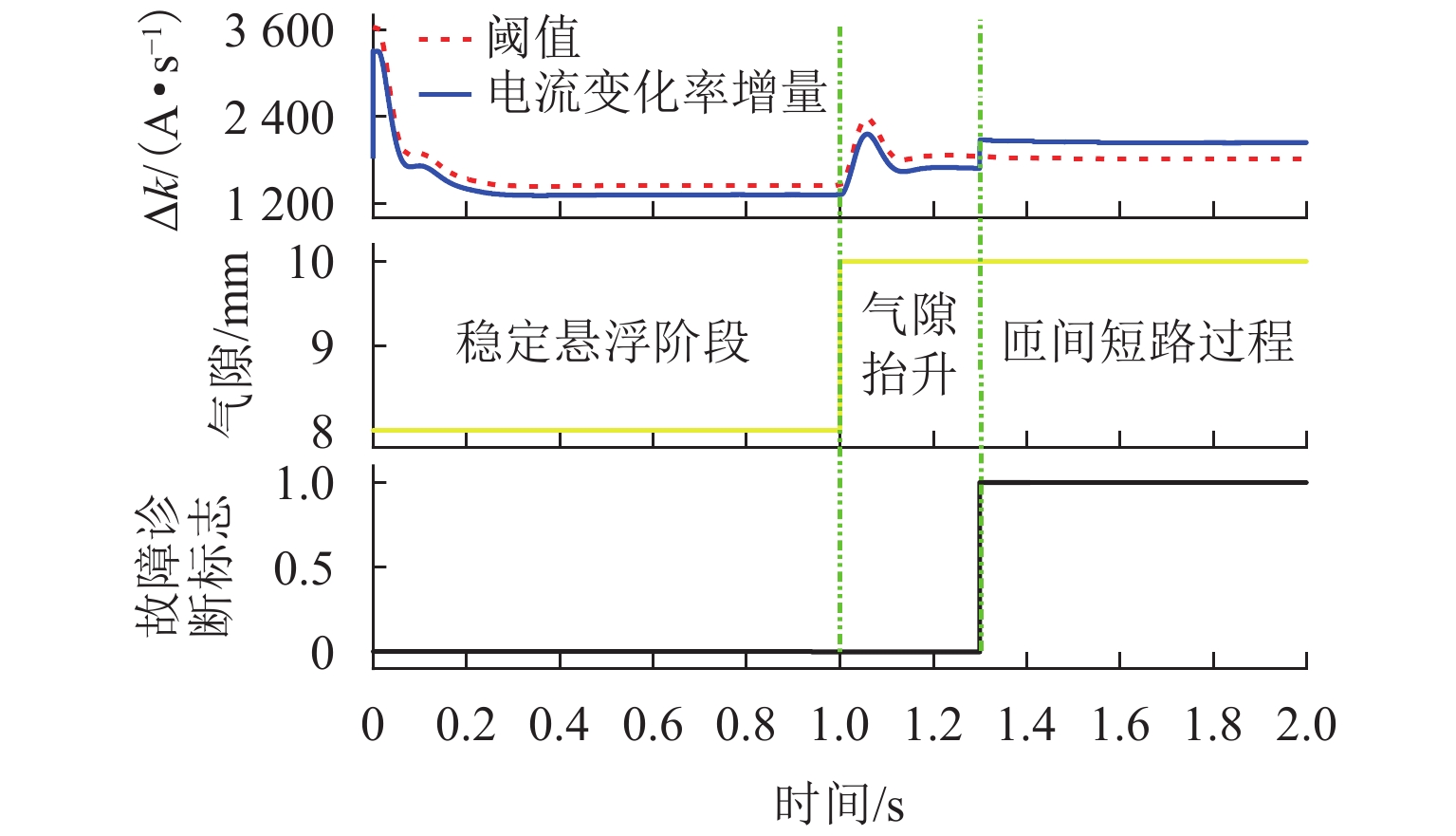
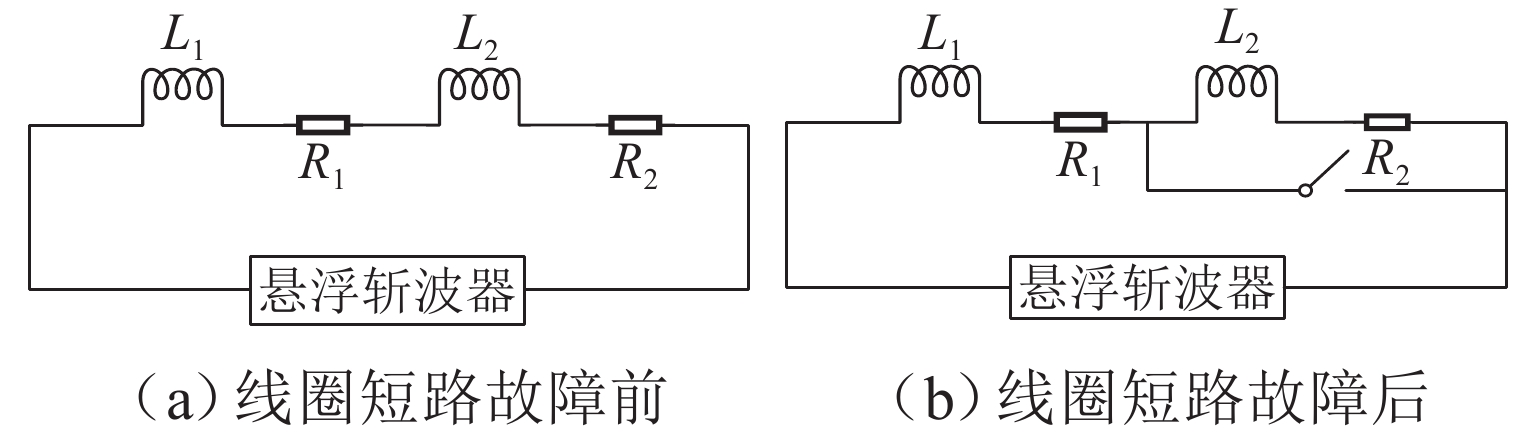
为提高复杂工况下悬浮电磁铁线圈故障诊断的准确性，基于故障前、后电流特性变化，考虑温度、加减载、气隙扰动等因素的影响，提出一种基于周期内电流变化率增量的电磁铁线圈故障诊断方法. 通过建立两电平控制下电磁铁线圈输出电流变化率增量的数学模型，分析得到电流变化特性，明确电磁铁线圈匝间短路是电流变化率增量异常的本质因素，即可通过检测电流变化率增量变化来作为故障判断条件；针对间隙变化导致电流变化率增量改变触发误诊断的问题，采用最小二乘法求解实际间隙与正常状态下电量变化率增量的关系式，建立查找表，从而根据间隙变化来实时调整电流变化率增量阈值. 经过仿真和实验验证：该算法适用于磁浮列车的各种工况，鲁棒性强；在线圈短路比5%时，故障诊断准确率高达97%，灵敏度高；能够在一个基波周期内完成故障诊断，诊断速度快.
- 磁浮列车 /
- 悬浮电磁铁 /
- 电流变化率增量 /
- 故障诊断 /
- 最小二乘法
Abstract:
To improve the accuracy of fault diagnosis for suspended electromagnet coils under complex operating conditions, a fault diagnosis method for electromagnet coils based on the increment of current change rate within a cycle was proposed based on the changes in current characteristics before and after the failure, taking into account the effects of temperature, load variation, and air gap disturbances. By establishing a mathematical model for the increment of the electromagnet coil’s output current change rate under two-level control, the current variation characteristics were analyzed. It was clarified that an interturn short circuit in the electromagnet coil was the fundamental cause of abnormal current change rate increment, making it feasible to use the variation in current change rate increment as a criterion for fault detection. Moreover, to address the issue of false diagnoses triggered by changes in the air gap that affected the current change rate increment, the least squares method was used to derive the relationship between the actual air gap and the current change rate increment under normal conditions. A lookup table was then established to dynamically adjust the threshold of the current change rate increment in real time based on air gap variations. Simulation and experimental results verify that the proposed algorithm is suitable for various operating conditions of maglev trains, demonstrating strong robustness. When the coil’s short circuit ratio is less than 5%, the fault diagnosis accuracy reaches as high as 97%, with high sensitivity. Moreover, the algorithm is capable of completing fault diagnosis within a single fundamental cycle, ensuring rapid detection.
- maglev train /
- suspended electromagnet /
- current change rate increment /
- fault diagnosis /
- least squares method

HTML全文

作为一种新型的轨道交通方式，磁浮列车以悬浮力取代传统的车轮作为支撑，实现了与轨道的非接触^[1-2]. 悬浮系统是列车悬浮的关键子系统，其稳定性和可靠性对列车的运行尤为重要. 然而，开关器件非常高的电流变化率和电压变化率、振动引起线圈与铁芯的摩擦以及工作环境中的温度、湿度等多种因素都可能导致线圈的绝缘失效. 若不及时处理，该故障轻则导致电流控制异常，相应的悬浮点失效，列车减速运行，重则会导致严重的落车事故. 为提高电磁铁线圈运行的可靠性，目前解决方案大多是进行容错控制. 准确有效的故障诊断是实现容错控制的首要条件^[3-7]. 因此，有必要对悬浮电磁铁线圈进行故障诊断算法研究.

选择合适的故障特征以及提取方法对故障诊断至关重要^[8-11]. 文献[12]从量化线圈故障程度的角度出发，提出一种将系统参数变化等效转化为控制输入百分比的方法，可以对线圈故障程度进行评估. 文献[13]考虑A/D转换器的量化误差，采用局部放大算法估算电磁铁的电阻和电感，作为对电磁铁故障的判断. 文献[14]考虑模型非线性、不确定外力干扰和轨道不平顺性，设计一种基于系统辨识理论模型的磁悬浮系统电磁铁线圈故障诊断算法. 文献[15]分析了磁轴承电磁线圈故障对电流斜率的影响，提出一种在线电磁线圈故障诊断方法. 文献[16]提出一种基于数据残差的磁悬浮列车悬挂系统故障诊断方法，将基于模型的故障诊断方法和基于数据的方法相结合，通过模型设计和数据实现，最大限度地发挥模型和数据优势. 文献[17]采用多个传感器对相关故障特征量进行监测，提出一种基于神经网络的执行器/传感器的故障诊断方法.

然而，上述方法存在一些不足：文献[12-15]所提方法对悬浮间隙改变导致线圈参数改变的情况并未考虑，容易造成误诊断；文献[16-17]的诊断方法复杂，需要大量的数据，在线识别困难，成本高. 本文在上述文献的基础上，综合考虑温度变化以及多工况下间隙变化的影响，提出一种基于电流变化率增量的在线故障诊断方法. 该方法更多考虑列车运行的复杂场景对电磁铁线圈参数的影响，提高诊断算法的可靠性以及有效性.

1. 悬浮电磁铁匝间短路特性分析

中低速磁浮列车大多采用U型悬浮电磁铁结构. U型电磁铁主要由铁芯和绕组构成，铁芯中被绕组包裹且产生磁力线的部分为芯柱，未被绕组包裹且只导磁而不产生磁力线的部分为磁轭. 绕组采用矩形截面的漆包线顺接绕制而成，层间走线的连接方式为U型，绕组匝间、层间以及绕组与铁芯间都有绝缘材料填充.

假设磁场均匀分布，不考虑漏磁通和铁芯磁压降的影响，可以得到间隙磁感应强度为

${B_{\mathrm{m}}} = \frac{{{\mu _0}Ni}}{{2{\textit{z}}}} \text{，}$

(1)

式中： ${\mu _0}$ 为空气磁导率， $N$ 为电磁铁线圈匝数， $i$ 为电磁铁线圈电流， ${\textit{z}}$ 为悬浮间隙.

用磁路分析法求得电磁铁线圈等效电感为

$L = \frac{\psi }{i} = \frac{{N{B_{\text{m}}}S}}{i} = \frac{{{\mu _0}{N^2}S}}{{2{\textit{z}}}} \text{，}$

(2)

式中： $\psi$ 为磁链， $S$ 为铁芯磁极面积.

由式（2）可得，在不考虑漏磁通和铁芯磁压降影响的前提下，稳定悬浮时，电磁铁线圈的电感参数与匝数的平方成正比. 当电磁铁线圈发生匝间短路时，电磁铁线圈有效匝数减小，电磁铁线圈的等效电感显著减小，意味着在恒定电压激励下的电磁铁线圈电流特性势必会发生变化. 因此，本文从分析电磁铁线圈匝间短路对线圈电流特性影响出发，提取故障特征，并设计相应的故障诊断策略.

2. 基于周期内电流变化率增量的电磁铁线圈故障诊断

2.1 两电平控制下的电流变化率增量数学模型

中低速磁浮列车大多采用两电平的控制方式. 因此，本文只针对两电平控制下悬浮电磁铁线圈的故障诊断算法进行研究.

当开关管 ${{\text{S}}_1}$ 、 ${{\text{S}}_2}$ 同时导通或关断时，不同开关状态下对应的电路模态如所示^[18]. 图中： $R$ 为电磁铁线圈等效电阻， ${U_{{\mathrm{dc}}}}$ 为直流电源电压， ${{\text{D}}_1}$ 、 ${{\text{D}}_2}$ 为续流二极管. 如（a）所示，电磁铁线圈处于充电状态时， ${{\text{S}}_1}$ 和 ${{\text{S}}_2}$ 导通， ${{\text{D}}_1}$ 和 ${{\text{D}}_2}$ 关断，直流电源 ${U_{{\mathrm{dc}}}}$ 向负载线圈充电. 如（b）所示， ${{\text{S}}_1}$ 和 ${{\text{S}}_2}$ 关断， ${{\text{D}}_1}$ 和 ${{\text{D}}_2}$ 由于电磁铁线圈的大电感作用导致线圈电流不能突变而导通，电磁铁线圈放电.

图 1 正常状态下不同开关状态的电路模态

Figure 1. Circuit modes of different switching states under normal condition

下载: 全尺寸图片幻灯片

在一个开关周期内，根据电路关系，可得微分方程为

$\left\{ {\begin{array}{*{20}{l}} {{U_{{\mathrm{dc}}}} = L\dfrac{{{\mathrm{d}}i}}{{{\mathrm{d}}t}} + Ri + 2{U_{\mathrm{s}}}}, \\ { - {U_{{\mathrm{dc}}}} = L\dfrac{{{\mathrm{d}}i}}{{{\mathrm{d}}t}} + Ri + 2{U_{\mathrm{d}}}}, \end{array}} \right.$

(3)

式中： ${U_{\mathrm{s}}}$ 为开关管导通压降， ${U_{\mathrm{d}}}$ 为续流二极管导通压降.

对式（3）求导可得

$\left\{ {\begin{array}{*{20}{c}} {{k_{{\mathrm{inc}}}} = \dfrac{{{\mathrm{d}}i}}{{{\mathrm{d}}t}} = \dfrac{{{U_{{\mathrm{dc}}}} - 2{U_{\mathrm{s}}}}}{L}{{\mathrm{e}}^{ - {t}/{\tau }}} - \dfrac{{{i_0}}}{\tau }{{\mathrm{e}}^{ - {t}/{\tau }}}}, \\ {{k_{{\mathrm{dec}}}} = \dfrac{{{\mathrm{d}}i}}{{{\mathrm{d}}t}} = - \dfrac{{{U_{{\mathrm{dc}}}} + 2{U_{\mathrm{d}}}}}{L}{{\mathrm{e}}^{ - {t}/{\tau }}} - \dfrac{{{i_{01}}}}{\tau }{{\mathrm{e}}^{ - {t}/{\tau }}}} , \end{array}} \right.$

(4)

式中： ${k_{{\mathrm{inc}}}}$ 、 ${k_{{\mathrm{dec}}}}$ 分别为充、放电电流斜率， ${i_0}$ 为电磁铁线圈充电过程中的起始电流， $\tau$ 为电磁铁线圈的充电时间常数， ${i_{01}}$ 为电磁铁线圈放电过程中的起始电流，t为时间.

考虑到列车长时间的低速行驶、到站静浮以及开关器件极高的电流变化率和电压变化率，电磁铁线圈的温度会剧烈波动，从零摄氏度迅速攀升到几百摄氏度，从而导致电磁铁线圈电阻显著变化^[19].

电磁铁线圈电阻随着温度的上升而增加，其计算式为

${R}_{1}={R}_2\left({k}_{1} + {T}_{1}\right)/\left({k}_{1} + 20\right) \text{，}$

(5)

式中： ${R_1}$ 为测定时线圈平均温度 ${T_1}$ 下的线圈电阻；R₂为20 ℃时线圈的电阻值； ${k_1}$ 为电阻温度常数，铜材时取235.

中低速磁浮列车稳定悬浮时的工作电流较大，导致温度引起的 $Ri$ 变化也较大，无法忽略，电流变化率也出现较大波动. 若将电流变化率作为故障特征量，通过设置阈值进行判别，很可能会产生误诊断，降低故障诊断的准确率. 本文在上述模型基础上，考虑温度改变引起电流变化率的变化对故障诊断准确率的影响，将式（5）代入式（4）可得

$\left\{\begin{array}{l} {k}_{{\mathrm{inc}}}=\dfrac{{U}_{{\mathrm{dc}}}-2{U}_{{\mathrm{s}}}}{L}-\dfrac{{R}_{2}\left({k}_{1} + {T}_{1}\right)/\left({k}_{1} + 20\right)}{L}{i}_{0}, \\ {k}_{{\mathrm{dec}}}=-\dfrac{{U}_{{\mathrm{dc}}} + 2{U}_{{\mathrm{d}}}}{L}-\dfrac{{R}_{2}\left({k}_{1} + {T}_{1}\right)/\left({k}_{1} + 20\right)}{L}{i}_{01}. \end{array}\right.$

(6)

模拟信号的漂移和噪声、电路的增益误差以及间隙的波动都会影响电流变化率识别精度. 充电斜率和放电斜率都是在一个开关周期内计算均值所得，间隔时间很短，可以认为2个量的计算误差相等，并且充、放电电流初值差很小，可忽略. 式（6）中的两式相减得

$\Delta k = {k_{{\mathrm{inc}}}} - {k_{{\mathrm{dec}}}} = \frac{{2{U_{{\mathrm{dc}}}} - 2{U_{\mathrm{s}}} + 2{U_{\mathrm{d}}}}}{L},$

(7)

式中： $\Delta k$ 为电流变化率增量.

由式（7）可知， $\Delta k$ 不受测量噪声、温度和外界因素波动的影响，仅与电磁铁线圈参数有关. 本文通过式（7）来估算电磁铁线圈电流变化率增量的实时变化，从而对电磁铁线圈匝间短路故障进行诊断.

2.2 电磁铁线圈故障诊断算法设计

为提高算法的实时性，对相邻2个采样点之间的斜率求平均值，从而计算充电或者放电电流斜率. 在一个开关周期内，当前时刻采样点斜率可表示为

${k_n} = \frac{{{i_n} - {i_{n - 1}}}}{{{T_{{\mathrm{sample}}}}}} \text{，}$

(8)

式中： ${i_{{n}}}$ 为当前采样时刻n的电流值， $n \in \{ r,d \} , r、d$ 分别为充放电过程的时间长度； ${T_{{\mathrm{sample}}}}$ 为采样周期.

以电磁铁线圈充电过程为例，其 ${k_{{\mathrm{inc}}}}$ 可由式（9）计算^[20].

${k_{{\mathrm{inc}}}} = \frac{{{k_1} + {k_2} + \cdots +{k_{r - 1}} + {k_r}}}{r} .$

(9)

同理可得

${k_{{\mathrm{dec}}}} = \frac{{{k_1} + {k_2} + \cdots +{k_{d - 1}} + {k_d}}}{d} .$

(10)

由式（9）、（10）可以计算故障诊断指标量，即周期内电流变化率增量 $\Delta k$ ，如式（11）所示.

$\Delta k = {k_{{\mathrm{inc}}}} - {k_{{\mathrm{dec}}}}.$

(11)

通过实际采样计算的 $\Delta k$ 与故障预警阈值作比较来判断检测故障^[21-23]. 电磁铁线圈的故障诊断算法流程如所示. 图中： ${k_j}$ 为剔除奇异点后的电流斜率（ $j\leqslant n$ ）. 通过初始化程序完成对相关变量的赋值以及A/D转换器采样模块设置；将A/D转换器采样到的电流进行数字滤波处理，由 $i_n$ 和 $i_ {n - 1}$ 计算 ${k_n}$ . 若 ${k_n}$ 满足有效性原则，则被纳入到电磁铁线圈电流变化率增量计算，否则，被剔除. 最后，根据电流变化率增量与阈值的大小比较结果，判别电磁铁线圈是否存在故障. 若电磁铁线圈电流变化率增量超出阈值范围，则报故障给上位机^[24-25].

图 2 电磁铁线圈故障诊断算法

Figure 2. Electromagnet coil fault diagnosis algorithm

下载: 全尺寸图片幻灯片

2.3 阈值自适应调整

根据电磁铁线圈电感的计算式可知，电磁铁线圈的电感不仅与电磁铁线圈的故障情况有关（发生故障后线圈匝数 $N$ 会发生变化），还与悬浮间隙有关. 悬浮点变化或者处于起浮工况都会导致悬浮间隙的变化，悬浮电磁铁线圈的电感也就随之变化，从而导致电流变化率增量值发生变化. 因此，仅凭一个固定的阈值无法检测所有工况下的故障.

为解决间隙的变化导致电流变化率增量发生改变而触发误诊断的问题，采用离线整定的方法，测量出悬浮间隙与正常电磁铁线圈电流变化率增量的关系，如图3所示.

图 3 正常状态下电流变化率增量拟合曲线

Figure 3. Fitting curve of current change rate increment under normal condition

下载: 全尺寸图片幻灯片

采用最小二乘法拟合，得到 ${\textit{z}}$ 与正常电磁铁线圈电流变化率增量 $\Delta k$ 的关系式为

$\Delta k = 0.02{{\textit{z}}^2} + 164.76{\textit{z}} - 2.29.$

(12)

取正常状态下电流变化率增量的1.1倍作为故障预警阈值 $\Delta \overline k$ ，如式（13）所示.

$\Delta \overline {k} = 1.1 \Delta {{k}}.$

(13)

根据测量出的悬浮间隙与正常线圈电流变化率增量之间的关系，形成一个查找表. 在实时诊断的过程中，可以根据查找表以及实际间隙值来选定阈值，从而提高故障诊断的自适应性和准确性.

3. 仿真与实验验证

3.1 电磁铁线圈故障诊断算法设计

3.1.1 灵敏度测试仿真

早期电磁铁线圈发生匝间短路故障时，故障特征并不明显，极容易被测量噪声淹没. 通过改变线圈的匝数来模拟短路比不同时的情形，来对比分析采用电流斜率和电流变化率增量方法在不同情况下的灵敏度.

所示为电磁铁线圈不同匝间短路比下的故障指标量变化结果. 从图中可见：采用电流斜率作为故障特征量，当匝间短路比分别为5%、10%和20%时，其 $\Delta k$ 分别为609、685、884 A/s；相比之下，采用电流变化率增量作为故障特征量，其值分别为1463、1629、2063 A/s；相同匝间短路比下，采用电流变化率增量作为故障特征量的变化更加明显，其特征更不容易被淹没在测量噪声中. 因此，采用电流变化率增量作为故障特征量的故障诊断方法对电磁铁线圈早期微弱故障的检测能力更强，灵敏度更高.

图 4 不同短路比下故障特征对比曲线

Figure 4. Fault characteristic comparison curves under different short circuit ratios

下载: 全尺寸图片幻灯片

短路比1%～100%变化并添加测量白噪声，进行100次仿真试验，得到不同方法下的故障诊断结果，如所示. 从表中可以看出，采用 $\Delta k$ 的故障诊断方法要优于采用电流斜率的方法. 其主要原因是采用电流斜率的故障诊断方法在列车起浮、气隙扰动以及线圈温度变化过程中容易发生误诊断，与式（6）分析一致. 而本文所提方法（式（7））不受这些因素影响，所以故障诊断准确率高.

表 1 诊断性能对比

Table 1. Comparison of diagnosis performance %

诊断方法	准确诊断率	误报率	漏诊率
电流斜率	90	2	8
Δk	97	1	2

下载: 导出CSV

| 显示表格

3.1.2 匝间短路故障

为模拟电磁铁线圈发生匝间短路情形，在1.3 s时改变电磁铁线圈的匝数，匝间短路比为5%. 图5（a）为测到的电磁铁线圈匝间短路仿真波形. 图5（b）为故障前、后的局部放大对比.

图 5 匝间短路故障仿真波形

Figure 5. Simulation waveforms of interturn short circuit fault

下载: 全尺寸图片幻灯片

根据图5（b）可以得出，匝间短路前、后，电磁铁线圈电流纹波发生显著变化，起浮过程中，间隙会发生变化，悬浮电磁铁的等效电感值也会随之改变. 通过式（12）、（13）设置电流变化率增量的阈值，实现阈值的动态自适应调整，如图6、7的红色虚线所示；通过式（11）实时计算电流变化率增量的数值，如图6、7的蓝实线所示. 根据图6仿真结果可知，本文所提的故障诊断算法可以很好地解决起浮过程中间隙变化所带来的误诊断问题，并且也可以在1.3 s发生匝间短路时快速地诊断该故障.

图 6 电磁铁匝间短路故障仿真结果

Figure 6. Simulation results of electromagnet’s interturn short circuit fault

下载: 全尺寸图片幻灯片

图 7 电磁铁线圈匝间短路加载仿真

Figure 7. Simulation of electromagnet coil’s interturn short circuit loading

下载: 全尺寸图片幻灯片

3.1.3 负载变化

为研究荷载量变化是否影响电磁铁线圈故障诊断结果，进行如下验证. 在0.8 s加载50%并在1.3 s时发生匝间短路（短路比5%）（结果如图7）. 从图7可知：当负载发生变化时，电流值会发生变化，导致间隙发生波动，从而电流变化率增量发生波动，但此时由于间隙变化，阈值也随之调整，不报故障；当再次趋于稳定时，悬浮间隙不变，为8 mm，由式（7）可知，电流变化率增量不发生变化；在1.3 s时发生匝间短路，由于匝数的变化导致电磁铁线圈的电感减小，电磁铁线圈电流变化率增量数值增大，超过阈值，触发报警. 从故障预警结果可知，所提出的故障诊断算法可以适应磁浮列车荷载量频繁变化的情况.

3.1.4 温度变化

由前面分析可知，电磁铁线圈的工作环境比较复杂，自身温度变化比较大，由温度变化引起的电阻值变化也就较大. 由电流变化率公式可知，电阻变化势必导致电流变化率大小发生较大波动，如果采用电流变化率作为故障判别指标就容易造成误诊断. 而本文所提出的故障诊断算法可以很好地适应电磁铁线圈的工作环境，仿真结果如图8所示. 在0.8 s时，温度由室温20 ℃陡增到180 ℃，电磁铁线圈的电阻由于温度的变化导致自身电阻值由2.000 Ω变为3.255 Ω，电流变化率增量几乎不发生改变，与前面的分析基本吻合，电流变化率增量不受线圈温度变化影响；在1.3 s时发生匝间短路，电阻值略有减小，此时电磁铁线圈的电感值发生极大变化，从而导致电流变化率增量发生改变，超出预警阈值触发报警.

图 8 电磁铁线圈匝间短路温度变化仿真

Figure 8. Simulation of temperature change during electromagnet coil’s interturn short circuit

下载: 全尺寸图片幻灯片

3.1.5 间隙扰动

在1.0 s时稳定悬浮间隙由8 mm变为10 mm，仿真结果如图9所示.

图 9 电磁铁线圈匝间短路间隙扰动仿真

Figure 9. Simulation of air gap disturbance during electromagnet coil’s interturn short circuit

下载: 全尺寸图片幻灯片

间隙的变化会导致电磁铁线圈的等效电感发生改变，从而导致电流变化率的增量发生变化. 通过间隙值实时调整电流变化率增量阈值，该故障诊断算法不报故障；当发生匝间短路时，其可以很快地检出故障.

3.2 实验验证

本文搭建的故障诊断实验平台如图10所示.

图 10 基于Cspace悬浮控制单元故障诊断实验平台

Figure 10. Fault diagnosis experiment platform based on CSpace suspension control unit

下载: 全尺寸图片幻灯片

在电磁线圈故障诊断中，线圈正常时合上开关，模拟线圈局部短路故障. 原理如所示. 中： ${L_1}$ 、 ${R_1}$ 分别为未发生故障电磁铁线圈的等效电阻和等效电感， ${L_2}$ 、 ${R_2}$ 为发生故障电磁铁线圈的等效电阻和等效电感.

图 11 线圈短路故障模拟

Figure 11. Short circuit fault simulation of coil

下载: 全尺寸图片幻灯片

线圈发生局部短路时，故障前、后的电流变化波形如图12所示. 从图中可以看出，当线圈发生匝间短路故障时，电流纹波明显增大，只需要70 µs左右的时间就可快速检出线圈的匝间短路故障.

图 12 电磁铁线圈匝间短路实验波形

Figure 12. Interturn short circuit test waveforms of electromagnet coil

下载: 全尺寸图片幻灯片

4. 结　论

本文建立了基于电流变化率增量的电磁铁线圈故障诊断模型. 针对间隙变化影响电流变化率增量的问题，采用最小二乘法求解悬浮间隙与正常状态下电量变化率增量的关系式，根据间隙变化实时调整电流变化率增量的阈值，从而避免误诊断，提高诊断的准确率. 最后，在各种工况下进行仿真和实验验证，结论如下：

1）根据间隙实时调整周期内电流变化率增量的阈值，提高了诊断算法对复杂工况的抗干扰能力.

2）在短路比5%时就可以检出电磁铁线圈匝间短路故障，灵敏度高.

3）故障后大约一个基波周期内就可以实现故障预警，诊断速度快，不受温度等因素的影响，自适应性强.

致谢：国家重点实验室基金项目（Q110422Q02003）

图 1 正常状态下不同开关状态的电路模态

Figure 1. Circuit modes of different switching states under normal condition

下载: 全尺寸图片幻灯片

图 2 电磁铁线圈故障诊断算法

Figure 2. Electromagnet coil fault diagnosis algorithm

下载: 全尺寸图片幻灯片

图 3 正常状态下电流变化率增量拟合曲线

Figure 3. Fitting curve of current change rate increment under normal condition

下载: 全尺寸图片幻灯片

图 4 不同短路比下故障特征对比曲线

Figure 4. Fault characteristic comparison curves under different short circuit ratios

下载: 全尺寸图片幻灯片

图 5 匝间短路故障仿真波形

Figure 5. Simulation waveforms of interturn short circuit fault

下载: 全尺寸图片幻灯片

图 6 电磁铁匝间短路故障仿真结果

Figure 6. Simulation results of electromagnet’s interturn short circuit fault

下载: 全尺寸图片幻灯片

图 7 电磁铁线圈匝间短路加载仿真

Figure 7. Simulation of electromagnet coil’s interturn short circuit loading

下载: 全尺寸图片幻灯片

图 8 电磁铁线圈匝间短路温度变化仿真

Figure 8. Simulation of temperature change during electromagnet coil’s interturn short circuit

下载: 全尺寸图片幻灯片

图 9 电磁铁线圈匝间短路间隙扰动仿真

Figure 9. Simulation of air gap disturbance during electromagnet coil’s interturn short circuit

下载: 全尺寸图片幻灯片

图 10 基于Cspace悬浮控制单元故障诊断实验平台

Figure 10. Fault diagnosis experiment platform based on CSpace suspension control unit

下载: 全尺寸图片幻灯片

图 11 线圈短路故障模拟

Figure 11. Short circuit fault simulation of coil

下载: 全尺寸图片幻灯片

图 12 电磁铁线圈匝间短路实验波形

Figure 12. Interturn short circuit test waveforms of electromagnet coil

下载: 全尺寸图片幻灯片

表 1 诊断性能对比

Table 1. Comparison of diagnosis performance %

诊断方法准确诊断率误报率漏诊率

电流斜率 90 2 8

Δk 97 1 2

下载: 导出CSV

参考文献(25)

[1]	KWONG R H, YONGE-MALLO D L. Fault diagnosis in discrete-event systems: incomplete models and learning[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2011, 41(1): 118-130. doi: 10.1109/TSMCB.2010.2047257
[2]	LEI Y G, JIA F, LIN J, et al. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3137-3147. doi: 10.1109/TIE.2016.2519325
[3]	BOBTSOV A A, PYRKIN A A, ORTEGA R S, et al. A state observer for sensorless control of magnetic levitation systems[J]. Automatica, 2018, 97: 263-270. doi: 10.1016/j.automatica.2018.08.004
[4]	高彩霞,冯凌云,党建军. 基于双级PNN的直驱永磁同步电机匝间短路故障诊断方法[J]. 河南理工大学学报(自然科学版),2025,44(2): 116-127. GAO Caixia, FENG Lingyun, DANG Jianjun. Interturn short circuit fault diagnosis method of direct-drive permanent magnet synchronous motor based on two-stage PNN[J]. Journal of Henan Polytechnic University (Natural Science), 2025, 44(2): 116-127.
[5]	吴振宇,王慧,胡存刚,等. 基于多路漏磁信号阵列的无刷直流电机匝间短路故障诊断[J]. 电工技术学报,2025,40(4): 1105-1116. WU Zhenyu, WANG Hui, HU Cungang, et al. Turn-to-turn short circuit fault diagnosis of brushless DC motor based on multiple magnetic flux leakage signal arrays[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1105-1116.
[6]	阚超豪,姚骁键,齐安康,等. 三相异步电机匝间短路故障的诊断方法[J]. 电气传动,2024,54(11): 76-80. KAN Chaohao, YAO Xiaojian, QI Ankang, et al. Diagnosis method of inter-turn short circuit fault of three-phase induction motor[J]. Electric Drive, 2024, 54(11): 76-80.
[7]	段汝鹏. 双三相永磁同步电机匝间短路故障诊断与容错控制研究[D]. 杭州:浙江大学,2024.
[8]	THIBEAULT N M, SMITH R S. Magnetic bearing measurement configurations and associated robustness and performance limitations[J]. Journal of Dynamic Systems, Measurement, and Control, 2002, 124(4): 589-598. doi: 10.1115/1.1514671
[9]	VISCHER D, BLEULER H. Self-sensing active magnetic levitation[J]. IEEE Transactions on Magnetics, 1993, 29(2): 1276-1281. doi: 10.1109/20.250632
[10]	TANG M, ZHU C S. New method of position estimation for self-sensing active magnetic bearings based on artificial neural network[C]//2010 International Conference on Electrical and Control Engineering. Wuhan: IEEE, 2010: 1355-1358.
[11]	TABREZ M, BAKHSH F I, HASSAN M, et al. A comparative simulation study of different sensorless permanent magnet synchronous motor drives using neural network and fuzzy logic[J]. Journal of Intelligent & Fuzzy Systems, 2018, 35(5): 5177-5184.
[12]	LONG Z Q, LI Y, HE G. Research on electromagnet fault diagnosis technology of suspension control system of maglev train[J]. Control and Decision, 2010, 25(7): 1004-1009.
[13]	WANG P, LONG Z Q, XU Y S. Component-level fault detection for suspension system of maglev trains based on autocorrelation length and stable kernel representation[J]. IEEE Transactions on Vehicular Technology, 2021, 70(8): 7594-7604. doi: 10.1109/TVT.2021.3096732
[14]	LI H H, WU L J, SU Z Z, et al. Detection of inter-turn short circuit fault of active magnetic bearing based on least mean square algorithm[C]//2021 24th International Conference on Electrical Machines and Systems (ICEMS). Gyeongju: IEEE, 2021: 1049-1053.
[15]	CHENG X, CHENG B X, LU M Q, et al. An online fault-diagnosis of electromagnetic actuator based on variation characteristics of load current[J]. Automatika, 2020, 61(1): 11-20. doi: 10.1080/00051144.2019.1654652
[16]	王志强. 高速磁浮列车悬浮系统故障诊断与容错控制研究[D]. 长沙:国防科技大学,2019.
[17]	YETENDJE A, SERON M M, DE DONÁ J A. Multisensor fusion fault-tolerant control of a magnetic levitation system[C]//18th Mediterranean Conference on Control and Automation, MED10. Marrakech: IEEE, 2010: 1055-1060.
[18]	梁达,张昆仑,肖嵩. 考虑电流振铃特性的悬浮电磁铁等效电路模型[J]. 西南交通大学学报,2022,57(3): 588-596. doi: 10.3969/j.issn.0258-2724.20210886 LIANG Da, ZHANG Kunlun, XIAO Song. Equivalent circuit model of suspension electromagnet with current ringing characteristics[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 588-596. doi: 10.3969/j.issn.0258-2724.20210886
[19]	孙超,张昆仑. 基于遗传算法的悬浮电磁铁磁热耦合参数优化[J]. 电气工程学报,2024,19(2): 344-352. SUN Chao, ZHANG Kunlun. Optimization of magnetothermal coupling parameters of suspension electromagnet based on genetic algorithm[J]. Journal of Electrical Engineering, 2024, 19(2): 344-352.
[20]	朱瑞雨,崔江. 一种航空发电机电枢绕组匝间短路故障诊断技术[J]. 电机与控制应用,2025,52(1): 22-35. doi: 10.12177/emca.2024.147 ZHU Ruiyu, CUI Jiang. A fault diagnosis technique for armature winding inter-turn short circuit in aerospace generators[J]. Electric Machines & Control Application, 2025, 52(1): 22-35. doi: 10.12177/emca.2024.147
[21]	马杰,都业林,金涛,等. 动车组牵引电机匝间短路故障诊断方法研究[J]. 铁道机车车辆,2025,45(1): 144-151. doi: 10.3969/j.issn.1008-7842.2025.01.20 MA Jie, DU Yelin, JIN Tao, et al. Research on fault diagnosis method for EMU traction motor inter-turn short circuit fault[J]. Railway Locomotive & Car, 2025, 45(1): 144-151. doi: 10.3969/j.issn.1008-7842.2025.01.20
[22]	王雅宁. 基于反电动势残差的永磁同步电机匝间短路故障检测与定位[D]. 西安:西安理工大学,2024.
[23]	LUO P E, YIN Z G, ZHANG Z, et al. Diversified diagnosis strategy for PMSM inter-turn short-circuit fault via novel sliding mode observer[J]. IEEE Transactions on Power Electronics, 2024, 39(4): 4149-4159. doi: 10.1109/TPEL.2024.3352077
[24]	NIU G, DONG X, CHEN Y J. Motor fault diagnostics based on current signatures: a review[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 3520919.1-3520919.19.
[25]	刘君,李中祥,李堃,等. 变压器绕组短路故障多特征融合诊断[J]. 湖南大学学报(自然科学版),2023,50(4): 210-216. LIU Jun, LI Zhongxiang, LI Kun, et al. Multi-feature fusion detection method for interturn short-circuit faults of transformers[J]. Journal of Hunan University (Natural Sciences), 2023, 50(4): 210-216.