Adaptive Terminal Sliding Mode Control Strategy for Electromagnetic Levitation System Based on Disturbance Compensation
-
摘要:
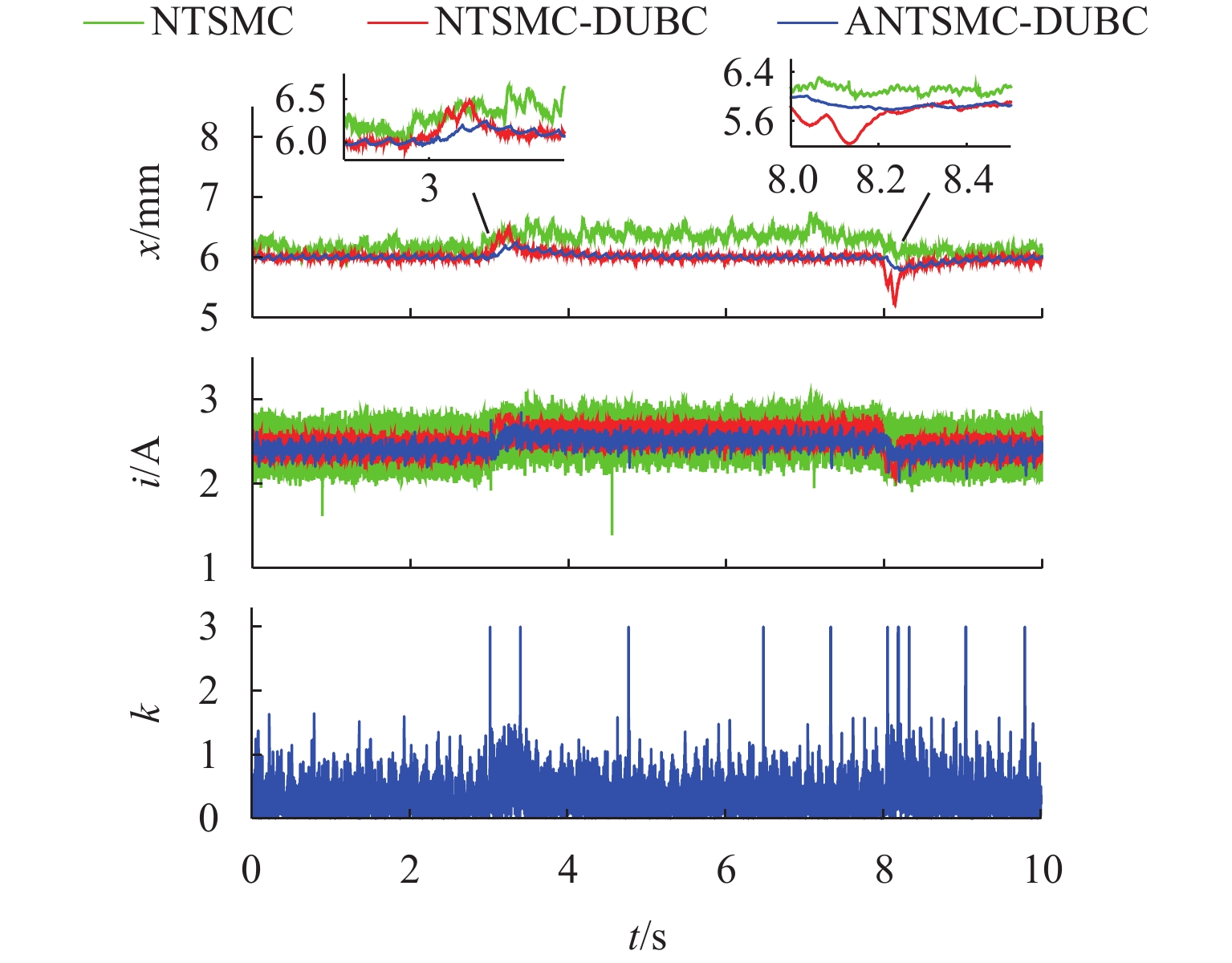
为提高电磁悬浮系统抗干扰能力,提出一种基于扰动上界补偿的自适应非奇异终端滑模控制(ANTSMC-DUBC)策略. 该策略采用基于扰动上界补偿的非奇异终端滑模控制(NTSMC-DUBC)加快系统状态的收敛速度并避免奇异性, 到达控制律中的扰动补偿项能够抑制集总扰动,从而选择更小的开关增益来减小抖振;设计一种可随滑模函数状态自适应变化的开关增益,在保证系统动态性能的同时提高系统的稳态性能和扰动补偿效率;理论推导证明了所设计的悬浮控制器满足李雅普诺夫稳定性判据. 实验结果表明:所提出的ANTSMC-DUBC控制器在信号跟随、抗干扰和加减载实验中表现出良好的稳态性能和动态性能,并在面对系统内外扰动时具有出色的抗干扰能力;相较于NTSMC,ANTSMC-DUBC面对等效外力干扰时间隙波动小于0.21 mm,系统均方根误差和时间乘积绝对值误差分别降低56.26%和57.57%;进行1.5 kg加减载时最大间隙波动为0.22 mm,没有稳态误差.
Abstract:To improve the anti-disturbance capability of the electromagnetic levitation system, an adaptive nonsingular terminal sliding mode control based on disturbance upper bound compensation (ANTSMC-DUBC) was proposed. The strategy used nonsingular terminal sliding mode control based on disturbance upper bound compensation (NTSMC-DUBC) to speed up the convergence of the system state and avoid singularity. The disturbance compensation term in the reaching control law can suppress the lumped disturbance, so that a smaller switching gain can be selected to reduce chattering. A switching gain that can adaptively change with the state of the sliding mode function was designed to ensure the dynamic performance of the system while improving the steady state performance and the efficiency of disturbance compensation. The theoretical derivation proved that the designed levitation controller satisfied the Lyapunov stability criterion. The experimental results show that the proposed ANTSMC-DUBC controller exhibits good steady state and dynamic performance in signal tracking, anti-disturbance, and load variation tests, and demonstrates excellent anti-disturbance when facing internal and external disturbances in the system. Compared with that of NTSMC, the gap fluctuation of ANTSMC-DUBC is less than 0.21 mm under the equivalent external disturbance, and the system root mean square error and time-weighted absolute error are reduced by 56.26% and 57.57%, respectively. The maximum gap fluctuation is 0.22 mm with no steady state error when the 1.5 kg load variation is performed.
-
表 2 悬浮控制器参数
Table 2. Parameters of levitation controllers
参数 NTSMC NTSMC-DUBC ANTSMC-DUBC a0 2420 2420 2420 b0 −6.05 −6.05 −6.05 β 25 25 25 p/q 19/13 19/13 19/13 k 3 1.5 μ 1000 1000 l 3 c 2000 ϕ 0.001 表 1 电磁悬浮系统参数
Table 1. Parameters of electromagnetic levitation system
参数 数值 悬浮质量/kg 4.43 电磁铁线圈匝数/匝 525 电磁铁磁极面积/mm2 3144.2 平衡点悬浮间隙/mm 6 平衡点线圈电流/A 2.4 电磁铁线圈电阻/Ω 2 电磁铁线圈电感/mH 91 表 3 实验性能比较
Table 3. Experimental performance comparison
实验 指标 NTSMC NTSMC-DUBC ANTSMC-
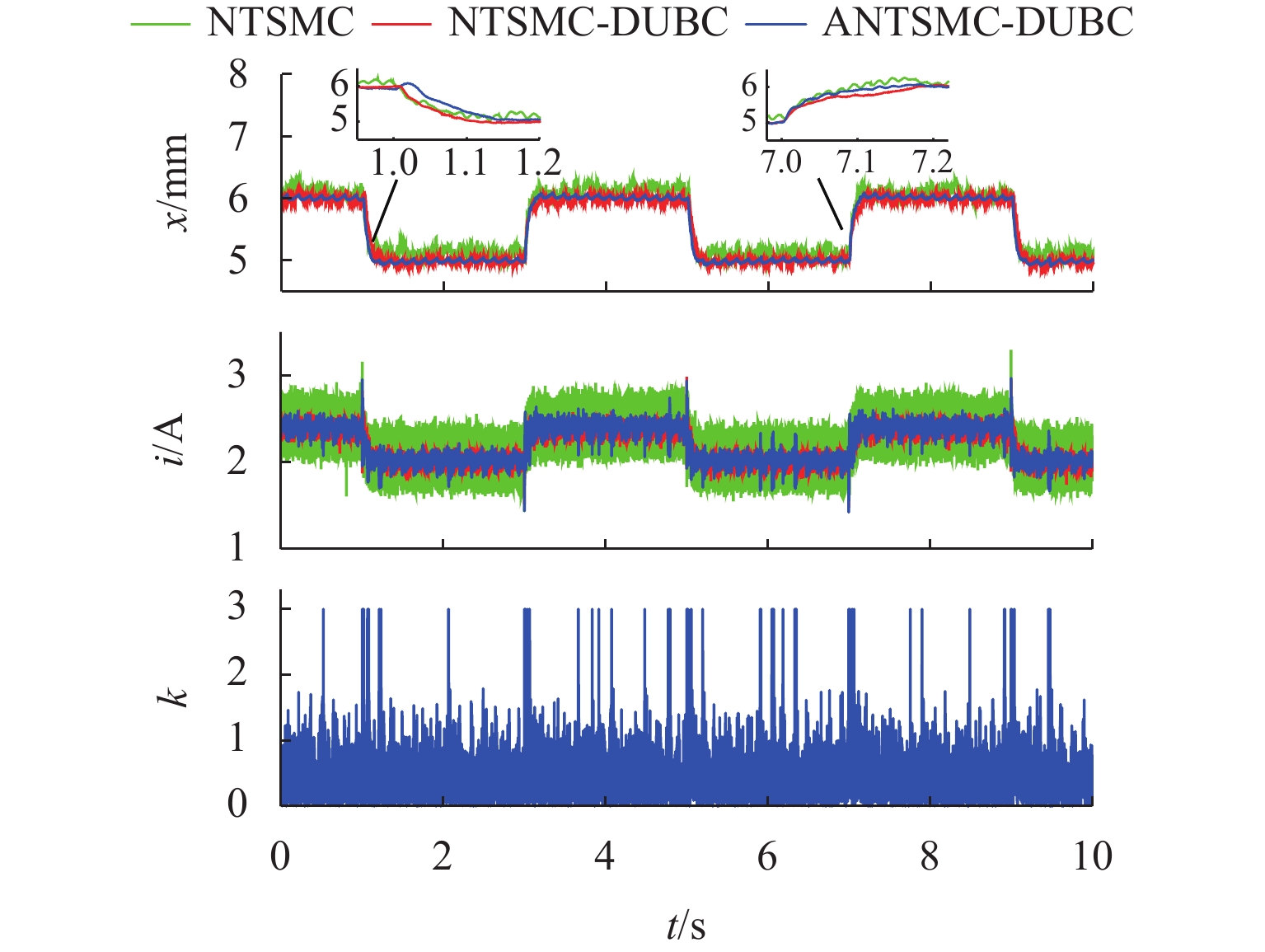
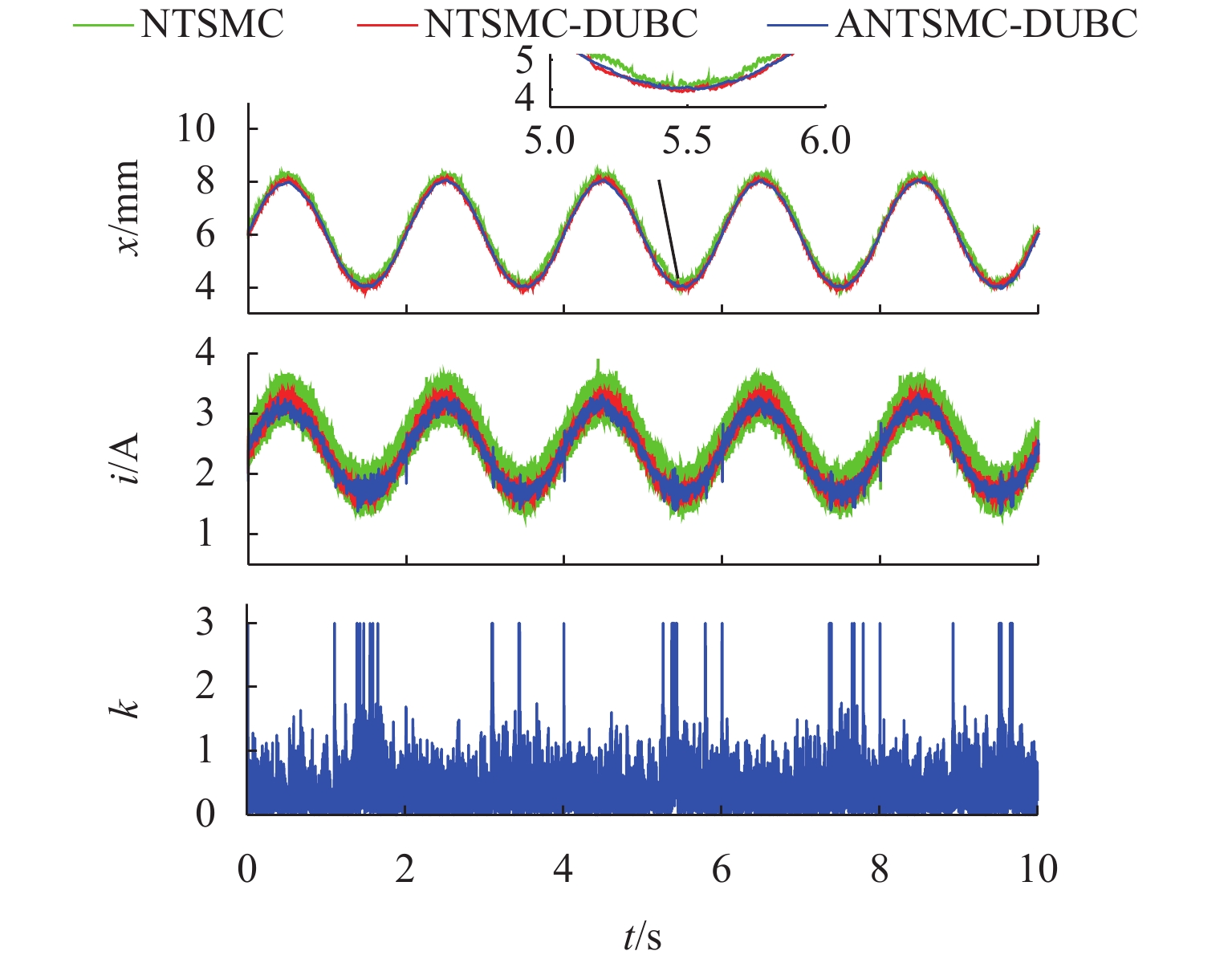
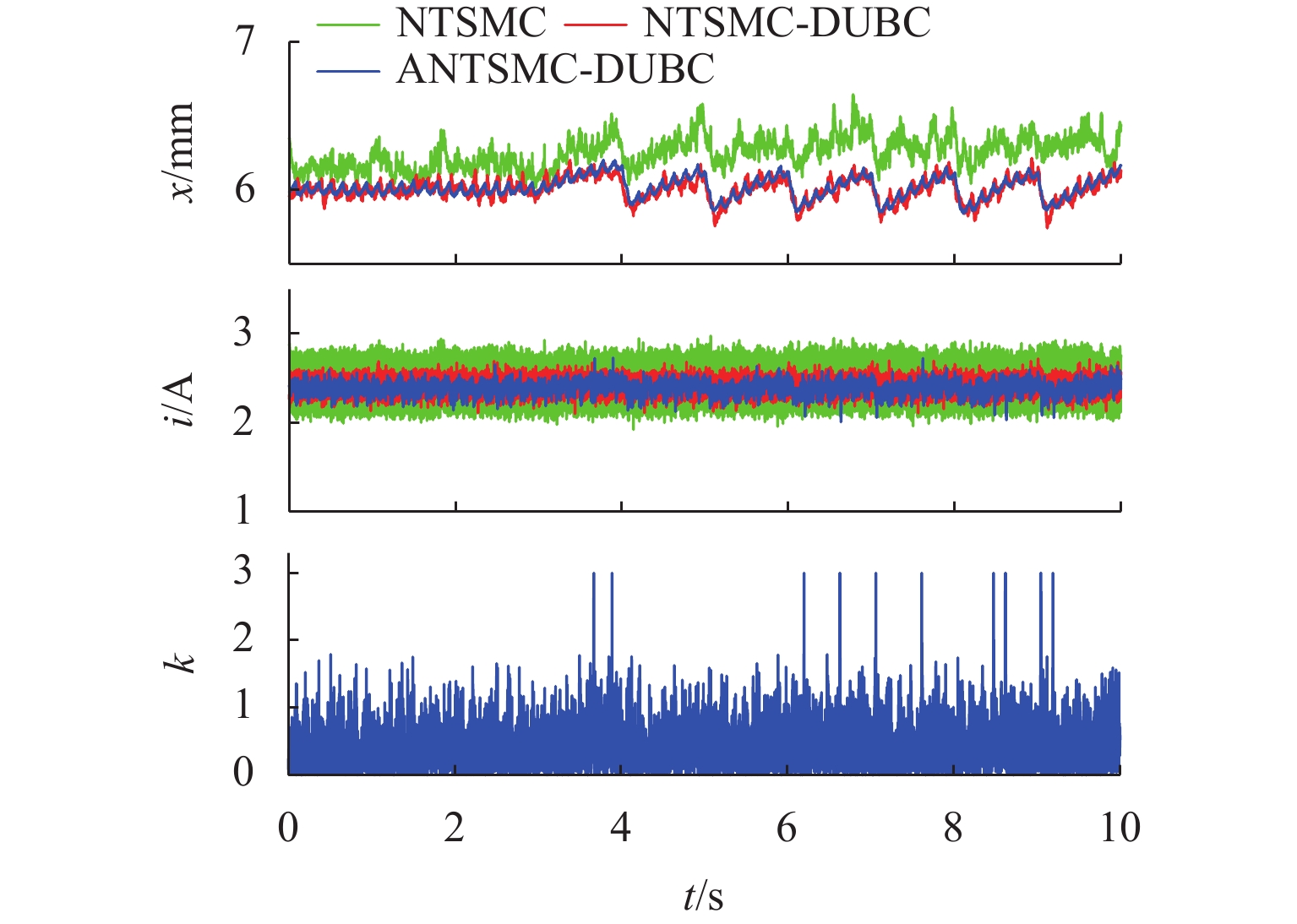
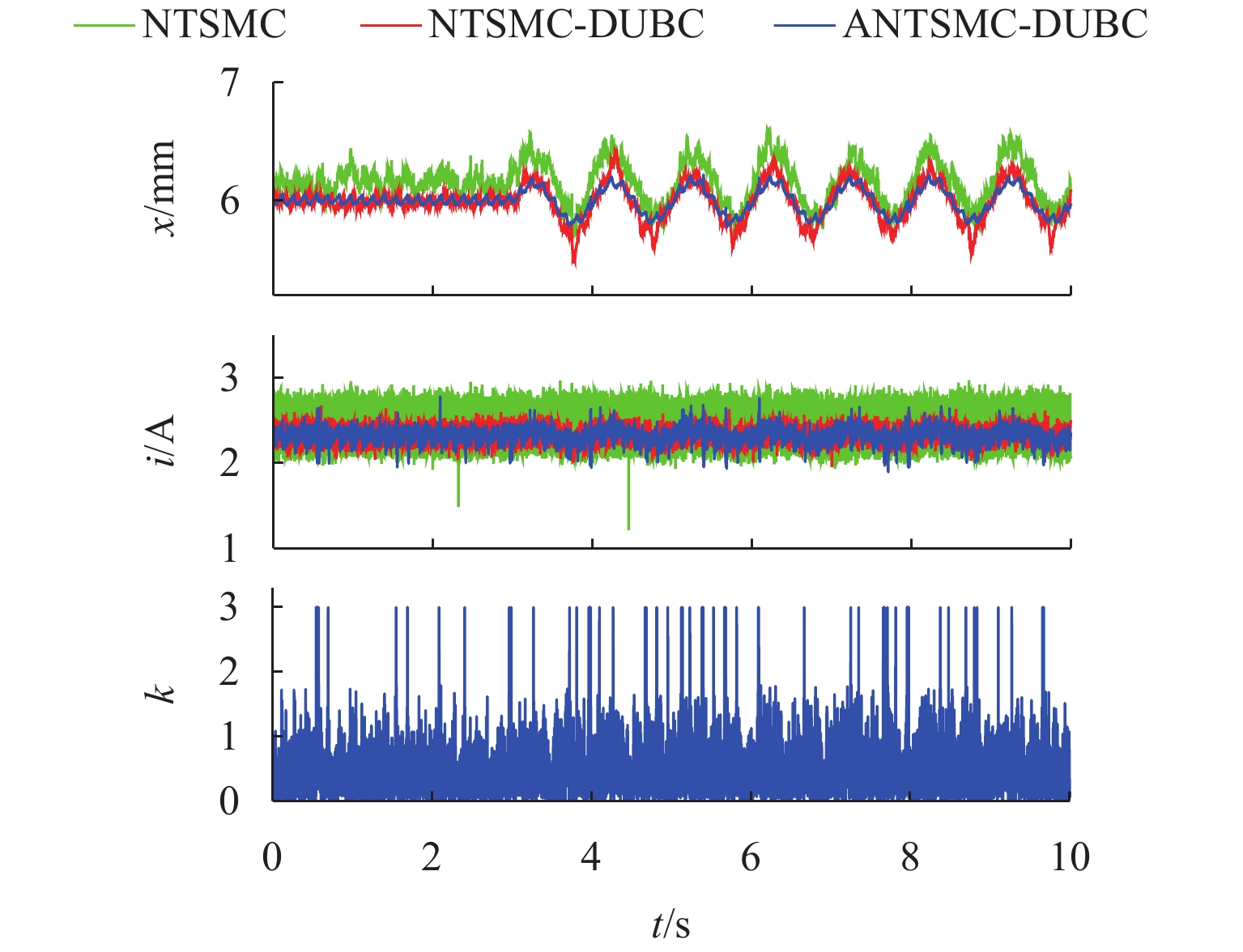
DUBC方波跟随 eRMSE 0.1767 0.1505 0.1141 eITAE 13.1130 6.7114 4.2928 正弦波跟随 eRMSE 0.2212 0.0930 0.0622 eITAE 20.0883 7.7549 5.0415 锯齿波干扰 eRMSE 0.2721 0.0775 0.0717 eITAE 25.0468 6.2254 5.6861 正弦波干扰 eRMSE 0.2302 0.1546 0.1007 eITAE 19.1406 11.7254 8.1219 加减载实验 eRMSE 0.3018 0.1043 0.0609 eITAE 26.3091 5.5048 4.0449 -
[1] 朱进权, 葛琼璇, 张波, 等. 考虑悬浮系统影响的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2022, 37(12): 3087-3096.Zhu Jinquan, Ge Qiongxuan, Zhang Bo, et al. Traction control strategy of high-speed maglev considering the influence of suspension system[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3087-3096. [2] 袁野, 施天宇, 孙玉坤, 等. 12/14磁悬浮开关磁阻电机悬浮系统解耦控制策略[J]. 中国电机工程学报, 2023, 43(23): 9310-9319. doi: 10.13334/j.0258-8013.pcsee.221678Yuan Ye, Shi Tianyu, Sun Yukun, et al. Decoupling control of suspension system for 12/14 bearingless switched reluctance motor[J]. Proceedings of the CSEE, 2023, 43(23): 9310-9319. doi: 10.13334/j.0258-8013.pcsee.221678 [3] 刘程子, 奚志胜, 杨艳, 等. 一种应用于磁悬浮轴承的具有容错功能的多桥臂开关功放电路[J]. 中国电机工程学报, 2023, 43(17): 6828-6840. doi: 10.13334/j.0258-8013.pcsee.220920Liu Chengzi, Xi Zhisheng, Yang Yan, et al. Utility model relates to a fault-tolerant multi-leg switch power amplifier circuit applied to magnetic bearing[J]. Proceedings of the CSEE, 2023, 43(17): 6828-6840. doi: 10.13334/j.0258-8013.pcsee.220920 [4] Zhang T, Le Q Y, Zhu W G. Structure and suspension force analysis of six-pole five degrees of freedom AC hybrid magnetic bearing[J]. IEEE Transactions on Magnetics, 2021, 57(6): 8001404. [5] Sun Y G, Xu J Q, Qiang H Y, et al. Adaptive neural-fuzzy robust position control scheme for maglev train systems with experimental verification[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8589-8599. doi: 10.1109/TIE.2019.2891409 [6] 陈萍, 史天成, 于明月, 等. 基于模型参考自适应的自学习悬浮控制策略[J]. 西南交通大学学报, 2023, 58(4): 799-807.Chen Ping, Shi Tiancheng, Yu Mingyue, et al. Self-learning model reference adaptive levitation control strategy[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 799-807. [7] 王浩, 黄翠翠, 丁明强, 等. 基于非线性最小方差的磁浮列车悬浮系统性能评估[J]. 铁道科学与工程学报, 2025, 22(6): 2457-2466. doi: 10.19713/j.cnki.43-1423/u.T20241304Wang Hao, Huang Cuicui, Ding Mingqiang, et al. Performance evaluation of maglev train suspension system based on nonlinear minimum variance[J]. Journal of Railway Science and Engineering, 2025, 22(6): 2457-2466. doi: 10.19713/j.cnki.43-1423/u.T20241304 [8] 翟明达, 张博, 李晓龙, 等. 基于模糊PID控制的准零刚度磁悬浮隔振平台的设计与实现[J]. 西南交通大学学报, 2023, 58(4): 886-895. doi: 10.3969/j.issn.0258-2724.20220880Zhai Mingda, Zhang Bo, Li Xiaolong, et al. Design and implementation of magnetic suspension vibration isolation platform with quasi-zero stiffness based on fuzzy PID control[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 886-895. doi: 10.3969/j.issn.0258-2724.20220880 [9] 杨杰, 杨星, 高涛, 等. 电磁悬浮系统的改进线性自抗扰控制方法[J]. 电机与控制学报, 2024, 28(1): 131-141.Yang Jie, Yang Xing, Gao Tao, et al. Improved linear active disturbance rejection control method for electromagnetic levitation system[J]. Electric Machines and Control, 2024, 28(1): 131-141. [10] 林俊亭, 陈信州. 基于高增益扰动观测器的磁悬浮球系统滑模控制[J]. 北京航空航天大学学报, 2025, 51(6): 1897-1906. doi: 10.13700/j.bh.1001-5965.2024.0518Lin Junting, Chen Xinzhou. Sliding mode control of magnetic levitation ball systems based on a high-gain disturbance observer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2025, 51(6): 1897-1906. doi: 10.13700/j.bh.1001-5965.2024.0518 [11] 曹学谦, 葛琼璇, 朱进权, 等. 基于积分滑模的高速磁悬浮列车谐波电流抑制策略[J]. 电工技术学报, 2022, 37(22): 5817-5825, 5861.Cao Xueqian, Ge Qiongxuan, Zhu Jinquan, et al. Harmonic current suppression strategy for high-speed maglev train based on integral sliding mode[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5817-5825,5861. [12] Fu D X, Zhao X M, Zhu J G. A novel robust super-twisting nonsingular terminal sliding mode controller for permanent magnet linear synchronous motors[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 2936-2945. doi: 10.1109/TPEL.2021.3119029 [13] Hou S X, Wang C, Chu Y D, et al. Neural-observer-based terminal sliding mode control: design and application[J]. IEEE Transactions on Fuzzy Systems, 2022, 30(11): 4800-4814. doi: 10.1109/TFUZZ.2022.3160614 [14] Wang J X, Zhao L, Yu L. Adaptive terminal sliding mode control for magnetic levitation systems with enhanced disturbance compensation[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 756-766. doi: 10.1109/TIE.2020.2975487 [15] 张文静, 阮玉鑫, 高亚苹, 等. 中速磁悬浮列车的滑模周期自适应学习控制方法[J]. 交通运输工程学报, 2023, 23(2): 264-272.Zhang Wenjing, Ruan Yuxin, Gao Yaping, et al. Sliding mode periodic adaptive learning control method for medium-speed maglev trains[J]. Journal of Traffic and Transportation Engineering, 2023, 23(2): 264-272. [16] Kang J S, Huang X Y, Xia C, et al. Ultralocal model-free adaptive supertwisting nonsingular terminal sliding mode control for magnetic levitation system[J]. IEEE Transactions on Industrial Electronics, 2024, 71(5): 5187-5194. doi: 10.1109/TIE.2023.3285925 [17] 雷城, 蓝益鹏, 孙云鹏. 直线同步电动机磁悬浮系统的模糊分数阶滑模控制[J]. 电机与控制学报, 2022, 26(3): 94-100.Lei Cheng, Lan Yipeng, Sun Yunpeng. Fuzzy fractional sliding mode control of magnetic levitation system of linear synchronous motors[J]. Electric Machines and Control, 2022, 26(3): 94-100. [18] 许贤泽, 宋明星, 龚勇兴, 等. 基于扰动补偿的磁悬浮转台分数阶滑模控制[J]. 西南交通大学学报, 2024, 59(4): 766-775. doi: 10.3969/j.issn.0258-2724.20230412Xu Xianze, Song Mingxing, Gong Yongxing, et al. Fractional-order sliding mode control for maglev rotary table based on disturbance compensation[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 766-775. doi: 10.3969/j.issn.0258-2724.20230412 [19] 魏静波, 罗浩, 关子津. 基于干扰观测器的磁悬浮球系统全局快速终端滑模控制[J]. 西南交通大学学报, 2023, 58(4): 836-844.Wei Jingbo, Luo Hao, Guan Zijin. Global fast terminal sliding mode control for maglev ball system based on disturbance observer[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 836-844. [20] 张艳, 王丽梅, 方馨. 基于三阶超螺旋扰动观测器的PMLSM全局自适应滑模控制[J]. 电机与控制学报, 2024, 28(6): 76-86. doi: 10.15938/j.emc.2024.06.008Zhang Yan, Wang Limei, Fang Xin. Global adaptive sliding mode control for PMLSM based on third-order super-twisting disturbance observer[J]. Electric Machines and Control, 2024, 28(6): 76-86. doi: 10.15938/j.emc.2024.06.008 [21] Wang J X, Rong J Y, Yang J. Adaptive fixed-time position precision control for magnetic levitation systems[J]. IEEE Transactions on Automation Science and Engineering, 2023, 20(1): 458-469. doi: 10.1109/TASE.2022.3156943 [22] Huang X Y, Kang J S, Ding H, et al. Adjacent cross-coupling control for magnetic levitation system with ultra-local sliding mode algorithm[J]. IEEE Transactions on Vehicular Technology, 2025, 74(2): 2418-2428. doi: 10.1109/TVT.2024.3472221 [23] Chen C, Xu J Q, Lin G B, et al. Sliding mode bifurcation control based on acceleration feedback correction adaptive compensation for maglev train suspension system with time-varying disturbance[J]. IEEE Transactions on Transportation Electrification, 2022, 8(2): 2273-2287. doi: 10.1109/TTE.2022.3144518 [24] 徐园平, 袁高展, 周瑾, 等. 基于电磁感应的抗磁悬浮倾角传感器[J]. 仪器仪表学报, 2024, 45(12): 63-73. doi: 10.19650/j.cnki.cjsi.J2413282Xu Yuanping, Yuan Gaozhan, Zhou Jin, et al. Diamagnetic levitation inclinometer based on electromagnetic induction[J]. Chinese Journal of Scientific Instrument, 2024, 45(12): 63-73. doi: 10.19650/j.cnki.cjsi.J2413282 [25] Wang J X, Yu L. Adaptive resonant-EIDO-based optimized position precision control for magnetic levitation system[J]. IEEE Transactions on Industrial Electronics, 2023, 70(5): 5013-5023. doi: 10.1109/TIE.2022.3186348 -




 下载:
下载: