Size Effect Model for Red-Bed Soft Rock Based on Machine Learning Algorithm
-
摘要:
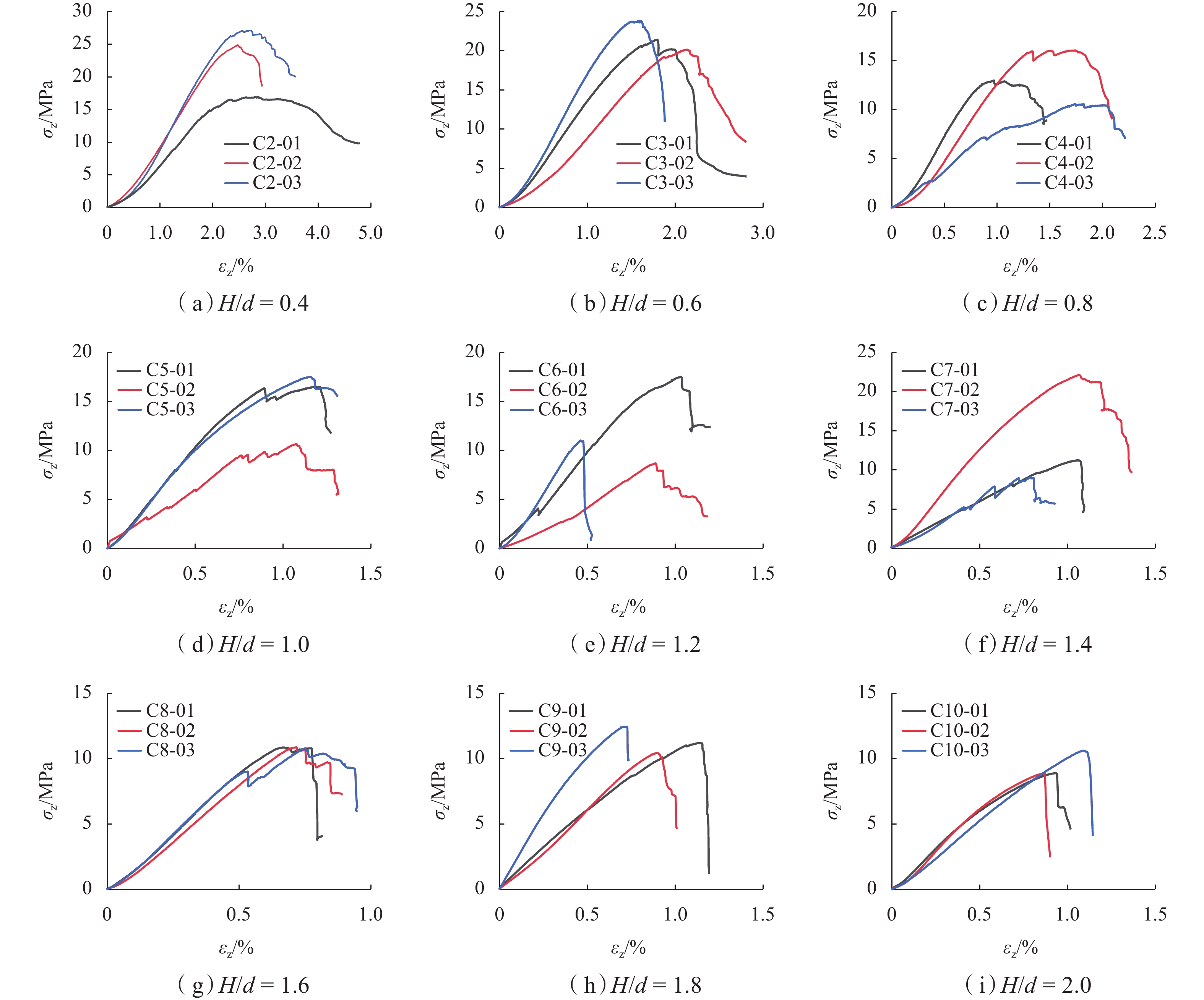
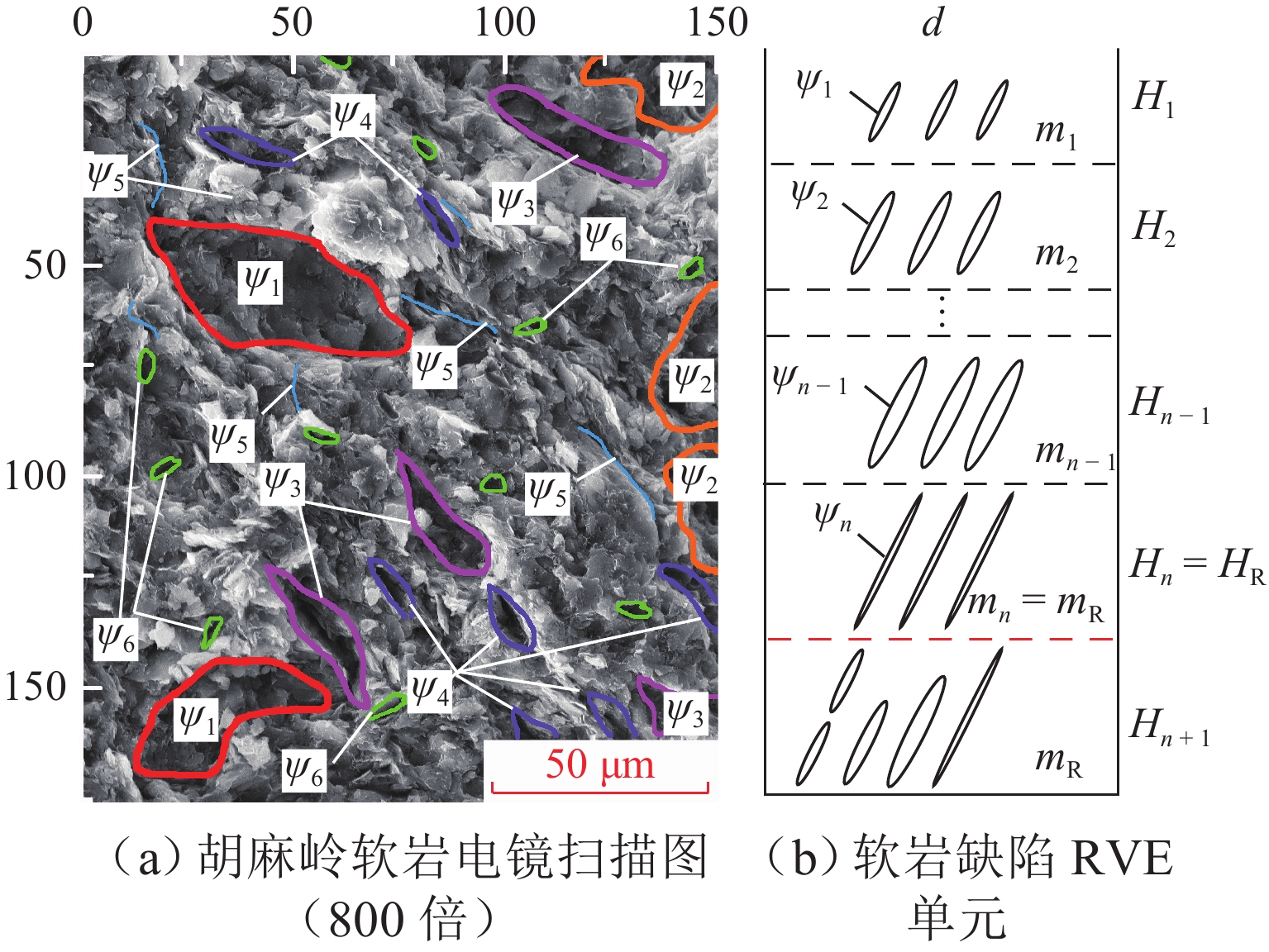
构建精准的尺寸效应预测模型对使用室内试验单元强度设计大尺度构件结构具有重要的工程意义. 对不同高径比红层软岩试样进行无侧限单轴压缩试验,并评价现有尺寸效应模型对本文数据的可靠性;提出参数离散度,定义为每组试样的多个力学特征参数变异系数的均值,对试验结果的离散性进行分析;采用决策树回归、支持向量回归、多层感知机、随机森林回归、极限梯度提升回归5种机器学习模型预测不同尺寸红层软岩及其他岩类的单轴抗压强度,并引入SHAP (shapley additive explanations)方法揭示特征对预测结果的影响及贡献. 结果表明:随着试样高径比的降低,单轴抗压强度
σ P、峰值轴应变ε P均逐渐增加,应力-应变曲线会由脆性向延性模式转换;胡麻岭红层软岩很难适应现有基于硬质岩提出的尺寸效应模型;高径比对试样离散度影响显著,离散度会随高径比增加先增加后迅速降低;极限梯度提升回归模型对红层软岩抗压强度的预测精度最高,测试集R 2为0.989,多层感知机模型能够预测非标准尺寸煤岩、贫矿、大理岩的峰值应力,误差小于20%;岩石的微观排列更致密会导致模型预测值较真实值偏低;弹性模量权重过高会使模型高估目标值.Abstract:Objective Red-bed soft rock is highly susceptible to softening, swelling, and disintegration upon water exposure and exhibits pronounced rheological behavior, which often leads to structural deformation and failure in engineering constructions. The rock has attracted widespread attention in geotechnical research. The mechanical properties of rocks are significantly influenced by sample size and geometry, yet existing size effect models are typically tailored to specific rock types. Therefore, establishing a unified size effect model and understanding the influence of size on the mechanical behavior of red-bed soft rocks are of considerable significance.
Method A series of unconfined uniaxial compression tests was conducted on red-bed soft rock specimens with varying height-to-diameter ratios (
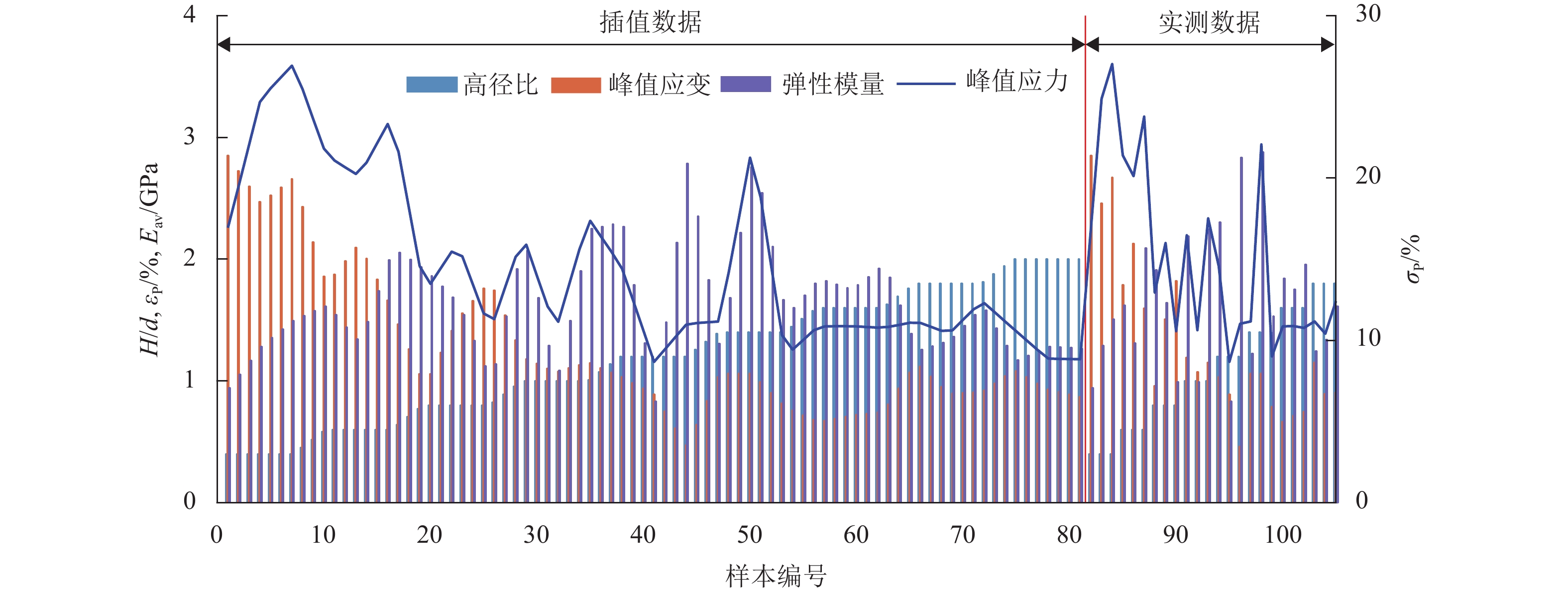
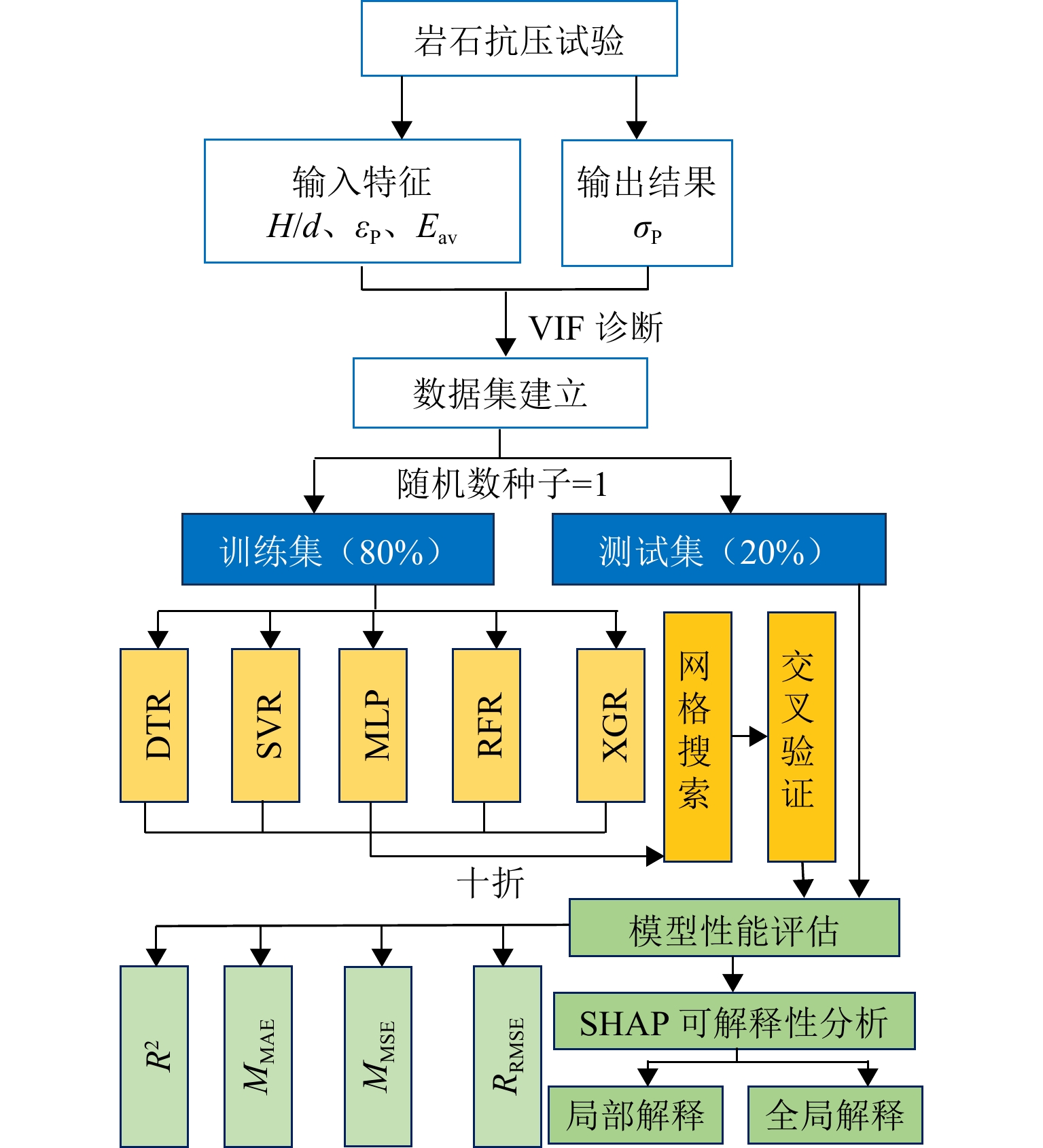
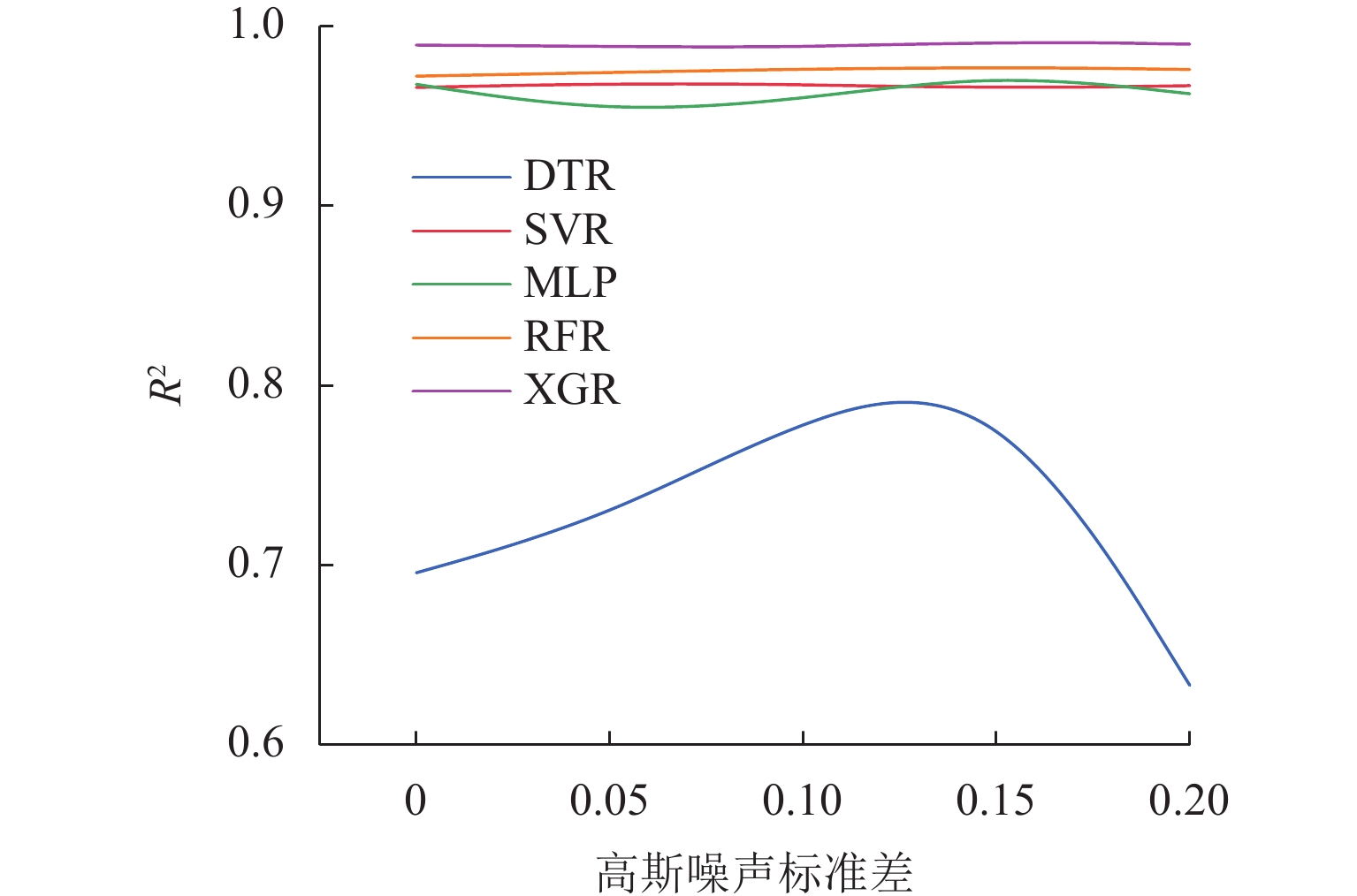
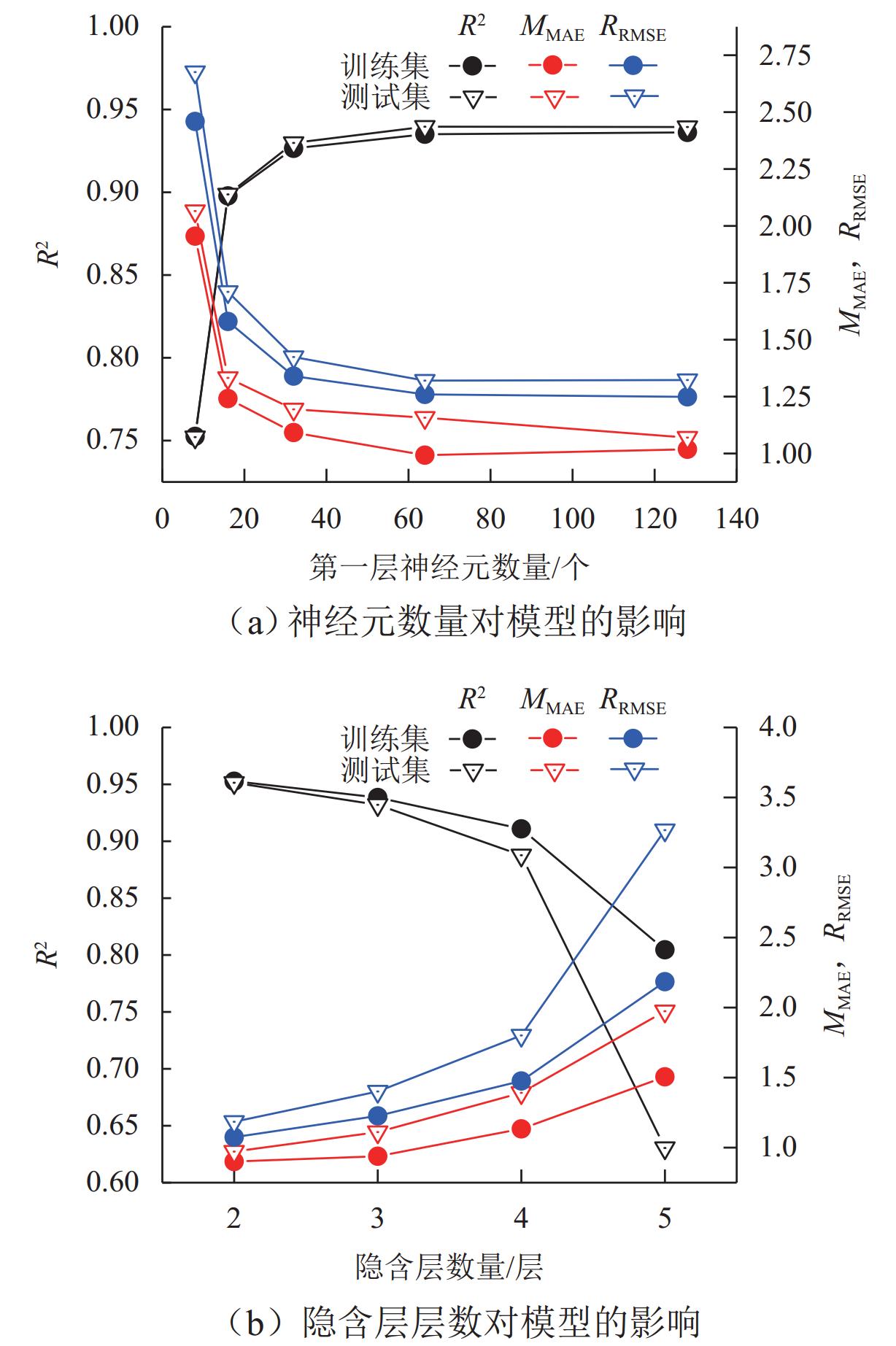
H/d ) to investigate their peak stress (σ P), peak axial strain (ε P), and average elastic modulus (E av). The dispersion of mechanical parameters under differentH/d ratios was analyzed using a dispersion parameter defined as the mean coefficient of variation across these key mechanical properties. Subsequently, five machine learning algorithms, decision tree regression (DTR), support vector regression (SVR), multilayer perceptron (MLP), random forest regression (RFR), and extreme gradient boosting regression (XGR), were employed to model the size effect of red-bed soft rocks. The original dataset was expanded through linear interpolation, and the influence of Gaussian noise of varying intensities was investigated. The hyperparameters of DTR, SVR, RFR, and XGR were determined through grid search, and the network structure of MLP was determined through manual tuning, while model robustness was evaluated using 10-fold cross-validation. Performance metrics on both training and test datasets were reported. In addition, a global interpretability analysis of the optimal XGR model was conducted using Shapley additive explanations (SHAP) to rank feature importance and perform local interpretations on three representative actual test samples (H/d = 0.40, 1.00, and 2.00). To assess model generalizability, the trained models were used to predict the uniaxial compressive strength of rock types with non-standard sizes.Result As the
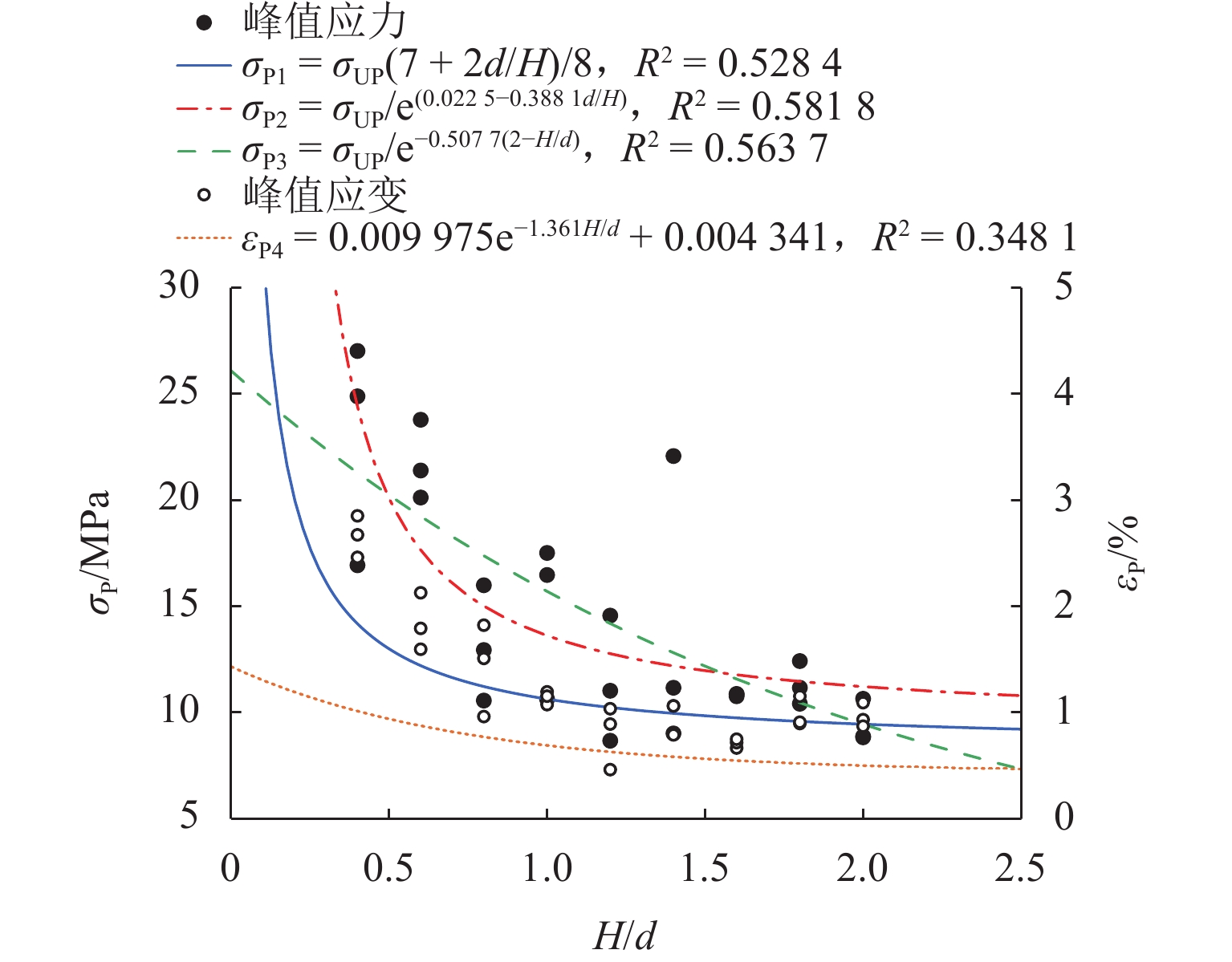
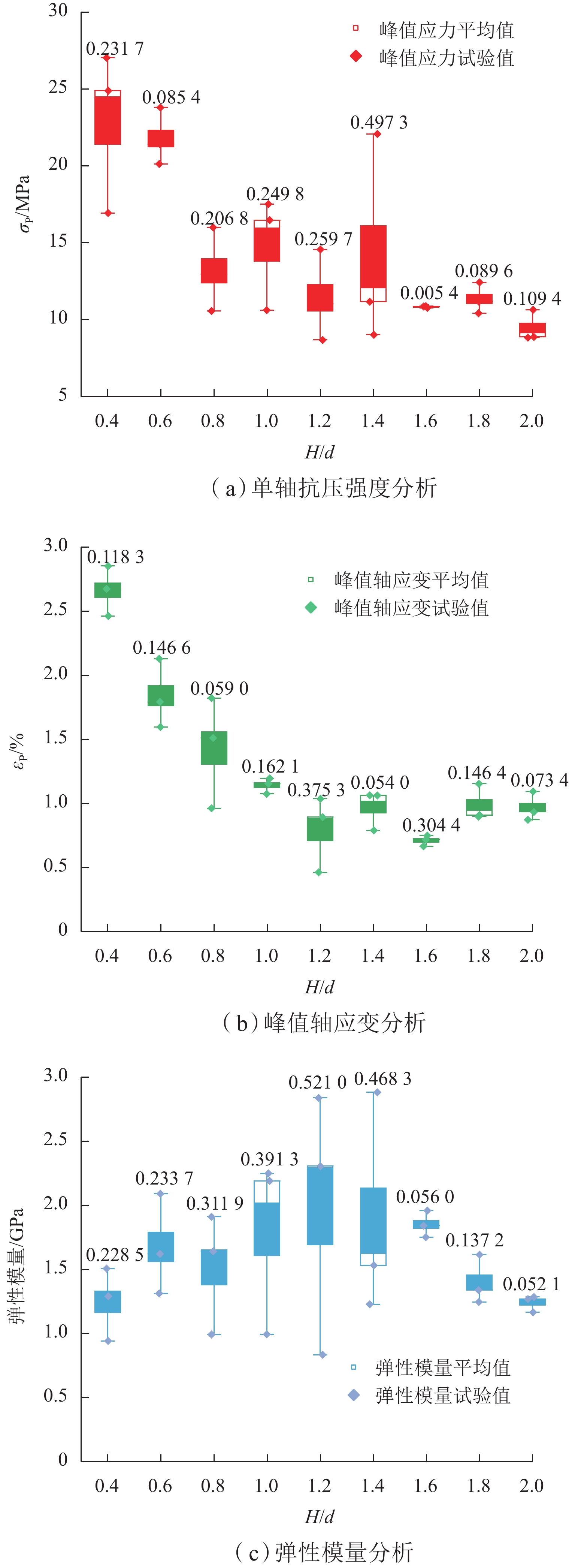
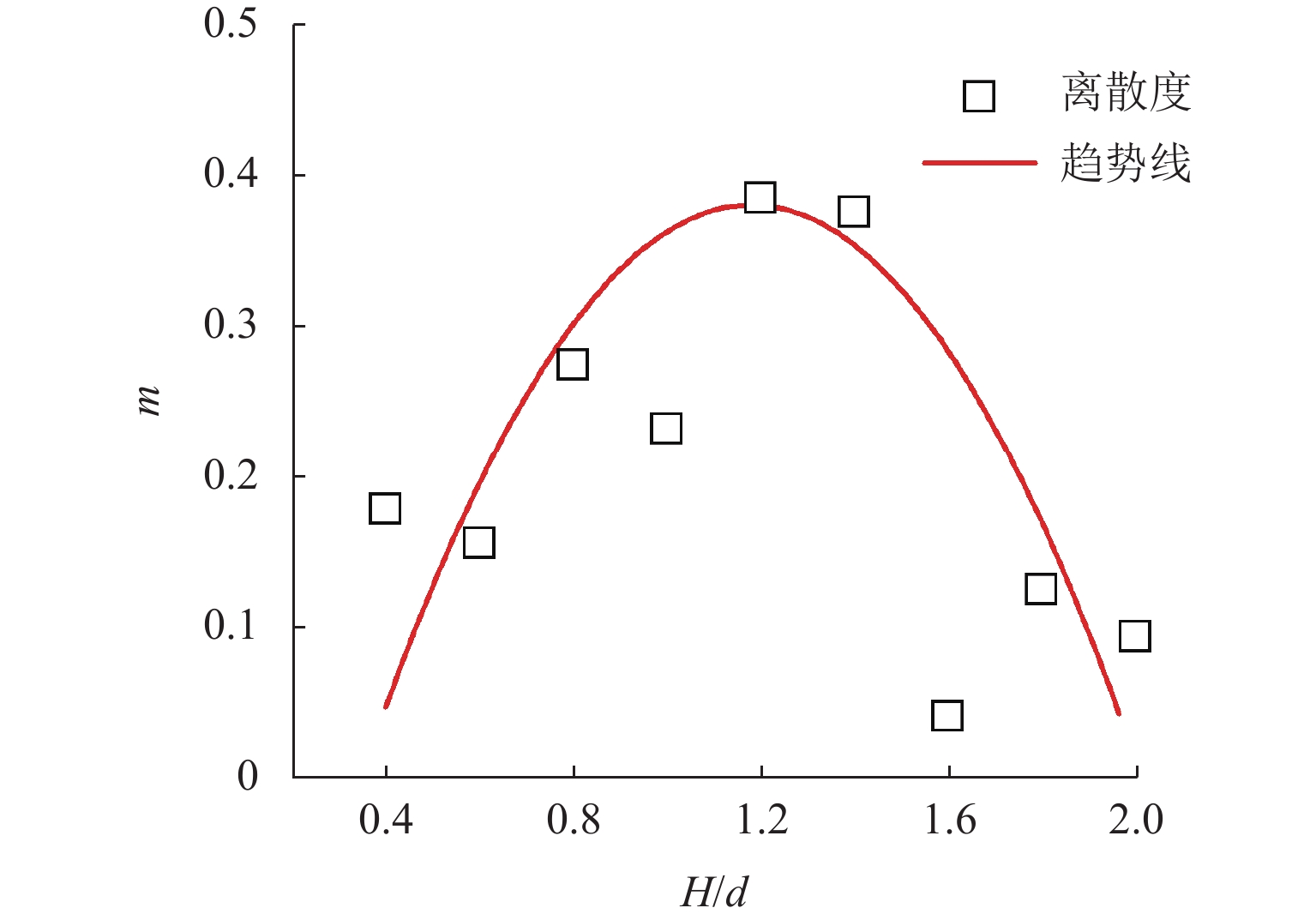
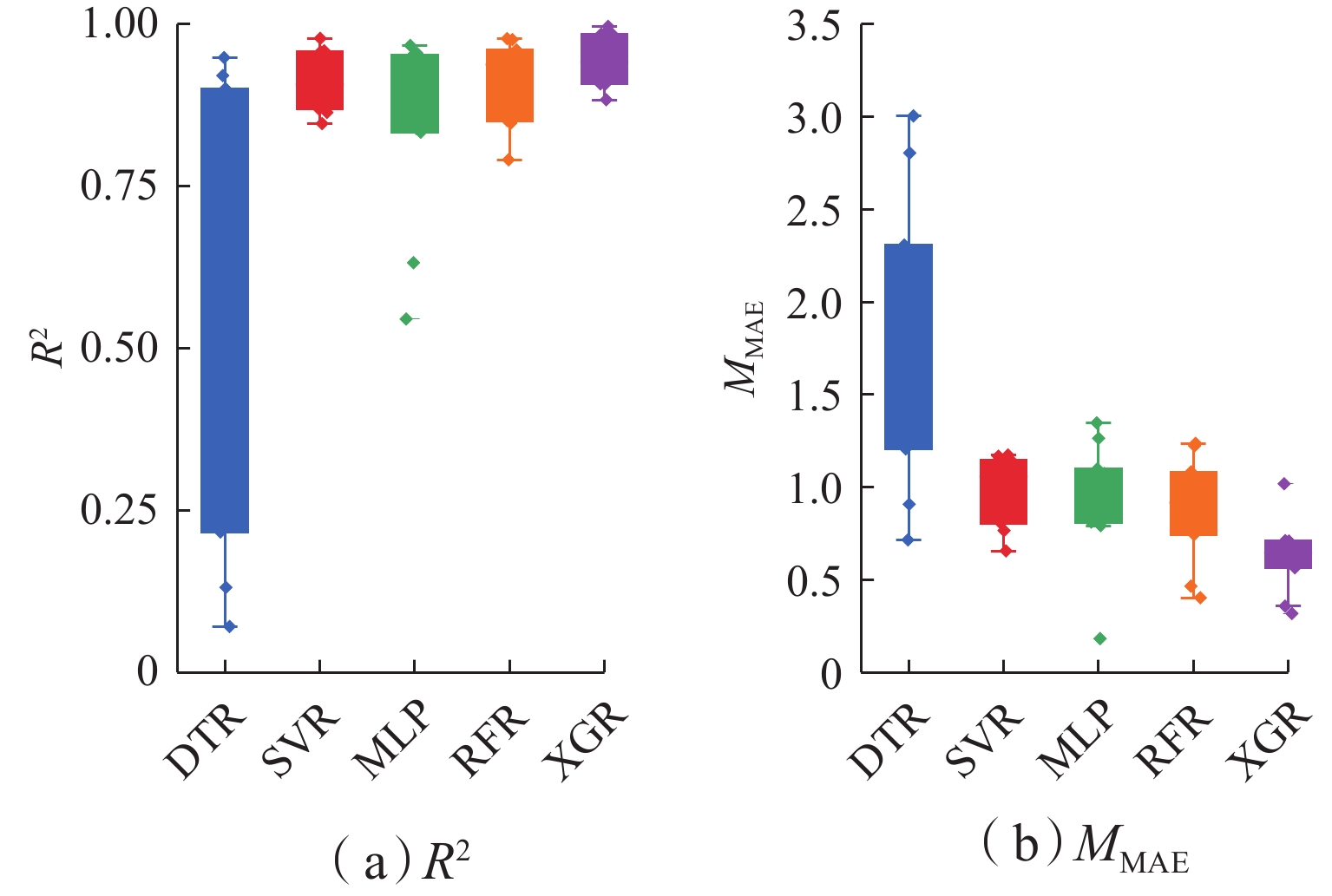
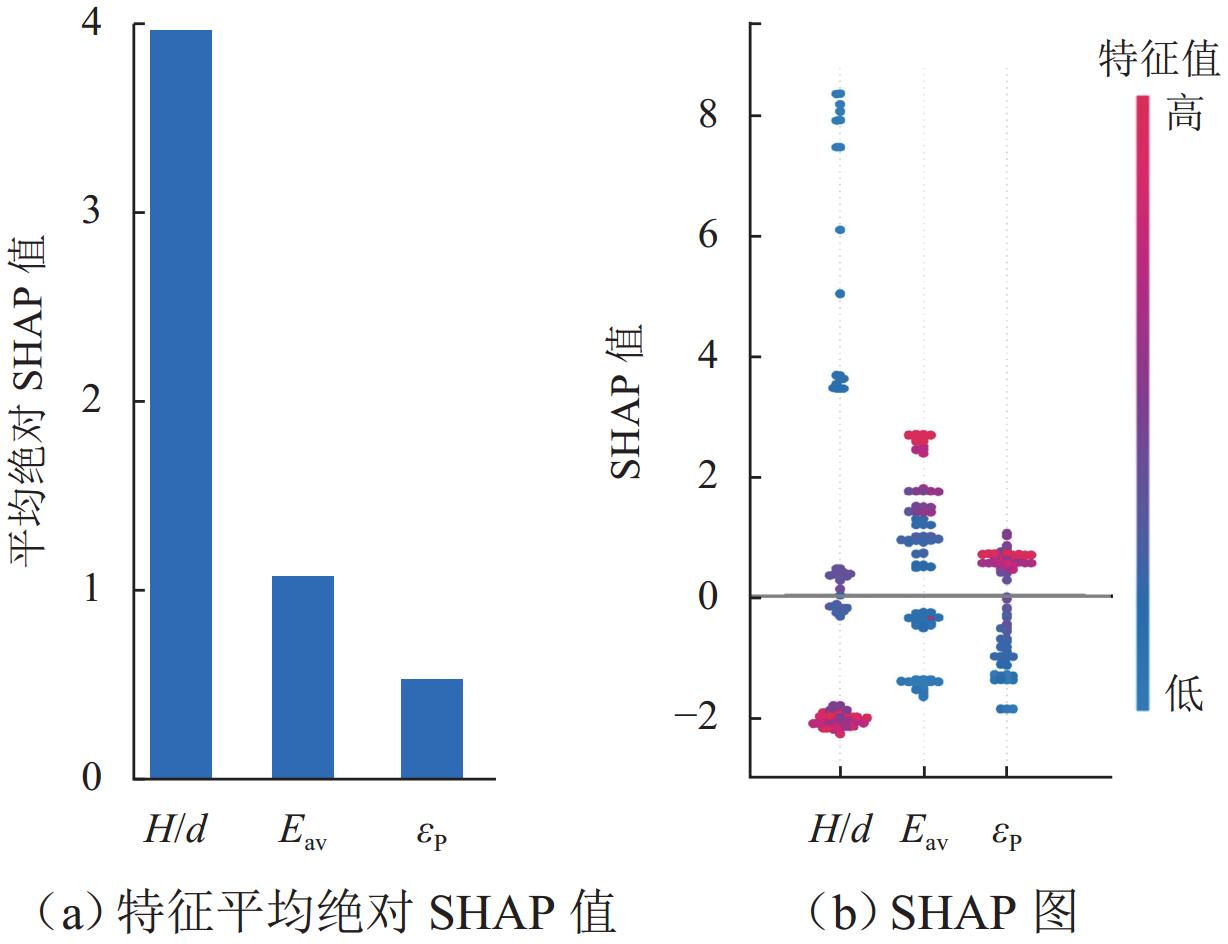
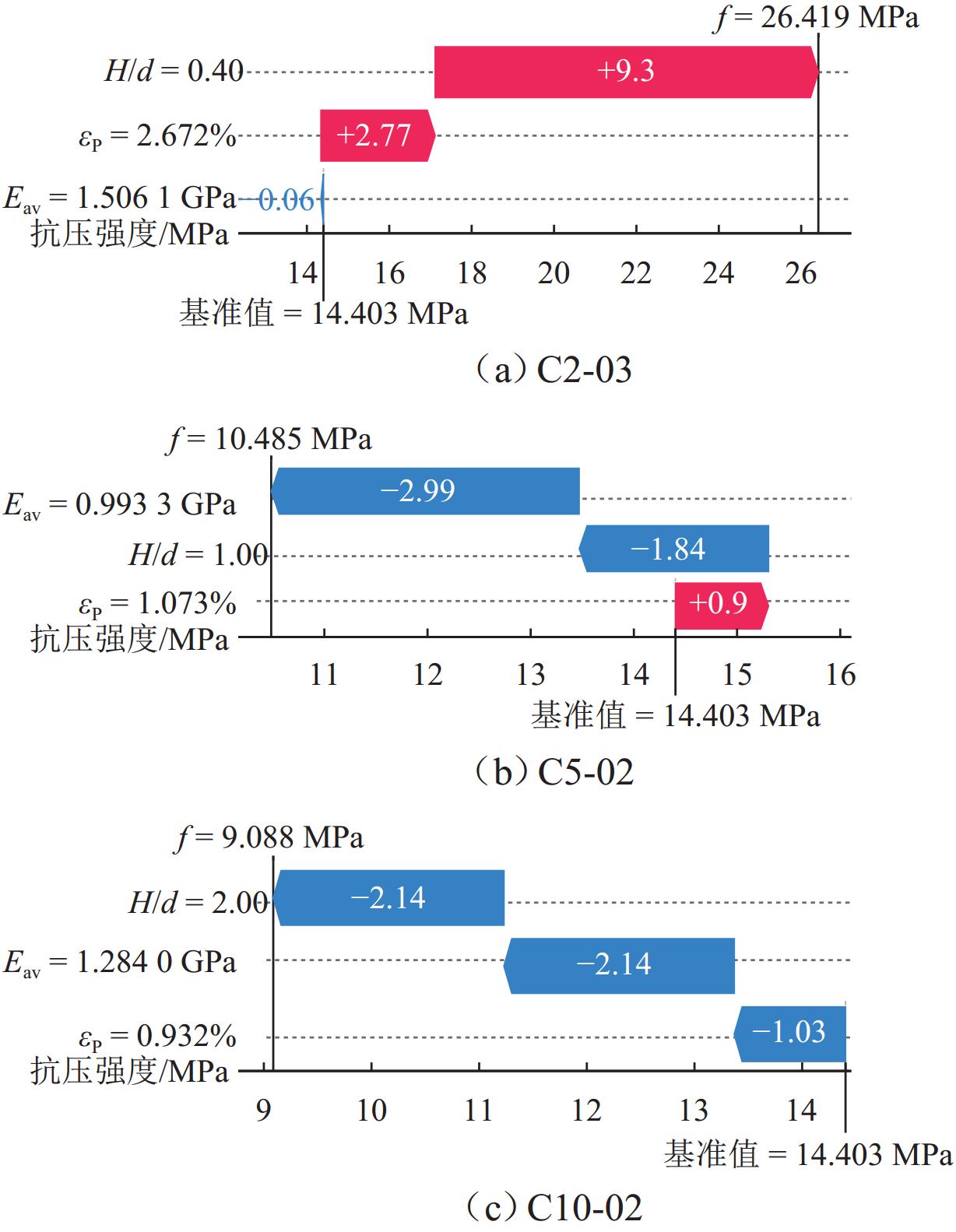
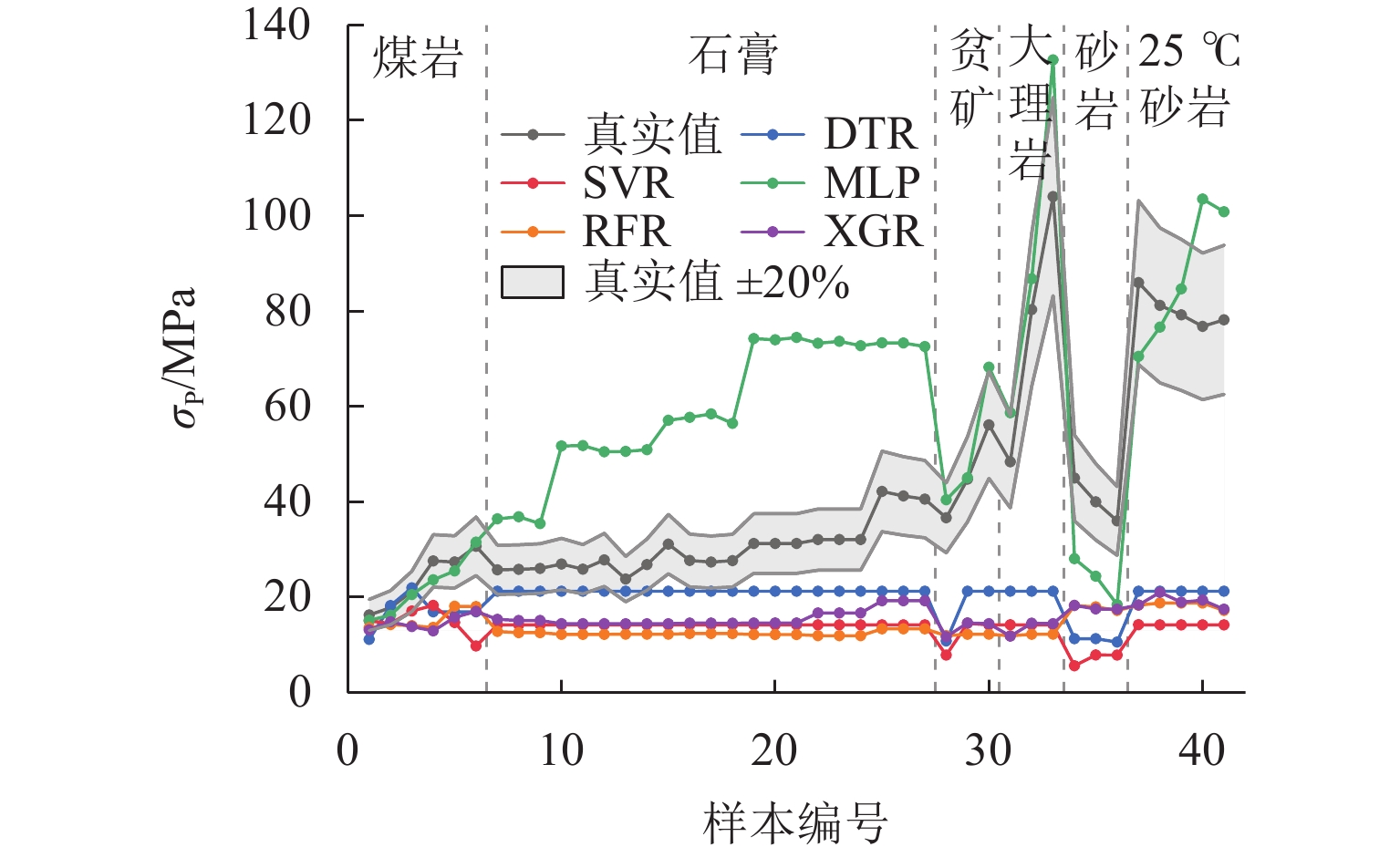
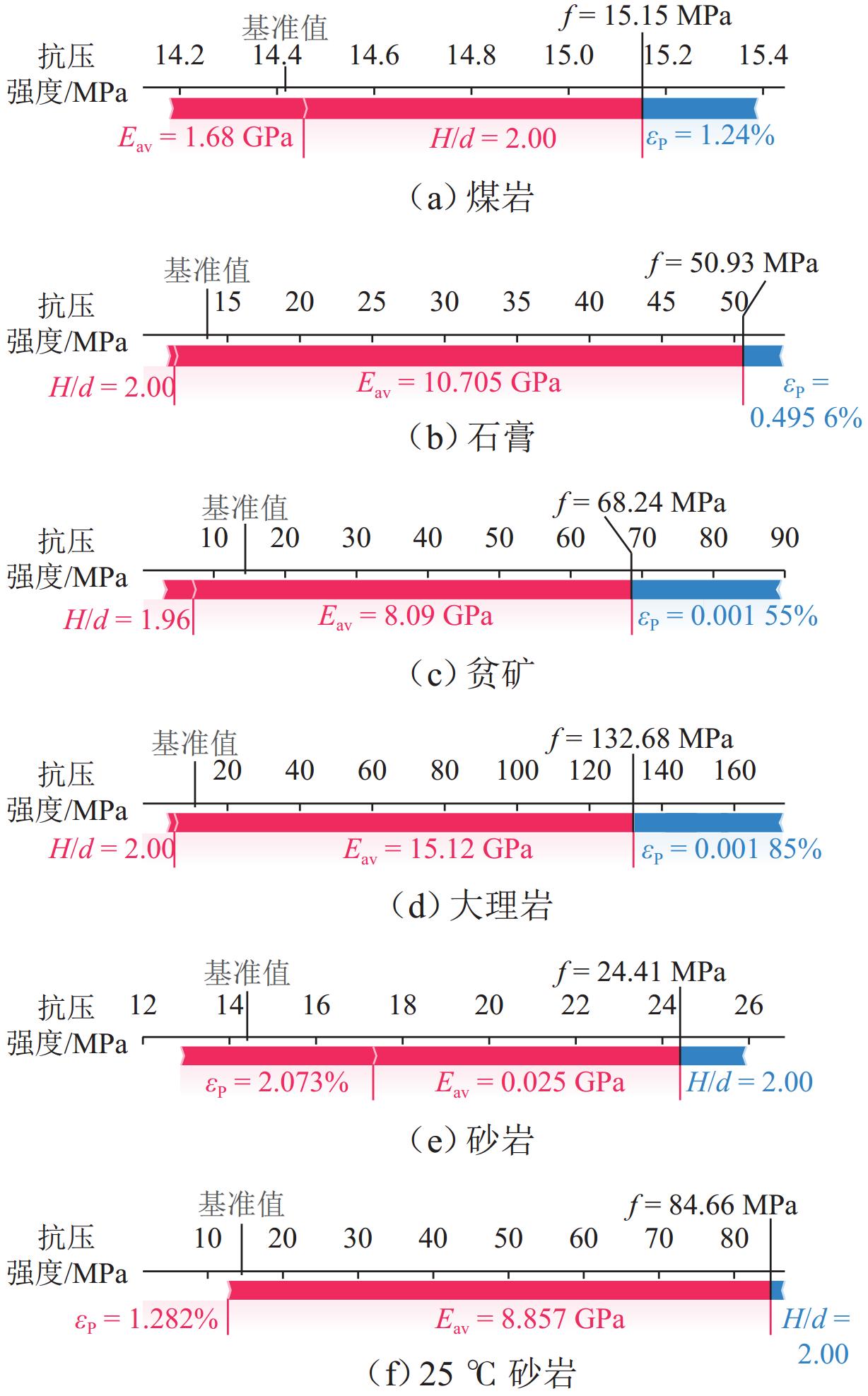
H/d ratio decreased, both uniaxial compressive strength and peak axial strain increased. The uniaxial compressive strength of the 0.40H/d ratio group specimen was 1.6–2.1 times that of the 2.00H/d ratio group specimen, and the peak axial strain was 2.3–3.3 times that of the latter. The stress–strain curves exhibited a transition from brittle to ductile failure modes. The failure mode of the specimen gradually changed from shear failure to splitting failure, and then to complex failure modes. Existing empirical models failed to accurately fit the size effect on uniaxial compressive strength of red-bed soft rock from the Huma Ridge area, withR 2 values below 0.6. Among the mechanical parameters, the dispersion order from highest to lowest wasE av,σ P, andε P. The dispersion parameter of mechanical characteristics increased and then decreased withH/d ratio, peaking betweenH/d = 1.20–1.40. Among the five machine learning algorithms, DTR was the most sensitive to noise and exhibited the lowest stability and predictive performance (minimumR 2 = 0.175). In contrast, XGR, RFR, MLP, and SVR effectively captured the complex nonlinear relationships between input features andσ P, with testR 2 values of 0.989, 0.972, 0.967, and 0.965, respectively. SHAP-based analysis of the XGR model revealed thatH/d was the most influential feature, followed byE av andε P. The average absolute SHAP values are 3.98, 1.09, and 0.56. HigherH/d values had a negative impact on model predictions, whileE av andε P showed positive contributions. Local interpretation indicated that asH/d increased from 0.40 to 2.00, its contribution weight declined and shifted from positive to negative. For sample C5-02 (H/d = 1.00),E av exhibited a strong negative contribution to the predictedσ P. When applied to predictσ P of other rock types, the MLP model demonstrated relatively better generalizability, accurately estimatingσ P for coal rock, lean ore, and marble. However, it tended to overestimateσ P for gypsum and underestimate it for sandstone. This discrepancy was attributed not only to differences in microstructural characteristics but also to variation in feature contributions. Specifically, SHAP analysis showed thatE av had the highest contribution weight in gypsum, lean ore, and marble predictions, whereasH/d dominated in sandstone predictions, resulting in prediction bias.Conclusion Changes in various mechanical properties are obtained as the
H/d ratio decreases through uniaxial compression tests, and the discreteness of these indicators is analyzed. Among all models tested, XGR achieves the highest accuracy in predictingσ P of red-bed soft rocks. In terms of model consistency, the MLP model trained on the red-bed soft rock dataset can predict theσ P of other non-standard sized rocks with an error of less than 20%. While the MLP model shows promising results in predictingσ P of other rock types, its accuracy remains limited due to insufficient training diversity. To improve model generalizability and applicability, future work should incorporate additional rock types and features such as rock density and fracture parameters. This result provides a preliminary exploration and reference for the construction of more universal rock strength prediction models in the future.-
Key words:
- red-bed soft rock /
- size effect model /
- height-diameter ratio /
- machine learning /
- prediction model
-
表 1 红层软岩物理力学参数
Table 1. Physical and mechanical parameters of red-bed soft rock
参数 取值范围 孔隙比 e0 0.196~0.217 颗粒密度 ds/(g•cm−3) 2.639~2.643 含水率 w/% 7.61~8.10 崩解系数 Id/% 71.59~74.81 单轴抗压强度 σP/MPa 8.84~10.65 抗拉强度 σt/MPa 0.45~0.63 纵波波速 νw/(km•s−1) 2.59~2.71 表 2 因子共线性诊断
Table 2. Factor collinearity diagnosis
影响因子 VIF 容忍度 H/d 3.045 0.328 $ {\varepsilon _{\text{P}}} $/% 3.454 0.290 $ {E_{{\text{av}}}} $/GPa 1.426 0.701 表 3 实测值与插值数据统计参数
Table 3. Statistical parameters of measured and interpolated data
指标 数据类型 H/d $ {\varepsilon _{_{\text{P}}}} $/% $ {E_{{\text{av}}}} $/GPa $ {\sigma _{_{\text{P}}}} $/MPa 最大值 实测值 2.00 2.851 2.881 27.020 插值 2.00* 2.724 2.787 26.913 最小值 实测值 0.40 0.461 0.834 8.670 插值 0.40* 0.472 1.055 8.843 均值 实测值 1.20 1.277 1.623 14.426 插值 1.20* 1.252 1.660 14.579 标准差 实测值 0.50 0.615 0.532 5.374 插值 0.50* 0.555 0.385 4.944 注:*表示插值中H/d统计参数没有变化,由于设置多组高径比相同的平行试验,线性插值不会显著影响统计指标. 表 4 各模型超参数设置
Table 4. Hyperparameter settings of each model
模型 超参数名称 搜索空间 最优取值 DTR ccp_alpha 0~0.5 0.1 max_depth 1.0~15.0 6.0 SVR C 0.1~100.0 100.0 epsilon 0.01~0.50 0.50 gamma 0.01~10.00 0.01 RFR n_estimators 100~300 200 max_depth 5~30 10 min_samples_split 2~10 2 min_samples_leaf 1~2 1 XGR gamma 0~1 0 learning_rate 0.01~0.50 0.10 max_depth 3~7 3 n_estimators 50~200 200 alpha 0~1 0 lambda 1~2 2 subsample 0.5~1.0 0.5 表 5 模型预测结果
Table 5. Model prediction results
模型 类型 R2 MMAE MMSE RRMSE DTR 训练集 0.996 0.203 0.084 0.289 测试集 0.807 1.582 6.550 2.650 SVR 训练集 0.988 0.142 0.278 0.528 测试集 0.965 0.573 0.536 0.732 MLP 训练集 0.949 0.787 1.098 1.048 测试集 0.967 0.803 1.107 1.052 RFR 训练集 0.981 0.371 0.399 0.632 测试集 0.972 0.644 0.937 0.968 XGR 训练集 0.992 0.204 0.169 0.411 测试集 0.989 0.485 0.395 0.629 -
[1] 吕龙龙, 廖红建, 伏映鹏, 等. 干湿状态对红层软岩脆延特性影响的试验研究[J]. 西安交通大学学报, 2021, 55(4): 162-171. doi: 10.7652/xjtuxb202104018LÜ Longlong, LIAO Hongjian, FU Yingpeng, et al. Experimental research on effects of dry and natural states on brittle-ductile transition property for red-bed soft rock[J]. Journal of Xi’an Jiaotong University, 2021, 55(4): 162-171. doi: 10.7652/xjtuxb202104018 [2] 张俊云, 张乐, 高福洲, 等. 干湿循环下红层土石混合料强度及变形特性的试验研究[J]. 西南交通大学学报, 2023, 58(6): 1394-1404. doi: 10.3969/j.issn.0258-2724.20220343ZHANG Junyun, ZHANG Le, GAO Fuzhou, et al. Experimental study on strength and deformation characteristics of red-bed soil-rock mixture under wetting-drying cycles[J]. Journal of Southwest Jiaotong University, 2023, 58(6): 1394-1404. doi: 10.3969/j.issn.0258-2724.20220343 [3] 和铭, 魏良帅, 贾逸, 等. 红层软岩膨胀力学特性试验研究[J]. 水利水电技术, 2019, 50(4): 171-178.HE Ming, WEI Liangshuai, JIA Yi, et al. Experimental study on expansive mechanical characteristics of red-bed soft rock[J]. Water Resources and Hydropower Engineering, 2019, 50(4): 171-178. [4] ZHANG G D, LING S X, LIAO Z X, et al. Mechanism and influence on red-bed soft rock disintegration durability of particle roughness based on experiment and fractal theory[J]. Construction and Building Materials, 2024, 419: 135504. doi: 10.1016/j.conbuildmat.2024.135504 [5] 陈从新, 卢海峰, 袁从华, 等. 红层软岩变形特性试验研究[J]. 岩石力学与工程学报, 2010, 29(2): 261-270.CHEN Congxin, LU Haifeng, YUAN Conghua, et al. Experimental research on deformation propertities of red-bed soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 261-270. [6] 周翠英, 梁宁, 刘镇. 红层软岩压缩破坏的分形特征与级联失效过程[J]. 岩土力学, 2019, 40(增1): 21-31.ZHOU Cuiying, LIANG Ning, LIU Zhen. Fractal characteristics of compression failure of red soft rock and cascading failure process[J]. Rock and Soil Mechanics, 2019, 40(S1): 21-31. [7] 中华人民共和国住房和城乡建设部. 工程岩体试验方法标准: GB/T 50266—2013[S]. 北京: 中国计划出版社, 2013. [8] 江权, 崔洁, 冯夏庭, 等. 玄武岩力学参数的随机性统计与概率分布估计[J]. 岩土力学, 2017, 38(3): 784-792.JIANG Quan, CUI Jie, FENG Xiating, et al. Stochastic statistics and probability distribution estimation of mechanical parameters of basalt[J]. Rock and Soil Mechanics, 2017, 38(3): 784-792. [9] 杨同, 王宝学, 张磊. 非标准岩样室内力学试验的几种处理方法[J]. 中国矿业, 2007, 16(2): 87-89. doi: 10.3969/j.issn.1004-4051.2007.02.027YANG Tong, WANG Baoxue, ZHANG Lei. Several processing methods in indoor mechanics tests of the non-standard rock samples[J]. China Mining Magazine, 2007, 16(2): 87-89. doi: 10.3969/j.issn.1004-4051.2007.02.027 [10] CHEN L, LIU T Y, JIA B X, et al. Acoustic emission and fractal characteristics of red beds soft rock under water-force coupling[J]. Scientific Reports, 2024, 14: 4424. doi: 10.1038/s41598-024-54814-2 [11] 朱其志, 闵中泽, 王岩岩, 等. 粉砂岩三轴压缩试验中的试样尺寸效应研究[J]. 岩石力学与工程学报, 2019, 38(增2): 3296-3303.ZHU Qizhi, MIN Zhongze, WANG Yanyan, et al. Study on the size effect of silty sandstone samples under conventional triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S2): 3296-3303. [12] 侍倩, 曾亚武. 岩土力学实验[M]. 2版. 武汉: 武汉大学出版社, 2010. [13] 蔡美峰. 岩石力学与工程[M]. 2版. 北京: 科学出版社, 2013. [14] 杨圣奇, 苏承东, 徐卫亚. 岩石材料尺寸效应的试验和理论研究[J]. 工程力学, 2005, 22(4): 112-118. doi: 10.3969/j.issn.1000-4750.2005.04.022YANG Shengqi, SU Chengdong, XU Weiya. Experimental and theoretical study of size effect of rock material[J]. Engineering Mechanics, 2005, 22(4): 112-118. doi: 10.3969/j.issn.1000-4750.2005.04.022 [15] 朱珍德, 邢福东, 王军, 等. 基于灰色理论的脆性岩石抗压强度尺寸效应试验研究[J]. 岩土力学, 2004, 25(8): 1234-1238.ZHU Zhende, XING Fudong, WANG Jun, et al. Experimental study on size effect on comperession strength of brittle rock based on grey theory[J]. Rock and Soil Mechanics, 2004, 25(8): 1234-1238. [16] 刘宝琛, 张家生, 杜奇中, 等. 岩石抗压强度的尺寸效应[J]. 岩石力学与工程学报, 1998, 17(6): 611-614. doi: 10.3321/j.issn:1000-6915.1998.06.001LIU Baochen, ZHANG Jiasheng, DU Qizhong, et al. A study of size effect for compression strength of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 611-614. doi: 10.3321/j.issn:1000-6915.1998.06.001 [17] HASHEMINEJAD M M, SOHANKAR N, HAJIANNIA A. Predicting the collapsibility potential of unsaturated soils using adaptive neural fuzzy inference system and particle swarm optimization[J]. Scientia Iranica, 2018, 25(6): 2980-2996. [18] TIE J H, MENG W Z, WEI M D, et al. Loading rate and mineralogical controls on tensile strength of rocks: a machine learning view[J]. Rock Mechanics and Rock Engineering, 2023, 56(8): 6119-6125. doi: 10.1007/s00603-023-03354-8 [19] ZHANG P, YIN Z Y, JIN Y F, et al. A novel hybrid surrogate intelligent model for creep index prediction based on particle swarm optimization and random forest[J]. Engineering Geology, 2020, 265: 105328. doi: 10.1016/j.enggeo.2019.105328 [20] 赵奎, 杨道学, 曾鹏, 等. 单轴压缩条件下花岗岩声学信号频域特征分析[J]. 岩土工程学报, 2020, 42(12): 2189-2197. doi: 10.11779/CJGE202012004ZHAO Kui, YANG Daoxue, ZENG Peng, et al. Frequency-domain characteristics of acoustic signals of granite under uniaxial compression[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2189-2197. doi: 10.11779/CJGE202012004 [21] TOUPIN R A. Saint-venant’s principle[J]. Archive for Rational Mechanics and Analysis, 1965, 18(2): 83-96. doi: 10.1007/BF00282253 [22] WITCZAK M, KALOUSH K, PENLLINEN T, et al. Simple performance test for superpave mix deesign[M]. Cambridge: Nation academy press, 2002. [23] 陈瑜, 黄永恒, 曹平, 等. 不同高径比时软岩强度与变形尺寸效应试验研究[J]. 中南大学学报(自然科学版), 2010, 41(3): 1073-1078.CHEN Yu, HUANG Yongheng, CAO Ping, et al. Size effect experimental study of strength and deformation in different height-to-diameter ratio soft rocks[J]. Journal of Central South University (Science and Technology), 2010, 41(3): 1073-1078. [24] ALBULAYHI K, ABU AL-HAIJA Q, ALSUHIBANY S A, et al. IoT intrusion detection using machine learning with a novel high performing feature selection method[J]. Applied Sciences, 2022, 12(10): 5015. doi: 10.3390/app12105015 [25] 张林, 郭郑曦, 齐实, 等. 基于机器学习模型的高植被覆盖区浅层滑坡预测[J]. 农业工程学报, 2024, 40(17): 149-160.ZHANG Lin, GUO Zhengxi, QI Shi, et al. Predicting shallow landslides in highly vegetation-covered areas using machine learning models[J]. Transactions of the Chinese Society of Agricultural Engineering, 2024, 40(17): 149-160. [26] ZHANG J R, NIU W J, YANG Y Z, et al. Machine learning prediction models for compressive strength of calcined sludge-cement composites[J]. Construction and Building Materials, 2022, 346: 128442. doi: 10.1016/j.conbuildmat.2022.128442 [27] CZAJKOWSKI M, KRETOWSKI M. The role of decision tree representation in regression problems–An evolutionary perspective[J]. Applied Soft Computing, 2016, 48: 458-475. doi: 10.1016/j.asoc.2016.07.007 [28] CAI R, HAN T H, LIAO W Y, et al. Prediction of surface chloride concentration of marine concrete using ensemble machine learning[J]. Cement and Concrete Research, 2020, 136: 106164. doi: 10.1016/j.cemconres.2020.106164 [29] 郝建, 刘河清, 刘建康, 等. 基于振动信号的岩石单轴抗压强度钻进预测实验研究[J]. 岩石力学与工程学报, 2024, 43(6): 1406-1424.HAO Jian, LIU Heqing, LIU Jiankang, et al. Experimental study of rock uniaxial compressive strength prediction with drilling based on vibration signals[J]. Chinese Journal of Rock Mechanics and Engineering, 2024, 43(6): 1406-1424. [30] YANG Y R, YUAN Y, HAN Z, et al. Interpretability analysis for thermal sensation machine learning models: an exploration based on the SHAP approach[J]. Indoor Air, 2022, 32(2): e12984. [31] 张玉江, 邵珠娟, 袁红辉, 等. 不同高径比煤岩力学性能及破坏特征实验研究[J]. 中国矿业, 2020, 29(5): 110-114. doi: 10.12075/j.issn.1004-4051.2020.05.021ZHANG Yujiang, SHAO Zhujuan, YUAN Honghui, et al. Experimental study on mechanical properties and failure characteristics of coal rocks with different aspect ratios[J]. China Mining Magazine, 2020, 29(5): 110-114. doi: 10.12075/j.issn.1004-4051.2020.05.021 [32] 贺桂成, 李玉兰, 丁德馨. 不同高径比石膏试样强度与尺寸效应的试验研究[J]. 地下空间与工程学报, 2016, 12(6): 1464-1470.HE Guicheng, LI Yulan, DING Dexin. Experimental investigation on strength and size effect of the gypsum sample in different height to diameter ratios[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(6): 1464-1470. [33] ZHANG C L, LI M J, YAN X, et al. Fracture process and failure characteristics of sandstone with different height-to-diameter ratios[J]. Processes, 2023, 11(11): 3069. doi: 10.3390/pr11113069 [34] SU H J, JING H W, MAO X B, et al. Size effect of sandstone after high temperature under uniaxial compression[J]. Journal of Central South University, 2015, 22(5): 1901-1908. doi: 10.1007/s11771-015-2709-1 -




 下载:
下载: