Uncertainty Quantification for Seismic Vulnerability of Bridge Based on Bootstrap Method
-
摘要:
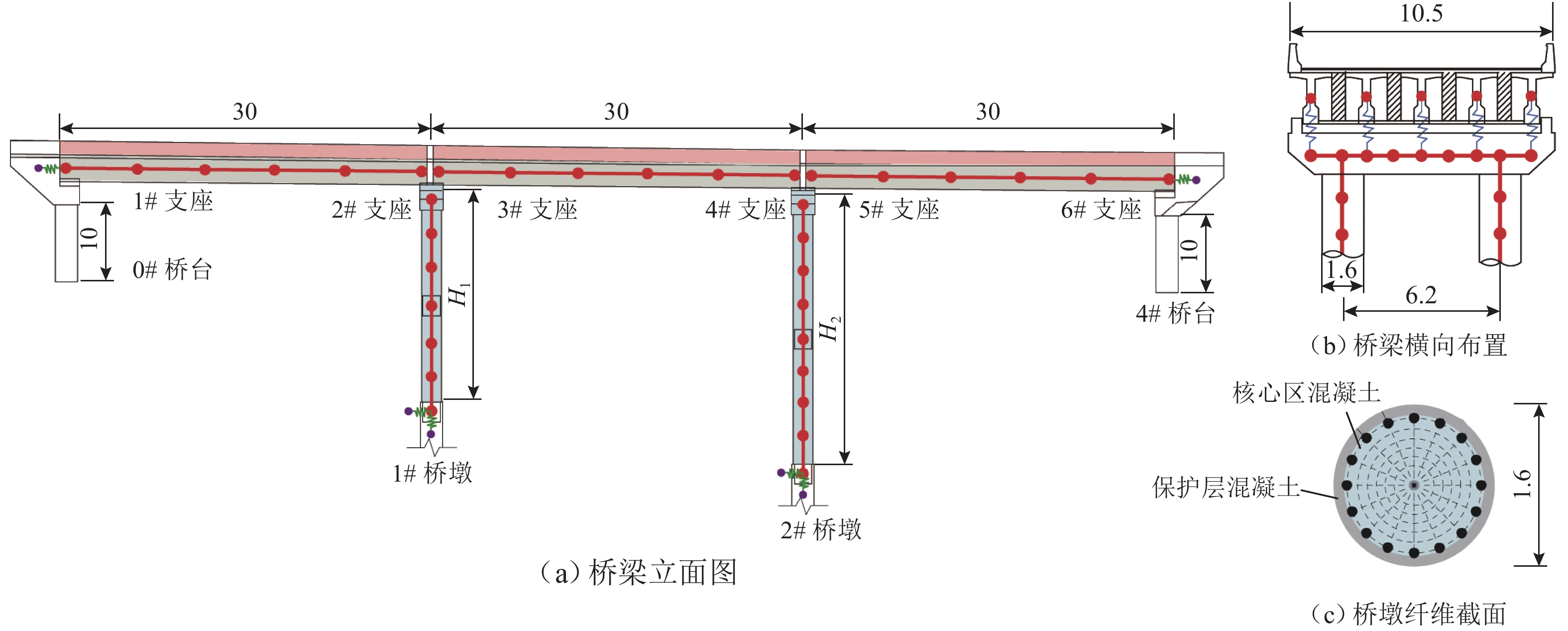
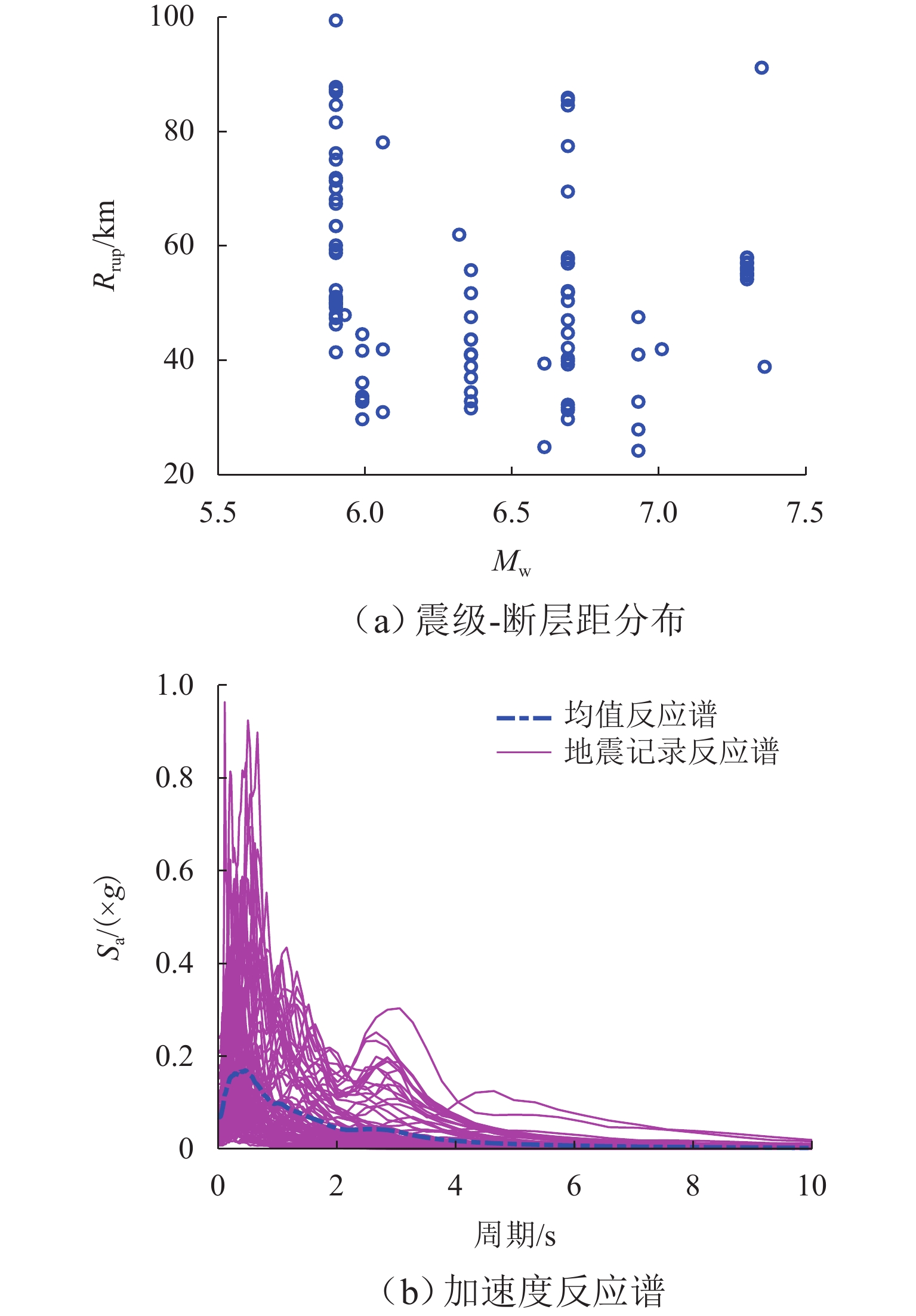
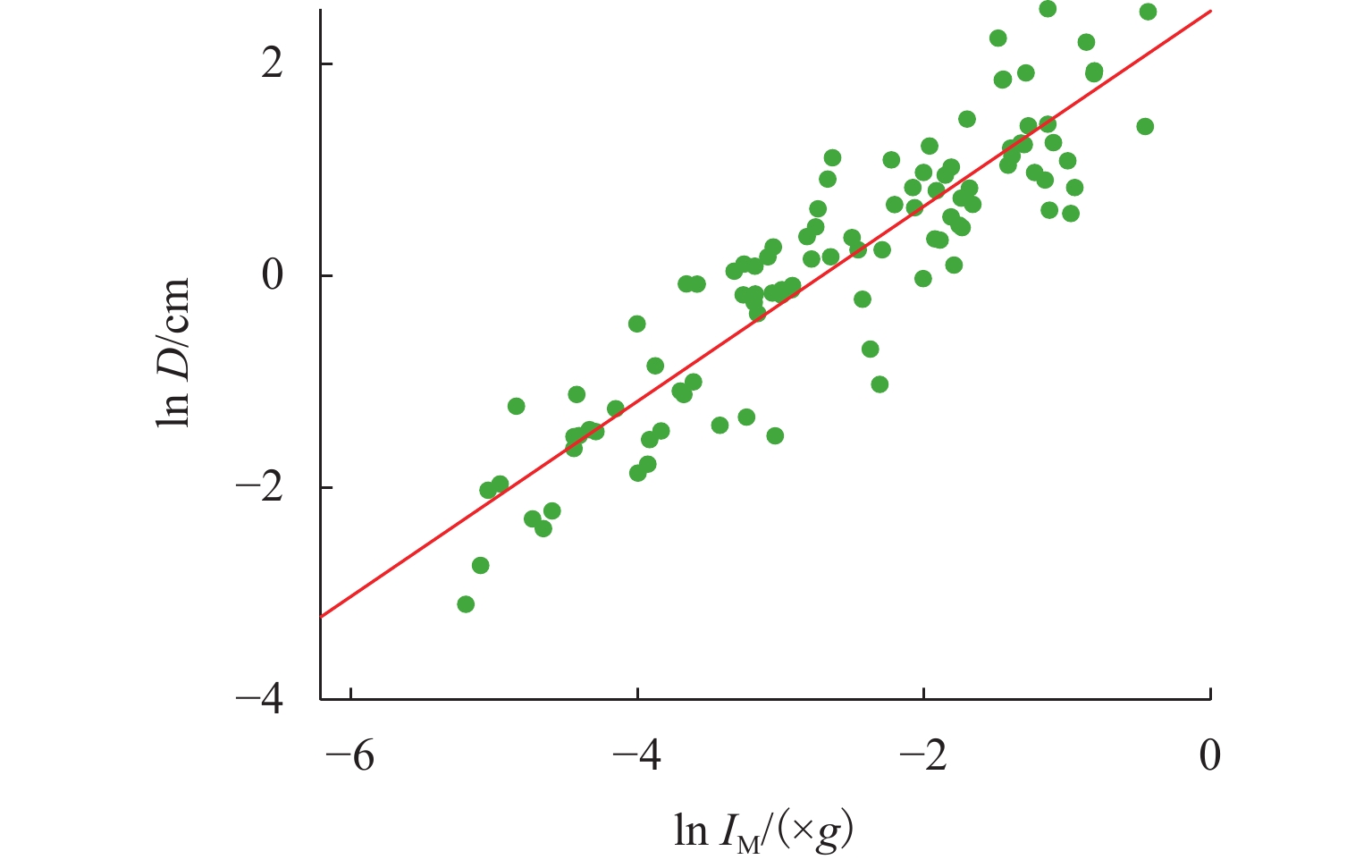
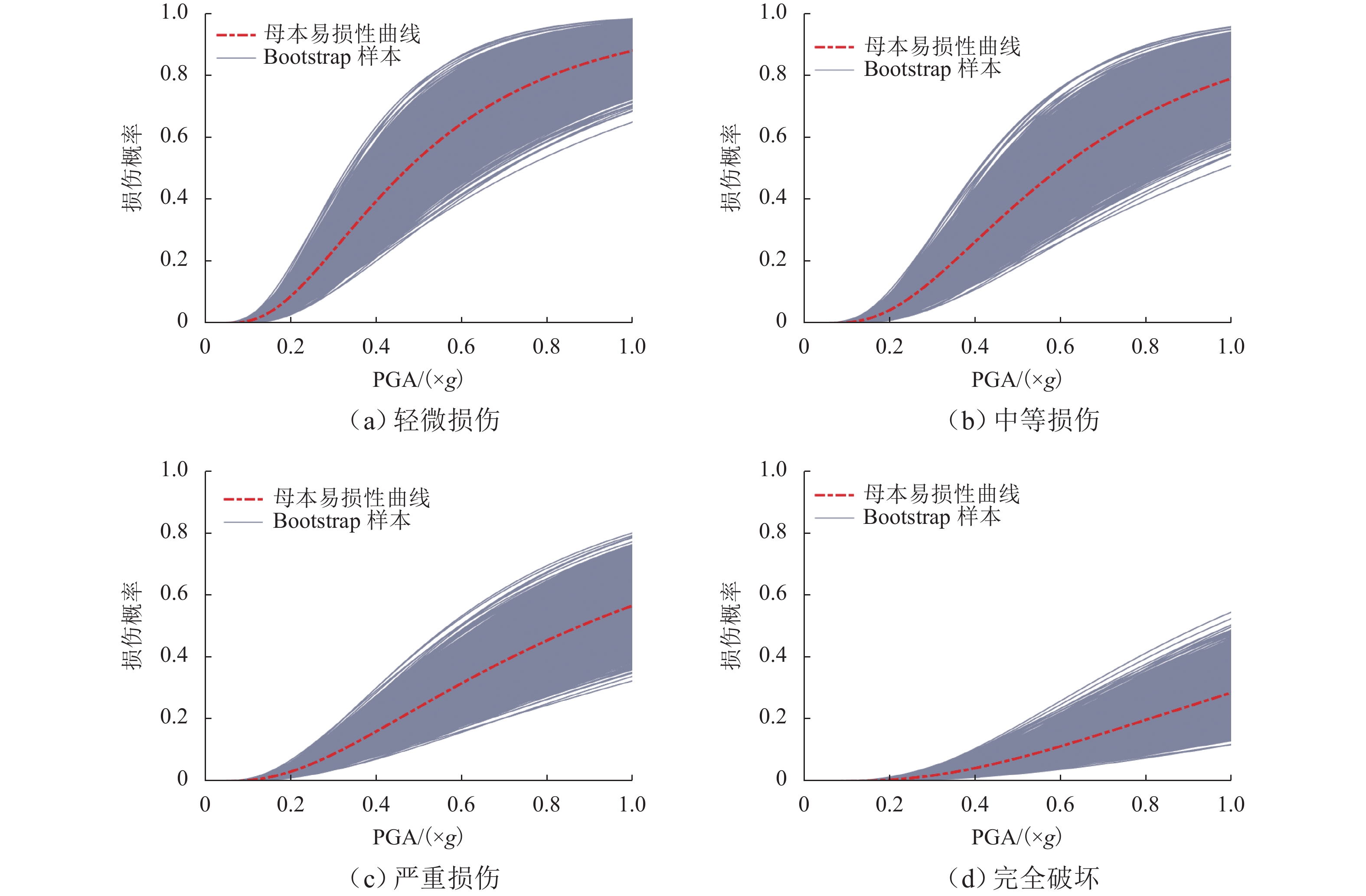
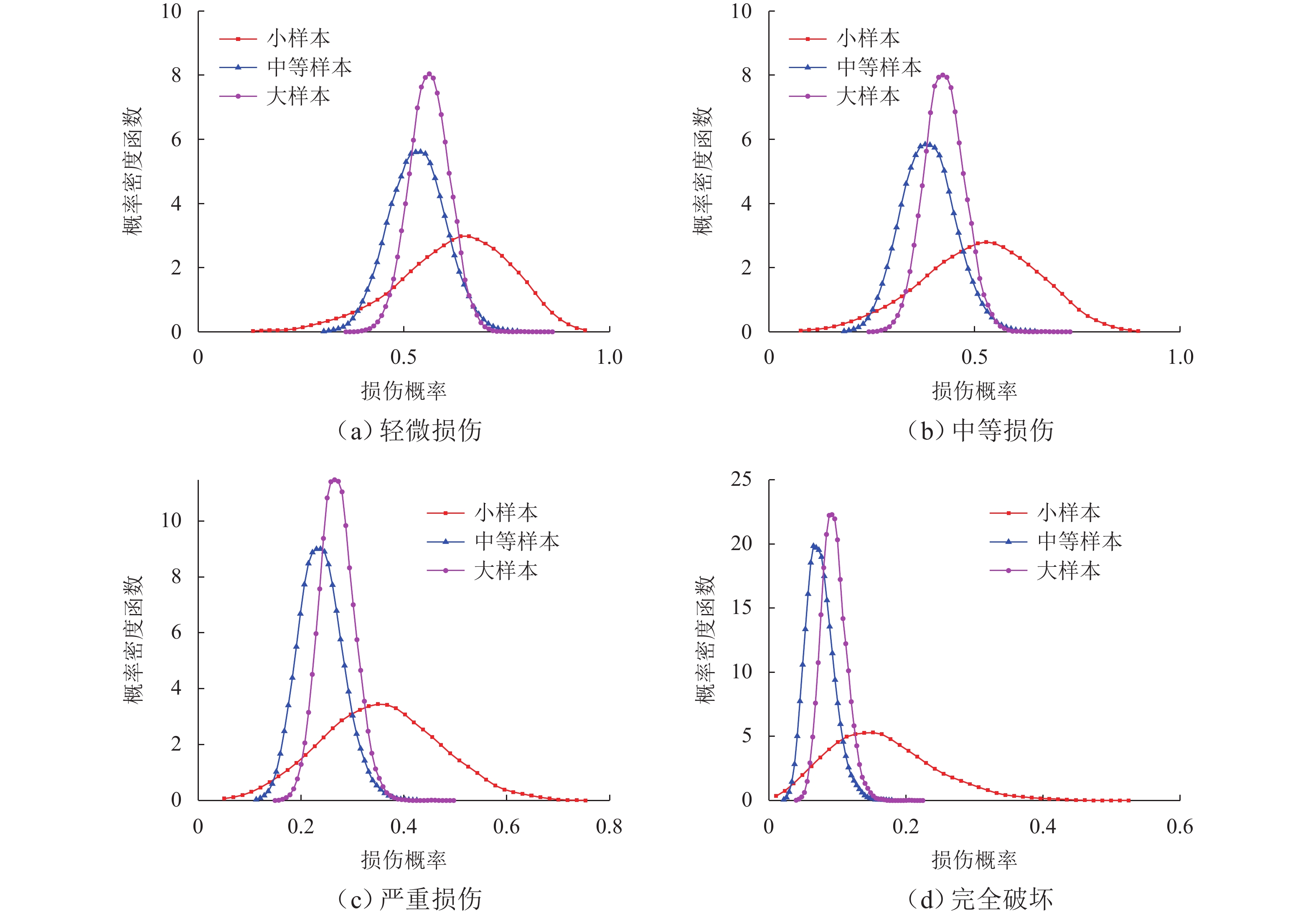
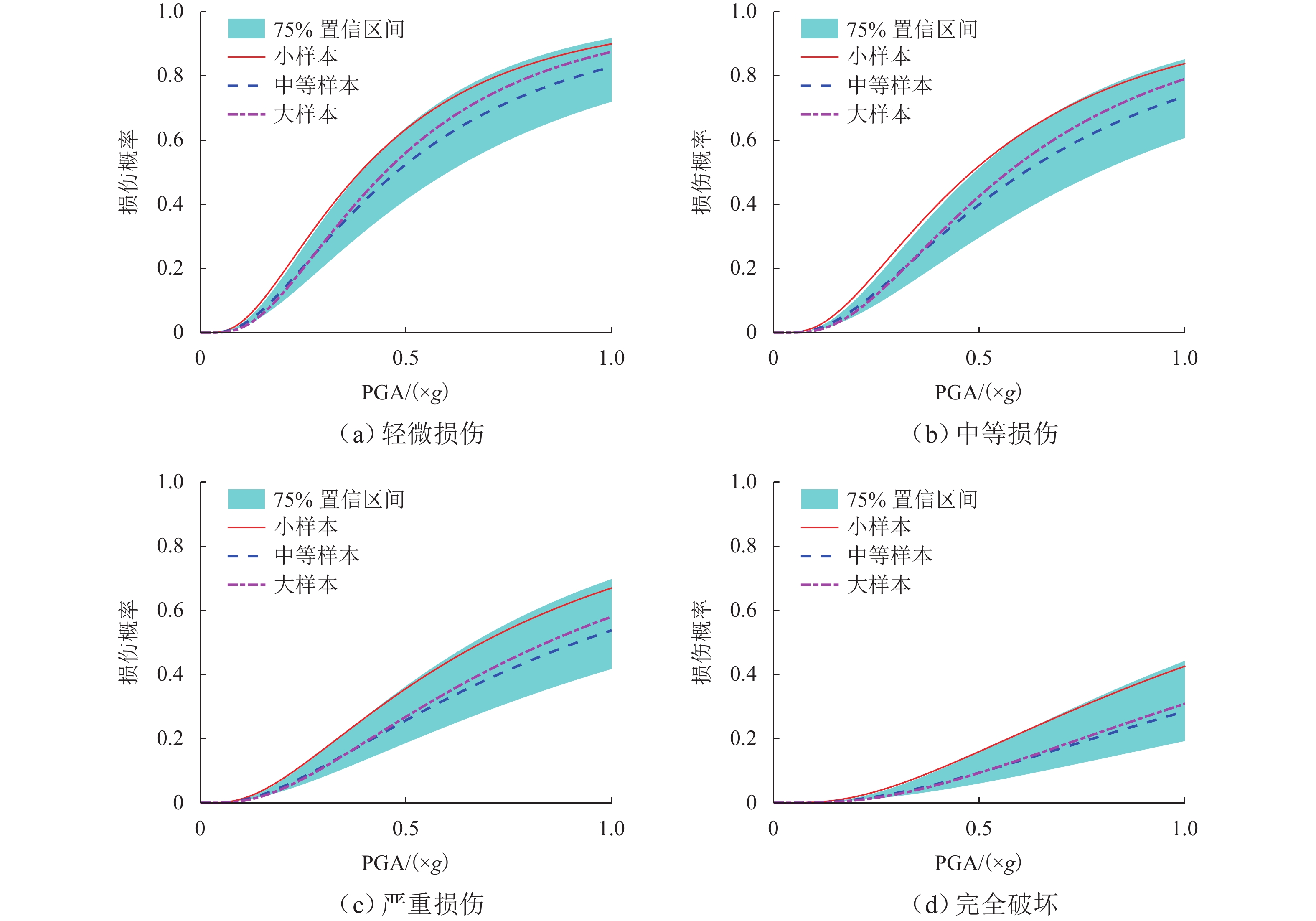
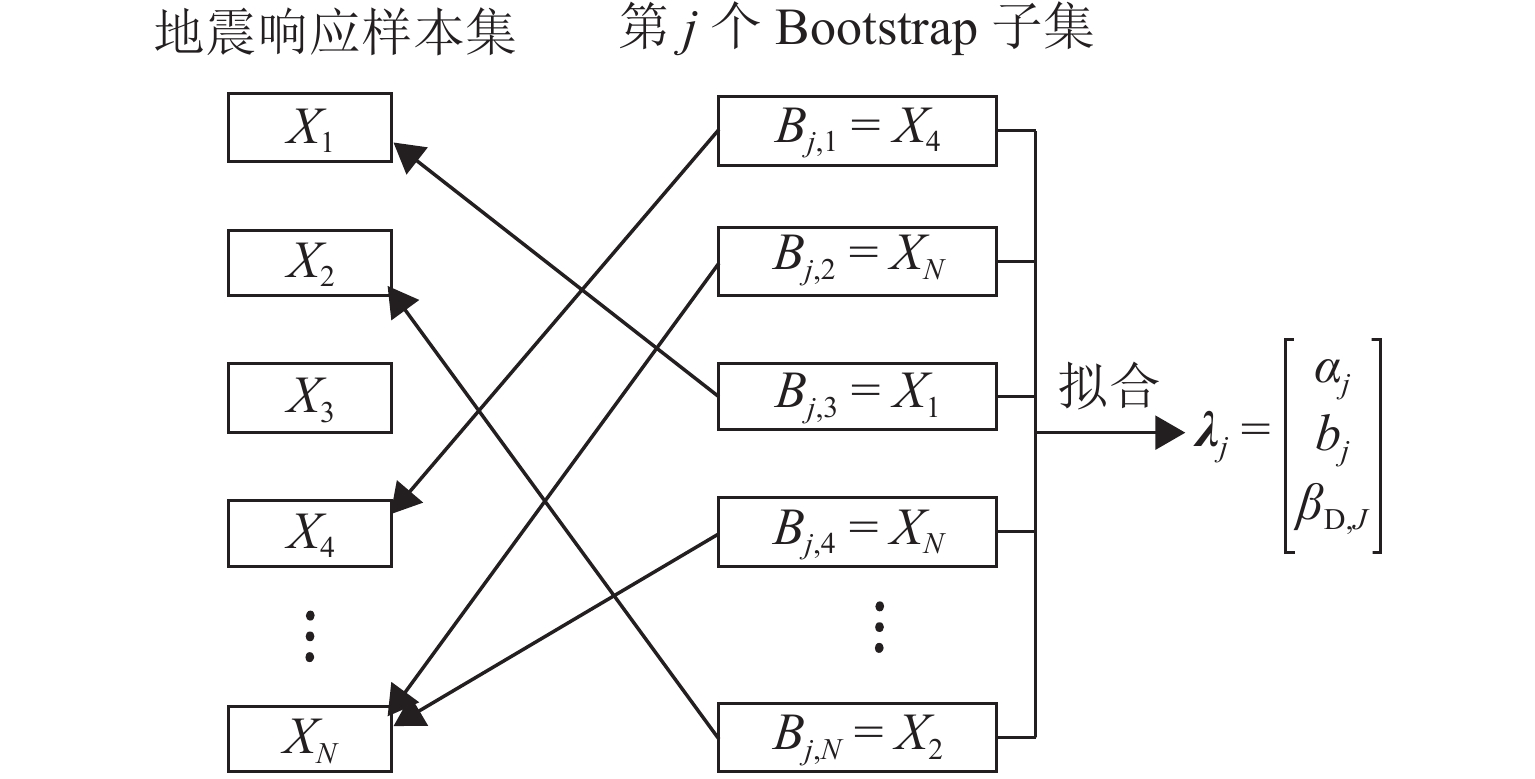
为研究地震动不确定性对桥梁结构地震需求和易损性的影响，明确地震动不确定性在其地震易损性分析中的传播规律，提出一种基于Bootstrap的桥梁地震易损性不确定性量化方法. 首先，通过概率地震需求分析确定地震动强度指标与桥梁结构地震需求之间的对应关系；其次，考虑地震动样本数量对桥梁结构地震需求模型和易损性的影响，采用Bootstrap方法对概率地震需求模型参数和易损性曲线的不确定性进行模拟；最后，以一座3跨简支梁桥为例，分别采用50、100、300条地震记录对其进行地震易损性分析，量化不同地震样本下概率地震需求模型和易损性的变异性. 研究结果表明：地震作用下，桥梁结构的地震需求和易损性均具有较大的不确定性，当采用100条地震记录进行分析时，桥梁各个损伤状态下失效概率的变异性都在10%以上，严重损伤状态下失效概率的变异性甚至高达30%；在进行桥梁地震易损性分析时，宜将不同地震动强度下桥梁结构的失效概率表示为区间随机变量，从而考虑由于地震记录样本所导致的地震易损性变异性；Bootstrap方法可以有效模拟桥梁结构地震需求和地震易损性的不确定性，为小样本情况下桥梁结构概率地震需求模型统计不确定性模拟和地震易损性分析提供了一条有效途径.
Abstract:To investigate the influence of ground motion uncertainty on the seismic demand and vulnerability of bridge structures and to clarify the propagation of this uncertainty in seismic vulnerability analysis, a quantitative method based on the Bootstrap method was proposed for assessing the uncertainty in the seismic vulnerability of bridges. Firstly, the relationship between the ground motion intensity index and the seismic demand of bridge structures was determined through probabilistic seismic demand analysis. Secondly, by considering the influence of ground motion sample size on the seismic demand model and vulnerability of bridge structures, the Bootstrap method was used to simulate the uncertainties in both probabilistic seismic demand model parameters and vulnerability curves. Finally, by taking a three-span simply supported beam bridge as an example, seismic vulnerability analyses were conducted using 50, 100, and 300 seismic records to quantify the variability of probabilistic seismic demand models and vulnerability under different ground motion samples. The results indicate that the seismic demand and vulnerability of bridge structures are subject to significant uncertainties under the ground motion. When 100 seismic records are used, the variability in failure probability of the bridge under various damage states exceeds 10%, and that under severe damage states reaches up to 30%. In seismic vulnerability analysis of bridges, it is advisable to represent the failure probability of bridge structures under different ground motion intensities as interval random variables to account for variability in seismic vulnerability due to seismic record samples. The Bootstrap method can effectively simulate the uncertainty in the seismic demand and vulnerability of bridge structures, providing an effective approach for statistical uncertainty simulation and seismic vulnerability analysis of probabilistic seismic demand models of bridge structures under small sample sizes.
-
Key words:
- bridge /
- seismic vulnerability /
- uncertainty quantification /
- Bootstrap /
- probabilistic seismic demand
-
图 4 100条地震波下概率地震需求模型
Figure 4. Probabilistic seismic demand model under 100 ground motions
图 5 概率地震需求模型拟合参数的概率密度函数
Figure 5. Probability density function of fitted parameters of probabilistic seismic demand model
图 6 Bootstrap重抽样易损性曲线与母本易损性曲线的对比（100条地震记录）
Figure 6. Comparison between Bootstrap resampled vulnerability curves and parent vulnerability curves （100 seismic records）
图 7 损伤超越的概率密度函数（PGA=0.5g）
Figure 7. Probability density function of damage exceedance （PGA = 0.5g）
表 1 随机变量统计信息
Table 1. Statistical information of random parameters
随机参数 分布类型 均值 变异系数 $ {f_{{\mathrm{c,core}}}} $/MPa 对数正态 43.34 0.216 $ {\varepsilon _{{\mathrm{c,core}}}} $ 0.00206 0.185 $ {f_{{\mathrm{cu,core}}}} $/MPa 8.87 0.216 $ {\varepsilon _{{\mathrm{cu,core}}}} $ 0.0073 0.524 $ {f_{{\mathrm{c,cover}}}} $/MPa 35.99 0.156 $ {\varepsilon _{{\mathrm{c,cover}}}} $ 0.002 0.2 $ {\varepsilon _{{\mathrm{cu,cover}}}} $ 0.004 0.2 ${E_{\text{s}}}$/MPa 200000 0.03 ${f_{\mathrm{y}}}$/MPa 381.65 0.0743 B 0.02 0.2 α 正态 0.02 0.5 ζ 0.05 0.2 
下载: 导出CSV
表 2 概率地震需求模型参数变异性
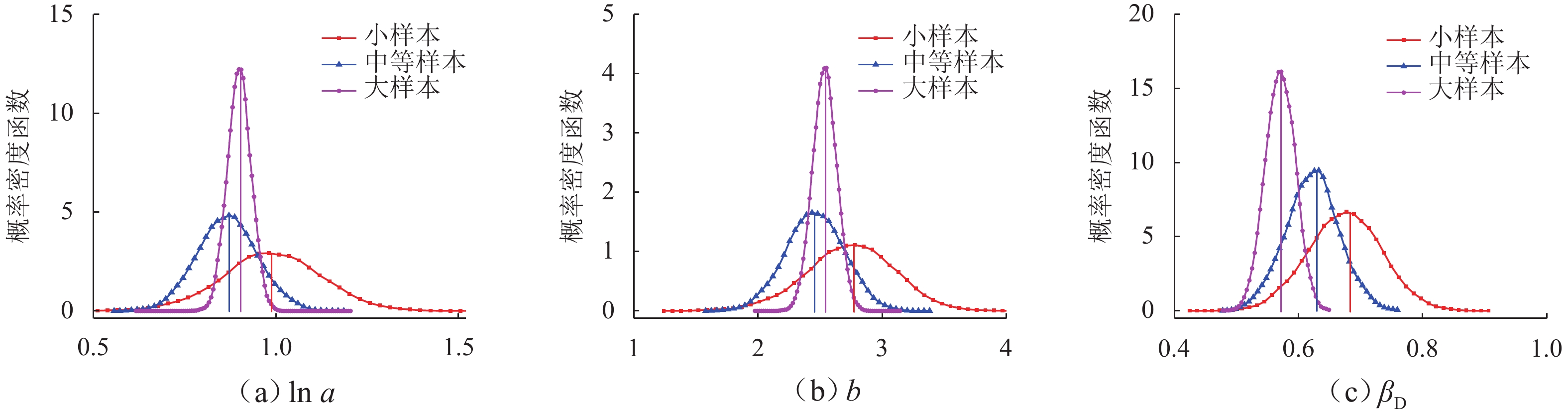
Table 2. Parameter variability of probabilistic seismic demand models
样本
数/条ln a b $ {\beta _{\mathrm{D}}} $ 直接
估计Bootstrap
均值变异
系数/%直接
估计Bootstrap
均值变异
系数/%直接
估计Bootstrap
均值变异
系数/%50 0.993 0.989 13.72 2.755 2.741 13.03 0.690 0.675 8.95 100 0.866 0.866 9.50 2.457 2.458 9.52 0.630 0.622 6.76 300 0.899 0.899 3.58 2.535 2.536 3.79 0.573 0.570 4.30
下载: 导出CSV
表 3 Bootstrap方法计算的桥梁结构失效概率
Table 3. Failure probabilities of bridge structures calculated by Bootstrap method
极限状态 小样本 中等样本 大样本 直接估计 均值 变异系数 直接估计 均值 变异系数 直接估计 均值 变异系数 轻微损伤 0.634 0.621 0.216 0.533 0.532 0.128 0.561 0.562 0.086 中等损伤 0.521 0.512 0.273 0.389 0.387 0.169 0.425 0.426 0.113 严重损伤 0.357 0.354 0.318 0.239 0.238 0.179 0.269 0.270 0.125 完全破坏 0.160 0.164 0.464 0.074 0.075 0.271 0.094 0.095 0.188
下载: 导出CSV
-
[1] 管仲国, 黄勇, 张昊宇, 等. 青海玛多7.4级地震桥梁工程震害特性分析[J]. 世界地震工程, 2021, 37(3): 38-45.GUAN Zhongguo, HUANG Yong, ZHANG Haoyu, et al. Damage characteristics and analysis of bridge engineering in M7.4 Qinghai Maduo earthquake[J]. World Earthquake Engineering, 2021, 37(3): 38-45. [2] 周海涛. 公路工程抗震减灾技术回顾与展望[J]. 公路交通科技, 2010, 27(9): 39-43.ZHOU Haitao. Review and prospect of earthquake resistance and disaster mitigation technology of highway engineering[J]. Journal of Highway and Transportation Research and Development, 2010, 27(9): 39-43. [3] 陈志强. 基于动力可靠度的高墩桥梁抗震性能概率分析理论及应用[D]. 成都: 西南交通大学, 2022. [4] CUI S G, GUO C, ZENG G, et al. Influence of hydrodynamic pressure on fragility of high-pier continuous rigid frame bridge subjected to ground motion[J]. Ocean Engineering, 2022, 264: 112516. doi: 10.1016/j.oceaneng.2022.112516 [5] YAN J L, GUO A X, LI H. Comparative analysis of different types of damage indexes of coastal bridges based on time-varying seismic fragility[J]. Marine Structures, 2022, 86: 103288. doi: 10.1016/j.marstruc.2022.103288 [6] LI S Q, LIU H B. Analysis of probability matrix model for seismic damage vulnerability of highway bridges[J]. Geomatics, Natural Hazards and Risk, 2022, 13(1): 1395-1421. doi: 10.1080/19475705.2022.2077146 [7] SKOULIDOU D, ROMÃO X. Uncertainty quantification of fragility and risk estimates due to seismic input variability and capacity model uncertainty[J]. Engineering Structures, 2019, 195: 425-437. doi: 10.1016/j.engstruct.2019.05.067 [8] SOLEIMANI F. Propagation and quantification of uncertainty in the vulnerability estimation of tall concrete bridges[J]. Engineering Structures, 2020, 202: 109812. doi: 10.1016/j.engstruct.2019.109812 [9] IERVOLINO I. Assessing uncertainty in estimation of seismic response for PBEE[J]. Earthquake Engineering & Structural Dynamics, 2017, 46(10): 1711-1723. [10] HU Y, GUO W. Seismic response of high-speed railway bridge-track system considering unequal-height pier configurations[J]. Soil Dynamics and Earthquake Engineering, 2020, 137: 106250. doi: 10.1016/j.soildyn.2020.106250 [11] NIELSON B G. Analytical fragility curves for highway bridges in moderate seismic zones [D]. Atlanta: Georgia Institute of Technology, 2005. [12] 谢明志, 杨永清, 庄重, 等. 结构不确定性对高速铁路矮塔斜拉桥概率地震需求的影响[J]. 铁道科学与工程学报, 2022, 19(6): 1475-1484.XIE Mingzhi, YANG Yongqing, ZHUANG Zhong, et al. Influence of structural uncertainty on probabilistic seismic demand of high-speed railway extradosed cable-stayed bridge[J]. Journal of Railway Science and Engineering, 2022, 19(6): 1475-1484. [13] CORNELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526-533. doi: 10.1061/(ASCE)0733-9445(2002)128:4(526) [14] 郭怿品, 李典庆, 唐小松, 等. 基于Bootstrap方法的堆石坝坝坡稳定可靠度分析[J]. 武汉大学学报(工学版), 2019, 52(2): 106-115.GUO Yipin, LI Dianqing, TANG Xiaosong, et al. Slope stability reliability of rockfill dams based on Bootstrap method[J]. Engineering Journal of Wuhan University, 2019, 52(2): 106-115. [15] LUO Z, ATAMTURKTUR S, JUANG C H. Bootstrapping for characterizing the effect of uncertainty in sample statistics for braced excavations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(1): 13-23. doi: 10.1061/(ASCE)GT.1943-5606.0000734 [16] MENEGOTTO M. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C]//Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads. Lisbon: IABSE, 1973: 15-22. [17] KENT D C, PARK R. Flexural members with confined concrete[J]. Journal of the Structural Division, 1971, 97(7): 1969-1990. doi: 10.1061/JSDEAG.0002957 [18] 招商局重庆交通科研设计院有限公司. 公路桥梁抗震设计规范: JTG/T 2231-01—2020[S]. 北京: 人民交通出版社股份有限公司, 2020. [19] 李辉辉, 李立峰. 考虑变量相关性的桥梁时变地震易损性研究[J]. 振动与冲击, 2019, 38(9): 173-183.LI Huihui, LI Lifeng. Bridge time-varying seismic fragility considering variables' correlation[J]. Journal of Vibration and Shock, 2019, 38(9): 173-183. [20] CHEN Z Q, ZHENG S X, ZHANG J, et al. Seismic reliability analysis of high-pier railway bridges with correlated random parameters via an improved maximum entropy method[J]. Structures, 2021, 33: 4538-4555. doi: 10.1016/j.istruc.2021.07.039 [21] LI H H, LI L F, WU W P, et al. Seismic fragility assessment framework for highway bridges based on an improved uniform design-response surface model methodology[J]. Bulletin of Earthquake Engineering, 2020, 18(5): 2329-2353. doi: 10.1007/s10518-019-00783-1 -
下载:
点击查看大图
计量
- 文章访问数: 54
- HTML全文浏览量: 31
- PDF下载量: 15
- 被引次数: 0