基于数字孪生模型的磁浮平面电机剩磁补偿

徐逢秋; 邱熠; 何加文; 许贤泽

doi:10.3969/j.issn.0258-2724.20240556

基于数字孪生模型的磁浮平面电机剩磁补偿

doi: 10.3969/j.issn.0258-2724.20240556

武汉大学电子信息学院，湖北武汉 430072

基金项目: 国家重点研发计划（2022YFF0605400）；湖北省科技创新人才计划项目（2024DJC046）

详细信息

作者简介:
徐逢秋（1990—），男，副教授，博士，研究方向为磁悬浮系统设计和磁悬浮平面电机运动控制，E-mail：hncxu@whu.edu.cn

通讯作者:
许贤泽（1967—），男，教授，博士，研究方向为精密测量与控制和磁悬浮控制技术，E-mail：xuxianze@whu.edu.cn

中图分类号: TM351
计量
- 文章访问数: 213
- HTML全文浏览量: 84
- PDF下载量: 26
- 被引次数: 0
出版历程
- 收稿日期: 2024-10-30
- 修回日期: 2025-02-28
- 网络出版日期: 2025-05-20
- 刊出日期: 2025-04-03

Remanence Compensation of Maglev Planar Motor Based on Digital Twin Model

Electronic Information School, Wuhan University, Wuhan 430072, China

摘要

摘要:
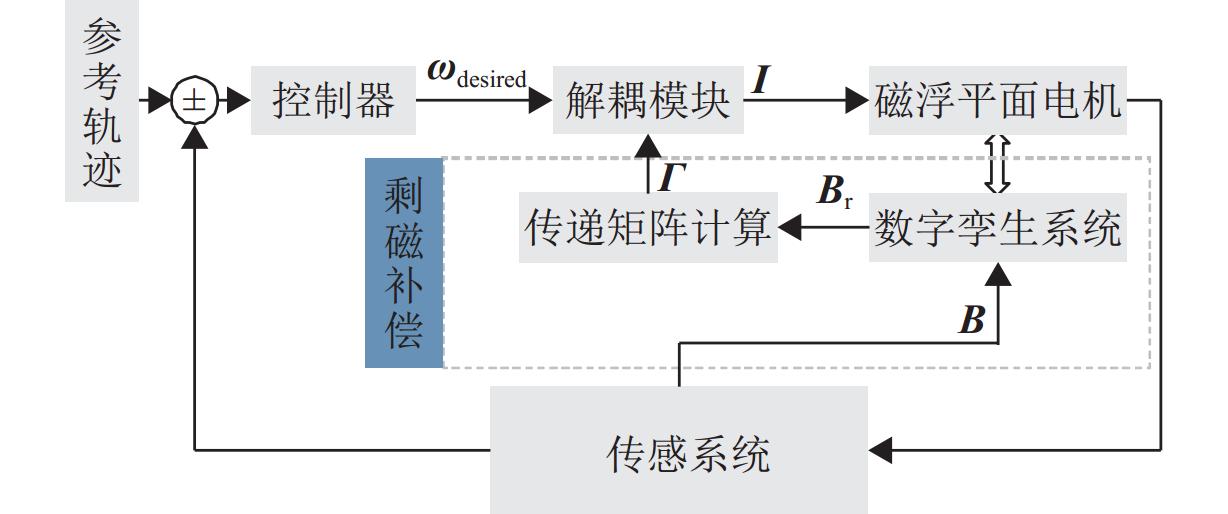
为提升磁浮平面电机发生退磁故障后的控制性能，提出一种针对永磁体阵列的剩磁补偿方法，并通过数字孪生模型对所提方法进行有效性验证. 首先，构建基于数字孪生五维模型的磁浮平面电机数字孪生框架，明确5层架构的组成部分；其次，利用磁荷节点模型探讨动子周围磁场与剩余磁化强度的关系，获得剩磁反演表达式，并在运动解耦过程中引入反演获得的剩磁数据，得出剩磁补偿后的控制电流；最后，利用不同退磁分布的磁浮平面电机孪生体数据，反演得到剩磁数值，通过多组轨迹跟踪仿真实验，对比无退磁、忽视退磁影响、剩磁反演补偿3种情况下的运动模拟. 研究结果表明：与忽视退磁影响相比，采用剩磁反演补偿方法，水平方向上进行斜坡轨迹跟踪的均方根误差减小56.5%，最大误差减小40.9%；平面运动阶跃响应稳定时间减少41.3%，超调量减少15.7%；圆轮廓跟踪时，轮廓误差的均方根减小85.0%，最大误差减小38.9%.
- 磁浮平面电机 /
- 数字孪生 /
- 剩磁补偿 /
- 轨迹跟踪
Abstract:
A remanence compensation method for permanent magnet arrays was proposed to enhance the control performance of maglev planar motors after demagnetization faults, and the effectiveness of the proposed method was verified by a digital twin model. Firstly, a digital twin framework for maglev planar motors based on a five-dimensional digital twin model was constructed, and the components of the five-layer architecture were clarified. Secondly, the relationship between the magnetic field around the mover and the residual magnetization intensity was explored by using a magnetic charge node model to obtain a remanence inversion expression. Then, the inverted remanence data were introduced into the motion decoupling process to derive the control current after remanence compensation. Digital twin data of maglev planar motors with different demagnetization distributions were used to obtain remanence values through inversion. Multiple trajectory tracking simulation experiments were conducted to compare motion simulations under three conditions: no demagnetization, neglecting demagnetization effects, and remanence inversion compensation. The results show that compared with neglecting demagnetization effects, the remanence inversion compensation method reduces the root mean square error of horizontal ramp trajectory tracking by 56.5% and the maximum error by 40.9%. The setting time in planar motion step response is decreased by 41.3%, and the overshoot is reduced by 15.7%. When a circle contour is tracked, the root mean square of contour error is decreased by 85.0%, and the maximum error is reduced by 38.9%.
- maglev planar motor /
- digital twin /
- remanence compensation /
- trajectory tracking

HTML全文

图 1 磁浮平面电机的数字孪生系统框架

Figure 1. Digital twin system framework for maglev planar motor

下载: 全尺寸图片幻灯片

图 2 磁浮平面电机数字孪生体

Figure 2. Digital twin of maglev planar motor

下载: 全尺寸图片幻灯片

图 3 磁浮平面电机结构及磁荷节点分布

Figure 3. Structure of maglev planar motor and distribution of magnetic charge nodes

下载: 全尺寸图片幻灯片

图 4 剩磁补偿控制流程

Figure 4. Remanence compensation control process

下载: 全尺寸图片幻灯片

图 5 磁场测量传感系统

Figure 5. Magnetic field measurement sensor system

下载: 全尺寸图片幻灯片

图 6 磁浮平面电机退磁率分布

Figure 6. Demagnetization rate distribution of maglev planar motor

下载: 全尺寸图片幻灯片

图 7 剩磁反演结果

Figure 7. Results of remanence inversion

下载: 全尺寸图片幻灯片

图 8 气隙磁场对比

Figure 8. Air gap magnetic field comparison

下载: 全尺寸图片幻灯片

图 9 斜坡轨迹跟踪实验结果

Figure 9. Experimental results for ramp trajectory tracking

下载: 全尺寸图片幻灯片

图 10 阶跃响应实验结果

Figure 10. Experimental results for step response

下载: 全尺寸图片幻灯片

图 11 圆轮廓的跟踪误差

Figure 11. Tracking errors of circular contour

下载: 全尺寸图片幻灯片

图 12 圆轮廓跟踪

Figure 12. Circular contour tracking

下载: 全尺寸图片幻灯片

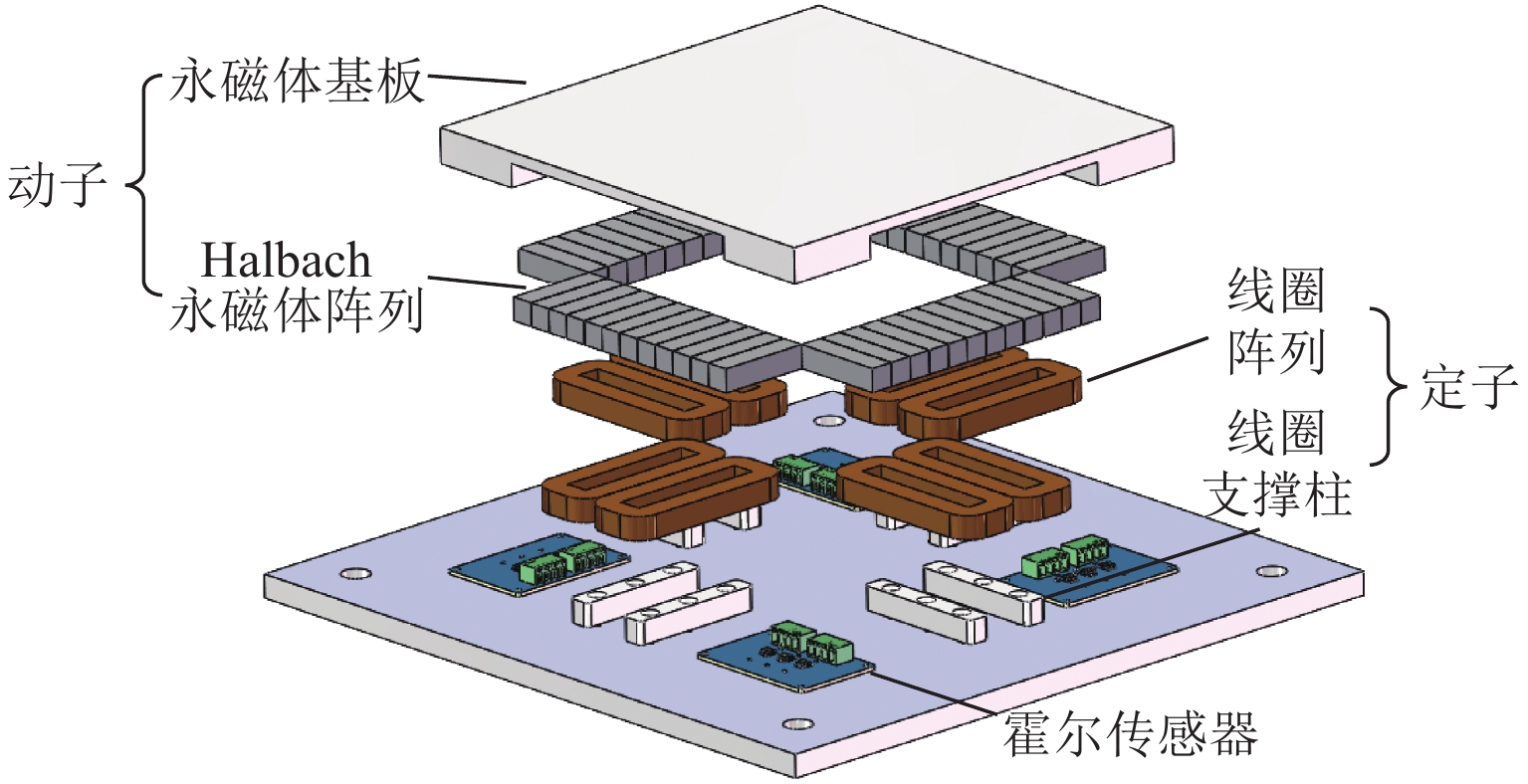
表 1 磁浮平面电机结构参数

Table 1. Structural parameters of maglev planar motor

参数	数值
L_m/mm W_m/mm H_m/mm	40 10 10
动子质量/kg	2.37
L_c/mm W_c/mm H_c/mm R_c/mm	60 10 10 10
线圈匝数/匝	300
I_x/（×10⁻³ kg•m²） I_y/（×10⁻³ kg•m²） I_z/（×10⁻³ kg•m²）	9.38 9.38 18.70

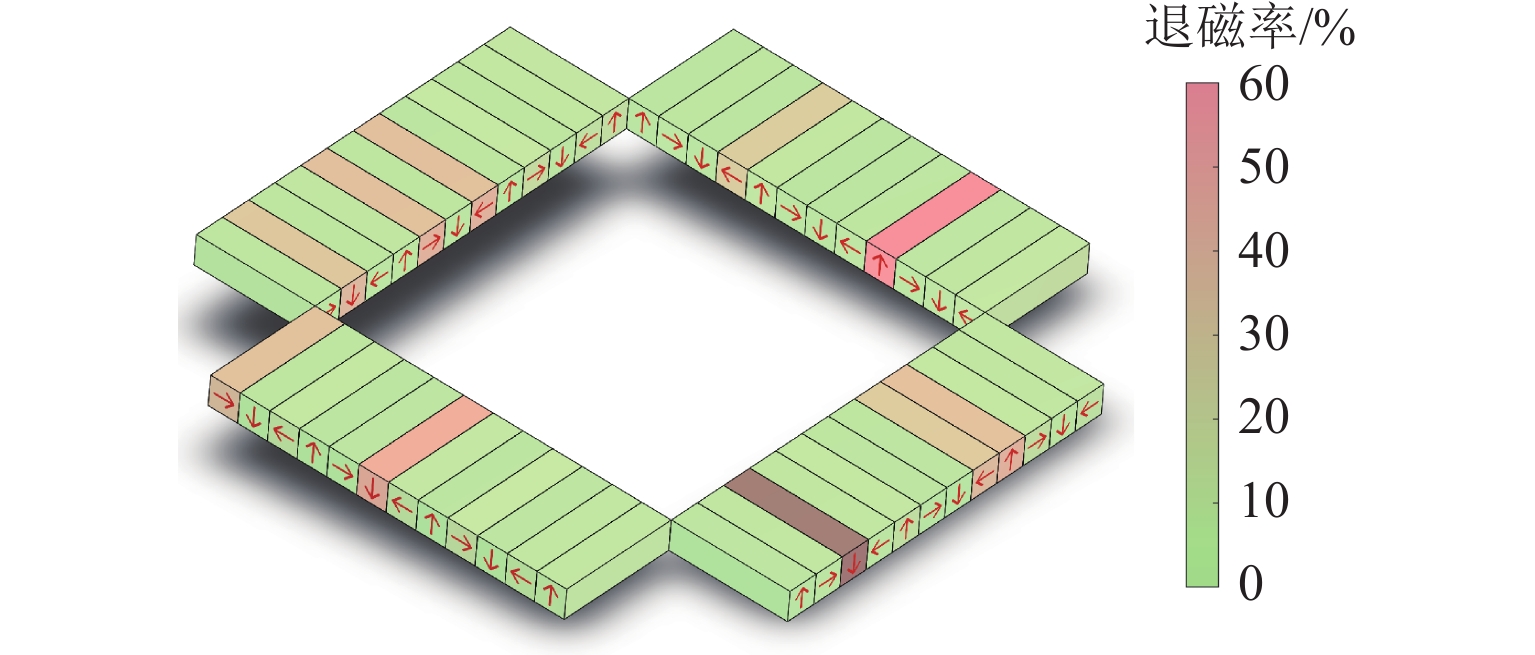
下载: 导出CSV

表 2 永磁体退磁率分布

Table 2. Demagnetization rate distribution of permanent magnets

阵列	基本无退磁	轻度退磁	重度退磁
阵列 1	2,3,4,5,7,8,9,10,11,12	1	6
阵列 2	1,2,4,5,6,7,10,11,12	3,8,9
阵列 3	1,2,3,5,6,7,8,10,11,12	9	4
阵列 4	1,2,3,4,5,7,9,10,12	6,8,11

下载: 导出CSV

表 3 剩磁反演误差分析

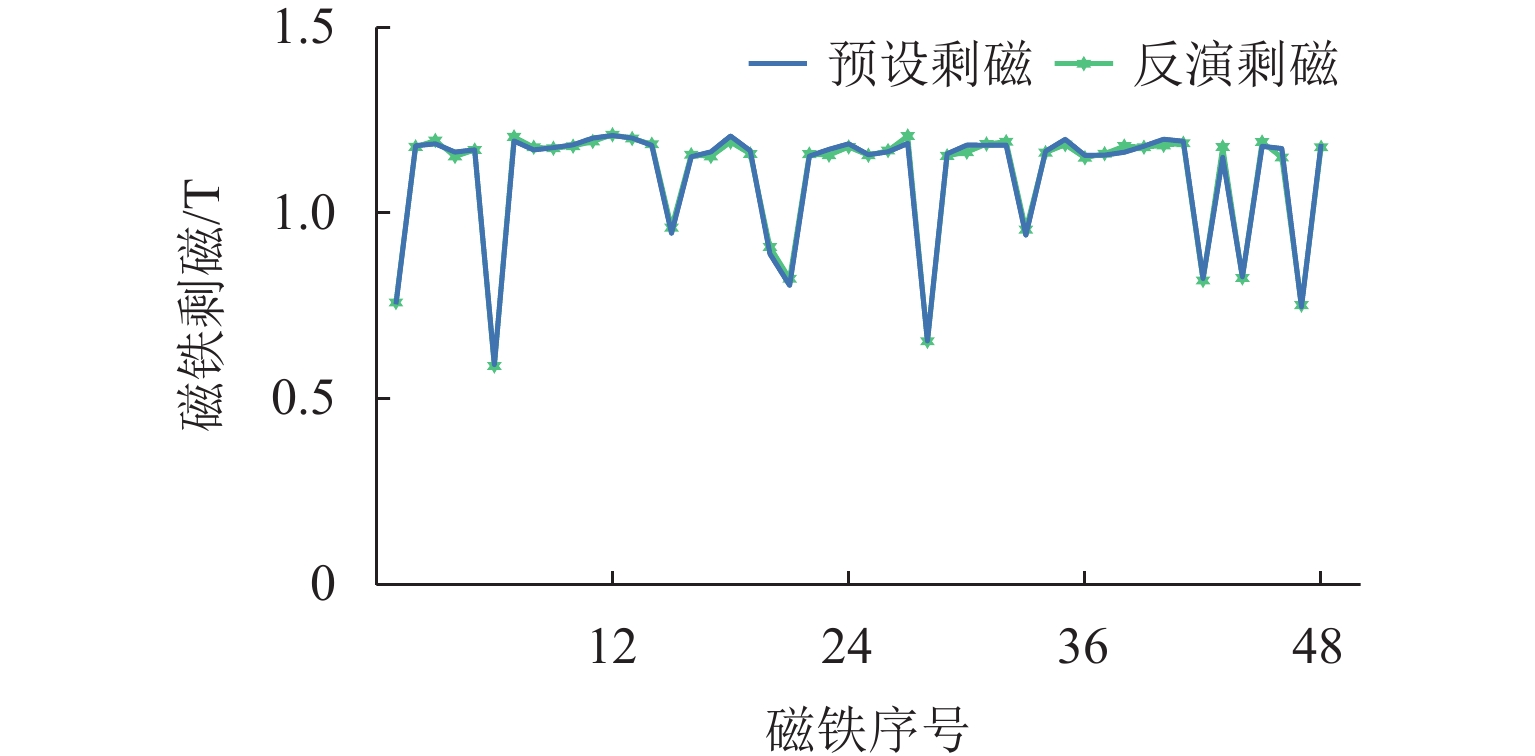
Table 3. Error analysis of remanence inversion

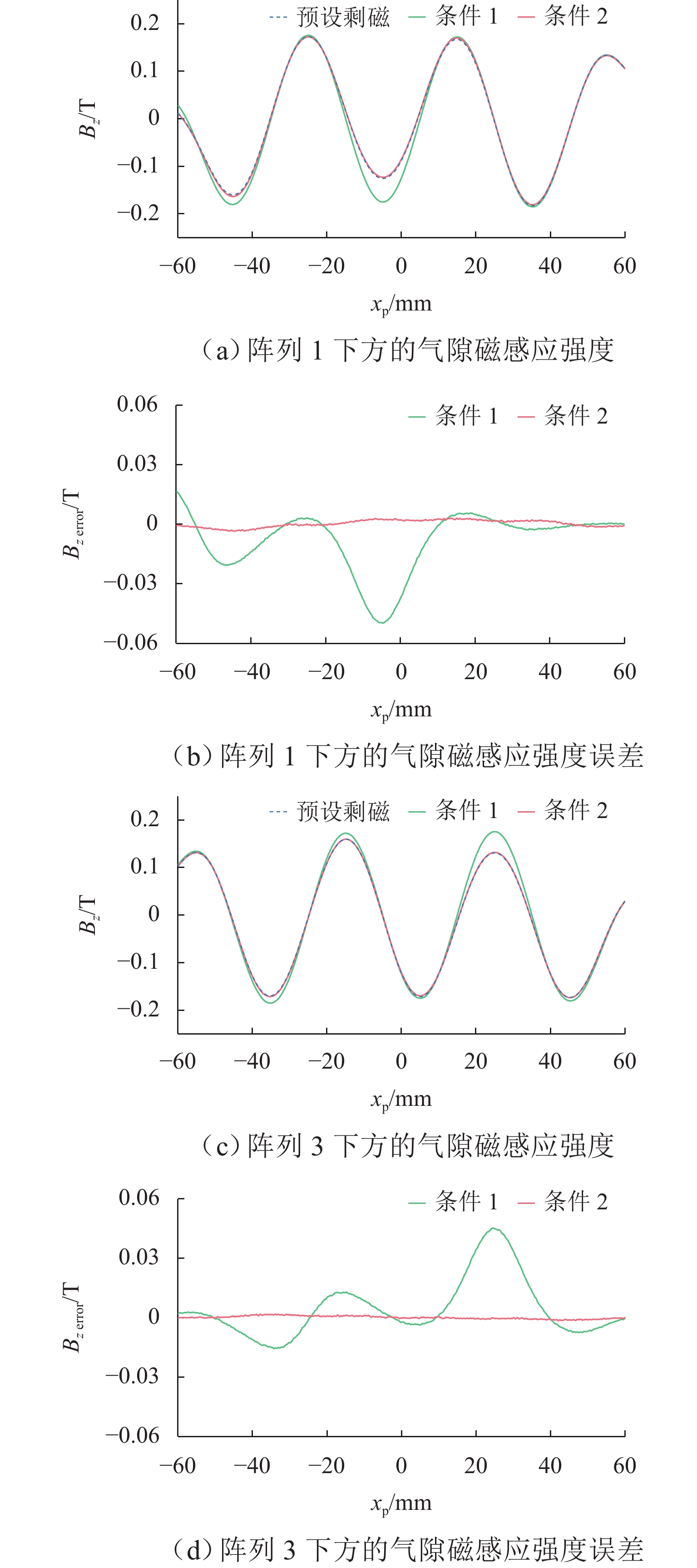
参数	e_rms,B/T	e_map/%	R²
取值	0.011	0.67738	0.99549

下载: 导出CSV

表 4 气隙磁感应强度误差分析

Table 4. Error analysis of air gap magnetic flux density

阵列位置	条件	e_rms,B/T	e_map/%
阵列 1	条件 1	0.016939	45.1079
阵列 1	条件 2	0.001293	3.6183
阵列 3	条件 1	0.015386	28.4291
阵列 3	条件 2	0.001790	3.9413

下载: 导出CSV

表 5 斜坡轨迹跟踪控制性能

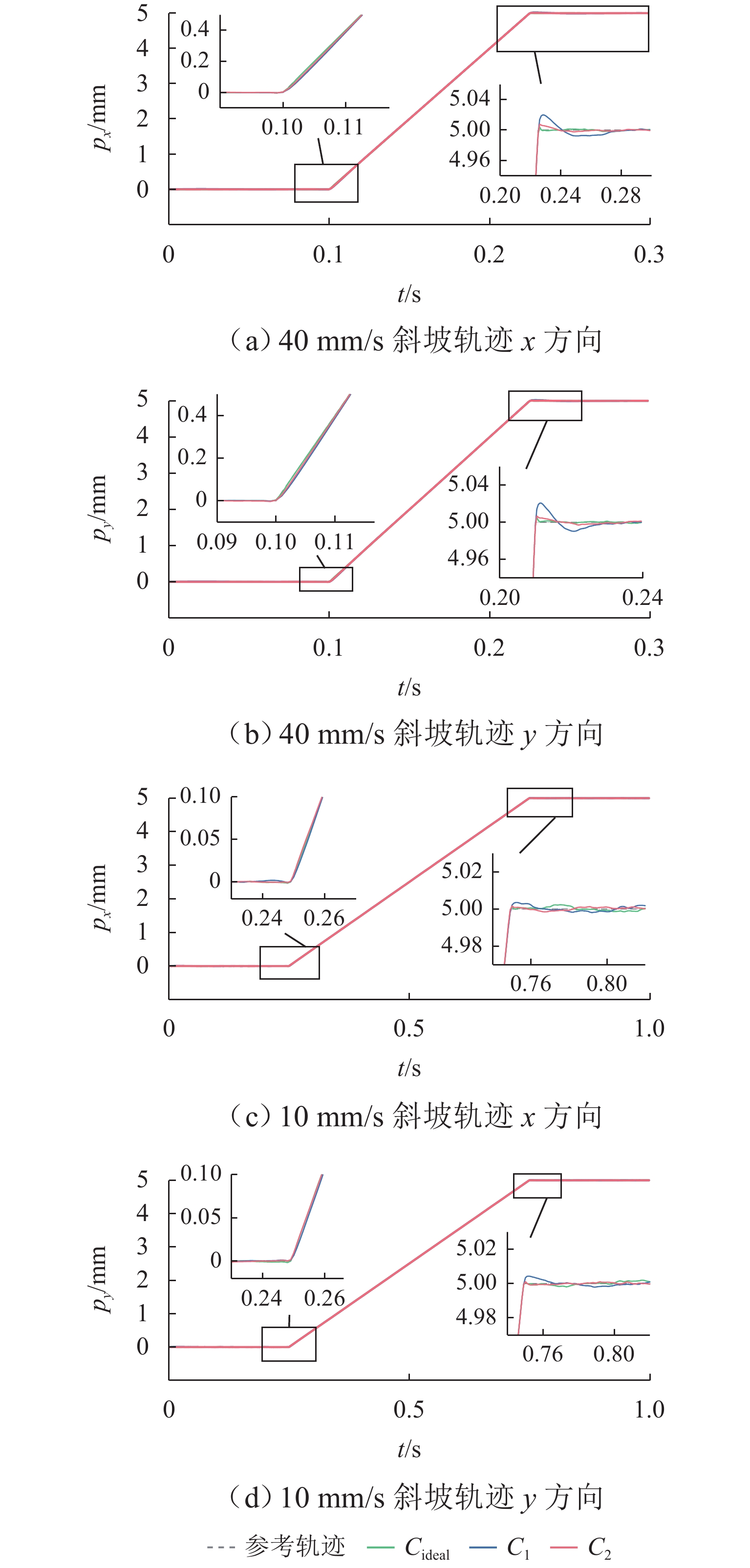
Table 5. Control performance for ramp trajectory tracking mm

速度/（mm·s⁻¹）	情况	x 方向		y 方向
速度/（mm·s⁻¹）	情况	e_rms	e_max	e_rms	e_max
40	C_ideal	0.00099	0.00527	0.00074	0.00224
	C₁	0.00586	0.02266	0.00171	0.00699
	C₂	0.00265	0.01344	0.00079	0.00236
10	C_ideal	0.00089	0.00551	0.00070	0.00221
	C₁	0.00616	0.02436	0.00160	0.00702
	C₂	0.00268	0.01440	0.00091	0.00223

下载: 导出CSV

表 6 阶跃响应性能指标

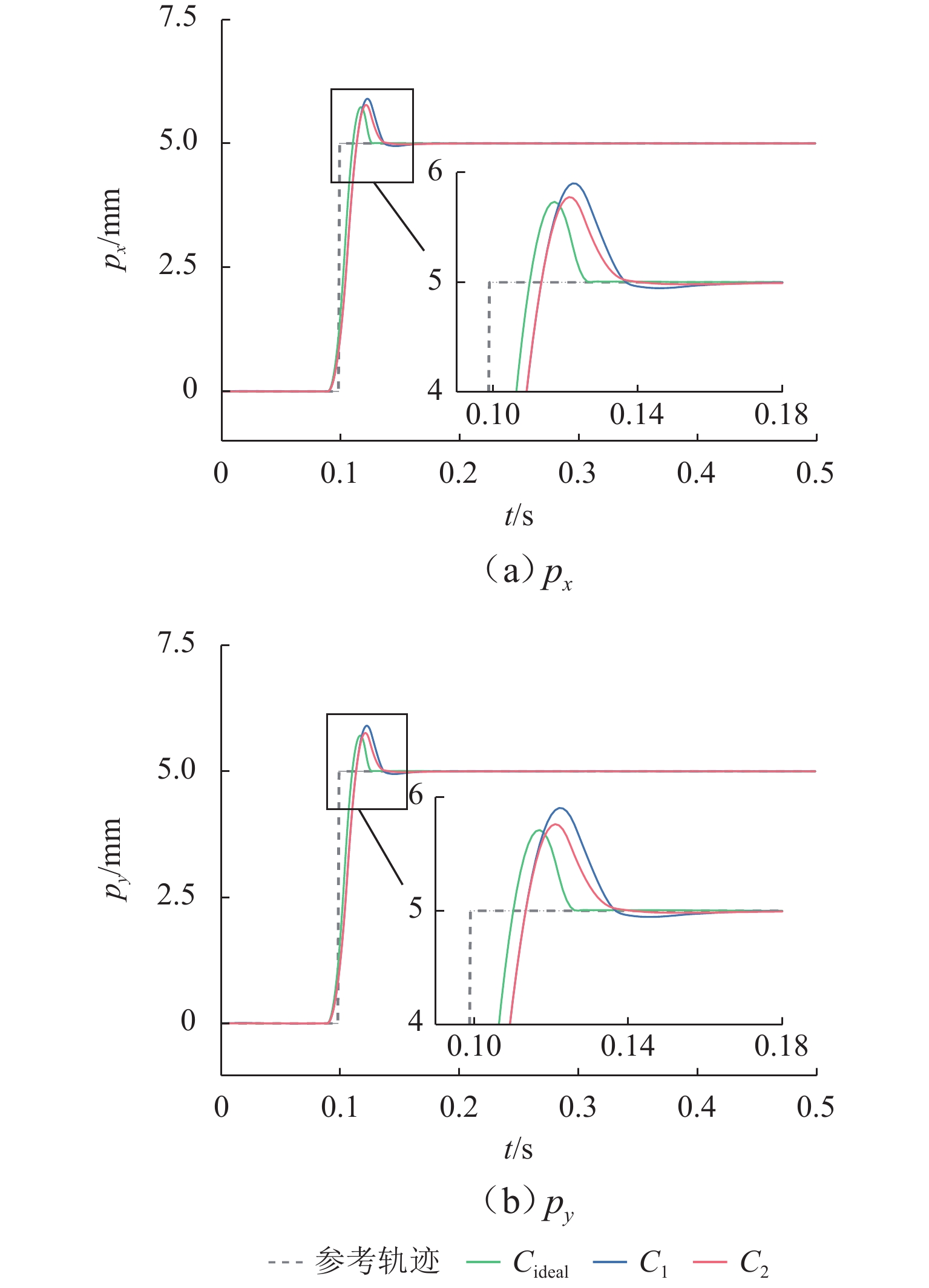
Table 6. Performance metrics for step response

情况	方向	响应时间/ms	超调量/mm
C_ideal	x	24	0.7327
C_ideal	y	27	0.7077
C₁	x	63	0.9007
C₁	y	63	0.9034
C₂	x	37	0.7758
C₂	y	39	0.7616

下载: 导出CSV

表 7 圆轮廓跟踪性能

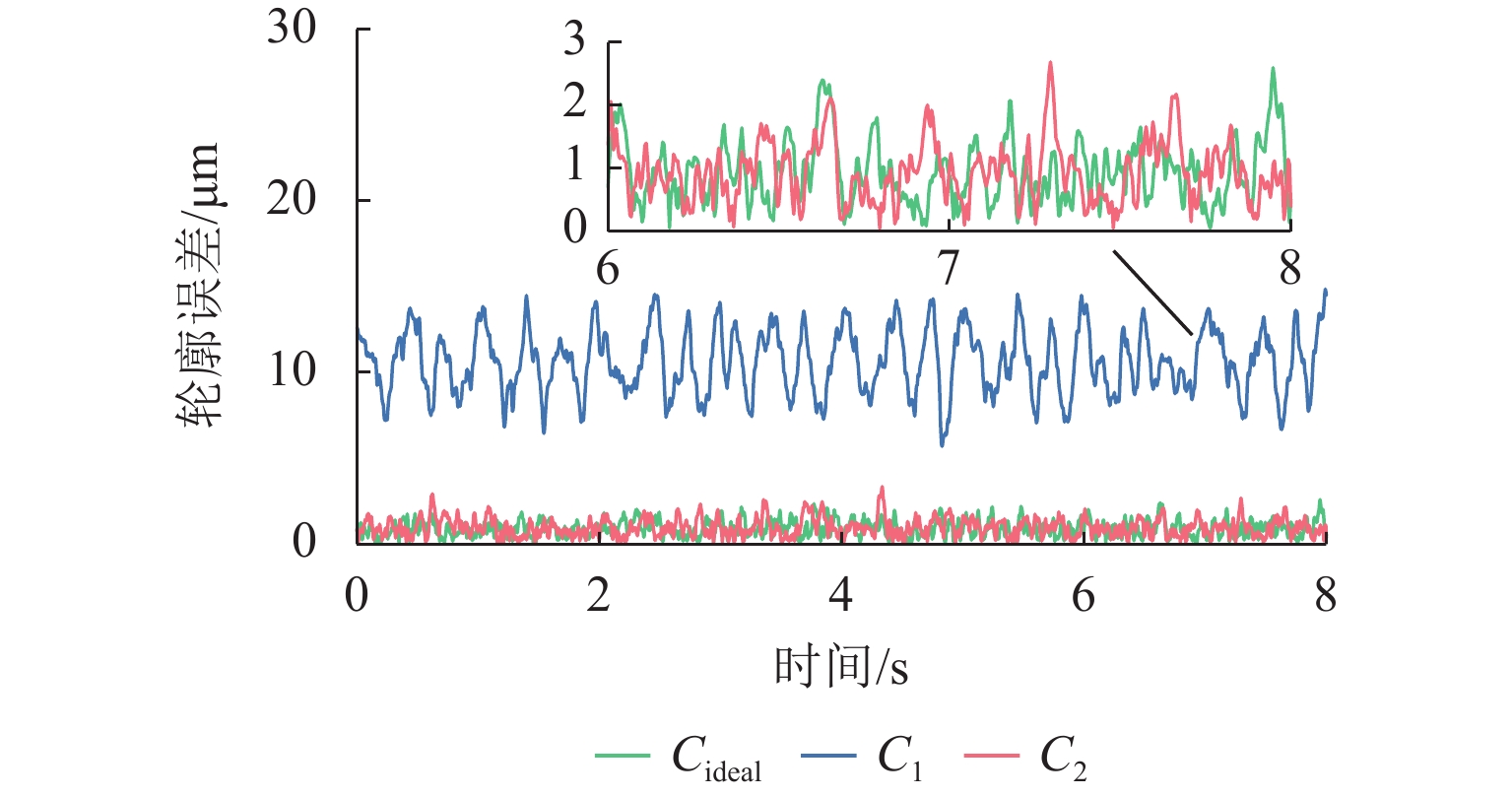
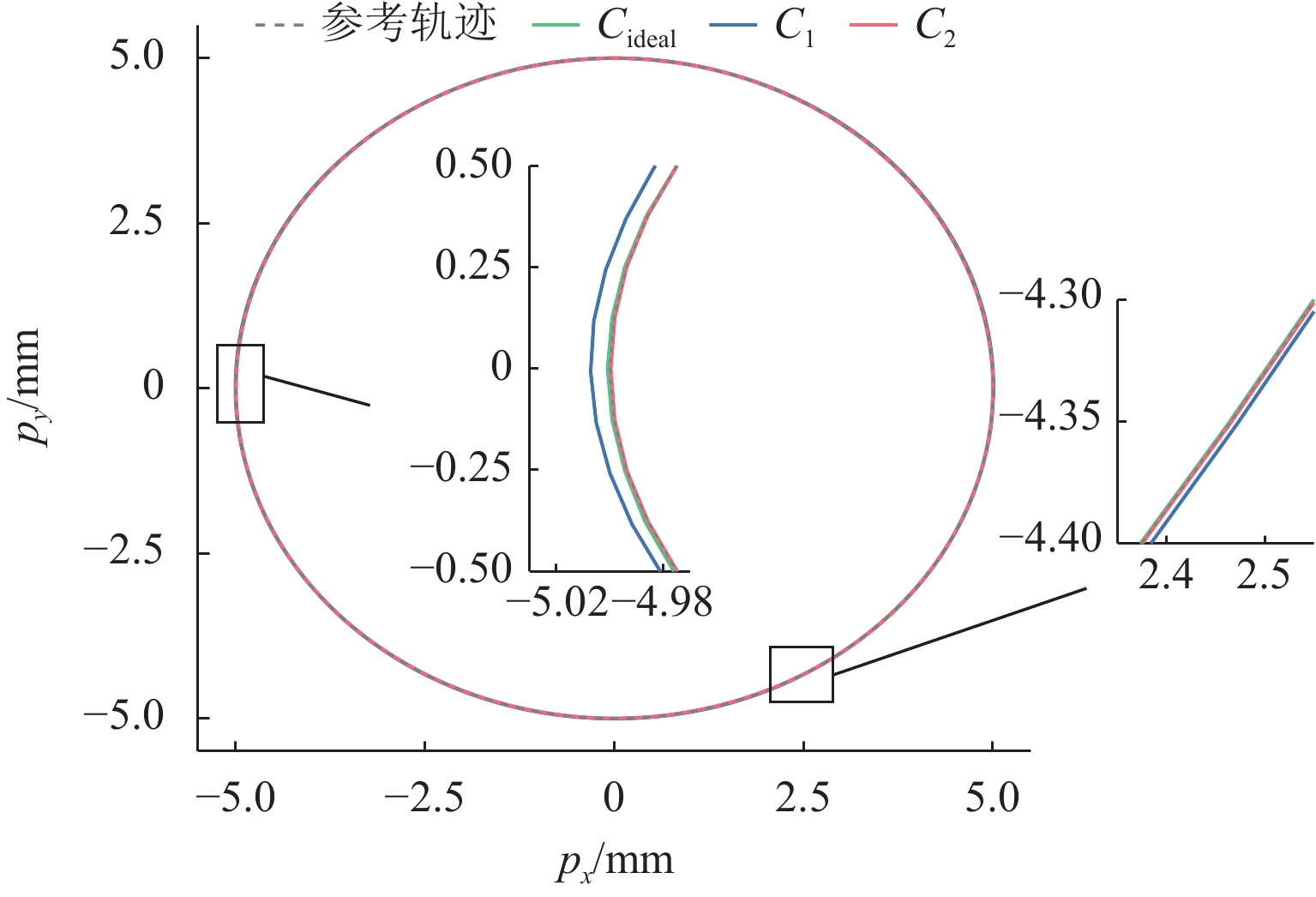
Table 7. Performance of circular contour tracking

性能指标	ε_rms/mm	ε_max/mm
C_ideal	0.0015	0.0156
C₁	0.0113	0.0275
C₂	0.0017	0.0168

下载: 导出CSV

参考文献(25)

[1]	郭东明. 高性能制造[J]. 机械工程学报,2022,58(21): 225-242. doi: 10.3901/JME.2022.21.225 GUO Dongming. High performance manufacturing[J]. Journal of Mechanical Engineering, 2022, 58(21): 225-242. doi: 10.3901/JME.2022.21.225
[2]	ZHOU L, WU J J. Magnetic levitation technology for precision motion systems: a review and future perspectives[J]. International Journal of Automation Technology, 2022, 16(4): 386-402. doi: 10.20965/ijat.2022.p0386
[3]	FU H, HU C X, YU D D, et al. Cascaded iterative learning motion control of precision maglev planar motor with experimental investigation[J]. ISA Transactions, 2023, 139: 463-474. doi: 10.1016/j.isatra.2023.03.031
[4]	FAIZ J, NEJADI-KOTI H. Demagnetization fault indexes in permanent magnet synchronous motors: an overview[J]. IEEE Transactions on Magnetics, 2016, 52(4): 1-11.
[5]	NAIR S S, PATEL V I, WANG J B. Post-demagnetization performance assessment for interior permanent magnet AC machines[J]. IEEE Transactions on Magnetics, 2016, 52(4): 1-10.
[6]	WOO D K, JEONG B H. Irreversible demagnetization of permanent magnet in a surface-mounted permanent magnet motor with overhang structure[J]. IEEE Transactions on Magnetics, 2016, 52(4): 1-6.
[7]	JANSEN J W, VAN LIEROP C M M, LOMONOVA E A, et al. Modeling of magnetically levitated planar actuators with moving magnets[J]. IEEE Transactions on Magnetics, 2007, 43(1): 15-25.
[8]	HUANG S D, LIN Z X, CAO G Z, et al. Nonlinear dynamic model-based position control parameter optimization method of planar switched reluctance motors[J]. Mathematics, 2023, 11(19): 4067.1-4067.19.
[9]	周扬,周瑾,王艺宇,等. 考虑界面接触的磁悬浮轴承-转子系统建模及鲁棒控制[J]. 西南交通大学学报,2024,59(4): 755-765. ZHOU Yang, ZHOU Jin, WANG Yiyu, et al. Modeling and robust control of magnetic bearing-rotor system considering interface contact[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 755-765.
[10]	HUANG S D, XU Z H, CAO G Z, et al. Nonlinear-disturbance-observer-based predictive control for trajectory tracking of planar motors[J]. IET Electric Power Applications, 2024, 18(4): 389-399. doi: 10.1049/elp2.12398
[11]	PARK Y, FERNANDEZ D, LEE S B, et al. Online detection of rotor eccentricity and demagnetization faults in PMSMs based on Hall-effect field sensor measurements[J]. IEEE Transactions on Industry Applications, 2019, 55(3): 2499-2509.
[12]	BRAUN J, DOPPELBAUER M, BRAUN J, et al. Calculation of the demagnetization for permanent magnet synchronous machines[C]//2016 XXII International Conference on Electrical Machines (ICEM). Lausanne: ACM, 2016: 173-179.
[13]	HUANG L, ZHOU F L, WANG W, et al. Digital twin method and application practice of spacecraft system driven by mechanism data[J]. Digital Twin, 2024, 4: 1-16. doi: 10.12688/digitaltwin.17918.1
[14]	丁国富,何旭,张海柱,等. 数字孪生在高速列车生命周期中的应用与挑战[J]. 西南交通大学学报,2023,58(1): 58-73. doi: 10.3969/j.issn.0258-2724.20210573 DING Guofu, HE Xu, ZHANG Haizhu, et al. Application and challenges of digital twin in life cycle of high-speed trains[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 58-73. doi: 10.3969/j.issn.0258-2724.20210573
[15]	TUEGEL E J, INGRAFFEA A R, EASON T G, et al. Reengineering aircraft structural life prediction using a digital twin[J]. International Journal of Aerospace Engineering, 2011, 2011: 154798.1-154798.14.
[16]	陶飞,程颖,程江峰,等. 数字孪生车间信息物理融合理论与技术[J]. 计算机集成制造系统,2017,23(8): 1603-1611. TAO Fei, CHENG Ying, CHENG Jiangfeng, et al. Theories and technologies for cyber-physical fusion in digital twin shop-floor[J]. Computer Integrated Manufacturing Systems, 2017, 23(8): 1603-1611.
[17]	KOHTZ S, ZHAO J H, RENTERIA A, et al. Optimal sensor placement for permanent magnet synchronous motor condition monitoring using a digital twin-assisted fault diagnosis approach[J]. Reliability Engineering & System Safety, 2024, 242: 109714.1-109714.12.
[18]	陶飞,刘蔚然,刘检华,等. 数字孪生及其应用探索[J]. 计算机集成制造系统,2018,24(1): 1-18. TAO Fei, LIU Weiran, LIU Jianhua, et al. Digital twin and its potential application exploration[J]. Computer Integrated Manufacturing Systems, 2018, 24(1): 1-18.
[19]	BANCEL F. Magnetic nodes[J]. Journal of Physics D: Applied Physics, 1999, 32(17): 2155-2161. doi: 10.1088/0022-3727/32/17/304
[20]	MAHMOUDITABAR F, VAHEDI A, MARIGNETTI F. The demagnetization phenomenon in PM machines: principles, modeling, and design considerations[J]. IEEE Access, 2023, 11: 47750-47773. doi: 10.1109/ACCESS.2023.3274701
[21]	LI W L, ZHANG M W, ZHAO X, et al. Effect of demagnetization fault on electromagnetic field and related parameters in permanent magnet wind generator[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS). Harbin: ACM, 2019: 1-7.
[22]	CHOI G, JAHNS T M. Investigation of key factors influencing the response of permanent magnet synchronous machines to three-phase symmetrical short-circuit faults[J]. IEEE Transactions on Energy Conversion, 2019, 31(4): 1488-1497.
[23]	ZHAN H L, WU L J, LYU Z K, et al. Uneven demagnetization fault diagnosis in dual three-phase permanent magnet machines based on electrical signal difference[J]. IEEE Transactions on Transportation Electrification, 2023, 9(2): 3026-3039.
[24]	XU F Q, PENG R T, ZHENG T, et al. Development and validation of numerical magnetic force and torque model for magnetically levitated actuator[J]. IEEE Transactions on Magnetics, 2022, 55(1): 1-9.
[25]	XU F Q, SHI Y, ZHANG K Y, et al. Real-time application of robust offset-free MPC in maglev planar machine[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 6121-6130.